Engineering Applications with Stress-Strength for a New Flexible Extension of Inverse Lomax Model: Bayesian and Non-Bayesian Inference
Abstract
1. Introduction
- To produce several forms for the HF and PDF.
- To improve the ILo distribution’s flexibility for modeling various data.
- To enhance the adaptability of the standard ILo distribution’s mean, variance, skewness, and kurtosis properties.
- To estimate the TTLILo distribution parameters using Bayesian and non-Bayesian approaches.
- To construct the ACIs (approximate confidence intervals), Bayesian credible intervals, and BCIs (bootstrap confidence intervals).
- To take the the data analysis of jute fiber-breaking strengths at two different gauge lengths and investigate for SS application purposes and compare to some other models.
- To model skewed data, which are difficult to examine with other traditional models.
- To demonstrate with two engineering datasets that the TTLILo distribution gives a better fit than some other models.
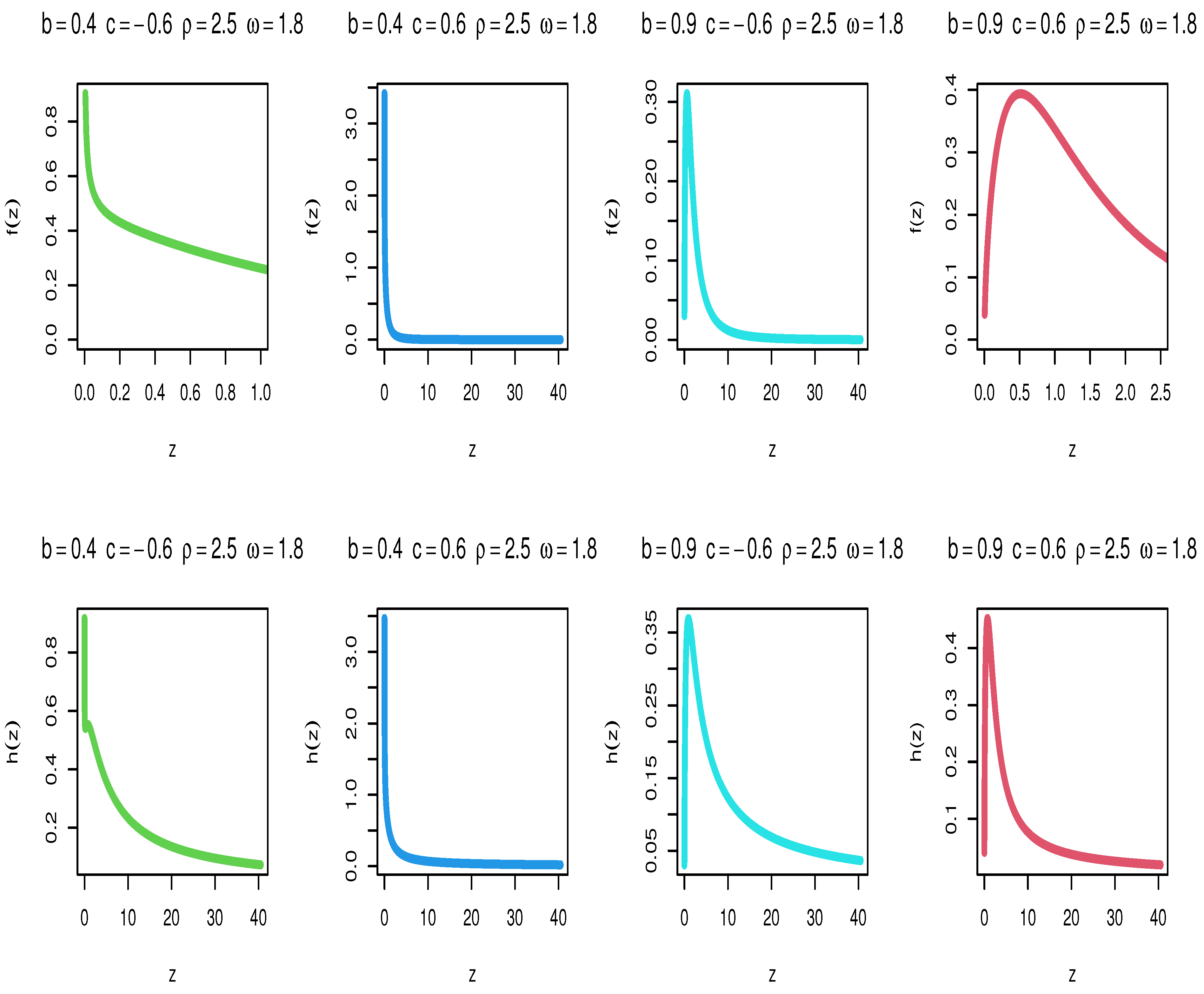
2. The Construction of the TTLILo Distribution
2.1. Usefuel Expansions of the TTLILo Model
2.2. Quantile Function
3. Structural Properties
3.1. Stochastic Ordering
3.2. Moments and Incomplete Moments
3.3. Variability Measures
- The values of and when are greater than the values of and at . Then, it can be concluded that the values of decrease as the value of increases, whereas the values increase, for all the values of the selected parameters.
- At the measure’s value is lower than the values for the other two measures, which indicate more information.
- For the same set of parameters, all the measures have values that are lower for the positive transmuted parameter values than for the negative transmuted parameter values. For example, the results of (1.5, −0.5, 1.5, 0.5) and (1.5, 0.5, 1.5, 0.5).
- There is less uncertainty in all the measure values in accordance with their smaller values, as the value of b increases with the same values of the other parameters. For example, see the results of (1.5, −0.5, 1.5, 0.5) and (2.5, −0.5, 1.5, 0.5).
- All the uncertainty measures decrease as the value of increases with the same values of the other parameters, suggesting less uncertainty. For example, see the results of (1.5, −0.5, 1.5, 0.5) and (1.5, −0.5, 3, 0.5).
4. Characterizations
5. Bayesian and Non-Bayesian Inference
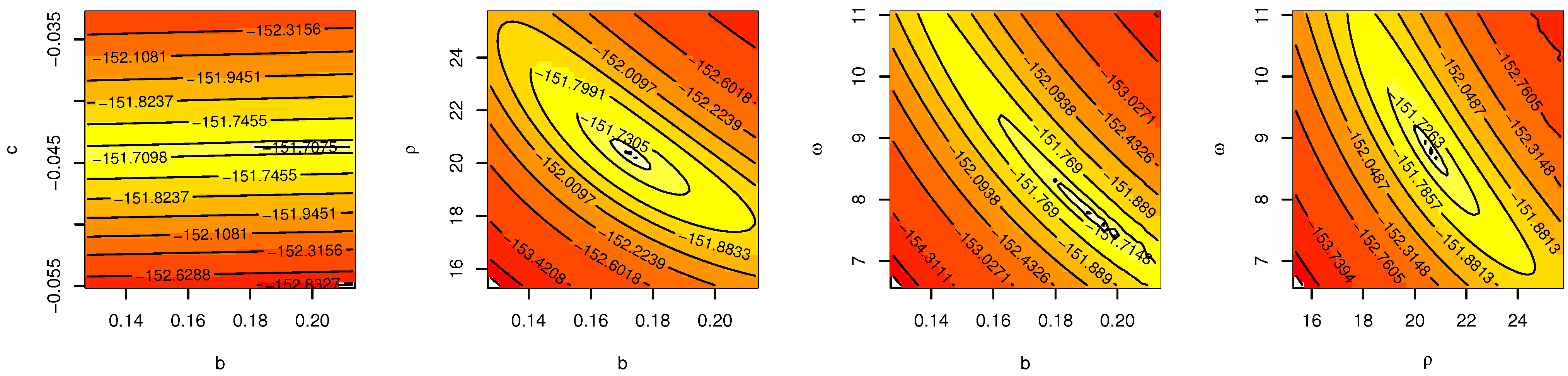
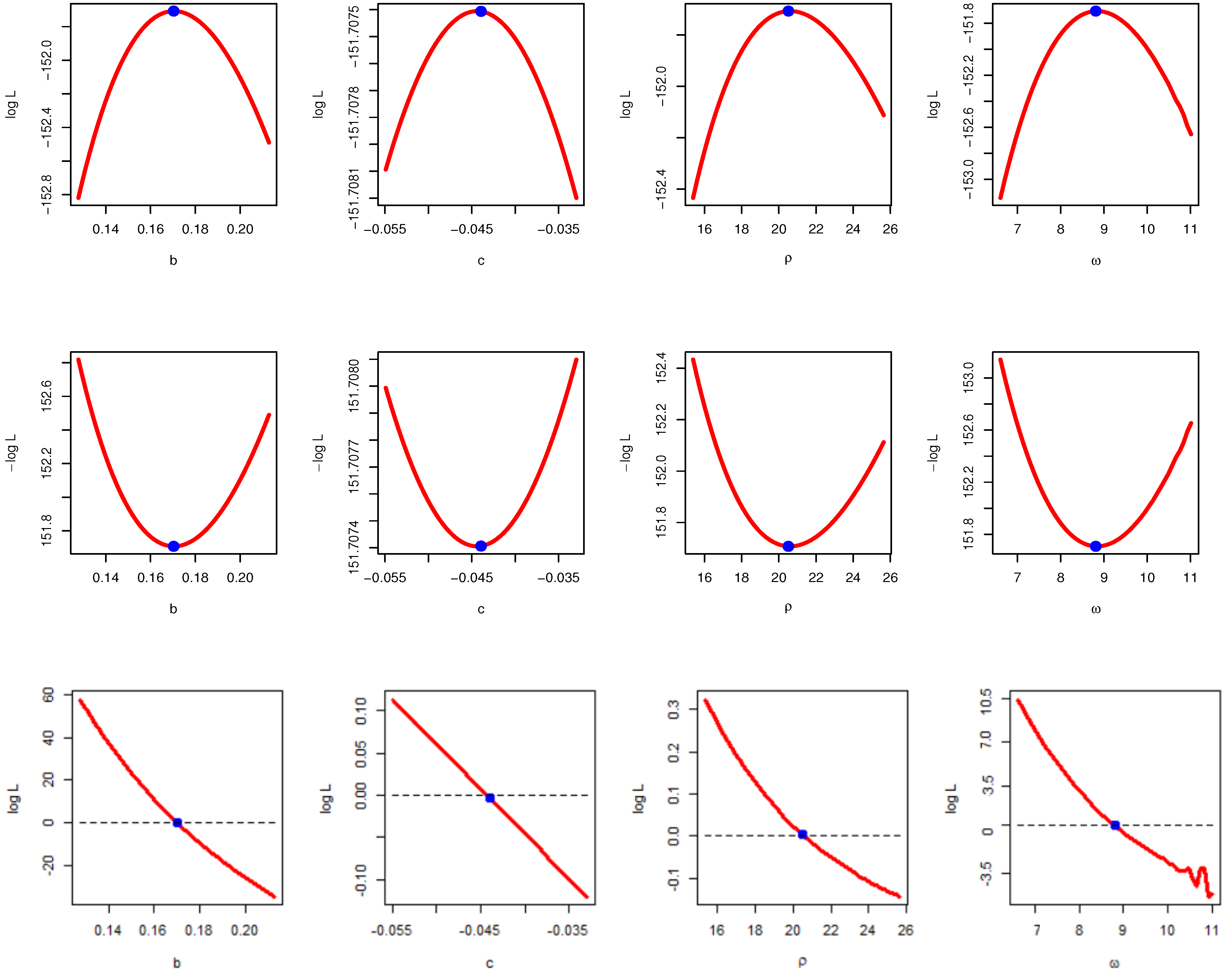
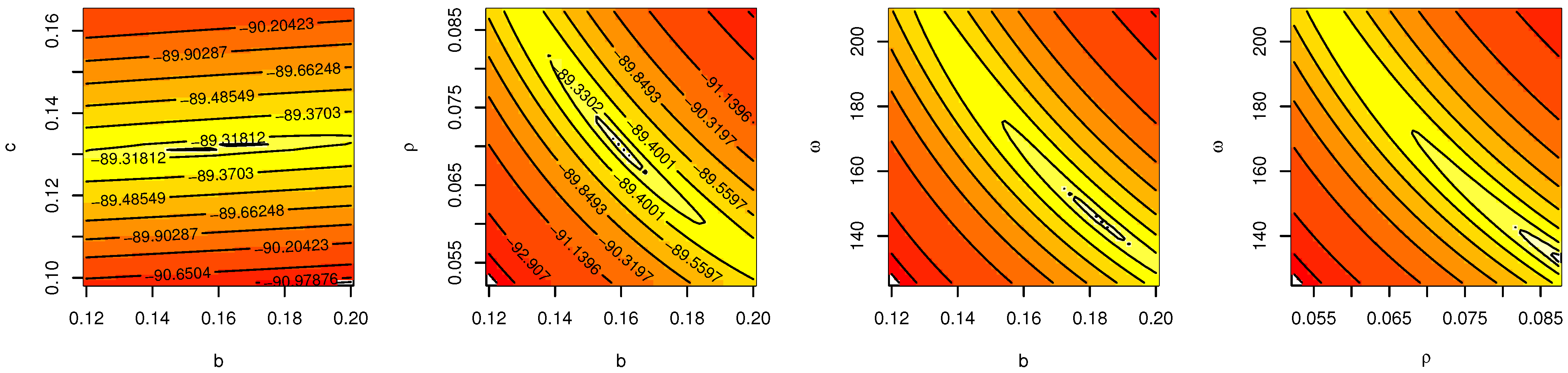
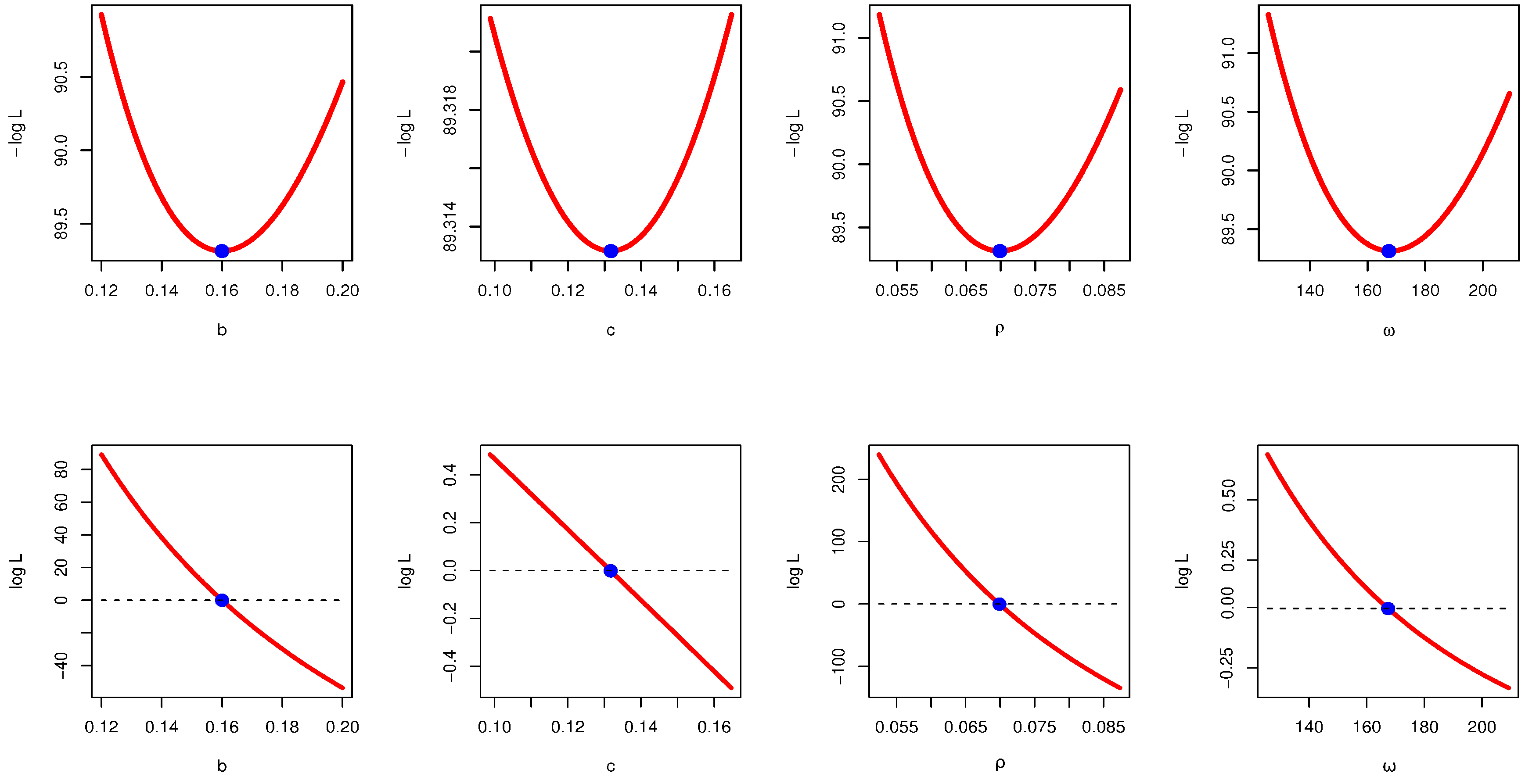
5.1. Maximum Likelihood Estimator
5.2. Bayesian Estimator
5.3. Bootstrap Confidence Intervals
- i.
- Algorithm Percentile BCIsFor the PBCIs (percentile BCIs) approach, the following steps were executed:
- 1.
- Compute the estimators of for the TTILo distribution.
- 2.
- Generate a bootstrap sample using b, c, , and to obtain the bootstrap estimate of b say , c say , say , and say using the bootstrap sample.
- 3.
- Repeat step 2 N times to obtain , , , and .
- 4.
- Arrange , , , and in ascending order as , , , and .
- 5.
- Set a two-sided PBCI for the unknown parameters b, c, and by , , , and .
- ii.
- Algorithm Bootstrap-t CIsFor the BTCIs (bootstrap-t CIs) approach, we follow the outlined steps below:
- 1.
- Follow the same steps as (1–2) in the previous algorithm.
- 2.
- Compute the t-statistic of as where j = 1, 2, 3, 4, and is the asymptotic variance of and it can be obtained using the Fisher information matrix.
- 3.
- Repeat steps 2–3 B times and obtain .
- 4.
- Arrange in ascending order as .
- 5.
- A two-sided BTCI for the unknown parameters b, c, , and is given by
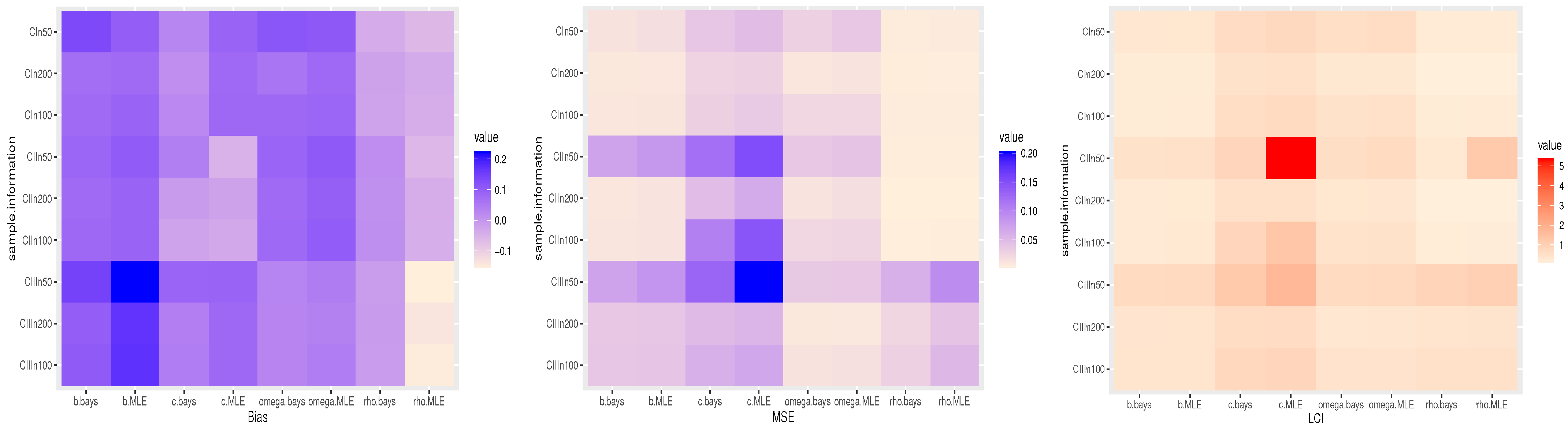
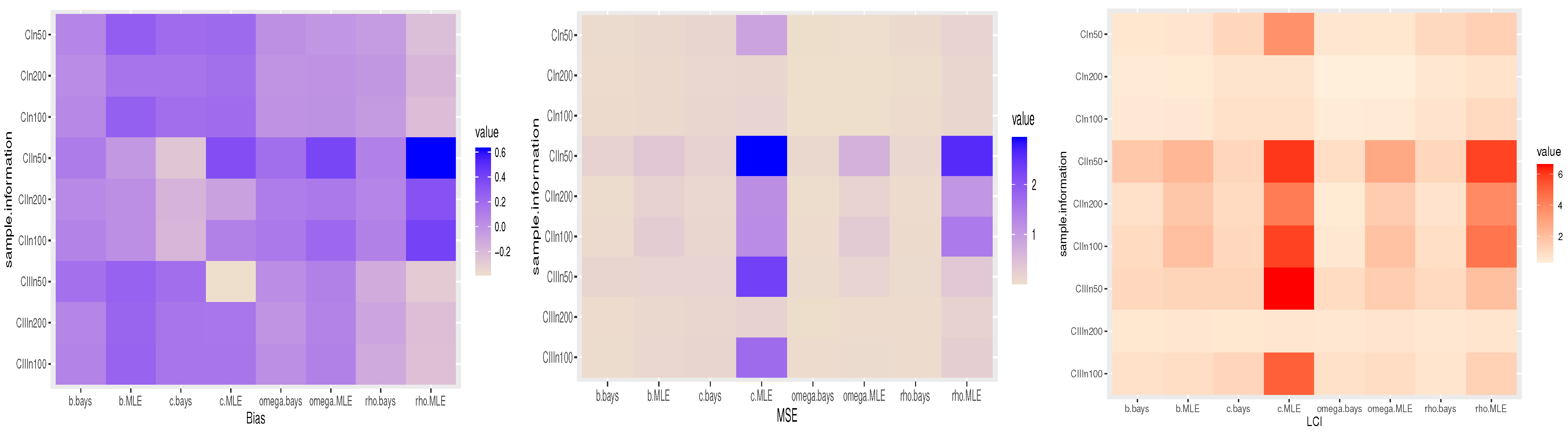
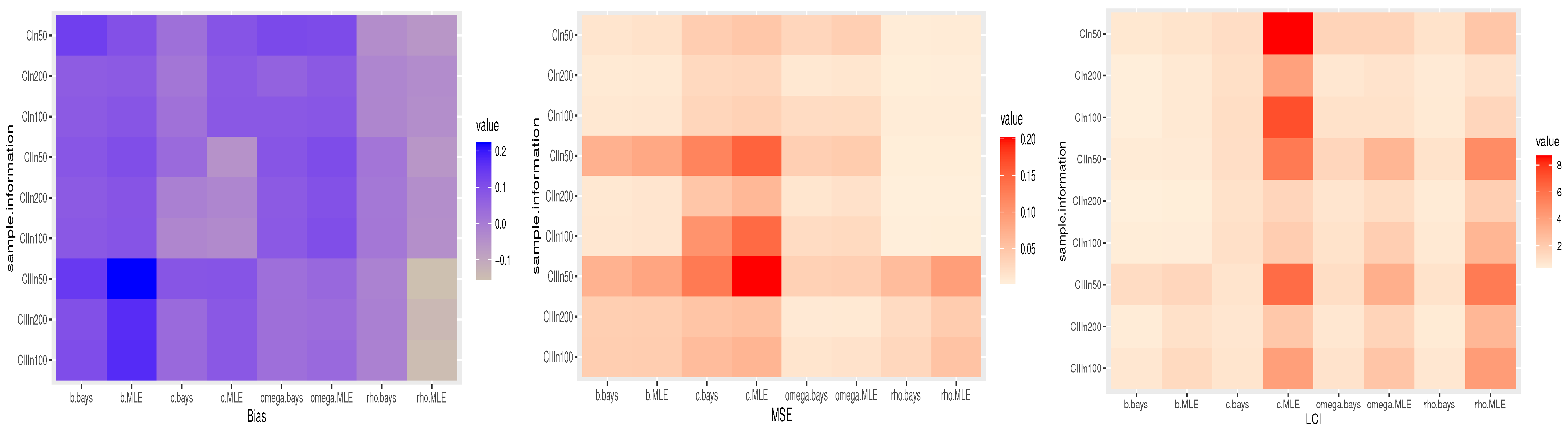
6. Simulation Study
- The suggested point or interval estimates for , and have demonstrated strong performance across the provided parameter sets.
- As the value of n grows, all the recommended estimates perform effectively, thus confirming the consistency property of the obtained estimates.
- The Bayes estimating approach performs better than the maximum likelihood method.
- The Bayes estimation approach is the most effective for the TTLILo distribution.
- The BCIs have the shortest CIs.
- The CCIs are better than ACIs in terms of their shortest length.
- In roughly most scenarios, the CP of the CI estimates increases as the sample sizes rise.
- The CP of the estimates at a negative true value of c has larger values compared to the corresponding at a positive true value.
- For all choices of n, the CP is quite near the desired level of significance.
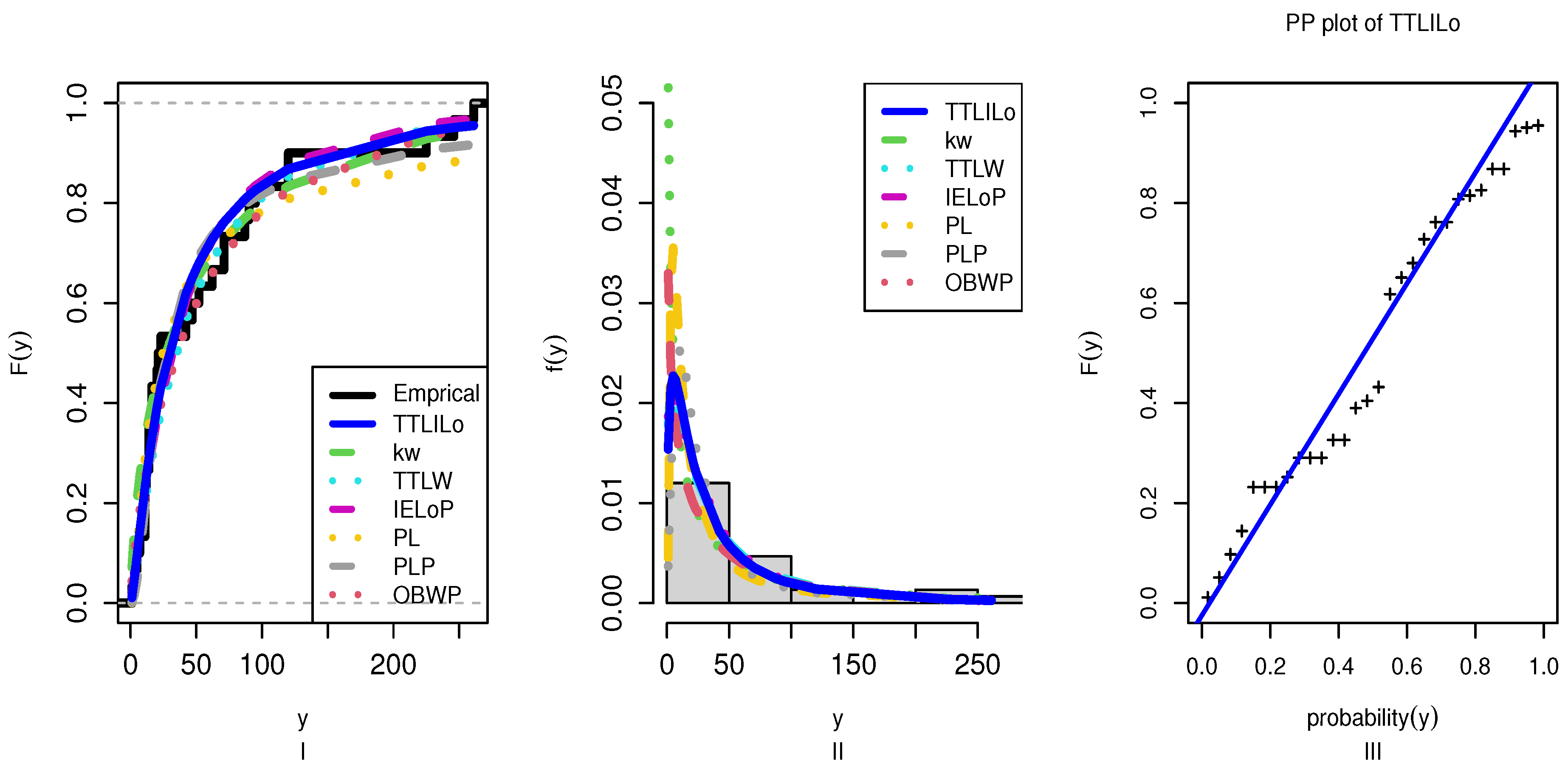
7. Real Data Analysis
8. Stress-Strength Application
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Acronyms
| AD | Anderson–Darling | MLEs | Maximum likelihood estimates |
| BIC | Bayesian IC | Probability density function | |
| PBCIs | Percentile BCIs | SS | Stress-strength |
| LPB | Length of percentile bootstrap | TTL-G | Transmuted Topp–Leone generated |
| LPB.Bayes | Length of percentile bootstrap for BE | TTLILo | Transmuted Topp–Leone inverse Lomax |
| CVM | Cramér–von Mises | SE | Squared error |
| KS | Kolmogorov–Smirnov | MCMC | Markov Chain Monte Carlo |
| LRO | Likelihood ratio ordering | ACIs | Approximate confidence intervals |
| LPB.MLE | Length of percentile bootstrap for MLE | LACI | Length of ACI |
| SO | Stochastic ordering | BEs | Bayesian estimates |
| TTT | Total time on test | CDF | Cumulative distribution function |
| PL | Poisson–Lomax | CCI | Credible CI interval |
| PLP | Power Lomax–Poisson | LCCI | Length of CCI |
| MH | Metropolis–Hastings | KW | Kumaraswamy–Weibull |
| AIC | Akaike information criteria | LBT.MLE | Length of bootstrap-t for MLE |
| BCIs | Bootstrap confidence intervals | IELoP | Inverse exponentiated Lomax–Poisson |
| BTCI | Bootstrap-t CI | TL-G | Topp–Leone generated |
| LBT | Length of bootstrap-t | CP | Coverage probability |
| LBT.Bayes | Length of bootstrap-t for BE | TTLW | TTL Weibull |
| HF | Hazard function | MSEs | Mean squared error |
| ILo | Inverse Lomax | OBWP | Odd Burr–Weibull–Poisson |
Appendix A
Appendix A.1. Second-Order Derivatives of the Log-Likelihood Function to Make Hessian Matrix
Appendix A.2. Simulation Results
| MLE | Bayesian | CI | Bootstraping | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Bias | MSE | Bias | MSE | LACI | CP | LCCI | CP | LBP.MLE | LBT.MLE | LBP.Bayes | LBT.Bayes | |||
| 0.2 | −0.3 | 50 | b | 0.0987 | 0.0180 | 0.1347 | 0.0142 | 0.3568 | 94.0% | 0.3456 | 95.5% | 0.0244 | 0.0249 | 0.1037 | 0.1025 |
| c | 0.0911 | 0.0479 | 0.0294 | 0.0411 | 0.7820 | 94.6% | 0.6818 | 94.4% | 0.0526 | 0.0552 | 0.0958 | 0.0957 | |||
| −0.0587 | 0.0065 | −0.0374 | 0.0058 | 0.2185 | 93.5% | 0.2098 | 94.5% | 0.0542 | 0.0554 | 0.0260 | 0.0268 | ||||
| 0.1097 | 0.0389 | 0.1140 | 0.0310 | 0.6443 | 93.5% | 0.6010 | 96.0% | 0.0473 | 0.0471 | 0.0776 | 0.0764 | ||||
| 100 | b | 0.0896 | 0.0111 | 0.0781 | 0.0106 | 0.2164 | 94.5% | 0.1932 | 96.3% | 0.0151 | 0.0149 | 0.0665 | 0.0665 | ||
| c | 0.0813 | 0.0363 | 0.0251 | 0.0312 | 0.7189 | 95.0% | 0.6176 | 94.5% | 0.0469 | 0.0419 | 0.0810 | 0.0808 | |||
| −0.0407 | 0.0064 | −0.0226 | 0.0056 | 0.2099 | 94.5% | 0.2018 | 95.5% | 0.0516 | 0.0511 | 0.0167 | 0.0165 | ||||
| 0.0873 | 0.0247 | 0.0821 | 0.0240 | 0.5136 | 96.5% | 0.5074 | 98.0% | 0.0358 | 0.0356 | 0.0535 | 0.0543 | ||||
| 200 | b | 0.0784 | 0.0093 | 0.0729 | 0.0084 | 0.2021 | 98.5% | 0.1917 | 96.5% | 0.0146 | 0.0137 | 0.0539 | 0.0539 | ||
| c | 0.0804 | 0.0302 | 0.0145 | 0.0277 | 0.5468 | 95.3% | 0.5100 | 95.5% | 0.0378 | 0.0377 | 0.0747 | 0.0749 | |||
| −0.0360 | 0.0044 | −0.0214 | 0.0041 | 0.1115 | 95.0% | 0.1048 | 96.5% | 0.0083 | 0.0083 | 0.0109 | 0.0108 | ||||
| 0.0798 | 0.0131 | 0.0593 | 0.0102 | 0.3214 | 96.8% | 0.3052 | 99.5% | 0.0232 | 0.0233 | 0.0352 | 0.0354 | ||||
| 0.2 | 50 | b | 0.1040 | 0.0830 | 0.0874 | 0.0727 | 0.5438 | 95.5% | 0.5060 | 95.5% | 0.0379 | 0.0385 | 0.1404 | 0.1395 | |
| c | −0.0487 | 0.1529 | 0.0421 | 0.1216 | 5.3828 | 96.2% | 0.8769 | 94.5% | 0.3498 | 0.5153 | 0.0673 | 0.0678 | |||
| −0.0578 | 0.0041 | 0.0163 | 0.0040 | 1.2462 | 96.5% | 0.2798 | 95.5% | 0.0860 | 0.1147 | 0.0204 | 0.0206 | ||||
| 0.1082 | 0.0432 | 0.0894 | 0.0391 | 0.6969 | 94.3% | 0.6135 | 94.5% | 0.0504 | 0.0504 | 0.0888 | 0.0886 | ||||
| 100 | b | 0.0906 | 0.0137 | 0.0819 | 0.0117 | 0.2919 | 95.8% | 0.2498 | 96.3% | 0.0204 | 0.0210 | 0.0667 | 0.0657 | ||
| c | −0.0318 | 0.1465 | −0.0229 | 0.1054 | 1.3318 | 96.5% | 0.8691 | 94.9% | 0.0944 | 0.1096 | 0.0636 | 0.0638 | |||
| −0.0418 | 0.0038 | 0.0135 | 0.0031 | 0.1788 | 97.5% | 0.1625 | 95.8% | 0.0122 | 0.0125 | 0.0192 | 0.0190 | ||||
| 0.1035 | 0.0267 | 0.0809 | 0.0246 | 0.4969 | 94.5% | 0.4720 | 97.5% | 0.0356 | 0.0358 | 0.0614 | 0.0613 | ||||
| 200 | b | 0.0901 | 0.0137 | 0.0781 | 0.0103 | 0.2557 | 95.9% | 0.2476 | 96.6% | 0.0185 | 0.0181 | 0.0532 | 0.0529 | ||
| c | −0.0212 | 0.0655 | −0.0080 | 0.0494 | 0.5662 | 96.9% | 0.5175 | 95.5% | 0.0396 | 0.0401 | 0.0627 | 0.0619 | |||
| −0.0406 | 0.0028 | 0.0113 | 0.0024 | 0.1064 | 97.9% | 0.0998 | 96.9% | 0.0079 | 0.0079 | 0.0174 | 0.0174 | ||||
| 0.0981 | 0.0181 | 0.0781 | 0.0132 | 0.3616 | 96.0% | 0.3529 | 99.0% | 0.0262 | 0.0263 | 0.0380 | 0.0379 | ||||
| 0.7 | −0.3 | 50 | b | 0.2234 | 0.0861 | 0.1473 | 0.0724 | 0.7480 | 93.5% | 0.7111 | 94.5% | 0.1316 | 0.1330 | 0.0539 | 0.0533 |
| c | 0.0909 | 0.2026 | 0.0891 | 0.1310 | 1.7325 | 95.0% | 1.2359 | 94.5% | 0.1193 | 0.1342 | 0.0951 | 0.0951 | |||
| −0.1550 | 0.0943 | −0.0116 | 0.0610 | 1.0418 | 97.5% | 0.9226 | 95.0% | 0.0756 | 0.0783 | 0.0737 | 0.0737 | ||||
| 0.0467 | 0.0388 | 0.0313 | 0.0374 | 0.7520 | 94.0% | 0.7107 | 94.5% | 0.0866 | 0.0881 | 0.0520 | 0.0518 | ||||
| 100 | b | 0.1737 | 0.0417 | 0.1061 | 0.0406 | 0.4213 | 93.9% | 0.3992 | 95.5% | 0.0678 | 0.0683 | 0.0295 | 0.0304 | ||
| c | 0.0815 | 0.0692 | 0.0450 | 0.0610 | 0.8503 | 96.5% | 0.8118 | 94.9% | 0.0860 | 0.0864 | 0.0609 | 0.0612 | |||
| −0.1484 | 0.0533 | −0.0097 | 0.0301 | 0.5489 | 97.8% | 0.5373 | 98.0% | 0.0403 | 0.0413 | 0.0398 | 0.0399 | ||||
| 0.0453 | 0.0171 | 0.0304 | 0.0144 | 0.4690 | 95.0% | 0.4567 | 98.0% | 0.0518 | 0.0566 | 0.0343 | 0.0350 | ||||
| 200 | b | 0.1709 | 0.0406 | 0.1003 | 0.0395 | 0.4015 | 95.5% | 0.3972 | 95.7% | 0.0512 | 0.0513 | 0.0279 | 0.0282 | ||
| c | 0.0816 | 0.0555 | 0.0426 | 0.0508 | 0.6682 | 98.5% | 0.6605 | 96.5% | 0.0779 | 0.0786 | 0.0459 | 0.0454 | |||
| −0.1375 | 0.0423 | −0.0081 | 0.0256 | 0.4238 | 98.5% | 0.4174 | 98.5% | 0.0317 | 0.0319 | 0.0294 | 0.0292 | ||||
| 0.0371 | 0.0099 | 0.0301 | 0.0090 | 0.3623 | 97.5% | 0.3467 | 99.5% | 0.0332 | 0.0327 | 0.0252 | 0.0250 | ||||
| 0.2 | 50 | b | 0.1274 | 0.1538 | 0.1181 | 0.1490 | 1.4575 | 92.0% | 1.4219 | 94.5% | 0.1121 | 0.1117 | 0.1043 | 0.1041 | |
| c | 0.7316 | 5.1970 | -0.0191 | 0.0534 | 7.0476 | 95.5% | 0.8373 | 94.5% | 0.8035 | 0.8260 | 0.0664 | 0.0666 | |||
| 0.1820 | 1.1833 | 0.0576 | 0.0864 | 4.2146 | 92.5% | 1.0963 | 94.5% | 0.2836 | 0.3248 | 0.0799 | 0.0793 | ||||
| 0.1665 | 0.1865 | 0.1833 | 0.1077 | 1.5658 | 95.5% | 1.0288 | 96.0% | 0.1089 | 0.1095 | 0.0730 | 0.0729 | ||||
| 100 | b | 0.1141 | 0.0583 | 0.0979 | 0.0568 | 0.7709 | 95.5% | 0.7093 | 95.7% | 0.0565 | 0.0568 | 0.0603 | 0.0607 | ||
| c | 0.0607 | 1.0970 | 0.0030 | 0.0500 | 2.9508 | 95.7% | 0.8093 | 94.9% | 0.5583 | 0.4704 | 0.0634 | 0.0644 | |||
| −0.0494 | 0.1924 | 0.0186 | 0.0356 | 1.7128 | 97.5% | 0.6662 | 97.5% | 0.1197 | 0.1376 | 0.0522 | 0.0535 | ||||
| 0.0745 | 0.0325 | 0.1395 | 0.0304 | 0.6451 | 97.0% | 0.5851 | 97.5% | 0.0440 | 0.0447 | 0.0408 | 0.0404 | ||||
| 200 | b | 0.0914 | 0.0338 | 0.0983 | 0.0305 | 0.4517 | 96.0% | 0.4174 | 96.2% | 0.0313 | 0.0313 | 0.0539 | 0.0546 | ||
| c | −0.0508 | 0.1535 | 0.0029 | 0.0453 | 1.1830 | 96.0% | 0.7982 | 95.1% | 0.0854 | 0.0897 | 0.0567 | 0.0561 | |||
| −0.0461 | 0.0939 | −0.0091 | 0.0218 | 1.0921 | 97.7% | 0.5316 | 98.0% | 0.0747 | 0.0844 | 0.0398 | 0.0400 | ||||
| 0.0513 | 0.0093 | 0.1187 | 0.0030 | 0.3199 | 97.6% | 0.3059 | 98.5% | 0.0228 | 0.0225 | 0.0386 | 0.0390 | ||||
| MLE | Bayesian | CI | Bootstraping | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Bias | MSE | Bias | MSE | LACI | CP | LCCI | CP | LBP.MLE | LBP.MLE | LBP.Bayes | LBP.Bayes | |||
| 0.8 | −0.5 | 50 | b | 0.2785 | 0.1057 | 0.0733 | 0.0807 | 0.6597 | 95.0% | 0.6343 | 95.5% | 0.1143 | 0.1159 | 0.0455 | 0.0463 |
| c | 0.2140 | 0.8928 | 0.2016 | 0.1466 | 3.6167 | 94.0% | 1.1627 | 94.5% | 0.2511 | 0.3356 | 0.0862 | 0.0855 | |||
| −0.2215 | 0.1791 | −0.0437 | 0.0933 | 1.4172 | 94.7% | 1.1076 | 95.5% | 0.0999 | 0.0970 | 0.0889 | 0.0864 | ||||
| −0.0135 | 0.0267 | 0.0127 | 0.0196 | 0.6402 | 95.0% | 0.6178 | 94.5% | 0.0665 | 0.0666 | 0.0458 | 0.0456 | ||||
| 100 | b | 0.2648 | 0.0894 | 0.0557 | 0.0599 | 0.5462 | 95.5% | 0.5089 | 95.8% | 0.0649 | 0.0667 | 0.0384 | 0.0388 | ||
| c | 0.2034 | 0.1626 | 0.1921 | 0.1360 | 0.8246 | 96.0% | 0.8091 | 94.9% | 0.0849 | 0.0847 | 0.0609 | 0.0601 | |||
| −0.2157 | 0.1434 | −0.0381 | 0.0447 | 1.0911 | 95.0% | 0.7314 | 95.6% | 0.0788 | 0.0786 | 0.0545 | 0.0547 | ||||
| 0.0058 | 0.0140 | 0.0042 | 0.0125 | 0.4648 | 95.5% | 0.4574 | 95.0% | 0.0435 | 0.0435 | 0.0334 | 0.0328 | ||||
| 200 | b | 0.1604 | 0.0856 | 0.0381 | 0.0431 | 0.4918 | 96.0% | 0.4745 | 99.5% | 0.0523 | 0.0525 | 0.0331 | 0.0334 | ||
| c | 0.1832 | 0.1352 | 0.1621 | 0.1259 | 0.7091 | 98.5% | 0.6913 | 95.5% | 0.0792 | 0.0790 | 0.0491 | 0.0492 | |||
| −0.1831 | 0.1353 | −0.0213 | 0.0400 | 0.7600 | 96.0% | 0.5897 | 99.0% | 0.0554 | 0.0554 | 0.0444 | 0.0444 | ||||
| 0.0041 | 0.0066 | −0.0038 | 0.0051 | 0.3170 | 95.9% | 0.3045 | 95.9% | 0.0321 | 0.0321 | 0.0225 | 0.0221 | ||||
| 0.5 | 50 | b | −0.0261 | 0.3511 | 0.1189 | 0.2015 | 2.3262 | 88.0% | 1.7245 | 94.5% | 0.1599 | 0.1635 | 0.1202 | 0.1213 | |
| c | 0.3539 | 2.9478 | −0.2588 | 0.1927 | 6.0802 | 94.0% | 1.1817 | 94.5% | 0.5993 | 0.5021 | 0.0996 | 0.0997 | |||
| 0.6329 | 2.6104 | 0.0967 | 0.1214 | 5.8418 | 91.5% | 1.1861 | 94.8% | 0.4255 | 0.4246 | 0.0875 | 0.0869 | ||||
| 0.3925 | 0.6845 | 0.1867 | 0.1121 | 2.8622 | 91.5% | 0.9358 | 97.0% | 0.2001 | 0.2049 | 0.0761 | 0.0789 | ||||
| 100 | b | 0.0234 | 0.2686 | 0.0814 | 0.0741 | 2.0322 | 89.5% | 1.0189 | 95.5% | 0.1496 | 0.1493 | 0.0725 | 0.0718 | ||
| c | 0.0911 | 1.2316 | −0.1835 | 0.1331 | 5.8596 | 96.5% | 1.1397 | 94.6% | 0.3931 | 0.4560 | 0.0849 | 0.0851 | |||
| 0.4104 | 1.5044 | 0.0912 | 0.0691 | 4.5422 | 92.0% | 0.8662 | 95.8% | 0.3243 | 0.3327 | 0.0622 | 0.0616 | ||||
| 0.2200 | 0.2939 | 0.1356 | 0.0438 | 1.9471 | 92.0% | 0.5704 | 97.5% | 0.1345 | 0.1340 | 0.0461 | 0.0469 | ||||
| 200 | b | 0.0225 | 0.1988 | 0.0520 | 0.0480 | 1.7411 | 92.0% | 0.8353 | 95.8% | 0.1236 | 0.1224 | 0.0600 | 0.0601 | ||
| c | −0.0707 | 1.2063 | −0.1723 | 0.1240 | 4.3073 | 97.5% | 1.0516 | 95.5% | 0.3071 | 0.3297 | 0.0804 | 0.0805 | |||
| 0.3335 | 1.0860 | 0.0718 | 0.0466 | 3.8800 | 95.0% | 0.7355 | 99.5% | 0.2778 | 0.2920 | 0.0593 | 0.0584 | ||||
| 0.1370 | 0.1788 | 0.1124 | 0.0322 | 1.5720 | 95.0% | 0.4989 | 98.0% | 0.1116 | 0.1141 | 0.0393 | 0.0396 | ||||
| 1.3 | −0.5 | 50 | b | 0.2524 | 0.1641 | 0.1804 | 0.1521 | 1.2449 | 95.0% | 1.1570 | 94.8% | 0.0884 | 0.0897 | 0.1143 | 0.1137 |
| c | −0.3919 | 2.3380 | 0.1912 | 0.1628 | 6.6250 | 95.7% | 1.2487 | 94.5% | 0.5645 | 0.5381 | 0.1110 | 0.1097 | |||
| −0.2872 | 0.3443 | −0.1272 | 0.0822 | 2.0107 | 94.6% | 1.0862 | 95.5% | 0.1467 | 0.1458 | 0.0829 | 0.0827 | ||||
| 0.0929 | 0.1613 | 0.0331 | 0.0789 | 1.5356 | 92.0% | 1.0154 | 94.5% | 0.1105 | 0.1097 | 0.0770 | 0.0764 | ||||
| 100 | b | 0.2483 | 0.1176 | 0.0821 | 0.0536 | 0.9294 | 96.0% | 0.8459 | 95.9% | 0.0652 | 0.0683 | 0.0596 | 0.0594 | ||
| c | 0.1503 | 1.7181 | 0.1479 | 0.1563 | 5.1474 | 96.5% | 1.2020 | 94.6% | 0.3521 | 0.4778 | 0.1003 | 0.1003 | |||
| −0.2359 | 0.2577 | −0.1198 | 0.0462 | 1.4106 | 95.9% | 0.6865 | 97.9% | 0.1006 | 0.1074 | 0.0486 | 0.0483 | ||||
| 0.0911 | 0.0749 | 0.0240 | 0.0455 | 0.9781 | 93.5% | 0.8103 | 97.9% | 0.0717 | 0.0723 | 0.0597 | 0.0598 | ||||
| 200 | b | 0.2393 | 0.1110 | 0.0711 | 0.0444 | 0.6195 | 96.5% | 0.6079 | 96.5% | 0.0456 | 0.0474 | 0.0527 | 0.0524 | ||
| c | 0.1472 | 0.1915 | 0.1485 | 0.1420 | 0.6256 | 97.0% | 0.6110 | 96.5% | 0.0451 | 0.0451 | 0.0901 | 0.0881 | |||
| −0.2240 | 0.1903 | −0.0915 | 0.0445 | 0.6672 | 96.3% | 0.5760 | 98.9% | 0.0457 | 0.0455 | 0.0398 | 0.0399 | ||||
| 0.0813 | 0.0442 | −0.0081 | 0.0263 | 0.6525 | 96.5% | 0.6021 | 98.5% | 0.0474 | 0.0472 | 0.0449 | 0.0439 | ||||
| 0.5 | 50 | b | 0.1251 | 0.3617 | 0.1713 | 0.1775 | 2.3613 | 92.5% | 1.4204 | 93.9% | 0.1648 | 0.1612 | 0.1088 | 0.1083 | |
| c | 0.5983 | 5.1007 | −0.2273 | 0.1846 | 7.9351 | 94.5% | 1.1812 | 94.5% | 0.7939 | 0.8247 | 0.1004 | 0.1011 | |||
| 0.5473 | 2.9872 | 0.1371 | 0.1294 | 6.4427 | 92.5% | 1.2650 | 98.0% | 0.4600 | 0.4776 | 0.0922 | 0.0910 | ||||
| 0.5010 | 0.8039 | 0.2085 | 0.1681 | 2.9219 | 93.0% | 1.2700 | 94.2% | 0.2204 | 0.2224 | 0.0980 | 0.0989 | ||||
| 100 | b | −0.0446 | 0.2835 | 0.0945 | 0.0458 | 2.0850 | 93.5% | 0.7416 | 94.5% | 0.1466 | 0.1492 | 0.0561 | 0.0571 | ||
| c | 0.1286 | 3.6066 | −0.1031 | 0.1721 | 7.4623 | 96.5% | 1.1750 | 94.7% | 0.5298 | 0.5228 | 0.0935 | 0.0930 | |||
| 0.5306 | 2.3538 | 0.0791 | 0.0543 | 5.6571 | 93.5% | 0.8181 | 99.5% | 0.4259 | 0.4255 | 0.0580 | 0.0580 | ||||
| 0.3782 | 0.5966 | 0.1372 | 0.0584 | 2.6468 | 93.5% | 0.7643 | 94.5% | 0.1903 | 0.1910 | 0.0502 | 0.0497 | ||||
| 200 | b | 0.0381 | 0.1578 | 0.0861 | 0.0325 | 1.5540 | 94.2% | 0.6116 | 94.8% | 0.1110 | 0.1122 | 0.0420 | 0.0419 | ||
| c | −0.1006 | 0.4073 | −0.0925 | 0.1565 | 2.3810 | 97.5% | 1.0812 | 95.5% | 0.1619 | 0.1602 | 0.0836 | 0.0840 | |||
| 0.1848 | 0.9123 | 0.0634 | 0.0452 | 3.6827 | 94.0% | 0.7640 | 99.6% | 0.2573 | 0.2591 | 0.0572 | 0.0582 | ||||
| 0.2342 | 0.1536 | 0.1270 | 0.0346 | 1.2350 | 95.5% | 0.5240 | 95.9% | 0.0888 | 0.0896 | 0.0372 | 0.0368 | ||||
| MLE | Bayesian | CI | Bootstraping | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Bias | MSE | Bias | MSE | LACI | CP | LCCI | CP | LBP.MLE | LBP.MLE | LBP.Bayes | LBP.Bayes | |||
| 0.4 | −0.6 | 50 | b | 0.1596 | 0.0552 | 0.0534 | 0.0399 | 0.8929 | 94.7% | 0.7023 | 94.5% | 0.0645 | 0.0634 | 0.0543 | 0.0553 |
| c | −0.7587 | 4.7153 | 0.3274 | 0.2938 | 8.6923 | 95.5% | 1.1968 | 94.3% | 0.9750 | 0.9979 | 0.0987 | 0.0986 | |||
| −0.2257 | 0.3981 | −0.0296 | 0.0591 | 2.3154 | 95.7% | 0.9447 | 94.3% | 0.1544 | 0.1527 | 0.0664 | 0.0662 | ||||
| −0.2204 | 0.2213 | −0.0933 | 0.1645 | 1.6331 | 95.5% | 1.6324 | 93.6% | 0.1157 | 0.1156 | 0.1186 | 0.1173 | ||||
| 100 | b | 0.1483 | 0.0348 | 0.0272 | 0.0119 | 0.6554 | 95.5% | 0.3919 | 97.1% | 0.0457 | 0.0459 | 0.0294 | 0.0298 | ||
| c | −0.4509 | 3.4587 | 0.3041 | 0.2316 | 7.3058 | 96.0% | 1.1679 | 94.5% | 0.4991 | 0.5519 | 0.0977 | 0.0984 | |||
| −0.2135 | 0.2755 | −0.0187 | 0.0323 | 1.5268 | 96.5% | 0.6005 | 94.5% | 0.1156 | 0.1142 | 0.0427 | 0.0420 | ||||
| −0.2070 | 0.1356 | −0.0746 | 0.0664 | 0.9842 | 97.5% | 0.9768 | 94.5% | 0.0671 | 0.0667 | 0.0684 | 0.0682 | ||||
| 200 | b | 0.1411 | 0.0335 | 0.0234 | 0.0116 | 0.6468 | 96.2% | 0.3888 | 97.5% | 0.0438 | 0.0437 | 0.0278 | 0.0278 | ||
| c | 0.2555 | 1.1127 | 0.2658 | 0.2258 | 4.0219 | 96.4% | 1.0907 | 95.5% | 0.2880 | 0.3111 | 0.0908 | 0.0905 | |||
| −0.2099 | 0.1273 | −0.0113 | 0.0313 | 0.9972 | 96.6% | 0.5724 | 94.8% | 0.0729 | 0.0732 | 0.0394 | 0.0396 | ||||
| −0.1833 | 0.1263 | −0.0510 | 0.0506 | 0.9047 | 97.7% | 0.7390 | 94.8% | 0.0640 | 0.0632 | 0.0566 | 0.0563 | ||||
| 0.6 | 50 | b | 0.0658 | 0.0259 | 0.0650 | 0.0236 | 0.5766 | 93.5% | 0.5387 | 94.6% | 0.0408 | 0.0408 | 0.0450 | 0.0449 | |
| c | −0.3979 | 2.1328 | −0.3706 | 0.2493 | 5.7371 | 95.0% | 1.1482 | 94.5% | 0.3900 | 0.4161 | 0.0961 | 0.0957 | |||
| 0.3901 | 1.7463 | 0.1207 | 0.0703 | 4.9618 | 94.0% | 0.9433 | 94.5% | 0.3700 | 0.3715 | 0.0669 | 0.0659 | ||||
| 0.2069 | 0.6551 | 0.1561 | 0.2030 | 3.0751 | 94.5% | 1.5362 | 94.3% | 0.2110 | 0.2109 | 0.1150 | 0.1157 | ||||
| 100 | b | 0.0582 | 0.0209 | 0.0482 | 0.0202 | 0.4686 | 94.0% | 0.4488 | 96.0% | 0.0315 | 0.0319 | 0.0342 | 0.0342 | ||
| c | −0.3192 | 0.3495 | −0.3041 | 0.2377 | 1.9554 | 95.4% | 1.0745 | 94.6% | 0.1398 | 0.1413 | 0.0897 | 0.0908 | |||
| 0.1867 | 0.6496 | 0.0604 | 0.0311 | 3.0812 | 94.5% | 0.6434 | 94.7% | 0.2182 | 0.2202 | 0.0464 | 0.0463 | ||||
| 0.0815 | 0.2393 | 0.0597 | 0.0665 | 1.9214 | 95.0% | 0.9357 | 94.5% | 0.1367 | 0.1360 | 0.0708 | 0.0703 | ||||
| 200 | b | 0.0410 | 0.0206 | 0.0378 | 0.0140 | 0.4061 | 94.6% | 0.3436 | 98.5% | 0.0289 | 0.0289 | 0.0241 | 0.0241 | ||
| c | −0.2857 | 0.3102 | −0.2406 | 0.2040 | 1.5790 | 95.6% | 0.9900 | 95.5% | 0.1064 | 0.1065 | 0.0732 | 0.0722 | |||
| 0.0252 | 0.2286 | 0.0239 | 0.0213 | 1.8765 | 95.5% | 0.5135 | 96.1% | 0.1264 | 0.1289 | 0.0385 | 0.0387 | ||||
| −0.0786 | 0.1024 | 0.0279 | 0.0448 | 1.2191 | 95.5% | 0.8127 | 99.0% | 0.0902 | 0.0901 | 0.0603 | 0.0611 | ||||
| 0.9 | 0.2 | 50 | b | 0.1503 | 0.1753 | 0.1426 | 0.1292 | 1.5358 | 95.1% | 1.2499 | 95.5% | 0.1119 | 0.1116 | 0.0949 | 0.0991 |
| c | 0.2925 | 2.6366 | 0.0032 | 0.0480 | 6.2768 | 95.0% | 0.8870 | 94.5% | 0.4647 | 0.4918 | 0.0671 | 0.0642 | |||
| 0.1919 | 2.1393 | 0.0524 | 0.0634 | 5.6982 | 92.5% | 0.9463 | 96.1% | 0.3972 | 0.3998 | 0.0661 | 0.0667 | ||||
| 0.3002 | 0.8372 | 0.0694 | 0.1031 | 3.3967 | 92.5% | 1.1605 | 94.9% | 0.2489 | 0.2531 | 0.0870 | 0.0888 | ||||
| 100 | b | 0.1500 | 0.1444 | 0.1406 | 0.0662 | 1.3720 | 95.3% | 0.7227 | 98.9% | 0.0985 | 0.0983 | 0.0576 | 0.0577 | ||
| c | −0.0300 | 1.1120 | −0.0018 | 0.0465 | 4.1424 | 95.5% | 0.8220 | 94.7% | 0.2943 | 0.3082 | 0.0597 | 0.0598 | |||
| 0.1012 | 1.1802 | 0.0108 | 0.0306 | 4.2506 | 94.5% | 0.7183 | 96.7% | 0.2953 | 0.2950 | 0.0466 | 0.0470 | ||||
| 0.1769 | 0.3890 | 0.0527 | 0.0764 | 2.3504 | 93.5% | 0.9299 | 95.5% | 0.1685 | 0.1675 | 0.0728 | 0.0730 | ||||
| 200 | b | 0.1422 | 0.1141 | 0.1363 | 0.0433 | 1.0162 | 95.5% | 0.5090 | 99.0% | 0.0749 | 0.0751 | 0.0381 | 0.0385 | ||
| c | −0.0267 | 0.3299 | −0.0010 | 0.0387 | 2.2017 | 96.5% | 0.7541 | 94.9% | 0.1601 | 0.1655 | 0.0533 | 0.0531 | |||
| −0.0914 | 0.6118 | −0.0098 | 0.0223 | 3.0202 | 96.2% | 0.5550 | 96.9% | 0.2140 | 0.2153 | 0.0422 | 0.0421 | ||||
| −0.0515 | 0.1718 | 0.0485 | 0.0364 | 1.6277 | 93.9% | 0.7128 | 96.3% | 0.1126 | 0.1147 | 0.0507 | 0.0509 | ||||
| 0.6 | 50 | b | 0.1124 | 0.1803 | 0.1023 | 0.1504 | 1.6092 | 96.5% | 1.1377 | 97.5% | 0.1174 | 0.1169 | 0.0852 | 0.0852 | |
| c | 0.1933 | 2.9809 | −0.1907 | 0.2650 | 6.7845 | 95.2% | 1.1380 | 94.4% | 0.5019 | 0.5148 | 0.0938 | 0.0962 | |||
| 0.3246 | 2.9453 | 0.0816 | 0.0768 | 6.6226 | 93.5% | 1.0038 | 94.5% | 0.4767 | 0.4759 | 0.0713 | 0.0714 | ||||
| 0.4664 | 1.2229 | 0.1084 | 0.1337 | 3.9404 | 93.5% | 1.3896 | 98.3% | 0.2839 | 0.2847 | 0.0967 | 0.0980 | ||||
| 100 | b | 0.1026 | 0.1051 | 0.0911 | 0.0491 | 1.1742 | 96.7% | 0.7275 | 99.0% | 0.0849 | 0.0840 | 0.0520 | 0.0515 | ||
| c | −0.1876 | 0.3729 | −0.1743 | 0.2580 | 1.8901 | 95.4% | 1.1119 | 94.5% | 0.1377 | 0.1391 | 0.0807 | 0.0809 | |||
| 0.0544 | 0.8320 | 0.0536 | 0.0280 | 3.5783 | 93.7% | 0.6422 | 94.6% | 0.2536 | 0.2539 | 0.0432 | 0.0430 | ||||
| 0.1637 | 0.2831 | 0.0987 | 0.0539 | 1.9894 | 93.7% | 0.8245 | 98.5% | 0.1441 | 0.1445 | 0.0582 | 0.0581 | ||||
| 200 | b | 0.0916 | 0.0912 | 0.0851 | 0.0426 | 1.1237 | 97.5% | 0.5620 | 99.5% | 0.0838 | 0.0828 | 0.0445 | 0.0453 | ||
| c | −0.1721 | 0.3255 | −0.1706 | 0.2112 | 1.0657 | 99.5% | 0.9882 | 95.0% | 0.1259 | 0.1243 | 0.0714 | 0.0713 | |||
| 0.0507 | 0.7463 | 0.0315 | 0.0220 | 2.7135 | 97.5% | 0.5842 | 94.7% | 0.2401 | 0.2336 | 0.0397 | 0.0399 | ||||
| 0.1384 | 0.2556 | 0.0726 | 0.0446 | 1.8537 | 97.5% | 0.7275 | 99.5% | 0.1369 | 0.1309 | 0.0526 | 0.0533 | ||||
References
- Weibull, W. A Statistical Distribution Function of Wide Applicability. Asme J. Appl. Mech. 1951, 103, 293–297. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus-motor-failure data. Technometrics 1995, 37, 436–445. [Google Scholar] [CrossRef]
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Liu, L.; Strawderman, R.L.; Johnson, B.A.; O’Quigley, J.M. Analyzing repeated measures semi-continuous data, with application to an alcohol dependence study. Stat. Methods Med. Res. 2016, 25, 133–152. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Tapert, S.; Fan, C.C.; Thompson, W.K. A semi-parametric Bayesian model for semi-continuous longitudinal data. Stat. Med. 2022, 41, 2354–2374. [Google Scholar] [CrossRef] [PubMed]
- Kleiber, C.; Kotz, S.S. Statistical Size Distributions in Economics and Actuarial Sciences; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kleiber, C. Lorenz ordering of order statistics from log-logistic and related distributions. J. Stat. Plan. Inference 2004, 120, 13–19. [Google Scholar] [CrossRef]
- McKenzie, D.; Miller, C.; Falk, D.A. The Landscape Ecology of Fire; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- Rahman, J.; Aslam, M. Interval prediction of future order statistics in two-component mixture inverse Lomax model: A Bayesian approach. Am. J. Math. Manag. Sci. 2014, 33, 216–227. [Google Scholar] [CrossRef]
- Yadav, A.S.; Singh, S.K.; Singh, U. On hybrid censored inverse Lomax distribution: Application to the survival data. Statistica 2016, 76, 185–203. [Google Scholar]
- Rahman, J.; Aslam, M. On estimation of two-component mixture inverse Lomax model via Bayesian approach. Int. J. Syst. Assur. 2017, 8, 99–109. [Google Scholar] [CrossRef]
- Jan, U.; Ahmad, S.P. Bayesian analysis of inverse Lomax distribution using approximation techniques. Bayesian Anal. 2017, 7, 1–12. [Google Scholar]
- Hassan, A.S.; Mohamed, R.E. Weibull inverse Lomax distribution. Pak. J. Stat. Oper. Res. 2019, 33, 587–603. [Google Scholar] [CrossRef][Green Version]
- Maxwell, O.; Chukwu, A.U.; Oyamakin, O.S.; Khaleel, M.A. The Marshall-Olkin inverse Lomax distribution (MO-ILD) with application on cancer stem cell. J. Adv. Math. Compu. 2019, 33, 1–12. [Google Scholar] [CrossRef]
- ZeinEldin, R.A.; Haq, M.A.; Hashmi, S.; Elsehetry, M. Alpha power transformed inverse Lomax distribution with different methods of estimation and applications. Complexity 2020, 2020, 1860813. [Google Scholar] [CrossRef]
- Hassan, A.S.; Ismail, D. Parameters of Topp-Leone inverse Lomax distribution in presence of right censored samples. Gazi Univ. J. Sci. 2021, 34, 1193–1208. [Google Scholar]
- Ahmadini, A.A.H.; Hassan, A.S.; Elgarhy, M.; Elsehetry, M.; Alshqaq, S.S.; Nassr, S.G. Inference of truncated Lomax inverse Lomax distribution with applications. Intell. Autom. Soft Comput. 2021, 29, 199–212. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Hassan, A.S.; Alotaibi, N.; Shrahili, M.; Nagy, H.F. Reliability estimation of inverse Lomax distribution using extreme ranked set sampling. Adv. Math. Phys. 2021, 2021, 4599872. [Google Scholar] [CrossRef]
- Hassan, A.; Elshaarawy, R.; Heba, N.A.G.Y. Estimation Study of Multicomponent Stress-Strength Reliability Using Advanced Sampling Approach. Gazi Univ. J. Sci. 2024, 37, 465–481. [Google Scholar] [CrossRef]
- Yousof, H.M.; Alizadeh, M.; Jahanshahi, S.M.A.; Ramires, T.G.; Ghosh, I.; Hamedani, G.G. The transmuted Topp-Leone-G family of distributions: Theory, characterizations and applications. J. Data Sci. 2017, 15, 723–740. [Google Scholar] [CrossRef]
- Rezaei, S.; Sadr, B.B.; Alizadeh, M.; Nadarajah, S. Topp-Leone generated family of distributions: Properties and applications. Commun. Stat. Theory Methods 2017, 46, 2893–2909. [Google Scholar] [CrossRef]
- Shaw, W.T.; Buckley, I.R.C. The alchemy of probability distributions: Beyond Gram-Charlier expansions and a skew-kurtotic-normal distribution from a rank transmutation map. arXiv 2007, arXiv:0901.0434. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; The Regents of the University of California: Oakland, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 79–487. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On a generalized entropy measure leading to the pathway model with a preliminary application to solar neutrino data. Entropy 2013, 15, 4011–4025. [Google Scholar] [CrossRef]
- Glänzel, W. A characterization theorem based on truncated moments and its application to some distribution families. In Mathematical Statistics and Probability Theory; Springer: Dordrecht, The Netherlands, 1987; pp. 75–84. [Google Scholar]
- Glänzel, W. Some consequences of a characterization theorem based on truncated moments. J. Theor. Appl. Stat. 1990, 21, 613–618. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Zhang, M.H.; Liu, X.T.; Wang, Y.S.; Wang, X. Parameters distribution characteristics of material fatigue life based on improved bootstrap method. Int. J. Damage Mech. 2019, 28, 772–793. [Google Scholar] [CrossRef]
- Ge, H.Y.; Liu, X.T.; Fang, Y.; Wang, H.X.; Zhang, M.H. An improved bootstrap method introducing error ellipse for numerical analysis of fatigue life parameters. Eng. Comput. 2021, 38, 289–312. [Google Scholar] [CrossRef]
- Ibrahim, M.; Yousof, H. Transmuted Topp-Leone Weibull lifetime distribution: Statistical properties and different method of estimation. Pak. J. Stat. Oper. Res. 2020, 16, 501–515. [Google Scholar] [CrossRef]
- Hassan, A.S.; Almetwally, E.M.; Gamoura, S.C.; Metwally, A.S.M. Inverse Exponentiated Lomax Power Series Distribution: Model, Estimation and Application. J. Math. 2022, 2022, 1998653. [Google Scholar] [CrossRef]
- Al-Zahrani, B.; Sagor, H.H. The Poisson-Lomax distribution. Rev. Colomb. Estad. 2014, 37, 225–245. [Google Scholar] [CrossRef]
- Hassan, A.S.; Nassr, S.G. Power Lomax Poisson distribution: Properties and estimation. J. Data Sci. 2018, 18, 105–128. [Google Scholar] [CrossRef]
- Nasir, M.A.; Jamal, F.; Silva, G.O.; Tahir, M.H. Odd Burr-G Poisson family of distributions. J. Stat. Appl. Prob. 2018, 7, 9–28. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Franklin Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to gamma and Weibull distributions. Biom J. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Antoniou, A.; Lu, W.S. Practical Optimization: Algorithms and Engineering Applications; Springer: New York, NY, USA, 2007; Volume 19, p. 669. [Google Scholar]
- Jorgensen, B. Statistical Properties of the Generalized Inverse Gaussian Distribution; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 9. [Google Scholar]
- Xia, Z.P.; Yu, J.Y.; Cheng, L.D.; Liu, L.F.; Wang, W.M. Study on the breaking strength of jute fibres using modified Weibull distribution. Compos. Part Appl. Sci. Manuf. 2009, 40, 54–59. [Google Scholar] [CrossRef]
- Saracoglu, B.; Kinaci, I.; Kundu, D. On estimation of R = P (Y < X) for exponential distribution under progressive type-II censoring. J. Stat. Comput. Simul. 2012, 82, 729–744. [Google Scholar]
- Alshenawy, R.; Sabry, M.A.; Almetwally, E.M.; Almongy, H.M. Product spacing of stress-strength under progressive hybrid censored for exponentiated-gumbel distribution. Comput. Mater. Contin. 2021, 66, 2973–2995. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Tolba, A.H. Stress-Strength Reliability Under Partially Accelerated Life Testing Using Weibull Model. Sci. Afr. 2023, 20, e01733. [Google Scholar] [CrossRef]
- Abu El Azm, W.S.; Almetwally, E.M.; Alghamdi, A.S.; Aljohani, H.M.; Muse, A.H.; Abo-Kasem, O.E. Stress-strength reliability for exponentiated inverted Weibull distribution with application on breaking of Jute fiber and Carbon fibers. Comput. Intell. Neurosci. 2021, 2021, 4227346. [Google Scholar]
- Nassar, M.; Alotaibi, R.; Zhang, C. Product of Spacing Estimation of Stress-Strength Reliability for Alpha Power Exponential Progressively Type-II Censored Data. Axioms 2023, 12, 752. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, Y.; Bai, X.; Zhan, P. Reliability estimation of a NM-cold-standby redundancy system in a multicomponent stress-strength model with generalized half-logistic distribution. Phys. Stat. Mech. Its Appl. 2018, 490, 231–249. [Google Scholar] [CrossRef]
- Kang, S.G.; Lee, W.D.; Kim, Y. Objective Bayesian analysis for generalized exponential stress-strength model. Comput. Stat. 2021, 36, 2079–2109. [Google Scholar] [CrossRef]
- Fayomi, A.; Hassan, A.S.; Baaqeel, H.; Almetwally, E.M. Bayesian Inference and Data Analysis of the Unit–Power Burr X Distribution. Axioms 2023, 12, 297. [Google Scholar] [CrossRef]
- Singh, D.P.; Jha, M.K.; Tripathi, Y.M.; Wang, L. Inference on a multicomponent stress-strength model based on unit-Burr III distributions. Ann. Data Sci. 2023, 10, 1329–1359. [Google Scholar] [CrossRef]
- Saini, S.; Tomer, S.; Garg, R. On the reliability estimation of multicomponent stress-strength model for Burr XII distribution using progressively first-failure censored samples. J. Stat. Comput. Simul. 2022, 92, 667–704. [Google Scholar] [CrossRef]








| (1.5, −0.5, 1.5, 0.5) | 1.176 | 1.326 | 0.629 | 0.453 | 0.406 | 3.97 |
| (2.5, −0.5, 1.5, 0.5) | 1.588 | 1.869 | 1.047 | 1.013 | 0.795 | 5.014 |
| (4, −0.5, 1.5, 0.5) | 1.906 | 2.32 | 1.313 | 1.376 | 0.995 | 6.048 |
| (1.5, −0.5, 3, 0.5) | 1.87 | 2.267 | 1.195 | 1.147 | 0.873 | 6.443 |
| (2.5, −0.5, 3, 0.5) | 2.281 | 2.891 | 1.559 | 1.706 | 1.148 | 7.919 |
| (4, −0.5, 3, 0.5) | 2.599 | 3.408 | 1.79 | 2.07 | 1.289 | 9.382 |
| (1.5, 0.5, 1.5, 0.5) | 0.352 | 0.365 | −0.287 | −0.571 | −0.661 | 2.255 |
| (2.5, 0.5, 1.5, 0.5) | 0.889 | 0.973 | 0.415 | 0.253 | 0.237 | 3.121 |
| (4, 0.5, 1.5, 0.5) | 1.273 | 1.45 | 0.803 | 0.724 | 0.607 | 3.965 |
| (1.5, 0.5, 3, 0.5) | 1.045 | 1.162 | 0.398 | 0.122 | 0.118 | 4.018 |
| (2.5, 0.5, 3, 0.5) | 1.583 | 1.862 | 1.008 | 0.946 | 0.754 | 5.242 |
| (4, 0.5, 3, 0.5) | 1.966 | 2.409 | 1.347 | 1.417 | 1.015 | 6.436 |
| b | c | KS | p-Value | CVM | AD | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TTLILo | estimates | 0.1703 | −0.0439 | 20.5164 | 8.8115 | 0.1072 | 0.8807 | 0.0795 | 0.4333 | 311.4148 | 317.0196 | |
| SE | 0.0582 | 0.5545 | 0.3608 | 0.3567 | ||||||||
| KW | estimates | 1.2367 | 0.6078 | 1.4584 | 0.0804 | 0.1941 | 0.2083 | 0.0862 | 0.4687 | 313.9641 | 319.5689 | |
| SE | 0.5945 | 0.0020 | 0.6861 | 0.0149 | ||||||||
| TTLW | estimates | 3.4231 | 0.0955 | 0.0210 | 0.4761 | 0.1473 | 0.5334 | 0.0810 | 0.4358 | 311.7251 | 317.3299 | |
| SE | 4.6060 | 0.7433 | 0.0349 | 0.2882 | ||||||||
| IELoP | estimates | 86.7457 | 1.1845 | 0.4980 | 2.5505 | 0.1258 | 0.7296 | 0.0905 | 0.4791 | 311.5726 | 317.1774 | |
| SE | 21.3210 | 0.3504 | 1.8010 | 2.1276 | ||||||||
| PL | estimates | 0.7387 | 15.2763 | 54.7040 | 0.1570 | 0.4503 | 0.1010 | 0.7367 | 315.9373 | 320.1409 | ||
| SE | 0.0942 | 2.5666 | 3.6562 | |||||||||
| PLP | estimates | 0.0104 | 2.1150 | 39.1073 | 230.6120 | 0.1210 | 0.7720 | 0.0904 | 0.5829 | 315.5517 | 321.1565 | |
| SE | 0.0047 | 0.8415 | 17.1134 | 51.1562 | ||||||||
| OBWP | estimates | 0.0025 | 0.6161 | 1.2651 | 10.7397 | 8.0621 | 0.1354 | 0.6409 | 0.0950 | 0.5201 | 321.8135 | 328.8195 |
| SE | 0.0005 | 0.0765 | 0.1629 | 5.3759 | 4.9321 |
| Hessian Matrix | Eigenvectors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Eigenvalues | |||||||||
| b | 1011.2481 | 1019.3303 | 0.9960 | 0.0206 | 0.0107 | −0.0862 | |||
| c | −87.4628 | 10.6091 | 17.8560 | −0.0864 | 0.0037 | 0.0153 | −0.9961 | ||
| 5.5160 | −0.6141 | 12.6414 | 12.4330 | 0.0055 | 0.1822 | −0.9831 | −0.0149 | ||
| 21.4747 | −1.9702 | −0.8537 | 18.1396 | 3.0188 | 0.0215 | −0.9830 | −0.1820 | −0.0083 | |
| b | c | KS | p-Value | CVM | AD | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TTLILo | Estimates | 0.1600 | 0.1317 | 0.0699 | 167.4198 | 0.1202 | 0.6104 | 0.0543 | 0.3589 | 186.6263 | 193.3818 | |
| SE | 0.1535 | 0.5072 | 0.0716 | 3.8966 | ||||||||
| TTLW | Estimates | 58.1011 | 0.1803 | 8.0034 | 0.2664 | 0.1533 | 0.3038 | 0.0606 | 0.4152 | 188.0099 | 194.7654 | |
| SE | 48.8839 | 0.4997 | 9.2094 | 0.0450 | ||||||||
| IELoP | Estimates | 0.1669 | 12.8608 | 0.0827 | 1.5100 | 0.122 | 0.603 | 0.0638 | 0.4102 | 187.5061 | 194.2616 | |
| SE | 0.1185 | 7.9279 | 1.3748 | 0.4414 | ||||||||
| PLP | Estimates | 0.0822 | 2.4468 | 6.6152 | 1.9044 | 0.1278 | 0.5844 | 0.1024 | 0.6467 | 192.1852 | 198.9407 | |
| SE | 0.1923 | 2.3213 | 5.2638 | 4.9810 | ||||||||
| OBWP | Estimates | 0.0026 | 1.0358 | 0.9683 | 9.4829 | 9.2072 | 0.1279 | 0.5297 | 0.1226 | 0.8713 | 202.9075 | 211.3519 |
| SE | 0.0006 | 0.2114 | 0.1557 | 6.7102 | 6.7098 | |||||||
| KW | Estimates | 3.8258 | 0.6738 | 13.9079 | 0.1657 | 0.1277 | 0.6014 | 0.0553 | 0.3958 | 187.5262 | 194.2817 | |
| SE | 0.0073 | 0.0078 | 1.0124 | 0.0269 |
| Hessian Matrix | Eigenvectors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Eigenvalues | |||||||||
| b | 1675.1444 | 11,569.5888 | 0.3759 | 0.9142 | 0.1515 | −0.0005 | |||
| c | −118.8257 | 14.8123 | 47.7700 | −0.0289 | 0.1750 | −0.9841 | 0.0008 | ||
| 4012.4206 | −312.9006 | 9931.1742 | 3.7739 | 0.9262 | −0.3656 | −0.0922 | −0.0002 | ||
| 1.7366 | −0.1332 | 4.2407 | 0.0677 | 0.0659 | 0.0004 | 0.0003 | 0.0008 | 1.0000 | |
| b | c | KS | p-Value | CVM | AD | AIC | BIC | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | Estimates | 7.4166 | −0.5586 | 172.9725 | 0.6006 | 0.2147 | 0.1081 | 0.0897 | 0.6820 | 419.5942 | 425.1990 |
| SE | 44.1519 | 0.5949 | 323.2337 | 2.8588 | |||||||
| Z | Estimates | 31.8271 | −0.2593 | 342.4166 | 0.1634 | 0.1676 | 0.3307 | 0.1214 | 0.8252 | 418.6250 | 424.2298 |
| SE | 8.1252 | 0.6559 | 14.1515 | 0.0915 |
| Maximum Likelihood | Bayesian | |||
|---|---|---|---|---|
| Estimate | SE | Estimate | SE | |
| 13.6892 | 96.5180 | 5.9063 | 4.6592 | |
| −0.5568 | 0.6069 | −0.0853 | 0.2912 | |
| 0.3726 | 1.8839 | 0.2542 | 0.1439 | |
| 3.6497 | 17.5410 | 4.5396 | 3.6980 | |
| −0.2449 | 0.6666 | −0.3828 | 0.3578 | |
| 0.7876 | 3.2043 | 0.6023 | 0.5364 | |
| 207.0288 | 340.0919 | 640.5580 | 252.2402 | |
| R | 0.5974 | 0.8003 | ||
| TTLILo (New) | 13.6892 | −0.5568 | 0.3726 | 3.6497 | −0.2449 | 0.7876 | 207.0288 | 0.5974 |
| Exponential [44] | 356.7297 | - | 340.74 | - | 0.5177 | |||
| Exponentiated Gumbel Distribution [45] | 3.360852 | - | 223.3009 | - | 0.51816 | |||
| Weibull [46] | 389.3 | 1.71 | - | 372.17 | 1.36 | - | 2.21 | 0.5384 |
| Exponentiated Inverted Weibull [47] | 441.8773 | - | 315.0805 | - | 1.1569 | 0.5838 | ||
| Alpha Power Exponential [48] | 23.44078 | - | 5.6544 | - | 0.004932 | 0.4019 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alyami, S.A.; Elbatal, I.; Hassan, A.S.; Almetwally, E.M. Engineering Applications with Stress-Strength for a New Flexible Extension of Inverse Lomax Model: Bayesian and Non-Bayesian Inference. Axioms 2023, 12, 1097. https://doi.org/10.3390/axioms12121097
Alyami SA, Elbatal I, Hassan AS, Almetwally EM. Engineering Applications with Stress-Strength for a New Flexible Extension of Inverse Lomax Model: Bayesian and Non-Bayesian Inference. Axioms. 2023; 12(12):1097. https://doi.org/10.3390/axioms12121097
Chicago/Turabian StyleAlyami, Salem A., I. Elbatal, Amal S. Hassan, and Ehab M. Almetwally. 2023. "Engineering Applications with Stress-Strength for a New Flexible Extension of Inverse Lomax Model: Bayesian and Non-Bayesian Inference" Axioms 12, no. 12: 1097. https://doi.org/10.3390/axioms12121097
APA StyleAlyami, S. A., Elbatal, I., Hassan, A. S., & Almetwally, E. M. (2023). Engineering Applications with Stress-Strength for a New Flexible Extension of Inverse Lomax Model: Bayesian and Non-Bayesian Inference. Axioms, 12(12), 1097. https://doi.org/10.3390/axioms12121097






