Fixed Point Theorems in Rectangular b-Metric Space Endowed with a Partial Order

Abstract

The purpose of this paper is to present some fixed-point results for self-generalized contractions in ordered rectangular b-metric spaces. We also provide some examples that illustrate the non-triviality and richness of this area of research.

1. Introduction

The importance of fixed-point theory is shaped out by Felix Browder [1] in the following sentences “Among the most original and far-reaching of the contributions made by Henri Poincaré to mathematics was his introduction of the use of topological or ’qualitative’ methods in the study of nonlinear problems in analysis… The ideas introduced by Poincaré include the use of fixed-point theorems, the continuation method and the general concept of global analysis”.

Initially, the fixed-point theory was used to prove the existence of solutions of differential equations; see the work of Joseph Liouville around 1837. Later on, in 1890, the method of successive approximations was introduced by Charles Emile Picard and, after that, in 1922, with the well known contraction principle, Stefan Banach initiated the modern fixed-point theory. The diverse results of the existence of fixed points have relevant applications in many branches of mathematical analysis, algebra, topology, etc., see [2]. Via a fixed-point result it is possible to solve some nonlinear functional equations or some optimization problem or some variational inequalities.

For short, a fixed point of a map f is a solution of the equation $x=f\left(x\right)$. For the state of the art, let X be a nonempty set and $f:X\to X$ be a map. The set of all fixed points of f is $Fix\left(f\right)=\left\{x\in X,f\left(x\right)=x\right\}$. If we denote the graph of the function f by ${\mathcal{G}}_f$, i.e., ${\mathcal{G}}_f=\left\{\left(x,f\left(x\right)\right),x\in X\right\}\subset X\times X$ and ${\Delta }_X=\left\{\left(x,x\right),x\in X\right\}$ is the diagonal-set of X, then $Fix\left(f\right)={\mathcal{G}}_f\cap {\Delta }_X$. This equality permits a connection between classical metric fixed-point theory and another mathematics subject like graph theory. This direction of research was initiated by J. Jakhymski [3], who demonstrated how his theorem could be used to prove the Kelisky–Rivlin theorem on the convergence of the Bernstein operators on the space of continuous functions on $\left[0, 1\right]$. Since then, graphical fixed-point theory has been widely studied, and some significant results are presented in the book [4] and the recent paper [5].

There are at least two methods to study the non-emptiness of the set $Fix\left(f\right)$. On the one hand, we can study the convergence of the successive approximations sequence $\left\{f^n\left(x_0\right)\right\}$, where $x_0\in X$. On the other hand, we can study the zeroes of the function $F:\left(X,d\right)\to \left[0,\infty \right)$ given by $F\left(x\right)=d\left(x,f\left(x\right)\right)$. Both methods can be enriched by adding some extra assumptions on the function or the space. This is especially interesting when dealing with ordered algebraic structures. This research direction has been the subject of extensive coverage in the literature, with numerous references available, including Ran and Reurings [6], O’Regan and Petrusel [7], Alfuraidan et al. [4] and Khan [8]. These works underscore the importance of studying this subject in a variety of research fields, including the theory of automata (which explores the fundamental principles of computation and the behavior of abstract machines), mathematical linguistics (which investigates the mathematical properties of language and its structures), approximation theory and the theory of critical points. Given the breadth of coverage, it is clear that investigating this topic is essential for advancing understanding in these fields.

In fact, the metric contractive conditions are based on comparing the distances between different points in the domain and their images under the mapping. Some of the conditions involve some of the following six displacements $d\left(f\left(x\right),f\left(y\right)\right)$, $d\left(x,y\right)$, $d\left(x,f\left(x\right)\right)$, $d\left(y,f\left(y\right)\right)$, $d\left(x,f\left(y\right)\right)$ and $d\left(y,\left(x\right)\right)$ such that it can be possible to prove non-emptiness of the set $Fix\left(f\right)$.

For example, one way to understand the Kannan contraction condition is to use a geometric interpretation. Suppose that $f:X\to X$ is a map that satisfies the inequality

$$d(f\left(x\right),f\left(y\right))\le a[d(x,f\left(x\right))+d(y,f\left(y\right))],\forall x,y\in X,$$

(1)

where $a\in \left(0,\frac{1}{2}\right)$ and $\left(X,d\right)$ is a metric space. Then, for any two points $x,y\in X$, we can draw a quadrilateral with vertices x, $f\left(x\right)$, $f\left(y\right)$, y, as shown in Figure 1.

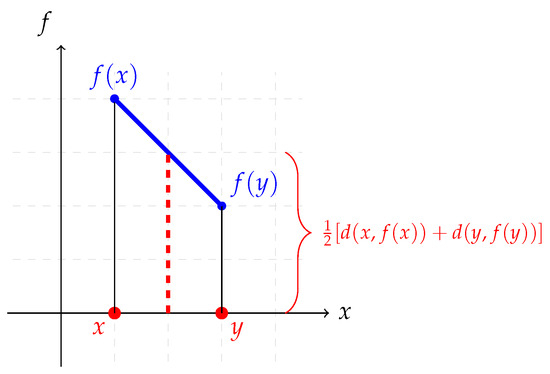
Figure 1. A geometric interpretation of Kannan contractive condition [9].

The inequality (1) tells us that the length of the side $f\left(x\right)-f\left(y\right)$ is smaller than the length of the midsegment that connects the midpoints of the sides $x-f\left(x\right)$ and $y-f\left(y\right)$. This shows that the map f shrinks the distances between points in some sense, which is a key property for proving the existence and uniqueness of fixed points. So, we have the fixed-point theorem due to Kannan [10]:

Theorem 1

([10]). Let $(X,d)$ be a complete metric space. If the mapping $f:X\to X$ satisfies (1), with $0<a<\frac{1}{2}$, then f has a unique fixed point.

A number of recent studies have explored fixed-point results that rely on Kannan contraction conditions. Specifically, Debnath, P.; Srivastava, H.M. [11] and Konwar, N. et al. [12] have extended Kannan’s fixed-point theorem to the case of multivalued maps using Wardowski’s type contraction.

One of the main topics in fixed-point theory is to extend the classical or recent results of metric fixed-point theory to some more general settings, such as generalized metric spaces, and to consider some nonlinear mappings that are more general than Banach’s contraction. In [13], some equivalent conditions for generalized contractions are given and we state one of them as follows.

Theorem 2

([13]). Let f be a self map of a metric space $\left(X,d\right)$. The following statements are equivalent:

(E-i.)

There exist $\psi ,\eta :\left[0,\infty \right)\to \left[0,\infty \right)$ two continuous and nondecreasing maps such that ${\psi }^{-1}\left(\left\{0\right\}\right)={\eta }^{-1}\left(\left\{0\right\}\right)=\left\{0\right\}$ and, for any $x,y\in X$,

$$\psi \left(d\left(f\left(x\right),f\left(y\right)\right)\right)\le \psi \left(d\left(x,y\right)\right)-\eta \left(d\left(x,y\right)\right)$$

holds;

(E-ii.)

There exist $\alpha \in \left[0,1\right)$ and $\psi :\left[0,\infty \right)\to \left[0,\infty \right)$ a continuous and nondecreasing function such that ${\psi }^{-1}\left(\left\{0\right\}\right)=\left\{0\right\}$ and, for any $x,y\in X$,

$$\psi \left(d\left(f\left(x\right),f\left(y\right)\right)\right)\le \alpha ·\psi \left(d\left(x,y\right)\right)$$

holds;

(E-iii.)

There exists a continuous and nondecreasing function $\phi :\left[0,\infty \right)\to \left[0,\infty \right)$ such that $\phi \left(t\right)<t$ for all $t>0$ and, for any $x,y\in X$,

$$d\left(f\left(x\right),f\left(y\right)\right)\le \phi \left(d\left(x,y\right)\right).$$

Besides Banach’s contraction principle, an important tool in fixed-point theory is Caristi’s theorem; for details see [14,15]. In [16] it is proved that the analog of Caristi’s theorem does not hold in some rectangular metric space but in [17] there is a proposal to transpose the Caristi type theorems in b-metric spaces.

Acording to Berinde & Păcurar [18], the concept of b-metric space was introduced in 1981 as quasimetric space. About 20 years ago, Branciari [19] introduced the new type of metric space by replacing the triangle inequality with the rectangular inequality in the definition of a metric space. George et al. [20] further extended this idea by introducing the rectangular b-metric space, which has been studied by many authors, such as Öztürk, V. [21] and Kari, A. et al. [22]. The existence of a fixed point in an ordered metric space has its starting point in work of Ran et al. [6] and was continued by many other researchers like Harjani [23].

Considering the discussion above, we establish in this paper a fixed-point theorem for a generalized contraction in a rectangular b-metric space endowed with a partial order. As a consequence of the main result, we obtain a fixed-point result for a mapping satisfying contractive conditions of integral type in a complete rectangular b-metric space endowed with a partial order. For the rest of the manuscript we make the following arrangement: in Section 2, we state some basic definitions and notations to be used throughout this paper. The main result is given in Section 3.

2. Preliminaries

2.1. Partially Ordered Sets

In what follows, let X be a nonempty set and ⪯ be a reflexive, transitive and anti-symmetric relation on X, i.e., $\left(X,⪯\right)$ is a partially ordered set. Denote

$$X_{⪯}=\left\{\left(x,y\right)\in X\times X,x⪯y \mathrm{or} y⪯x\right\}.$$

Definition 1.

Let $\left(X,⪯\right)$ be a partially ordered set and $f:X\to X$ be a given mapping. We say that f is an isotone if $x⪯y$ implies $f\left(x\right)⪯f\left(y\right)$.

Definition 2.

Let $\left(X,⪯\right)$ be a partially ordered set and $\left\{x_n\right\}$ be a sequence from X. We say that $\left\{x_n\right\}$ is a nondecreasing sequence if $x_n⪯x_{n+1}$ for all $n\ge 0$.

Remark 1.

If $f:X\to X$ is an isotone and there is $x_0\in X$ such that $x_0⪯f\left(x_0\right)$, then $\left\{f^n\left(x_0\right)\right\}$ is a nondecreasing sequence.

In the literature, there exist many examples of partially ordered sets; see [24,25] and references therein. We mention here two of them.

Example 1.

Let $X=C\left(a,b,{\mathbb{R}}_{+}\right)$ be the set of all continuous functions from compact subset $\left[a,b\right]\subset \mathbb{R}$ to the set of non-negative real numbers. Let $\left[c,d\right]\subset \left[a,b\right]$ be a compact subset and $\mu \in \left(0,1\right)$, $t^{\prime }\in \left[c,d\right]$ be two positive real numbers. For any $u,v\in X$, if we consider that $u\preccurlyeq v$ if and only if $\mu ·v\left(t\right)-v\left(t^{\prime }\right)\le \mu ·u\left(t\right)-u\left(t^{\prime }\right)$ for all $t\in \left[a,b\right]$, then $\left(X,\preccurlyeq \right)$ is a partially ordered set of continuous functions.

Example 2.

Let $X=C\left(\left[a,b\right],\mathbb{R}\right)$ be the set of all continuous functions from $\left[a,b\right]$ into $\mathbb{R}$ endowed with the distance d related to the usual supremum norm, i.e., $d\left(h_1,h_2\right)=\underset{t\in \left[a,b\right]}{max}\left|h_1\left(t\right)-h_2\left(t\right)\right|$ for all $h_1,h_2\in C\left(\left[a,b\right],\mathbb{R}\right)$. Consider on X the partial order ⪯ defined by $h_1⪯h_2$ if and only if $h_1\left(t\right)\ge h_2\left(t\right)$ for any $t\in \left[a,b\right]$, where $h_1,h_2\in C\left(\left[a,b\right],\mathbb{R}\right)$. Then, $\left(X,d,⪯\right)$ is an ordered and complete metric space.

In ordered metric spaces, the following principle of Banach–Caccioppoli type was established by Ran and Reurings [6].

Theorem 3

([6]). Let $\left(X,⪯\right)$ be a partially ordered set such that every pair $x,y\in X$ has a lower and an upper bound. Let $\left(X,d\right)$ be a complete metric space and $f:X\to X$ be a continuous and monotone (i.e., either decreasing or increasing) operator. Suppose that the following two assertions hold:

(H-i.)

There exists $a\in \left(0,1\right)$ such that $d\left(f\left(x\right),f\left(y\right)\right)\le a·d\left(x,y\right)$ for each $x,y\in X$, with $x,y\in X_{⪯}$;

(H-ii.)

There exists $x_0\in X$ such that $\left(x_0,f\left(x_0\right)\right)\in X_{⪯}$.

Then, f has an unique fixed point $x^{*}\in X$, i.e., $f\left(x^{*}\right)=x^{*}$, and for each $x\in X$ the sequence $\left\{f^n\left(x\right)\right\}$ of successive approximations of f starting from x converges to $x^{*}\in X$.

The existence of fixed points on partially ordered metric spaces is a topic that has attracted a lot of attention in recent years. Many researchers have contributed to this field by establishing various results and applications, see [7,23,26,27,28,29].

2.2. Rectangular b-Metric Spaces

Let X be a nonempty set and $d:X\times X\to \left[0,\infty \right)$ be a map providing the following axioms.

(M-i.)

$d\left(x,y\right)=0$ if and only if $x=y$ for all $x,y\in X$;

(M-ii.)

$d\left(x,y\right)=d\left(y,x\right)$ for all $x,y\in X$;

(M-iii.)

There exists $s\ge 1$, a real number, such that

$$d\left(x,y\right)\le s·\left(d\left(x,z\right)+d\left(z,y\right)\right) \mathrm{for} \mathrm{all} x,y,z\in X;$$

(bM)

(M-iv.)

there is $s\ge 1$ a real number such that

$$d\left(x,y\right)\le s·\left(d\left(x,z_1\right)+d\left(z_1,z_2\right)+d\left(z_2,y\right)\right)$$

(rbM)

is satisfied for all $x,y\in X$, $z_1,z_2\in X\setminus \left\{x,y\right\}$, with $x\ne y$ and $z_1\ne z_2$.

The following definitions are consistent with [30,31], respectively [19].

Definition 3.

Let X be a nonempty set, $d:X\times X\to \left[0,\infty \right)$ and $s\ge 1$ be a given real number. The pair $\left(X,d\right)$ is a b-metric space with coefficient s if axioms axioms (M-i.), (M-ii.) and (M-iii.) hold.

Definition 4.

Let X be a nonempty set, $d:X\times X\to \left[0,\infty \right)$ and $s\ge 1$ be a given real number. The pair $\left(X,d\right)$ is a rectangular b-metric space with coefficient s if axioms (M-i.), (M-ii.) and (M-iv.) hold.

Remark 2.

For $s=1$, the axiom (M-iii.) is the triangle inequality and $\left(X,d\right)$ is a metric space introduced by Fréchet in [32].

For a brief history of the concept of b-metric space, we refer to [18,26].

Remark 3.

For $s=1$, the axiom (M-iv.) is a rectangular inequality and $\left(X,d\right)$ is a rectangular metric space introduced by Branciari in [19].

Note that a rectangular metric space is a generalization of a metric space, where the triangle inequality is replaced by a weaker condition. Any metric space is also a rectangular metric space and any rectangular metric space is a special case of a rectangular b-metric space. Moreover, if a b-metric space has a coefficient s, then it is also a rectangular b-metric space with coefficient $s^2$. For more details and examples of these spaces, see [20,33]. One way to construct a rectangular metric space is given in [34].

Example 3.

Let $\left(X,d\right)$ be a complete metric space, $u,v\in X$ and $\left\{u_n\right\}$ be a convergent sequence such that $u_n\in X\setminus \left\{u,v\right\}$ for all $n\ge 1$ and $\underset{n\to \infty }{lim}{u}_n=u$. Denote by σ the set of all elements of the considered sequence $\left\{u_n\right\}$, and $P_u=\left(\sigma \times \left\{u\right\}\right)\cup \left(\left\{u\right\}\times \sigma \right)$, $P_v=\left(\sigma \times \left\{v\right\}\right)\cup \left(\left\{v\right\}\times \sigma \right)$ and $\Sigma =\sigma \cup \left\{u,v\right\}$. Define a function $d_{\Sigma }$ from $\Sigma \times \Sigma$ into $\left[0,\infty \right)$ by

$$d_{\Sigma }\left(x,y\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if} x=y\hfill \\ d\left(u,u_n\right),\hfill & \mathrm{if} \left(x,y\right)\in P_u\cup P_v\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Then, $\left(\Sigma ,d_{\Sigma }\right)$ is a rectangular metric space which is not a metric space.

Since $\left\{u_n\right\}$ is a Cauchy sequence and $\left(X,d\right)$ is complete, there exists $N\ge 1$ such that $d\left(u_n,u\right)\le \frac{1}{2}$ for all $n\ge N$, so, we have

$$d_{\Sigma }\left(u_m,u_n\right)=1=\frac{1}{2}+\frac{1}{2}\ge d\left(u,u_m\right)+d\left(u,u_n\right)=d_{\Sigma }\left(u_m,u\right)+d_{\Sigma }\left(u_n,u\right),$$

inequality which proves that $\left(\Sigma ,d_{\Sigma }\right)$ is not a metric space. On the other hand, for $s\ge 1$ and for all positive integers $m\ge N$, $n\ge N$, with $m\ne n$, we have

$$\begin{array}{cc}\hfill d_{\Sigma }\left(u_m,u_n\right)& =1\le s=s·d\left(u,v\right)\hfill \\ & \le s·d\left(u_m,u\right)+s·d\left(u,v\right)+s·d\left(u_n,u\right)\hfill \\ & =s·\left(d_{\Sigma }\left(u_m,u\right)+d_{\Sigma }\left(u,v\right)+d_{\Sigma }\left(v,u_n\right)\right).\hfill \end{array}$$

Therefore, there are elements in set Σ for which the triangle inequality does not hold, instead the rectangular inequality (with coefficient s) holds.

Remark that Example 3 is a generalization of Example 1.3 from [35].

Example 4.

Let $\left(X,d\right)$ be a complete metric space, $u,v,w\in X$ and $\left\{u_n\right\}$ be a convergent sequence such that $u_n\in X\setminus \left\{u,v,w\right\}$ for all $n\ge 1$ and $\underset{n\to \infty }{lim}{u}_n=u$. Denote by σ the set of all elements of the considered sequence $\left\{u_n\right\}$, and $P_v=\left(\sigma \times \left\{v\right\}\right)\cup \left(\left\{v\right\}\times \sigma \right)$, $P_w=\left(\sigma \times \left\{w\right\}\right)\cup \left(\left\{w\right\}\times \sigma \right)$ and $\Sigma =\sigma \cup \left\{u,v,w\right\}$. Define a function ${\delta }_{\Sigma }$ from $\Sigma \times \Sigma$ into $\left[0,\infty \right)$ by

$${\delta }_{\Sigma }\left(x,y\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if} x=y\hfill \\ 2·\kappa ,\hfill & \mathrm{if} \left(x,y\right)\in \sigma \times \sigma \hfill \\ \frac{\kappa }{2}·d\left(u,u_n\right),\hfill & \mathrm{if} \left(x,y\right)\in P_v\cup P_w\hfill \\ \kappa ,\hfill & \mathrm{otherise}\hfill \end{array}\right.$$

where $\kappa >0$ is positive real constant. Then, $\left(\Sigma ,{\delta }_{\Sigma }\right)$ is a rectangular b-metric space.

Since $\left\{u_n\right\}$ is a Cauchy sequence and $\left(X,d\right)$ is complete, there exists $N\ge 1$ such that $d\left(u_n,u\right)\le 1$ for all $n\ge N$. Hence, for all positive integers $m\ge N$, $n\ge N$, with $m\ne n$, we have

$$\begin{array}{cc}\hfill {\delta }_{\Sigma }\left(u_m,u_n\right)& =2\kappa =\frac{\kappa }{2}+\kappa +\frac{\kappa }{2}\hfill \\ & \ge \frac{\kappa }{2}·d\left(u_m,u\right)+{\delta }_{\Sigma }\left(v,w\right)+\frac{\kappa }{2}·d\left(u_m,u\right)\hfill \\ & ={\delta }_{\Sigma }\left(u_m,v\right)+{\delta }_{\Sigma }\left(v,w\right)+{\delta }_{\Sigma }\left(w,u_n\right).\hfill \end{array}$$

Hence, there are elements in set Σ for which the rectangular inequality does not hold. On the other hand, since $\kappa ={\delta }_{\Sigma }\left(u,v\right)={\delta }_{\Sigma }\left(v,w\right)={\delta }_{\Sigma }\left(w,u\right)$, we have

$${\delta }_{\Sigma }\left(u_m,u_n\right)=2\kappa =2·{\delta }_{\Sigma }\left(z_1,z_2\right)\le 2·\left(d_{\Sigma }\left(u_m,z_1\right)+d_{\Sigma }\left(z_1,z_2\right)+{\delta }_{\Sigma }\left(z_2,u_n\right)\right),$$

where $z_1,z_2\in \left\{u,v,w\right\}$ with $z_1\ne z_2$. Thus, (rbM) is satified for all $x,y\in \sigma$, $x\ne y$ and $z_1,z_2\in \left\{u,v,w\right\}$ with respect to coefficient $s=2$. Similarly, we can treat all cases that must be considered to finish the proof that $\left(\Sigma ,{\delta }_{\Sigma }\right)$ is a rectangular b-metric space with coefficient $s=2$.

Following the idea from [34], the notion from Definition 4 can be generalized. We say that $\left(X,d\right)$ is an n-gon rectangular b-metric space, if n is a given positive integer, $n\ge 4$, X is a nonempty set and the function $d:X\times X\to \left[0,\infty \right)$ satisfies the axioms (M-i.), (M-ii.) and

$$d\left(x,y\right)\le s·\left(d\left(x,z_1\right)+\sum _{k=1}^{n-2}d\left(z_k,z_{k+1}\right)+d\left(z_{n-1},y\right)\right),$$

(nrbM)

where $x,y\in X$, $z_k\in X\setminus \left\{x,y\right\}$, with $x\ne y$ and $z_k\ne z_l$ for all $k,l\in \left\{1,2,\dots ,n-1\right\}$, with $k\ne l$.

Example 5.

Let $p\ge 2$ be a positive integer and $X={\mathcal{L}}^2\left[0,1\right]$ be the set of Lebesgue measurable functions on $\left[0,1\right]$ such that ${\displaystyle \underset{0}{\overset{1}{\int }}{\left|f\left(t\right)\right|}^{2}dt<\infty }$. Define $D_p:X\times X\to \left[0,\infty \right)$ by

$$D_p\left(f,g\right)=\underset{0}{\overset{1}{\int }}{\left|f\left(t\right)-g\left(t\right)\right|}^{2}dt \mathrm{for} \mathrm{all} f,g\in X.$$

(2)

Then, $\left(X,D_p\right)$ is a p-gon rectangular b-metric space with coefficient $s=p$. Indeed, it is obvious that the axioms (M-i.) and (M-ii.) are satisfied by $D_p$. Now, consider $f,g\in X$ and $h_k\in X\setminus \left\{f,g\right\}$, with $f\ne g$ and $h_k\ne h_l$ for all $k,l\in \left\{1,2,\dots ,p-1\right\}$, with $k\ne l$. We have

$$\frac{f-g}{p}=\frac{f-h_1}{p}+\frac{1}{p}·\sum _{k=1}^{p-2}\left(h_k-h_{k+1}\right)+\frac{h_{p-1}-g}{p}$$

and by quadratic mean we obtain

$${\left|f-g\right|}^2\le p·\left({\left|f-h_1\right|}^2+\sum _{k=1}^{p-2}{\left|h_k-h_{k+1}\right|}^2+{\left|h_{p-1}-g\right|}^2\right).$$

(3)

Hence, by (2) and (5), the inequality

$$D_p\left(f,g\right)\le p·\left(D_p\left(f,h_1\right)+\sum _{k=1}^{p-2}d\left(h_k,h_{k+1}\right)+d\left(h_{n-1},g\right)\right)$$

(4)

holds for all $f,g\in X$ and $h_k\in X\setminus \left\{f,g\right\}$, with $f\ne g$ and $h_k\ne h_l$ for all $k,l\in \left\{1,2,\dots ,p-1\right\}$, with $k\ne l$. That is, (nrbM); therefore, $\left(X,D_p\right)$ is a p-gon rectangular b-metric space.

Remark that, if in Example 5 we consider $p=2$, then we obtain the particular case given by Example 1 from [36].

2.3. Rectangular b-Metric Spaces Endowed with a Partial Order

Definition 5.

Let $\left(X,⪯\right)$ be a partially ordered set and $s\ge 1$ be a given real number. We say that $\left(X,d,⪯\right)$ is a partially ordered rectangular b-metric space if $\left(X,d\right)$ is rectangular b-metric space.

The basic topological properties, such as convergence and completeness, can be defined in a manner similar to that of metric spaces. These properties are analogous to the ones defined for metric spaces, but they may have different implications or consequences.

Definition 6.

Let $\left(X,d\right)$ be a rectangular b-metric space with coefficient s, $x\in X$ and $\left\{x_n\right\}$ be a sequence in X. We say that the sequence $\left\{x_n\right\}$ is $Rb$-convergent in $\left(X,d\right)$ and converges to x if, for every $\epsilon >0$, there exists $n_0\in \mathbb{N}$ such that $d\left(x_n,x\right)<\epsilon$ for all $n>n_0$. In this case, we write $\underset{n\to \infty }{lim}{x}_n=x$.

Note that the limits are not unique in rectangular b-metric space. For example, if we consider the sequence $\left\{u_n\right\}$ given by Example 3, then both equality $\underset{n\to \infty }{lim}{d}_{\Sigma }\left(u_n,u\right)=\underset{n\to \infty }{lim}d\left(u_n,u\right)=0$ and $\underset{n\to \infty }{lim}{d}_{\Sigma }\left(u_n,v\right)=\underset{n\to \infty }{lim}d\left(u_n,u\right)=0$ hold, so $\left\{u_n\right\}$ is $Rb$-convergent to u and v, but $u\ne v$.

Lemma 1

([33]). Let $\left(X,d\right)$ be a rectangular b-metric space with coefficient $s\ge 1$ and $\left\{x_n\right\}$, $\left\{y_n\right\}$ be two b-convergent sequences, with $\underset{n\to \infty }{lim}{x}_n=x$ and $\underset{n\to \infty }{lim}{y}_n=y$, respectively. The following inequalities

$$\frac{1}{s}·d\left(x,y\right)\le \underset{n\to infty}{lim\; inf}d\left(x_n,y_n\right)\le \underset{n\to \infty }{lim\; sup}d\left(x_n,y_n\right)\le s·d\left(x,y\right)$$

(5)

hold.

Definition 7.

Let $\left(X,d\right)$ be a rectangular b-metric space with coefficient s. The sequence $\left\{x_n\right\}$ is said to be $Rb$-Cauchy if $\underset{n\to \infty }{lim}d\left(x_{n+p},x_n\right)=0$ for all $p\in \mathbb{N}$.

In fact, $\left\{x_n\right\}$ is an $Rb$-Cauchy sequence if, for every $\epsilon >0$, there exists $n_0\in \mathbb{N}$ such that $d\left(x_{n+p},x_n\right)<\epsilon$ for all $n>n_0$ and $p>0$. Note that the sequence $\left\{u_n\right\}$ from Example 3 is not an $Rb$-Cauchy sequence because $d_S\left(u_m.u_n\right)=1$ for all $m,n\in \mathbb{N}$ with $m\ne n$.

Definition 8.

A rectangular b-metric space $\left(X,d\right)$ is called Rb-complete if any $Rb$-Cauchy sequence is convergent in $\left(X,d\right)$.

3. Main Result

In the sequel, we make the notations

$${\mathcal{M}}_{x,y}^f=max\left\{d\left(x,y\right),d\left(x,f\left(x\right)\right),d\left(y,f\left(y\right)\right)\right\}$$

(6)

and

$$m_{x,y}^f=min\left\{d\left(x,f\left(x\right)\right),d\left(y,f\left(y\right)\right),d\left(x,f\left(y\right)\right),d\left(y,f\left(x\right)\right)\right\}.$$

(7)

If $y=f\left(x\right)$, then

$${\mathcal{M}}_{x,f\left(x\right)}^f=max\left\{d\left(x,f\left(x\right)\right),d\left(f\left(x\right),f^2\left(x\right)\right)\right\}$$

(8)

and

$$m_{x,f\left(x\right)}^f=0 \mathrm{for} \mathrm{all} x\in X.$$

(9)

Let $\mathcal{S}$ denote the class of those continuous and increasing functions $\psi :\left[0,\infty \right)\to \left[0,\infty \right)$ and $\mathcal{E}$ be the class of lower semicontinuous functions $\phi :\left[0,\infty \right)\to \left[0,\infty \right)$ for which the equality $\phi \left(t\right)=0$ holds only for $t=0$.

Theorem 4.

Let $\left(X,d,⪯\right)$ be a partially ordered rectangular b-metric space with coefficient s, with $s\ge 1$ a given real number. Let $f:X\to X$ be an isotone mapping such that

(T-i.)

There exists $x_0\in X$ such that $x_0⪯f\left(x_0\right)$;

(T-ii.)

There exist $\psi \in \mathcal{S}$ and $\phi \in \mathcal{E}$ and $L\in \left(0,\infty \right)$ such that

$$\psi \left(s^2·d\left(f\left(x\right)\right),f\left(y\right)\right)\le \psi \left({\mathcal{M}}_{x,y}^f\right)-\phi \left({\mathcal{M}}_{x,y}^f\right)+L·m_{x,y}^f$$

(10)

for all $x,y\in X_{\le }$;

Then, f has a fixed point in X.

Proof. 

Let $\left\{y_n\right\}$ be the Picard iteration defined by $y_0=x_0$ and $y_n=f\left(y_{n-1}\right)$ for all $n\ge 1$. By Remark 1, the hypothesis (T-i.) ensures that the sequence $\left\{y_n\right\}$ is nondecreasing, so $y_n⪯y_{n+1}$ for all $n\ge 0$; thus, $\left(y_m,y_n\right)\in X_{⪯}$ for all $m,n\in \mathbb{N}$, $m\ne n$.

If there is $n_0\in \mathbb{N}$ such that $y_{n_0}=y_{n_0+1}$, then $y_{n_0}$ is a fixed point of f, so there is nothing to prove.

Assume that $y_n\ne y_{n+1}$ for all $n\in \mathbb{N}$, so $d\left(y_n,y_{n+1}\right)\ne 0$ for all $n\in \mathbb{N}$. Substitute $x=y_n$ and $y=y_{n+1}$ in (10); by (8) and (9), we obtain

$$\psi \left(d\left(y_{n+1},y_{n+2}\right)\right)\le \psi \left(s·d\left(y_{n+1},y_{n+2}\right)\right)\le \psi \left({\mathcal{M}}_{y_n,y_{n+1}}^f\right)-\phi \left({\mathcal{M}}_{y_n,y_{n+1}}^f\right),$$

(11)

where ${\mathcal{M}}_{y_n,y_{n+1}}^f=max\left\{\left\{d\left(y_n,y_{n+1}\right),d\left(y_{n+1},y_{n+2}\right)\right\}\right\}$.

If ${\mathcal{M}}_{y_n,y_{n+1}}^f=d\left(y_{n+1},y_{n+2}\right)$, then (11) turns into

$$\psi \left(d\left(y_{n+1},y_{n+2}\right)\right)\le \psi \left(d\left(y_{n+1},y_{n+2}\right)\right)-\phi \left(d\left(y_{n+1},y_{n+2}\right)\right),$$

which implies $\phi \left(d\left(y_{n+1},y_{n+2}\right)\right)=0$. This contradicts the properties of $\phi$ and the hypothesis $d\left(y_n,y_{n+1}\right)\ne 0$. Therefore, ${\mathcal{M}}_{y_n,y_{n+1}}^f=d\left(y_n,y_{n+1}\right)$. Hence, by (11), we must have

$$\psi \left(d\left(y_{n+1},y_{n+2}\right)\right)\le \psi \left(d\left(y_n,y_{n+1}\right)\right)-\phi \left(d\left(y_n,y_{n+1}\right)\right)\le \psi \left(d\left(y_n,y_{n+1}\right)\right).$$

(12)

Since $\psi$ is increasing, (12) holds only if $d\left(y_{n+1},y_{n+2}\right)\le d\left(y_n,y_{n+1}\right)$ for all $n\in \mathbb{N}$. So $\left\{d\left(y_n,y_{n+1}\right)\right\}$ is a real number sequence which is decreasing and positive. Hence, the sequence $\left\{d\left(y_n,y_{n+1}\right)\right\}$ converges to a positive number, so there exists $\ell \in \left[0,\infty \right)$ such that $\underset{n\to \infty }{lim}d\left(y_n,y_{n+1}\right)=\ell$. Taking limits as $n\to \infty$ in (12), we obtain $\psi \left(\ell \right)\le \psi \left(\ell \right)-\phi \left(\ell \right)$, which leads to $\phi \left(\ell \right)=0$. Hence, $\ell =0$, that is

$$\underset{n\to \infty }{lim}d\left(y_n,y_{n+1}\right)=0.$$

(13)

By (13), we have $\underset{n\to \infty }{lim}{\mathcal{M}}_{y_n,y_{n+1}}^f=0$ and

$$\underset{n\to \infty }{lim}{\mathcal{M}}_{y_n,y_p}^f=\underset{n\to \infty }{lim}d\left(y_n,y_p\right) \mathrm{for} \mathrm{all} p\in \mathbb{N}.$$

(14)

In order to prove that $\left\{y_n\right\}$ is an $Rb$-Cauchy sequence in $\left(X,d\right)$ we will use the proof by contradiction. Assume that $y_n\ne y_{n+1}$ for all $n\in \mathbb{N}$ and we can find two subsequences $\left\{y_n^{\prime }\right\}$ and $\left\{y_n^{\prime \prime }\right\}$ of $\left\{y_n\right\}$ such that $\underset{n\to \infty }{lim}d\left(y_n^{\prime },y_n^{\prime \prime }\right)\ne 0$. Without losing the generality, we can consider that there exist $k,p\in \mathbb{N}$, which depend on $i\in \mathbb{N}$, such that $y_n^{\prime }=y_{k\left(i\right)}$, $y_n^{\prime \prime }=y_{p\left(i\right)}$ with $i<k\left(i\right)<p\left(i\right)$, and there exists $\epsilon >0$ for which the inequalities

$$d\left(y_{k\left(i\right)},y_{p\left(i\right)}\right)\ge \epsilon$$

(15)

$$d\left(y_{k\left(i\right)},y_{p\left(i\right)-1}\right)<\epsilon$$

(16)

hold. In fact, (15) implies that $\left\{y_n\right\}$ is not an $Rb$-Cauchy sequence in $\left(X,d\right)$ and (16) ensures that $p\left(i\right)$ is the smallest integer satisfying (15). For simplicity, we use $d^{*}\left(k_i,p_i\right)$ instead of $d\left(y_{k\left(i\right)},y_{p\left(i\right)}\right)$, i.e.,

$$d^{*}\left(k_i,p_i\right)=d\left(y_{k\left(i\right)},y_{p\left(i\right)}\right).$$

By (rbM) from axiom (M-iv), with $x=y_{k\left(i\right)}$, $y=y_{p\left(i\right)}$, $z=y_{p\left(i\right)-2}$ and $w=y_{p\left(i\right)-1}$, and using (15) and (16), we obtain

$$\begin{array}{cc}\hfill \epsilon & \le d^{*}\left(k_i,p_i\right)\le s·\left(d^{*}\left(k_i,p_i-2\right)+d^{*}\left(p_i-2,p_i-1\right)+d^{*}\left(p_i-1,p_i\right)\right)\hfill \\ & \le s·\epsilon +s·\left(d^{*}\left(p_i-2,p_i-1\right)+d^{*}\left(p_i-1,p_i\right)\right).\hfill \end{array}$$

(17)

Taking (13) into account, we find that

$$\underset{i\to \infty }{lim\; sup}{d}^{*}\left(k_i,p_i\right)\le s\epsilon .$$

(18)

By (rbM) from axiom (M-iv), with $x=y_{k\left(i\right)}$, $y=y_{p\left(i\right)}$, $z=y_{k\left(i\right)+1}$ and $w=y_{p\left(i\right)+1}$, and using (15) and (16), we obtain

$$\begin{array}{cc}\hfill \epsilon & \le d^{*}\left(k_i,p_i\right)\le s·\left(d^{*}\left(k_i,k_i+1\right)+d^{*}\left(k_i+1,p_i+1\right)+d^{*}\left(p_i+1,p_i\right)\right).\hfill \end{array}$$

(19)

Letting $i\to \infty$ in (19) and using (13), we have

$$\frac{\epsilon }{s}\le \underset{i\to \infty }{lim\; sup}{d}^{*}\left(k_i+1,p_i+1\right).$$

(20)

Since $\psi \left(d^{*}\left(k_i+1,p_i+1\right)\right)=\psi \left(d\left(f\left(y_{k\left(i\right)}\right),f\left(y_{p\left(i\right)}\right)\right)\right)\le \psi \left(s^2·d\left(f\left(y_{k\left(i\right)}\right),\right.\right.$$\left.\left.f\left(y_{p\left(i\right)}\right)\right)\right)$, by (10), we conclude that

$$\psi \left(d^{*}\left(k_i+1,p_i+1\right)\right)\le \psi \left({\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\right)-\phi \left({\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\right)+L·m_{y_{k\left(i\right)},y_{p\left(i\right)}}^f,$$

(21)

where

$${\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f=max\left\{d^{*}\left(k_i,p_i\right),d^{*}\left(k_i,k_i+1\right),d^{*}\left(p_i,p_i+1\right)\right\}$$

(22)

and

$$m_{y_{k\left(i\right)},y_{p\left(i\right)}}^f=min\left\{d^{*}\left(k_i,k_i+1\right),d^{*}\left(p_i,p_i+1\right),d^{*}\left(k_i,p_i+1\right),d^{*}\left(k_i+1,p_i\right)\right\}.$$

(23)

Taking the upper limit as $i\to \infty$ in (22), respectively (23), and using (13) and (18), we obtain

$$\underset{i\to \infty }{lim\; sup}{\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f=\underset{i\to \infty }{lim\; sup}{d}^{*}\left(k_i,p_i\right)<s\epsilon ,$$

(24)

respectively

$$\underset{i\to \infty }{lim\; sup}{m}_{y_{k\left(i\right)},y_{p\left(i\right)-1}}^f=0.$$

(25)

Now, by (20) and the equality $\psi \left(s\epsilon \right)=\psi \left(s^2·{\displaystyle \frac{\epsilon }{s}}\right)$, we obtain

$$\psi \left(s\epsilon \right)\le \underset{i\to \infty }{lim\; sup}\psi \left(s^2·d^{*}\left(k_i+1,p_i+1\right)\right).$$

Taking the limit as $i\to \infty$ in (21), and using (16), (24) and (25), we have

$$\begin{array}{cc}\hfill \psi \left(s\epsilon \right)& \le \underset{i\to \infty }{lim\; sup}\psi \left({\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\right)-\underset{i\to \infty }{lim\; inf}\phi \left({\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\right)+L·\underset{i\to \infty }{lim\; sup}{m}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\hfill \\ \hfill & \le \psi \left(s\epsilon \right)-\underset{i\to \infty }{lim\; inf}\phi \left({\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\right).\hfill \end{array}$$

Due to the fact that $\phi \in \mathcal{E}$, we conclude that $\underset{i\to \infty }{lim\; inf}\phi \left({\mathcal{M}}_{y_{k\left(i\right)},y_{p\left(i\right)}}^f\right)=0$. Hence,

$$\underset{i\to \infty }{lim\; inf}\phi \left(d\left(y_{k\left(i\right)},y_{p\left(i\right)}\right)\right)=0.$$

Therefore, by properties of $\phi$,

$$\underset{i\to \infty }{lim}d\left(y_{k\left(i\right)},y_{p\left(i\right)}\right)=0,$$

which is a contradiction with respect to (15), so $\left\{y_n\right\}$ is an $Rb$-Cauchy sequence in $\left(X,d\right)$. By the $Rb$-completeness of $\left(X,d\right)$, this implies that $\left\{y_n\right\}$ has a limit point $u\in X$ or, equivalently,

$$\underset{n\to \infty }{lim}d\left(y_n,u\right)=0.$$

Suppose that $u\ne f\left(u\right)$. Then, from Lemma 1, we obtain

$$\begin{array}{cc}\hfill \frac{1}{s}·d\left(u,f\left(u\right)\right)& \le \underset{n\to infty}{lim\; inf}d\left(y_n,f\left(y_n\right)\right)\le \underset{n\to \infty }{lim\; sup}d\left(y_n,f\left(y_n\right)\right)\hfill \\ & =\underset{n\to \infty }{lim\; sup}d\left(y_n,y_{n+1}\right)=0.\hfill \end{array}$$

(26)

So, the above holds unless $d\left(u,f\left(u\right)\right)=0$; that is, $u=f\left(u\right)$ and u is a fixed point of f. □

A contractive condition given by (10) is commonly known as a generalized almost contraction. This type of contractive condition ensures the existence of a fixed point of a map that need not be continuous, like in Kannan’s theorem. There exist several other examples of contractive conditions that are closely connected to the notion of almost contractiveness. Studies indicate that, if we consider a specific type of metric space endowed with a partial order, we can modify the requirements imposed on the implicit functions $\psi$ and $\phi$ that define the contractive condition.

As a direct consequence of Theorem 4, we can derive a fixed-point theorem for mappings that fulfill contractive conditions of integral type. This result holds in any complete rectangular b-metric space equipped with a partial order. In line with the terminology used in the paper by Branciari [37], we denote by $\mathbb{L}$ the set of all functions Ł $:[0,\infty )\to [0,\infty ]$ which satisfy the following properties:

(I-i.)

The map Ł is Lebesque-integrable, i.e., Ł is summable on each compact subset of $[0,\infty )$;

(I-ii.)

$Ł\left(x\right)\ge 0$ for all $x\in \left[0,\infty \right)$;

(I-iii.)

${\displaystyle \underset{0}{\overset{\epsilon }{\int }}Ł\left(s\right)ds>0}$ for each $\epsilon >0$.

We state and prove the following result.

Theorem 5.

Let $\left(X,d,⪯\right)$ be a partial ordered rectangular b-metric space with coefficient s, with $s\ge 1$ a given real number. Let $f:X\to X$ be an isotone mapping such that

(IT-i.)

There exists $x_0\in X$ such that $x_0⪯f\left(x_0\right)$;

(IT-ii.)

There exist $Ł\in \mathbb{L}$, $\psi \in \mathcal{S}$ and $\phi \in \mathcal{E}$ and $L\in \left(0,\infty \right)$ such that

$${\int }_0^{\psi \left(s^2·d\left(f\left(x\right)\right),f\left(y\right)\right)}Ł\left(s\right)ds\le {\int }_0^{\psi \left({\mathcal{M}}_{x,y}^f\right)}Ł\left(s\right)ds-{\int }_0^{\phi \left({\mathcal{M}}_{x,y}^f\right)}Ł\left(s\right)ds+L·m_{x,y}^f$$

(27)

for all $x,y\in X_{\le }$.

Then, f has a fixed point in X.

Proof. 

Consider the function $h:\left[0,\infty \right)\to \left[0,\infty \right)$ given by ${\displaystyle h\left(t\right)={\int }_0^tŁ\left(ds\right)ds}$ and define $\Psi =h\circ \psi$, $\Phi =h\circ \phi$. By properties of composition of functions, we have that $\Psi \in \mathcal{S}$ and $\Phi \in \mathcal{E}$. Since the equalities

$${\displaystyle \Psi \left(s^2·d\left(f\left(x\right)\right),f\left(y\right)\right)={\int }_0^{\psi \left(s^2·d\left(f\left(x\right)\right),f\left(y\right)\right)}Ł\left(s\right)ds,}$$

${\displaystyle \Psi \left({\mathcal{M}}_{x,y}^f\right)={\int }_0^{\psi \left({\mathcal{M}}_{x,y}^f\right)}Ł\left(s\right)ds}$ and ${\displaystyle \Phi \left({\mathcal{M}}_{x,y}^f\right)={\int }_0^{\psi \left({\mathcal{M}}_{x,y}^f\right)}Ł\left(s\right)ds}$ hold, (27) can be expressed as

$$\Psi \left(s^2·d\left(f\left(x\right)\right),f\left(y\right)\right)\le \Psi \left({\mathcal{M}}_{x,y}^f\right)-\Phi \left({\mathcal{M}}_{x,y}^f\right)+L·m_{x,y}^f.$$

(28)

Hence, we have the contractive condition given by (10). Therefore, by Theorem 4 we can conclude that f has a fixed point in X. □

As a final remark, we consider the integral equation

$$x\left(\tau \right)=h\left(\tau \right)+\underset{0}{\overset{1}{\int }}{\rm Y}\left(\tau ,t,x\left(t\right)\right)dt,\tau \in \left[0,1\right]$$

(29)

under the following assumptions

(F-i.)

There exists $y\in C\left(\left[0,1\right],\mathbb{R}\right)$ such that ${\displaystyle y\left(\tau \right)\le h\left(\tau \right)+\underset{0}{\overset{1}{\int }}{\rm Y}\left(\tau ,t,y\left(t\right)\right)dt}$, for any $\tau \in \left[0,1\right]$;

(F-ii.)

$h:\left[0,1\right]\to \mathbb{R}$ and ${\rm Y}:\left[0,1\right]\times \left[0,1\right]\times \mathbb{R}\to \mathbb{R}$ are continuous mappings;

(F-iii.)

The function ${\rm Y}\left(\tau ,t,·\right)$ maps real numbers to real numbers and is increasing for each $\tau ,t\in \left[0,1\right]$;

(F-iv.)

There exist $\phi \in \mathcal{E}$ and a continuous function $\varpi$ from $\left[0,1\right]\times \left[0,1\right]$ to $\left[0,\infty \right)$, with ${\displaystyle \underset{t\in \left[0,1\right]}{sup}\underset{0}{\overset{1}{\int }}\varpi \left(t,s\right)ds\le 1}$ such that

$$\left|{\rm Y}\left(\tau ,t,s_1\right)-{\rm Y}\left(\tau ,t,s_2\right)\right|\le \varpi \left(\tau ,t\right)·\phi \left(\left|s_1-s_2\right|\right),foreach\tau ,t\in \left[0,1\right]$$

and $s_1,s_2\in \mathbb{R}$, with $s_1\le s_2$.

It can be shown through a relatively uncomplicated exercise that Equation (29) has a solution in $C\left(\left[0,1\right],\mathbb{R}\right)$.

4. Conclusions

In this article, we establish a fixed-point theorem in the setting of complete rectangular b-metric spaces endowed with a partial order. We note that several consequences can be obtained from the main result. As another remark, note that the partial order implies a relaxation of contractiveness. As a continuation of this work we indicate the extension of these results to the case of nonself mappings.