Abstract
Stress is the body’s response to something that requires action or attention. In general, anything that poses a real challenge or threat to a person’s well-being can cause stress. Stress can slow down a person’s well-being activities. Often, you might not know whether you are stressed, if you are under too much stress, or when it is time to seek help. This paper presents a mathematical model with time delay subject to a person’s stress for early stress detection to assess whether a person is stress-free, has stress but is undetected, or has stress in any specific state such as minor, moderate, or severe stress. Being more alert to the effects of stress and reducing the uncertainty of undetected stress, or better, preventing it, may help people, especially teens, manage it more effectively and cope better, even a person happens to be stressed. The model can be extended to study the effects of multiple stress factors in light of the prolonged COVID-19 pandemic on people’s mental stress.
1. Introduction
Stress is a natural feeling of not being able to cope with specific activities, and it can become harmful or a chronic condition if a person does not know how to handle it in certain situations. Such situations can be from work, relationships, and peers. It is difficult to live stress-free in our busy daily lives. Stress levels are higher than pre-pandemic levels according to the American Psychological Association (APA) [1]. According to the APA, the average reported level of stress during the pandemic in 2021 among all adults was 5.0, which was slightly higher than the pre-pandemic level in 2019, which was 4.9, and in 2017, which was 4.8.
The outbreak of COVID-19 rapidly spread to more than 220 countries around the world, including the United States [2]. As of 15 November 2022, there have been more than 98 million confirmed COVID-19 cases and more than 1 million reported deaths in the U.S. [3]. Worldwide, there have been over 635 million confirmed cases and more than 6.6 million reported deaths [3]. The COVID-19 pandemic has changed our daily lives, in which almost everyone depends on the internet. American users spent, on average, 65 min on social media daily in 2020 compared to 56 min in 2019 [4], and global internet users spent 2 h and 29 min on social media daily [5]. With our regular to-do list each day including the use of social media and networks such as emails, Facebook, etc., coping with stress in healthy ways can seem impossible to achieve. However, how do you know when you are under too much stress, and how much stress is too much?
Stress is considered to be something that causes distress and can cause mental health problems. If you experience lots of stress, for example, it might cause you to develop a mental health problem such as depression. However, not all stress is bad because, on some occasions, increased stress (i.e., healthy stress) results in increased productivity and even can help you survive in a dangerous situation. For example, the stress of having a project deadline for your job may push you to finish your project on time. Once you complete it, the stress may go away.
Many of us are often facing challenges related to work, school, financial burdens, or relationships, which can be stressful. Learning to cope with stress early on will help you and the people around you become more resilient. Stress can cause [6]:
- Anger, worry, frustration, and difficulty making decisions;
- Sleeping problems, headaches, chronic health problems, and mental health conditions.
The COVID-19 pandemic has significantly changed and affected our daily lives. It had a severe impact on the mental stress and health of people. According to The American Institute of Stress [7], about 33% of American people report feeling extreme stress; 77% of people experience stress that affects their physical health; 73% of people have stress that impacts their mental health; and 48% of people have trouble sleeping because of stress. Based on the APA [1], more than 60% of people had gained or lost an undesired amount of weight, at least 65% were not getting their desired amount of sleep, and about 48% said the level of stress in their life had increased compared with before the COVID-19 pandemic. The Global Organization for Stress [8] reported that stress is the number one health concern of high school students. A study conducted from January to June 2021 observed that 37% of U.S. high school students reported regular mental health struggles during the COVID-19 pandemic [9].
The Harris Poll conducted a survey in 2021 which showed that 32% of adults are sometimes stressed about the coronavirus pandemic, and 63% agreed that the uncertainty of the next few months likely causes them stress [10]. The pandemic also causes stress among different groups of people. For example, Hispanic adults were more likely than non-Hispanic White adults to say decision making has become more stressful compared with before the pandemic (day-to-day decisions: 44% vs. 34%; major decisions: 40% vs. 32%).
After School [11] polled high school students in the U.S. in 2018, and more than 35,500 students participated in the survey on the topic of stress and mental health. The results showed that: (i) about 45% of teens are stressed “all the time” and 37% of teens are “sometimes” stressed, but only 6.3% of teens are “never” stressed, and 27.22% of teens stated that relationships were the most likely cause of stress. The top five states in which teens say they are stressed “all the time” are New Mexico (57.8%), Rhode Island (56.8%), West Virginia (54.3%), Virginia (51.2%), and Kentucky (50.5%) based on the After School data. On the other hand, the top five states in which teens are “never” stressed include Hawaii (14.3%), Maryland (12%), the District of Columbia (10%), South Carolina (9.4%), and Florida (9.3%). The results also showed that more than 82% teens in Chicago and Houston Cityare stressed “sometimes” or “all the time”, whereas about 80% teens in Dallas (Texas) and New York (NY) are stressed “sometimes” or “all the time”.
Schokkenbroek et al. [12] conducted an online survey among 2889 respondents between 3 and 17 April 2020. Their findings showed that people experienced more stress during the COVID-19 pandemic lockdown than before the pandemic. According to the National Institute of Mental Health [13], 1 in 5 U.S. adults live with a moderate to severe mental health condition, and 1 in 20 U.S. adults experience serious mental illness each year [14]. The WHO [15] reported that there has been a sharp rise in the number of people experiencing mental health problems in recent years. The global prevalence of anxiety and depression increased by a massive 25% during the first year of the COVID-19 pandemic [15].
The pandemic may cause stress for many people as they deal with uncertainty and disruptions to their daily lives. Coronavirus has upended life in so many ways. Coping with COVID restrictions is only part of the disruption. Many of our everyday decisions can affect our health and safety. Quach et al. [16] conducted a study focusing on the Asian American community’s experiences during the COVID-19 pandemic in the San Francisco Bay area, California, between 20 May and 23 June 2020. They found that among 1297 Asian American respondents, about 67% and 22.6% reported feeling stressed and depressed, respectively. Daimer et al. [17] showed a strong impact of the COVID-19 pandemic and that related concerns and social adversity affected anxiety and depression based on an online survey in Germany and the United Kingdom over 1 year during the COVID-19 pandemic. Wani et al. [18] presented an approach for early depression detection using advanced natural language processing and deep learning techniques in designing an efficient system to detect major depressive symptoms at an early stage.
The COVID-19 pandemic has affected almost everyone. Schuller et al. [19] recently discussed the impacts on mental health due to the COVID-19 pandemic. In general, the effects of the COVID-19 pandemic were unanimously negative regarding stress, coping, and mental outcomes [15]. Loneliness, fear of infection, the suffering and death of loved ones, and financial worries have been cited as stressors leading to anxiety, stress, and depression [15]. In this paper, we present mathematical modeling of multi-stage early stress detection considering time-dependent delays using partial differential equations to determine whether a person is stress free or whether stress can be detected in its early stages. The model can also be used to study the effects of multiple stress factors—in light of the prolonged COVID-19 pandemic—on mental stress.
2. Relationship between Stress and Immune System
Stress is not normally considered a mental health problem. A stressor may be a one-time or short-term occurrence. If it happens repeatedly or lasts for days, weeks, or longer, this is called chronic stress or long-term stress (i.e., illness or losing your job). However, chronic stress can cause mental health problems and reduce the number of natural killer cells or lymphocytes in the body, which are needed to fight viruses [1].
How does stress get inside the body to affect the immune response?
Stress is how our brains and bodies respond to an external cause, such as having a lot of work or having an illness. Our body is well-equipped to handle stress in small doses, but when it becomes long-term, it can have serious effects on the body. Stress affects all systems of the body, including the cardiovascular and nervous systems. For example, heart and blood vessels comprise the two elements of the cardiovascular system that work together to provide oxygen to organs in the body. The activity of these two elements is coordinated in the body’s response to stress. Blood vessels direct blood to large muscles, therefore increasing the amount of blood pumped to these parts of the body and elevating blood pressure [1].
There are many factors that can contribute to stress. However, whatever the cause, stress creates a hormone in your body called cortisol [20]. When we are stressed out, our body is responding to stress, and it can raise our blood pressure, heart rate, and blood sugar levels, which is also called a “fight or flight” response. When the stressor goes away, our heart rate returns to normal, and our muscles relax. Cortisol can suppress our immune system’s effectiveness in fighting off invaders by lowering the number of lymphocytes present in the blood and interfering with normal white blood cell communication.
The immune system is a complex interconnected network consisting of many parts including organs, tissues, cells, molecules, and proteins that work together to protect the body from illness when germs enter the body. A body’s well-functioning immune system can prevent germs from entering the body and destroy any infectious microorganisms that do invade the body [21,22,23]. As long as by developing antibodies to attack it and protect us our immune system is working smoothly, we often do not pay much attention to or even know about it. However, if it stops working properly because it is weak or cannot fight particular germs or diseases, then we get sick. Germs that our body has never encountered before are likely to make us sick [24]. Some germs will only make you ill the first time you come into contact with them. When the body senses danger from a virus or infection, the immune system will respond from such specific virus and germs. The main tasks of the body’s immune system are to attack and destroy substances that are foreign to our body, such as bacteria and viruses, or limit the extent of their harm if they get in [25]. However, when our immune system is not working properly, the body attacks healthy cells in which there is no invader or does not stop an attack after an invader has been killed, resulting in autoimmune disease [26,27].
Developing mathematical models to predict the growth of virus-infected cells and immune cells has been of interest in the area of epidemiology research [28,29] and infectious disease epidemiology [30] in the past few decades. Many models [28,31] have been proposed, using partial differential equations in the past several decades and delay partial differential equations in recent years, to characterize tumor-immune dynamic growth, but various open research problems remain regarding modeling due to the complexity of virus infection and tumor cancer growth in the body’s immune systems [32]. There are many aspects yet to consider when factoring mental stress into the mathematical modeling of the immune system. Many researchers have developed models that related to COVID-19 disease analysis [2,30,33,34,35,36,37], yet they have not considered the uncertainty of the mental stress related to the COVID-19 pandemic.
Stress. Stress is the body’s natural defense against predators and danger. It causes the body to flood with hormones which prepare its systems to evade or confront danger. A life stressor is any event or experience that causes stress. Some stressors can be minor and relatively easy to manage, such as a lot of work to finish up quickly or a small disagreement with a good friend. Other stressors can be harder or more severe to handle, such as a disagreement with a loved one or severe illness such as COVID-19 infection. Some common stressors in life are [38]:
Death of a spouse;Divorce;The death of a close family member;Personal injury or illness;A difficult marriage;Being fired, laid off, or unemployed;Employer reorganization or downsizing;A change in residence;Changing work responsibilities;Retirement depression;Becoming a single parent;The Death of a close friend;Sexual harassment at work;Foreclosure on a loan or mortgage;Domestic violence or sexual abuse;Being disciplined at school or at work;Having a child with a behavior problem;Getting married or remarried;Infidelity;Experiencing or being involved in a car accident.
When humans face a challenge or threat, they have a partly physical response. The body activates resources that help people stay and confront the challenge as fast as possible. The body produces larger quantities of the chemical cortisol and can the physical reactions, for example, increased blood pressure, heightened muscle preparedness, sweating, and alertness.
These factors all improve a person’s ability to respond to a potentially challenging situation. Environmental factors that trigger this reaction are called stressors. Examples include noises, aggressive behavior, nervous moments during an interview, etc. Feelings of stress tend to increase in tandem with the number of stressors.
The relationship between stress and the immune system. Selye [39] discussed a model that shows how stress and immunity are related. Many researchers [40,41,42] studied a closer relationship between stress and immune function and showed the immunological changes associated with stress in response to infection. Futterman et al. [43] studied the immune system effects of emotional valence such as unhappiness vs. happiness, and Cohen et al. [44] focused on the immune system closely linked to emotional arousal (e.g., stimulation).
To our knowledge, this is the first study to develop a mathematical model for the multi-stage detection of stress which can be used to determine whether a person is stress-free using time-dependent delay differential equations. We discuss the model formulation in the next section.
3. Model Formulation
We first present some notations and model assumptions consisting of seven states that represent the stress levels of an individual, where
S1: Stress-free state (i.e., meaning a person has no stress);
S2: Undetected stress state: A person is stressed, but it is not detected
S3: Detected stress state: A person is stressed, and it is detected
S4: Detected minor stress state: Minor stress is detected in a person
S5: Detected moderate stress state: Moderate stress is detected in a person;
S6: Detected severe stress state: Severe stress is detected in a person;
S7: Death state due to stress;
P1(t): Probability that a person is stress-free at time t (i.e., P1(t) = P(S1(t));
P2(t): Probability that a person is stressed but it is not detected at time t;
P3(t): Probability that a person is stressed and it is detected at time t;
P4(t): Probability that minor stress is detected in a person at time t;
P5(t): Probability that moderate stress is detected in a person at time t;
P6(t): Probability that severe stress is detected in a person at time t;
P7(t): Probability that a person is dead due to stress at time t.
3.1. Notation
The following notations are used in the model formulation:
a: Undetected stress rate from stress-free state (normal, healthy state);
b: Rate of detected stress from the undetected stress state;
c: Death rate from the detected stress;
d1: Proportion of detected stress that is minor stress;
d2: Proportion of detected stress that is moderate stress;
d3: Proportion of severe stress that leads to death;
d4: Proportion of severe stress that recovers and goes back to the undetected stress state;
e: Rate of stress-free recovery from detected minor stress;
f: The detected stress rate;
g: Severe stress rate;
h: Moderate stress rate;
k: Constant healthy growth factor;
m: Constant coefficient of growth related to normal (healthy) state;
q: Proportion of normal recovery from detected moderate stress state;
u1: Rate of normal recovery from undetected stress state;
u2: Rate of detected moderate stress from undetected stress state;
v: Growth rate of related healthy (both external and internal) environments;
w: Undetected stress death rate;
z: Rate of detected severe stress from detected moderate stress state;
τ1, τ2,τ3,τ4: The time delays (i.e., τ1 is the period of time needed before detecting the stress).
3.2. Model Assumptions
The assumptions of the proposed stress model are as follows:
- All the coefficients in the model are positive constants.
- A stress-free growth rate m(t) (see Figure 1) is a time-dependent function with a constant coefficient k. In this study, we consider
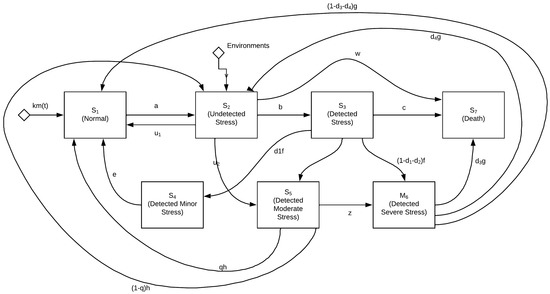 Figure 1. The proposed mental stress time delay model configuration.
Figure 1. The proposed mental stress time delay model configuration. - Upon being stress-free, a person will go to the undetected stress state at a rate a.
- In the undetected stress state, the stress is detected at the rate b. Likewise, a person is dead with a death rate c after detecting stress.
- Upon detecting stress, the proportions of detected stress with minor, moderate, or severe stress are d1, d2, and (1− d1 − d2), respectively.
- A person recovers as being stress-free or having undetected stress from the detected severe stress at the rate (1 − d3 − d4) and d4, respectively, and dies at the rate d3.
- There is a period time delay τ1 for a person who is stressed but between the undetected and detected stress.
- There is a period time delay τ2 between severe stress being detected in a person and the person becoming stress-free after recovery.
- There is a period time delay τ3 between stress not being detected in a person and the person becoming stress-free after recovery.
- There is the time delay τ4 required for a person to become severely stress from the moderate stress stage.
We can formulate a generalized stress model consisting of seven time-dependent probability functions: P1(t), P2(t),…, P7(t) based on the assumptions above and Figure 1 as follows:
Figure 1 demonstrates the proposed mathematical presentation of the above equations. We develop an algorithm using R software, version 4.0.3 to numerically obtain the results of Pi(t), for i = 1, 2,…, 7.
In this analysis, we calculate the probability that a person who has a stress at time t, which is defined as
Similarly, the probability that a person has no stress or has stress but has survived at time t is defined as
Entropy is a quantitative measure of randomness [45]. It is used to help model and represent the degree of uncertainty of a random variable. Here, we use entropy to explain the uncertainty of each state of the entire system.
After obtaining the probability of each state Pi(t), we compute the entropy value, H(X), which measures the randomness state of the system. A large entropy value indicates a higher level of uncertainty of the distribution function, meaning it is difficult to predict the state of the system. In other words, a large entropy value indicates it is harder to draw any conclusions from that information (i.e., the state of the system), meaning low information gain, whereas a low entropy value means high information gain, where the information gain can be thought of as the purity in the system and the amount of clean knowledge available in a system. Flipping a coin is an example of an action that provides information that is random. For discrete random variable X with values X1, X2,…, Xk and probabilities P(X1), P(X2)…, P(Xk), respectively, the entropy function H(X) is calculated as follows:
4. Numerical Results
In this section, we present the numerical results of the model using Equations (1)–(7). Obtaining the data to estimate all 19 parameter values in the model was a challenging task. This paper aims to present the first study of a new model with time delay subject to a person’s stress for early stress detection using time-delay partial differential equations to assess whether a person is stress-free, has undetected stress, or has detected stress. Our future work will be focused on estimating model parameter values based on empirical data from the literature including high school students’ data from After School [11]. For this reason, in this paper, we assume that the model parameter values are given as shown in Table 1 for the purpose of the illustration of the proposed modeling results. Researchers can apply the proposed model to obtain the results for their specific application’s set of parameter values.

Table 1.
Model parameter values.
In this analysis, we assume the initial conditions (i.e., time t = 0) are that a person is stress-free with the probability of 0.9 or is stressed but undetected with the probability of 0.1. That is,
P1(0) = 0.9; P2(0) = 0.1; P3(0) = P4(0) = P5(0) = P6(0) = P7(0) = 0.0.
It is worth noting that the results do not necessarily depend on the assumptions of these initial numbers; analysts can provide any numbers as initial values for the purpose of numerically solving a system of differential equations. We now present various cases with some parameter values of the related healthy growth rate, such as k and v, as well as the undetected stress death rate w, where the first, second, third and fourth time delays are 1, 5, 10, and 7 time units, respectively. Results can be obtained for various parameter values and delay times.
Case 1:k = 0.005, v = 0.001, and w = 0.0007
From Table 2 and Figure 2, we observe that in state S2 (i.e., undetected stress state) and state S3 (i.e., detected stress state), the probabilities that a person has undetected stress and detected stress both increase significantly at the beginning but start to decrease until it slowly stabilizes around the 50th time unit and 125th time unit, respectively. Similarly, in state S6 (i.e., severe stress state), the probability that a person is in severe stress increases slowly at the beginning and then continues to increase until it slowly stabilizes around the 185th time unit. We also observe that the probability that a person is stress-free (S1) decreases significantly at the beginning and then continues to decrease until it slowly stabilizes around the 115th time unit as time progresses.

Table 2.
The probability results of each state for Case 1 (k = 0.005, v = 0.001, w = 0.0007).
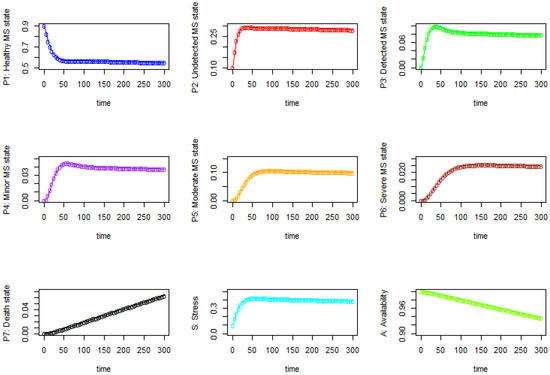
Figure 2.
The probability results of each state for Case 1, where the initial probabilities are P1(0) = 0.9, P2(0) = 0.1.
The probability that a person is stressed, either undetected or detected, (state S) significantly increases at the beginning and then continues to increase until around the 40th unit time. The probability of a person dying from stress follows an increasing function and is about 6.30% at time 300. The results from Table 3 and Figure 3 show that there are strong positive correlations between state S4 and S5 with 0.94, S2 and S3 with 0.96, and S5 and S6 with 0.94. Similarly, there are strong negative correlations between S1 and S2 with −0.91, S1 and S4 with −0.94, and S1 and S5 with −0.92. Figure 4 shows the results of each state, where the initial value P1(0) = 1.

Table 3.
The correlation results of the system state for Case 1 (k = 0.005, v = 0.001, w = 0.0007).
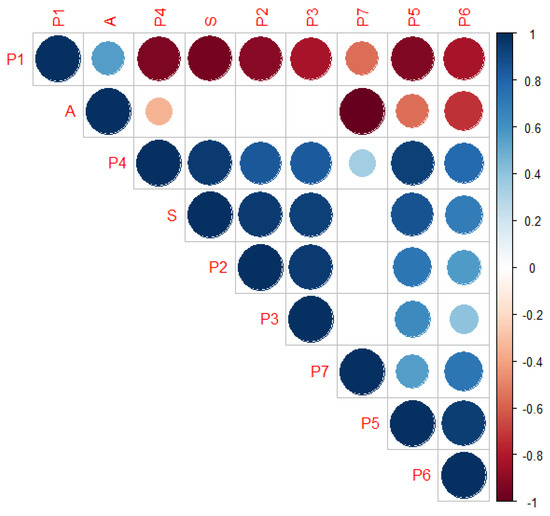
Figure 3.
The probability results of each state for Case 1: k = 0.005, v = 0.001, and w = 0.0007.
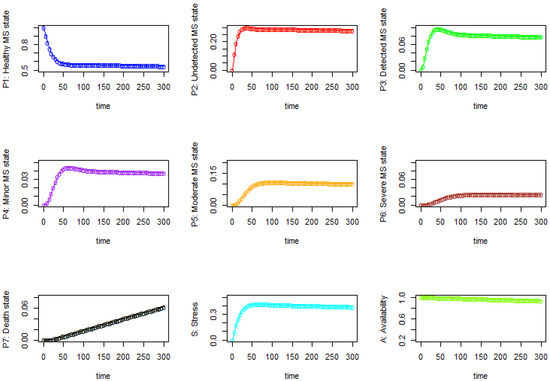
Figure 4.
The probability results of each state where the initial probability is P1(0) = 1.
Case 2:k = 0.01, v = 0.002, and w = 0.00035
From Figure 5, we observe that in state S2 (i.e., the undetected stress state) and state S6 (the severe stress state), the probabilities that a person is stressed but it is undetected or is in severe stress increase significantly at the beginning and continue to increase until they slowly stabilize around the 100th and 150th time unit, respectively. We also observe that the probability that a person is stress-free (S1) decreases significantly at the beginning and then continues to decrease until it slowly stabilizes around the 125th time unit as time progresses. The probability that a person is stressed, either undetected or detected (state S), significantly increases at the beginning until around the 35th time unit and then starts to decrease until it slowly stabilizes at around the 250th time unit.
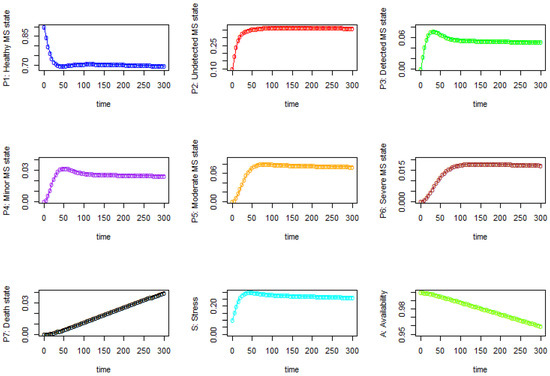
Figure 5.
The probability results of each state for Case 2: k = 0.01, v = 0.002, and w = 0.00035.
The results from Table 4 also show that there are strong positive correlations between state S2 and S4 with 0.89 and S2 and S5 with 0.91. In the contrast, there are strong negative correlations between S1 and S2 with −0.98, S1 and S4 with −0.92, and S1 and S5 with −0.87.

Table 4.
The correlation results of the system state for Case 2 (k = 0.01, v = 0.002, w = 0.00035).
Case 3: The same as Case 2, but there is no time delay (i.e., τ1 = τ2 = τ3 = τ4 = 0).
From Figure 6, we observe that in state S2 (i.e., the undetected stress state) and state S6 (the severe stress state), the probabilities that a person is stressed but undetected or is in severe stress increase significantly at the beginning and continue to increase until they slowly stabilize around the 55th and 125th time unit, respectively. We also observe that the probability that a person is stress-free (S1) decreases significantly at the beginning and then continues to decrease until it slowly stabilizes around the 75th time unit as time progresses. The probability that a person is stressed, either undetected or detected (state S), significantly increases at the beginning until around the 45th time unit and then starts to decrease until it slowly stabilizes at around the 275th time unit.
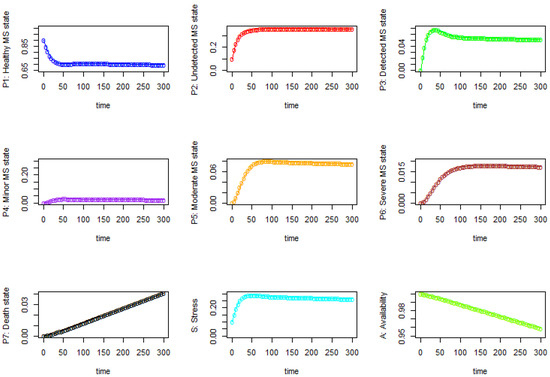
Figure 6.
The probability results of each state for Case 3 (i.e., τ1 = τ2 = τ3 = τ4 = 0).
The results from Table 5 show that there are strong positive correlations between state S2 and S4 with 0.92, S2 and S5 with 0.93, and S5 and S6 with 0.94. In the contrast, there are strong negative correlations between S1 and S2 with −0.99, S1 and S4 with −0.93, and S1 and S5 with −0.91.

Table 5.
The correlation results of the system state for Case 3.
Entropy Computation
We now compute the entropy values using Equation (10). Table 6 presents the entropy calculation results for all three cases as discussed above. In this example, shows that an undetected stress state (S2) is considered riskier than other states based on the entropy values as given in Table 6, since it indicates a high level of uncertainty of the distribution function, and it is difficult to predict the state of the system. On the other hand, a severe stress state (S6) has a small entropy value, meaning a large amount of information is gained about the state of the system, which implies a lower level of uncertainty.

Table 6.
Entropy results of the system for all three cases.
5. Conclusions
Stress is very subjective, and therefore, diagnosing stress can be challenging, because it depends on many uncertain factors. So, bringing more awareness to the effects of stress and developing coping strategies before stress—if it can be detected—becomes chronic or severe can help an individual manage it more effectively and maintain their physical health. This paper presented a mathematical time-delay model to determine whether a person is stress free, has undetected stress, or has detected stress in various states, including minor, moderate and severe. Further research in the future can be extended to incorporate the factors caused by theCOVID-19 pandemic and implement the model with real data sets to study the effects of specific stress factors using model selection strategies [46] due to the prolonged COVID-19 pandemic.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- APA. American Psychological Association. 2021. Available online: https://www.apa.org/ (accessed on 12 August 2022).
- Pham, H. On estimating the number of deaths related to COVID-19. Mathematics 2000, 8, 655. [Google Scholar] [CrossRef]
- John Hopkins Coronavirus Data Center. Available online: https://coronavirus.jhu.edu/ (accessed on 15 November 2022).
- Statista. 2022. Available online: https://www.statista.com/statistics/1018324/us-users-daily-social-media-minutes/ (accessed on 10 October 2022).
- Datareportal, Digital 2022: Global Overview Report. 2022. Available online: https://datareportal.com/reports/ (accessed on 5 November 2022).
- Centers for Disease Control and Prevention (CDC). 2022. Available online: https://www.cdc.gov/niosh/topics/stress/ (accessed on 5 November 2022).
- AIS: The American Institute of Stress. Available online: https://www.stress.org/daily-life (accessed on 5 November 2022).
- GOS: Global Organization for Stress. Available online: http://www.gostress.com/stress-facts/ (accessed on 10 November 2022).
- Centers for Disease Control and Prevention (CDC,b). 2022. Available online: https://www.cdc.gov/mentalhealth/stress-coping/cope-with-stress/index.html (accessed on 5 November 2022).
- Harris Poll, APA. 2021. Available online: https://www.apa.org/news/press/releases/stress/2021/ (accessed on 8 November 2022).
- After School. Available online: https://data.world (accessed on 10 September 2022).
- Schokkenbroek, J.M.; Hardyns, W.; Anrijs, S.; Ponnet, K. Partners in lockdown: Relationship stress in men and women during the COVID-19 pandemic. Couple Fam. Psychol. Res. Pract. 2021, 10, 149–157. [Google Scholar] [CrossRef]
- NIMH. National Institute of Mental Health (NIMH). Available online: https://www.nimh.nih.gov/ (accessed on 10 October 2022).
- NAMI. National Alliance Mental Illness (NAMI). Available online: https://www.nami.org/mhstats (accessed on 10 October 2022).
- WHO. The World Health Organization (WHO). Available online: https://who.int (accessed on 5 October 2022).
- Quach, T.; Ðoàn, L.N.; Liou, J.; Ponce, N.A. A rapid assessment of the impact of COVID-19 on asianamericans: Cross-sectional survey study. JMIR Public Health Surveill. 2021, 7, e23976. [Google Scholar] [CrossRef]
- Daimer, S.; Mihatsch, I.M.; Neufeld, S.; Murray, G.K.; Knolle, F. Investigating the relationship of COVID-19 related stress and media consumption with schizotypy, depression, and anxiety in cross-sectional surveys repeated throughout the pandemic in Germany and the UK. eLife 2022, 11, e75893. [Google Scholar] [CrossRef]
- Wani, M.A.; Elaffendi, M.A.; Shakil, K.A.; Imran, A.S.; El-Latif, A.A.A. Depression screening in Humans with AI and deep learning techniques. IEEE Trans. Comput. Soc. Syst. 2022, PP, 1. [Google Scholar] [CrossRef]
- Schuller, B.W.; Lochner, J.; Qian, K.; Hu, B. COVID-19′s impact on mental health—The hour of computational aid? IEEE Trans. Comput. Soc. Syst. 2022, 9, 967–973. [Google Scholar] [CrossRef]
- Medical News Today (Medical). Available online: https://www.medicalnewstoday.com/articles/145855 (accessed on 5 November 2022).
- Thompson, A.E. The immune system. J. Am. Med. Assoc. 2015, 313, 1686. [Google Scholar] [CrossRef] [PubMed]
- CRI Staff. How Does the Immune System Work? 30 April 2019. Available online: https://www.cancerresearch.org/blog/april-2019/how-does-the-immune-system-work-cancer?gclid=CjwKCAjwsNiIBhBdEiwAJK4khgG7w-9Ugv3HMGc1VWZbRuhFBOfIPMW2Qo3Dv1-VH1HGvmJruZjwxxoC3HYQAvD_BwE (accessed on 2 October 2022).
- Guide to Your Immune System. 2020. Available online: https://www.webmd.com/cold-and-flu/ss/slideshow-immune-system (accessed on 2 October 2022).
- Immune System, Cleveland Clinic. 2021. Available online: https://my.clevelandclinic.org/health/articles/21196-immune-system (accessed on 12 June 2022).
- Newman, T. How the immune system works. Med. News Today 2018. Available online: https://www.medicalnewstoday.com/articles/320101 (accessed on 5 June 2022).
- Pham, H. A dynamic model of multiple time-delay interactions between the virus cells and body’s immune system with autoimmune diseases. Axioms 2021, 10, 216. [Google Scholar] [CrossRef]
- Pham, H. Mathematical modeling the time-delay interactions between tumor viruses and the immune system with the effects of chemotherapy and autoimmune diseases. Mathematics 2022, 10, 756. [Google Scholar] [CrossRef]
- Vaghi, C.; Rodallec, A.; Fanciullino, R.; Ciccolini, J.; Mochel, J.P.; Mastri, M. Population Modeling of Tumor Growth Curves and the Reduced Gompertz Model Improve Prediction of the Age of Experimental Tumors. PLoS Comput. Biol. 2020. Available online: https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1007178 (accessed on 2 May 2022). [CrossRef] [PubMed]
- Ng, J.; Stovezky, Y.R.; Brenner, D.J.; Formenti, S.C.; Shuryak, I. Development of a model to estimate the association between delay in cancer treatment and local tumor control and risk of metastates. JAMA Netw. Open 2021, 4, e2034065. [Google Scholar] [CrossRef]
- Rothan, H.A.; Byrareddy, S.N. The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. J. Autoimmun. 2020, 109, 102433. [Google Scholar] [CrossRef]
- Meacham, C.E.; Morrison, S.J. Tumour heterogeneity and cancer cell plasticity. Nature 2013, 501, 328–337. [Google Scholar] [CrossRef]
- Talkington, A.; Durrett, R. Estimating tumor growth rates in vivo. Bull. Math Biol. 2015, 77, 1934–1954. [Google Scholar] [CrossRef] [PubMed]
- Pham, H. Estimating the COVID-19 death toll by considering the time-dependent effects of various pandemic restrictions. Mathematics 2020, 8, 1628. [Google Scholar] [CrossRef]
- Battegay, M.; Kuehl, R.; Tschudin-Sutter, S.; Hirsch, H.H.; Widmer, A.F.; Neher, R.A. 2019-Novel Coronavirus (2019-nCoV):Estimating the case fatality rate–a word of caution. Swiss Med. Wkly. 2020, 150, w20203. [Google Scholar] [CrossRef]
- Chin, A.W.H.; Chu, J.T.S.; Perera, M.R.A.; Hui, K.P.Y.; Yen, H.L.; Chan, M.C.W.; Peiris, M.; Poon, L.L.M. Stability of SARS-CoV-2 in different environmental conditions. Lancet Mircobe 2020, 1, e10. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Centre for Mathematical Modelling of Infectious Diseases COVID-19 Working Group. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Pham, H.; Pham, D.H. A novel generalized logistic dependent model to predict the presence of breast cancer based on biomarkers. Concurr. Comput. Pract. Exp. 2020, 32, e5467. [Google Scholar] [CrossRef]
- PsychCentral. Available online: https://psychcentral.com/stress/top-10-life-stressors-that-can-trigger-anxiety (accessed on 10 July 2022).
- Selye, H. The Stress of Life; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Maier, S.F.; Watkins, L.R. Cytokines for psychologists: Implications of bidirectional immune-to-brain communication for understanding behavior, mood, and cognition. Psychol. Rev. 1998, 105, 83–107. [Google Scholar] [CrossRef] [PubMed]
- Maier, S.F.; Watkins, L.R.; Fleshner, M. Psychoneuroimmunology: The interface between behavior, brain, and immunity. Am. Psychol. 1994, 49, 1004–1017. [Google Scholar] [CrossRef] [PubMed]
- Maier, K.J.; Waldstein, S.R.; Synowski, S.J. Relation of cognitive appraisal to cardiovascular reactivity, affect, and task engagement. Ann. Behav. Med. 2003, 26, 32–41. [Google Scholar] [CrossRef]
- Futterman, A.D.; Kemeny, M.E.; Shapiro, D.; Fahey, J.L. Immunological and physiological changes associated with induced positive and negative mood. Psychosom. Med. 1994, 56, 499–511. [Google Scholar] [CrossRef]
- Cohen, S.; Hamrick, N.; Rodriguez, M.S.; Feldman, P.J.; Rabin, B.S.; Manuck, S.B. The stability of and intercorrelations among cardiovascular, immune, endocrine, and psychological reactivity. Ann. Behav. Med. 2000, 22, 171–197. [Google Scholar] [CrossRef]
- Athanasios, P. Probability, Random Variables, and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Pham, H. Statistical Reliability Engineering; Springer: London, UK, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).