Employing an Effective Robust Optimization Approach for Cooperative Covering Facility Location Problem under Demand Uncertainty

Abstract

The traditional covering problem has two assumptions: “all or nothing coverage” and “individual coverage”. There are settings where the two assumptions may be unrealistic. In this research, we relax the two assumptions and study the cooperative covering facility location problem with demand uncertainty. Previous research on the covering problem has not considered cooperative covering under uncertain demand, particularly our approach to effectiveness maximization and offering full control of the conservatism of the model. We propose a cooperative covering model to maximize effectiveness, including the quality per dollar as a criterion. Then, the demand at each node is assumed to be uncertain, and the robust counterparts of the deterministic model are presented by considering the different degrees of conservatism of the robust solution. More importantly, the non-linear programming is transformed into equivalent linear programming by introducing auxiliary variables and using duality theory. The numerical examples show that the optimal location of the facility is affected by the protection level and the decision maker can make a trade-off between conservatism and effectiveness in an uncertain environment. Moreover, when the protection level is large, the objective function value makes a smaller sacrifice to get high robustness. In addition, two ways to measure the price of robustness are defined. The facility location decision can be made by evaluating the relative decrease in effectiveness compared to the nominal demand model or by evaluating the relative increase in effectiveness compared to the complete protection model.

1. Introduction

The covering facility location problem is one of the traditional facility location models. It was first introduced by Church and ReVelle [1] and is widely applied to various fields. For example, in the location of emergency facilities, to ensure that the travel distance between the facility and the customer does not exceed a predetermined threshold is very important. Some other applications include the location of retail stores (retail stores will receive the patronage of a customer only when their distance is within the trading area) and signal-transmission facilities (sensors, light posts, warning sirens, etc.). The literature on covering problem is quite rich, for a detailed investigation of this topic, the reader is referred to Farahani et al. [2]. Linear programming is applied to deal with the covering facility location problem, which is the frequently used method of optimal approach. A significant number of other optimal approaches are also used to solve problems such as multi-agent task planning [3], road traffic anti-collision warning system [4], and the multi-criteria supplier selection problem [5].

With the advance of research in the covering model, it is realized that some of the underlying assumptions are inconsistent with real situations. The traditional covering model has two assumptions: (A1) “all or nothing coverage” and (A2) “individual coverage”. In other words, customers who are within a certain predefined “service standard” of a facility are considered adequately served, while those who are not within those limits are considered as not being served at all. The service standard of a facility is typically defined in terms of distance or time. The demand is covered by only one facility, namely the closest one. The second-closest facility has nothing to do with the coverage. It is not difficult to imagine settings where the two assumptions may be impractical. For example, consider setting up a supermarket in a city. The trading area of a supermarket is usually centered on the supermarket and within 1–2 miles of it [6]. Suppose the coverage radius of the supermarket is 1.5 miles. Under the assumption of the traditional covering model, customers within 1.5 miles of the supermarket are completely covered; otherwise, they are not covered. The reality is that customers that are 1.49 miles away from the supermarket may not visit the supermarket, and customers who are 1.51 miles away from the supermarket may visit the supermarket. Therefore, assumption (A1) does not accurately describe the actual situation. A more reasonable assumption is that the coverage or service level of supermarkets for customers gradually declines as the distance between the two increases. Similarly, the same situation exists in assumption (A2). Let us suppose, for example, a customer has two supermarkets 1.6 miles away, but none within 1.5 miles. Another one only has one supermarket 1.5 miles away. The former has worse coverage than the latter according to assumption (A2), because the former is not covered at all and the latter is fully covered. However, the reality is that all supermarkets within a certain distance away from the customer have impacts on the customer’s purchasing behavior. Thus, the former is not necessarily worse than the latter.

The cooperative covering model seeks to soften the “all or nothing” and “individual coverage” assumptions, and was introduced by Berman et al. [7] and further investigated by many researchers. The cooperative coverage objective could be viewed to result from the following mechanism: a facility emits a "signal" whose strength declines with distance according to some signal decay function. The total signal received by a customer is the sum of all signals emitted by all located facilities. The signal can either be physical (e.g., in the case of the location of warning sirens or cell phone towers) or non-physical. For example, in retailing applications the signal reflects the attraction of the facility (i.e., customer awareness), with the assumption that closer facilities are more likely to enter the customer’s consideration set when shopping decisions are made. To simplify the presentation, we apply the term signal in the analysis. In most facility location problems, the goal of the cooperative covering model is to maximize the number of customers covered by locating P facilities (maximum covering), or to minimize the locating cost under the condition that all the customers are covered by the opened facilities (set covering) [8]. It is worth noting that the number of customers covered and the locating cost are equally important for most decision makers. It is not appropriate to only consider the number of customers covered or the locating cost in this situation. As with the criterion applied in the literature by Eiselt and Marianov [9], we maximize the effectiveness, including the quality per dollar as a criterion. The quality of service received by a customer is the sum of all signals provided to him by all located facilities. In other words, effectiveness is measured in terms of the ratio between output and input. In this context, we here consider quality as an output and put it in relation to an input that is measured in terms of the cost of opening new facilities. The model in this study can more accurately describe the location problem of facilities that propagate light, sound, and signals. The proposed formulation considers the effectiveness, which better serves policymaker’s needs.

Moreover, there is a growing recognition that in many real-world location problems there is a large number of uncertainties, such as the uncertainty in demands, travel time from facilities to customers, and cost parameters [10]. The influence of uncertainty is an important aspect, which should be taken into consideration in the facility location decision. If we do not consider the influence of uncertain factors for simplifying the problem, we may get a sub-optimal solution. It will lead to lower operation efficiency, lower service level, and the waste of resources once parameters deviate from the predicted value in the actual operation. With the rapid development of uncertain decision theory, using uncertain theories and methods to solve the facility location problem has become a hot spot for scholars at home and abroad. According to the probability distribution information of parameters, uncertain facility location problems fall into two categories: stochastic optimization and robust optimization. For the stochastic optimization problem, the probability distributions of uncertain parameters are known and the goal is to solve for the minimum expected cost (maximum expected profit) or maximize the probability of satisfying a certain constraint. For the robust optimization problem, the probability distributions of uncertain parameters are unknown and most of them are expressed by discrete scenarios or specific uncertain sets. The objective function optimizes the worst-case performance (cost, profit, etc.) or regret value of the system. Stochastic optimization provides a good method for the facility location problem with uncertain parameters, but it also has some limitations. It is very difficult to determine representative scenarios and their probabilities. A relatively small number of scenarios are often chosen, which limits the scope of decision making. In this study, we take the robust optimization approach, i.e., the precise probability distributions of the uncertain parameters are unknown. A novel robust optimization approach, i.e., the budget-of-uncertainty robust approach, is employed to formulate the robust cooperative covering model. The proposed robust model can not only adjust the degree of conservatism by changing the protection level, but also can be reformulated as an equivalent linear programming, which is computationally tractable.

In this research, a robust cooperative covering model is presented, in which the objective is to maximize effectiveness. Additionally, the effectiveness takes the quality per dollar as a criterion. The model we proposed generalizes the traditional facility location models by maximizing the ratio between output and input, and taking uncertain parameters into consideration as well. Assuming the demands are uncertain and take values within a bounded and symmetric multi-dimensional box, the concept of the budget-of-uncertainty is applied to solve the problem. Compared with the existing similar research, the main contributions and novelty of this paper are highlighted as follows:

(1) The effectiveness of opening new facilities is taken into consideration in the cooperative covering model. The cooperative covering model is a more accurate representation of the facilities that emit physical signals and non-physical signals as well. The measure of the quality received compared to locating cost is used, which is more in line with the need of policymaker.

(2) The demand at each node is assumed to be uncertain, which better describes the decision environment. The uncertain demand is assumed to be within a bounded and symmetric multi-dimensional box, and the precise probability distribution is unknown. The budget-of-uncertainty robust approach is employed to deal with the problem, which can completely control the conservatism of the model and adjust the effect on the objective function.

(3) The proposed non-linear model can be reformulated as a linear programming model equivalently by introducing auxiliary variables and using means of strong duality theory. The resulting linear programming is computationally tractable and easy to be applied to solve real-world problems.

(4) We provide insights into the different optimal locations corresponding to different protection levels. The trade-off between the degree of the conservatism of the robust solution and the effectiveness is investigated. A sensitivity analysis is conducted as well.

The remainder of this paper is structured as follows. Section 2 reviews the literature related to the facility location problem and robust optimization approaches. In Section 3, the nominal problem and the robust problem formulation are presented, analyzed, and reformulated. In Section 4, we compare the different optimal solutions under different conservatisms and analyze the impact of the protection level on the effectiveness. Finally, Section 5 contains some concluding remarks and several future research directions.

2. Literature Foundations

In this section, we briefly review some of the relevant studies in two streams of research that are related to our problems: the covering facility location problem and robust facility location problem. The facility location problem is an important strategic decision and is used to deal with various practical problems, including the location of manufacturing industries [11], vehicle inspection [12], electric vehicle charging stations [13], wireless sensor networks [14], healthcare facilities [15], public schools [16], and so on. For a detailed investigation into models, solution algorithms, and applications of facility location modeling, the reader is referred to Farahani et al. [17], Daskin [18], and Laporte et al. [19].

The problem of the covering location model is an important branch of the facility location problem, which was introduced by Church and ReVelle [1]. The classical covering location model can be broadly separated into two categories: the set covering model and the maximal covering location model. The aim of the former is to minimize the facility location cost required to cover each customer at least once, while the latter is to maximize the number of demands covered with a given number of facilities located. Both of the models can be applied to a wide variety of settings. Kolen and Tamir [20] and Farahani et al. [21] review covering models on discrete spaces, while Drezner [22] and Drezner [23] review the models on continuous space. Interested readers can also refer to Farahani et al. [2] for detailed discussions on models, solutions, and applications related to the covering problem.

A new development in covering location models is the cooperative covering model which soft the “all or nothing” and “individual coverage” assumptions, and first officially introduced by Berman et al. [7]. The new covering constructs are then further investigated by many researchers. Berman et al. [24] analyze the cooperative covering model on the network. The goal is to find the best location on the network to maximize the coverage. In addition, an optimal algorithm is proposed for the location of one and two facilities. While, for more than two facilities, the heuristic algorithm is proposed. Karatas and Dasci [25] propose a two-level facility location and sizing problem to determine the location of base stations and mobile switching centers. A more realistic covering concept, i.e., cooperative covering, is adopted in the setting. Karatas [26] presents a multi-objective facility location problem in the presence of cooperative covering. A combined solution procedure is provided to solve the problem. Morohosi and Furuta [27] use the cooperative covering location concept to deploy the location of an ambulance. Li et al. [28] develop a cooperative maximal covering model to maximize appeal coverage. Jayalakshmi and Singh [29] present a cooperative maximum covering location model, and a hybrid artificial bee colony algorithm is devised to solve the problem. Drezner and Drezner [30] analyze the maximum area covered by the cooperative cover model, and the steps are proposed. Bagherinejad et al. [31] generalize the maximal covering location by taking cooperative and gradual covering concepts into consideration simultaneously. Berman et al. [32] elaborate on new problems in the covering location model, including the gradual cover problem, cooperative cover problem, and variable radius problem. Drezner et al. [33] apply the cooperative covering model to locate cell phone towers in Orange County, California. The case study shows that, compared with the existing procedures, cooperative covering offers better total coverage.

There is a growing recognition that a large number of uncertainties affect real-world facility location problems, and a considerable body of the literature attempts to solve the problem with uncertain parameters. One of the prominent approaches to dealing with parameter uncertainty is robust optimization. Compared with stochastic optimization, robust optimization neither needs to know the precise probability distributions of the random parameters nor tackle large amounts of discrete scenarios. In recent years, robust optimization has emerged as a preeminent methodology to deal with facility location problems with uncertainty. The robust optimization in this direction was originally studied by Soyster [34]. It assumes that the uncertain parameters take values in a convex set, and the objective is to optimize the worst case. This robust optimization approach remains the linear construction of the deterministic model, but may excessively affect the objective function. We refer to it as the complete protection robust model below. A major step in addressing a theory for robust optimization was made independently by Ben-Tal and Nemirovski [35], El-Ghaoui and Lebret [36], and El-Ghaoui et al. [37]. To overcome the problem of over conservatism, these researchers suppose the uncertain parameters are within a multi-dimensional ellipsoid, which changes the linear framework of the deterministic problem and results in solving conic quadratic problems. To deal with the above drawbacks, the budget-of-uncertainty robust approach is introduced by Bertsimas and Sim [38]. This robust optimization approach not only offers full control of the degree of conservatism by adjusting the protection level, but also can be reformulated as a linear programming model, which is particularly attractive for solving robust discrete optimization models. Baron et al. [39] apply the robust optimization approach to a multi-period fixed-charge facility location and production planning problem with demand uncertainty. Two uncertain sets, i.e., a bounded and symmetric multi-dimensional box and a multi-dimensional ellipsoid, are considered. Li et al. [40] assume the flow between each pair of nodes to be uncertain and correlated. The single and multiple allocation hub location problems are proposed. Solyali et al. [41] study robust inventory routing problem under demand uncertainty, and two robust mixed integer programming formulations for the problem are presented. Alem and Morabito [42] propose a robust production planning problem for furniture companies when production costs and product demands are uncertain, and the relations between the conservative budgets of uncertainty and global costs are deeply analyzed. Zhou et al. [43] present a multi-capacity hierarchical location-routing robust optimization problem under carbon trading policies, and the risk preferences of decision makers are measured by indeterminate levels. Gregory et al. [44] propose two models for portfolio selection by using the budget-of-uncertainty robust approach. The cost of robustness is analyzed and the properties of robust models with respect to portfolio composition are examined.

Many other standards are used to measure robustness. Kouvelis et al. [45] present that the relative regret values for all scenarios are no more than p, while p is an exogenous variable. Snyder and Daskin [46] refer to the measure as p-robustness, and solution that satisfies the p-robustness constraint is called a p-robust solution. The facility layout problem is considered by Kouvelis et al. [45], the aim of which is to construct a series p-robust solutions. Gutierrez and Kouvelis [47] use the concept of p-robust to an international procurement environment. The research studies how to select suppliers worldwide to avoid exchange rate and local price changes. Gutierrez et al. [48] propose the is-equal-to network design problem with p-solution restrictions, and Benders decomposition method is devised to solve the problem. Snyder and Daskin [46] combine the concept of minimizing expected cost and p-robust solution, and apply it to P-median problem and fixed cost facility location problem, respectively. Daskin et al. [49] and Owen [50] introduce the $\alpha$-reliable minimax model. The traditional model minimizes the maximal regret, even though the probability of the worst scenario happening is very small. Daskin et al. [49] present the $\alpha$-reliable minimax model, whose aim is to optimize the worst-case performance over an endogenously generated set of scenarios. The collective probability of occurrence of the endogenously selected set is no less than some given value $\alpha$, which is called the reliability level. In this way, the planner can be 100$\alpha$% sure that the regret will be no more than that found by the model. Daskin et al. [49] solve the problem using the standard branch and bound method. Owen [50] designed a genetic algorithm to solve this problem. Chen et al. [51] present a model called the $\alpha$-reliable mean-excess regret model. In contrast to the $\alpha$-reliable minimax model where the regret that defines the $\alpha$-quantile of all regrets is minimized, the $\alpha$-reliable mean-excess regret model minimizes the expectation of the regrets associated with the scenarios in the tail, which has a collective probability of 1 −$\alpha$.

The influence of uncertainty is also considered in the integrating location and routing problems. Schiffer and Walther [52] present a robust location-routing approach that considers simultaneous decisions on routing vehicles and locating charging stations for strategic network design of electric logistics fleets. Shang et al. [53] present a real-world case of a medical implant supply network integrating location-inventory routing and direct shipping. Mohammadi et al. [54] develop a model to integrate reliable location and routing decisions under fairness concerns. Tavana et al. [55] formulate a novel bi-objective mixed-integer linear programming model to solve the location-inventory routing problems in green supply chains with low-carbon emissions under uncertainty. Various objectives have been considered for the optimization problem. Bevrani et al. [56] develop a model that can integrate various transportation modes while maximizing the flow of multi-modal transportation systems. Szeto et al. [57] consider a sustainable road network design and land-use problem. The social, economic, and environmental impacts on commuters are considered using a multi-objective bi-level optimization model. Bevrani et al. [58] propose a multi-criteria multi-commodity network flow model to determine Pareto optimal solutions that simultaneously maximize the flow and minimize the cost for commuters and other commodities.

3. Problem Description and Formulation

3.1. Nominal Problem Formulation

In this section, we consider a cooperative covering model based on the effectiveness of locating when customers’ demands are deterministic. A firm seeks to locate some facilities at a set of candidate nodes. Each facility is assumed to emit a signal whose strength declines with distance according to some signal strength function. The total signal received by a customer is the sum of all signals provided to him by all located facilities, which is referred to as quality of service. The objective is to maximize the effectiveness, which includes the quality per dollar as a criterion. The quality of service received by a customer is the sum of all signals provided to him by all located facilities. In other words, effectiveness is measured in terms of the ratio between output and input. In this context, we here consider quality as an output and put it in relation to an input that is measured in terms of the cost of opening new facilities. Meanwhile, the quality of service received by each demand is no less than a certain acceptable threshold. We refer to it as threshold quality, which guarantees the minimal quality of service received by each customer. Whether each customer can enjoy a certain minimum quality of service is an important issue in the location decision, such as locating a facility for signal coverage, such as a car rental office, post office, park, or other convenient public service facilities.

The nominal problem is formulated by assuming that all parameters in the model are static and exactly known, including the demands. Let G(N, A) be a connected graph with node set N and arc set A. N represents both the potential demand nodes and the candidate facilities. For the convenience of exposition, the following notations are defined.

Parameters
$f_i$	The fixed cost of opening a facility at node i, $i\in \mathbb{N}$
$d_i$	The demand at node i, $i\in \mathbb{N}$
Q	The predetermined quality threshold
$c_{ij}$	The distance between node i and node j, $i,j\in \mathbb{N}$
$g\left(c_{ij}\right)$	Signal strength function, which is a monotonic nonincreasing function of distance $c_{ij}$
Decision variables
$x_j$	$\left\{\begin{array}{c}1,\mathrm{if}\mathrm{a}\mathrm{facility}\mathrm{is}\mathrm{located}\mathrm{at}\mathrm{candidate}\mathrm{node}j\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.,j\in \mathbb{N}$

The nominal problem we considered is formulated as follows:

Model (DM):

$$\begin{array}{c}\hfill \max \frac{{\displaystyle \sum _{i\in \mathbb{N}}}{\displaystyle \sum _{j\in \mathbb{N}}}{d}_{i}g\left(c_{ij}\right)x_j}{{\displaystyle \sum _{j\in \mathbb{N}}}{f}_j{x}_j}\end{array}$$

(1)

$$\begin{array}{cc}\hfill s.t.& \sum _{j\in \mathbb{N}}g\left(c_{ij}\right)x_j\ge Q,\forall i\in \mathbb{N}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & x_j\in \left\{0,1\right\},\forall j\in \mathbb{N}\hfill \end{array}$$

(3)

The aim of the objective function (1) is to maximize the effectiveness, i.e., the quality per dollar. Constraint (2) ensures that the quality of service received by each demand is not below a given acceptable threshold Q. When the value of Q is 0, Constraint (2) is meaningless. The maximum value of Q is $min\left\{{\displaystyle \sum _{j\in \mathbb{N}}}g\left(c_{ij}\right)\right\}$, in which case facilities are established at all demand nodes. Constraint (3) refers to the domain of the decision variables.

The cooperative covering model can describe more accurately the location problem of facilities that emit physical signals and non-physical signals as well. Compared to the cooperative covering model presented in the previous research, our model takes effectiveness into consideration, which measures effectiveness as the total quality in relation to the total cost. It is more in line with the need of decision makers.

Clearly, this formulation is non-linear, and there is a fraction in the objective function. The following theorem describes procedures to remove the fraction in the objective function and reformulates model (DM).

Theorem 1.

Model (DM) is equivalent to the following programming:

Model (DM’):

$$\begin{array}{c}\hfill max\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{d}_{i}g\left(c_{ij}\right)X_j\end{array}$$

(4)

$$\begin{array}{cc}\hfill s.t.& \sum _{j\in \mathbb{N}}g\left(c_{ij}\right)X_j\ge Qv,\forall i\in \mathbb{N}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \sum _{j\in \mathbb{N}}{f}_j{X}_j=1 \hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & v\ge 0 \hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & X_j\in \left\{0,\nu \right\},\forall j\in \mathbb{N}\hfill \end{array}$$

(8)

Proof of Theorem 1. 

Since no less than one facility is located, i.e., ${\displaystyle \sum _{j\in \mathbb{N}}}{f}_j{x}_j>0$, a new auxiliary variable $v=\frac{1}{{\displaystyle \sum _{j\in \mathbb{N}}}{f}_j{x}_j}$ is introduced. Additional variables $X_j=v{x}_j$ for all $j\in \mathbb{N}$ are defined. The objective function (1) can be reformulated as follows:

$$\begin{array}{cc}\hfill & \frac{{\displaystyle \sum _{i\in N}}{\displaystyle \sum _{j\in N}}{d}_{i}g\left(c_{ij}\right)x_j}{{\displaystyle \sum _{j\in N}}{f}_j{x}_j}\hfill \\ \hfill & ={\displaystyle \sum _{i\in N}}\sum _{j\in N}{d}_{i}g\left(c_{ij}\right)x_j\nu \hfill \\ \hfill & =\sum _{i\in N}\sum _{j\in N}{d}_{i}g\left(c_{ij}\right)X_j\hfill \end{array}$$

Additionally, objective function (1) can be reformulated as objective function (4).

Constraint (2) can be reformulated as follows:

$$\begin{array}{cc}\hfill & \sum _{j\in N}g\left(c_{ij}\right)x_j\ge Q,\forall i\in N\hfill \\ \hfill & \iff \sum _{j\in N}g\left(c_{ij}\right)x_j\nu \ge Q\nu ,\forall i\in N\hfill \\ \hfill & \iff \sum _{j\in N}g\left(c_{ij}\right)X_j\ge Q\nu ,\forall i\in N\hfill \end{array}$$

Constraint (6) arises from the definition of v. To guarantee that $x_j\in \left\{0,1\right\}$, we require that $X_j\in \left\{0,\nu \right\},\forall j\in \mathbb{N}$.

Using the transformation above, the problem (DM) can be reformulated as (DM’), equivalently. □

The cooperative covering model we proposed aims at maximizing the effectiveness, and takes quality and the locating cost into consideration simultaneously. However, the nominal problem assumes the values of all the parameters are precisely known. In the real world, some of the parameters are inevitably exposed to many uncertain factors during the operational lifetime of a facility. Hence, it is important to consider uncertainty in this cooperative covering modeling.

3.2. The Robust Problem

In practical issues, there are a lot of uncertainties in the facility location problem, such as the uncertainty in demand, travel time between facilities, and demand and cost parameters. The influence of uncertainty is an important aspect that should be taken into consideration by investors in locating. In this section, the demand at each node is assumed to be uncertain, and the precise probability distribution is unknown. Let ${\stackrel{\sim }{d}}_i$ denotes the uncertain demand at node i($i\in \mathbb{N}$). Additionally, ${\stackrel{\sim }{d}}_i$ takes value in a symmetric interval $\left[{\overline{d}}_i-{\widehat{d}}_i,{\overline{d}}_i+{\widehat{d}}_i\right]$, where ${\overline{d}}_i$ is the mean or nominal value of ${\stackrel{\sim }{d}}_i$ and ${\widehat{d}}_i$ is the maximal deviation from the nominal value. Define the box uncertainty set $U_i=\left[{\overline{d}}_i-{\widehat{d}}_i,{\overline{d}}_i+{\widehat{d}}_i\right]$, then ${\stackrel{\sim }{d}}_i\in U_i$.

To withstand parameter uncertainty without excessively affecting the objective function, the budget-of-uncertainty robust approach is employed. This robust approach overcomes the shortcomings of over conservatism, and provides full control of the conservatism of the solution by adjusting the protection level. The robust counterparts of the problem (DM’) are formulated as follows:

Model (RM):

$$\begin{array}{c}\hfill max\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{\overline{d}}_{i}g\left(c_{ij}\right)X_j-\varphi (X,\mathrm{\Gamma })\end{array}$$

(9)

subject to Constraints (5)–(8).

Where

$$\varphi (X,\mathrm{\Gamma })=\underset{\left\{S\cup \left\{t\right\}\left|S\subseteq \mathbb{N},\left|S\right|=⌊\mathrm{\Gamma }⌋,t\in \mathbb{N}\backslash S\right.\right\}}{max}\left\{\sum _{i\in S}\sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j+\sum _{j\in \mathbb{N}}\left(\mathrm{\Gamma }-⌊\mathrm{\Gamma }⌋\right){\widehat{d}}_{t}g\left(c_{tj}\right)X_j\right\}$$

$\varphi (X,\mathrm{\Gamma })$ is defined as protection function. In this setting, $\mathrm{\Gamma }$ is the protection level of the actual effectiveness, which is used to measure the degree of conservatism of the solution. As will become clear below, not all demands will change, only some of them deviate from the nominal values. More importantly, the objective function is to maximize the worst case, in which up to $⌊\mathrm{\Gamma }⌋$ of these uncertain demands change and one uncertain demand changes by $\left(\mathrm{\Gamma }-⌊\mathrm{\Gamma }⌋\right){\widehat{d}}_i$. The role of the protection level $\mathrm{\Gamma }$ is to adjust the risk appetite of the decision maker such that the larger $\mathrm{\Gamma }$ is, the more conservative the model is [40]. If $\mathrm{\Gamma }$ is equal to 0, that means the decision maker is not risk-averse at all. In this setting, the locating decision is made according to the nominal demands. On the contrary, $\mathrm{\Gamma }$ is equal to N, which means that the decision maker is absolute risk-averse, and the locating decision is made based on the worst case. 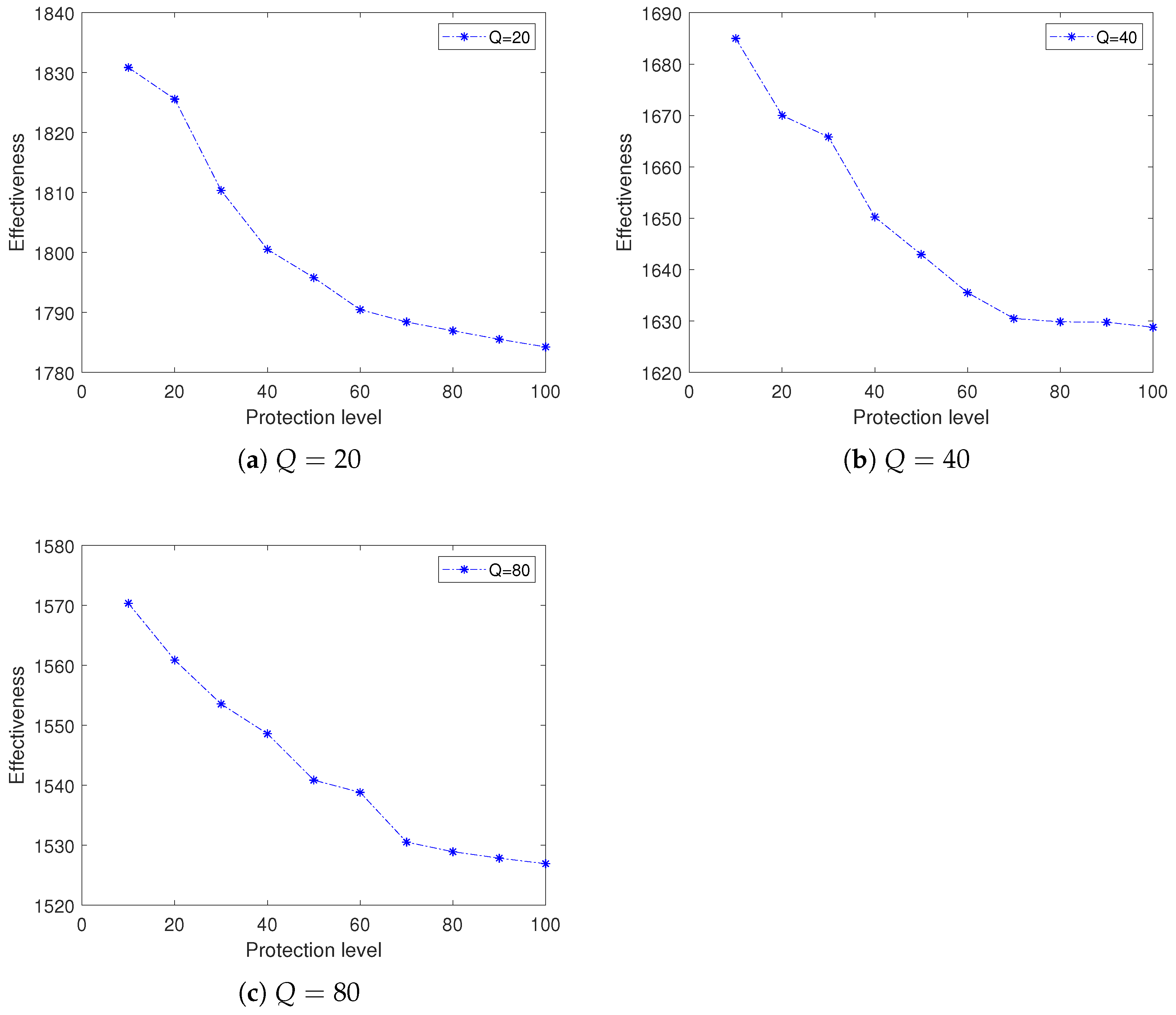With the increase of protection level $\mathrm{\Gamma }$, the degree of risk aversion increases as well. In other words, the higher the protection level, the more risk-averse the decision maker is. The decision maker can make trade-offs between the protection level and effectiveness according to the model we propose.

In order to reformulate the objective function as a linear optimization, the following theorem is presented.

Theorem 2.

The robust model (RM) can be reformulated as the following programming (RM′) equivalently.

Model (RM’):

$$\begin{array}{c}\hfill max\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{\overline{d}}_{i}g\left(c_{ij}\right)X_j-\left(\alpha \mathrm{\Gamma }+\sum _{i\in \mathbb{N}}{\beta }_i\right)\end{array}$$

(10)

$$\begin{array}{cc}\hfill s.t.& \alpha +{\beta }_i\ge \sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j,\forall i\in \mathbb{N}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \alpha \ge 0 \hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & {\beta }_i\ge 0,\forall i\in \mathbb{N} \hfill \\ \hfill & constrains\left(5\right)\sim \left(8\right) \hfill \end{array}$$

(13)

Proof of Theorem 2. 

Similar to the method in Bertsimas and Sim [38], $\varphi (X,\mathrm{\Gamma })$ equals the following linear optimization programming:

$$\varphi (X,\mathrm{\Gamma })=\left\{\max \sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j{D}_i:\sum _{i\in \mathbb{N}}{D}_i=\mathrm{\Gamma },0\le D_i\le 1,\forall i\in \mathbb{N}\right\}$$

(14)

By introducing dual variables associated with the constraints in problem (14), the following dual problem of (14) is obtained:

$$\varphi (X,\mathrm{\Gamma })=\left\{\min \alpha \mathrm{\Gamma }+\sum _{i\in \mathbb{N}}{\beta }_i:\alpha +{\beta }_i\ge \sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j,\alpha \ge 0,{\beta }_i\ge 0,\forall i\in \mathbb{N}\right\}$$

(15)

Incorporating problem (15) into the objective function (9), the Theorem 2 is obtained. □

Theorem 3.

When $\mathrm{\Gamma }=0$, the model (RM) is transformed into the nominal model (DM).

Proof of Theorem 3. 

It is clear in (14) that when $\mathrm{\Gamma }=0$, $\varphi (X,\mathrm{\Gamma })$ equals to 0. Then the model (RM) is transformed into the model (DM) based on the objective function (9). □

In other words, the problem (RM) naturally generalizes the deterministic counterpart problem (DM).

3.3. Linearization of the Robust Model

The formulation (RM’) is clearly non-linear. In Constraint (8), the variables $X_j(\forall j\in \mathbb{N})$ take values 0 or v. In this section, the robust model (RM’) is rewritten as a linear programming model, which can be readily solved through standard optimization tools.

To reformulate model (RM’) as a linear optimization model, we define new binary variables $Y_j\in \left\{0,1\right\}(\forall j\in N)$, and adding the constraints:

$$\begin{array}{cc}\hfill & X_j\le v,\forall j\in \mathbb{N}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & X_j\le \left(1-Y_j\right)M_1,\forall j\in \mathbb{N} \hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & X_j\ge v-Y_j{M}_2,\forall j\in \mathbb{N} \hfill \end{array}$$

(18)

where, $M_1,M_2>max\left\{v\right\}$. The maximum value of v is counted by $max\left\{v\right\}=\frac{1}{min{\displaystyle \sum _{j\in N}}{f}_j{x}_j}$. At least one facility should be opened, then $\frac{1}{min{\displaystyle \sum _{j\in N}}{f}_j{x}_j}\le \frac{1}{min\left\{f_i\right\}}$. Here we choose $M_1=M_2=\frac{1}{min\left\{f_i\right\}}$.

To demonstrate the validity of these new constraints, first assume that $Y_j=0$. In such a case, the Constraints (16)–(18) read $X_j\le v,X_j\le M_1$ and $X_j\ge v$, forcing $X_j=v$. If on the other hand, $Y_j=1$, then the constraints read $X_j\le v{X}_j\le 0$ and $X_j\ge v-M_2$, resulting in $X_j=0$, which is the desired result. Note that $X_j=\left(1-Y_j\right)\nu$ and $x_j=1-Y_j$.

The full formulation is then

Model (LRM):

$$\begin{array}{c}\hfill max\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{\overline{d}}_{i}g\left(c_{ij}\right)X_j-\left(\alpha \mathrm{\Gamma }+\sum _{i\in \mathbb{N}}{\beta }_i\right)\end{array}$$

$$\begin{array}{cc}\hfill s.t.& X_j\le v,\forall j\in \mathbb{N}\hfill \\ \hfill & X_j\le \left(1-Y_j\right)M_1,\forall j\in \mathbb{N}\hfill \\ \hfill & X_j\ge v-Y_j{M}_2,\forall j\in \mathbb{N}\hfill \\ \hfill & X_j\ge 0,\forall j\in \mathbb{N}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & Y_j\in \left\{0,1\right\},\forall j\in \mathbb{N} \hfill \\ \hfill & \left(5\right)\sim \left(7\right),\left(11\right)\sim \left(13\right) \hfill \end{array}$$

(20)

The robust model (RM’) is equivalent to mixed integer programming (LRM) and the mixed integer programming can be solved by branch and bound algorithm. We can also use commercial software to solve the problem, such as IBM IOG CPLEX and Lingo.

4. Numerical Study and Analysis

4.1. Test Environment

In this section, we conduct experiments to illustrate the robust solution to the cooperative covering model with demand uncertainty. N nodes on the square $[0,100]\times [0,100]$ are randomly generated, representing both the candidate facility locations and the potential demand nodes. The nominal demand at each demand node $d_i$ is independent of all others and is generated from the uniform distribution $Uniform[3000,5000]$. The fixed facility location cost $f_i$ is drawn from the uniform distribution $Uniform[\mathrm{17,500},\mathrm{22,500}]$ (see Baron et al. [39]). The distance between node i and node j, $c_{ij}$ equals the Euclidean distance between the two nodes. Assume ${\widehat{d}}_i={\epsilon }_i{\overline{d}}_i$, where $0\le {\epsilon }_i\le 1$ is called disturbance ratio, which measures the uncertainty size at node i. The disturbance ratio ${\epsilon }_i$ can be estimated based on historical data. The prediction method, such as artificial neural network and time series prediction, can also be used to obtain the disturbance ratio. In this numerical study, ${\epsilon }_i$ is drawn from the uniform distribution $Uniform[0.05,0.2]$. The signal strength function can be defined as the piecewise function (Berman et al. [8]), and is given by

$$\begin{array}{c}\hfill g\left(c_{ij}\right)=\left\{\begin{array}{c}20,if{c}_{ij}\le 10\hfill \\ 30-c_{ij},if10<c_{ij}<30\hfill \\ 0,otherwise\hfill \end{array}\right.\end{array}$$

We compare the solutions of the nominal problem (DM) to those of the robust problem (RM) with different protection levels. We do so by first considering the optimal locations of facilities established corresponding to the different protection levels of $\mathrm{\Gamma }$. Second, the effects of the protection level on the objective function value for various protection levels are deeply analyzed. Moreover, two ways to measure the price of robustness are defined, and the changes in the effectiveness are investigated. Finally, a sensitivity analysis of important parameters is conducted.

4.2. Comparing the Solution Corresponding to Different Protection Level

To investigate the solution of the formulation (RM) corresponding to different protection levels, we first solve problem (RM) for various protection levels. The quality threshold is set to be 60, and 100 nodes on the square $[0,100]\times [0,100]$ are randomly generated (see Figure 1a). In Figure 1, we present typical solutions of the model (RM). In the figures, a black point denotes the potential demand nodes, as well as the candidate facility locations; a red plus sign denotes an opened facility when the protection level is 0; a blue square denotes an opened facility when the protection level is 40; a green circle denotes an opened facility when protection level is 80.

According to Theorem 3, the robust optimization problem (RM) is exactly the nominal problem (DM) when we set the protection level to be 0. Figure 1 compares the optimal location for different protection levels, and we can compare the results of the solution’s topology for different protection levels. When the protection level is 0, i.e., all demands are exactly known and take their nominal values, 36 facilities will be opened. When the protection level is 40, there are 43 facilities located. As is shown in Figure 1, although most of the locating sites under $\mathrm{\Gamma }=40$ and 80 are the same as the deterministic problem, several of them are different from the deterministic problem. The number of the opening facilities is larger than the deterministic problem when considering demand uncertainty. Moreover, the locating site has significant differences corresponding to different protection levels. Therefore, the optimal location of the facility is indeed affected by the protection level, which cannot be ignored in the complex decision-making environment.

Next, we present the objective function value of the model (RM) for various protection levels under three different values of quality threshold, and to investigate how changes in the protection level affect effectiveness. The experimental results are depicted in Figure 2. Figure 2 illustrates the performance of effectiveness as a function of the protection level, while the quality threshold equals $20,40$, and 80, respectively. It can be seen that with the increase in protection level, the effectiveness decreases. This result can be explained by the protection function:

$$\varphi (X,\mathrm{\Gamma })=\underset{\left\{S\cup \left\{t\right\}\left|S\subseteq \mathbb{N},\left|S\right|=⌊\mathrm{\Gamma }⌋,t\in \mathbb{N}\backslash S\right.\right\}}{max}\left\{\sum _{i\in S}\sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j+\sum _{j\in \mathbb{N}}\left(\mathrm{\Gamma }-⌊\mathrm{\Gamma }⌋\right){\widehat{d}}_{t}g\left(c_{tj}\right)X_j\right\}$$

From the above formula, when the protection level increases, there are more demands deviating from their nominal values to the worst case, the protection function also increases. Therefore, the objective function value decreases. We make several observations. Obviously, the effectiveness decreases with the protection level. Moreover, some interesting “phase transitions” are observed in Figure 2 as the protection level increases. When the protection level is small, the curve drops faster, in which case the conservatism of the decision maker has a greater impact on effectiveness. On the contrary, when the protection level is large, the curve seems to be flattening out, which means that the conservatism of the decision maker hardly affects the effectiveness. The decision maker can make a trade-off between conservatism and effectiveness in an uncertain environment.

4.3. The Price of Robustness

It is obvious from the above analysis that the effectiveness is sacrificed to withstand the demand fluctuation. The robust solution of the model (RM) has an objective function value much worse than the objective function value of the solution of the nominal problem (DM). That is, compared with the nominal model (DM), the effectiveness is decreased. The more conservative, the bigger the decrease in the effectiveness. The above qualitative analysis shows the trend of the curves and gives us an intuitive picture of how the protection level affects effectiveness. Next, we analyze the trade-offs between the protection level and the effectiveness quantitatively, and provide two criteria to measure the price of robustness.

Let $P_0^{\ast }$ and $P_1^{\ast }$ denote the optimal objective values resulting from the model (DM) and (RM), respectively. The price of robustness is defined as follows (Liu et al., [59]):

$$\begin{array}{c}\hfill Price1=\frac{P_0^{\ast }-P_1^{\ast }}{P_0^{\ast }}\ast 100\%\end{array}$$

(21)

$Price1$, defined by Equation (21), measures the relative difference in effectiveness resulting from the nominal model and the robust model. Because $P_0^{\ast }\ge P_1^{\ast }$, $Price1\ge 0$. $Price1$ illustrates the relative reduction in the effectiveness when considering demand uncertainty. Figure 3 is plotted to illustrate how the sacrifice made for the robustness of the model when the quality threshold equals $20,40$, and 80, respectively. As shown in Figure 3, when the protection level is low, the curves increase slowly. However, when the protection level becomes higher, the curves increase sharply. It is shown that large increases in the protection level are not necessary with large increases in the price of robustness. This demonstrates that a higher level of conservatism can be attained without large increases in $Price1$. That is, a higher level of conservatism does not always necessarily result in much sacrifice in effectiveness. This is evident from Figure 3 since the trade-off curves are steep when the protection level is larger than about 50. According to the trade-offs between $Price1$ and the protection level, the decision maker can compute the $Price1$ based on the protection level or obtain the protection level depending on $Price1$.

Another commonly used means to deal with parameter uncertainty is Soyster’s approach, which formulates the robust model by considering the worst case of the uncertain parameter. It leads to the obtained solutions being too conservative, because in order to ensure the robustness of the solution it may sacrifice too much optimality for the nominal problem. Next, we will compare the relative difference between the resulting from the model (RM) and the model by Soyster’s approach. In fact, the model by Soyster’s approach can be obtained by generalizing the robust model (RM). Let protection level $\mathrm{\Gamma }=N$ (in the numerical experiments, $N=100$). In other words, all the demands deviate to the worst case. According to formula (14):

$$\varphi (X,\mathrm{\Gamma })=\left\{\max \sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j{D}_i:\sum _{i\in \mathbb{N}}{D}_i=\mathrm{\Gamma },0\le D_i\le \mathbb{N},\forall i\in \mathbb{N}\right\}$$

The optimal solution of (14) is $D_i=1$ for all $i\in \mathbb{N}$ when $\mathrm{\Gamma }=100$. In this case, the protection function is:

$$\begin{array}{c}\hfill \varphi (X,\mathrm{\Gamma })=\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}{\widehat{d}}_{i}g\left(c_{ij}\right)X_j\end{array}$$

Substituting the above protection function in the objective function of the model (RM), it is reformulated as:

$$\begin{array}{c}\hfill max\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}\left({\overline{d}}_i-{\widehat{d}}_i\right)g\left(c_{ij}\right)X_j\end{array}$$

The robust counterpart of the problem (DM’) by using Soyster’s approach is formulated as follows:

(SRM)

$$\begin{array}{c}\hfill max\sum _{i\in \mathbb{N}}\sum _{j\in \mathbb{N}}\left({\overline{d}}_i-{\widehat{d}}_i\right)g\left(c_{ij}\right)X_j\end{array}$$

subject to Constraints (5)–(8).

The robust model (SRM) provides full protection from demand deviation by considering the minimum value of demand, which we call it complete protection robust approach. Obviously, Soyster’s approach is too conservative, and may excessively affect the objective function. To measure the effects of Soyster’s approach to effectiveness, we define the following price of robustness. Let $P_c^{\ast }$ denote the optimal objective value resulting from the model (SRM). Another price of robustness is defined as follows (Liu et al. [59]):

$$\begin{array}{c}\hfill Price2=\frac{P_1^{\ast }-P_c^{\ast }}{P_c^{\ast }}\ast 100\%\end{array}$$

(22)

$Price2$, defined by Equation (22), measures the relative difference of effectiveness between the complete protection robust model and the budget-of-uncertainty robust model. Because $P_c^{\ast }\le P_1^{\ast }$, $Price2\ge 0$. $Price2$ illustrates the relative increase in the effectiveness when considering demand uncertainty, compared to the complete protection case.

In

Table 1. The price of robustness for various quality thresholds.

$\mathbf{\Gamma }$	Quality Threshold Q
	Price of Robustness 1 (%) (Compared to the Nominal Model)			Price of Robustness 2 (%) (Compared to the Complete Protection Model)
	20	40	80	20	40	80
0	0	0	0	3.3314	4.5801	3.7513
10	0.6964	1.0802	0.8736	2.6117	3.4504	2.8449
20	0.9823	1.9596	1.4714	2.3164	2.5307	2.2247
30	1.8083	2.2056	1.9341	1.4628	2.2735	1.7447
40	2.3415	3.1196	2.2478	0.9119	1.3175	1.4192
50	2.597	3.5488	2.7358	0.6479	0.8687	0.9129
60	2.8871	3.9844	2.8645	0.348	0.4132	0.7793
70	2.9983	4.2797	3.3878	0.2331	0.1044	0.2364
80	3.078	4.3172	3.4895	0.1508	0.0651	0.131
90	3.1551	4.3219	3.557	0.0712	0.0602	0.0609
100	3.224	4.3795	3.6157	0	0	0

, we present the values of $Price1$ and $Price2$ for various protection levels under three different quality thresholds. The facility location decision can be made from Table 1. For risk-appetite decision makers, the original decision by considering nominal demand may be changed. They can make the decisions by evaluating the relative decrease in effectiveness and the protection level. While for risk-averse decision makers, the original decision by considering minimum demand may also be changed. They can make the decisions by evaluating the relative increase in effectiveness and the protection level as well. In summary, decision makers can make trade-offs between the price of robustness and the protection level according to Table 1.

4.4. Sensitivity Analysis

In this section, we perform a sensitivity analysis of two important parameters. Furthermore, how the quality threshold and disturbance ratio of demand affect the model is analyzed in detail.

The specific operation is as follows. First, we set the quality threshold equal to 40, which we call the benchmark quality threshold. The model (RM) is solved for various protection levels. Then, decrease the quality threshold by $5\%$ and solve the model (RM) for various protection levels. Increasing the quality threshold by $5\%$ does the same thing. The results are depicted in Figure 4. The three lines describe the change in the effectiveness with protection level when the quality threshold fluctuates slightly. As is shown in Figure 4, when the quality threshold decreases by $5\%$, the effectiveness decreases; when the quality threshold increases by $5\%$, the effectiveness increases. Therefore, the effectiveness is sensitive to the quality threshold. Moreover, the gap between the three curves has not changed much with different protection levels. In other words, the sensitivity of effectiveness to the quality threshold is almost uniform for various protection levels.

The disturbance ratio of demand, ${\epsilon }_i$, is an important parameter to the robust optimization model. We next analyze how the fluctuation in disturbance ratio affects the optimal value of the robust model. First, the disturbance ratio of demand at node i, i.e., ${\epsilon }_i$, is drawn from the uniform distribution $Uniform[0.05,0.2]$ randomly, which we call the benchmark disturbance ratio. The robust model (RM) is solved for various protection levels. Then, decrease and increase the disturbance ratio by $5\%$ and solve the model (RM) for various protection levels, respectively.

In Figure 5, we present the solutions of the models. The three lines describe the change in the effectiveness with protection level when the disturbance ratio of the demand fluctuates slightly. The effectiveness changes in the opposite direction to the disturbance ratio. Under the same protection level, the effectiveness decreases (increases) with the disturbance ratio increase (decreases). Therefore, the effectiveness is sensitive to the disturbance ratio. More importantly, the gap between the three curves has changed with different protection levels. The gap becomes wider as the protection level increases. When the protection level is 0, i.e., no demand deviates from the nominal value, the effectiveness is $1703.40$. It is the optimal solution to the deterministic problem (DM). When the protection level increases to 30, the optimal solutions are $1665.05$ (benchmark disturbance ratio), $1655.01$ (increase the disturbance ratio by $5\%$), and $1675.02$ (decrease the disturbance ratio by $5\%$). The absolute values of the difference between the fluctuated problems and the benchmark are $10.04$ and $9.97$, respectively. When the protection level increases to 80, the optimal solutions are $1630.65$ (benchmark disturbance ratio), $1602.03$ (increase the disturbance ratio by $5\%$), and $1652.78$ (decrease the disturbance ratio by $5\%$). The absolute values of the difference between the fluctuated problems and the benchmark are $28.63$ and $22.13$, respectively.

Some key insights can be gained from Figure 5. When the protection level is low, the effectiveness under different disturbances does not change much. With the improvement in the protection level, the gap between the effectiveness for different disturbances grows. This phenomenon is also easy to be explained by the definition of protection level. When the protection level is low, the number of demands that deviate to the worst-case scenario is small. If $\mathrm{\Gamma }$ is chosen as an integer, up to $\mathrm{\Gamma }$ of these demands are allowed to change. So, in this case, the disturbance ratio of demand has little impact on the objective function value of the problem. On the contrary, the number of demands that deviate from the worst-case scenario becomes larger as the protection level increases. Obviously, the disturbance ratio of demand has a bigger impact on the objective function of the problem in this setting. The sensitivity analysis of the demand disturbance ratio shows that the effectiveness becomes more sensitive to demand disturbance with the improvement of the protection level.

5. Conclusions and Future Work

This article has employed an effective robust optimization approach for the cooperative covering facility location problem under demand uncertainty. The objective of this paper is to maximize the effectiveness with uncertain demand. A more realistic covering concept, i.e., cooperative covering, is adopted in the setting. The model in this study can more accurately describe the location problem of facilities that propagate light, sound, and microwave signals. The research is to maximize the ratio between output and input, and take uncertain parameters into consideration as well. The classical facility location model is to develop a model that assumes that the input data is precisely known and equal to some nominal values. It is therefore conceivable that as the data take values different than the nominal ones, several constraints may be violated, and the optimal solution may no longer be optimal or even feasible. In contrast, our approach can offer full control of the conservatism of the model and adjust the effect on the objective function.

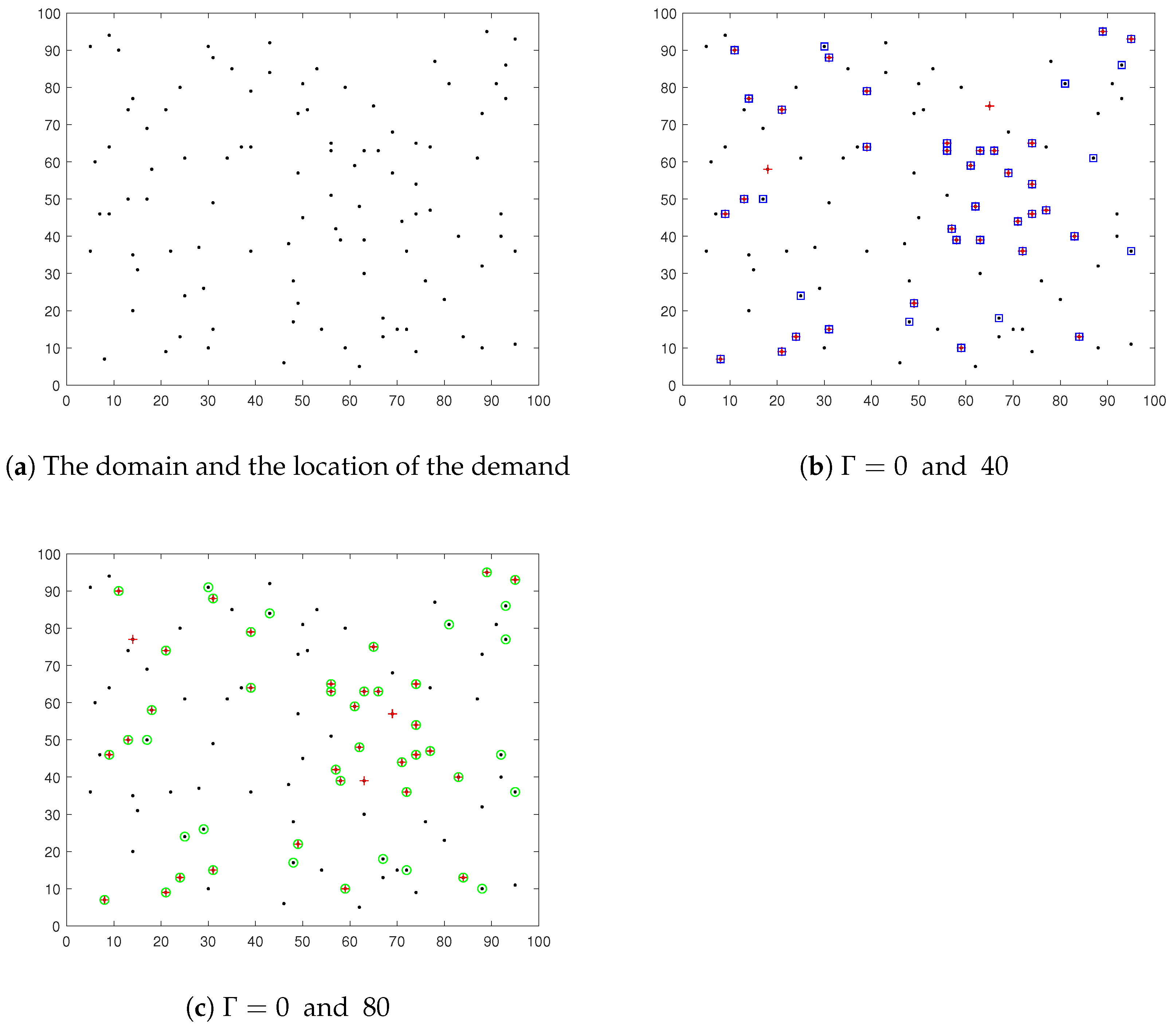
Numerical examples highlight that the optimal location of the facility is indeed affected by the protection level, and it is therefore important to take into consideration the demand uncertainty when facility location decisions are made. The number of the opening facilities is larger than the deterministic problem when considering demand uncertainty. Moreover, the best location of the facility is influenced by uncertain parameters, which cannot be ignored in the complex decision-making environment.

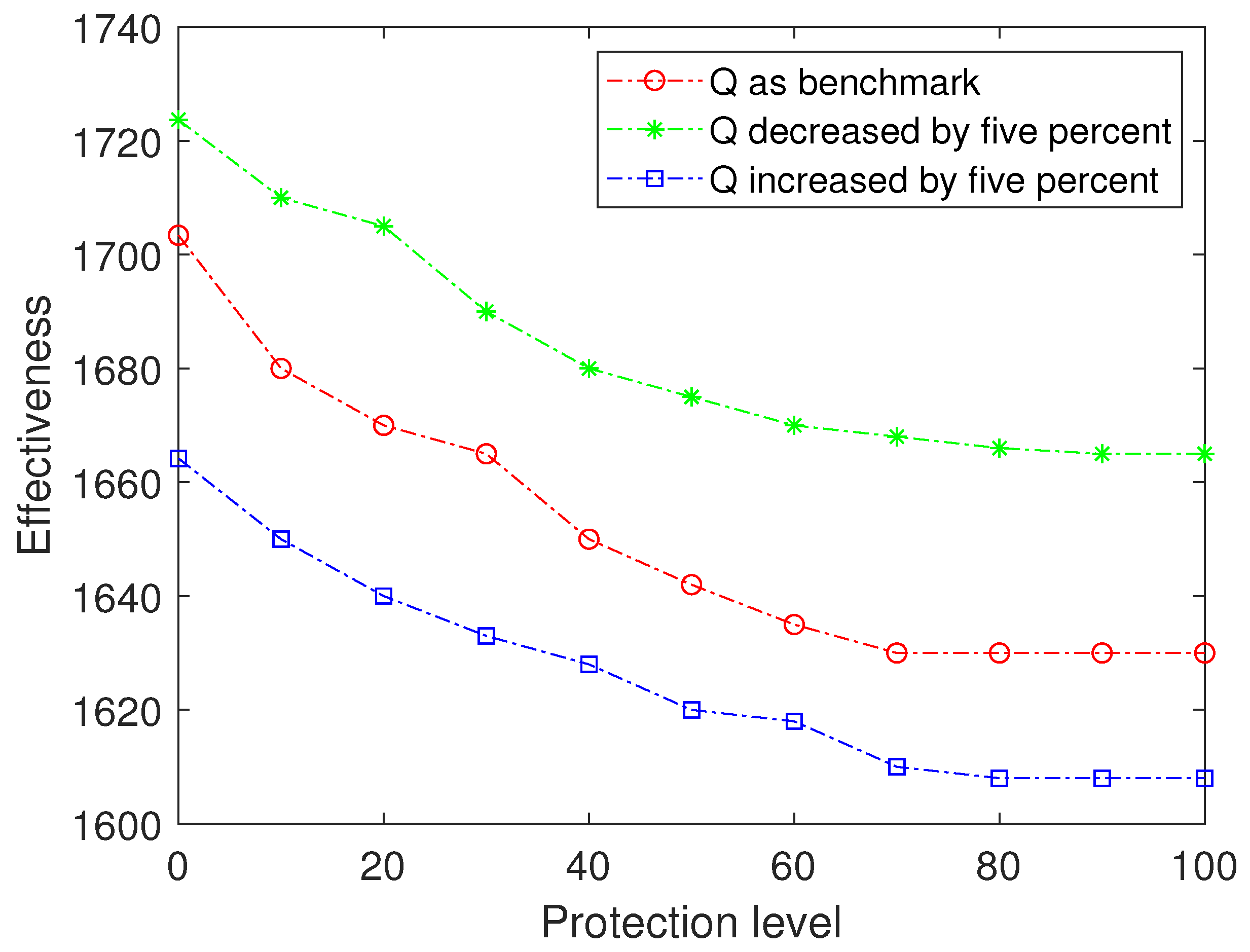
Two ways to measure the price of robustness are defined. The facility location decision can be made by evaluating the relative decrease in effectiveness compared to the nominal demand model, or by evaluating the relative increase in effectiveness compared to the complete protection model.

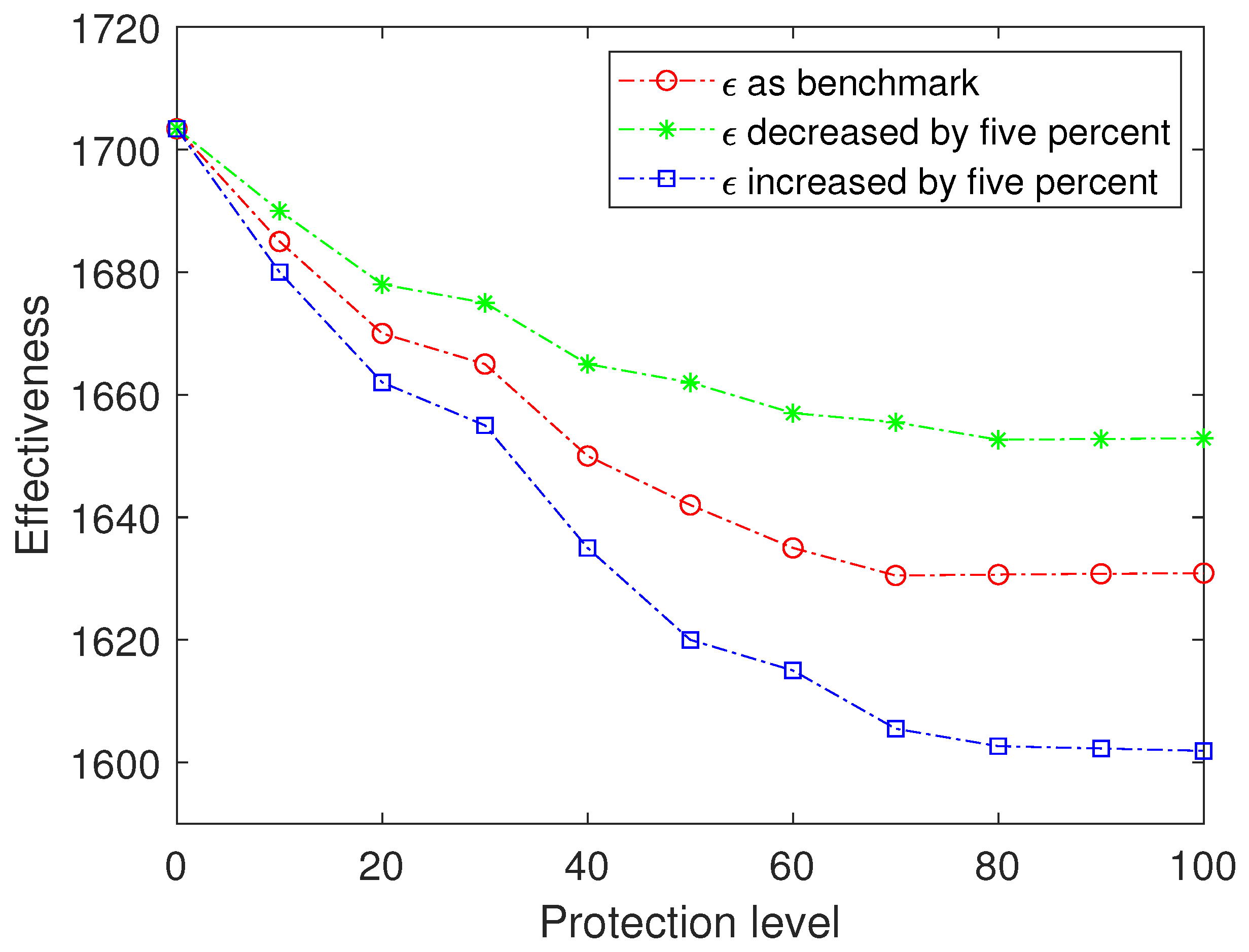
Sensitivity analysis of two important parameters has been performed. We can summarize the key insights in the numerical examples. The effectiveness is sensitive to the quality threshold. Moreover, the sensitivity of effectiveness to the quality threshold is almost uniform for various protection levels. The effectiveness becomes more sensitive to demand disturbance with the improvement on protection level.

In future research, additional objectives such as total distance traveled and travel time may be considered, and a multi-objective programming will be formulated, which is inspired by the model and criteria in Bevrani et al. [58]. Travel distance and travel time are perhaps important aspects in retailing applications, as customers are highly sensitive to the distance and time it takes to reach their destination. We find the solutions given by the robust model with a box. Future work may consider additional uncertainty sets such as polyhedra, e.g., an intersection of a box with an L1 norm. In addition, we assume that the demand at each node is independent of all others. However it turns out that it is not in some practical problems and demands are correlated. We will continue this work to make deep research in this direction.