Homogeneity of Complex Fuzzy Operations

Abstract

The homogeneity of binary functions on the unit interval [0, 1] is a very useful property in many real practical applications. This paper studies the homogeneity of binary functions on the unit circle of the complex plane. The homogeneity is a generalization of both rotational invariance and ratio scale invariance for complex fuzzy operations. We show that a binary function is homogeneous if and only if it is both rotationally invariant and ratio scale invariant. Moreover, we consider the simplification of the homogeneity for complex fuzzy binary operators.

1. Introduction

Ramot et al. [1,2] proposed the concept of complex fuzzy sets (CFSs), and complex fuzzy theories and complex fuzzy methods have been successfully applied to many fields. In many theoretical and application studies, complex fuzzy operations play an important role. In Ramot et al.’s initial paper [1], complex fuzzy operations are set-theoretic operations on complex fuzzy sets. For example, a complex fuzzy binary operation is defined as a function G: ${\mathbf{O}}^U\times {\mathbf{O}}^U\to {\mathbf{O}}^U$, where U is a universe of discourse, $\mathbf{O}=\left\{\alpha \in \mathbb{C}\left|\right|\alpha |\le 1\right\}$ is the unit disc of the complex plane and ${\mathbf{O}}^U$ is a mapping from U to $\mathbf{O}$. Ramot et al. [1,2] proposed several set-theoretic operations of complement, union and intersection. Zhang et al. [3] gave some new set-theoretic operations of CFSs and studied their operation properties. Dick, Yager and Yazdanbahksh [4] presented some set-theoretic operations of CFSs based on thoses of Pythagorean fuzzy sets, which was developed by Liu et al. [5]. Dick [6] also introduced S-implications of CFSs. Dai [7] gave some quasi-MV algebras for complex fuzzy logic. Hu et al. [8] investigated the orthogonality preserving operators of CFSs. Hu et al. [9] studied the continuity of complex fuzzy operations. Xu et al. [10] investigated the migrativity of complex fuzzy operations.

For convenience, many scholars have studied complex fuzzy binary operation as a function F: $\mathbf{O}\times \mathbf{O}\to \mathbf{O}$. Dick [11] asserted that a complex fuzzy binary operation should be rotationally invariant, i.e., $F(\mu ·e^{j\theta },\nu ·e^{j\theta })=F(\mu ,\nu )·e^{j\theta }$ for any $\mu ,\nu \in \mathbf{O}$ and $\theta \in \mathbf{R}$. Dai [12,13] generalized Dick’s rotational invariance and examined the rotational invariance of the order of CFSs. Greenfield et al. [14] examined the rotational invariance of interval-valued complex fuzzy operations.

Note that rotational invariance is a special case of the homogeneity of complex fuzzy binary operations, i.e., $F(\mu ·\alpha ,\nu ·\alpha )=F(\mu ,\nu )·\alpha$ for any $\mu ,\nu ,\alpha \in \mathbf{O}$. When $\alpha$ is limited within the boundary point set $\overline{\mathbf{O}}=\left\{\alpha \in \mathbb{C}\left|\right|\alpha |=1\right\}$, it is the rotational invariance. When $\mu ,\nu ,\alpha$ are limited within the unit interval $\mathbf{I}=[0,1]$, it is the homogeneity of traditional fuzzy binary operations. The homogeneity of traditional fuzzy binary functions, such as t-norms, t-conorms, copulas, uninorms, aggregation operators, overlap and grouping functions, has been studied extensively [15,16,17,18,19,20,21,22,23].

As mentioned above, on the one hand, there exist many discussions on the homogeneity of traditional fuzzy binary operations. On the other hand, complex fuzzy operations have developed rapidly recently. In particular, as listed above, the parallelity preserving, orthogonality preserving, continuity and rotational invariance of complex fuzzy operations have been discussed in the literature. However, as far as we know, to date, there has not been any discussion about the homogeneity of complex fuzzy operations. Note that rotational invariance, as a special case of homogeneity, has been well studied in the field of complex fuzzy operations. Therefore, in this paper, we focus on the homogeneity of complex fuzzy binary operations. The major contributions of this paper are as follows:

• The proposed complex-valued homogeneity is more general than the classical real-valued homogeneity of fuzzy operations.
• The proposed homogeneity is more comprehensive than the rotational invariance [11] because the latter is a special case of the proposed homogeneity.
• The proposed homogeneity can be simplified. We give several simplified versions of the proposed homogeneity.
• The relationship among homogeneity, rotational invariance and ratio scale invariance is given.

This article is structured as follows. In Section 2, we present some preliminary concepts of homogeneity, rotational invariance and scale invariance for complex fuzzy binary operations. In Section 3, we study the relationship among homogeneity, rotational invariance and ratio scale invariance. In Section 4, we discuss the simplification of the homogeneity. In Section 5, we give some characterizations of the homogeneity, rotational invariance and ratio scale invariance of complex fuzzy binary operations. In Section 6, a discussion of different properties of complex fuzzy operations are offered. In Section 7, concluding remarks are given.

2. Homogeneity

In this section, we introduce the concepts of homogeneity, rotational invariance and ratio scale invariance for complex fuzzy binary operations.

Definition 1.

A binary operation$F:{\mathit{O}}^2\to \mathit{O}$is said to be homogeneous of order$k\in ]0,\infty [$if

$$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu ,\alpha \in \mathit{O}.$$

(1)

In fact, it is a definition of the complex-valued homogeneity for complex fuzzy binary function.

In 2005, Dick [11] introduced the following concept of rotational invariance.

Definition 2

([11]). A binary operation $F:{\mathit{O}}^2\to \mathit{O}$ is rotationally invariant if, for all $\mu ,\nu \in \mathit{O}$ and $\theta \in \mathit{R}$,

$$F(e^{j\theta }\mu ,e^{j\theta }\nu )=e^{j\theta }F(\mu ,\nu ).$$

(2)

Note that Dick’s rotational invariance is a special case of homogeneity when we limit $\alpha \in \overline{\mathbf{O}}$ and $k=1$ in Definition 1. For convenience, we consider the following more general concept of rotational invariance.

Definition 3.

A binary operation$F:{\mathit{O}}^2\to \mathit{O}$is rotationally invariant of order$k\in ]0,\infty [$if, for all$\mu ,\nu \in \mathit{O}$and$\theta \in \mathit{R}$,

$$F(e^{j\theta }\mu ,e^{j\theta }\nu )=e^{jk\theta }F(\mu ,\nu ).$$

(3)

Then we introduce the following concept of ratio scale invariance for complex fuzzy binary operations.

Definition 4.

A binary operation$F:{\mathit{O}}^2\to \mathit{O}$is ratio scale invariant of order$k\in ]0,\infty [$if, for all$\mu ,\nu \in \mathit{O}$and$\gamma \in [0,1]$,

$$F(\gamma \mu ,\gamma \nu )={\gamma }^{k}F(\mu ,\nu ).$$

(4)

Clearly, ratio scale invariance is a special case of homogeneity when we limit $\alpha \in [0,1]$ in Definition 1. Note that the ratio scale invariance of binary functions on $\mathbf{I}$ has been well discussed in [24].

3. Relationship

In this section, we study the relationship among homogeneity, rotational invariance and ratio scale invariance.

First, we rewrite the homogeneity in another form.

Theorem 1.

A binary operation$F:{\mathit{O}}^2\to \mathit{O}$is homogeneous of order$k\in ]0,\infty [$if and only if, for all$\mu ,\nu \in \mathit{O}$, $r\in \mathit{I}$and$\theta \in \mathbb{R}$,

$$\left.\begin{array}{c}F(e^{j\theta }\mu ,e^{j\theta }\nu )=e^{jk\theta }F(\mu ,\nu ),\hfill \\ F(r\mu ,r\nu )=r^{k}F(\mu ,\nu )\hfill \end{array}\right\}$$

(5)

Proof. 

(⇒) Trivial.

(⇐) For any $\alpha \in \mathbf{O}$, denote $\alpha =r_{\alpha }·e^{j{\theta }_{\alpha }}$ where $r_{\alpha }\in \mathbf{I}$. Then,

$$\begin{array}{ccc}\hfill F(\alpha \mu ,\alpha \nu )& =& F(r_{\alpha }·e^{j{\theta }_{\alpha }}\mu ,r_{\alpha }·e^{j{\theta }_{\alpha }}\nu )\hfill \\ & =& \left(r_{\alpha }^k\right)·F(e^{j{\theta }_{\alpha }}\mu ,e^{j{\theta }_{\alpha }}\nu )\hfill \\ & =& {\left(r_{\alpha }\right)}^k·e^{jk{\theta }_{\alpha }}·F(\mu ,\nu )\hfill \\ & =& {\alpha }^{k}F(\mu ,\nu ).\hfill \end{array}$$

□

Thus, Equation (1) is equivalent to Equation (5). From the above theorem, we have the following corollary.

Corollary 1.

A binary operation$F:{\mathit{O}}^2\to \mathit{O}$is homogeneous of order$k\in ]0,\infty [$, if and only if it is both rotationally invariant and ratio scale invariant of order k.

From the definitions of homogeneity, rotational invariance and ratio scale invariance, we know that rotational invariance and ratio scale invariance are two special cases of homogeneity. From this corollary, homogeneity equals rotational invariance plus ratio scale invariance, i.e.,

$$\begin{array}{c}\mathrm{Homogeneity}=\mathrm{Rotational}\mathrm{invariance}+\mathrm{Ratio}\mathrm{scale}\mathrm{invariance}.\hfill \end{array}$$

If each variable is decreased by a factor $\alpha =r·e^{j\theta }$, then the output is both rotated by $k\theta$ degrees and decreased by k power of the factor r.

Example 1.

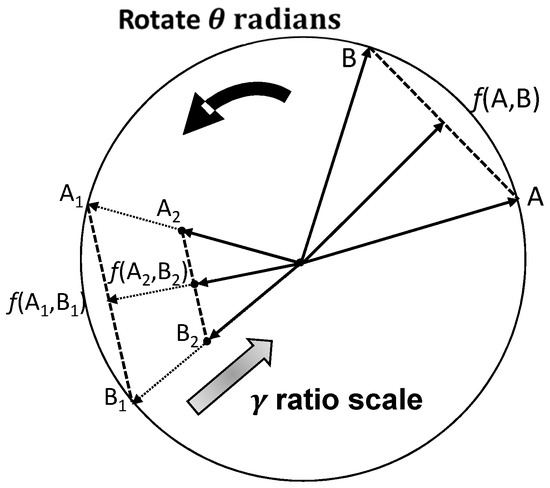
The average operation$F:{\mathit{O}}^2\to \mathit{O}$is defined by

$$\begin{array}{cc}\hfill F(\mu ,\nu )& =\frac{\mu +\nu }{2}.\hfill \end{array}$$

(6)

Obviously, F is homogeneous of order 1 because$F(\alpha \mu ,\alpha \nu )=\frac{\alpha \mu +\alpha \nu }{2}=\alpha ·\frac{\mu +\nu }{2}=\alpha ·F(\mu ,\nu )$for any$\alpha \in \mathit{O}$. As shown in Figure 1, if each variable of the average operation f is decreased by a factor$\alpha =r·e^{j\theta }$, then the output is both rotated by θ degrees and decreased by the factor r.

Figure 1. Homogeneity = Rotational invariance + Ratio scale invariance.

Example 2.

The weight average operation$F:{\mathit{O}}^2\to \mathit{O}$is defined by

$$\begin{array}{cc}\hfill F(\mu ,\nu )& =w_1\mu +w_2\nu ,\hfill \end{array}$$

(7)

where$w_1,w_2\in \mathit{O}$and$w_1+w_2=1$. Note that we use complex weights in this equation.

Then, F is homogeneous of order 1 because$F(\alpha \mu ,\alpha \nu )=w_1\left(\alpha \mu \right)+w_2\left(\alpha \nu \right)=\alpha ·(w_1\mu +w_2\nu )=\alpha ·F(\mu ,\nu )$for any$\alpha \in \mathit{O}$.

Example 3.

The product operation$F:{\mathit{O}}^2\to \mathit{O}$is defined by

$$\begin{array}{cc}\hfill F(\mu ,\nu )& =\mu ·\nu .\hfill \end{array}$$

(8)

Obviously, F is homogeneous of order 2 because$F(\alpha \mu ,\alpha \nu )=\left(\alpha \mu \right)·\left(\alpha \nu \right)=(\alpha ·\alpha )·(\mu ·\nu )={\alpha }^2·F(\mu ,\nu )$for any$\alpha \in \mathit{O}$.

4. Simplification

In this section, several simplified versions of the homogeneity are given. First, the following is a straightforward result from Theorem 1.

Theorem 2.

Let$F:{\mathit{O}}^2\to \mathit{O}$be a binary operation. Then, the following statements are equivalent.

1. 

$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu \in \mathit{O}and\alpha \in \mathit{O}$;

2. 

$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu \in \mathit{O}and\alpha \in \mathit{I}\cup \overline{\mathit{O}}$.

Note that F is homogeneous if Equation (1) holds for all $\alpha \in \mathbf{O}$. From the above result, we know that F is homogeneous if Equation (1) holds for all $\alpha \in \mathbf{I}\cup \overline{\mathbf{O}}$. This is very interesting because $\mathbf{I}\cup \overline{\mathbf{O}}$ is a proper subset of $\mathbf{O}$, i.e., $\left(\mathbf{I}\cup \overline{\mathbf{O}}\right)⫋\mathbf{O}$, and the size of $\mathbf{I}\cup \overline{\mathbf{O}}$ is much smaller than that of $\mathbf{O}$.

Then, there are two questions. The first question is: could $\mathbf{I}\cup \overline{\mathbf{O}}$ be replaced by other subset of $\mathbf{O}$? The answer is positive. In the following, we show that $\mathbf{I}\cup \overline{\mathbf{O}}$ could replaced by $[-1,0]\cup \overline{\mathbf{O}}$.

Theorem 3.

Let$F:{\mathit{O}}^2\to \mathit{O}$be a binary operation. Then, the following statements are equivalent.

1. 

$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu \in \mathit{O}and\alpha \in \mathit{O}$;

2. 

$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu \in \mathit{O}and\alpha \in [-1,0]\cup \overline{\mathbf{O}}$.

Proof. 

(⇒) Trivial.

(⇐) For any $\alpha \in \mathbf{O}$, denote $\alpha =r_{\alpha }·e^{j{\theta }_{\alpha }}$ where $r_{\alpha }\in \mathbf{I}$. Then, we have $\alpha =r_{\alpha }·e^{j{\theta }_{\alpha }}=(-r_{\alpha })·e^{j({\theta }_{\alpha }-\pi )}$ where $-r_{\alpha }\in [-1,0]$. Then,

$$\begin{array}{ccc}\hfill F(\alpha \mu ,\alpha \nu )& =& F\left((-r_{\alpha })·e^{j({\theta }_{\alpha }-\pi )}\mu ,(-r_{\alpha })·e^{j({\theta }_{\alpha }-\pi )}\nu \right)\hfill \\ & =& \left({(-r_{\alpha })}^k\right)·F(e^{j({\theta }_{\alpha }-\pi )}\mu ,e^{j({\theta }_{\alpha }-\pi )}\nu )\hfill \\ & =& {(-r_{\alpha })}^k·e^{jk({\theta }_{\alpha }-\pi )}·F(\mu ,\nu )\hfill \\ & =& {(-r_{\alpha }·e^{j({\theta }_{\alpha }-\pi )})}^k·F(\mu ,\nu ).\hfill \\ & =& {\alpha }^{k}F(\mu ,\nu ).\hfill \end{array}$$

□

The second question is: can we use a smaller subset to replace $\mathbf{I}\cup \overline{\mathbf{O}}$ (or $[-1,0]\cup \overline{\mathbf{O}}$)? The answer is also positive.

Theorem 4.

Let$\mathit{V}=\{e^{j\theta }:-\pi /2\le \theta \le \pi /2\}$and$F:{\mathit{O}}^2\to \mathit{O}$be a binary operation. Then, the following statements are equivalent.

1. 

$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu \in \mathit{O}and\alpha \in \mathit{O}$;

2. 

$F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu ),forall\mu ,\nu \in \mathit{O}and\alpha \in [-1,0]\cup \mathit{V}$.

Proof. 

(⇒) Trivial.

(⇐) For any $e^{j\theta }$ where $\frac{\pi }{2}\le \theta \le \frac{3\pi }{2}$, we have $e^{j\theta }=-e^{j(\theta -\pi )}$ where $\theta -\pi \in [-\frac{\pi }{2},\frac{\pi }{2}]$. Then,

$$\begin{array}{ccc}\hfill F(e^{j\theta }\mu ,e^{j\theta }\nu )& =& F\left((-1)·e^{j(\theta -\pi )}\mu ,(-1)·e^{j({\theta }_{\alpha }-\pi )}\nu \right)\hfill \\ & =& \left({(-1)}^k\right)·F(e^{j({\theta }_{\alpha }-\pi )}\mu ,e^{j({\theta }_{\alpha }-\pi )}\nu )\hfill \\ & =& {(-1)}^k·e^{jk({\theta }_{\alpha }-\pi )}·F(\mu ,\nu )\hfill \\ & =& {(-1·e^{j({\theta }_{\alpha }-\pi )})}^k·F(\mu ,\nu ).\hfill \\ & =& {\left(e^{j\theta }\right)}^{k}F(\mu ,\nu ).\hfill \end{array}$$

Thus, we show $F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu )$ for all $\alpha \in \{e^{j\theta }:\frac{\pi }{2}\le \theta \le \frac{3\pi }{2}\}$. Since it also holds for all $\alpha \in [-1,0]\cup \mathbf{V}$, it holds for all $\alpha \in [-1,0]\cup \overline{\mathbf{O}}$. Then, from Theorem 3, it holds for all $\alpha \in \mathbf{O}$. □

This is very interesting because $[-1,0]\cup \mathbf{V}$ is also a proper subset of $[-1,0]\cup \overline{\mathbf{O}}$, i.e.,

$$\left([-1,0]\cup \mathbf{V}\right)⫋\left([-1,0]\cup \overline{\mathbf{O}}\right),$$

and the size of $[-1,0]\cup \mathbf{V}$ is much smaller than that of $[-1,0]\cup \overline{\mathbf{O}}$.

Now, we give the proper subsets of $\mathbf{O}$, as shown in Figure 2. Note that f is homogeneous of order k if Equation (1) holds for all $\alpha \in \mathbf{O}$. These results have simplified the homogeneity proof of complex fuzzy binary operation. From the above results, we only need to prove that Equation (1) holds for one of the three subsets.

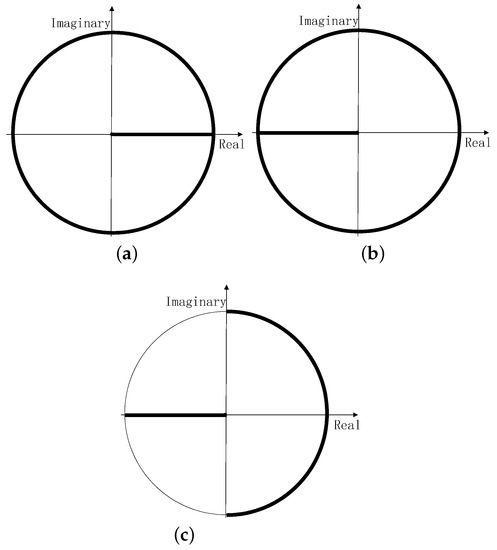
Figure 2. Three subsets: (a) $\mathbf{I}\cup \overline{\mathbf{O}}$, (b) $[-\mathbf{1},\mathbf{0}]\cup \overline{\mathbf{O}}$ (c) $[-\mathbf{1},\mathbf{0}]\cup \mathbf{V}$.

5. Further Characterization

In this section, the homogeneity, rotational invariance and ratio scale invariance are further characterized. First, we have the following results for the homogeneity.

Theorem 5.

Let$F:{\mathit{O}}^2\to \mathit{O}$be a binary operation. If F is homogeneous of order k, then

1. 

$F(0,0)=0$;

2. 

$F(\mu ,\mu )={\mu }^k·F(1,1)$;

3. 

$F(-\mu ,-\nu )=F(\mu ,\nu )$and$F(-\mu ,\nu )=F(\mu ,-\nu )$when k is an even number;

4. 

$F(-\mu ,-\nu )=-F(\mu ,\nu )$and$F(-\mu ,\nu )=-F(\mu ,-\nu )$when k is an odd number.

Proof. 

1. $F(0,0)=0^k·F(0,0)=0$.

2.

$F(\mu ,\mu )=F(\mu ·1,\mu ·1)={\mu }^k·f(1,1)$.

3.

k is an even number, then $F(-\mu ,-\nu )={(-1)}^{k}F(\mu ,\nu )=F(\mu ,\nu )$, and $F(-\mu ,\nu )={(-1)}^{k}F(\mu ,-\nu )=F(\mu ,-\nu )$.

4.

k is an odd number, then $F(-\mu ,-\nu )={(-1)}^{k}F(\mu ,\nu )=-F(\mu ,\nu )$, and $F(-\mu ,\nu )={(-1)}^{k}F(\mu ,-\nu )=-F(\mu ,-\nu )$.

□

Rotational invariance and ratio scale invariance are two special cases of the homogeneity. Moreover, they are weaker conditions than the homogeneity for complex fuzzy binary operations. Some results of Theorem 5 also can be obtained for the rotational invariance (or ratio scale invariance) of complex fuzzy operations.

Corollary 2.

If a binary operation$F:{\mathit{O}}^2\to \mathit{O}$is ratio scale invariant of order k, then

1. 

$F(0,0)=0$

2. 

$F(-\mu ,-\nu )=F(\mu ,\nu )$and$F(-\mu ,\nu )=F(\mu ,-\nu )$when k is an even number;

3. 

$F(-\mu ,-\nu )=-F(\mu ,\nu )$and$F(-\mu ,\nu )=-F(\mu ,-\nu )$when k is an odd number.

Corollary 3.

If a binary operation$f:{\mathit{O}}^2\to \mathit{O}$is rotationally invariant of order k, then, for all$\mu ,\nu \in \mathit{O}$,

1. 

$F(-\mu ,-\nu )=F(\mu ,\nu )$and$F(-\mu ,\nu )=F(\mu ,-\nu )$when k is an even number then;

2. 

$F(-\mu ,-\nu )=-F(\mu ,\nu )$and$F(-\mu ,\nu )=-F(\mu ,-\nu )$when k is an odd number then.

Moreover, we have the following characterizations for the homogeneity, rotational invariance and ratio scale invariance of a complex fuzzy binary operation.

Theorem 6.

A binary operation$F:{\mathit{O}}^2\to \mathit{O}$is homogeneous of order k if and only if it is the convex sum of a finite family of homogeneous functions of order k.

Proof. 

(⇒) F is the convex sum of itself.

(⇐) Let $F(\mu ,\nu )={\sum }_{i=1}^n{w}_i{F}_i(\mu ,\nu )$ with ${\sum }_{i=1}^n{w}_i=1$ and $w_i\in \mathbf{I}$. If $F_i$ ($i=12,...,n$) is homogeneous of order k, then, for any $\alpha \in \mathbf{O}$, and all $\mu ,\nu \in \mathbf{O}$,

$$\begin{array}{ccc}& F(\alpha \mu ,\alpha \nu )& =\sum _{i=1}^n{w}_i{F}_i(\alpha \mu ,\alpha \nu )\hfill \\ & & =\sum _{i=1}^n{w}_i{\alpha }^k{F}_i(\mu ,\nu )\hfill \\ & & ={\alpha }^k\left(\sum _{i=1}^n{w}_i{F}_i(\mu ,\nu )\right)\hfill \\ & & ={\alpha }^{k}F(\mu ,\nu ).\hfill \end{array}$$

Then, F is homogeneous of order k. □

Similarly to Theorem 6, we have the following characterizations of rotational invariance and ratio scale invariance.

Theorem 7.

A binary operation $F:{\mathit{O}}^2\to \mathit{O}$ is rotationally invariant of order k if and only if it is the convex sum of a finite family of rotationally invariant functions of order k.

Proof. 

Similar to that of Theorem 6. □

Theorem 8.

A binary operation $F:{\mathit{O}}^2\to \mathit{O}$ is scale invariant of order k if and only if it is the convex sum of a finite family of scale invariant functions of order k.

Proof. 

Similar to that of Theorem 6. □

6. Discussion

The recent development of complex fuzzy sets and logic has made us more concerned with the issue of complex fuzzy operations. An important question is: what properties does a useful complex fuzzy operation have?

First, a complex fuzzy operation should be a generation of one traditional fuzzy operation. Therefore, we should consider the question of whether the properties of the traditional fuzzy operation still hold for complex fuzzy operations, such as continuity [9] and migrativity [10]. These properties are important for both traditional fuzzy operations and complex fuzzy operations.

Second, we should consider some special properties for complex fuzzy operations, such as rotational invariance [11] and preserving orthogonality [8]. These properties are important only for complex fuzzy operations, not for traditional fuzzy operations.

Both ways will lead to a large number of properties for complex fuzzy operations. Then, it is important to clarify the relationships among these properties. Recently, we have found that the research works on these two types of properties have not been developed independently. In this paper, the complex-valued homogeneity of complex fuzzy operations not only is a general property of real-valued homogeneity of traditional fuzzy operations, but also a general property of the rotational invariance of complex fuzzy operations.

7. Concluding Remarks

In this paper, we studied the homogeneity of complex fuzzy binary operators. First, we showed that homogeneity equaled rotational invariance plus ratio scale invariance. Then, we gave three simplified versions of the homogeneity, i.e., for any $\mu ,\nu \in \mathbf{O}$, the equation $F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu )$ holds for all $\alpha \in \mathbf{O}$ if and only it holds for all $\alpha \in \mathbf{I}\cup \overline{\mathbf{O}}$ or $\alpha \in [-1,0]\cup \overline{\mathbf{O}}$ or $\alpha \in [-1,0]\cup \mathbf{V}$. Note that these subsets $\mathbf{I}\cup \overline{\mathbf{O}}$, $[-1,0]\cup \overline{\mathbf{O}}$ and $\alpha \in [-1,0]\cup \mathbf{V}$ are much smaller than $\mathbf{O}$. It will be meaningful to further discuss the simplification of the homogeneity for complex fuzzy operators.

Note that this paper focused on the homogeneity of binary complex fuzzy operators, i.e., $F(\alpha \mu ,\alpha \nu )={\alpha }^{k}F(\mu ,\nu )$. However, two variables use the same parameter $\alpha$, which restricts the potential applications of the concept of homogeneity in complex fuzzy theories. Furthermore, this paper only considered the binary complex fuzzy operators. Therefore, the following general function

$$F({\alpha }_1{\mu }_1,{\alpha }_2{\mu }_2,\cdots ,{\alpha }_n{\mu }_n)=G({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)F({\mu }_1,{\mu }_2,\cdots ,{\mu }_n)$$

is worth investigating. Moreover, there are a number of complex fuzzy aggregation operators which are useful tools in decision-making, and future research should consider the homogeneity of n-dimensional complex fuzzy aggregation operators and their applications. Naturally, other properties and their relationship with the homogeneity of complex fuzzy operators are possible topics for future consideration.