The Boundary Value Problem with Stationary Inhomogeneities for a Hyperbolic-Type Equation with a Fractional Derivative

Abstract

The paper presents an analytical solution of a partial differential equation of hyperbolic-type, containing both second-order partial derivatives and fractional derivatives of order below the second. Examples of applying the solution of a boundary value problem with stationary inhomogeneities for a hyperbolic-type equation with a fractional derivative in modeling the behavior of polymer concrete under the action of loads are considered.

1. Introduction

Differential equations with fractional derivatives are actively used in mathematical modeling of objects of various nature. The eight volumes of the publication [1] present both the main theoretical facts on the theory of fractional calculus and examples of the application of this theory in various fields of natural science. Currently, fractional spatial derivatives are used in mathematical modeling of anomalous diffusions or dispersions, and fractional time derivatives are used to model processes with <<memory>>. In particular, a partial differential equation of hyperbolic-type, containing both second-order partial derivatives and fractional derivatives of order below the second, can be applied to describe the vibration of a string, taking into account friction in a medium with a fractal geometry [2]. Differential equations with fractional derivatives play an important role in engineering problem solving [3,4], as well as in physics [5,6], finance [7,8] and even in biology [9,10]. In the present paper, this equation is used in modeling the change in the deformation-strength characteristics of polymer concrete under the action of loads. Particular cases of the problem under consideration can be found in [11]. The present results are a generalization of the author’s results [11].

2. Problem Statement and Solution Method

Let us consider in the domain $G=\left\{0\le x\le \aleph ;0\le t\le \Theta \right\}$ an inhomogeneous equation of hyperbolic-type containing a fractional derivative with respect to the variable x, that is, equations of the form:

$$\frac{{\partial }^{2}v\left(x,t\right)}{\partial t^2}+f_0\left(x\right)=\frac{{\partial }^{2}v\left(x,t\right)}{\partial x^2}+c·D_{ox}^{\gamma }v\left(x,t\right).$$

(1)

The Dirichlet (or first-type) boundary condition:

$$v\left(0,t\right)=v_0;v\left(\aleph ,t\right)=v_{\aleph }.$$

(2)

Initial conditions:

$$v\left(x,0\right)=\phi \left(x\right).$$

(3)

$$v_t^{{}^{\prime }}\left(x,0\right)=\varpi \left(x\right).$$

(4)

Here, $c;v_0;v_{\aleph }$ are constants; $D_{ox}^{\gamma }v$ is the left Riemann–Liouville fractional derivative (fractional differentiation operator) with respect to a variable x of order $\gamma \in \left(1;2\right)$:

$$D_{ox}^{\gamma }v\left(x\right)={\frac{1}{\Gamma \left(2-\gamma \right)}\left({\int }_0^x\frac{v\left(\zeta \right)d\zeta }{{\left(x-\zeta \right)}^{\gamma -1}}\right)}_{xx}^{{}^{″}}.$$

The problem solution (1)–(4) is found by the standard analytical method for solving hyperbolic equations—the method of separation of variables. That is, the problem solution (1)–(4) is the sum of the two functions:

$$v\left(x,t\right)=V\left(x\right)+w\left(x,t\right).$$

(5)

The physical meaning of the function $V\left(x\right)$ is a stationary state of the process. This function is a solution of the first boundary-value problem:

$$V^{″}\left(x\right)+c·D_{ox}^{\gamma }V\left(x\right)=f_0\left(x\right).$$

(6)

$$V\left(0\right)=v_0;V\left(\aleph \right)=v_{\aleph }$$

(7)

The physical meaning of the function $w\left(x,t\right)$ is a deviation from the stationary state. This function is a solution to the corresponding homogeneous hyperbolic equation:

$$\frac{{\partial }^{2}w}{\partial t^2}=\frac{{\partial }^{2}w}{\partial x^2}+c·D_{ox}^{\gamma }w;$$

(8)

with homogeneous boundary conditions:

$$w\left(0,t\right)=w\left(\aleph ,t\right)=0;$$

(9)

and initial conditions:

$$w\left(x,0\right)=\omega \left(x\right);\omega \left(x\right)=\phi \left(x\right)-V\left(x\right);w_t^{{}^{\prime }}\left(x,0\right)=\varpi \left(x\right).$$

(10)

For the functions $\omega \left(x\right)$ and $\varpi \left(x\right)$ from conditions (10), which determine the initial position of the points of the sample and the initial speed of the points of the sample, the following conditions must be met:

$$\omega \left(0\right)=\omega \left(\aleph \right)=0;{\omega }^{″}\left(0\right)={\omega }^{″}\left(\aleph \right)=0;\varpi \left(0\right)=\varpi \left(\aleph \right)=0;$$

$$\omega \left(x\right)\in C^2\left(0;\aleph \right);{\omega }^{‴}\left(x\right)\in C\left(0;\aleph \right);{\varpi }^{″}\left(x\right)\in C\left(0;\aleph \right).$$

The series that will be constructed below for the functions $v(x,t)$, $\frac{{\partial }^{2}v}{\partial t^2}$, and $\frac{{\partial }^{2}v}{\partial x^2}$ when solving problems (1)–(4) if the above conditions are met, will converge uniformly [12], since the fractional differentiation operator of order at most two $D^{\gamma },0<\gamma <2$ is subordinate to the second-order differentiation operator $D^2$.

We will solve problems (8)–(10) using the Fourier method (separation of variables) from [11]

$$w\left(x,t\right)=\sum _{m=1}^{\infty }{X}_m\left(x\right)\left\{A_{m}sin\left(t{\sqrt{\lambda }}_m\right){+B}_{m}cos\left(t{\sqrt{\lambda }}_m\right)\right\}.$$

(11)

There

$$X_j\left(x\right)=x+\sum _{n=1}^{\infty }{(-1)}^n\sum _{k=0}^n\frac{\left(\begin{array}{c}n\\ k\end{array}\right)c^k{\lambda }_j^{n-k}}{\Gamma (2n+2-k\gamma )}{x}^{2n+1-k\gamma };j=1;2;...$$

(12)

eigenfunctions of the problem:

$$X^{{}^{″}}\left(x\right)+c·D_{ox}^{\gamma }X\left(x\right)+\lambda X\left(x\right)=0;X\left(0\right)=0;X\left(\aleph \right)=0.$$

(13)

We use the following notation for the dot product of two functions $f\left(x\right)$ and $g\left(x\right)$:

$$⟨f\left(x\right),g\left(x\right)⟩=\underset{0}{\overset{\aleph }{\int }}f\left(x\right)·g\left(x\right)dx.$$

We find the coefficients $A_m$ and $B_m$ from Formula (11) using the dot product:

$$A_m=\frac{⟨\varpi ,X_m(\aleph -x)⟩}{\sqrt{{\lambda }_m}⟨X_m(\aleph -x),X_m⟩},B_m=\frac{⟨\omega ,X_m(\aleph -x)⟩}{⟨X_m(\aleph -x),X_m⟩};m=1;2;\cdots$$

(14)

The numbers ${\lambda }_j$ are the eigenvalues of the problem (8)–(10), or the numbers ${\lambda }_j$ are zeros of the function $\mathsf{\Lambda }$:

$$\mathsf{\Lambda }\left(\lambda \right)=\aleph +\sum _{n=1}^{\infty }{(-1)}^n\sum _{k=0}^n\frac{\left(\begin{array}{c}n\\ k\end{array}\right)c^k{\lambda }^{n-k}}{\Gamma \left(2(n+1)-k\gamma \right)}{\aleph }^{2n+1-k\gamma }.$$

The solution to problems (6) and (7) also is found by the analytical method, by reducing to the Volterra equation. A particular case $f_0\left(x\right)\equiv const$ of problems (6) and (7) was considered in [11]. Now consider the solution of problems (6) and (7) for an arbitrary continuous function $f_0\left(x\right)$. Let us integrate both parts of Equation (6) twice and substitute the boundary condition $V\left(0\right)=v_0$ from (7):

$$V\left(x\right)+\frac{c}{\Gamma \left(2-\gamma \right)}\underset{0}{\overset{x}{\int }}\frac{V\left(\zeta \right)d\zeta }{{(x-\zeta )}^{\gamma -1}}=\underset{0}{\overset{x}{\int }}\left\{\underset{0}{\overset{\xi }{\int }}{f}_0\left(\zeta \right)d\zeta \right\}d\xi +G·x+v_0.$$

Denote

$$F_0\left(x\right)=\underset{0}{\overset{x}{\int }}\left\{\underset{0}{\overset{\xi }{\int }}{f}_0\left(\zeta \right)d\zeta \right\}d\xi .$$

We obtain the integral equation

$$V\left(x\right)=u_0+G·x+F_0\left(x\right)+\frac{-c}{\Gamma \left(2-\gamma \right)}\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{1-\gamma }V\left(s\right)ds,x\in \left(0;\aleph \right).$$

(15)

This integral equation is an inhomogeneous Volterra equation of the 2nd kind with a difference kernel (a special case of the Fredholm equation). In [13], the solution of Equation (15) is written out in terms of a function of the Mittag-Leffler type:

$$E_{\rho }\left(z,\mu \right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma \left(\mu +\frac{k}{\rho }\right)}.$$

Thus, in accordance with [13], the solution to problems (6) and (7) is

$$V\left(x\right)=u_0+G·x+F_0\left(x\right)-$$

$$+(-c)\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{1-\gamma }{E}_{\frac{1}{2-\gamma }}\left[-c{\left(x-s\right)}^{2-\gamma };2-\gamma \right]\left\{u_0+G·x+F_0\left(x\right)\right\}ds.$$

That is,

$$V\left(x\right)=v_0+G·x+F_0\left(x\right)+\underset{0}{\overset{x}{\int }}\sum _{k=0}^{\infty }\frac{{\left(-c\right)}^{k+1}{\left(x-s\right)}^{2k+1-\gamma (k+1)}}{\Gamma \left((1+k)\left(2-\gamma \right)\right)}\left\{v_0+G·s+F_0\left(s\right)\right\}ds.$$

Let us transform the last expression for the function $V\left(x\right)$,

$$V\left(x\right)=v_0+v_0\sum _{k=0}^{\infty }\frac{{\left(-c\right)}^{k+1}}{\Gamma \left(\left(1+k\right)\left(2-\gamma \right)\right)}\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{2k+1-\gamma \left(k+1\right)}ds+$$

$$+G·x+G\sum _{k=0}^{\infty }\frac{{\left(-c\right)}^{k+1}}{\Gamma \left((1+k)\left(2-\gamma \right)\right)}\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{2k+1-\gamma (k+1)}·sds+$$

$$+F_0\left(x\right)+\sum _{k=0}^{\infty }\frac{{\left(-c\right)}^{k+1}}{\Gamma \left((1+k)\left(2-\gamma \right)\right)}\underset{0}{\overset{x}{\int }}{{\left(x-s\right)}^{2k+1-\gamma (k+1)}F}_0\left(s\right)ds.$$

Let us introduce the notation for the third term:

$${\check{F}}_0\left(x\right)=F_0\left(x\right)+\sum _{k=0}^{\infty }\frac{{\left(-c\right)}^{k+1}}{\Gamma \left((k+1)\left(2-\gamma \right)\right)}\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{2k+1-\gamma (k+1)}{F}_0\left(s\right)ds.$$

We simplify the expression for the first two terms of the expression for the function $V\left(x\right)$ and obtain that

$$V\left(x\right)=v_0{E}_{\frac{1}{2-\gamma }}\left(-c·x^{\left(2-\gamma \right)},1\right)+G·x·E_{\frac{1}{2-\gamma }}\left(-c·x^{\left(2-\gamma \right)},2\right)+{\check{F}}_0\left(x\right).$$

(16)

It remains for us to determine the value of the constant G in expression (16). We substitute $x=\aleph$ into the expression (16) and use the boundary condition $V\left(\aleph \right)=v_{\aleph }$ from (7) to find this constant. Then

$$G=\frac{v_{\aleph }{-v}_0·E_{\frac{1}{2-\gamma }}\left(-c·{\aleph }^{\left(2-\gamma \right)},1\right)-{\check{F}}_0\left(\aleph \right)}{\aleph ·E_{\frac{1}{2-\gamma }}\left(-c·{\aleph }^{\left(2-\gamma \right)},2\right)}.$$

(17)

We obtain an explicit expression for solving problems (1)–(4) from (11) and (16):

$$v\left(x,t\right)=v_0{E}_{\frac{1}{2-\gamma }}\left(-c·x^{\left(2-\gamma \right)},1\right)+G·x·E_{\frac{1}{2-\gamma }}\left(-c·x^{\left(2-\gamma \right)},2\right)+{\check{F}}_0\left(x\right)+$$

$$+\sum _{m=1}^{\infty }{X}_m\left(x\right)\left[A_{m}sin\left(t{\sqrt{\lambda }}_m\right){+B}_{m}cos\left(t{\sqrt{\lambda }}_m\right)\right].$$

(18)

We will dwell in more detail on an important particular case, where a time-constant external action—the function $f_0\left(x\right)$—is a polynomial:

$$f_0\left(x\right)=\sum _{n=0}^N{a}_n{x}^n.$$

In this case,

$$F_0\left(x\right)=\sum _{n=0}^N{a}_n\underset{0}{\overset{x}{\int }}\left\{\underset{0}{\overset{\xi }{\int }}{\zeta }^{n}d\zeta \right\}d\xi =\sum _{n=0}^N\frac{a_n{x}^{n+2}}{\left(n+1\right)\left(n+2\right)}.$$

Consequently,

$${\check{F}}_0\left(x\right)=\sum _{n=0}^N\frac{a_n{x}^{n+2}}{\left(n+1\right)\left(n+2\right)}+$$

$$+\sum _{k=0}^{\infty }\frac{{\left(-c\right)}^{k+1}}{\Gamma \left(\left(k+1\right)\left(2-\gamma \right)\right)}\sum _{n=0}^N\frac{a_n}{\left(n+1\right)\left(n+2\right)}\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{2k+1-\gamma \left(k+1\right)}{s}^{n+2}ds$$

Notice, that,

$$\underset{0}{\overset{x}{\int }}{\left(x-s\right)}^{2k+1-\gamma \left(k+1\right)}{s}^{n+2}ds=x^{n+2k-\gamma \left(k+1\right)+4}\frac{\Gamma \left((2-\gamma )(k+1)\right)\Gamma \left(n+3\right)}{\Gamma \left(n+2k-\gamma \left(k+1\right)+5\right)}.$$

In this way:

$${\check{F}}_0\left(x\right)=\sum _{n=0}^N\frac{a_n{x}^{n+2}}{\left(n+1\right)\left(n+2\right)}+\sum _{k=0}^{\infty }\sum _{n=1}^N\frac{{{\left(-c\right)}^{k+1}a}_n{x}^{n+2+(2-\gamma )(k+1)}\Gamma \left(n+1\right)}{\Gamma \left(n+3+(2-\gamma )(k+1)\right)}=$$

$$=\sum _{n=0}^N\frac{a_n{x}^{n+2}}{\left(n+1\right)\left(n+2\right)}+\sum _{n=1}^N{a}_n{x}^{n+2}\Gamma \left(n+1\right)\sum _{k=0}^{\infty }\frac{{\left(-c·x^{2-\gamma }\right)}^{k+1}}{\Gamma \left(n+3+\left(2-\gamma \right)\left(k+1\right)\right)}=$$

$$=\sum _{n=0}^N{a}_n{x}^{n+2}\Gamma \left(n+1\right)\left\{\frac{1}{\Gamma \left(n+3\right)}+\sum _{k1=1}^{\infty }\frac{{\left(-c·x^{2-\gamma }\right)}^{k+1}}{\Gamma \left(n+3+\left(2-\gamma \right)k1\right)}\right\}=$$

$$=\sum _{n=0}^N{a}_n{x}^{n+2}\Gamma \left(n+1\right)E_{\frac{1}{2-\gamma }}\left(-c·x^{2-\gamma },n+3\right).$$

Finally,

$${\check{F}}_0\left(x\right)=\sum _{n=0}^N{a}_n{x}^{n+2}\Gamma \left(n+1\right)E_{\frac{1}{2-\gamma }}\left(-c·x^{2-\gamma },n+3\right)$$

(19)

In particular, for $N=2$ we obtain,

$$f_0\left(x\right)=a_0+a_{1}x+a_2{x}^2;F_0\left(x\right)=\frac{a_0{x}^2}{2}+\frac{a_1{x}^3}{6}+\frac{a_2{x}^4}{12};$$

$${\check{F}}_0\left(x\right)=a_0{x}^2{E}_{\frac{1}{2-\gamma }}\left(-c·x^{2-\gamma },3\right)+a_1{x}^3{E}_{\frac{1}{2-\gamma }}\left(-c·x^{2-\gamma },4\right)+{2a}_2{x}^4{E}_{\frac{1}{2-\gamma }}\left(-c·x^{2-\gamma },5\right)$$

3. Results

The results of solving problems (1)–(4), as shown in [14,15], can be used in modeling the behavior of polymer concrete under the influence of gravity. In this case, the constants in Equation (1) have the following physical meaning: $\gamma$ is the viscoelasticity parameter of the medium; c is the viscosity modulus of the medium. As shown in [16], for polymer concrete based on polyester resin (dian and dichloroanhydride-1,1-dichloro-2,2-diethylene), the parameter values are:

$$\gamma =1.472;c=1.8.$$

The function $f_0\left(x\right)$ characterizes the external force on the polymer concrete object in the situation under consideration.

We will provide examples in which we set $\aleph =0.4$, since such a size is present in the study of various properties of building materials, in particular, in the study of the properties of polymer concrete. The values of the remaining parameters will correspond to polymer concrete based on polyester resin (diana and diacyl chloride-1,1-dichloro-2,2-diethylene).

All calculations were carried out using the high-level programming language MATLAB.

The eigenvalues of problem (13) for $\aleph =0.4$ were found as zeros of the function:

$$\Lambda \left(\lambda \right)=0.4+\sum _{n=1}^{80}{(-1)}^n\sum _{j=0}^n\frac{\left(\begin{array}{c}n\\ j\end{array}\right){\left(1.8\right)}^j{\lambda }^{n-j}}{\Gamma \left(2(n+1)-1.472j\right)}{\left(0.4\right)}^{2n+1-1.472j}.$$

Note that the case $\aleph =1$ is presented in [17], and the case $\aleph =1.5$ is presented in [11].

The graph of the function $\Lambda \left(\lambda \right)$ at $\lambda \in (0;4000)$ for the considered parameter values is shown in Figure 1.

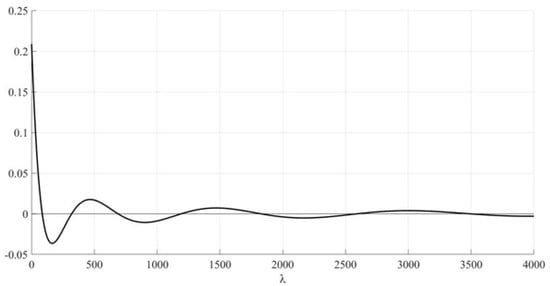
Figure 1. The function graph $\Lambda \left(\lambda \right)$ for $\lambda \in (0;4000)$.

The values of the first seven eigenvalues of problem (13) at $\aleph =0.4$; $\gamma =1.472$; $c=1.8$ are presented in Table 1.

Table 1. The first seven eigenvalues of problem (13) for $\aleph =0.4;\gamma =1.472;c=1.8$.

Designation	Values
${\lambda }_1$	85.95
${\lambda }_2$	319.99
${\lambda }_3$	689.11
${\lambda }_4$	1192.21
${\lambda }_5$	1826.89
${\lambda }_6$	2592.81
${\lambda }_7$	3488.83

The dot products values $⟨X_k(\aleph -x),X_k⟩$ at $\aleph =0.4;\gamma =1.472;c=1.8$ for the first seven eigenfunctions (12) with an accuracy of six decimal places are presented in Table 2.

Table 2. The dot products values $⟨X_k(\aleph -x),X_k⟩$ at $\aleph =0.4;\gamma =1.472;c=1.8$

k	$⟨{\mathit{X}}_{\mathit{k}}(0.4-\mathit{x}),{\mathit{X}}_{\mathit{k}}⟩$
1	0.001162
2	−0.000245
3	0.000096
4	−0.000047
5	0.000027
6	−0.000017
7	0.000011

The following three examples display the solution to problems (1)–(4).

The function $\widehat{v}\left(x,t\right)$ is taken as an approximate solution:

$$\widehat{v}\left(x,t\right)=V\left(x\right)+\sum _{k=1}^7{X}_k\left(x\right)\left[A_{k}sin\left(t{\sqrt{\lambda }}_k\right){+B}_{k}cos\left(t{\sqrt{\lambda }}_k\right)\right]$$

In accordance with Formulas (16), (17), and (19)

$$V\left(x\right)=v_0·E_{1.894}\left(-1.8·x^{0.528},1\right)+G·x·E_{1.894}\left(-1.8·x^{0.528},2\right)+{\check{F}}_0\left(x\right);$$

$${\check{F}}_0\left(x\right)=a_0{x}^2{E}_{1.894}\left(-c·x^{0.528},3\right)+a_1{x}^3{E}_{1.894}\left(-c·x^{0.528},4\right)+{2a}_2{x}^4{E}_{1.894}\left(-c·x^{0.528},5\right);$$

$$G=\frac{v_{\aleph }{-v}_0·E_{1.894}\left(-1.11,1\right)-{\check{F}}_0\left(0.4\right)}{0.4·E_{1.894}\left(-1.11,2\right)}.$$

According to Formulas (12) and (14):

$$X_k\left(x\right)=x+\sum _{n=1}^{80}{(-1)}^n\sum _{j=0}^n\frac{\left(\begin{array}{c}n\\ j\end{array}\right){\left(1.8\right)}^j{\lambda }_k^{n-j}}{\Gamma \left(2\right(n+1)-1.472j)}{x}^{2n+1-1.472j};k=1;2;...;7;$$

$$A_k=\frac{⟨\varpi ,X_k(0.4-x)⟩}{{\sqrt{\lambda }}_k⟨X_k,X_k(0.4-x)⟩};B_k=\frac{⟨\omega ,X_k(0.4-x)⟩}{⟨X_k,X_k(0.4-x)⟩};k=1;2;...7.$$

In calculations, the time step was $\Delta t=0.01$ and the spatial variable step was $\Delta x=0.002$. When calculating the function of the Mittag-Leffler type, 500 terms were used.

The relation following from (15) will be used as a test of the approximately found function $V\left(x\right)$:

$$G_{pr}=\frac{1}{\aleph }\left\{v_{\aleph }-v_0+\frac{-c}{\Gamma \left(2-\gamma \right)}\underset{0}{\overset{\aleph }{\int }}\frac{V\left(\zeta \right)d\zeta }{{(\aleph -\zeta )}^{\gamma -1}}-F_0\left(\aleph \right)\right\}$$

Example 1.

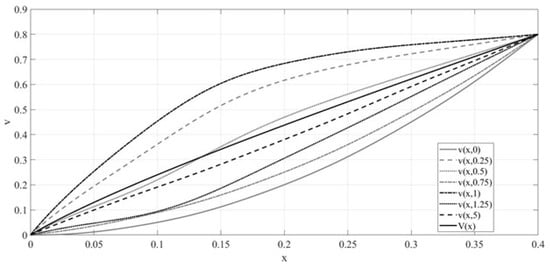
Let $\Theta =1.5;v_0=0;v_{0.4}=0.8;\phi \left(x\right)=5x^2;f_0\left(x\right)=2+x;\varpi \left(x\right)\equiv 0$

In this case,

$${\check{F}}_0\left(x\right)={2x}^2{E}_{1.894}\left(-1.8·x^{0.528},3\right)+x^3{E}_{1.894}\left(-1.8·x^{0.528},4\right)$$

Figure 2 shows the function $\widehat{v}\left(x,t\right)$, the approximate solution of problems (1)–(4).

Figure 2. The function $\widehat{v}$$\left(x,t\right)$ under the conditions of Example 1.

The values of the constants for checking the accuracy of calculations are:

$$G=3.27;G_{pr}=3.17.$$

The relative error is 3%.

Figure 3 shows the graphs of the sections of the function $\widehat{v}\left(x,t\right)$ at the time $t_0=0;$$t_1=0.25;$ $t_2=0.5;$$t_3=0.75;$$t_4=1;$$t_5=1.25;$$t_6=1.5$ and limit-state function $V\left(x\right)$.

Figure 3. The graphs of the sections of the function $\widehat{v}\left(x,t\right)$ at the time $t_0=0;$$t_1=0.25;$$t_2=0.5;$$t_3=0.75;$$t_4=1;$$t_5=1.25;$$t_6=1.5$ and limit-state function $V\left(x\right)$ in the conditions of Example 1.

Example 2.

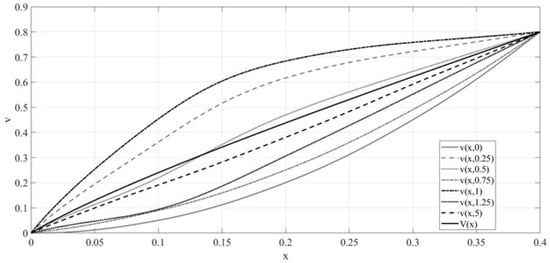
Let $\Theta =1.5;v_0=0;v_{0.4}=0.8;\phi \left(x\right)=5x^2;f_0\left(x\right)=0.4x-x^2;\varpi \left(x\right)\equiv 0$

The values of the constants for checking the accuracy of calculations are:

$$G=3.65;G_{pr}=3.64.$$

The relative error is 0.3%.

Figure 4 shows the graphs of the sections of the function $\widehat{v}\left(x,t\right)$ at the time $t_0=0;$$t_1=0.25;$ $t_2=0.5;$$t_3=0.75;$$t_4=1;$$t_5=1.25;$$t_6=1.5$ and limit state—function $V\left(x\right)$.

Figure 4. The graphs of the sections of the function $\widehat{v}\left(x,t\right)$ at the time $t_0=0;$$t_1=0.25;$$t_2=0.5;$$t_3=0.75;$$t_4=1;$$t_5=1.25;$$t_6=1.5$ and limit-state function $V\left(x\right)$ in the conditions of Example 2.

Example 3.

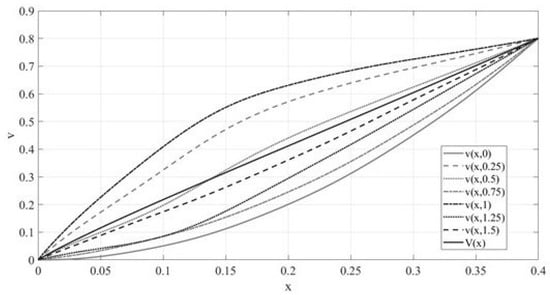
Let $\Theta =1.5;v_0=0;v_{0.4}=0.8;\phi \left(x\right)=5x^2;f_0\left(x\right)=4+0.4x-x^2;\varpi \left(x\right)\equiv 0$

The values of the constants for checking the accuracy of calculations are:

$$G=2.85;G_{pr}=2.74.$$

The relative error is 4%.

Figure 5 shows the graphs of the sections of the function $\widehat{v}\left(x,t\right)$ at the time $t_0=0;$$t_1=0.25;$$t_2=0.5;$$t_3=0.75;$$t_4=1;$$t_5=1.25;$$t_6=1.5$ and limit-state function $V\left(x\right)$.

Figure 5. The graphs of the sections of the function $\widehat{v}\left(x,t\right)$ at the time $t_0=0;$$t_1=0.25;$$t_2=0.5;$$t_3=0.75;$$t_4=1;$$t_5=1.25;$$t_6=1.5$ and limit state-function $V\left(x\right)$ in the conditions of Example 3.

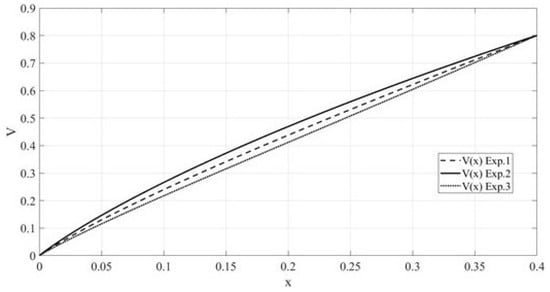
To compare the limit state under the same initial conditions and different external influences, we combine the functions $V\left(x\right)$ in the same figure under the conditions of Examples 1–3. Figure 6 shows, for comparison, the limit-state graphs under the conditions of Examples 1–3.

Figure 6. The limit-state graphs under the conditions of Examples 1–3.

4. Discussion

Thus, we have solved problems (1)–(4) by analytical methods and we have given three examples, which can be used in modeling the behavior of polymer concrete under the influence of gravity. We note that, works by [18,19] considered numerical schemes for solving partial differential hyperbolic-type equations with a fractional derivative. In [18], a generalization of the inhomogeneous Equation (1) to the case of an arbitrary external action, but for homogeneous initial and boundary conditions, is considered. In [19], approaches from [18] are used to solve a homogeneous hyperbolic-type equation with fractional derivatives of two types and with homogeneous boundary conditions of the first kind. In addition, it was shown in [19] that the numerical solutions of the equation under consideration coincided with a high degree of accuracy with the solution from the author’s work [11] for the corresponding homogeneous equation.