Abstract
Multi-secret image sharing technology shares multiple secret images among shared images for participants and the recovery requires enough shared images for fulfilling the security property. Simultaneously, the adopted Boolean method preserves high performance. The proposed (k, n, m) multi-secret image sharing scheme shares m secret images among n participants and gathering k participants’ shared images perfectly recovers these m secret images. The proposed scheme exhibits high performance because of the usage of Boolean-based processing. Moreover, the usage of a sharing matrix based strategy acquires perfect reconstruction of the secret images under (k, n) thresholds. Two proposed schemes, the source-random-mixed (SRM) and the source-random-separate (SRS) methods, are presented in this study from different strategies of sharing the random image mixed with the secret images or separated to the secret images, respectively. Moreover, the proposed SRS method exhibits the better sharing capacity. Experimental results show that the proposed schemes perform well on sharing efficiency and security.
MSC:
94A62
1. Introduction
The popular usage of multimedia content leads to a security problem on transmission or storage being increasingly more important. Secret image sharing technique, aiming to protect the multimedia content among participants, is one of the protection methods and has become an important research field [1].
The secret image sharing problem was first presented by Thien and Lin [2] with solving by the Shamir–Lagrange method [3]. The secret image sharing technique is then extended to various research areas, such as sharing among host images [4,5], sharing using Boolean operations [6,7], progressive sharing [8,9,10], sharing with visual cryptography property [11], multiple sharing [12,13], and scalable sharing [14]. Among these research topics, sharing multiple secret images efficiently is an important topic in real cases. Moreover, the Boolean-based scheme outperforms the functional-based schemes on computational complexity but is hard to achieve various properties such as (k, n) partial recovery, multiple sharing, or progressive sharing. Therefore, a Boolean-based secret image sharing scheme with (k, n) thresholds on multiple secret images sharing is very important and merits our study.
The Boolean-based approaches can be classified into two categories, the stacking-based and the XOR-based methods. The stacking-based methods [15,16,17,18], which are based on visual cryptography [19], are the least computational Boolean-based methods. However, the stacking-based methods always lead to a rough visual effect. Consequently, the XOR-based methods are the key technique having both efficient computation complexity and perfect recovered results. Therefore, our proposed method is based on XOR-based technique. Moreover, sharing matrix strategy [20] is an efficient method to achieve perfect recovery. Therefore, the proposed scheme is based on XOR operations and the concept of sharing matrix.
Over the past years, several Boolean-based approaches have been presented. Wang et al. [6] adopted simple Boolean operations to present an (n, n) threshold scheme. Chen and Wu [12] proposed a Boolean-based multiple secret image sharing method which used n − 1 secret images to generate n shared images. Collecting all shared images is the requirement of their proposed method. The Boolean-based multiple secret image sharing method [12] was then improved by Chen and Wu [13] by using a random number image generation function, which obtains the same random image from secret images or shared images. Therefore, the sharing capacity is increased due to the no random image requirement. Chen et al. [21] further modified the usage of random image generation to a Boolean-based symmetric recovery function. Notice that most previous Boolean-based schemes are mainly for (n, n) thresholds. Bao et al. [20] proposed the sharing matrix to acquire Boolean-based (k, n) secret image sharing. Prasetyo and Jing [22] present the Chinese remainder theorem and XOR-based (n, n) secret image sharing. Chattopadhyay et al. [23] acquired (n, n) secret image sharing with scalable shared images. Kabirirad and Eslami [24] present (k, n) secret image sharing with recovery by consecutive k shared images. Kabirirad and Eslami [25] proposed a Boolean-based multiple secret image sharing scheme. However, the size of the generated shared image must be the same as the secret image. Azza and Lian [26] present a multi-secret image sharing scheme using cellular automaton with steganography. Chen and Wu [27] proposed a multi-secret sharing scheme based on Boolean operation. Based on the proposed predefined access structure, the recovery of secret images does not require collection of all the shared images. Moreover, the way to construct multi-secret image sharing with general (k, n) thresholds is still not well solved.
This paper proposes a secure Boolean-based (k, n, m) multiple secret image sharing approach that shares m secret images among n shared images, and collecting k shared images perfectly recovers these m secret images. Two schemes are presented in this study: the source-random-mixed scheme (SRM) sharing the XOR result among each shared image and the random image, and the source-random-separate scheme (SRS) that shares the random image individually. Experimental results show the novel properties of the two proposed approaches. Moreover, the proposed SRS scheme outperforms others for its usage of sharing matrix on secret images distribution.
The paper is organized into the following sections. Section 2 gives a brief review of related works [20,21]. Section 3 presents details of two proposed sharing and recovery approaches, the source-random-mixed scheme (SRM) and the source-random-separate scheme (SRS). Section 4 presents the experimental results. Section 5 offers concluding remarks.
2. Review of Related Literature
This section briefly reviews the state-of-art in Boolean-based secret sharing schemes with the function of multiple images sharing. Section 2.1 introduces the secret sharing of multiple images based on the Boolean function proposed by Chen et al. [21]. Section 2.2 introduces the sharing matrix-based (k, n) secret image sharing method by Bao et al. [20].
2.1. Multiple Secret Images Sharing Scheme
Chen et al. [21] proposed a Boolean-based (n, n) secret image sharing scheme, in which n secret images are shared among n shared images and by Boolean operation. The sharing steps are introduced as follows.
- 1.
- Acquire the random image R with the secret images by Equation (1):
- 2.
- Shift the random image with different pixels to acquire a series of random images , as given in Equation (2):
- 3.
- Acquire shared images for participant i from Equation (3):
The recovery steps are introduced as follows.
- 1.
- Collect all n shared images and perform XOR operation on all shared images, as defined by Equation (4):
- 2.
- Apply the result of Equation (4) to Equations (1) and (2) to obtain a series of random images .
- 3.
- Acquire the recovered secret images by applying and to Equation (5):
The recovered secret images and original secret images are consistent when all the shared images are correctly acquired. Moreover, Chen et al.’s scheme [21] only exhibits (n, n) secret image sharing for sharing among n shared images and recovery requirement is all n shared images. For acquiring a Boolean-based and robust (k, n) secret image sharing scheme, Bao et al. [22] presented sharing an important matrix-based method, which is introduced in the next section.
2.2. Boolean-Based (k, n) Secret Image Sharing Scheme
The Boolean-based scheme is difficult to achieve with (k, n) secret image sharing when . Bao et al. [20] present a novel (k, n) secret image sharing scheme by using the proposed sharing matrix to achieve the recovery of only acquiring k shared images rather than n shared images. Assume that a secret image with size r × c is shared among n shared images with recovery thresholds (k, n); their sharing algorithm is introduced as follows.
- Generate a series of n binary sharing matrices Mi(0 ≤ i ≤ n − 1) with size r × c, in which each matrix should satisfy the following two criteria:
- Gathering k sharing matrices leads to each entry containing at least a 1 among these sharing matrices.
- Gathering less than k sharing matrices leads to at least an entry without finding a 1 among these sharing matrices.
- Encrypt the secret image I to acquire a randomlike image R.
- For a sharing matrix Mi, each entry Mi(j,k)(0 ≤ j≤ r − 1,0 ≤ k ≤ c − 1) determines the corresponding shared image entry Si(j,k), as defined in Equation (6):
Since the encrypted image R in Step 2 is a randomlike image, Step 3 acquires a shared image that is also randomlike because part of the entries of R are and other entries are random numbers. According to the novel arrangement of the sharing matrices , gathering k shared images can acquire all entries Si(j,k)(0 ≤ j ≤ r − 1, 0 ≤ k ≤ c − 1) of R and then decrypt to the secret image I perfectly. However, gathering less than k shared images cannot acquire all entries of R and the secret image cannot then be decrypted.
The recovery algorithm is introduced as follows.
- Reconstruct the same series of n binary sharing matrices Mi(0 ≤ I ≤ n − 1) as applied in the sharing algorithm.
- Acquire the encrypted image R from and by applying Equation (7)
- 3.
- Decrypt the secret image from R to acquire the recovered secret image.
In Step 2, each entry of the randomlike image R will be correctly recovered because of the property of binary sharing matrices Mi, as introduced in Step 1 of the sharing algorithm.
3. The Proposed Approach
This section introduces our proposed XOR-based (k, n, m) multi-secret image sharing scheme, in which m secret images are shared among n participants with k thresholds for perfectly recovering all secret images.
Section 3.1 introduces the generation of the sharing matrix, Section 3.2 and Section 3.3 introduce two proposed XOR-based (k, n, m) multi-secret image sharing algorithms: the source-random-mixed method (SRM) and source-random-separate method (SRS), respectively. Examples of the proposed SRS sharing and recovery with thresholds (2, 3, 2) are demonstrated in Section 3.4.
3.1. Sharing Matrix Generation
Since the sharing matrix has to acquire the property of (k, n) thresholds, all secret images are consistent in size and the sharing matrices Pi(i = 1, 2, …, n) have the following properties:
- Each sharing matrix Pi has the same size with secret images.
- Each element in Pi are either 0 or 1.
- Selecting p matrices of Pi, for example, i = 1, 2, …, p, the following criteria should be satisfied.
- 3.1
- When p ≥ k, at least one matrix has the value of 1 in all entries among these p matrices.
- 3.2
- When p < k, at least one entry has the value of 0 in all p matrices.
Above three properties construct the sharing matrices Pi(i = 1, 2, …, n) that will be used in our two proposed methods. Without loss of generality, an example of (k, n) using threshold (3, 4) and matrix size 4 × 6 is illustrated in Figure 1. The predetermined selection of n = 4 acquires 4 sharing matrices P1 to P4 and k = 3 shows that selecting 3 sharing matrices should fit the above criterion 3.1. For example, the selection of P1, P2, and P3 fits the requirement of 3.1 being at least one matrix having the value of 1 in all entries. However, the selection of , and fits the criterion of Step 3.2, with entries such as P1(1,1) = P2(1,1) = 0 or P1(2,6) = P2(2,6) = 0. Therefore, the (k, n) thresholds determine the collection of k sharing matrices acquires at least one matrix that has the value of 1 in all entries and the collection of k − 1 sharing matrices at least have the value of 0 in one entry among sharing matrices.

Figure 1.
A sharing matrix example of (3, 4) thresholds with 4 × 6 matrix size.
The sharing matrix generation algorithm, a modification of Bao et al.’s method [20], is illustrated as follows for obtaining sharing matrices Pi(i = 1, 2, …, n) for (k, n, m) thresholds with r × c secret image size.
- 1.
- Use Equation (8) to acquire an n × 1 binary vector M:
- 2.
- Acquire initial matrix N by permuting through M as Equation (9):
- 3.
- Extend one row vector of N, denoted by N(i,:), to acquire an extended matrix Ni with size r × t by using Equation (10):
- 4.
- Exchange rows of to acquire exchanged matrix :
- 5.
- Extend the matrix to fit the sizes of secret image for obtaining sharing matrix :
Figure 2 shows sharing matrices generation step by step. Since the (k, n) thresholds are (3, 4), the generated binary vector M, as shown in Figure 2a, is 4 × 1 and 2 of these 4 elements are 1, as denoted in Step 1 of Equation (8). Figure 2b shows the generated initial matrix N, as defined in Step 2 and Equation (9). Figure 2c–e shows a series of extended matrix N1, exchanged matrix , and sharing matrix , respectively. These matrices are acquired from Steps 3–5. In Figure 2c, N1 is acquired from the first row of N with one position circular shift. Moreover, Figure 2f of N2 is acquired from the second row of N with one positioned circular shift.
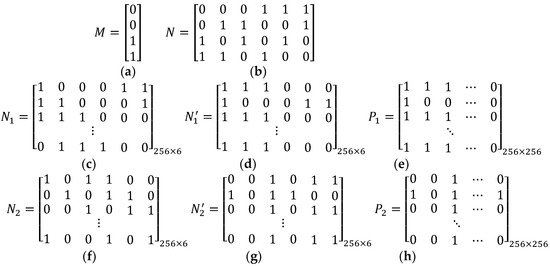
Figure 2.
An example of (3, 4) thresholds sharing matrix generation method size 256 × 256: (a) binary vector M, (b) initial matrix N, (c) extended matrix N1, (d) exchanged matrix , (e) sharing matrix , (f) extended matrix N2, (g) exchanged matrix , (h) sharing matrix P2.
Figure 3 shows the sharing strategy of the proposed algorithms. The input images Ii are processed to acquire temporary images Ei. On the other hand, sharing matrices Pi are calculated from thresholds (k, n), as introduced in Equations (8)–(12). At last, shared images Sj are acquired from temporary images Ei and sharing matrices Pi.
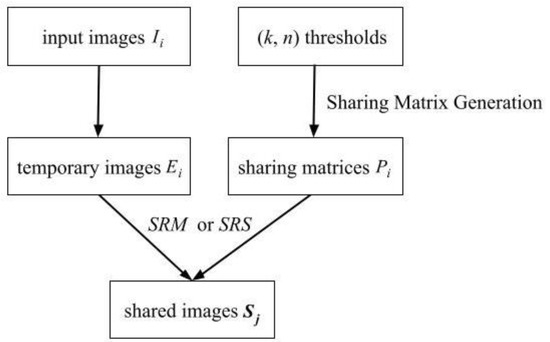
Figure 3.
Sharing strategy of the proposed two algorithms.
3.2. The Proposed (k, n, m) Source-Random-Mixed (SRM) Algorithm
This section shows our first proposed (k, n, m) SRM sharing algorithm, in which m secret images with identical size are shared among n shared images and collecting k shared images perfectly recover these n secret images. Assume all the secret images are denoted by Ii(1 ≤ i ≤ m) with the same size r × c, and the generated shared images are Sj(1 ≤ j ≤ n). The sharing matrices introduced in Section 3.1 are needed in the proposed sharing and recovery algorithms. Figure 4 shows the proposed SRM sharing steps and the proposed SRM sharing algorithm is introduced as follows.
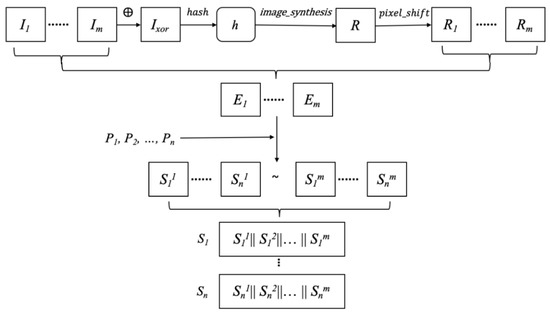
Figure 4.
Processes of the first proposed source-random-mixed (SRM) sharing algorithm.
- 1.
- Apply m secret images Ii (1 ≤ i ≤ m) to XOR operation for acquiring IXOR by Equation (13):
- 2.
- Generate a random image R by Equation (14):
- 3.
- Generate a series of randomlike images Ri (1 ≤ i ≤ m) from Equation (15):
- 4.
- A series of temporary images Ei (1 ≤ i ≤ m) are acquired from Ii and Ri by Equation (16):
- 5.
- Based on (k, n) thresholds, generate sharing matrix Pj (1 ≤ j ≤ n) from Equations (8)–(12).
- 6.
- Calculate initial shared images Sji by images Ei (1 ≤ i ≤ m) and Pj (1 ≤ j ≤ n), which is defined as:
- 7.
- Obtain shared images Sj (1 ≤ j ≤ n) by concatenating initial shared images Sji(1 ≤ I ≤ m), as shown in Equation (18):
At last, the size of Sj is m × (r × c).
Figure 5 shows a shared image example of (3, 4, 5) thresholds. In the proposed (3, 4, 5) SRM sharing method, 5 secret images are shared to 4 shared images and collecting 3 shared images perfectly recovers these 5 secret images. Figure 5a–e shows 5 secret images and Figure 5f shows one of shared image , which is a concatenation of 5 initial shared images as virtually segmented by dotted lines.

Figure 5.
Example of generated shared image by (3, 4, 5) thresholds: (a–e) secret images, (f) the generated shared image S1.
The recovery algorithm requires k shared images with the same size m × r × c. The proposed recovery algorithm of SRM is introduced as follows.
- Collect k shared images and denote them by S1, S2, …, Sk.
- Separate all collected shared images Si(1 ≤ i ≤ k) to recovered shared images Sij(1 ≤ j ≤ m) with size r × c.
- Check all entries (k, l)(1 ≤ j ≤ k, 1 ≤ l ≤ c) among the images Sij(1 ≤ j ≤ k) to acquire the temporary image . For the entry (k, l) with one of the pixel , assign by the value of If all values in the entry (k, l) are 0, then assign by 0.
- Acquire the temporary image by Equation (19):
- 5.
- Apply to Equation (14) for acquiring the random image .
- 6.
- Apply to Equation (15) for acquiring randomlike images (1 ≤ i ≤ m).
- 7.
- Apply and to Equation (20) for obtaining recovered secret images :
After applying the above recovery algorithm by k correct shared images, the recovered secret images (1 ≤ i ≤ m) are consistent with the original secret images. For the recovery of less than k correct shared images, all randomlike images are acquired. Moreover, in Step 3, the nonzero values of all (k,l)(1 ≤ i ≤ k) should be consistent when no malicious attacks on shared images are applied.
Furthermore, the proposed SRM method assigns 0 to pixels of shared images when the corresponding coordinates of the sharing matrix are 0, as shown in Equation (17). Therefore, each shared image appears dark, as shown in Figure 5f.
3.3. The Proposed (k, n, m) Source-Random-Separate (SRS) Algorithm
This section introduces our second proposed (k, n, m) source-random-separate (SRS) algorithm. The sharing matrices introduced in Section 3.1 are also needed in the proposed sharing and recovery algorithms. Figure 6 shows the proposed SRS sharing steps, and the proposed SRS sharing algorithm is introduced as follows.
- Apply m secret images Ii(1 ≤ i ≤ m) to XOR operation for acquiring IXOR by Equation (13).
- Generate a randomlike image Z with size r × c by the function image_synthesis(b,r,c) defined in Equation (14). The seed b is the same seed as used to generate the exchanged matrix in Equation (11).
- Apply the XOR operation between IXOR and Z to acquire the randomlike image by Equation (21):
- 4.
- Based on (k, n) thresholds, generate sharing matrix Pj(1 ≤ j ≤ n) by Equations (8)–(12).
- 5.
- Use Equation (22) to calculate images SRj(1 ≤ j ≤ n) by sharing matrix Pj.
- 6.
- Apply IXOR and Equation (14) to generate the random image R.
- 7.
- Generate a series of randomlike images Ri(1 ≤ i ≤ m) from the random image R by Equation (15).
- 8.
- Apply Ii and Ri by Equation (16) to obtain encrypted images Ei(1 ≤ i ≤ m).
- 9.
- Randomly select m columns from the initial matrix N in Equation (9) to acquire matrix Npart, i.e.,
- 10.
- Use Equation (24) to acquire share by the matrix value of Npart:
- 11.
- Concatenate SRj and (1 ≤ i ≤ m) to acquire shared images Sj, i.e.,
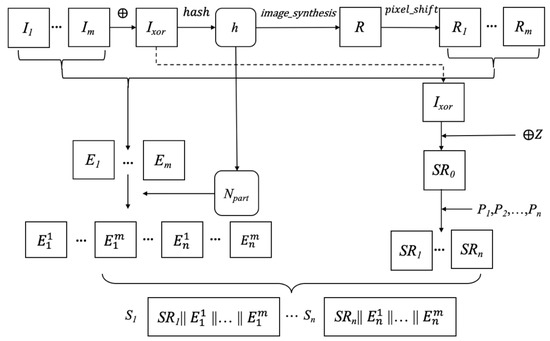
Figure 6.
Processes of the second proposed source-random-separate (SRS) algorithm.
The proposed SRS method shares XOR result IXOR and the randomlike images Ri(1 ≤ i ≤ m) with secret images Ii (1 ≤ i ≤ m) separately. Especially, in Step 10, the images are selected according to the matrix. Assume in the proposed (3, 4, 5) SRS method with the encrypted images Ei(1 ≤ i ≤ 5) and the matrix the concatenation of images is acquired from the matrix element of . In the first row, the 1st and 3rd elements being 1 leads to share From the Npart matrix, we can also acquire shares ,and Therefore, gathering 3 shares among acquires all for the further recovery processing. Furthermore, size of the shared images is determined by the number of elements containing 1 in each row of the matrix. Therefore, size of shared image is t × r × c, in which t is equal to and denoted number of elements with 1 in the j rows of matrix .
The recovery algorithm of the proposed (k, n, m) SRS is introduced as follows.
- Collect k shared images and denote them by Sj(1 ≤ j ≤ k).
- Extract each shared image with size r × c to acquire SRj(1 ≤ j ≤ k).
- Generate an initial matrix N and sharing matrix through Equations (8)–(12).
- Generate a randomlike image Z with size r × c by the function image_synthesis(b,r,c) defined in Equation (14), in which the seed b is the same seed as used to generate the exchanged matrix in sharing matrix generation step of Equation (11).
- Use Equation (26) to acquire :
- 6.
- Apply XOR operation between the and the randomlike image Z to acquire random image IXOR, i.e.,
- 7.
- Apply Equations (14) and (15) with IXOR to acquire h, R, and .
- 8.
- Apply the initial matrix N and coefficient h with Equation (23) to acquire the matrix Npart.
- 9.
- Split the remaining shared image in Step 2 to groups of r × c matrices and assign each r × c share to by Equation (28):
- 10.
- Replace by extracting the nonempty matrix to share . Moreover, two nonempty elements among r × c share should be identical.
- 11.
- Apply and to Equation (29) for covering the secret images , i.e.,
In Step 10, if two nonempty r × c sharing are not identical, at least one of the r × c shares is maliciously modified.
3.4. Examples of Sharing and Recovery of the Proposed SRS with Thresholds (2, 3, 2)
In this section, examples of the (2, 3, 2) SRS sharing and recovery processes are introduced. The first way is to generate sharing matrix by the predefined (2, 3, 2) thresholds as follows.
- Use Equation (8) to generate matrix by threshold k = 2, n = 3.
- Apply matrix to Equation (9) for acquiring matrix N, i.e.,
- 3.
- Acquire matrices N1, N2, and N3 by applying matrix N to Equation (10), i.e.,
- 4.
- Acquire exchanged matrix by applying matrices to Equation (11), i.e.,
- 5.
- Acquire sharing matrices P1, P2, and P3 by applying matrices to Equation (12):
Figure 7 shows an example of the proposed SRS method with thresholds (2, 3, 2). In the proposed (2, 3, 2) method, 2 secret images are shared among 3 shared images with XOR operations and gathering 2 of these 3 shared images perfectly recover these 2 secret images. Figure 7a,b shows two secret images with size 256 × 256 and Figure 7c,d shows two encrypted images in Step 8 of sharing algorithm. Figure 7e–g shows three generated shared images with size 256 × 512, 256 × 512, 256 × 768, respectively. The recovery of acquiring two secret images should collect 2 shared images. Applying Figure 7e,f to the proposed recovery algorithm acquires 2 secret images, as shown in Figure 7a,b.

Figure 7.
A sharing example of the proposed (2, 3, 2) SRS method: (a,b) two secret images, (c,d) two encrypted images, (e–g) shared images, (h,i) the recovered images from (e,f).
The sharing processes of the proposed (2, 3, 2) SRS method is introduced as follows.
- Apply secret images and to Equation (13) for obtaining .
- Generate randomlike image Z by Equation (14).
- Generate randomlike image by Equation (21).
- Generate the sharing matrices Pi(1 ≤ i ≤ 3) above by thresholds (2, 3, 2) with size 256 × 256 by Equations (8)–(12).
- Applying and to Equation (22) acquires .
- Apply and Equation (14) to generate the random image .
- Generate randomlike images and from the random image by Equation (15).
- Apply and by Equation (16) to obtain encrypted images , as shown in Figure 7c,d, respectively.
- Randomly select two columns of to acquire matrix .
- Apply and , to Equation (24) to generate , .
- Acquire shared images by , as shown in Figure 7e–g, respectively.
The recovery processes of the proposed (2, 3, 2) SRS method is introduced as follows.
- Collect two shared images S1 and S2.
- Extract SR1, SR2 from S1, S2 with size of 256 × 256.
- Generate the initial matrix and sharing matrix P1, P2, P3 from Equations (8)–(12).
- Generate a randomlike image Z with size r × c by Equation (14).
- Use Equation (26) with P1, P2 and SR1, SR2 to recover .
- Use Equation (27) with SR0 and Z to acquire IXOR.
- Apply Equations (14) and (15) with IXOR to acquire R1 and R2.
- Acquire the matrix .
- Assign the remaining part of shared images S1 and S2 to E1 and E2, respectively.
- Apply Equation (29) with R1, R2 and E1, E2 to recover secret images I1, I2.
4. Experimental Results and Discussions
This section demonstrates the experimental results of our proposed (k, n, m) approach. Section 4.1 presents experimental results of the proposed approach with different thresholds and recovery of attacked shared images. All experiments are performed on a PC with an Intel i7-4720HQ CPU, and 16 G RAM, using MATLAB 9.10 software. The size of all secret images is 256 × 256. Section 4.2 presents the performance of the proposed approach with comparing other multiple secret image sharing methods.
4.1. Experimental Results
Figure 8 and Figure 9 show the experimental results of two proposed schemes, the SRM and SRS methods, by sharing with thresholds (k, n, m) = (3, 4, 5) for sharing 5 secret images among 4 shared images and collecting 3 shared images that perfectly recover these 5 secret images. Figure 8 shows the results of our SRM method presented first. Figure 8a–e shows the 5 secret images: Lenna, Baboon, House, Cameraman, and Barbara with size 256 × 256. Figure 8f–i shows 4 shared images with size 256 × 1280, in which each shared image is the combination of five parts for every secret image with size 256 × 256. Therefore, the size of the shared images is proportional to the number of secret images as 5 times 256 × 256 in this example. Two kinds of recovered secret images are provided. Figure 8j–n shows 5 recovered secret images from Figure 8f–h, and Figure 8o–s shows 5 recovered secret images from the Figure 8f,g collection. Figure 8f–h fits the recovery threshold k = 3 for perfectly acquiring the images in Figure 8j–n that are identical to the original secret images. However, the collection shown in Figure 8f,g cannot satisfy the recovery threshold k = 3 and the recovered secret images all appear as noise images because of the failed acquisition of in Equation (19). Moreover, the proposed SRM method uses a sharing matrix to assign part of pixels in shared images to 0, as defined in Equation (17). Therefore, the shared images all appear darker than the random images. Moreover, because of the large usage of 0 pixels, some kinds of regularity can also be found.

Figure 8.
Results of the first proposed (3, 4, 5) SRM method. (a–e): 5 secret images with size 256 × 256; (f–i): 4 shared images with size 256 × 1280; (j–n): 5 recovered secret images from (f–h); (o–s): 5 recovered secret images from (f,g).

Figure 9.
Results of the second proposed (3, 4, 5) SRS method. (a–e): 5 secret images with size 256 × 256; (f–g): 2 shared images with size 256 × 768; (h,i): 2 shared images with size 256 × 1024; (j–n): 5 recovered secret images from (f–h); (o–s): 5 recovered secret images from (g,i).
Figure 9 shows the results of our second proposed SRS method. Figure 9a–e shows the same 5 secret images with size 256 × 256. Figure 9f–i shows 4 shared images of the parameter b = 1 in step 2 of sharing algorithm and generating matrix of size 4 × 5 as in Equation (23). The first and third elements in the first row of the matrix exhibit the element 1 and it leads the shares of and as defined in Equation (24). These two shares with the sharing of lead to the shared image with a size that is three times that of the secret image. Therefore, the first shared image is shown in Figure 9f with the size 256 × 768, which is three times the secret image size 256 × 256. Moreover, the third row of leads to the share of , , and that are needed. Consequently, four times the secret image size is obtained, as shown in Figure 9h, with the size 256 × 1024. Therefore, sizes of shared images are according to the number of elements with 1, as shown in Figure 9f–i, being 256 × 768, 256 × 768, 256 × 1024, and 256 × 1024, respectively. In the recovery process, collecting k = 3 number of shared images is needed for perfect recovery. Collecting shared images shown in Figure 9f–h recovers the reconstructed images, as shown in Figure 9j–n. The collected shared images less than k, as shown in Figure 9g,i, recover the reconstructed images, as shown in Figure 9o–s, in which all recovered images appear as noise images.
Table 1 shows the computation time of the two proposed schemes, SRM and SRS, among three different thresholds. The two proposed XOR-based schemes require limited CPU computation time, and the performances of the proposed schemes are exhibited. Moreover, the computation complexities between the two proposed schemes, SRM and SRS, are different. In our first proposed SRM method, the complexity of the sharing and recovery algorithms are O(nm) and O(km), respectively. Furthermore, the sharing and recovery complexities of our second SRS method are O(n) and O(k), respectively.

Table 1.
Performance of sharing and recovery procedures at different thresholds.
Since our second proposed SRS method outperforms our first proposed SRM method in both less computation time and smaller size of shared images, more experimental results for our second proposed SRS method are illustrated. Figure 10 shows experimental results of the proposed (3, 5, 3) SRS method by the shared images with homogeneous regions. Figure 10a–c are three generated secret images, which are constructed by simple color regions with size 256 × 256. The generated is defined by with size 5 × 3, the size that is determined by n × m under thresholds (k, n, m). From definition of the first row in , the first shared image, shown in Figure 10d, includes the random image and one share of the third secret image from Figure 10c. Therefore, the size of the first shared image is twice the secret images at 256 × 512. Moreover, Figure 10e shows the second shared image of the combination of the random image and two shares of the first and the second secret images from Figure 10a,b, respectively. Therefore, the size of the second shared image is three times that of the secret images at 256 × 768. At last, the fourth shared image, shown in Figure 10g with size 256 × 1024, includes the random image and three shares of the first, second, and third secret images from Figure 10a–c, respectively. Therefore, three different kind of sizes are found in the proposed (3, 5, 3) SRS method, as shown in Figure 10d–h, and these shared images all exhibit randomlike images. Two kinds of recovery results are also provided. Figure 10i–k are the recovered secret images from Figure 10d–f. Figure 10l–n are the recovered secret images from Figure 10g,h. Since the collected number of shared images is less than threshold k, the recovered secret images are all noiselike images that exhibit the threshold recovery property of our proposed scheme.

Figure 10.
Results of the second proposed (3, 5, 3) SRS method. (a–c): secret images with size 256 × 256; (d): the first shared image with size 256 × 512; (e,f): the second and third shared images with size 256 × 768; (g): the fourth shared image with size 256 × 1024; (h): the fifth shared image with size 256 × 512; (i–k): recovered secret images from (d–f); (l–n): recovered secret images from (g,h).
Figure 11 shows the recovery results of applying attacks on shared images of homogeneous secret images. Figure 11a–e exhibit five shared images, which are the same as Figure 10d–h as the shared images of Figure 11a–c. Figure 11f shows a malicious attack result on Figure 11a by replacing one small black block in the left area. Figure 11g–i shows the recovered shared image from Figure 11a–c. The recovery of Figure 11b,c,f is shown in Figure 11j–l, which shows that any attack leads to false recovery because of the incorrect random image generated. Therefore, security of the proposed scheme is identified.

Figure 11.
Results of the recovery of attacked shared images in the proposed (3, 5, 3) SRS method. (a–e): 5 shared images as in Figure 10d–h; (f) maliciously attacked shared image of (a); (g–i): 3 recovered secret images from (a–c); (j–l): 3 recovered secret images from (f,b,c).
4.2. Comparison and Discussion
This section compares the proposed method with other stacking or XOR-based secret image sharing methods. The comparison metrics include lossless recovery or not, recovery strategy, sharing threshold, multiple sharing or not, and sharing capacity. The stacking-based schemes generate visual similarity on recovered secret images. Therefore, only stacking-based schemes are not lossless recovery and other XOR-based methods can recover without loss all secret images. In sharing thresholds, the method of Kabirirad and Eslami [24] satisfies restrictively consecutive k shared images and only adopt sharing matrix strategies that satisfy the general (k, n) threshold property with . Other methods, such as stacking-based or XOR-based, only have (2, 2) or (n, n) thresholds. It should be noted that many related methods cannot solve the way to construct multi-secret image sharing with general (k, n) thresholds; however, the proposed multiple sharing property exhibits the structure of sharing several secret images simultaneously. In a Boolean-based (n, n) secret image sharing method, all the secret and shared images are the same size. The sharing capacity is the measurement of dividing the number of secret images by the number of shared images required to recover secret images. Therefore, in a Boolean-based (k, n) secret image sharing method, the sharing capacity is extended to dividing the size of secret images by the size of shared images required to recover secret images. Large sharing capacity means smaller shared image acquired. The sharing capacities of the proposed SRM method and SRS method are and with < n, respectively. Furthermore, the value is determined by the matrix as the number of elements with 1 in the corresponding row.
Table 2 shows that the proposed SRM and SRS methods are the only XOR and sharing matrix-based methods that can perform (k, n) thresholds on multiple sharing with good sharing capacity.

Table 2.
Comparisons between the two proposed approaches and related multiple secret image sharing methods.
Table 3 shows an example of sharing capacity comparisons between the two proposed methods and other related methods. Since some conventional methods [6,12,13,15,16,17,18,21] only have the (n, n) thresholds; therefore, these methods are restricted to (2, 2) and (3, 3) sharing capacities. Moreover, only Bao et al. [20] and our two proposed methods satisfy the requirement of (k, n) thresholds. Therefore, these three methods have (2, 3) and (3, 4) sharing capacities. Although the method of Bao et al. [20] can only share one image secretly, its sharing capacity is higher because of adopting an encryption method during the sharing process. Finally, the two proposed schemes are the only methods for sharing multiple images secretly. Moreover, the proposed SRS method outperforms the proposed SRM method on more randomly shared images and better sharing capacity.

Table 3.
Sharing capacity comparisons among the proposed approaches and related multiple secret image sharing methods.
5. Conclusions
In this study, our contribution is a novel framework that can share m secret images among n participants, and gathering k participants’ shared images perfectly recover these m secret images. We propose two XOR-based (k, n, m) multi-secret image sharing schemes. The first is the source-random-mixed (SRM) method, which mixes the random image and secret images to generate shares for each secret image. The second is the source-random-separate (SRS) method, which separates the random image and secret images for constructing the shares for each secret image. Both of the proposed schemes reach the general (k, n) threshold by the usage of a sharing matrix, which is a popular property in mathematical-calculation-based methods such as the Shamir–Lagrange-based method. The proposed schemes have the properties of lossless recovery on collecting k shared images and no useful information acquired on collecting less than k shared images. The proposed schemes outperform other multiple sharing methods on the sharing rate of larger than or equal to 1. Therefore, these two proposed schemes exhibit good improvements on sharing multiple secret images through (k, n) thresholds by using XOR and a sharing matrix based Boolean operations.
In this study, we propose two efficient XOR-based (k, n, m) multi-secret image sharing schemes; however, there are several challenges and limitations to the proposed approach. First, the size of all the secret images used in the proposed approach must be equal, the multiple shared images generated are affected by the randomly generated matrix, and the sizes of each shared image are likely to be different. Second, the performance is relatively low compared to the secret image sharing method that simply uses Boolean operations. Based on these challenges and limitations, how to improve our proposed SRS method to identical size and how to apply the proposed approach in various actual applications, such as share authentication [28,29] and e-voting [30], merit our future study.
Author Contributions
Conceptualization, C.-S.L. and C.-C.C.; methodology, C.-C.C.; validation,C.-S.L., C.-C.C. and J.-Z.C.; formal analysis, C.-S.L. and C.-C.C.; investigation, J.-Z.C.; writing—original draft preparation, writing—review and editing, C.-S.L., C.-C.C. and J.-Z.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Ministry of Science and Technology, Taiwan, Republic of China under Grants MOST-110-2221-E-032-027 and MOST-110-2221-E-032-032.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chanu, O.B.; Neelima, A. A survey paper on secret image sharing schemes. Int. J. Multimed. Inf. Retr. 2019, 8, 195–215. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Ulutas, M.; Ulutas, G.; Nabiyev, V.V. Invertible secret image sharing for gray level and dithered cover images. J. Syst. Softw. 2013, 86, 485–500. [Google Scholar] [CrossRef]
- Wu, X.; Ou, D.; Liang, Q.; Sun, W. A user-friendly secret image sharing scheme with reversible steganography based on cellular automata. J. Syst. Softw. 2012, 85, 1852–1863. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, L.; Ma, N.; Li, X. Two secret sharing schemes based on Boolean operations. Pattern Recognit. 2007, 40, 2776–2785. [Google Scholar] [CrossRef]
- Kabirirad, S.; Eslami, Z. Improvement of (n, n)-multi-secret image sharing schemes based on Boolean operations. J. Inf. Secur. Appl. 2019, 47, 16–27. [Google Scholar] [CrossRef]
- Dhara, B.C.; Chanda, B. A fast progressive image transmission scheme using block truncation coding by pattern fitting. J. Vis. Commun. Image Represent. 2012, 23, 313–322. [Google Scholar] [CrossRef]
- Fang, W.-P. Friendly progressive visual secret sharing. Pattern Recognit. 2008, 41, 1410–1414. [Google Scholar] [CrossRef]
- Huang, C.-P.; Hsieh, C.-H.; Huang, P.S. Progressive sharing for a secret image. J. Syst. Softw. 2009, 83, 517–527. [Google Scholar] [CrossRef]
- Lin, S.-J.; Lin, J.-C. VCPSS: A two-in-one two-decoding-options image sharing method combining visual cryptography (VC) and polynomial-style sharing (PSS) approaches. Pattern Recognit. 2007, 40, 3652–3666. [Google Scholar] [CrossRef]
- Chen, T.-H.; Wu, C.-S. Efficient multi-secret image sharing based on Boolean operations. Signal Process. 2011, 91, 90–97. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-J. A secure Boolean-based multi-secret image sharing scheme. J. Syst. Softw. 2014, 92, 107–114. [Google Scholar] [CrossRef]
- Wang, R.-Z.; Su, C.-H. Secret image sharing with smaller shadow images. Pattern Recognit. Lett. 2006, 27, 551–555. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.S.; Hsu, H.C.; Chen, H.W. New visual cryptography system based on circular shadow image and fixed angle segmentation. J. Electron. Imaging 2005, 14, 033018-1–033018-5. [Google Scholar] [CrossRef]
- Shyu, S.J.; Huang, S.-Y.; Lee, Y.-K.; Wang, R.-Z.; Chen, K. Sharing multiple secrets in visual cryptography. Pattern Recognit. 2007, 40, 3633–3651. [Google Scholar] [CrossRef]
- Lin, S.-J.; Chen, S.-K.; Lin, J.-C. Flip visual cryptography (FVC) with perfect security, conditionally-optimal contrast, and no expansion. J. Vis. Commun. Image Represent. 2010, 21, 900–916. [Google Scholar] [CrossRef]
- Wu, H.-C.; Chang, C.-C. Sharing visual multi-secrets using circle shares. Comput. Stand. Interfaces 2005, 28, 123–135. [Google Scholar] [CrossRef]
- Naor, M.; Shamir, A. Visual Cryptography. Proc. Int. Conf. Adv. Cryptol. 1995, 1–12. [Google Scholar]
- Bao, L.; Yi, S.; Zhou, Y. Combination of Sharing Matrix and Image Encryption for Lossless (k,n)-Secret Image Sharing. IEEE Trans. Image Process. 2017, 26, 5618–5631. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-J.; Chen, J.-L. Highly efficient and secure multi-secret image sharing scheme. Multimed. Tools Appl. 2016, 75, 7113–7128. [Google Scholar] [CrossRef]
- Prasetyo, H.; Jing, G.J. A note on multiple secret sharing using Chinese remainder theorem and exclusive-or. IEEE Access 2019, 7, 37473–37497. [Google Scholar] [CrossRef]
- Chattopadhyay, A.K.; Ghosh, D.; Maitra, P.; Nag, A.; Saha, H.N. A Verifiable (n, n) Secret Image Sharing Scheme Using XOR Operations. In Proceedings of the 2018 9th IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 8–10 November 2018; pp. 1025–1031. [Google Scholar]
- Kabirirad, S.; Eslami, Z. A(t,n)-multi secret image sharing scheme based on Boolean operations. J. Vis. Commun. Image Represent. 2018, 57, 39–47. [Google Scholar] [CrossRef]
- Bhattacharjee, T.; Maity, S.P.; Islam, S.R. Hierarchical secret image sharing scheme in compressed sensing. Signal Process. Image Commun. 2018, 61, 21–32. [Google Scholar] [CrossRef]
- Azza, A.A.; Lian, S. Multi-secret image sharing based on elementary cellular automata with steganography. Multimed. Tools Appl. 2020, 79, 21241–21264. [Google Scholar] [CrossRef]
- Chen, T.-H.; Wu, X.-W. Multiple secret image sharing with general access structure. Multimed. Tools Appl. 2020, 79, 13247–13265. [Google Scholar] [CrossRef]
- Yan, X.; Lu, Y.; Yang, C.-N.; Zhang, X.; Wang, S. A Common Method of Share Authentication in Image Secret Sharing. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2896–2908. [Google Scholar] [CrossRef]
- Jiang, Y.; Yan, X.; Qi, J.; Lu, Y.; Zhou, X. Secret image sharing with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities. Mathematics 2020, 8, 234. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, X.; Huang, Z.; Wang, L.; Xiang, Y. Multi-level multi-secret sharing scheme for decentralized e-voting in cloud computing. J. Parallel Distrib. Comput. 2019, 130, 91–97. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).