Abstract
Λ-Fractional analysis was introduced to fill up the mathematical gap exhibited in fractional calculus, where the various fractional derivatives fail to fulfill the prerequisites demanded by differential topology. Nevertheless, the various advantages exhibited by the fractional derivatives, and especially their non-local character, attracted the interest of physicists, although the majority of them try to avoid it. The introduced Λ-fractional analysis can generate fractional geometry since the Λ-fractional derivatives generate differentials. The Λ-fractional analysis is introduced to mechanics to formulate non-local response problems with the demanded mathematical accuracy. Further, fractional peridynamic problems with horizon are suggested.
Keywords:
fractional order; fractal dimension; fractional integral; fractional derivative; Riemann–Liouville fractional derivative; Λ-fractional derivative; left and right Λ-spaces; Cantor set; fractional horizon MSC:
74Β15
1. Introduction
Most of the natural materials are heterogeneous and with non-smooth geometry. Approximation models have been adopted in continuum physics, for smoothing the geometry of those physics materials. Further, a lot of theories are restricted to local action approximations, where conventional local derivatives are satisfying the postulated physics. Indeed, Noll, Truesdell et al. [1] postulated the local action axiom. Mandelbrot [2], responding to the need of adopting non-smooth geometries, closer to real physics, introduced the geometry of fractals, which are continuous geometrical objects but without smooth derivatives. There exists a broad literature concerning fractal structures and also their applications in various scientific areas, such as physics, mechanics, biology, biomechanics, economy, etc. [3,4,5,6]. Moreover, the fractals were combined with fractional calculus, just to add mathematical tools, for better analysis and numerical procedures. It is recalled that fractional calculus introduces non-local analysis, which is important in physics, especially in nano- and micro-physics. Eringen [7] proposed non-local extensions of two fundamental laws in physics: (a) the energy balance law to remain in global form and (b) a material point is considered to be attracted by all points of the body, at all past times.
Lastly, the fractal geometries were connected with fractional calculus for a better description of fractal geometries. However, fractals exhibit a non-smooth geometry. Nevertheless, fractional calculus cannot generate fractional geometry, since the fractional derivatives are not real mathematical derivatives but functional operators [8,9,10,11]. The richness of rigorous information included, not only in those references but in many other places, is valuable for any worker on fractional calculus. Those texts have been recognized as dictionaries for fractional calculus information. However, some procedures have been presented, proposing homogenization of the fractal geometries using fractional differentials [12,13,14,15]. In reality, fractional differentials do not mathematically exist, since fractional derivatives do not satisfy the prerequisites, demanded by differential geometry, for generating differentials. There exist extensions of the properties demanded from differential topology, such as the extensions of the Leibniz rule and the chain rule. However, differential topology does not accept extensions, only exact forms of the rules. The most striking is that the fractal geometrical physical objects are homogenized following local geometry through fractional calculus, inherently a non-local procedure, not capable of generating geometry, as stated by Lazopoulos [16]. The present work presents the Λ-fractional geometry of fractals and its application to mechanics. The Λ-fractional analysis is used for defining the Λ-fractional derivative and Λ-fractional space, where the Λ-fractional derivative is a local derivative equipped with all the properties of a derivative, corresponding to the differential. It would have been more prosperous for the fractional calculus worker to be able to use all the existing rigorous information. However, geometrical problems demand the existence of the differential. Hence, fractional differential geometry may be generated in the Λ-fractional space. Further, results may be transferred in the initial space. Specifically, the fractal structures will be transferred into the Λ-space. Those fractional fractal structures in the Λ-space may geometrically be transformed, following conventional differential geometry procedures. The results may be transferred into the initial space. The method has been applied to mechanics [17,18]. It should be pointed out that the present version of Λ-fractional analysis presented here has been adjusted to conform with the fractional rules that are broadly accepted. The present work discusses the idea of homogenization of fractal geometries [12,13,14,15,19,20,21,22] and considering the fractal Cantor bar concludes that the procedure fails. Nevertheless, the Λ-fractional Cantor bar could be used in physics and its geometry may be used in studying its axial deformation. Further, the Λ-fractional analysis with the horizon is introduced just to take care of possible homogenization procedures in fractal media. Hence, the Λ-fractional analysis works out, whereas the fractional homogenization procedure of fractal structures fails. The present work may be considered as a precursor for studying the homogenization procedure of the fractal continuum mechanics media.
2. The Fractional Calculus
Fractional Calculus has already been a well-organized branch of applied mathematics with many applications in physics, biology, economy, etc. There exist a lot of books for the interested reader [8,9,10,11,23], concerning the theory and its applications in various areas, offering sophisticated methods and rigorous approaches. A summary is presented.
Starting from the definition of the fractional integrals, the left and right fractional integrals for a fractional dimension 0 < γ ≤ 1 are defined by:
where Γ(γ) is Euler’s Gamma function and γ is the order of fractional integrals. There exist quite a few fractional derivatives. One of the first is the Riemann–Liouville fractional derivative (FR). Further, the left RL derivative is defined by:
Likewise, the right Riemann–Liouville’s fractional derivative (RL) is defined by:
The relation between fractional integrals and derivatives is expressed by:
The right fractional derivative and the right fractional integrals are connected by similar relations. It is quite evident that all the fractional derivatives are non-local and they yield the conventional local derivative at the point x when:
Although The RL fractional derivative does not acquire all the properties required by differential analysis, the most important defect of that derivative was considered to be its non-zero value of the constant. Hence it was proposed that the Caputo fractional derivative take care of that handicap. Caputo’s fractional derivative is defined by:
Nevertheless, that fractional derivative is very popular, although the properties of the derivative are not valid except for the linearity. There also exist some other fractional derivatives, such as Grunwald–Letnikov, Marchaud, and many others referred to in various texts [10,11].
All those derivatives are non-local and may be useful in non-local field theories. However, they lack basic properties for corresponding to differentials. So they are not able to generate differential geometry demanded by real problems.
3. The Homogenization of the Fractals Procedure
There exists an effort of embedding the fractal geometry into Euclidean geometry through fractional analysis. The idea was started by Stillinger [12] and applied by Palmer et al. [13]. Tarasov [14,21] and Balanking [15] presented the homogenized fractal spaces and embedded them into fractional spaces. Ostoja-Starzewsky et al. [18,20,22] presented continuum mechanics applications of homogenized fractal media based upon Tarasovs’ procedure. Tarasov proposed the homogenization of the mass law:
where D is the fractal dimension of the mass. Tarasov used the fractional integral for representing the mass volume in some fractal regions embedded in the Euclidean three-dimensional space. However, that embedding is mathematically questionable since fractional derivative does not exist in the mathematical sense. Indeed, fractional derivatives do not comply with the requirements of differential topology and fractional differential geometry could not be generated. Nevertheless, Tarasov [14,21] presents the homogenization of the fractals procedure and applies it in fields theory. The mass integral is defined for a fractal region W by:
the magnitude R of the position vector R, and the gamma function Γ. Further, the homogenization procedure is used to apply Green–Gauss field’s theorem, valid for local derivatives. For the one-dimensional fractals, the coefficient becomes:
Hence the mass of a fractal bar of unit length is:
Let us consider a bar of unit length with the fractal geometry of the Cantor set with fractal dimension γ = 0.6309 [23]. Then, the coefficient c equals c = 0.8805. Hence, the mass of the Cantor fractal bar, according to the homogenization procedure, is equal to:
However, it is well known that the measure of the length of the unit Cantor bar is equal to 1 [24]. Consequently, homogenization of the fractals procedure is not mathematically correct. That is due to the embedding procedure into fractional spaces, not being able to generate geometry. However, Λ-fractional derivatives generate geometry in the Λ-space since they correspond to differentials. That analysis will be presented in the next chapter.
4. The Λ-Fractional Analysis
The need for encoding fractional calculus was pointed out by Davis [25] in 1927. “The great elegance that can be secured by the proper use of fractional operators and the power they have in simplifying the solution of complicated functional equations should more than justify a more general recognition and use”. Further, at an International Conference in 1973, Ross [26,27] postulated the specific characteristics of fractional derivatives as follows:
- If f(z) is an analytic function of the complex variable z (or z = x a real variable), the derivative Dγ(f(z)) is the analytic function of γ and z.
- The operation Dγf must produce the same result as the ordinary differentiation when γ is a positive integer: Dγf(x) = fγ(x). If γ = −n, a negative integer, Dγ f(x) must produce the same result as ordinary n-fold integration, and g(x) = D(−n)f(x) must vanish together with all its n-l derivatives at x = the lower terminal of integration.
- The fractional operators must be linear.
- The operation of order zero leaves the function unchanged: Do f = f.
- The law of exponents (indices) holds for integration of arbitrary order:
D−μD−vf = D−μ−νf, Re(μ) and R(v) > O.
Nevertheless, all the well-known fractional derivatives do not access all the properties of the derivatives because they fail to satisfy differential topology rules for corresponding to differentials, generating differential geometry. Those well-known rules are Chillingworth [10]:
Atanackovic et al. [28] presented a book concerning fractional calculus with applications to mechanics. Lazopoulos [16,29,30] presented a fractional derivative satisfying both the prerequisites of differential topology in addition to the fractional postulates of the well-known fractional derivatives. The Λ-fractional analysis was proposed with the basic characteristics of the Λ-fractional derivative and Λ-fractional space where the fractional derivatives behave as local ones.
The Λ-fractional derivative (Λ-FD) is defined as:
Recalling the definition of Riemann–Liouville’s fractional derivative, Equation (3), the Λ-FD is expressed by:
Further, the Λ-fractional space is defined by (X, F(X)) with:
The Λ-FD exhibits all the properties of the conventional local derivatives in the Λ-fractional space (X, F(X)). Hence, fractional differential geometry may be generated as a conventional differential geometry in the fractional Λ-space, (X, F(X)). Then, the results may be transferred to the initial one using the relation:
Therefore, the various metrics, such as Riemannian, etc., and the frame indifference (translations and rotations) are valid in the Λ-fractional space, where the differential geometry may be any known differential geometry. No derivative exists in the initial space. On the contrary, derivatives exist in the Λ-fractional space. Then, the results may be transferred only as functions from the Λ-fractional space to the initial one.
In case the contribution of the right side fractional derivative should be taken into consideration, the Λ-fractional space may be defined with:
Just to understand the difference between the Λ-fractional derivative and the other derivatives, let us consider the function:
y = x3.
Figure 1 depicts the functions of the various derivatives, such as the conventional derivative, the fractional Riemann–Liouville derivative, and the Λ-derivative as a function in the initial space.
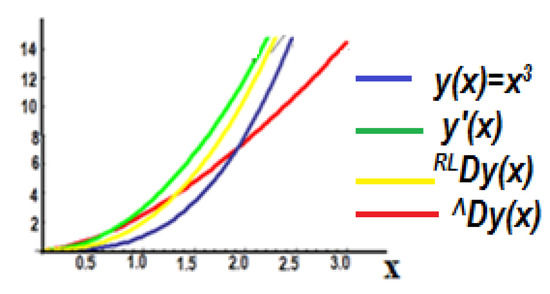
Figure 1.
The various derivatives of the function y = x3.
The blue curve indicates the function y = x3 and the green one is the conventional derivative. Furthermore, the yellow one is the well-known Riemann–Liouville fractional derivative. However, the red one is the function of the Λ-fractional derivative transferred into the initial space. The action of the Λ-fractional derivative is more intense than the other ones.
5. The Λ-Fractional Fractal Bar Extension
In the present section, the Λ-fractional deformation of a fractal bar under axial loading is discussed. Suppose that a bar, fixed at one end, is deformed by the application of an axial load p at its other end. The bar is Λ-fractionally deformed. Figure 2 shows the undeformed xo and the deformed ψ(xο) placements of the bar in the initial space.
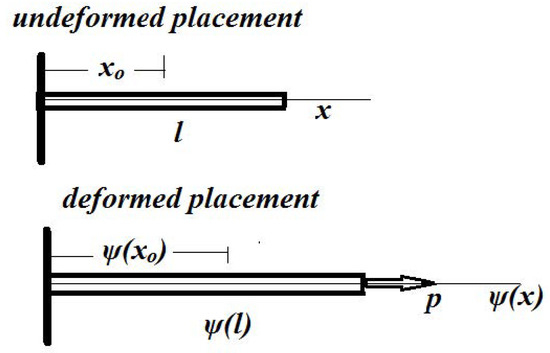
Figure 2.
The bar in the initial space.
The Λ-fractional analysis is connected with the Λ-fractional space, where the x-coordinate is transformed as:
Further, the load P in the Λ-space, corresponding to the axial load p in the initial space, is defined by:
In addition, the axial length l of the bar, in the initial space, becomes in the Λ-space:
Figure 3 shows the undeformed and deformed placements in the Λ-space.
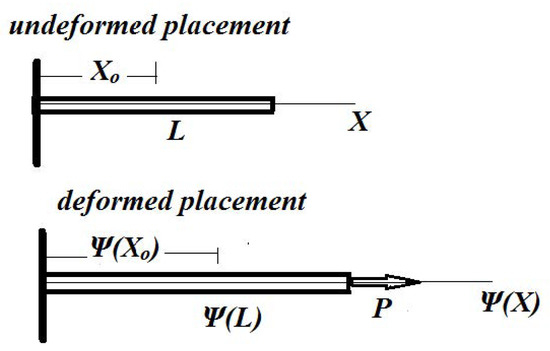
Figure 3.
The bar in the fractional Λ-space.
Moreover, the constant elastic modulus E in the initial space is transferred in the Λ-fractional space as non-constant EΛ along the x-axis. Indeed:
In addition, the constant cross section area in the initial space is transferred in the Λ-fractional space by:
Since the derivatives in the Λ-space are local, the strain of the bar in the Λ-fractional space is defined by:
Recalling further Equation (22), , the fractional strain is equal to:
Hence, Equation (28) yields:
with Y(Χ) denoting the displacement in the fractional Λ-space, with the boundary condition, Y(0) = 0. Further, Equation (29) may be expressed in the variable x of the initial space by:
Further, the displacement Y in the Λ-space may be expressed through Equation (22) as a function of the initial space. Indeed:
Recalling Equation (5), the displacement Y(X) in the Λ-space is transferred to y(x) in the initial plane (x, y) through:
Hence, the displacement field in the initial space is defined by:
For the fractal bar with dimension γ = 0.63 and with (unit length), the non-dimensional displacement y(x) has been shown in Figure 4.
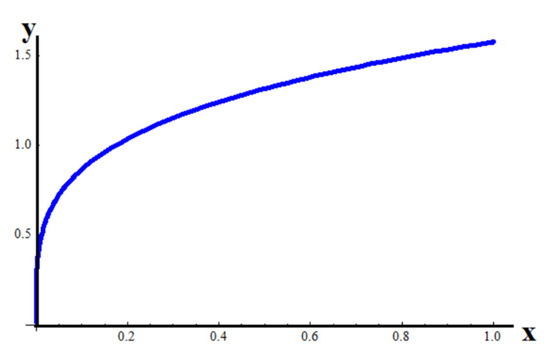
Figure 4.
The non-dimensional axial displacement of the fractional bar with γ = 0.63.
Further, for the Λ-fractional deformation for dimension γ = 0.8, the displacement function is shown in Figure 5.
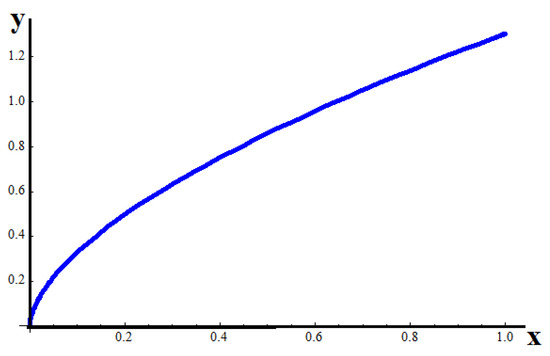
Figure 5.
The non-dimensional axial displacement of the fractional bar for γ = 0.8.
Considering that in the Λ-space the conventional mechanics’ rules are valid, the axial stress Σ(Χ) in the Λ-space is defined by:
Consequently, the axial stress, along the bar in the initial space, is defined through the relation:
Figure 6 shows the distribution of the real stresses in the initial space.
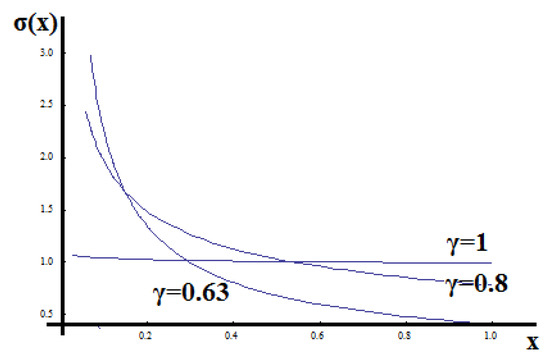
Figure 6.
The non-dimensional stresses along the x-axis of the bar.
It is evident that the present method exhibits the size effect phenomenon, which is well known by gradient theories, see Aifantis [31].
Likewise, the right RL derivative, Equation (4), may also be considered since there is not any direction preference. Figure 7 shows the stress distribution along the unit rod with fractal dimension d = 0.63 and fractal dimension d = 0.8.
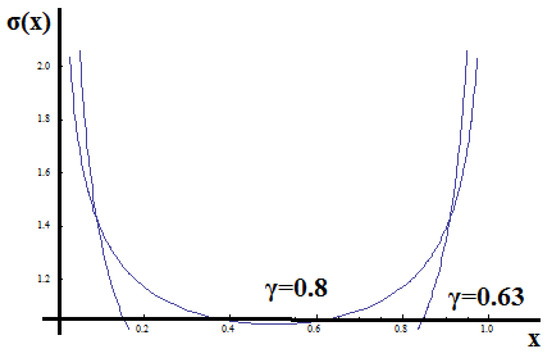
Figure 7.
Non-dimensional stress distribution of the bar with left and right.
Non-Local Action
The non-dimensional displacement of the fractional unit bar for the fractional-order γ = 0.63 is shown in Figure 8.
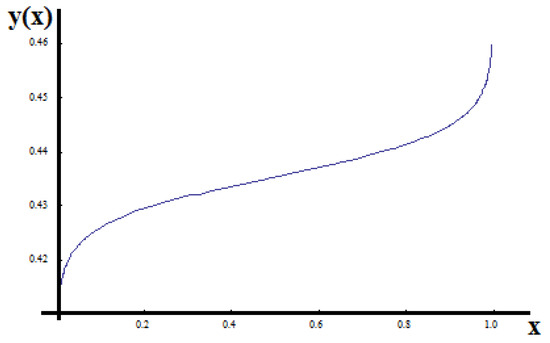
Figure 8.
The non-dimensional displacement of the symmetric fractional fractal bar of order γ = 0.63.
Figure 9 shows the distribution of the displacement field in the initial space for the left and right fractional deformation.
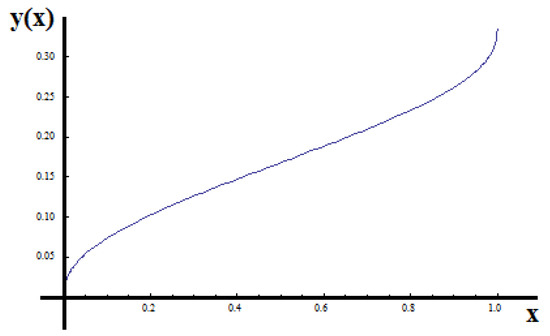
Figure 9.
The non-dimensional displacement of the symmetric fractional fractal bar of order γ = 0.80.
The present theory may be extended to any continuum media, just to describe the fractional response of fractal media.
6. The Extension of a Bar with Fractal Cross-Section Area Distribution
6.1. The Left Λ-Fractional Analysis
The present section deals with the fractional deformation of a bar with an order different from the fractal dimension of the distribution of the cross-section area of the bar. The distribution of the cross-section area along the bar is characterized by the Hausdorff dimension dH = 1.5, and it is defined by:
Restricting to n = 5 for computation reasons, the cross-section area is defined by:
Transferring the cross-section area in the Λ-space, the area function A(x) is defined by:
Recall from Equation (22):
Through the analysis of the problem, the fractional order γ = 0.6 will be considered. Then, introducing the variable X into Equation (39) through Equation (40), the area of the cross section A(X) is defined in the Λ-space as a function of X. Therefore, the fractal cross-section area a(x), Figure 10 in the initial space, is transferred into the dual Λ-space as shown in Figure 11.
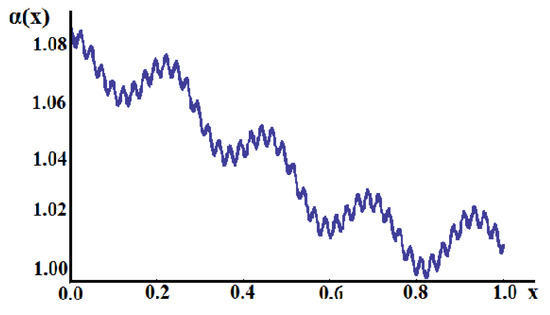
Figure 10.
The (dimensionless) distribution of the cross-sectional area a(x).
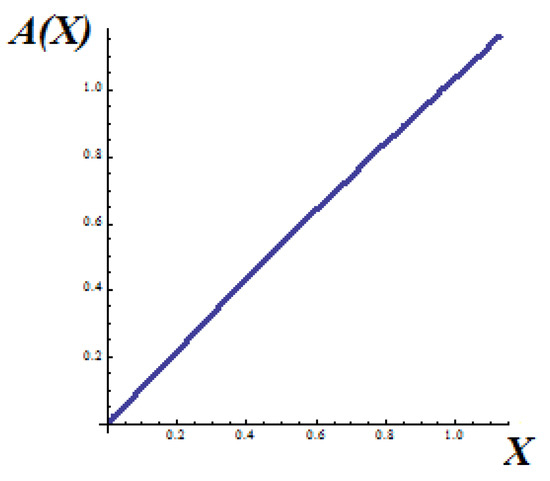
Figure 11.
The distribution of the cross-sectional area A(X) in the Λ-space.
Further, the length of the bar l in the initial space becomes L in the fractional Λ-space through Equation (24). The axial force p applied at the right end of the bar corresponds to the P load in the Λ-space defined by Equation (23). In addition, Young’s modulus of elasticity E corresponds to EΛ defined by Equation (25).
Since in the Λ-space everything works conventionally, the equilibrating axial stress in the Λ-space, shown in Figure 12, is defined by:
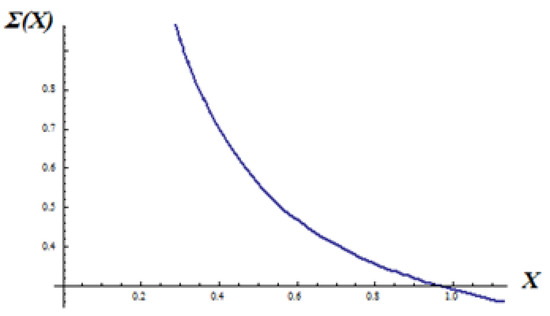
Figure 12.
The distribution of the stress Σ(X) in the Λ-space.
The real stress is applied to the initial space. Therefore, the stress Σ(Χ) function corresponding to the axial stress applied in the Λ-space is transferred as the real stress Σ(x), distributed along the bar in the initial space, and is defined through the relation:
The stress function Σ(x), applied in the Λ-space, is expressed in the variable x of the initial space. The distribution of the axial stress function Σ(x) in the initial space is shown in Figure 13.
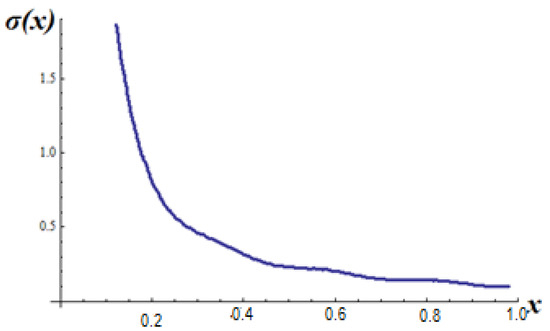
Figure 13.
The distribution of the stress Σ(x) in the initial space.
Recalling Equations (23)–(26), the strain in the Λ-space is defined by:
Let us point out that strain, as a derivative of the displacement function, is valid only in the Λ-space. No derivative exists in the initial space. However, the displacement function exists in the initial space and may be found as transferring the displacement function in the Λ-space. Therefore, integrating the strain, Equation (43), the displacement in the Λ-space is defined. Hence:
The displacement Y(X) has been computed for γ = 0.6. In addition, the displacement Y(x) in the Λ-space may be computed concerning the x variable of the initial space, which may be defined through the equation:
Further, the displacement function y(x) in the initial space is defined through the equation:
For the present case, the non-dimensional displacement is shown in Figure 14.
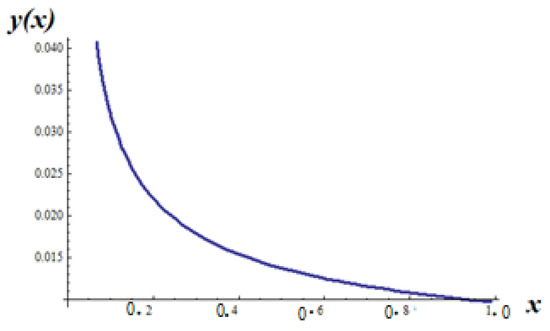
Figure 14.
The non-dimensional displacement field y(x) in the initial space.
The present problem indicates the methodology for discussing the fractional deformation of a fractal medium of different dimensions from the fractional order.
6.2. The Right Λ-Fractional Analysis
The right Λ-fractional space is defined considering the variable z = 1 − x. Then, the function α(z) denoting the distribution of the cross-section area of the fractal bar, corresponding to α(x), is defined by, see Equation (37):
Again, restricting to n = 5 for computation reasons, the cross-section area is defined by:
Transferring the cross-section area in the right Λ-space, the area function A(z) is defined by:
Recall from Equation (40):
Then, introducing the variable Z into Equation (49) through Equation (70), the area of the cross section A(Z) is defined in the Λ-space as a function of Z. Therefore, the fractal cross-section area a(z), Figure 15 in the initial space, is transferred into the dual Λ-space having the Figure 16.
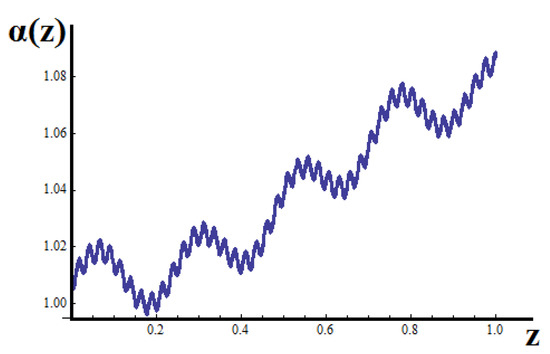
Figure 15.
The (dimensionless) distribution of the cross-sectional area α(z).
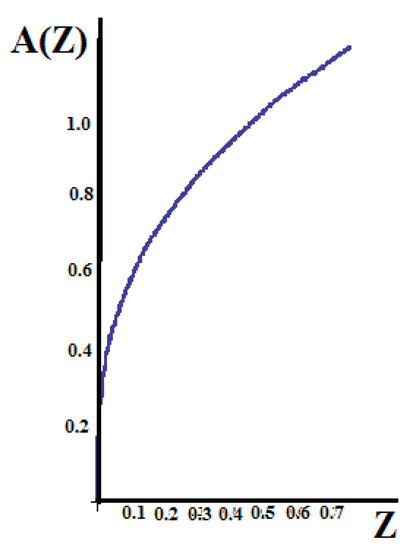
Figure 16.
The distribution of the cross-sectional area A(Z) in the Λ-space.
Further, the length of the bar l in the initial space becomes L in the fractional Λ-space through Equation (24). The axial force p applied at the right end of the bar corresponds to the P load in the Λ-space defined by Equation (23). In addition, Young’s modulus of elasticity E corresponds to EΛ defined by Equation (25).
Since in the Λ-space everything works conventionally, the equilibrating axial stress, shown in Figure 17, in the Λ-space is defined by:
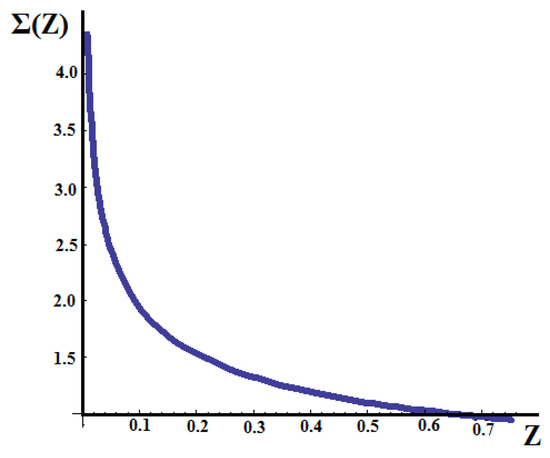
Figure 17.
The distribution of the stress Σ(Z) in the right Λ-space.
Hence, the stress Σ(Z) function corresponding to the axial stress applied in the Λ-space is transferred as the real stress, Σ(z), distributed along the bar in the initial space, and is defined through the relation:
The stress function Σ(z), applied in the Λ-space, is expressed in the variable z in the initial space. The distribution of the axial stress function Σ(z) in the initial space is shown in Figure 18.
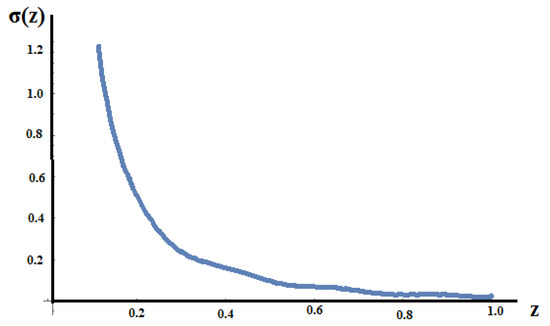
Figure 18.
The distribution of the stress Σ(z) in the initial space.
The final result concerning the stresses in the right initial space is defined reminding that z = 1 − x.
Following the same procedure as in the previous section for defining the strain, the strain in the right Λ-space is defined by:
Therefore, integrating the right Λ-fractional strain, Equation (53), the displacement in the right Λ-space is defined. Hence:
The displacement Y(X) has been computed for γ = 0.6. In addition, the displacement Y(z) in the Λ-space may be computed concerning the z variable of the initial space, which may be defined through the equation:
Further, the displacement function y(z) in the initial space is defined through the equation:
For the present case, the non-dimensional displacement is shown in Figure 19.
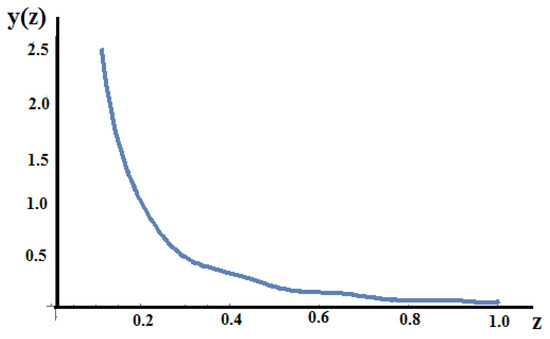
Figure 19.
The non-dimensional displacement field y(z) in the initial space.
However, recalling that z = 1 − x, Figure 19 is transferred into the x initial plane with Figure 20.
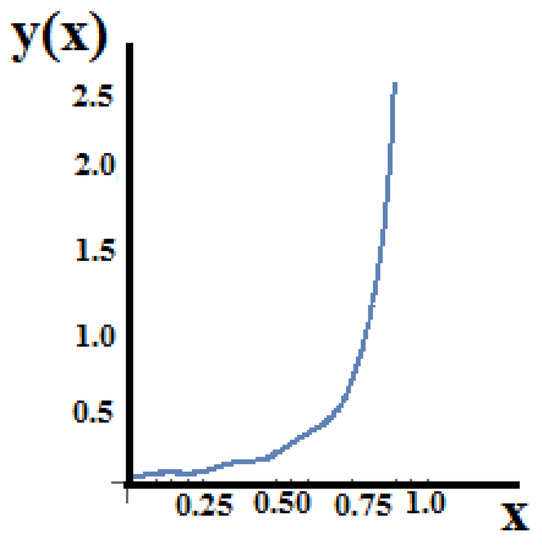
Figure 20.
The displacement field y(x) in the initial space.
The next step is the interconnection and combination of the left and right fractional Λ-solutions.
6.3. The Two Side Λ-Fractional Analysis
The final results in stresses and displacements in the initial space are defined as the mean values of the left and right results. Therefore, recalling Figure 13 concerning the stresses in the left initial space and Figure 18 indicating the distribution of the stresses in the right initial space, the distribution of the stresses in the fractal bar, that is the mean value of the left and right distribution of the stresses, is described in Figure 21.
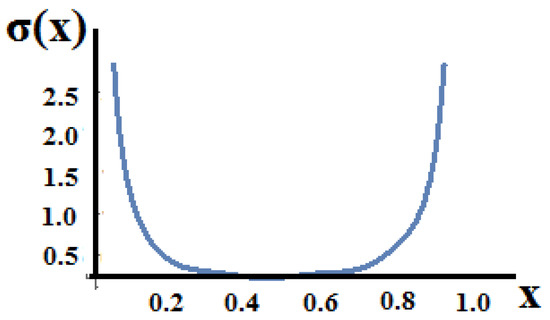
Figure 21.
The distribution of the two side fractional stresses along the fractal bar.
The maximum stresses are located around the poles.
Further, proceeding to the final distribution of the displacement field is the mean value of the left and right distribution of the displacement fields of the fractal bar, as shown in Figure 22.
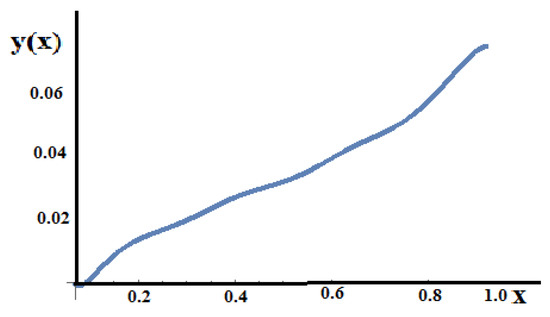
Figure 22.
The distribution of the two side fractional stresses along the fractal bar.
The present chapter completes the discussion of the Λ-fractional deformation of the fractal bar, which may also serve as a model for the discussion of Λ-fractional deformation of any structure.
7. Λ-Fractional Deformation with a Horizon
Fractional analysis has been applied to homogenize fractals media. Indeed, Ostoja-Starzewsky et al. [18,20,22] used Tarasov’s [14,21] homogenization of fractal spaces. Nevertheless, Tarasov’s proposal contradicts measure theory [24] because the length of Cantor’s rod is found as different from a unit, contrary to the exact mathematical procedure. Therefore, that approach is not reliable.
Trying to develop a mathematically correct procedure similar to the homogenization of the fractals into the context of fractional analysis, an analog of peridynamic theory Refs. [32,33] is proposed in the Λ-fractional analysis. Indeed, horizon h is considered in the Λ-space in the various problems with fractal functions. Let us consider a function f(x) in the initial space (x, f(x)). The corresponding function in the Λ-fractional space is defined by (X, F(X)). Nevertheless, for the existence of a horizon h, the function f(x) corresponds, in the Λ-fractional space, to F(X) − F(X − h) function. In addition, the derivatives of the functions F(X) in the Λ-fractional space are local. Further, Taylor expansion of the F(X − h) yields with horizon h << 1:
F(X − H) ≈ F(X) − F′(X)H + o(h).
Therefore, the function in the Λ-fractional space with the horizon h becomes:
F(X) − F(X − H) = F′(X)H.
Let us apply the proposed method of Λ-fractional analysis to the extension of the Cantor rod under axial load p applied to its end. Considering the constant cross-section area a in the initial space, the corresponding cross-section area A in the Λ-fractional space is defined by:
Therefore, the corresponding load P in the Λ-fractional space is defined by:
Then, the stress S(X) in the Λ-space is defined by:
Further, the Λ-fractional stress Σ(Χ) with horizon H is defined by:
The non-dimensional diagram of the Λ-fractional stress Σ(Χ) in the Λ-space, with, , is shown in Figure 23.
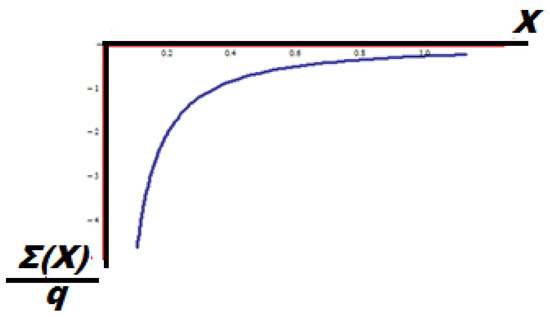
Figure 23.
The diagram of the Λ-fractional stress Σ(Χ) in the Λ-space.
It is quite strange that the values of the Λ-fractional stress with horizon H in the Λ-space are negative. Likewise, the stress Σ(x) in the Λ-space expressed with the variable x of the initial space is:
Hence, the true stress Σ(x) in the initial space is defined by:
The left Λ-fractional stress in the initial space with is shown in Figure 24.
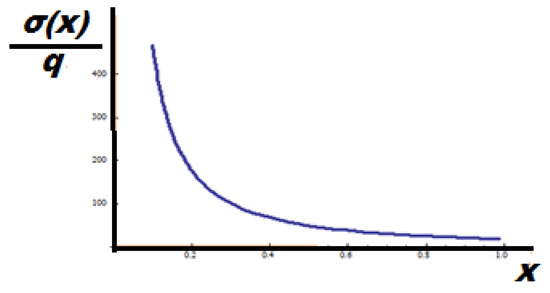
Figure 24.
The diagram of the true stress in the initial space.
Proceeding, the average of the left and right fractional stresses is shown in Figure 25.
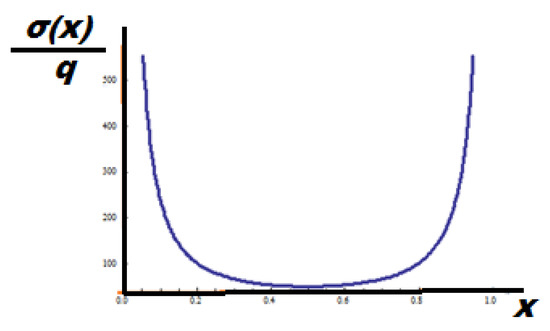
Figure 25.
The average left and right fractional stresses in the initial space with a horizon.
Those stresses are the true stresses for the fractional tension of the Cantor rod in the initial space.
Proceeding further, to the definition of the displacement field in the initial space, Young’s modulus EΛ in the Λ-fractional space is defined by, see Equation (59):
Then, the strain εΛ in the Λ-fractional space is defined by:
In addition, the Λ-fractional strain εΛH with horizon H is defined by:
Furthermore, the displacement in the Λ-fractional space is defined by:
Expressing the displacement in the Λ-space Y(x) with the variable x of the initial space through:
The displacement in the initial space is defined through the relation:
The left Λ-fractional displacement of the Cantor rod is shown in Figure 26.
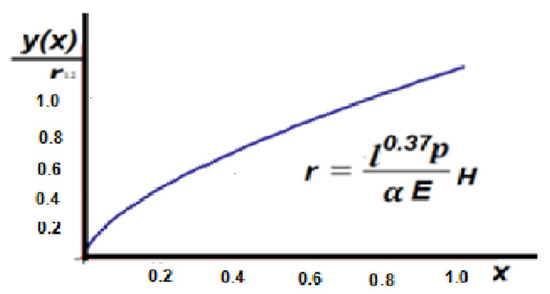
Figure 26.
The left Λ-fractional displacement of the Cantor rod in the initial space.
Further, the average left and right displacement of the extended Cantor rod is shown in Figure 27.
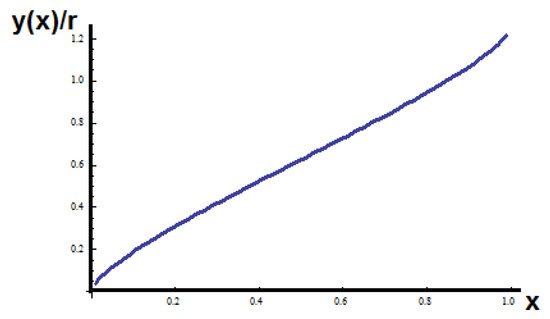
Figure 27.
The average left and right Λ-fractional displacement of the Cantor rod in the initial space.
The present section introduces the fractional deformation of a body with horizon. The present theory may be transferred into fractional deformation problems with horizon.
8. Conclusions
The relation between fractional calculus and fractal geometries is explored in the present study. Specifically, the idea of using fractional calculus for the homogenization of fractal structures is discussed. It is pointed out that fractional calculus is a non-local analysis, contrary to the homogenization procedure, considered as local. Further, fractional derivatives do not satisfy the prerequisites of differential topology for corresponding to differentials. Therefore, fractional differential geometry does not exist and its use in real problems is not correct. Nevertheless, a homogenization fractal method has been presented and supported in physics and mechanics [12,13,14,15,18,20,21,22]. That method accepts differential in fractional calculus, not mathematically existing. In addition, it uses a non-existing “differential” in a non-local (fractional) analysis to generate a local analysis of fractal geometries. Further, that method allows the application of field theorems valid in the conventional local analysis. The proposed homogenization method of fractals fails as a mathematical tool.
Applying Λ-fractional analysis with the Λ-fractional derivative and Λ-fractional space, the non-local fractional calculus in the initial space is transformed into conventional calculus in the Λ-space. The results may be transferred into the initial space. That analysis has been applied to a fractal rod of constant cross section and under axial deformation. Further, the procedure has been applied to a rod with a fractal distribution of the cross-section area along the bar. The applications indicate how Λ-fractional analysis and fractal geometries may co-operate, contrary to the existing homogenization procedure, which is a non-convincing concept. The Λ-fractional analysis with horizon is introduced to take care of the deformation of the fractal structures with horizon. The presented theory may be applied to fractional problems in continuum mechanics of fractal media.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
No conflict of interest exists in the present study.
References
- Truesdell, C.; Noll, W. The non-linear field theories of mechanics. In Handbuch der Physik, Vol. III/3; Berlin, S., Ed.; Springer: Berling, Germany, 1965. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1983. [Google Scholar]
- Aharony, A. Fractals in Physics. Europhys. News 1986, 17, 41–43. [Google Scholar] [CrossRef] [Green Version]
- Havlin, S.; Buldyrev, S.V.; Goldberger, A.L.; Mantegna, R.N.; Ossadnik, S.M.; Peng, C.K.; Simons, M.; Stanley, H.E. Fractals in Biology and Medicine; Elsevier: Amsterdam, The Netherlands, 1995; Volume 6, pp. 171–201. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Orlando, FL, USA, 1998. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA; London, UK, 1988. [Google Scholar]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations (An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications); Academic Press: San Diego, CA, USA; Boston, MA, USA; New York, NY, USA; London, UK; Tokyo, Japan; Toronto, OH, USA, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Stillinger, F.H. Axiomatic basis for spaces with non-integer dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Palmer, C.; Stavrinou, P.N. Equations of motion in a non-integer-dimensional space. J. Phys. A 2004, 37, 6987–7003. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields, and Media; Springer-Verlag: Berlin, Germany, 2010. [Google Scholar]
- Balankin, A.A. Continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. B 2015, 88, 90. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. On the Mathematical Formulation of Fractional Derivatives. Prog. Fract. Diff. Appl. 2019, 5, 261–267. [Google Scholar]
- Lazopoulos, K.A.; Lazopoulos, A.K. On plane Λ-fractional linear elasticity theory. Theor. Appl. Mech. Lett. 2020, 10, 270–275. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Electromagnetism on anisotropic fractal media. ZAMP 2012, 64, 381–390. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. On fractional bending of beams with Λ-fractional derivative. Arch. Appl. Mech. 2020, 90, 573–584. [Google Scholar] [CrossRef]
- Ostoja-Starzewsky, M.; Li, J.; Demmie, P. Continuum Homogenization of Fractal Media, Handbook of Nonlocal Continuum Mechanics for Materials and Structures; Vojadjis, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 904–935. [Google Scholar]
- Tarasov, V. Anisotropic fractal media by vector calculus in non-integer dimensional space. J. Math. Phys. 2014, 55, 083510. [Google Scholar] [CrossRef] [Green Version]
- Ostoja-Starzewski, M.; Li, J.; Joumaa, H.; Demmie, P. From fractal media to continuum mechanics. ZAMM 2014, 94, 401–573. [Google Scholar] [CrossRef]
- Carpinteri, A.; Mainardi, F. Fractals and Fractionals in Continuum Mechanics; CISM Courses and Lectures, No378; Springer: Wien, Austria, 1997. [Google Scholar]
- Kolmogorov, A.; Fomin, S. Introductory Real Analysis; Dover: New York, NY, USA, 1970. [Google Scholar]
- Davis, H.T. The application of fractional operators to fractional equations. Amer. J. Math. 1927, 49, 123–142. [Google Scholar] [CrossRef]
- Ross, B. (Ed.) Fractional Calculus and Its Applications; Lecture notes of Mathematics, No 457; Springer: Berlin, Germany, 1974. [Google Scholar]
- Ross, B. The development of fractional calculus 1695–1900. Hist. Math. 1977, 4, 75–89. [Google Scholar] [CrossRef] [Green Version]
- Atanackovic, T.; Philipovic, S.; Stankovic, B.; Zorica, D. Fractional Calculus with Applications in Mechanics, Vibrations and Diffusion Processes; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lazopoulos, K.A.; Lazopoulos, A.K. On Λ-fractional Elastic Solid Mechanics. Meccanica 2021, online. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. On fractional geometry of curves. Fractal Fract. 2021, 5, 161. [Google Scholar] [CrossRef]
- Aifantis, E.C. On the Microstructural Origin of Certain Inelastic Models. J. Eng. Mater. Technol. 1984, 106, 326–330. [Google Scholar] [CrossRef]
- Silling, S.A.; Zimmermann, M.; Abeyaratne, R. Deformation of a Peridynamic Bar. J. Elast. 2003, 73, 173–190. [Google Scholar] [CrossRef]
- Silling, S.A.; Lehoucq, R.B. Peridynamic Theory of Solid Mechanics. Adv. App. Mech. 2010, 5, 73–168. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).