Mathematical Modeling to Study Optimal Allocation of Vaccines against COVID-19 Using an Age-Structured Population
Abstract
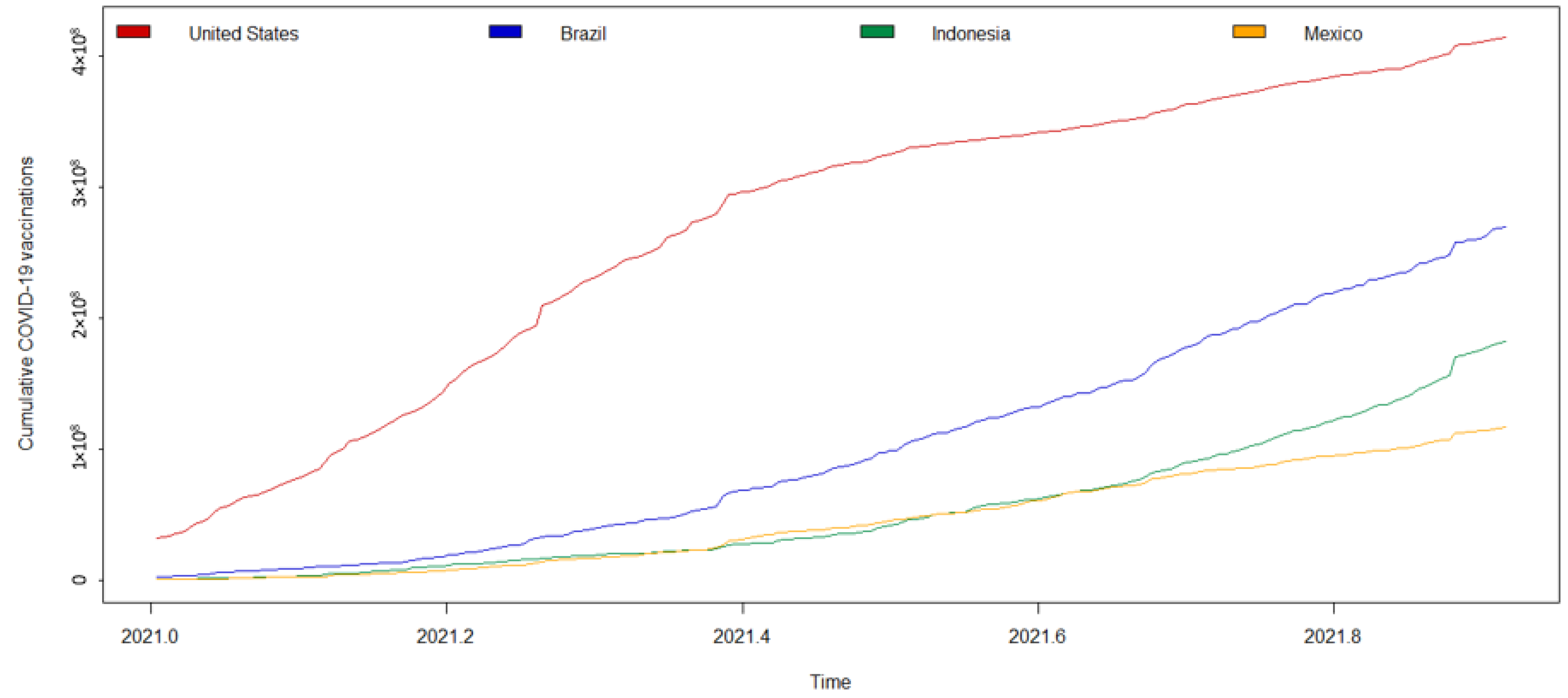
1. Introduction
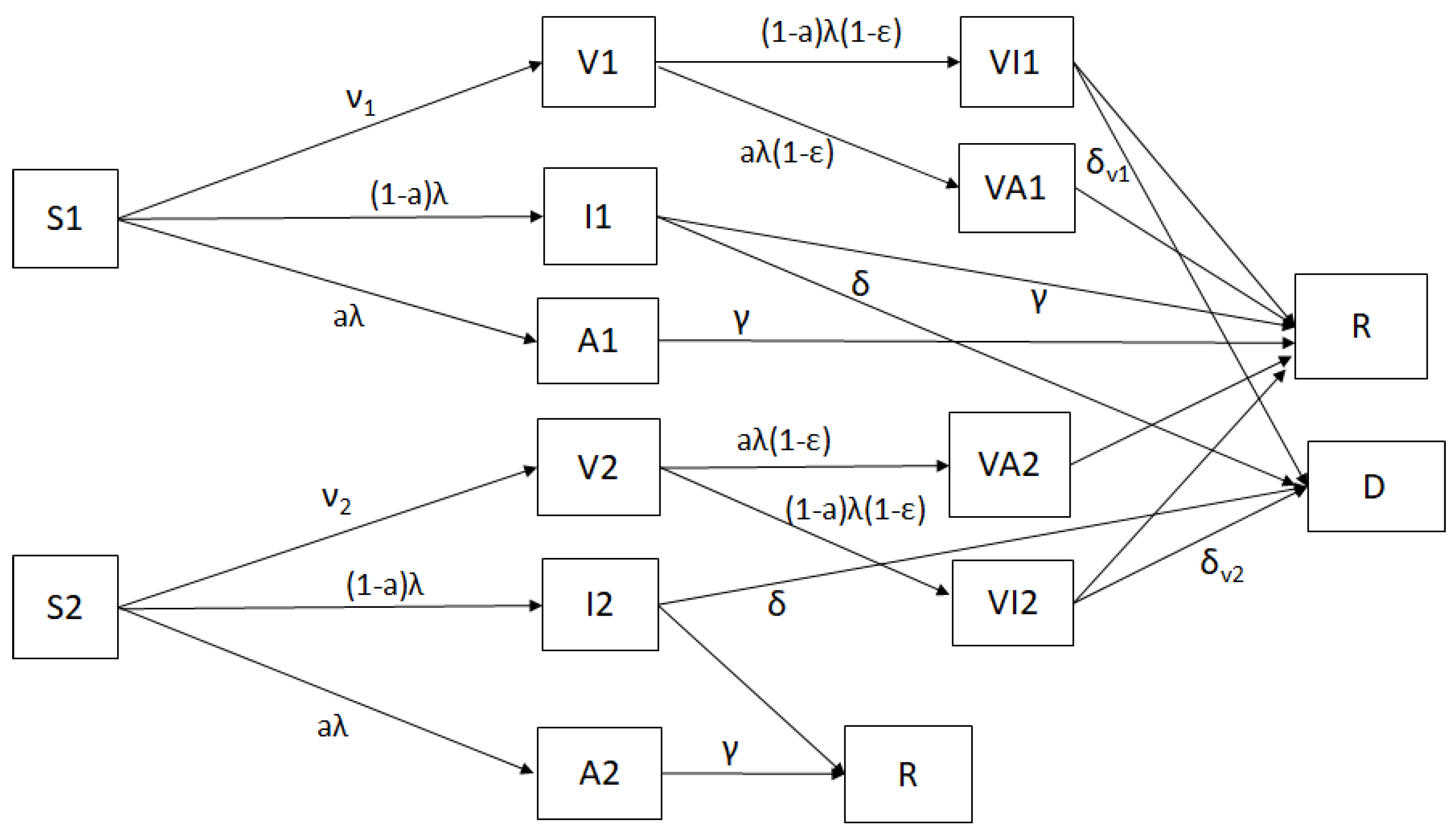
2. Materials and Methods
Positive Solutions
3. Results
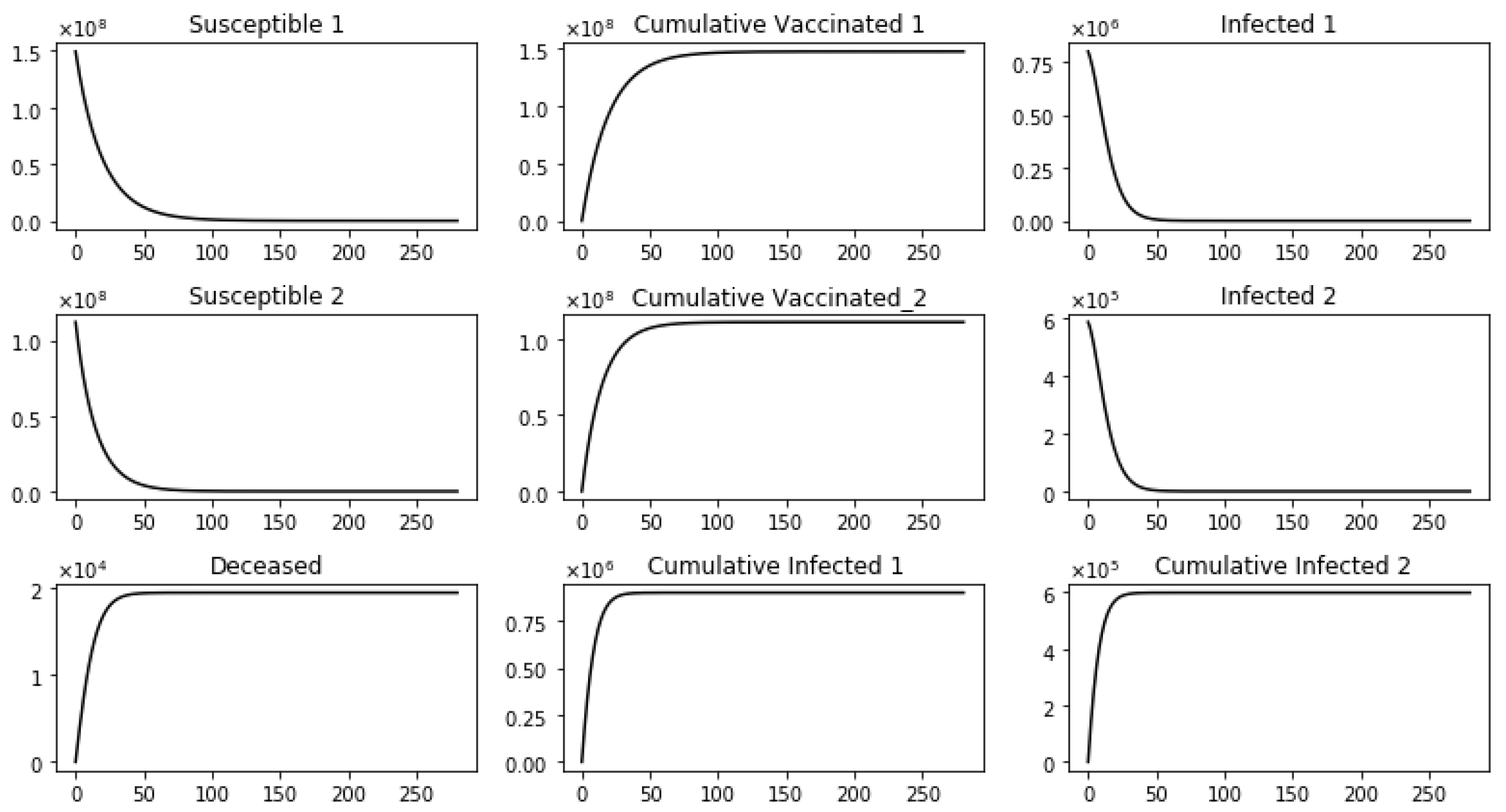
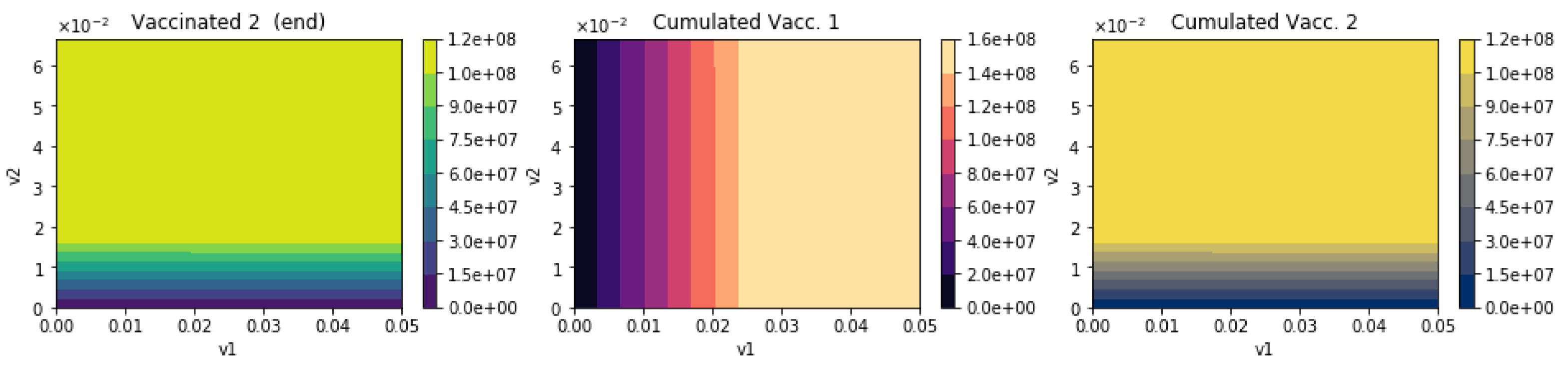
3.1. Scenarios with Proportional Vaccination Rates
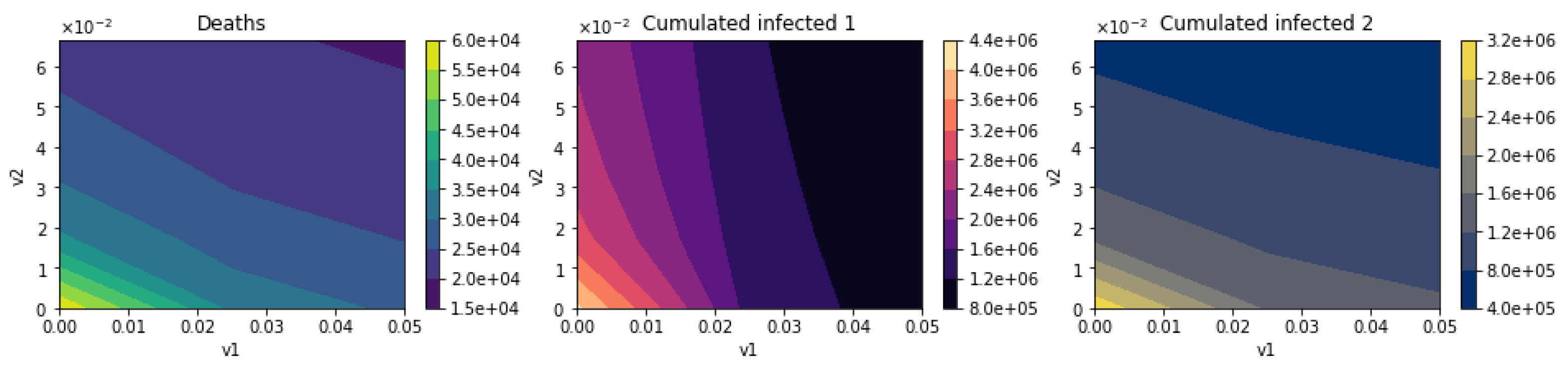
3.2. Scenarios with Fixed Numbers of Vaccines
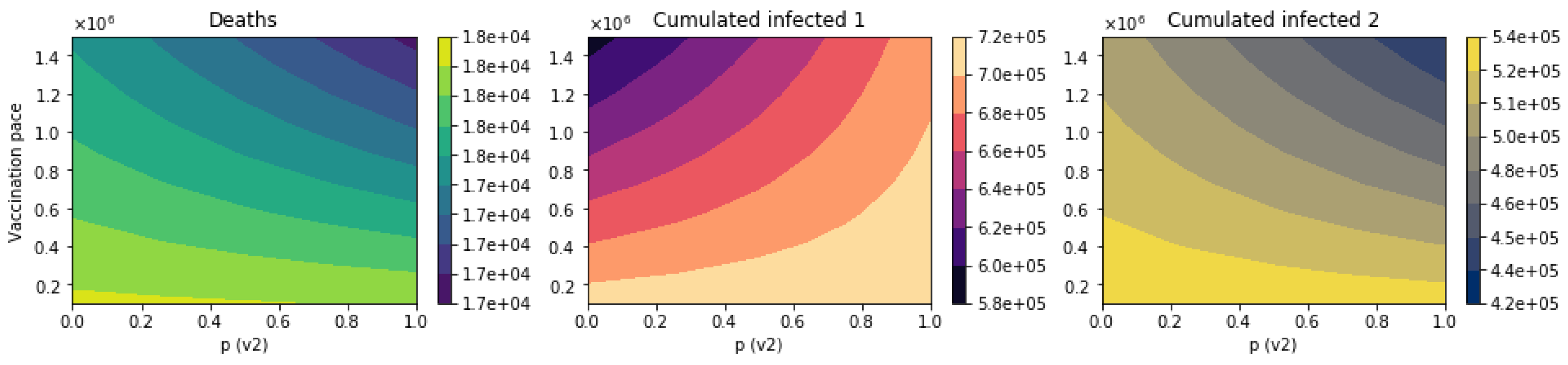
3.2.1. Scenarios Varying Vaccination Pace
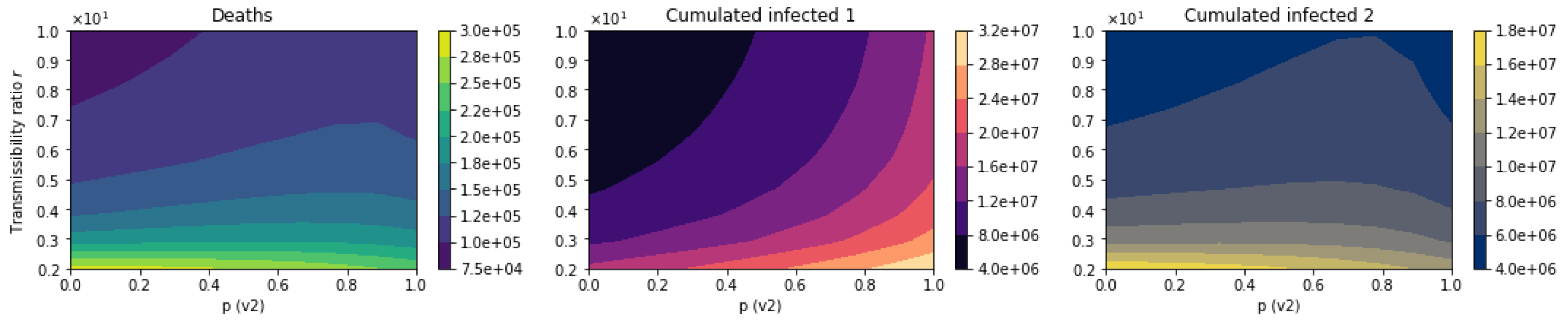
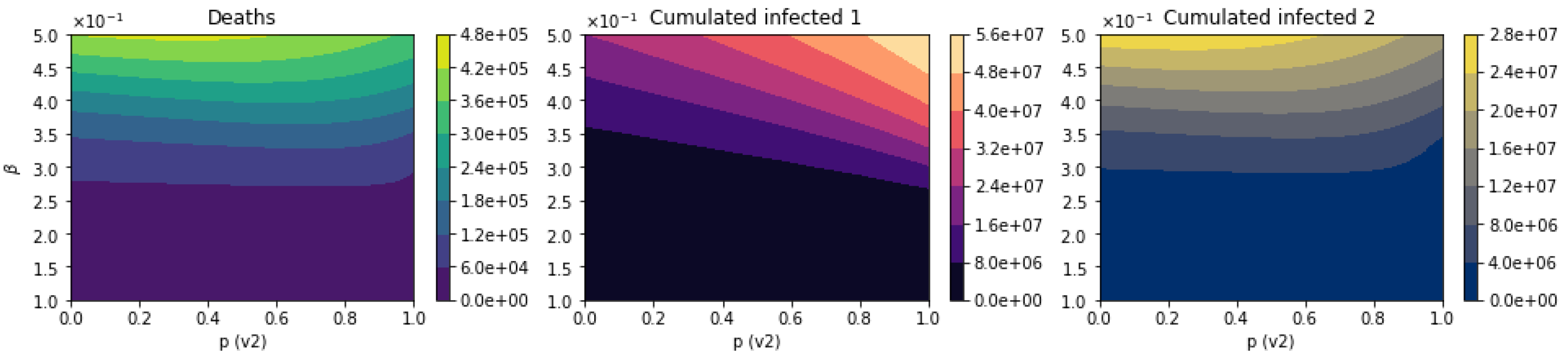
3.2.2. Scenarios Varying the Transmission Rate of the Age Group
3.2.3. Scenarios Varying SARS-CoV-2 Transmission Rate
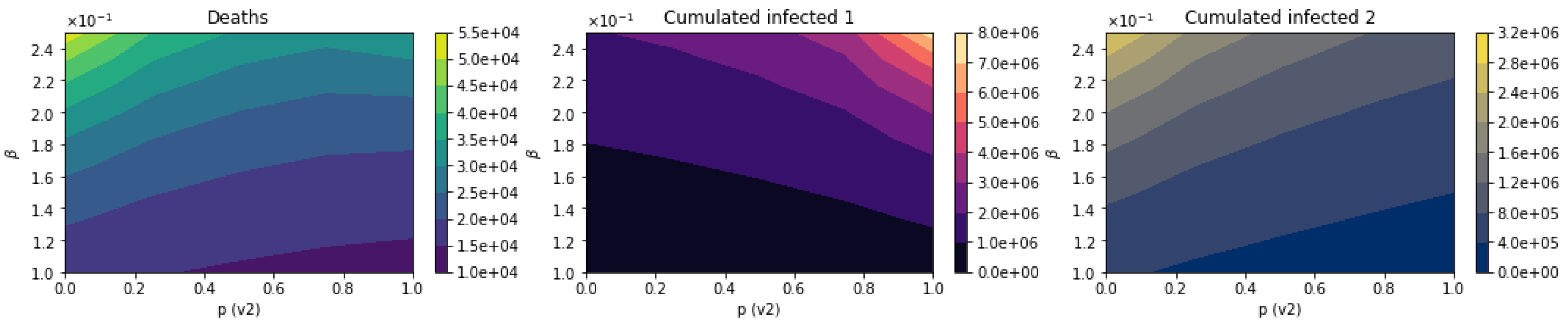
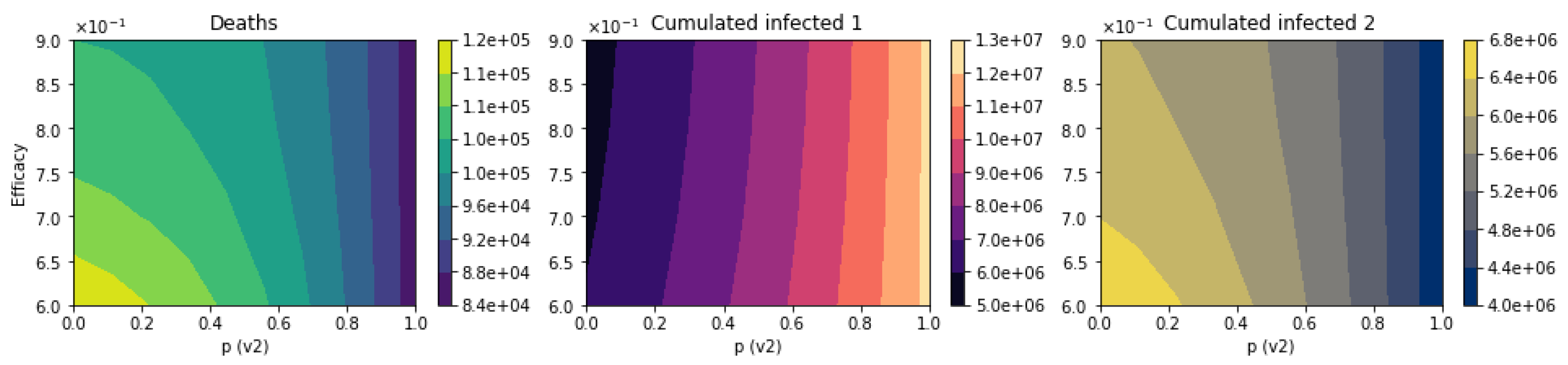
3.2.4. Scenarios Varying the Efficacy of the Vaccine
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johns Hopkins University and Medicine. 2022. Available online: https://coronavirus.jhu.edu (accessed on 1 March 2022).
- Centers for Disease Control and Prevention. 2020. Available online: https://www.cdc.gov/coronavirus/2019-nCoV/index.html (accessed on 1 March 2022).
- Asamoah, J.K.K.; Owusu, M.A.; Jin, Z.; Oduro, F.; Abidemi, A.; Gyasi, E.O. Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: Using data from Ghana. Chaos Solitons Fractals 2020, 140, 110103. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College: London, UK, 2020. [Google Scholar]
- Haushofer, J.; Metcalf, C.J.E. Which interventions work best in a pandemic? Science 2020, 368, 1063–1065. [Google Scholar] [CrossRef]
- Moore, S.; Hill, E.M.; Tildesley, M.J.; Dyson, L.; Keeling, M.J. Vaccination and non-pharmaceutical interventions for COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2021, 21, 793–802. [Google Scholar] [CrossRef]
- Mandal, S.; Bhatnagar, T.; Arinaminpathy, N.; Agarwal, A.; Chowdhury, A.; Murhekar, M.; Gangakhedkar, R.R.; Sarkar, S. Prudent public health intervention strategies to control the coronavirus disease 2019 transmission in India: A mathematical model-based approach. Indian J. Med Res. 2020, 151, 190. [Google Scholar]
- Reis, R.F.; de Melo Quintela, B.; de Oliveira Campos, J.; Gomes, J.M.; Rocha, B.M.; Lobosco, M.; dos Santos, R.W. Characterization of the COVID-19 pandemic and the impact of uncertainties, mitigation strategies, and underreporting of cases in South Korea, Italy, and Brazil. Chaos Solitons Fractals 2020, 136, 109888. [Google Scholar] [CrossRef]
- Wang, X.; Pasco, R.F.; Du, Z.; Petty, M.; Fox, S.J.; Galvani, A.P.; Pignone, M.; Johnston, S.C.; Meyers, L.A. Impact of social distancing measures on coronavirus disease healthcare demand, central Texas, USA. Emerg. Infect. Dis. 2020, 26, 2361. [Google Scholar] [CrossRef]
- Pinky, L.; Dobrovolny, H.M. SARS-CoV-2 coinfections: Could influenza and the common cold be beneficial? J. Med. Virol. 2020, 92, 2623–2630. [Google Scholar] [CrossRef]
- Dobrovolny, H.M. Modeling the role of asymptomatics in infection spread with application to SARS-CoV-2. PLoS ONE 2020, 15, e0236976. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, Y.; Ling, Y.; Lu, G.; Liu, F.; Yi, Z.; Jia, X.; Wu, M.; Shi, B.; Xu, S.; et al. Viral and host factors related to the clinical outcome of COVID-19. Nature 2020, 583, 437–440. [Google Scholar] [CrossRef]
- Ran, L.; Chen, X.; Wang, Y.; Wu, W.; Zhang, L.; Tan, X. Risk factors of healthcare workers with corona virus disease 2019: A retrospective cohort study in a designated hospital of Wuhan in China. Clin. Infect. Dis. 2020, 71, 2218–2222. [Google Scholar] [CrossRef]
- Yang, H.; Duan, G. Analysis on the epidemic factors for the corona virus disease. Zhonghua Yu Fang Yi Xue Za Zhi [Chinese J. Prev. Med. 2020, 54, E021. [Google Scholar]
- Block, P.; Hoffman, M.; Raabe, I.J.; Dowd, J.B.; Rahal, C.; Kashyap, R.; Mills, M.C. Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav. 2020, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Eker, S. Validity and usefulness of COVID-19 models. Humanit. Soc. Sci. Commun. 2020, 7, 1–5. [Google Scholar] [CrossRef]
- Jentsch, P.C.; Anand, M.; Bauch, C.T. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: A mathematical modelling study. Lancet Infect. Dis. 2021, 21, 1097–1106. [Google Scholar] [CrossRef]
- Qazi, A.; Qazi, J.; Naseer, K.; Zeeshan, M.; Hardaker, G.; Maitama, J.Z.; Haruna, K. Analyzing situational awareness through public opinion to predict adoption of social distancing amid pandemic COVID-19. J. Med. Virol. 2020, 92, 849–855. [Google Scholar] [CrossRef] [PubMed]
- Altmann, D.M.; Boyton, R.J.; Beale, R. Immunity to SARS-CoV-2 variants of concern. Science 2021, 371, 1103–1104. [Google Scholar] [CrossRef]
- Roda, W.C.; Varughese, M.B.; Han, D.; Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281. [Google Scholar] [CrossRef]
- Gonzalez-Parra, G.; Martínez-Rodríguez, D.; Villanueva-Micó, R.J. Impact of a new SARS-CoV-2 variant on the population: A mathematical modeling approach. Math. Comput. Appl. 2021, 26, 25. [Google Scholar] [CrossRef]
- Holmdahl, I.; Buckee, C. Wrong but useful- what COVID-19 epidemiologic models can and cannot tell us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef]
- Jewell, N.P.; Lewnard, J.A.; Jewell, B.L. Caution warranted: Using the Institute for Health Metrics and Evaluation model for predicting the course of the COVID-19 pandemic. Ann. Intern. Med. 2020, 173, 226–227. [Google Scholar] [CrossRef]
- Kuniya, T. Prediction of the Epidemic Peak of Coronavirus Disease in Japan, 2020. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Rodríguez, D.; Gonzalez-Parra, G.; Villanueva, R.J. Analysis of key factors of a SARS-CoV-2 vaccination program: A mathematical modeling approach. Epidemiologia 2021, 2, 140–161. [Google Scholar] [CrossRef]
- Walensky, R.P.; Walke, H.T.; Fauci, A.S. SARS-CoV-2 variants of concern in the United States—Challenges and opportunities. JAMA 2021, 325, 1037–1038. [Google Scholar] [CrossRef] [PubMed]
- Al-Qaness, M.A.; Ewees, A.A.; Fan, H.; Abd Elaziz, M. Optimized forecasting method for weekly influenza confirmed cases. Int. J. Environ. Res. Public Health 2020, 17, 3510. [Google Scholar] [CrossRef] [PubMed]
- Araz, O.M.; Bentley, D.; Muelleman, R.L. Using Google Flu Trends data in forecasting influenza-like–illness related ED visits in Omaha, Nebraska. Am. J. Emerg. Med. 2014, 32, 1016–1023. [Google Scholar] [CrossRef] [PubMed]
- Chretien, J.P.; George, D.; Shaman, J.; Chitale, R.A.; McKenzie, F.E. Influenza forecasting in human populations: A scoping review. PLoS ONE 2014, 9, e94130. [Google Scholar] [CrossRef]
- Hogan, A.B.; Anderssen, R.S.; Davis, S.; Moore, H.C.; Lim, F.J.; Fathima, P.; Glass, K. Time series analysis of RSV and bronchiolitis seasonality in temperate and tropical Western Australia. Epidemics 2016, 16, 49–55. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.; Diego, F.; Aranda, L.S. Modeling the epidemic waves of AH1N1/09 influenza around the world. Spat. Spatio-Temporal Epidemiol. 2011, 2, 219–226. [Google Scholar] [CrossRef]
- González-Parra, G.; Villanueva, R.J.; Ruiz-Baragaño, J.; Moraño, J.A. Modelling influenza A (H1N1) 2009 epidemics using a random network in a distributed computing environment. Acta Trop. 2015, 143, 29–35. [Google Scholar] [CrossRef]
- Moore, H.C.; Jacoby, P.; Hogan, A.B.; Blyth, C.C.; Mercer, G.N. Modelling the seasonal epidemics of respiratory syncytial virus in young children. PLoS ONE 2014, 9, e100422. [Google Scholar] [CrossRef]
- Osthus, D.; Hickmann, K.S.; Caragea, P.C.; Higdon, D.; Del Valle, S.Y. Forecasting seasonal influenza with a state-space SIR model. Ann. Appl. Stat. 2017, 11, 202. [Google Scholar] [CrossRef] [PubMed]
- Reich, N.G.; Brooks, L.C.; Fox, S.J.; Kandula, S.; McGowan, C.J.; Moore, E.; Osthus, D.; Ray, E.L.; Tushar, A.; Yamana, T.K.; et al. A collaborative multiyear, multimodel assessment of seasonal influenza forecasting in the United States. Proc. Natl. Acad. Sci. USA 2019, 116, 3146–3154. [Google Scholar] [CrossRef] [PubMed]
- Shaman, J.; Karspeck, A. Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. USA 2012, 109, 20425–20430. [Google Scholar] [CrossRef] [PubMed]
- Shaman, J.; Karspeck, A.; Yang, W.; Tamerius, J.; Lipsitch, M. Real-time influenza forecasts during the 2012–2013 season. Nat. Commun. 2013, 4, 2837. [Google Scholar] [CrossRef] [PubMed]
- Sloan, C.; Heaton, M.; Kang, S.; Berrett, C.; Wu, P.; Gebretsadik, T.; Sicignano, N.; Evans, A.; Lee, R.; Hartert, T. The impact of temperature and relative humidity on spatiotemporal patterns of infant bronchiolitis epidemics in the contiguous United States. Health Place 2017, 45, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Soliman, M.; Lyubchich, V.; Gel, Y.R. Complementing the power of deep learning with statistical model fusion: Probabilistic forecasting of influenza in Dallas County, Texas, USA. Epidemics 2019, 28, 100345. [Google Scholar] [CrossRef]
- Yang, W.; Cowling, B.J.; Lau, E.H.; Shaman, J. Forecasting influenza epidemics in Hong Kong. PLoS Comput. Biol. 2015, 11, e1004383. [Google Scholar] [CrossRef]
- Walton, N.A.; Poynton, M.R.; Gesteland, P.H.; Maloney, C.; Staes, C.; Facelli, J.C. Predicting the start week of respiratory syncytial virus outbreaks using real time weather variables. BMC Med. Inform. Decis. Mak. 2010, 10, 68. [Google Scholar] [CrossRef]
- Robertson, J.F.; Sewell, H.F.; Stewart, M. Delayed second dose of the BNT162b2 vaccine: Innovation or misguided conjecture? Lancet 2021, 397, 879–880. [Google Scholar] [CrossRef]
- Acedo, L.; Cortés, J.C.; Díez-Domingo, J.; Sánchez-Alonso, V.; Tuells, J.; Villanueva, R.J. Uncertainty and sensitivity of the sexual behavior changes to the current human papillomavirus vaccination campaign in Spain. Math. Methods Appl. Sci. 2021, 44, 7845–7857. [Google Scholar] [CrossRef]
- Acuña-Zegarra, M.A.; Díaz-Infante, S.; Baca-Carrasco, D.; Olmos-Liceaga, D. COVID-19 optimal vaccination policies: A modeling study on efficacy, natural and vaccine-induced immunity responses. Math. Biosci. 2021, 337, 108614. [Google Scholar] [CrossRef] [PubMed]
- Paltiel, A.D.; Schwartz, J.L.; Zheng, A.; Walensky, R.P. Clinical Outcomes Of A COVID-19 Vaccine: Implementation Over Efficacy: Study examines how definitions and thresholds of vaccine efficacy, coupled with different levels of implementation effectiveness and background epidemic severity, translate into outcomes. Health Aff. 2021, 40, 42–52. [Google Scholar]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ferranna, M.; Cadarette, D.; Bloom, D.E. COVID-19 Vaccine Allocation: Modeling Health Outcomes and Equity Implications of Alternative Strategies. Engineering 2021, 7, 924–935. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Parra, G. Analysis of Delayed Vaccination Regimens: A Mathematical Modeling Approach. Epidemiologia 2021, 2, 271–293. [Google Scholar] [CrossRef]
- I Arolas, H.P.; Acosta, E.; Myrskylä, M. Optimal vaccination age varies across countries. Proc. Natl. Acad. Sci. USA 2021, 118, e2105987118. [Google Scholar] [CrossRef]
- Kadire, S.R.; Wachter, R.M.; Lurie, N. Delayed second dose versus standard regimen for COVID-19 vaccination. N. Engl. J. Med. 2021, 384, e28. [Google Scholar] [CrossRef]
- Moghadas, S.M.; Vilches, T.N.; Zhang, K.; Nourbakhsh, S.; Sah, P.; Fitzpatrick, M.C.; Galvani, A.P. Evaluation of COVID-19 vaccination strategies with a delayed second dose. PLoS Biol. 2021, 19, e3001211. [Google Scholar] [CrossRef]
- Alvarez, M.M.; Bravo-González, S.; Trujillo-de Santiago, G. Modeling vaccination strategies in an Excel spreadsheet: Increasing the rate of vaccination is more effective than increasing the vaccination coverage for containing COVID-19. PLoS ONE 2021, 16, e0254430. [Google Scholar] [CrossRef]
- Shim, E. Optimal Allocation of the Limited COVID-19 Vaccine Supply in South Korea. J. Clin. Med. 2021, 10, 591. [Google Scholar] [CrossRef]
- Tuite, A.R.; Zhu, L.; Fisman, D.N.; Salomon, J.A. Alternative dose allocation strategies to increase benefits from constrained COVID-19 vaccine supply. Ann. Intern. Med. 2021, 174, 570–572. [Google Scholar] [CrossRef] [PubMed]
- Romero-Brufau, Santiago, e.a. Public health impact of delaying second dose of BNT162b2 or mRNA-1273 COVID-19 vaccine: Simulation agent based modeling study. BMJ 2021, 373, n1334. [Google Scholar] [CrossRef]
- Wikipedia. 2021. Available online: https://en.wikipedia.org/wiki/COVID-19vaccineclinicalresearch (accessed on 1 July 2021).
- Mohamadi, M.; Lin, Y.; Vulliet, M.V.S.; Flahault, A.; Rozanova, L.; Fabre, G. COVID-19 Vaccination Strategy in China: A Case Study. Epidemiologia 2021, 2, 402–425. [Google Scholar] [CrossRef]
- Afzal, A.; Saleel, C.A.; Bhattacharyya, S.; Satish, N.; Samuel, O.D.; Badruddin, I.A. Merits and Limitations of Mathematical Modeling and Computational Simulations in Mitigation of COVID-19 Pandemic: A Comprehensive Review. Arch. Comput. Methods Eng. 2021, 29, 1–27. [Google Scholar] [CrossRef]
- Din, A.; Khan, A.; Zeb, A.; Sidi Ammi, M.R.; Tilioua, M.; Torres, D.F. Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application. Axioms 2021, 10, 290. [Google Scholar] [CrossRef]
- Padmanabhan, R.; Abed, H.S.; Meskin, N.; Khattab, T.; Shraim, M.; Al-Hitmi, M.A. A review of mathematical model-based scenario analysis and interventions for COVID-19. Comput. Methods Programs Biomed. 2021, 206, 106301. [Google Scholar] [CrossRef]
- Mahrouf, M.; Boukhouima, A.; Zine, H.; Lotfi, E.M.; Torres, D.F.; Yousfi, N. Modeling and forecasting of COVID-19 spreading by delayed stochastic differential equations. Axioms 2021, 10, 18. [Google Scholar] [CrossRef]
- Rowan, N.J.; Moral, R.A. Disposable face masks and reusable face coverings as non-pharmaceutical interventions (NPIs) to prevent transmission of SARS-CoV-2 variants that cause Coronavirus disease (COVID-19): Role of new sustainable NPI design innovations and predictive mathematical modelling. Sci. Total Environ. 2021, 772, 145530. [Google Scholar]
- Wintachai, P.; Prathom, K. Stability analysis of SEIR model related to efficiency of vaccines for COVID-19 situation. Heliyon 2021, 7, e06812. [Google Scholar] [CrossRef]
- Allegretti, S.; Bulai, I.M.; Marino, R.; Menandro, M.A.; Parisi, K. Vaccination effect conjoint to fraction of avoided contacts for a Sars-Cov-2 mathematical model. Math. Model. Numer. Simul. Appl. 2021, 1, 56–66. [Google Scholar] [CrossRef]
- Ikram, R.; Khan, A.; Zahri, M.; Saeed, A.; Yavuz, M.; Kumam, P. Extinction and stationary distribution of a stochastic COVID-19 epidemic model with time-delay. Comput. Biol. Med. 2022, 141, 105115. [Google Scholar] [CrossRef] [PubMed]
- Tchoumi, S.Y.; Rwezaura, H.; Diagne, M.L.; González-Parra, G.; Tchuenche, J. Impact of Infective Immigrants on COVID-19 Dynamics. Math. Comput. Appl. 2022, 27, 11. [Google Scholar] [CrossRef]
- Yavuz, M.; Coşar, F.Ö.; Günay, F.; Özdemir, F.N. A new mathematical modeling of the COVID-19 pandemic including the vaccination campaign. Open J. Model. Simul. 2021, 9, 299–321. [Google Scholar] [CrossRef]
- Albani, V.V.; Loria, J.; Massad, E.; Zubelli, J.P. The impact of COVID-19 vaccination delay: A data-driven modeling analysis for Chicago and New York City. Vaccine 2021, 39, 6088–6094. [Google Scholar] [CrossRef]
- Abila, D.B.; Dei-Tumi, S.D.; Humura, F.; Aja, G.N. We need to start thinking about promoting the demand, uptake, and equitable distribution of COVID-19 vaccines NOW! Public Health Pract. 2020, 1, 100063. [Google Scholar] [CrossRef] [PubMed]
- Dermody, T.S.; DiMaio, D.; Enquist, L.W. Vaccine Safety, Efficacy, and Trust Take Time. Annu. Rev. Virol. 2020, 8, iii–iv. [Google Scholar] [CrossRef]
- Buonomo, B.; Della Marca, R.; d’Onofrio, A.; Groppi, M. A behavioural modelling approach to assess the impact of COVID-19 vaccine hesitancy. J. Theor. Biol. 2022, 534, 110973. [Google Scholar] [CrossRef]
- Bentout, S.; Tridane, A.; Djilali, S.; Touaoula, T.M. Age-structured modeling of COVID-19 epidemic in the USA, UAE and Algeria. Alex. Eng. J. 2021, 60, 401–411. [Google Scholar] [CrossRef]
- Simoy, M.; Aparicio, J. Socially structured model for COVID-19 pandemic: Design and evaluation of control measures. Comput. Appl. Math. 2021, 41. [Google Scholar] [CrossRef]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.Y.; Chen, L.; Wang, M. Presumed asymptomatic carrier transmission of COVID-19. JAMA 2020, 323, 1406–1407. [Google Scholar] [CrossRef]
- Buitrago-Garcia, D.; Egli-Gany, D.; Counotte, M.J.; Hossmann, S.; Imeri, H.; Ipekci, A.M.; Salanti, G.; Low, N. Occurrence and transmission potential of asymptomatic and presymptomatic SARS-CoV-2 infections: A living systematic review and meta-analysis. PLoS Med. 2020, 17, e1003346. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zhang, X.; Zhang, X.; Wei, Z.; Zhang, L.; Xu, J.; Liang, P.; Xu, Y.; Zhang, C.; Xu, A. Rapid asymptomatic transmission of COVID-19 during the incubation period demonstrating strong infectivity in a cluster of youngsters aged 16–23 years outside Wuhan and characteristics of young patients with COVID-19: A prospective contact-tracing study. J. Infect. 2020, 80, e1–e13. [Google Scholar] [CrossRef] [PubMed]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef] [PubMed]
- Park, S.W.; Cornforth, D.M.; Dushoff, J.; Weitz, J.S. The time scale of asymptomatic transmission affects estimates of epidemic potential in the COVID-19 outbreak. Epidemics 2020, 31, 100392. [Google Scholar] [CrossRef]
- Shao, S.; Zhou, D.; He, R.; Li, J.; Zou, S.; Mallery, K.; Kumar, S.; Yang, S.; Hong, J. Risk assessment of airborne transmission of COVID-19 by asymptomatic individuals under different practical settings. J. Aerosol Sci. 2020, 151, 105661. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, M.; Yokoe, D.S.; Havlir, D.V. Asymptomatic Transmission, the Achilles’ Heel of Current Strategies to Control COVID-19. N. Engl. J. Med. 2020, 382, 2158–2160. [Google Scholar] [CrossRef]
- Kinoshita, R.; Anzai, A.; Jung, S.m.; Linton, N.M.; Miyama, T.; Kobayashi, T.; Hayashi, K.; Suzuki, A.; Yang, Y.; Akhmetzhanov, A.R.; et al. Containment, Contact Tracing and Asymptomatic Transmission of Novel Coronavirus Disease (COVID-19): A Modelling Study. J. Clin. Med. 2020, 9, 3125. [Google Scholar] [CrossRef]
- Han, D.; Li, R.; Han, Y.; Zhang, R.; Li, J. COVID-19: Insight into the asymptomatic SARS-CoV-2 infection and transmission. Int. J. Biol. Sci. 2020, 16, 2803. [Google Scholar] [CrossRef]
- Teixeira, S.C. Mild and asymptomatic cases of COVID-19 are potential threat for faecal–oral transmission. Braz. J. Infect. Dis. 2020, 24, 368. [Google Scholar] [CrossRef]
- Pollán, M.; Pérez-Gómez, B.; Pastor-Barriuso, R.; Oteo, J.; Hernán, M.A.; Pérez-Olmeda, M.; Sanmartín, J.L.; Fernández-García, A.; Cruz, I.; de Larrea, N.F.; et al. Prevalence of SARS-CoV-2 in Spain (ENE-COVID): A nationwide, population-based seroepidemiological study. Lancet 2020, 396, 535–544. [Google Scholar] [CrossRef]
- Nikolai, L.A.; Meyer, C.G.; Kremsner, P.G.; Velavan, T.P. Asymptomatic SARS Coronavirus 2 infection: Invisible yet invincible. Int. J. Infect. Dis. 2020, 100, 112–116. [Google Scholar] [CrossRef] [PubMed]
- Kronbichler, A.; Kresse, D.; Yoon, S.; Lee, K.H.; Effenberger, M.; Shin, J.I. Asymptomatic patients as a source of COVID-19 infections: A systematic review and meta-analysis. Int. J. Infect. Dis. 2020, 98, 180–186. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Guo, Y.; Mao, R.; Zhang, J. Proportion of asymptomatic coronavirus disease 2019: A systematic review and meta-analysis. J. Med. Virol. 2021, 93, 820–830. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.A.; Quandelacy, T.M.; Kada, S.; Prasad, P.V.; Steele, M.; Brooks, J.T.; Slayton, R.B.; Biggerstaff, M.; Butler, J.C. SARS-CoV-2 Transmission From People Without COVID-19 Symptoms. JAMA Netw. Open 2021, 4, e2035057. [Google Scholar] [CrossRef]
- İşlier, Z.G.; Güllü, R.; Hörmann, W. An exact and implementable computation of the final outbreak size distribution under Erlang distributed infectious period. Math. Biosci. 2020, 325, 108363. [Google Scholar] [CrossRef] [PubMed]
- González-Parra, G.; Acedo, L.; Villanueva-Micó, R.J.; Arenas, A.J. Modeling the social obesity epidemic with stochastic networks. Phys. A Stat. Mech. Its Appl. 2010, 389, 3692–3701. [Google Scholar] [CrossRef]
- Roberts, M.; Andreasen, V.; Lloyd, A.; Pellis, L. Nine challenges for deterministic epidemic models. Epidemics 2015, 10, 49–53. [Google Scholar] [CrossRef] [PubMed]
- González-Parra, G.; Dobrovolny, H.M. Assessing uncertainty in A2 respiratory syncytial virus viral dynamics. Comput. Math. Methods Med. 2015, 2015, 567589. [Google Scholar] [CrossRef]
- Wearing, H.J.; Rohani, P.; Keeling, M.J. Appropriate models for the management of infectious diseases. PLoS Med 2005, 2, e174. [Google Scholar] [CrossRef]
- Faes, C.; Abrams, S.; Van Beckhoven, D.; Meyfroidt, G.; Vlieghe, E.; Hens, N.; Belgian Collaborative Group on COVID-19 Hospital Surveillance. Time between symptom onset, hospitalisation and recovery or death: Statistical analysis of belgian COVID-19 patients. Int. J. Environ. Res. Public Health 2020, 17, 7560. [Google Scholar] [CrossRef]
- Faust, J.S.; del Rio, C. Assessment of Deaths From COVID-19 and From Seasonal Influenza. JAMA Intern. Med. 2020, 180, 1045–1046. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Matrajt, L.; Eaton, J.; Leung, T.; Brown, E.R. Vaccine optimization for COVID-19, who to vaccinate first? Science Advances 2021, 7, eabf1374. [Google Scholar] [CrossRef]
- Walsh, F. Loss and resilience in the time of COVID-19: Meaning making, hope, and transcendence. Fam. Process 2020, 59, 898–911. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, B.B.; Wiegand, S.d.C.B. Losses in times of a pandemic: Bioethical perceptions about mourning caused by COVID-19 in Brazil. Voices Bioeth. 2020, 6. [Google Scholar] [CrossRef]
- Zhai, Y.; Du, X. Loss and grief amidst COVID-19: A path to adaptation and resilience. Brain, Behav. Immun. 2020, 87, 80–81. [Google Scholar] [CrossRef]
- Knoll, M.D.; Wonodi, C. Oxford–AstraZeneca COVID-19 vaccine efficacy. Lancet 2020, 397, 72–74. [Google Scholar] [CrossRef]
- Krause, P.; Fleming, T.R.; Longini, I.; Henao-Restrepo, A.M.; Peto, R.; Dean, N.; Halloran, M.; Huang, Y.; Fleming, T.; Gilbert, P.; et al. COVID-19 vaccine trials should seek worthwhile efficacy. Lancet 2020, 396, 741–743. [Google Scholar] [CrossRef]
- Hodgson, S.H.; Mansatta, K.; Mallett, G.; Harris, V.; Emary, K.R.; Pollard, A.J. What defines an efficacious COVID-19 vaccine? A review of the challenges assessing the clinical efficacy of vaccines against SARS-CoV-2. Lancet Infect. Dis. 2020, 21, e26–e35. [Google Scholar] [CrossRef]
- Lipsitch, M.; Dean, N.E. Understanding COVID-19 vaccine efficacy. Science 2020, 370, 763–765. [Google Scholar] [CrossRef]
- Bartsch, S.M.; O’Shea, K.J.; Ferguson, M.C.; Bottazzi, M.E.; Wedlock, P.T.; Strych, U.; McKinnell, J.A.; Siegmund, S.S.; Cox, S.N.; Hotez, P.J.; et al. Vaccine efficacy needed for a COVID-19 coronavirus vaccine to prevent or stop an epidemic as the sole intervention. Am. J. Prev. Med. 2020, 59, 493–503. [Google Scholar] [CrossRef] [PubMed]
- Dubé, E.; MacDonald, N.E. How can a global pandemic affect vaccine hesitancy? Expert Rev. Vaccines 2020, 19, 899–901. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, A.; Yi, B.; Ding, K.; Wang, H.; Wang, J.; Xu, G. The epidemiological characteristics of infection in close contacts of COVID-19 in Ningbo city. Chin. J. Epidemiol. 2020, 41, 668–672. [Google Scholar]
- Mc Evoy, D.; McAloon, C.G.; Collins, A.B.; Hunt, K.; Butler, F.; Byrne, A.W.; Casey, M.; Barber, A.; Griffin, J.M.; Lane, E.A.; et al. Relative infectiousness of asymptomatic SARS-CoV-2 infected persons compared with symptomatic individuals: A rapid scoping review. BMJ Open 2021, 11, e042354. [Google Scholar] [CrossRef]
- Santarpia, J.L.; Rivera, D.N.; Herrera, V.; Morwitzer, M.J.; Creager, H.; Santarpia, G.W.; Crown, K.K.; Brett-Major, D.; Schnaubelt, E.; Broadhurst, M.J.; et al. Aerosol and surface contamination of SARS-CoV-2 observed in quarantine and isolation care. Sci. Rep. 2020, 110, 12732. [Google Scholar] [CrossRef]
- Zhao, H.j.; Lu, X.x.; Deng, Y.b.; Tang, Y.j.; Lu, J.c. COVID-19: Asymptomatic carrier transmission is an underestimated problem. Epidemiol. Infect. 2020, 148, 1–7. [Google Scholar] [CrossRef]
- Driver, R.D. Ordinary and Delay Differential Equations, 1st ed.; Applied Mathematical Sciences 20; Springer: New York, NY, USA, 1977. [Google Scholar]
- Luis Barreira, C.V. Ordinary Differential Equations: Qualitative Theory, 1st ed.; Graduate Studies in Mathematics, American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.; Lau, E.H.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus—Infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Statista. 2021. Available online: https://www.statista.com/statistics/1105431/covidcasefatalityratesUSbyagegroup/ (accessed on 1 August 2021).
- Oran, D.P.; Topol, E.J. Prevalence of Asymptomatic SARS-CoV-2 Infection: A Narrative Review. Ann. Intern. Med. 2020, 173, 362–367. [Google Scholar] [CrossRef]
- Ahn, D.G.; Shin, H.J.; Kim, M.H.; Lee, S.; Kim, H.S.; Myoung, J.; Kim, B.T.; Kim, S.J. Current status of epidemiology, diagnosis, therapeutics, and vaccines for novel coronavirus disease 2019 (COVID-19). J. Microbiol. Biotechnol. 2020, 30, 313–324. [Google Scholar] [CrossRef]
- Burki, T.K. The Russian vaccine for COVID-19. Lancet Respir. Med. 2020, 8, e85–e86. [Google Scholar] [CrossRef]
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and efficacy of the BNT162b2 mRNA Covid-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef] [PubMed]
- Tregoning, J.S.; Brown, E.S.; Cheeseman, H.M.; Flight, K.E.; Higham, S.L.; Lemm, N.M.; Pierce, B.F.; Stirling, D.C.; Wang, Z.; Pollock, K.M. Vaccines for COVID-19. Clin. Exp. Immunol. 2020, 202, 162–192. [Google Scholar] [CrossRef] [PubMed]
- Dinleyici, E.C.; Borrow, R.; Safadi, M.A.P.; van Damme, P.; Munoz, F.M. Vaccines and routine immunization strategies during the COVID-19 pandemic. Hum. Vaccines Immunother. 2020, 17, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Yamey, G.; Schaferhoff, M.; Hatchett, R.; Pate, M.; Zhao, F.; McDade, K.K. Ensuring global access to COVID-19 vaccines. Lancet 2020, 395, 1405–1406. [Google Scholar] [CrossRef]
- Goldstein, J.R.; Cassidy, T.; Wachter, K.W. Vaccinating the oldest against COVID-19 saves both the most lives and most years of life. Proc. Natl. Acad. Sci. USA 2021, 118, e2026322118. [Google Scholar] [CrossRef]
- Sperrin, M.; Grant, S.W.; Peek, N. Prediction models for diagnosis and prognosis in COVID-19. BMJ 2020, 369, m1464. [Google Scholar] [CrossRef]
- Stutt, R.O.; Retkute, R.; Bradley, M.; Gilligan, C.A.; Colvin, J. A modelling framework to assess the likely effectiveness of facemasks in combination with lock-down in managing the COVID-19 pandemic. Proc. R. Soc. A 2020, 476, 20200376. [Google Scholar] [CrossRef]
- Haque, A.; Pant, A.B. Efforts at COVID-19 Vaccine Development: Challenges and Successes. Vaccines 2020, 8, 739. [Google Scholar] [CrossRef]
- Verger, P.; Dubé, E. Restoring confidence in vaccines in the COVID-19 era. Expert Rev. Vaccines 2020, 19, 991–993. [Google Scholar] [CrossRef]
- Ayoub, H.H.; Chemaitelly, H.; Abu-Raddad, L.J. Epidemiological Impact of Novel Preventive and Therapeutic HSV-2 Vaccination in the United States: Mathematical Modeling Analyses. Vaccines 2020, 8, 366. [Google Scholar] [CrossRef]
- Benest, J.; Rhodes, S.; Quaife, M.; Evans, T.G.; White, R.G. Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy. Vaccines 2021, 9, 78. [Google Scholar] [CrossRef] [PubMed]
- Chaves, L.F.; Hurtado, L.A.; Rojas, M.R.; Friberg, M.D.; Rodríguez, R.M.; Avila-Aguero, M.L. COVID-19 basic reproduction number and assessment of initial suppression policies in Costa Rica. Math. Model. Nat. Phenom. 2020, 15, 32. [Google Scholar] [CrossRef]
- Contreras, S.; Villavicencio, H.A.; Medina-Ortiz, D.; Saavedra, C.P.; Olivera-Nappa, Á. Real-time estimation of Rt for supporting public-health policies against COVID-19. Front. Public Health 2020, 8, 556689. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Parra, G.; Díaz-Rodríguez, M.; Arenas, A.J. Mathematical modeling to design public health policies for Chikungunya epidemic using optimal control. Optim. Control Appl. Methods 2020, 41, 1584–1603. [Google Scholar] [CrossRef]
- Nistal, R.; de la Sen, M.; Gabirondo, J.; Alonso-Quesada, S.; Garrido, A.J.; Garrido, I. A Modelization of the Propagation of COVID-19 in Regions of Spain and Italy with Evaluation of the Transmission Rates Related to the Intervention Measures. Biology 2021, 10, 121. [Google Scholar] [CrossRef]
- van Oosterhout, C.; Hall, N.; Ly, H.; Tyler, K.M. COVID-19 evolution during the pandemic–Implications of new SARS-CoV-2 variants on disease control and public health policies. Virulence 2021, 12, 507. [Google Scholar] [CrossRef]
- Zenk, L.; Steiner, G.; Pina e Cunha, M.; Laubichler, M.D.; Bertau, M.; Kainz, M.J.; Jäger, C.; Schernhammer, E.S. Fast Response to Superspreading: Uncertainty and Complexity in the Context of COVID-19. Int. J. Environ. Res. Public Health 2020, 17, 7884. [Google Scholar] [CrossRef]
- Hethcote, H.W. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef]
- Gumel, A.B.; Iboi, E.A.; Ngonghala, C.N.; Elbasha, E.H. A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations. Infect. Dis. Model. 2021, 6, 148–168. [Google Scholar] [CrossRef]





| Parameter | Symbol | Value |
|---|---|---|
| Susceptible 1 | 149,284,000 | |
| Asymptomatic 1 | 798,000 | |
| Infected (symptomatic) 1 | 798,000 | |
| Susceptible 2 | 112,104,000 | |
| Asymptomatic 2 | 588,000 | |
| Infected (symptomatic) 2 | 588,000 | |
| Recovered | 16,000,000 | |
| Total population | 300,705,643 |
| Parameter | Symbol | Value (Days) |
|---|---|---|
| Infectious period | 7 days [113] | |
| Case fatality ratio (rate) age group 1 | ≈0.01 [114] | |
| Case fatality ratio (rate) age group 2 | ≈0.1 [114] | |
| Case fatality ratio (rate) vaccinated age group 1 | assumed [114] | |
| Case fatality ratio (rate) vaccinated age group 2 | assumed [114] | |
| Probability of being asymptomatic | a | [2,115] |
| Efficacy of the vaccines | Varied | |
| Vaccination rate for age group i | Varied | |
| Fixed number of vaccines | 1.5× 10 | Varied |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Parra, G.; Cogollo, M.R.; Arenas, A.J. Mathematical Modeling to Study Optimal Allocation of Vaccines against COVID-19 Using an Age-Structured Population. Axioms 2022, 11, 109. https://doi.org/10.3390/axioms11030109
González-Parra G, Cogollo MR, Arenas AJ. Mathematical Modeling to Study Optimal Allocation of Vaccines against COVID-19 Using an Age-Structured Population. Axioms. 2022; 11(3):109. https://doi.org/10.3390/axioms11030109
Chicago/Turabian StyleGonzález-Parra, Gilberto, Myladis R. Cogollo, and Abraham J. Arenas. 2022. "Mathematical Modeling to Study Optimal Allocation of Vaccines against COVID-19 Using an Age-Structured Population" Axioms 11, no. 3: 109. https://doi.org/10.3390/axioms11030109
APA StyleGonzález-Parra, G., Cogollo, M. R., & Arenas, A. J. (2022). Mathematical Modeling to Study Optimal Allocation of Vaccines against COVID-19 Using an Age-Structured Population. Axioms, 11(3), 109. https://doi.org/10.3390/axioms11030109








