Perturbation of One-Dimensional Time-Independent Schrödinger Equation with a Near-Hyperbolic Potential

Abstract

The authors have recently investigated a type of Hyers–Ulam stability of one-dimensional time-independent Schrödinger equation with a symmetric parabolic potential wall. In this paper, we investigate a type of Hyers–Ulam stability of the Schrödinger equation with a near-hyperbolic potential.

1. Introduction

About 80 years ago, Ulam [1] proposed the following general stability problem concerning functional equations: Assume that we changed the mathematical equation to an inequality in some way. In this case, is there a solution to the equation near each solution to the inequality?

In 1941, Hyers [2] partially solved Ulam’s question for the approximately additive functions, assuming that $G_1$ and $G_2$ are Banach spaces. Indeed, he proved that each solution to the inequality $\parallel f(x+y)-f\left(x\right)-f\left(y\right)\parallel \le \epsilon$ (for all x and y) can be approximated by an exact solution, i.e., by an additive function. In that case, the Cauchy additive equation, $f(x+y)=f\left(x\right)+f\left(y\right)$, is said to have (or satisfy) the Hyers–Ulam stability.

Meanwhile, Rassias [3], trying not to strongly limit the Cauchy difference, attempted to weaken the condition for the Cauchy difference as follows:

$$\begin{array}{c}\hfill \parallel f(x+y)-f\left(x\right)-f\left(y\right)\parallel \le \epsilon \left({\parallel x\parallel }^p+{\parallel y\parallel }^p\right),\end{array}$$

where p is a fixed real number with $p<1$, and he proved the theorem of Hyers. That is, he proved the Hyers–Ulam-Rassias stability (or generalized Hyers–Ulam stability) of the Cauchy additive functional equation. Since then, Găvruţa [4] has published a paper that further expands the theorem of Rassias, both of which have been interesting enough to attract the attention of many mathematicians (see [5]).

Now we assume that $I=(a,b)$ is an open interval with $-\infty \le a<b\le +\infty$ and n is a fixed positive integer. We consider the linear differential equation of nth order

$$\begin{array}{c}\hfill a_n\left(x\right)y^{\left(n\right)}\left(x\right)+a_{n-1}\left(x\right)y^{(n-1)}\left(x\right)+\dots +a_1\left(x\right)y^{\prime }\left(x\right)+a_0\left(x\right)y\left(x\right)=g\left(x\right),\end{array}$$

(1)

where $y:I\to \mathbb{C}$ is an n times continuously differentiable function, $a_0,\dots ,a_n:I\to \mathbb{C}$ are given continuous functions, and $g:I\to \mathbb{C}$ is also a given continuous function.

In general, we say that the differential Equation (1) has the Hyers–Ulam stability if the following statement is true for all $\epsilon >0$: For any n times continuously differentiable (known) function $y:I\to \mathbb{C}$ that satisfies the inequality

$$\begin{array}{c}\hfill \left|a_n\left(x\right)y^{\left(n\right)}\left(x\right)+a_{n-1}\left(x\right)y^{(n-1)}\left(x\right)+\dots +a_1\left(x\right)y^{\prime }\left(x\right)+a_0\left(x\right)y\left(x\right)-g\left(x\right)\right|\le \epsilon \end{array}$$

for all $x\in I$, there is a solution $y_0:I\to \mathbb{C}$ of differential Equation (1) that satisfies

$$\begin{array}{c}\hfill |y\left(x\right)-y_0\left(x\right)|\le K(x,\epsilon )\end{array}$$

for each $x\in I$, where $K(x,\epsilon )$ depends only on x and $\epsilon$ and $\underset{\epsilon \to 0}{lim}K(x,\epsilon )=0$ for any fixed x.

If $K(x,\epsilon )$ really depends on the value of x, then in a broad sense (but not in its strict sense) this case seems somewhat suitable for Hyers–Ulam-Rassias stability. Since there is not yet an appropriate formal term for this case, in this paper we try to say that differential Equation (1) has a type of Hyers–Ulam stability. For a more detailed definition of Hyers–Ulam stability, see [5].

Obłoza is generally credited for being the first mathematician to study the Hyers–Ulam stability of differential equations (see [6,7]). Indeed, Obłoza perfectly demonstrated the Hyers–Ulam stability of linear differential equations of the form

$$\begin{array}{c}\hfill y^{\prime }\left(x\right)+f\left(x\right)y\left(x\right)=g\left(x\right).\end{array}$$

(2)

Since then, many mathematicians have dealt with this topic more broadly and in depth (see [8,9,10,11,12,13]).

In a recent paper [14], the authors investigated a type of Hyers–Ulam stability for the one-dimensional time-independent Schrödinger equation

$$\begin{array}{c}\hfill -\frac{{\hslash }^2}{2m}{\psi }^{″}\left(x\right)+V\left(x\right)\psi \left(x\right)=E\psi \left(x\right)\end{array}$$

(3)

when the system under observation has a symmetric parabolic potential wall.

In this paper, we prove a type of Hyers–Ulam stability of one-dimensional time-independent Schrödinger Equation (3) with a near-hyperbolic potential, where $\psi :(0,\infty )\to \mathbb{C}$ is the wave function, V is a hyperbolic potential function, ℏ is the reduced Planck constant, m is the mass of the particle, and E is the energy of the particle.

2. A Type of Hyers–Ulam Stability

In the following lemma, let $I=(a,b)$ be an open interval, where $-\infty \le a<b\le +\infty$, and let X be a Banach space over $\mathbb{K}$, where $\mathbb{K}$ denotes either $\mathbb{R}$ or $\mathbb{C}$.

Lemma 1

([11]). Assume that $y:I\to X$ is a continuously differentiable function and $\lambda :I\to \mathbb{K}$, and $f:I\to X$, $\phi :I\to [0,\infty )$ are continuous functions. If y satisfies the inequality

$$\begin{array}{c}\hfill \parallel y^{\prime }\left(x\right)-\lambda \left(x\right)y\left(x\right)-f\left(x\right)\parallel \le \phi \left(x\right)\end{array}$$

for all $x\in I$, then there exists a unique continuously differentiable function $z:I\to X$ such that

$$\begin{array}{c}\hfill z^{\prime }\left(x\right)-\lambda \left(x\right)z\left(x\right)=f\left(x\right)\end{array}$$

and

$$\begin{array}{c}\hfill \parallel y\left(x\right)-z\left(x\right)\parallel \le exp\left(\Re \left({\int }_a^x\lambda \left(s\right)ds\right)\right)\left|{\int }_a^{x}exp\left(-\Re \left({\int }_a^t\lambda \left(s\right)ds\right)\right)\phi \left(t\right)dt\right|\end{array}$$

for all $x\in I$.

From now on, let c and k be fixed positive real numbers. We assume that the potential functions $V_1:(0,c)\to \mathbb{R}$ and $V_2:(c,\infty )\to \mathbb{R}$ are given by

$$\begin{array}{c}\hfill V_1\left(x\right):=\frac{k}{c^2}x-\frac{2k}{c}and{V}_2\left(x\right):=-\frac{k}{x}.\end{array}$$

(4)

Roughly speaking, our potential function is near-hyperbolic (see Figure 1).

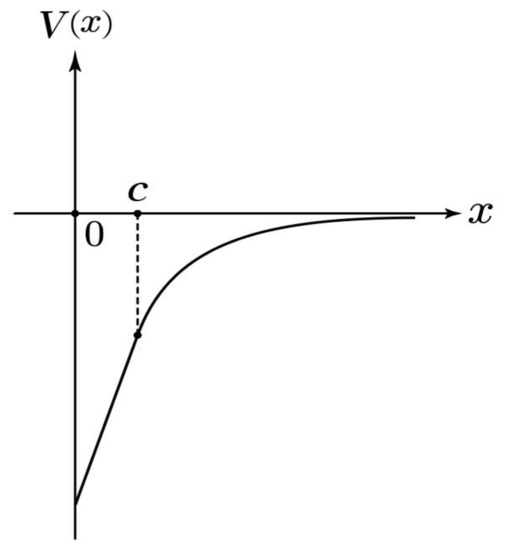
Figure 1. Near-hyperbolic potential function.

In the following theorem, we exclude the point c from each of the domains of $V_1$, ${\psi }_1$, ${\xi }_1$, $y_1$, and ${\varphi }_1$ to avoid trivially repeated calculations. We note that the following theorem is true whether or not we include the point c in their respective domains.

Theorem 1.

Assume that the potential functions $V_1:(0,c)\to \mathbb{R}$ and $V_2:(c,\infty )\to \mathbb{R}$ are given by (4). Let E be the energy of the particle under observation and let ε be any fixed positive real number. If twice continuously differentiable functions ${\psi }_1:(0,c)\to \mathbb{C}$ and ${\psi }_2:(c,\infty )\to \mathbb{C}$ satisfy the inequality

$$\begin{array}{c}\hfill \left|-\frac{{\hslash }^2}{2m}{\psi }_i^{″}\left(x\right)+V_i\left(x\right){\psi }_i\left(x\right)-E{\psi }_i\left(x\right)\right|\le \epsilon \end{array}$$

(5)

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$), then there exist twice continuously differentiable solutions ${\xi }_1:(0,c)\to \mathbb{C}$ and ${\xi }_2:(c,\infty )\to \mathbb{C}$ to the one-dimensional time-independent Schrödinger Equation (3) such that

$$\begin{array}{c}\hfill |{\psi }_i\left(x\right)-{\xi }_i\left(x\right)|\le \frac{2m}{{\hslash }^2}\epsilon {\int }_{\alpha }^x{\int }_{\alpha }^t\left|\frac{y_i\left(s\right)}{y_i\left(t\right)}\right|dsdt\end{array}$$

(6)

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$), where $y_1:(0,c)\to \mathbb{C}$ and $y_2:(c,\infty )\to \mathbb{C}$ are solutions to the second-order linear differential Equations in (10), respectively, and where $\alpha =0$ for $i=1$ and $\alpha =c$ for $i=2$.

Proof. 

Given an open subset D of $\mathbb{R}$, we use ${\mathcal{C}}^1\left(D\right)$ (${\mathcal{C}}^2\left(D\right)$) to denote the class of all (twice) continuously differentiable complex-valued functions defined on D. Considering the given potential functions $V_1:(0,c)\to \mathbb{R}$ and $V_2:(c,\infty )\to \mathbb{R}$, we define the differential operators ${\mathcal{L}}_a,{\mathcal{L}}_b:{\mathcal{C}}^2(0,c)\to {\mathcal{C}}^1(0,c)$ for $i=1$ and ${\mathcal{L}}_a,{\mathcal{L}}_b:{\mathcal{C}}^2(c,\infty )\to {\mathcal{C}}^1(c,\infty )$ for $i=2$ as follows:

$$\begin{array}{c}\hfill \left({\mathcal{L}}_a{\psi }_i\right)\left(x\right):={\psi }_i^{\prime }\left(x\right)+a\left(x\right){\psi }_i\left(x\right)\mathrm{and}\left({\mathcal{L}}_b{\psi }_i\right)\left(x\right):={\psi }_i^{\prime }\left(x\right)+b\left(x\right){\psi }_i\left(x\right)\end{array}$$

(7)

for all twice continuously differentiable functions ${\psi }_1:(0,c)\to \mathbb{C}$ and ${\psi }_2:(c,\infty )\to \mathbb{C}$, where $a,b:(0,\infty )\to \mathbb{C}$ are not known yet but they are continuously differentiable functions to be determined later. Then, it follows from (7) that

$$\begin{array}{c}\hfill -\frac{{\hslash }^2}{2m}\left(({\mathcal{L}}_b\circ {\mathcal{L}}_a){\psi }_i\right)\left(x\right)=-\frac{{\hslash }^2}{2m}\left({\psi }_i^{″}\left(x\right)+\left(a\left(x\right)+b\left(x\right)\right){\psi }_i^{\prime }\left(x\right)+\left(a^{\prime }\left(x\right)+a\left(x\right)b\left(x\right)\right){\psi }_i\left(x\right)\right)\end{array}$$

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$).

If we assume that

$$\begin{array}{c}\hfill -\frac{{\hslash }^2}{2m}\left(({\mathcal{L}}_b\circ {\mathcal{L}}_a){\psi }_i\right)\left(x\right)=-\frac{{\hslash }^2}{2m}{\psi }_i^{″}\left(x\right)+V_i\left(x\right){\psi }_i\left(x\right)-E{\psi }_i\left(x\right)\end{array}$$

(8)

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$), then

$$\begin{array}{c}\hfill b\left(x\right)=-a\left(x\right)\mathrm{and}{a}^{\prime }\left(x\right)+a\left(x\right)b\left(x\right)=-\frac{2m}{{\hslash }^2}\left(V_i\left(x\right)-E\right)\end{array}$$

for all $x>0$. That is, $a\left(x\right)$ is a solution to the Riccati equation

$$\begin{array}{c}\hfill a^{\prime }\left(x\right)-a{\left(x\right)}^2=-\frac{2m}{{\hslash }^2}\left(V_i\left(x\right)-E\right)\end{array}$$

(9)

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$).

If we set $a\left(x\right):=-\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}$ in the last equation, where the subindex $i=1$ for $0<x<c$ and $i=2$ for $x>c$, it then follows from (4) that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{y}_1^{″}\left(x\right)-{\displaystyle \frac{2m}{{\hslash }^2}}\left({\displaystyle \frac{k}{c^2}}x-{\displaystyle \frac{2k}{c}}-E\right)y_1\left(x\right)=0\hfill & \left(\mathrm{for}0<x<c\right),\hfill \\ y_2^{″}\left(x\right)+{\displaystyle \frac{2m}{{\hslash }^2}}\left({\displaystyle \frac{k}{x}}+E\right)y_2\left(x\right)=0\hfill & \left(\mathrm{for}x>c\right).\hfill \end{array}\right.\end{array}$$

(10)

Since every coefficient of each differential equation in (10) is continuous on the domain where the corresponding equation is defined, we confirm that the functions $y_1:(0,c)\to \mathbb{C}$ and $y_2:(c,\infty )\to \mathbb{C}$ exist.

Due to (5) and (8), we get

$$\begin{array}{c}\hfill \left|-\frac{{\hslash }^2}{2m}\left(({\mathcal{L}}_b\circ {\mathcal{L}}_a){\psi }_i\right)\left(x\right)\right|=\left|-\frac{{\hslash }^2}{2m}{\psi }_i^{″}\left(x\right)+V_i\left(x\right){\psi }_i\left(x\right)-E{\psi }_i\left(x\right)\right|\le \epsilon ,\end{array}$$

i.e.,

$$\begin{array}{c}\hfill \left|\left(({\mathcal{L}}_b\circ {\mathcal{L}}_a){\psi }_i\right)\left(x\right)\right|\le \frac{2m}{{\hslash }^2}\epsilon \end{array}$$

(11)

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$). If we set

$$\begin{array}{c}\hfill {\phi }_i\left(x\right):=\left({\mathcal{L}}_a{\psi }_i\right)\left(x\right)={\psi }_i^{\prime }\left(x\right)+a\left(x\right){\psi }_i\left(x\right)={\psi }_i^{\prime }\left(x\right)-\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}{\psi }_i\left(x\right),\end{array}$$

then it follows from (7) and (11) that

$$\begin{array}{c}\hfill \left|{\phi }_i^{\prime }\left(x\right)+\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}{\phi }_i\left(x\right)\right|=|{\phi }_i^{\prime }\left(x\right)-a\left(x\right){\phi }_i\left(x\right)|=\left|\left({\mathcal{L}}_b{\phi }_i\right)\left(x\right)\right|\le \frac{2m}{{\hslash }^2}\epsilon \end{array}$$

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$).

According to Lemma 1, there exists a unique function ${\varphi }_i\left(x\right)$ that satisfies

$$\begin{array}{c}\hfill {\varphi }_i^{\prime }\left(x\right)+\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}{\varphi }_i\left(x\right)=0\end{array}$$

(12)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\phi }_i\left(x\right)-{\varphi }_i\left(x\right)|& \le \frac{2m}{{\hslash }^2}\epsilon exp\left(-\Re \left({\int }_{\alpha }^x\frac{y_i^{\prime }\left(s\right)}{y_i\left(s\right)}ds\right)\right){\int }_{\alpha }^{x}exp\left(\Re \left({\int }_{\alpha }^t\frac{y_i^{\prime }\left(s\right)}{y_i\left(s\right)}ds\right)\right)dt\hfill \\ & \le \frac{2m}{{\hslash }^2}\epsilon {\int }_{\alpha }^x\left|\frac{y_i\left(t\right)}{y_i\left(x\right)}\right|dt\hfill \end{array}\end{array}$$

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$), where we set $\alpha =0$ for $i=1$ and $\alpha =c$ for $i=2$. That is, we get the following inequality

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left|{\psi }_i^{\prime }\left(x\right)-\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}{\psi }_i\left(x\right)-{\varphi }_i\left(x\right)\right|& =|{\psi }_i^{\prime }\left(x\right)+a\left(x\right){\psi }_i\left(x\right)-{\varphi }_i\left(x\right)|=|{\phi }_i\left(x\right)-{\varphi }_i\left(x\right)|\hfill \\ & \le \frac{2m}{{\hslash }^2}\epsilon {\int }_{\alpha }^x\left|\frac{y_i\left(t\right)}{y_i\left(x\right)}\right|dt\hfill \end{array}\end{array}$$

(13)

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$).

Due to Lemma 1 again, it follows from (13) that there exists a unique function ${\xi }_i\left(x\right)$ that satisfies

$$\begin{array}{c}\hfill {\xi }_i^{\prime }\left(x\right)-\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}{\xi }_i\left(x\right)={\varphi }_i\left(x\right)\end{array}$$

(14)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\psi }_i\left(x\right)-{\xi }_i\left(x\right)|& \le exp\left(\Re \left({\int }_{\alpha }^x\frac{y_i^{\prime }\left(s\right)}{y_i\left(s\right)}ds\right)\right){\int }_{\alpha }^{x}exp\left(-\Re \left({\int }_{\alpha }^t\frac{y_i^{\prime }\left(s\right)}{y_i\left(s\right)}ds\right)\right)\frac{2m}{{\hslash }^2}\epsilon {\int }_{\alpha }^t\left|\frac{y_i\left(s\right)}{y_i\left(x\right)}\right|dsdt\hfill \\ & \le \frac{2m}{{\hslash }^2}\epsilon {\int }_{\alpha }^x{\int }_{\alpha }^t\left|\frac{y_i\left(s\right)}{y_i\left(t\right)}\right|dsdt\hfill \end{array}\end{array}$$

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$).

Combining (12) and (14), we see that

$$\begin{array}{c}\hfill {\xi }_i^{″}\left(x\right)-\frac{y_i^{″}\left(x\right)}{y_i\left(x\right)}{\xi }_i\left(x\right)={\varphi }_i^{\prime }\left(x\right)+\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}{\varphi }_i\left(x\right)=0,\end{array}$$

(15)

and since $a\left(x\right)=-\frac{y_i^{\prime }\left(x\right)}{y_i\left(x\right)}$, it follows from (9) that $-\frac{y_i^{″}\left(x\right)}{y_i\left(x\right)}=a^{\prime }\left(x\right)-a{\left(x\right)}^2=-\frac{2m}{{\hslash }^2}(V_i\left(x\right)-E)$. Hence, by (15), we have

$$\begin{array}{c}\hfill {\xi }_i^{″}\left(x\right)-\frac{2m}{{\hslash }^2}\left(V_i\left(x\right)-E\right){\xi }_i\left(x\right)=0\end{array}$$

or

$$\begin{array}{c}\hfill -\frac{{\hslash }^2}{2m}{\xi }_i^{″}\left(x\right)+\left(V_i\left(x\right)-E\right){\xi }_i\left(x\right)=0\end{array}$$

for all $0<x<c$ (when $i=1$) and $x>c$ (when $i=2$).  □

To calculate the upper bound of inequality (6) in Theorem 1, we first have to solve differential equations of (10) to find $y_1\left(x\right)$ and $y_2\left(x\right)$. On account of [15], we can find the general solutions of the differential equations of (10). We select the appropriate $y_1\left(x\right)$ and $y_2\left(x\right)$ according to the formulas given in Remark 1 and estimate the upper bound of the inequality (6).

Remark 1.

$\left(i\right)$ The general solution of the first equation in (10) is given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill y_1\left(x\right)=c_1\mathrm{Ai}\left(\sqrt[3]{\frac{2m}{c^2{k}^2{\hslash }^2}}\left(kx-2ck-c^{2}E\right)\right)+c_2\mathrm{Bi}\left(\sqrt[3]{\frac{2m}{c^2{k}^2{\hslash }^2}}\left(kx-2ck-c^{2}E\right)\right),\end{array}\end{array}$$

where $c_1$ and $c_2$ are arbitrary complex numbers, $\mathrm{Ai}\left(x\right)$ is the Airy function and $\mathrm{Bi}\left(x\right)$ is the Airy Bi function. That is, $\mathrm{Ai}\left(x\right)$ and $\mathrm{Bi}\left(x\right)$ are linearly independent solutions of the Airy equation, $y^{″}\left(x\right)-xy\left(x\right)=0$. More precisely,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{Ai}\left(x\right)& =a_1\sum _{n=0}^{\infty }{3}^n{\left(\frac{1}{3}\right)}_n\frac{x^{3n}}{\left(3n\right)!}-a_2\sum _{n=0}^{\infty }{3}^n{\left(\frac{2}{3}\right)}_n\frac{x^{3n+1}}{(3n+1)!},\hfill \\ \hfill \mathrm{Bi}\left(x\right)& =b_1\sum _{n=0}^{\infty }{3}^n{\left(\frac{1}{3}\right)}_n\frac{x^{3n}}{\left(3n\right)!}+b_2\sum _{n=0}^{\infty }{3}^n{\left(\frac{2}{3}\right)}_n\frac{x^{3n+1}}{(3n+1)!},\hfill \end{array}\end{array}$$

where $a_1$, $a_2$, $b_1$, and $b_2$ are arbitrary complex constants and where we set ${\left(a\right)}_0=1$ and ${\left(a\right)}_n=a(a+1)(a+2)\cdots (a+n-1)$.

$\left(ii\right)$ The general solution of the second equation in (10) is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill y_2\left(x\right)& =c_{1}xexp\left(-\sqrt{\frac{-2mE}{{\hslash }^2}}x\right)U\left(\frac{k}{2E}\sqrt{\frac{-2mE}{{\hslash }^2}}+1,2,2\sqrt{\frac{-2mE}{{\hslash }^2}}x\right)\hfill \\ & +c_{2}xexp\left(-\sqrt{\frac{-2mE}{{\hslash }^2}}x\right){}_1{F}_1\left(\frac{k}{2E}\sqrt{\frac{-2mE}{{\hslash }^2}}+1;2;2\sqrt{\frac{-2mE}{{\hslash }^2}}x\right),\hfill \end{array}\end{array}$$

where $U(a,b,x)$ is the confluent hypergeometric function of the second kind and ${}_1{F}_1(a;b;x)$ is the Kummer confluent hypergeometric function. More precisely,

$$\begin{array}{c}\hfill \begin{array}{cc}& {}_1{F}_1(a;b;x)=\sum _{n=0}^{\infty }\frac{{\left(a\right)}_n{x}^n}{{\left(b\right)}_{n}n!},\hfill \\ & U(a,b,x)=\frac{\pi }{sin\left(b\pi \right)}\left(\frac{{}_1{F}_1(a;b;x)}{\Gamma (1+a-b)\Gamma \left(b\right)}-x^{1-b}\frac{{}_1{F}_1(1+a-b;2-b;x)}{\Gamma \left(a\right)\Gamma (2-b)}\right).\hfill \end{array}\end{array}$$

3. Examples

As examples related to the subject of this paper, we consider the case of the hydrogen atom in this section.

As we know, $\hslash \approx 1.055\times {10}^{-34}\mathrm{Js}$ is reduced Planck constant, $k=\frac{e^2}{4\pi {\epsilon }_0}\approx 2.307\times {10}^{-28}\mathrm{N}{\mathrm{m}}^2$, $m_e\approx 9.109\times {10}^{-31}\mathrm{kg}$ is the mass of electron, $E=-\frac{m_e{k}^2}{2{\hslash }^2}\approx -13.61\mathrm{eV}\approx -2.178\times {10}^{-18}\mathrm{J}$ is the electron energy at its ground state. Then, $\frac{-2m_{e}E}{{\hslash }^2}\approx 3.565\times {10}^{20}/{\mathrm{m}}^2$ and $\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}\approx 1.888\times {10}^{10}/\mathrm{m}$.

If we set $x=\tilde{x}{a}_0$, where $\tilde{x}$ is in units of Bohr radius and $a_0=\frac{{\hslash }^2}{m_{e}k}\approx 0.5296\times {10}^{-10}\mathrm{m}$ is the Bohr radius, then $\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}{a}_0=1$, $\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}x=\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}{a}_0\tilde{x}=\tilde{x}$, and $\frac{k}{2E}\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}=-1$.

$\left(a\right)$ For example, if we choose $c\approx 2.648\times {10}^{-11}\mathrm{m}$ so that $c\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}=1$, i.e., $c=\frac{{\hslash }^2}{2m_{e}k}=\frac{a_0}{2}$, then $\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}\approx 3.776\times {10}^{10}$, $\frac{1}{k}\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}(-c^{2}E)=0.25$, $\frac{1}{k}\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}(-2ck)=-2$, and $\frac{1}{k}\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}kx=\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}{a}_0\tilde{x}=2\tilde{x}$. Therefore, putting $c_1=1$ and $c_2=0$ in Remark 1 $\left(i\right)$ yields

$$\begin{array}{c}\hfill y_1\left(x\right)=\mathrm{Ai}\left(\frac{1}{k}\sqrt[3]{\frac{2m_{e}k}{c^2{\hslash }^2}}\left(-c^{2}E-2ck+kx\right)\right)=\mathrm{Ai}(-1.75+2\tilde{x}).\end{array}$$

As we see in Figure 2, $y_1\left(x\right)$ is positive and has no zeros on $(0,c)$, and hence, the upper bound for inequality (6) exists.

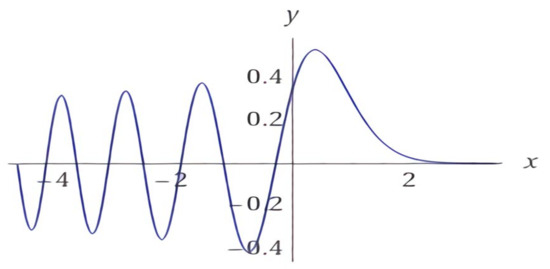
Figure 2. $y_1\left(x\right)$ has no zeros on $(0,c)$.

Moreover, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F_1\left(x\right)& :={\int }_0^x{\int }_0^t\frac{y_1\left(s\right)}{y_1\left(t\right)}dsdt={\int }_0^x\frac{1}{y_1\left(t\right)}\left({\int }_0^t{y}_1\left(s\right)ds\right)dt\hfill \\ & ={\int }_0^x\frac{1}{y_1\left(t\right)}\left(a_0{\int }_0^{\tilde{t}}\mathrm{Ai}(-1.75+2\tilde{s})d\tilde{s}\right)dt\hfill \\ & ={\int }_0^x\frac{a_0}{\mathrm{Ai}(-1.75+2\tilde{t})}{\int }_0^{\tilde{t}}\mathrm{Ai}(-1.75+2\tilde{s})d\tilde{s}dt\hfill \\ & =a_0^2{\int }_0^{\tilde{x}}\frac{1}{\mathrm{Ai}(-1.75+2\tilde{t})}{\int }_0^{\tilde{t}}\mathrm{Ai}(-1.75+2\tilde{s})d\tilde{s}d\tilde{t}\hfill \end{array}\end{array}$$

for all $0<x<c=\frac{a_0}{2}$, where $\tilde{t}=\frac{t}{a_0}$ and $\tilde{x}=\frac{x}{a_0}$. We know that $\frac{2m_e\epsilon }{{\hslash }^2}{F}_1\left(x\right)$ is an upper bound for inequality (6) when $0<x<c$.

Using Wolfram Alpha to compute the above double integral for small values of x, we get Table 1:

Table 1. In this table, $a_0$ denotes the Bohr radius of hydrogen atom.

x	$0.1a_0$	$0.2a_0$	$0.3a_0$	$0.4a_0$	$0.5a_0$
$F_1\left(x\right)$	$0.0047a_0^2$	$0.018a_0^2$	$0.040a_0^2$	$0.071a_0^2$	$0.113a_0^2$

$\left(b\right)$ If we put $c_1=\frac{1}{a_0}$ and $c_2=0$ in Remark 1 $\left(ii\right)$, then we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill y_2\left(x\right)& =\frac{1}{a_0}xexp\left(-\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}x\right)U\left(\frac{k}{2E}\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}+1,2,2\sqrt{\frac{-2m_{e}E}{{\hslash }^2}}x\right)\hfill \\ & =\tilde{x}{e}^{-\tilde{x}}U(0,2,2\tilde{x})=\tilde{x}{e}^{-\tilde{x}}\hfill \end{array}\end{array}$$

for $x>c=\frac{a_0}{2}$, where $\tilde{x}=\frac{x}{a_0}$ and $a_0$ is the Bohr radius. As we see in Figure 3, $y_2\left(x\right)$ has no zeros on $(c,\infty )$, and thus, the upper bound for inequality (6) exists.

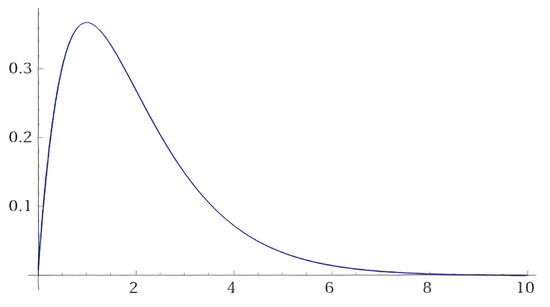
Figure 3. $y_2\left(x\right)$ has no zeros on $(c,\infty )$.

Furthermore, we see that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F_2\left(x\right)& :={\int }_0^x{\int }_0^t\frac{y_2\left(s\right)}{y_2\left(t\right)}dsdt={\int }_0^x\frac{1}{y_2\left(t\right)}\left({\int }_0^t{y}_2\left(s\right)ds\right)dt\hfill \\ & ={\int }_0^x\frac{1}{y_2\left(t\right)}\left(a_0{\int }_0^{\tilde{t}}\tilde{s}{e}^{-\tilde{s}}d\tilde{s}\right)dt={\int }_0^x\frac{a_0}{\tilde{t}{e}^{-\tilde{t}}}{\int }_0^{\tilde{t}}\tilde{s}{e}^{-\tilde{s}}d\tilde{s}dt\hfill \\ & =a_0^2{\int }_0^{\tilde{x}}\frac{1}{\tilde{t}{e}^{-\tilde{t}}}{\int }_0^{\tilde{t}}\tilde{s}{e}^{-\tilde{s}}d\tilde{s}d\tilde{t}\hfill \end{array}\end{array}$$

for any $x>c=\frac{a_0}{2}$, where $\tilde{t}=\frac{t}{a_0}$ and $\tilde{x}=\frac{x}{a_0}$. We know that $\frac{2m_e\epsilon }{{\hslash }^2}{F}_2\left(x\right)$ is an upper bound for inequality (6) when $x>c$.

Using Wolfram Alpha to compute the above double integral for some values of x, we get Table 2:

Table 2. In this table, $a_0$ denotes the Bohr radius of hydrogen atom.

x	$a_0$	$2a_0$	$3a_0$	$4a_0$	$5a_0$	$6a_0$	$7a_0$	$8a_0$	$9a_0$
$F_2\left(x\right)$	$0.32a_0^2$	$1.68a_0^2$	$5.26a_0^2$	$13.67a_0^2$	$32.99a_0^2$	$77.62a_0^2$	$181.98a_0^2$	$429.72a_0^2$	$1026.1a_0^2$

Unfortunately, $F_2\left(x\right)$ is a very fast increasing function.

4. Discussion

When it is difficult to find an exact solution of the Schrödinger equation for a particular potential, we can apply the perturbation theory to that equation. Moreover, we know that the one-dimensional Schrödinger equation can be applied to analyze the state of a particle reflected by a rectangular potential, which was the subject of a previous paper [16].

Since the difference between the perturbed solution ${\psi }_i$ and the exact solution ${\xi }_i$ of the one-dimensional time-independent Schrödinger Equation (3) is strongly influenced by x, we did not prove in Theorem 1 the exact Hyers–Ulam stability of the Schrödinger equation when the most of potential curve is hyperbolic. Therefore, it can be said that in this paper we dealt with a type of Hyers–Ulam stability.

The inequality (6) will be satisfied whatever $y_1\left(x\right)$ and $y_2\left(x\right)$ we choose which satisfy the formulas in Remark 1, but the upper bound of inequality (6) may depend strongly upon the choices of $y_1\left(x\right)$ and $y_2\left(x\right)$. Of course, the smaller the upper bound of the inequality, the better it is. But unfortunately we do not know what choices of $y_1\left(x\right)$ and $y_2\left(x\right)$ should be in order to reduce the upper bound of the inequality. We think that this question is worthy of another study separately from this paper.

5. Conclusions

In this paper, we investigated a type of Hyers–Ulam stability of the one-dimensional time-independent Schrödinger equation by using the operator method when the potential function is nearly expressed by a hyperbolic curve.

This problem is of great significance as it is suitable for describing the state of an electron of a hydrogen atom in nature. The electron may first be unstable in its transient state but it quickly reaches its stable state via the stability of the relevant Schrödinger equation. In other words, the stability of the Schrödinger equation with the relevant potential guarantees that the perturbed orbit will quickly come back to its corresponding stable orbit.

To the best of our knowledge, no papers have yet addressed this kind of stability problem. Therefore, it can be said that the value of this paper is high.