Accurate Time-Domain Modeling of Arbitrarily Shaped Graphene Layers Utilizing Unstructured Triangular Grids
Abstract
:1. Introduction
2. Theoretical Formulation
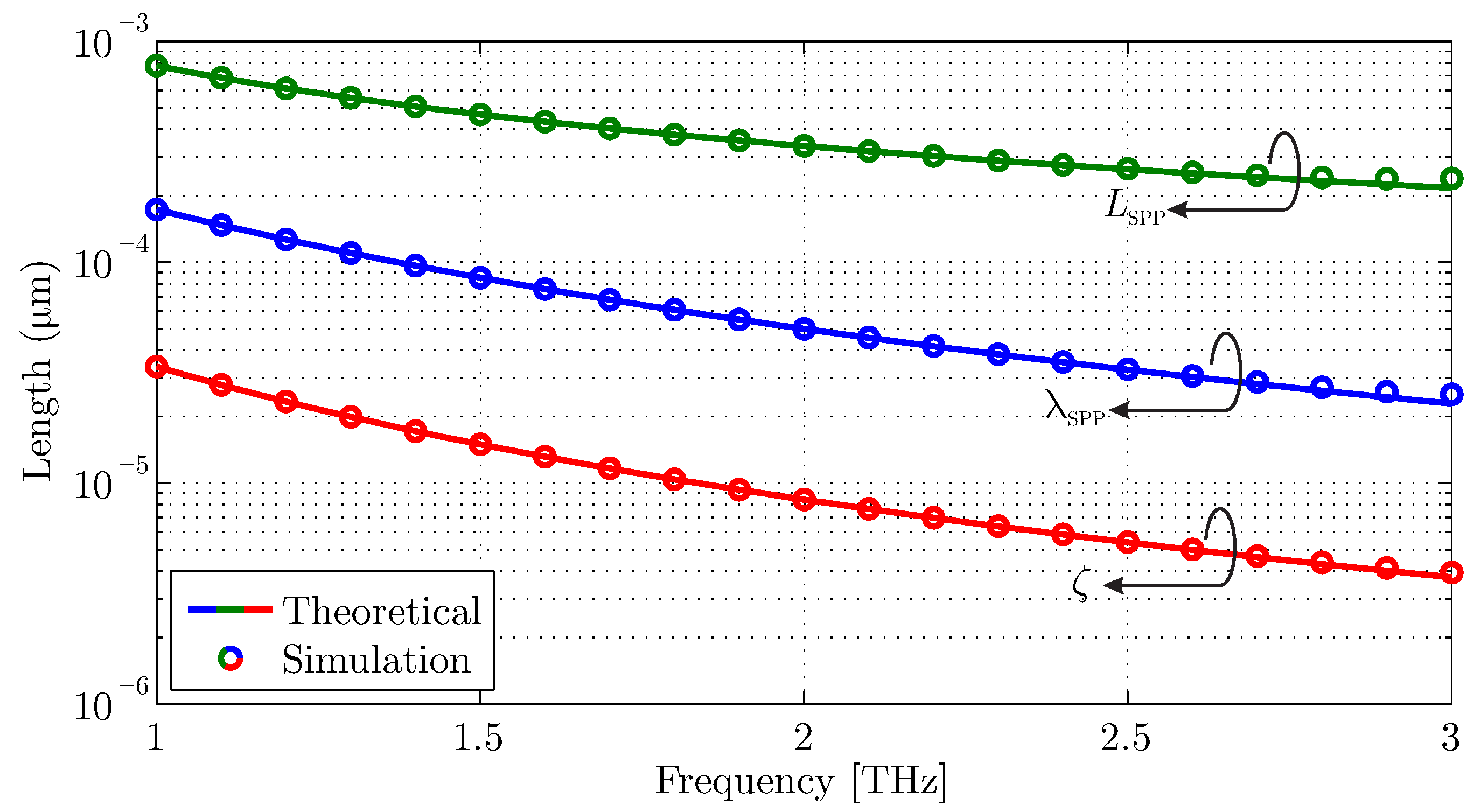
2.1. Graphene Surface Conductivity and Surface Wave Propagation Properties
2.2. Unstructured Triangular Grids for Electromagnetic Analysis in the Time Domain
2.3. Graphene Modeling within Unstructured Triangular Grids
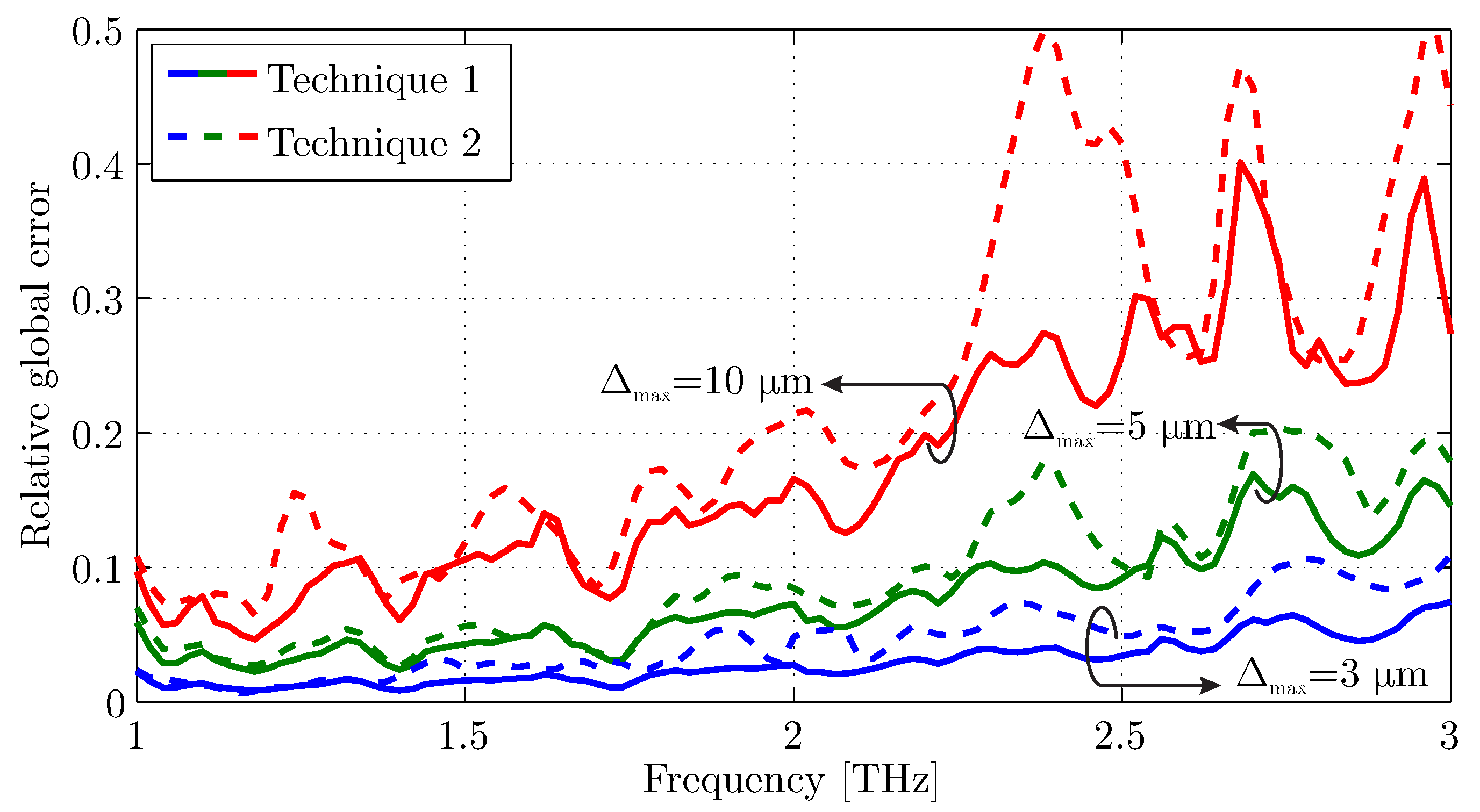
3. Proposed Algorithm Validation
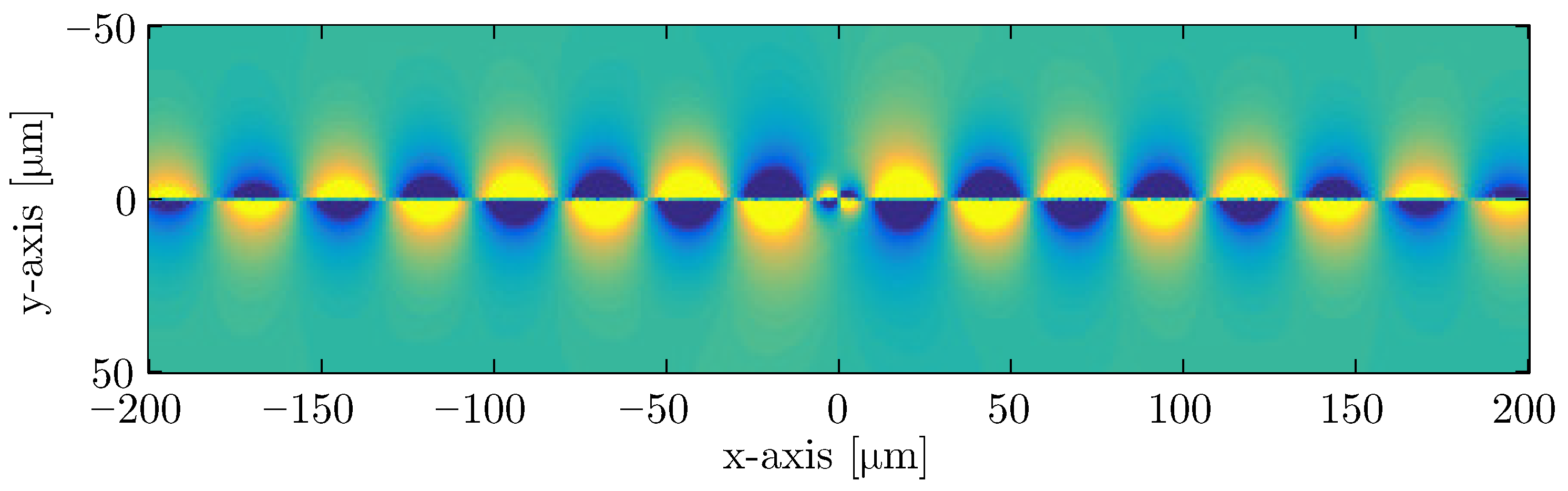
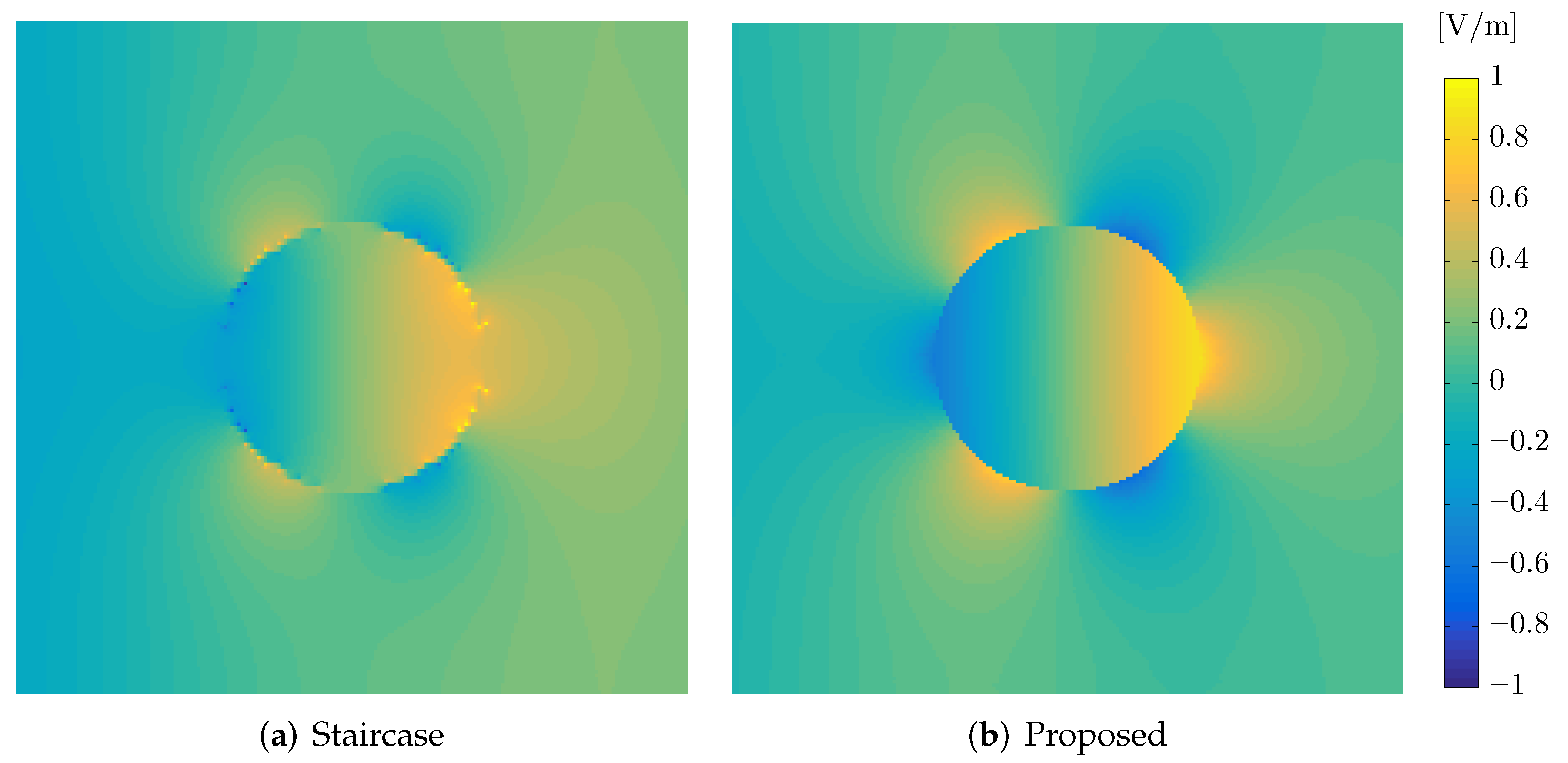
4. Incident Field toward a Circular Graphene Scatterer
5. Conclusions
Author Contributions
Funding
 .
.Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDTD | Finite-Difference Time-Domain |
| PML | Perfectly Matched Layer |
| RCM | Recursive Convolution Method |
| SPP | Surface Plasmon Polariton |
References
- Novoselov, K.; Geim, A.K.; Morozov, S.; Jiang, D.; Zhang, Y.; Dubonos, S.; Grigorieva, I.; Firsov, A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mikhailov, S.A.; Ziegler, K. New electromagnetic mode in graphene. Phys. Rev. Lett. 2007, 99, 016803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grigorenko, A.N.; Polini, M.; Novoselov, K. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.; Vasilevskiy, M.I. A primer on surface plasmon-polaritons in graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef] [Green Version]
- Ansell, D.; Radko, I.; Han, Z.; Rodriguez, F.; Bozhevolnyi, S.; Grigorenko, A. Hybrid graphene plasmonic waveguide modulators. Nat. Commun. 2015, 6, 8846. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Zhu, X.; Li, B.H.; Mortensen, N.A. Graphene-plasmon polaritons: From fundamental properties to potential applications. Front. Phys. 2016, 11, 117801. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Tantiwanichapan, K.; Swan, A.K.; Paiella, R. Graphene plasmonic devices for terahertz optoelectronics. Nanophotonics 2020, 9, 1901–1920. [Google Scholar] [CrossRef]
- Zhang, J.; Hong, Q.; Zou, J.; He, Y.; Yuan, X.; Zhu, Z.; Qin, S. Fano-resonance in hybrid metal-graphene metamaterial and its application as mid-infrared plasmonic sensor. Micromachines 2020, 11, 268. [Google Scholar] [CrossRef] [Green Version]
- Choroszucho, A. Analysis of the influence of the complex structure of clay hollow bricks on the values of electric field intensity by using the FDTD method. Arch. Electr. Eng. 2016, 65, 745–759. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Bouzianas, G.D.; Kantartzis, N.V.; Yioultsis, T.V.; Tsiboukis, T.D. Consistent study of graphene structures through the direct incorporation of surface conductivity. IEEE Trans. Magn. 2014, 50, 161–164. [Google Scholar] [CrossRef]
- Ramadan, O. Improved direct integration auxiliary differential equation FDTD scheme for modeling graphene drude dispersion. Optik 2020, 219, 165173. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Modeling graphene in the finite-difference time-domain method using a surface boundary condition. IEEE Trans. Antennas Propag. 2013, 61, 4176–4182. [Google Scholar] [CrossRef]
- Wang, X.H.; Yin, W.Y.; Chen, Z. Matrix exponential FDTD modeling of magnetized graphene sheet. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1129–1132. [Google Scholar] [CrossRef]
- Amanatiadis, S.A.; Kantartzis, N.V.; Ohtani, T.; Kanai, Y. Precise modeling of magnetically biased graphene through a recursive convolutional FDTD method. IEEE Trans. Magn. 2017, 54, 7201504. [Google Scholar] [CrossRef]
- Ramadan, O. Simplified FDTD Formulations for Magnetostatic Biased Graphene Simulations. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 2290–2294. [Google Scholar] [CrossRef]
- Mock, A. Modeling passive mode-locking via saturable absorption in graphene using the finite-difference time-domain method. IEEE J. Quantum Electron. 2017, 53, 1300210. [Google Scholar] [CrossRef]
- Amanatiadis, S.A.; Ohtani, T.; Zygiridis, T.T.; Kanai, Y.; Kantartzis, N.V. Modeling the Third-Order Electrodynamic Response of Graphene via an Efficient Finite-Difference Time-Domain Scheme. IEEE Trans. Magn. 2019, 56, 6700704. [Google Scholar] [CrossRef]
- Mock, A. Padé approximant spectral fit for FDTD simulation of graphene in the near infrared. Opt. Mater. Express 2012, 2, 771–781. [Google Scholar] [CrossRef]
- Amanatiadis, S.; Zygiridis, T.; Ohtani, T.; Kanai, Y.; Kantartzis, N. A Consistent Scheme for the Precise FDTD Modeling of the Graphene Interband Contribution. IEEE Trans. Magn. 2021, 57, 1600104. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, Y.; Xu, C.; Han, X.; Yan, X. Tunable light trapping and absorption enhancement with graphene ring arrays. Phys. Chem. Chem. Phys. 2016, 18, 26661–26669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.; Zhang, Z.; Wang, S.; Liu, Y.; Zhang, J.; Chen, D.; Ouyang, J.; Yang, J. Tunable graphene-based plasmon-induced transparency based on edge mode in the mid-infrared region. Nanomaterials 2019, 9, 448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, T.; Zhou, C.; Jiang, X.; Cheng, L.; Xu, C.; Xiao, S. Tunable light trapping and absorption enhancement with graphene-based complementary metasurfaces. Opt. Mater. Express 2019, 9, 1469–1478. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Cai, W.; Wang, L.; Zhang, X.; Xu, J. Tunable terahertz optical antennas based on graphene ring structures. Appl. Phys. Lett. 2012, 100, 153111. [Google Scholar] [CrossRef]
- Ye-xin, S.; Jiu-sheng, L.; Le, Z. Graphene-integrated split-ring resonator terahertz modulator. Opt. Quantum Electron. 2017, 49, 350. [Google Scholar] [CrossRef]
- Wu, L.; Liu, H.; Li, J.; Wang, S.; Qu, S.; Dong, L. A 130 GHz electro-optic ring modulator with double-layer graphene. Crystals 2017, 7, 65. [Google Scholar] [CrossRef] [Green Version]
- Bao, Z.; Tang, Y.; Hu, Z.D.; Zhang, C.; Balmakou, A.; Khakhomov, S.; Semchenko, I.; Wang, J. Inversion method characterization of graphene-based coordination absorbers incorporating periodically patterned metal ring metasurfaces. Nanomaterials 2020, 10, 1102. [Google Scholar] [CrossRef]
- Gusynin, V.; Sharapov, S.; Carbotte, J. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 2006, 19, 026222. [Google Scholar] [CrossRef] [Green Version]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef] [Green Version]
- Taflove, A.; Hagness, S.C.; Piket-May, M. Computational electromagnetics: The finite-difference time-domain method. In The Electrical Engineering Handbook; Elsevier Inc.: New York, NY, USA, 2005; Volume 3. [Google Scholar]
- Lee, C.; McCartin, B.; Shin, R.; Kong, J.A. A triangular-grid finite-difference time-domain method for electromagnetic scattering problems. J. Electromagn. Waves Appl. 1994, 8, 449–470. [Google Scholar] [CrossRef]
- Liu, Y.; Sarris, C.D.; Eleftheriades, G.V. Triangular-mesh-based FDTD analysis of two-dimensional plasmonic structures supporting backward waves at optical frequencies. J. Light. Technol. 2007, 25, 938–945. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 5.5, COMSOL AB. 2019. Available online: www.comsol.com (accessed on 1 November 2021).




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amanatiadis, S.; Zygiridis, T.; Kantartzis, N. Accurate Time-Domain Modeling of Arbitrarily Shaped Graphene Layers Utilizing Unstructured Triangular Grids. Axioms 2022, 11, 44. https://doi.org/10.3390/axioms11020044
Amanatiadis S, Zygiridis T, Kantartzis N. Accurate Time-Domain Modeling of Arbitrarily Shaped Graphene Layers Utilizing Unstructured Triangular Grids. Axioms. 2022; 11(2):44. https://doi.org/10.3390/axioms11020044
Chicago/Turabian StyleAmanatiadis, Stamatios, Theodoros Zygiridis, and Nikolaos Kantartzis. 2022. "Accurate Time-Domain Modeling of Arbitrarily Shaped Graphene Layers Utilizing Unstructured Triangular Grids" Axioms 11, no. 2: 44. https://doi.org/10.3390/axioms11020044
APA StyleAmanatiadis, S., Zygiridis, T., & Kantartzis, N. (2022). Accurate Time-Domain Modeling of Arbitrarily Shaped Graphene Layers Utilizing Unstructured Triangular Grids. Axioms, 11(2), 44. https://doi.org/10.3390/axioms11020044






