Optimal Location of Exit Doors for Efficient Evacuation of Crowds at Gathering Places
Abstract
1. Introduction
2. Materials and Methods
2.1. The State System
2.2. The Optimal Control Problem
2.3. Numerical Resolution
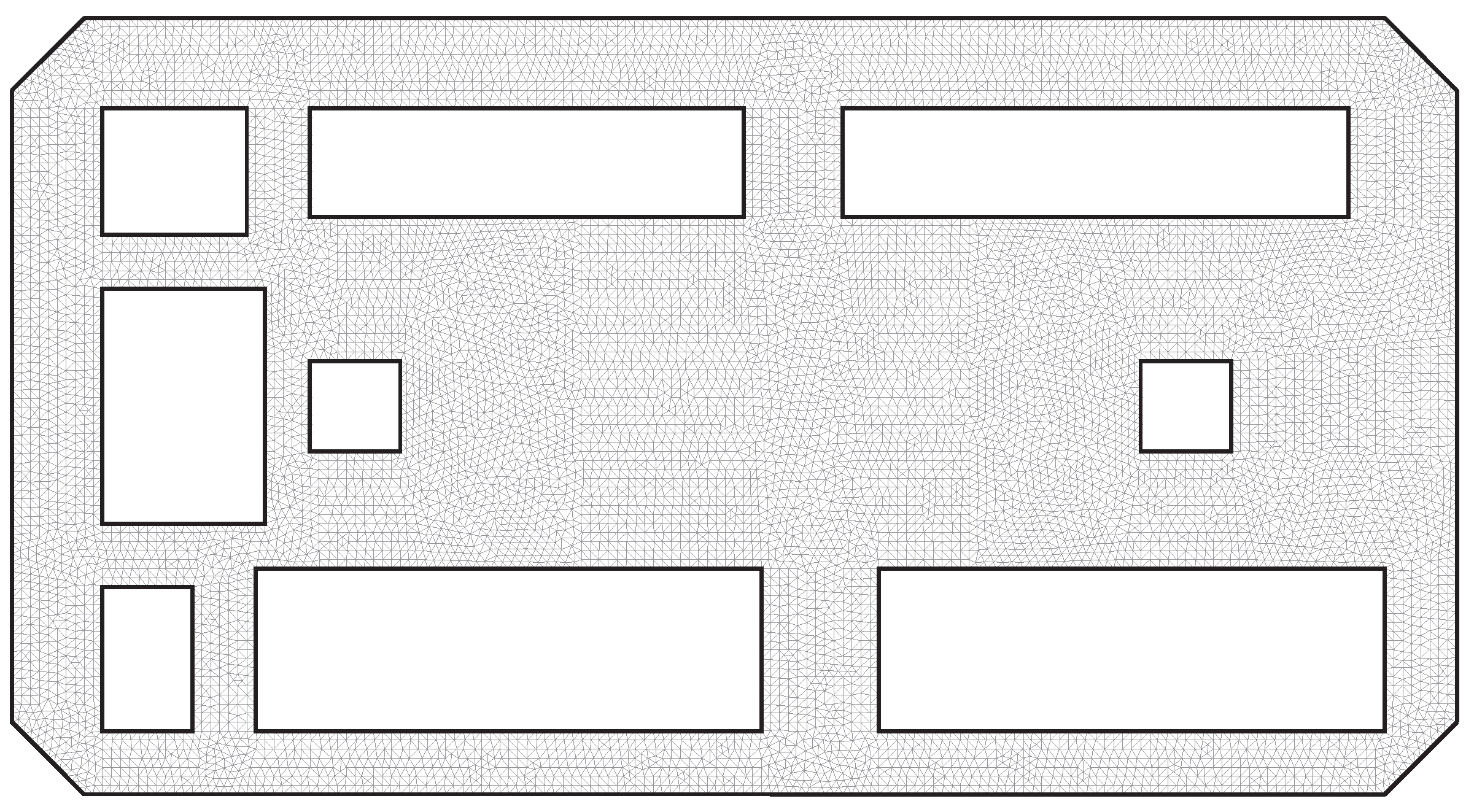
2.3.1. Space-Time Discretization
2.3.2. Numerical Optimization
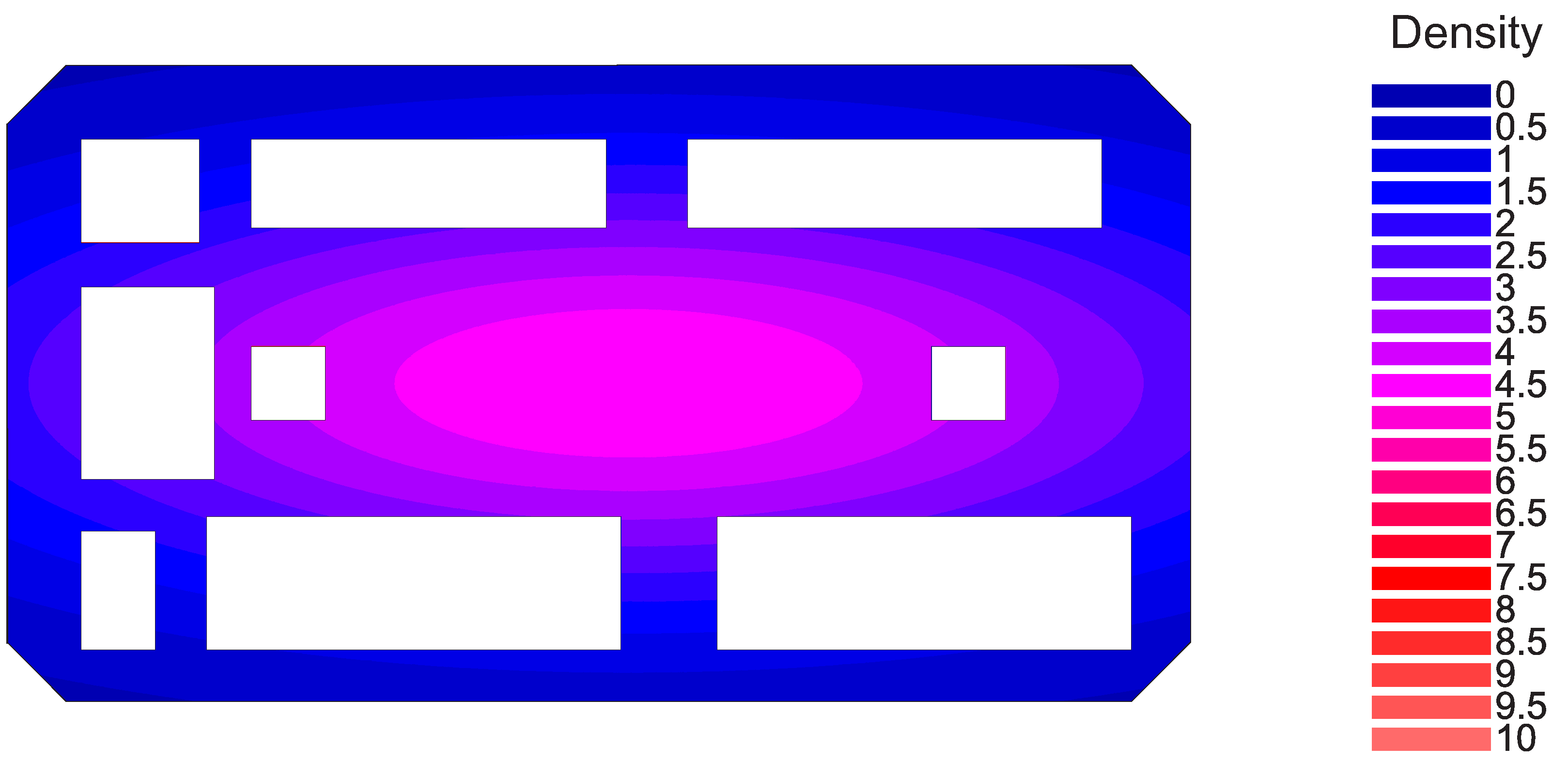
3. Results and Discussion
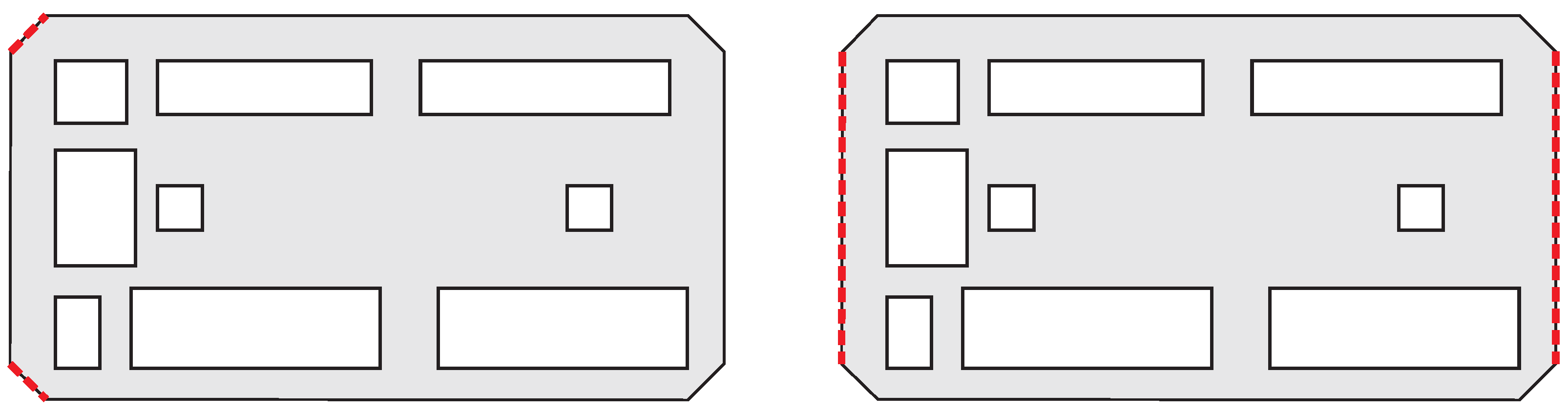
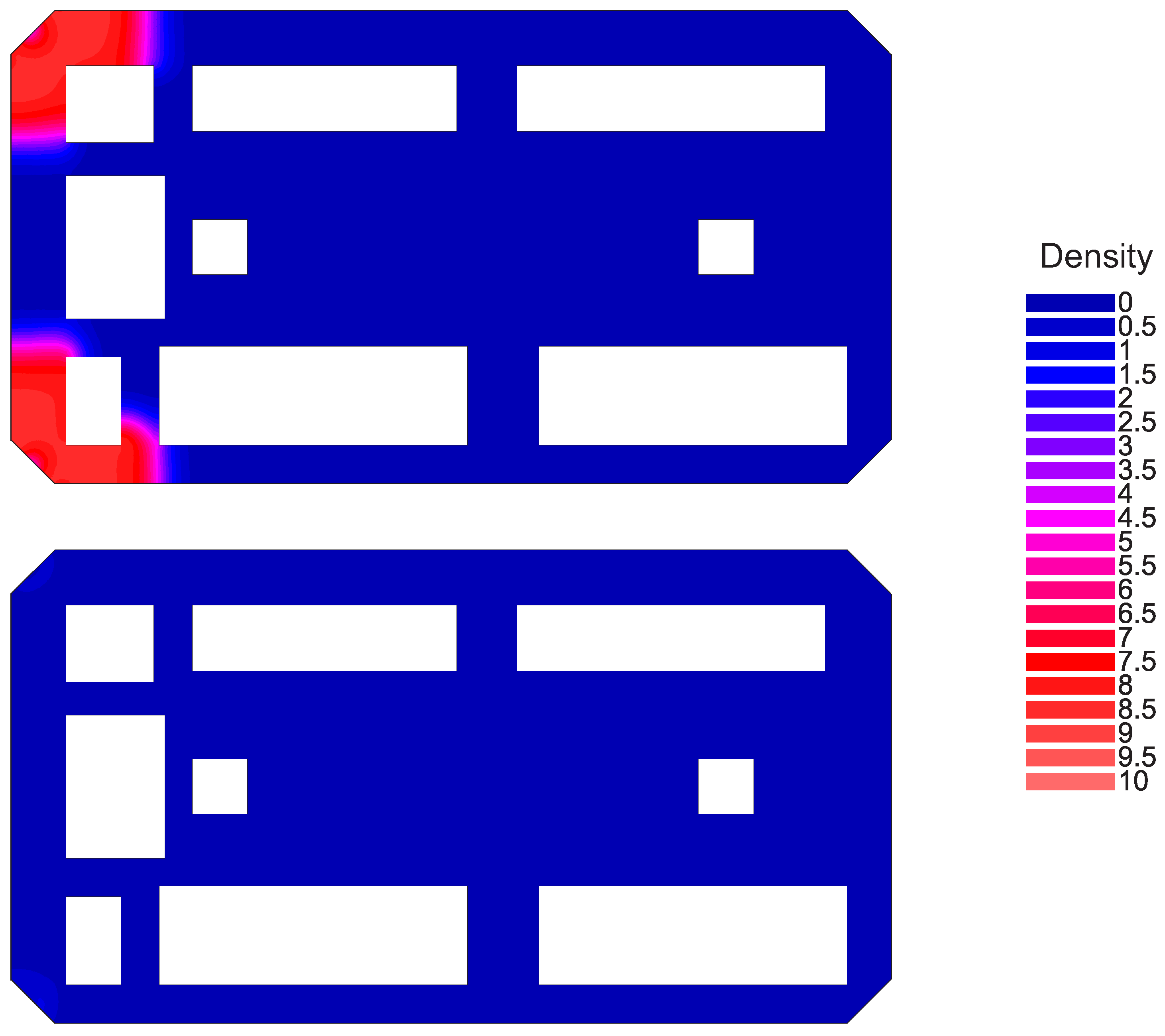
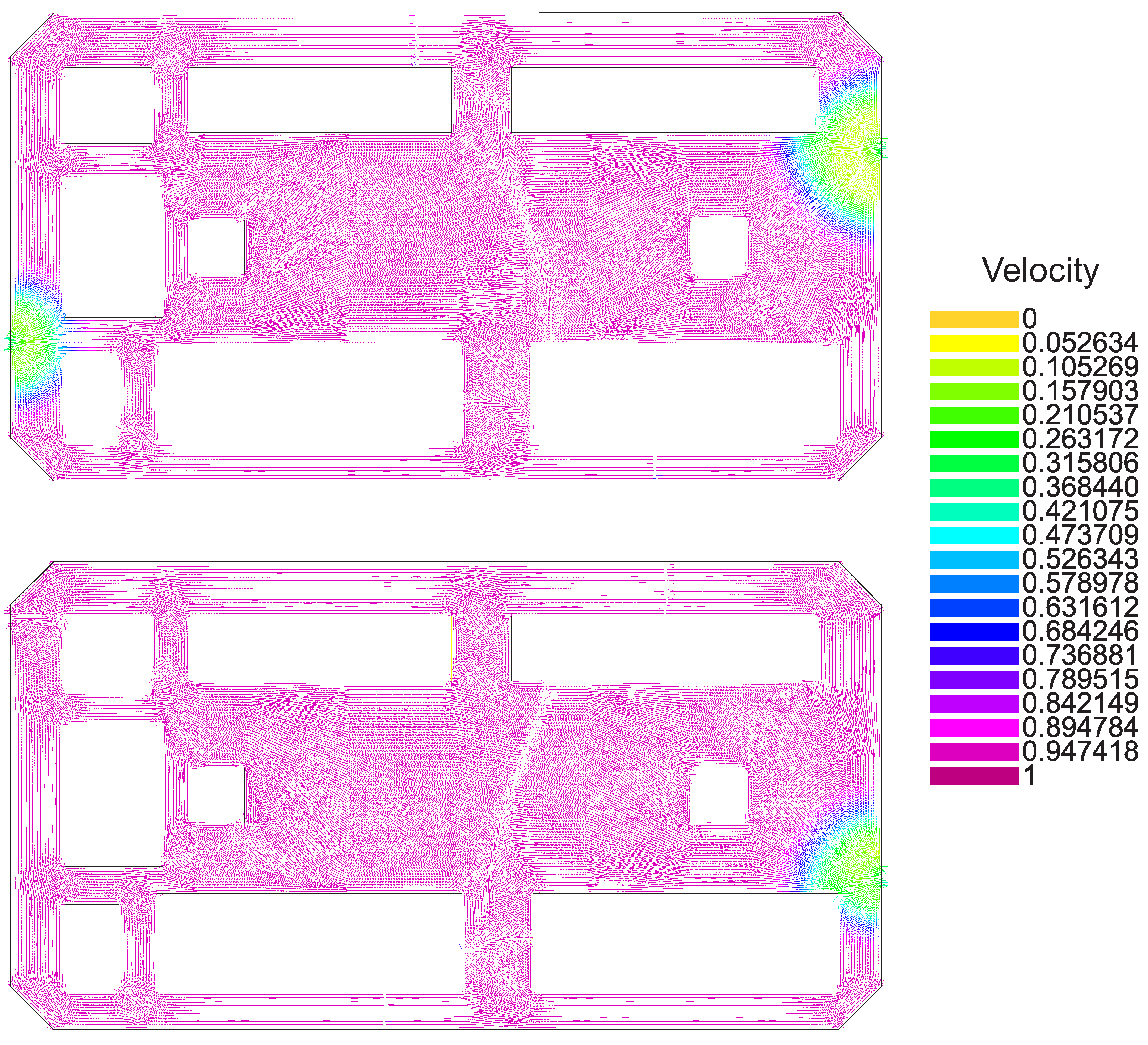
3.1. Case 1: Exit Doors in Left Corners
3.2. Case 2: Exit Doors in Left and Right Sides
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taneja, L.; Bolia, N.B. Network redesign for efficient crowd flow and evacuation. Appl. Math. Model. 2018, 53, 251–266. [Google Scholar] [CrossRef]
- Henderson, L.F. On the fluid mechanics of human crowd motion. Transp. Res. 1974, 8, 509–515. [Google Scholar] [CrossRef]
- Hirai, K.; Tarui, K. A simulation of the behavior of a crowd in panic. In Proceedings of the 1975 International Conference on Cybernetics and Society, San Francisco, CA, USA, 23–25 September 1975; pp. 409–411. [Google Scholar]
- Hughes, R. A continuum theory for the flow of pedestrians. Transp. Res. Part B Methodol. 2002, 36, 507–535. [Google Scholar] [CrossRef]
- Bellomo, N.; Dogbé, C. On the Modeling of Traffic and Crowds: A Survey of Models, Speculations, and Perspectives. SIAM Rev. 2011, 53, 409–463. [Google Scholar] [CrossRef]
- Martinez-Gil, F.; Lozano, M.; García-Fernandez, I.; Fernandez, F. Modeling, evaluation, and scale on artificial pedestrians: A literature review. ACM Comput. Surv. 2017, 50, 1–35. [Google Scholar] [CrossRef]
- Kachroo, P.; Al-nasur, S.J.; Wadoo, S.A.; Shende, A. Pedestrian Dynamics. Feedback Control of Crowd Evacuation, Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Cristiani, E.; Piccoli, B.; Tosin, A. Multiscale Modeling of Pedestrian Dynamics, Modeling, Simulation & Applications; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Maury, B.; Faure, S. Crowds in Equations. An Introduction to the Microscopic Modeling of Crowds; World Scientific: Singapore, 2019. [Google Scholar]
- Amadori, D.; Goatin, P.; Rosini, M.D. Existence results for Hughes’ model for pedestrian flows. J. Math. Anal. Appl. 2014, 420, 387–406. [Google Scholar]
- Di Francesco, M.; Fagioli, S.; Rosini, M.D.; Russo, G. Deterministic particle approximation of the Hughes model in one space dimension. Kinet. Rel. Mod. 2017, 10, 215–237. [Google Scholar] [CrossRef]
- Xia, Y.; Wong, S.C.; Zhang, M.; Shu, C.W.; Lam, W.H.K. An efficient discontinuous Galerkin method on triangular meshes for a pedestrian flow model. Int. J. Numer. Methods Eng. 2008, 76, 337–350. [Google Scholar] [CrossRef]
- Huang, L.; Wong, S.C.; Zhang, M.; Shu, C.W.; Lam, W.H.K. Revisiting Hughes’ dynamic continuum model for pedestrian flow and the development of an efficient solution algorithm. Transp. Res. Part Methodol. 2009, 53, 127–141. [Google Scholar]
- Piccoli, B.; Tosin, A. Time-Evolving Measures and Macroscopic Modeling of Pedestrian Flow. Arch. Ration. Mech. Anal. 2011, 199, 707–738. [Google Scholar] [CrossRef]
- Hoogendoorn, S.; Wageningen-Kessels, F.L.M.; Daamen, W.; Duives, D.C. Continuum modelling of pedestrian flows: From microscopic principles to self-organised macroscopic phenomena. Physica A 2014, 416, 684–694. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Martin, S.; Wolfram, M.T. An improved version of the Hughes model for pedestrian flow. Math. Models Methods Appl. Sci. 2016, 26, 671–697. [Google Scholar] [CrossRef]
- Carlini, E.; Festa, A.; Silva, F.J.; Wolfram, M.T. A Semi-Lagrangian Scheme for a Modified Version of the Hughes’ Model for Pedestrian Flow. Dyn. Games Appl. 2017, 7, 683–705. [Google Scholar] [CrossRef]
- Aghamohammadi, R.; Laval, J.A. Dynamic traffic assignment using the macroscopic fundamental diagram: A Review of vehicular and pedestrian flow models. Transp. Res. Part Methodol. 2020, 137, 99–118. [Google Scholar] [CrossRef]
- Cristiani, E.; De Santo, A.; Menci, M. A generalized mean-field game model for the dynamics of pedestrians with limited predictive abilities. Commun. Math. Sci. 2022; in press. [Google Scholar]
- Cristiani, E.; Priuli, F.S.; Tosin, A. Modeling rationality to control self-organization of crowds: An environmental approach. SIAM J. Appl. Math. 2015, 75, 605–619. [Google Scholar] [CrossRef]
- Hoogendoorn, S.; Bovy, P.H.L. Simulation of pedestrian flows by optimal control and differential games. Optim. Control Appl. Meth. 2003, 24, 53–172. [Google Scholar] [CrossRef]
- Molyneaux, N.; Scarinci, R.; Bierlaire, M. Design and analysis of control strategies for pedestrian flows. Transportation 2021, 48, 1767–1807. [Google Scholar] [CrossRef]
- Saadatseresht, M.; Mansourian, A.; Taleai, M. Evacuation planning using multiobjective evolutionary optimization approach. Eur. J. Oper. Res. 2009, 198, 305–314. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lu, X.; Tian, L.; Yu, Z.; Huang, K.; Wang, Y.; Li, T. Optimal layout design of obstacles for panic evacuation using differential evolution. Physica A 2017, 465, 175–194. [Google Scholar] [CrossRef]
- Cristiani, E.; Peri, D. Handling obstacles in pedestrian simulations: Models and optimization. Appl. Math. Model. 2017, 45, 285–302. [Google Scholar] [CrossRef]
- Shende, A.; Singh, M.P.; Kachroo, P. Optimization-based feedback control for pedestrian evacuation from an exit corridor. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1167–1176. [Google Scholar] [CrossRef]
- Kamkarian, P.; Hexmoor, H. Exploiting the Imperialist Competition algorithm to determine exit door efficacy for public buildings. Simulation 2014, 90, 24–51. [Google Scholar] [CrossRef]
- Tian, H.-H.; Dong, L.-Y.; Yu, X. Influence of the exits’ configuration on evacuation process in a room without obstacle. Physica A 2015, 420, 64–78. [Google Scholar]
- Wu, J.; Wang, X.; Chen, J.; Shu, G.; Li, Y. The position of a door can significantly impact on pedestrians’ evacuation time in an emergency. Appl. Math. Comput. 2015, 258, 29–35. [Google Scholar] [CrossRef]
- Khamis, N.; Selamat, H.; Ismail, F.S.; Lutfy, O.F.; Haniff, M.F.; Nordin, I.N. Optimized exit door locations for a safer emergency evacuation using crowd evacuation model and artificial bee colony optimization. Chaos Solitons Fractals 2020, 131, 109505. [Google Scholar] [CrossRef]
- Gurumoorthy, K.S.; Rangarajan, A. A Schrödinger equation for the fast computation of approximate Euclidean distance functions. In International Conference on Scale Space and Variational Methods in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2009; pp. 100–111. [Google Scholar]
- Churbanov, A.G.; Vabishchevich, P.N. Numerical solution of boundary value problems for the eikonal equation in an anisotropic medium. J. Comput. Appl. Math. 2019, 362, 55–67. [Google Scholar]
- Axthelm, R. Finite Element Simulation of a Macroscopic Model for Pedestrian Flow. In Traffic and Granular Flow’15; Springer: Cham, Switzerland, 2016; pp. 233–240. [Google Scholar]
- Herzog, R.A.; Pietschmann, J.F.; Winkler, M. Optimal control of Hughes’ model for pedestrian flow via local attraction. arXiv 2020, arXiv:2011.03580. [Google Scholar]
- Vázquez-Méndez, M.E.; Alvarez-Vázquez, L.J.; García-Chan, N.; Martinez, A. Optimal management of an urban road network with an environmental perspective. Comput. Math. Appl. 2019, 77, 1786–1797. [Google Scholar] [CrossRef]
- García-Chan, N.; Alvarez-Vázquez, L.J.; Martinez, A.; Vázquez-Méndez, M.E. Bilevel optimal control of urban traffic-related air pollution by means of Stackelberg strategies. Optim. Eng. 2022, 23, 1165–1188. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Price, W.L. A controlled random search procedure for global optimisation. Comput. J. 1977, 20, 367–370. [Google Scholar] [CrossRef]
- Hecht, F. New development in Freefem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarez-Vázquez, L.J.; García-Chan, N.; Martínez, A.; Rodríguez, C.; Vázquez-Méndez, M.E. Optimal Location of Exit Doors for Efficient Evacuation of Crowds at Gathering Places. Axioms 2022, 11, 592. https://doi.org/10.3390/axioms11110592
Alvarez-Vázquez LJ, García-Chan N, Martínez A, Rodríguez C, Vázquez-Méndez ME. Optimal Location of Exit Doors for Efficient Evacuation of Crowds at Gathering Places. Axioms. 2022; 11(11):592. https://doi.org/10.3390/axioms11110592
Chicago/Turabian StyleAlvarez-Vázquez, Lino J., Néstor García-Chan, Aurea Martínez, Carmen Rodríguez, and Miguel E. Vázquez-Méndez. 2022. "Optimal Location of Exit Doors for Efficient Evacuation of Crowds at Gathering Places" Axioms 11, no. 11: 592. https://doi.org/10.3390/axioms11110592
APA StyleAlvarez-Vázquez, L. J., García-Chan, N., Martínez, A., Rodríguez, C., & Vázquez-Méndez, M. E. (2022). Optimal Location of Exit Doors for Efficient Evacuation of Crowds at Gathering Places. Axioms, 11(11), 592. https://doi.org/10.3390/axioms11110592






