Logic, Game Theory, and Social Choice: What Do They Have in Common?

Abstract

The answer to the question above is that in all these domains axiomatic characterizations are given of, respectively, mathematical reasoning, certain notions from game theory, and certain social choice rules. The meaning of the completeness theorem in logic is that mathematical reasoning can be characterized by a handful of certain (logical) axioms and rules. If we apply mathematical reasoning to elementary arithmetic, i.e., the addition and multiplication of natural numbers, it turns out that almost all true arithmetical statements, for instance, $\forall x\forall y[x+y=y+x]$, can be logically deduced from the axioms of Peano. However, in 1931 Kurt Gődel showed that the axioms of Peano do not (fully) characterize the addition and multiplication of the natural numbers, more precisely, that there are certain special self-referential arithmetical sentences that, although true, cannot be deduced from Peano’s axioms. There are axiomatic characterizations of several social choice and ranking rules that say that a given rule is the only one satisfying a particular set of axioms. Arrow’s impossibility theorem in social choice theory tells us that a certain set of, at first sight, quite reasonable axioms for a social ranking rule turns out to be inconsistent. Consequently, a social ranking rule that satisfies the axioms in question cannot exist. Finally, many notions from game theory, such as the Shapley–Shubik and the Banzhaf index, may also be characterized by a set of axioms.

1. Logical Axioms and Rules

In logic, one studies how conclusions follow from certain given premisses. We shall restrict ourselves here to propositional logic, i.e., we shall restrict ourselves to arguments in which all premisses as well as the conclusion consist of propositions, atomic or built up from simpler propositions by means of the connectives ∧ (and), ∨ (or), → (if …, then …), and ¬ (not). The atomic propositions are rendered by letters P, Q, and R, and by means of the connectives one may build more complex propositions, such as $(P\vee Q)\to \neg R$. The latter formula may stand for ‘if it is raining or snowing, then we do not go for a walk’, for instance.

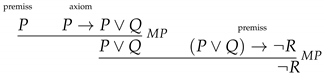
Now suppose that P and $(P\vee Q)\to \neg R$ are given premisses and that they are both true; then $\neg R$ must also be true. Why? Supposing P is true, then $P\vee Q$ is also true, and because $(P\vee Q)\to \neg R$ is supposed to be true, it follows that $\neg R$ must also be true. Schematically,

$$\begin{array}{c}\underline{P}\\ \underline{P\vee Q(P\vee Q)\to \neg R}\\ \neg R\end{array}$$

Note that the interpretation of the symbols P, Q, and R does not matter for the validity of the argument. P may stand for ‘it is raining’, but it may also stand for ‘I like honey’, for instance. Additionally, Q may stand for ‘I like sugar’ and R for ‘I like salt’, for instance. If the premisses P and $(P\vee Q)\to \neg R$ are both true, then the conclusion $\neg R$ must also be true, no matter what the precise interpretation (meaning) of P, Q, and R is. The validity of the argument is due to the meaning of the propositional connectives ∧ (and), ∨ (or), → (if …, then …), and ¬ (not) and does not depend on the content of P, Q, and R.

So, by definition, a formula B is a valid consequence of given premisses $A_1,\dots ,A_n$ iff for every interpretation of the atomic formulas P, Q, R, … occurring in $A_1,\dots A_n$, and B, whenever the premisses $A_1,\dots ,A_n$ are all true (under the given interpretation), then the conclusion B must also be true (under the given interpretation). Notation: $A_1,\dots ,A_n\vDash B$. As we have seen: $P,(P\vee Q)\to \neg R\vDash \neg R$.

One should realize that the validity of an argument does not say anything about the truth of the premisses. It only says that if the premisses are true (given a particular interpretation), then the conclusion must also be true (given the interpretation in question). For instance, the proposition ‘it is raining’ (P) may be false, in which case the conclusion ‘we do not go for a walk’ ($\neg R$) may be false too.

Now, it turns out that one may select a finite, small number of (logical) axioms, which characterize the meaning of the propositional connectives, and one rule, called Modus Ponens (MP), such that every valid consequence B of given premisses $A_1,\dots ,A_n$ can be deduced from the given premisses by applications of Modus Ponens and the axioms. Here are the (logical) axioms for the connectives:

	Introduction                              Elimination
∧	$A\to (B\to A\wedge B)$              $A\wedge B\to A$
	$A\wedge B\to B$
∨	$A\to A\vee B$         $(A\to C)\to \left(\right(B\to C)\to (A\vee B\to C\left)\right)$
	$B\to A\vee B$
→	$A\to (B\to A)$      $(A\to B)\to \left(\right(A\to (B\to C))\to (A\to C\left)\right)$
¬	$(A\to B)\to \left(\right(A\to \neg B)\to \neg A)$        $\neg \neg A\to A$

Additionally, the rule Modus Ponens (MP) is the following one: $\frac{AA\to B}{B}$.

For instance, the valid consequence $\neg R$ of the premisses P and $(P\vee Q)\to \neg R$ can be deduced from the given premisses by applications of the logical axioms and two applications of Modus Ponens:

The schema above is called a deduction of $\neg R$ from the premisses P and $(P\vee Q)\to \neg R$. Additionally, $\neg R$ is called deducible from P and $(P\vee Q)\to \neg R$, because there exists a deduction of $\neg R$ from the premisses P and $(P\vee Q)\to \neg R$; notation: $P,(P\vee Q)\to \neg R⊢\neg R$. More generally, B is deducible from$A_1,\dots ,A_n$, notation $A_1,\dots ,A_n⊢B$, if one can make a deduction of B from $A_1,\dots A_n$, using only Modus Ponens (MP) and the logical axioms.

It is easy to see that our logical deduction system is sound, i.e., logical deduction cannot lead from true premisses to false conclusions. That is, any formula B deducible from premisses $A_1,\dots ,A_n$ is a valid consequence of these premisses. In other words, if $A_1,\dots ,A_n⊢B$, then $A_1,\dots ,A_n\vDash B$. This is the soundness theorem for (classical) propositional logic.

Conversely, the completeness theorem for (classical) propositional logic says that every valid consequence B of given premisses $A_1,\dots ,A_n$ can be deduced from the premisses by using only the logical axioms for the connectives and Modus Ponens. In short: if $A_1,\dots ,A_n\vDash B$, then $A_1,\dots ,A_n⊢B$. For a proof, see any logic textbook, for instance de Swart [1]. This theorem says that any valid human mathematical argumentation can be simulated by using only the logical axioms and the rule Modus Ponens. In other words, the logical axioms for the connectives together with the rule Modus Ponens are a characterization of human mathematical reasoning. Because the rule Modus Ponens and these logical axioms can be captured in a computer program, in theory such a computer program can simulate human (mathematical) reasoning and hence is equipped with artificial intelligence.

It is important to notice that the right selection of the logical axioms and rules is a subtle one. For instance, although the formula of Peirce, $\left(\right(A\to B)\to A)\to A$, only contains the logical connective →, it cannot be deduced from the two axioms for → alone, see Exercise 2.44 in de Swart [1]. In addition, one needs the axioms for ¬. Additionally, in order to make a deduction of $A\vee \neg A$ (without using any premisses), one makes a deduction of $\neg \neg (A\vee \neg A)$ and next uses the axiom $\neg \neg C\to C$ and Modus Ponens, with C replaced by $A\vee \neg A$. If one replaces the axiom $\neg \neg A\to A$, for instance, by its converse, $A\to \neg \neg A$, then the completeness theorem does not hold anymore and $A\vee \neg A$ cannot be deduced anymore.

Interestingly, if one replaces the logical axiom $\neg \neg A\to A$ by $\neg A\to (A\to B)$, leaving all other axioms unchanged, a completely different logic results, called intuitionistic logic; see, for instance Chapter 8 in de Swart [1]. In intuitionistic logic, although $\neg \neg (A\vee \neg A)$ is deducible, $A\vee \neg A$ is no longer deducible and it should not be, because that would mean that for any proposition A, one has a proof of A or a proof of $\neg A$, which evidently is not the case: there are many unsolved problems A.

Additionally, it should be noted that mathematical (propositional) reasoning may be characterized by different sets of axioms. For instance, it turns out that the three axioms $A\to (B\to A)$, $(A\to B)\to \left(\right(A\to (B\to C))\to (A\to C\left)\right)$, and $(\neg A\to \neg B)\to (B\to A)$, together with Modus Ponens, constitute a different characterization, taking into account that conjunction (∧) and disjunction (∨) can be defined in terms of implication (→) and negation (¬). However, be aware: replacing $(\neg A\to \neg B)\to (B\to A)$ by $(A\to B)\to (\neg B\to \neg A)$ destroys the completeness theorem!

Basic propositions such as ‘john is a Philosopher’ typically consist of a subject (john) and a predicate (is a Philosopher). In predicate logic, one renders the subject–predicate structure of this basic proposition by, for instance, $P\left(j\right)$: the predicate ‘(being a) P(hilosopher)’ applies to j(ohn). In predicate logic, this subject–predicate structure of basic propositions is expressed by using predicate symbols and symbols to denote individuals. Consequently, one may deal with sentences such as ‘for all persons x, x is a Philosopher’, rendered by $\forall x\left[P\right(x\left)\right]$, and with sentences such as ‘there is at least one person x such that x is a Philosopher’, rendered by $\exists x\left[P\right(x\left)\right]$. The axioms for propositional logic now have to be supplemented by axioms for ∀ and ∃: $\forall x\left[A\right(x\left)\right]\to A\left(c\right)$ and $A\left(c\right)\to \exists x\left[A\right(x\left)\right]$, where c may indicate an individual such as j(ohn) or a variable such as $x,y,\dots$. Additionally, apart from the rule Modus Ponens, in predicate logic one also needs a rule for ∀ and a rule for ∃; in order to avoid some technical details we refer to, for instance, de Swart [1], Chapter 4.

The soundness and completeness theorem also hold for predicate logic: if $A_1,\dots ,A_n⊢B$, then $A_1,\dots ,A_n\vDash B$, and conversely, if $A_1,\dots ,A_n\vDash B$, then $A_1,\dots ,A_n⊢B$. The first one says that our deduction system is sound, i.e., it does not lead from true premisses to false conclusions. In other words, if B is deducible from $A_1,\dots ,A_n$ and $A_1,\dots ,A_n$ are true given an interpretation, then also B is true (given the same interpretation). The latter theorem says that we have enough axioms and rules to deduce any valid consequence of given premisses from those premisses by using the logical axioms and rules.

2. Arithmetical Axioms

In elementary arithmetic, one studies the properties of addition, +, and multiplication, ·, of the natural numbers $0,1,2,\dots$. From now on, we shall indicate the natural numbers by $0,s0,ss0,\dots$, where the symbol s stands for the successor function. We shall use letters $n,m,\dots$ as variables over natural numbers.

It became gradually clear that many arithmetical facts, such as $\forall n\forall m[n+m=m+n]$, can be logically deduced from a small number of more basic facts. In 1889, G. Peano proposed the following set of (arithmetical) axioms for addition and multiplication:

$\forall n[n+0=n]$	$\hspace{1em}\hspace{1em}\forall n[n·0=0]$
$\forall n\forall m[n+s(m)=s(n+m\left)\right]$	$\hspace{1em}\hspace{1em}\forall n\forall m[n·sm=n·m+n]$

Induction axiom: let $A\left(n\right)$ express a property of a natural number n.

$$A\left(0\right)\wedge \forall n\left[A\right(n)\to A(sn\left)\right]\to \forall n\left[A\right(n\left)\right]$$

For instance, to deduce $\forall n\forall m[n+m=m+n]$ from the Peano axioms, one needs the induction axiom. Together with the axioms for the successor function and equality (=), these axioms constitute the so-called Peano axioms for elementary arithmetic:

$\forall n[sn\ne 0]$

$\forall n\forall m[n=m\to sn=sm]$ and $\forall n\forall m[sn=sm\to n=m]$

$\forall n[n=n]$ (equality is reflexive)

$\forall n\forall m[n=m\to m=n]$ (equality is symmetric)

$\forall n\forall m\forall p\left[\right(n=m\wedge m=p)\to n=p]$ (equality is transitive)

Let us indicate the set of Peano axioms by $Peano$. Then, we know from the soundness and completeness theorem for predicate logic that $Peano⊢B$ iff $Peano\vDash B$. The latter means that any interpretation of $n,m,s,+$ and · that makes the Peano axioms true, will also make B true. However, doing arithmetic, we are not interested in all possible interpretations that make the Peano axioms true; we are only interested in the standard interpretation in which the variables are interpreted as natural numbers (and not as persons, for instance) and in which $s,+$ and · are interpreted as the successor function and the addition and multiplication of natural numbers, respectively (and not otherwise). Let us denote this standard interpretation by $\mathcal{N}$. Then, evidently, if $Peano⊢B$, then B is true under the standard interpretation $\mathcal{N}$ because the Peano axioms are true under $\mathcal{N}$. Experience now suggests that any formula B, such as $\forall n\forall m[n+m=m+n]$, which is true under the standard interpretation, may be deduced from the Peano axioms. That is, one might expect that if B is true under the standard interpretation $\mathcal{N}$, then $Peano⊢B$. In fact, Kleene [2] shows that many such formulas B actually can be deduced from the Peano axioms.

It was quite a surprise when K. Gödel, in 1931, proved that there are formulas B that are true under the standard interpretation $\mathcal{N}$ but that cannot be deduced from the Peano axioms. This is called Gődel’s incompleteness theorem: the Peano axioms are incomplete, i.e., they cannot deduce all formulas B that are true under the standard interpretation. In other words, it is impossible to fully characterize elementary number theory. Even more interestingly, the Peano axioms cannot even be extended in a consistent way in order to obtain the desired result. However, the formula B constructed by Gődel is a very special one: it says of itself that it is not deducible from the Peano axioms. For more details see, for instance, Kleene [2] or de Swart [1].

3. Axioms in Social Choice Theory

In traditional social choice theory, one assumes that each voter i gives as input a preference ordering $p\left(i\right)$ of the alternatives or candidates and a profile or vote configuration p is then a mapping that assigns to each voter i his preference ordering $p\left(i\right)$. Given such a profile p, a social ranking rule F assigns to p a social ranking ${⪰}_{F\left(p\right)}$ of the candidates and the highest ranked candidate in $F\left(p\right)$ is considered to be the winner.

$x{\approx }_{F\left(p\right)}y$:= $x{⪰}_{F\left(p\right)}y$ and $y{⪰}_{F\left(p\right)}x$, i.e., given profile p, the social ranking rule F declares x and y to be indifferent. Additionally, $x{\succ }_{F\left(p\right)}y$:= $x{⪰}_{F\left(p\right)}y$ and not $y{⪰}_{F\left(p\right)}x$, i.e., given profile p, the social ranking rule F prefers x to y.

The plurality rule (PR), for instance, is defined by $x{⪰}_{PR\left(p\right)}y$ iff the number of first votes for x in p is larger than or equal to the number of first votes for y in p. The majority rule (MR), on the other hand, is defined by $x{⪰}_{MR\left(p\right)}y$ iff x beats y, i.e., there are at least as many voters who prefer x to y in p than there are voters who prefer y to x in p. For illustration, consider the following profile p with five voters, numbered 1, 2, 3, 4 and 5, over four candidates, $a,b,c$, and d.

$p\left(1\right):abcd$

$p\left(2\right):acbd$

$p\left(3\right):bcad$

$p\left(4\right):cbad$

$p\left(5\right):dcab$

Then $PR\left(p\right)$: $a\left(bcd\right)$, i.e., $a{\succ }_{PR\left(p\right)}b{\approx }_{PR\left(p\right)}c{\approx }_{PR\left(p\right)}d$, where ≈ denotes indifference, because a is two times first in p, while b, c and d are only once first in p, while $MR\left(p\right)$: $cabd$, i.e., $c{\succ }_{MR\left(p\right)}a{\succ }_{MR\left(p\right)}b{\succ }_{MR\left(p\right)}d$ because c beats a with 3 against 2, a beats b with 3 against 2, and b beats d with 4 against 1. So, given this profile, the plurality rule would make a the winner, while the majority rule would make c the winner.

Notice that if there are only two alternatives, the plurality rule and the majority rule coincide.

Already in 1952, K. May [3] gave a characterization of the majority rule or the plurality rule in the case of only two alternatives.

Theorem 1.

In the case of only two alternatives, the majority (or plurality) rule is the only social ranking rule F that satisfies the following six axioms:

1 Based on comparing: the input for the social ranking rule F consists of profiles or vote configurations, which represent the individual preference orderings of the voters over the candidates.

2 Unrestricted domain: the social ranking rule F is defined over the set ofallpossible profiles, i.e., the social ranking rule F assigns a social ranking ${⪰}_{F\left(p\right)}$ to every (logically) possible vote configuration p.

3 Anonymity: the outcome of the social ranking rule F does not depend on the names of the voters.

4 Neutrality: the outcome of the social ranking rule F does not depend on the names of the candidates. More precisely, let q be the profile resulting from profile p by interchanging the names A and B and suppose $A{⪰}_{F\left(p\right)}B$, then $B{⪰}_{F\left(q\right)}A$.

5 Monotonicity: if $A{⪰}_{F\left(p\right)}B$ and A gets more support by at least one voter resulting in profile q, then $A{\succ }_{F\left(q\right)}B$.

6 Completeness: for each profile p and for all candidates A and B, $A{\succ }_{F\left(p\right)}B$ or $B{\succ }_{F\left(p\right)}A$ or $A{\approx }_{F\left(p\right)}B$.

Proof. 

Here, we present the proof as given by Balinski and Laraki [4]. Suppose the social ranking rule F satisfies all of the six axioms above. By anonymity, it follows that only the numbers count. Let $n_A$ be the number of voters in profile p who prefer A to B, $n_B$ the number of voters in p who prefer B to A, and $n_{AB}$ the number of voters in p who are indifferent between A and B. Completeness guarantees that there must be an outcome.

Suppose $n_A=n_B$ in profile p and $A{\succ }_{F\left(p\right)}B$. Neutrality implies that if q is the profile resulting from interchanging the names of A and B in p, $B{\succ }_{F\left(q\right)}A$. This is impossible because the new profile q is identical to the original profile p. Therefore, if $n_A=n_B$ in p, then $A{\approx }_{F\left(p\right)}B$. (*)

Suppose $n_A>n_B$ in p. Change the preferences of $n_A-n_B$ voters who prefer A to B in p into indifferences, resulting in a valid profile q in which the number of voters who prefer A to B equals the number of voters who prefer B to A; according to axiom 2, all profiles are allowed. For this new profile q, we have $A{\approx }_{F\left(q\right)}B$ because of (*). Next, by going back from profile q to the original profile p, the monotonicity axiom guarantees that $A{\succ }_{F\left(p\right)}B$. □

Assuming any number of candidates, Balinski and Laraki add the following two axioms to the six axioms just mentioned above:

7 Transitivity: if $X{⪰}_{F\left(p\right)}Y$ and $Y{⪰}_{F\left(p\right)}Z$, then $X{⪰}_{F\left(p\right)}Z$. We shall show below that the majority rule (MR) is not transitive, while the plurality rule (PR) clearly is.

8 Independence of Irrelevant Alternatives (IIA): If $A{⪰}_{F\left(p\right)}B$ and q is a profile resulting from profile p by adding or removing candidates, then still $A{⪰}_{F\left(q\right)}B$.

From its definition, it follows immediately that the majority rule is IIA, but we shall see below that the plurality rule is not.

In order to show that the majority rule (MR) is not transitive, one may consider the so-called Condorcet profile q:

1/3:	A	B	C
1/3:	B	C	A
1/3:	C	A	B

There is a majority, consisting of the first and the third group, which prefers A to B; therefore, A ${\succ }_{MR\left(q\right)}$ B. There is another majority, consisting of the first and second group, which prefers B to C; therefore, B ${\succ }_{MR\left(q\right)}$ C. But there is also a majority, consisting of the second and third group, which prefers C to A; therefore, C ${\succ }_{MR\left(q\right)}$ A and not A ${\succ }_{MR\left(q\right)}$ C, as transitivity would suggest. So, application of the majority rule to this Condorcet profile q yields a cyclic outcome: A ${\succ }_{MR\left(q\right)}$ B ${\succ }_{MR\left(q\right)}$ C ${\succ }_{MR\left(q\right)}$ A. There is no winner when the majority rule is applied to the Condorcet profile q.

In the literature, this is known as Condorcet’s paradox. One might guess that this problem hardly occurs in practice. However, Gehrlein [5] proved that in the case of three candidates and a large number of voters, the probability of a cyclic outcome under majority rule is about 1/16, assuming the impartial anonymous culture (IAC).

Next, we provide a real-life example showing that the plurality rule (PR) is not IIA. Let q be the following profile, which actually appeared in the year 2000 at the presidential elections in Florida.

profile q

profile q	2.912.790	49.18 % :	Bush
	2.912.253	49.17 % :	Gore
	97.488	01.65 % :	Nader	Gore	Bush

Let p be the profile resulting from profile q by leaving out candidate Nader. Then Gore ${\succ }_{PR\left(p\right)}$ Bush, because Gore has more first votes in p than Bush. However, profile q results from profile p by adding candidate Nader and applying plurality rule (PR) to profile q, Bush wins from Gore: Bush ${\succ }_{PR\left(q\right)}$ Gore, because the additon of candidate Nader lowers the number of voters for Gore. So, under the plurality rule in the competition between Bush and Gore, a third (irrelevant) candidate Nader plays a decisive role.

Theorem 2.

(Balinski and Laraki’s version of Arrow’s impossibility theorem): for more than two candidates, there is no social ranking rule F satisfying all axioms 1–8.

Proof. 

(Balinski and Laraki [4]) Suppose F satisfies all eight axioms and q is a profile. IIA says that in order to determine whether $A{⪰}_{F\left(q\right)}B$, we can leave out all other candidates and consider only these two. From axioms 1 till 6, it follows by May’s theorem that the social ranking rule F must be the majority rule (MR). However, the domain is unrestricted (axiom 2), so any Condorcet profile is allowed, and hence transitivity is violated. Therefore, there can be no social ranking rule that satisfies all axioms 1–8. □

In his original impossibility theorem, instead of the monotonicity axiom, Arrow [6] considered Pareto’s principle, which says that if all voters weakly prefer A to B ($A{⪰}_{p\left(i\right)}B$ for all voters i), then also society must weakly prefer A to B ($A{⪰}_{F\left(p\right)}B$). Arrow proved that any social ranking rule F that satisfies axioms 1–4, 6–8, and Pareto’s principle is a dictatorship, i.e., there is a voter d, called the dictator, such that the social outcome $F\left(p\right)$ is always the preference ordering $p\left(d\right)$ of d. In other words, axioms 1–4, 6–8, Pareto’s principle, and non-dictatorship are logically inconsistent; there can be no social ranking rule F that satisfies all these axioms.

Moreover, while the proof of Arrow’s impossibility theorem is relatively complicated, the proof of Balinski and Laraki’s version of Arrow’s theorem is relatively simple.

Van der Hout [7] et. al. proved that the plurality ranking (PR) rule can be characterized by the following three axioms or properties for a social ranking rule F:

Consistency: Let $V_1$ and $V_2$ be disjoint sets of voters, $p_1$ a profile for $V_1$, $p_2$ a profile for $V_2$, and $p_1+p_2$ the profile for $V_1\cup V_2$ that corresponds with $p_1$ on $V_1$ and with $p_2$ on $V_2$. F is consistent iff for all alternatives $x,y$, if $x{\succ }_{F\left(p_1\right)}y$ and $x{⪰}_{F\left(p_2\right)}y$, then $x{\succ }_{F(p_1+p_2)}y$.

Faithfulness: If F is applied to the profile $p\left(i\right)$ of $\left\{i\right\}$ alone, then the first element in the social preference ordering $F\left(\right(p\left(i\right)\left)\right)$ is the first element of i’s individual preference ordering $p\left(i\right)$.

FS-cancellation (FS stands for first score): given a profile p such that the number of voters who prefer x most in p equals the number of voters who prefer y most in p, then $x{\approx }_{F\left(p\right)}y$.

Theorem 3

([7]). The plurality ranking (PR) rule is the only social ranking rule that satisfies consistency, faithfulness, and FS-cancellation.

Proof. 

Let F be a social ranking rule satisfying the three axioms just mentioned. For p, a profile on the set V of voters, let ${\pi }_p\left(x\right)$ be the number of voters i in V for whom x is the most preferref alternative.

FS-cancellation says if ${\pi }_p\left(x\right)={\pi }_p\left(y\right)$, then $x{\approx }_{F\left(p\right)}y$. So, in order to show that F is the plurality rule, we still have to show that if ${\pi }_p\left(x\right)>{\pi }_p\left(y\right)$, then $x{\succ }_{F\left(p\right)}y$. So, suppose ${\pi }_p\left(x\right)>{\pi }_p\left(y\right)$.

• Case 1: if x is the most preferred alternative of all voters i, then—because F is faithful—x is the first element of $F\left(p\right(i\left)\right)$ for all voters i and hence, by repeated application of consistency, x is the first element of the social ranking $F\left(p\right)$ and hence $x{\succ }_{F\left(p\right)}y$. (*)
• Case 2: suppose on the other hand that there is some voter i in V for whom x is not the most preferred alternative in $p\left(i\right)$. Then, the set V of voters may be split into three disjoint subsets $V_1$, $V_2$, and $V_3$ such that (1) all voters in $V_1$ have x as the most preferred alternative, (2) the number of voters in $V_2$ with x as most preferred alternative equals the number of voters in $V_2$ with y as most preferred alternative, and (3) the voters in $V_3$ have neither x nor y as most preferred alternative. For instance, if profile p looks as follows: $\begin{array}{ll}p\left(1\right):& \hspace{1em}x\dots \\ p\left(2\right):& \hspace{1em}x\dots \\ p\left(3\right):& \hspace{1em}y\dots \\ p\left(4\right):& \hspace{1em}z\dots \end{array}$, then $V_1=\left\{1\right\}$, $V_2=\{2,3\}$, and $V_3=\left\{4\right\}$. Let $p_1,p_2,p_3$ be the profiles on respectively $V_1,V_2,V_3$, corresponding with p. We have already seen in (*) that $x{\succ }_{F\left(p_1\right)}y$. By FS-cancellation, $x{\approx }_{F\left(p_2\right)}y$. Additionally, because ${\pi }_{p_3}\left(x\right)={\pi }_{p_3}\left(y\right)=0$, again by FS cancellation, $x{\approx }_{F\left(p_3\right)}y$. Finally, since F is consistent, it follows that $x{\succ }_{F(p_1+p_2+p_3)}y$, i.e., $x{\succ }_{F\left(p\right)}y$. □

In [7], several other characterizations of the plurality ranking rule are given. Additionally, in the literature characterizations are given of several other social ranking and choice rules; see, for instance, [8,9,10].

4. Axioms in Game Theory

Let $N=\{1,\dots ,n\}$ denote a set of players, and let v be a function that assigns a real number to each non-empty subset S or coalition of N, such that $v(\varnothing )=0$. Then, the pair $(N,v)$ is called a cooperative transferable utility (TU) game. When N is clear from the context, we simply speak of the game v. A (0-1)-game is a game in which $v\left(S\right)=0$ or $v\left(S\right)=1$. It is a simple game if it is not identically 0 and satisfies the condition of monotonicity: $v\left(S\right)\le v\left(T\right)$ whenever $S\subseteq T$. In these games, a coalition S is called winning if $v\left(S\right)=1$ and losing if $v\left(S\right)=0$.

Collective decision-making procedures can be modelled by a (0-1)-game whose winning coalitions are those that can make a decision without the vote of the remaining players.

A winning coalition is minimal if it does not contain any other winning coalition. A player i is said to be a swinger in a coalition S, if S is winning and $S-\left\{i\right\}$ is not. A player i is said to be a null player if he or she is not a swinger in any coalition, i.e., $v\left(S\right)=v(S-\{i\left\}\right)$ for all S. In a simple game v, $W\left(v\right)$, respectively, $M\left(v\right)$, denotes the set of all winning, respectively, all minimal winning, coalitions. Any of these sets, $W\left(v\right)$ or $M\left(v\right)$, fully characterizes the game v.

A TU game is superadditive if $v(S\cup T)\ge v\left(S\right)+v\left(T\right)$ whenever $S\cap T=\varnothing$. In the context of simple games, the superadditivity property is equivalent to the following condition: $v\left(S\right)+v(N-S)\le 1$ for all $S\subseteq N$.

Let $S{G}_n$ denote the set of all simple superadditive n-person games.

A power index is a function $\Phi :S{G}_n\to {\mathbb{R}}^n$ that assigns to each simple superadditive game v a vector $\Phi \left(v\right)$ whose ith component is interpreted as a measure of the influence that player i can exert on the outcome. The best known power indices are the Shapley–Shubik [11] index and the Banzhaf [12] index. Shapley and Shubik interpreted the power of a player as the chance to be critical for the passage of a decision, while Banzhaf interpreted the power of a player as the probability that his vote is decisive assuming that all vote configurations are equally likely.

Example 1.

Suppose $N=\{1,2,3,4\}$ and a proposal is accepted iff at least three players/voters say ‘yes’; in other words, $v\left(S\right)=1$ iff S contains at least three players.

In order to determine the power of say voter/player 1, Banzhaf considers all $2^3$ coalitions S of which player 1 is a member and counts all such coalitions in which player 1 is decisive, i.e., if 1 withdraws from the coalition, then it is no longer winning; in other words, $v\left(S\right)-v(S-\{1\left\}\right)=1-0=1$. Below in

Table 1. Decisiveness of player 1 in game v.

1	2	3	4	1 is Decisive
+	+	+	+	no
+	+	+	-	yes
+	+	-	+	yes
+	+	-	-	no
+	-	+	+	yes
+	-	+	-	no
+	-	-	+	no
+	-	-	-	no

, we provide an overview of all coalitions player 1 belongs to and in which of these coalitions player 1 is decisive, given the game v:

So, in this example voter 1 is decisive in 3 out of 8 coalitions he belongs to. Therefore, Banzhaf defines the power of voter 1 to be $\frac{3}{8}$.

More generally, given a simple superadditive n-person game $(N,v)$, the Banzhaf power index $B{z}_i\left(v\right)$ of player/voter i is the probability that i is decisive, i.e., the number of winning coalitions i belongs to and such that without i the coalition becomes losing instead of winning, divided by the total number of coalitions i belongs to. Rendered in a formula:

$$B{z}_i\left(v\right)=\frac{1}{2^{n-1}}\sum _{S\subseteq N,i\in S}(v\left(S\right)-v(S-\left\{i\right\}))$$

The Shapley–Shubik index is based on a different idea. In the case of four voters there are 4! = 24 different ways in which a coalition may be formed. For instance, the order of joining the coalition may be 2 3 1 4 or 3 2 1 4, or 2 4 1 3 or 4 2 1 3, or 3 4 1 2 or 4 3 1 2. The total number of different orders of joining a coalition is 4! = 24 in case of 4 players. In order to determine the power of player 1, Shapley and Shubik look at the number of times that player 1 is critical for the passage of the decision. In our example, player 1 is critical for the passage of the decision if the coalition is formed in one of the six orders just mentioned. Therefore, the Shaply–Shubik power index of player 1, given the game $(N,v)$ with $N=\{1,2,3,4\}$ and $v\left(S\right)=1$ iff S contains at least three players, will be $\frac{6}{4!}=\frac{1}{4}$.

More generally, for a game $(N,v)$ the Shapley–Shubik power index of player i is given by

$$S{h}_i\left(v\right)=\sum _{S\subseteq N,i\in S}\frac{(s-1)!(n-s)!}{n!}(v\left(S\right)-v(S-\left\{i\right\})),$$

where s denotes the size of S, i.e., $s=\left|S\right|$. In our example, the summation is over the sets $\{2,3,1\}$ or $\{3,2,1\}$, $\{2,4,1\}$ or $\{4,2,1\}$ and $\{3,4,1\}$ or $\{4,3,1\}$ ($s=3$, $n-s=1$). Notice that when $v\left(S\right)-v(S-\{i\left\}\right)=1$, in other words, when player i is critical for the pasage of the decision, then $(s-1)!$ is the number of different orders of the players entering the coalition before i and $(n-s)!$ is the number of different orders of the players entering the coalition after i.

In [13] Annick Laruelle and Federico Valenciano provide a good characterization of both the Banzhaf and the Shapley–Shubik index in terms of four axioms for each of them, where the first three axioms are the same for both, and the difference is in the fourth axiom:

Anonymity (An):

the power of each player in a simple superadditive game does not depend on how the players are labelled. In other words, for all $v\in S{G}_n$, any permutation $\pi$ of N and any player $i\in N$, ${\Phi }_i\left(\pi v\right)={\Phi }_{\pi \left(i\right)}\left(v\right)$.

Null Player* (NP*):

being a null player is the worst role any player can expect to play, the role that yields a minimal measure of power. In other words, for all $v\in S{G}_n$ and all $i\in N$, i is a null player in v iff for all $w\in S{G}_n$, ${\Phi }_i\left(v\right)\le {\Phi }_i\left(w\right)$.

Symmetric Gain–Loss (SymGL):

the effect of eliminating a minimal winning coalition is the same for any two players belonging to it and for any two players outside it. In other words, for all $v\in S{G}_n$, for all $S\in M\left(v\right)$ ($S\ne N$), and for all $i,j\in S$, respectively, $i,j\in N-S$, ${\Phi }_i\left(v\right)-{\Phi }_i\left(v_S^{*}\right)$ = ${\Phi }_j\left(v\right)-{\Phi }_j\left(v_S^{*}\right)$. Here, $M\left(v\right)$ denotes the set of minimal winning coalitions and the modified game $v_S^{*}$ results from v by deleting just one single coalition S from the set of winning ones.

Let us illustrate this axiom for the Banzhaf and the Shapley–Shubik indices of the game v from our example above. Consider the minimal winning coalition $S=\{1,2,3\}$, and let $v_S^{*}$ be the game resulting from v by deleting $S=\{1,2,3\}$ from the set of winning ones. In

Table 2. Decisiveness of player 1 in game $v_S^{*}$ with $S=\{1,2,3\}$.

1	2	3	4	1 is Decisive
+	+	+	+	no
+	+	+	-	no
+	+	-	+	yes
+	+	-	-	no
+	-	+	+	yes
+	-	+	-	no
+	-	-	+	no
+	-	-	-	no

below, we give an overview of all coalitions player 1 belongs to and in which of these coalitions player 1 is decisive, but now given the game $v_S^{*}$:

So, $B{z}_1\left(v_S^{*}\right)=\frac{2}{8}$ and $B{z}_1\left(v\right)-B{z}_1\left(v_S^{*}\right)=\frac{3}{8}-\frac{2}{8}=\frac{1}{8}$. More generally, one easily checks that for all $i\in S=\{1,2,3\}$, $B{z}_i\left(v\right)-B{z}_i\left(v_S^{*}\right)=\frac{3}{8}-\frac{2}{8}=\frac{1}{8}$. However, for player $4\notin S=\{1,2,3\}$ we have $B{z}_4\left(v\right)-B{z}_4\left(v_S^{*}\right)=\frac{3}{8}-\frac{4}{8}=-\frac{1}{8}$.

For the Shapley–Shubik index, notice that given game $v_S^{*}$, player 1 is not critical anymore for the passage of the decision in the sequences 2 3 1 4 and 3 2 1 4 because $S=\{1,2,3\}$ is no longer winning anymore. At the same time, player 4 is now critical for the passage of the decision in the sequences 1 2 3 4, 1 3 2 4, 2 1 3 4, 2 3 1 4, 3 1 2 4, and 3 2 1 4, as well as for the passage of the decision in the sequences 1 2 4 3, 2 1 4 3, 1 3 4 2, 3 1 4 2, 2 3 4 1, and 3 2 4 1. So, $S{h}_1\left(v\right)-S{h}_1\left(v_S^{*}\right)=\frac{6}{24}-\frac{4}{24}=\frac{2}{24}$. More generally, for all $i\in S=\{1,2,3\}$, $S{h}_i\left(v\right)-S{h}_i\left(v_S^{*}\right)=\frac{6}{24}-\frac{4}{24}=\frac{2}{24}$. However, for player $4\notin S=\{1,2,3\}$, $S{h}_4\left(v\right)-S{h}_4\left(v_S^{*}\right)=\frac{6}{24}-\frac{12}{24}=-\frac{6}{24}$.

Both the Shapley–Shubik and the Banzhaf index satisfy the three axioms just mentioned. What distinguishes them is constant total gain–loss balance (CTGLB) and constant average gain–loss balance (CAGLB). Both axioms concern the effect of dropping a minimal winning coalition from the set of winning ones. The constant total, respectively, average gain–loss balance, postulates that the total, respectively, average loss of the players in the deleted coalition equals the total, respectively, average gain of the players outside it.

CTGLB: For all $v\in S{G}_n$ and all $S\in M\left(v\right)$ ($S\ne N$),

$$\sum _{i\in S}({\Phi }_i\left(v\right)-{\Phi }_i\left(v_S^{*}\right))=\sum _{j\in N-S}({\Phi }_j\left(v_S^{*}\right)-{\Phi }_j\left(v\right)).$$

For instance, given the games v and $v_S^{*}$ above with $S=\{1,2,3\}$, the total loss ${\sum }_{i\in S}(S{h}_i\left(v\right)-S{h}_i\left(v_S^{*}\right))$ of the players in S equals $3·\frac{2}{24}=\frac{1}{4}$, while the total gain ${\sum }_{j\in N-S}(S{h}_j\left(v_S^{*}\right)-S{h}_j\left(v\right))$ of the players outside S, i.e, $S{h}_4\left(v_S^{*}\right)-S{h}_4\left(v\right)$, also equals $\frac{6}{24}=\frac{1}{4}$.

CAGLB: For all $v\in S{G}_n$ and all $S\in M\left(v\right)$ ($S\ne N$),

$$\frac{1}{s}\sum _{i\in S}({\Phi }_i\left(v\right)-{\Phi }_i\left(v_S^{*}\right))=\frac{1}{n-s}\sum _{j\in N-S}({\Phi }_j\left(v_S^{*}\right)-{\Phi }_j\left(v\right)).$$

For instance, given the games v and $v_S^{*}$ above with $S=\{1,2,3\}$, the average loss of the players in S, i.e., $\frac{1}{3}{\sum }_{i\in S}(B{z}_i\left(v\right)-B{z}_i\left(v_S^{*}\right))$, equals $\frac{1}{3}·\frac{3}{8}=\frac{1}{8}$, while the average gain of the players outside S, i.e., $\frac{1}{4-3}{\sum }_{j\in N-S}(B{z}_j\left(v_S^{*}\right)-B{z}_j\left(v\right))$, i.e., $B{z}_4\left(v_S^{*}\right)-B{z}_4\left(v\right)$, also equals $\frac{1}{8}$.

In [13], the authors prove that the Shapley–Shubik index is characterized by (An), (NP*), (SymGL), and (CTGLB), while the Banzhaf index is characterized by (An), (NP*), (SymGL), and (CAGLB).

Theorem 4

([13]). Let $\Phi :S{G}_n\to {\mathbb{R}}^n$.

• (i) Φ satisfies (An), (NP*), (SymGL), and constanttotalgain–loss balance (CTGLB) iff $\Phi =\alpha Sh+\kappa \mathbf{1}$, for some $\alpha >0$ and $\kappa \in \mathbb{R}$, where 1:= $(1,\dots ,1)\in {\mathbb{R}}^n$. (ii) Φ satisfies (An), (NP*), (SymGL), and constantaveragegain–loss balance (CAGLB) iff $\Phi =\alpha Bz+\kappa \mathbf{1}$, for some $\alpha >0$ and $\kappa \in \mathbb{R}$.

For the proof, consisting of several pages, see [13].

5. Conclusions

Although the topics of logic, game theory, and social choice theory are quite different, it comes as no surprise that sometimes the same people are working in two or more of these fields. The common factor is that in all these studies axiomatic characterizations may be given of certain notions central to the field in question.