Abstract
This paper deals with the problem of goodness-of-fit tests (GFTs) for the weighted generalized quasi-Lindley distribution (WGQLD) using ranked set sampling (RSS) and simple random sampling (SRS) techniques. The tests are based on the empirical distribution function and sample entropy. These tests include the Kullback–Leibler, Kolomogorov–Smirnov, Anderson–Darling, Cramér–von Mises, Zhang, Liao, and Shimokawa, and Watson tests. The critical values (CV) and power of each test are obtained based on a simulation study by using SRS and RSS methods considering various sample sizes and alternatives. A rain data set is used to investigate the effectiveness of the suggested GFTs. Based on the same number of measured units for the various alternatives taken into consideration in this study, it is discovered that the RSS tests are more effective than those of their rivals in SRS. Additionally, as the set size increases, the GFTs’ power increases.
Keywords:
entropy; goodness-of-fit tests; critical values; generalized quasi-Lindley distribution; maximum likelihood estimation; ranked set sample; Shannon entropy MSC:
62G30; 46N30; 94A20
1. Introduction
The RSS method was first introduced by [1] as a new strategy for collecting data for estimating of pasture and forage yields mean in Australia. It is shown that the population mean estimation using RSS is more efficient than its competitor in simple random sampling. The RSS design is useful when the process of ranking the sample units is easier and less expensive than measuring them. The RSS can be described as follows:
- Draw a SRS of size from the study population. Then, partition them randomly into k sets each of size k, where k is the set size.
- Rank the k units within each set from the smallest to largest relative to the variable under consideration based on any free cost method.
- Obtain the ith ranked unit from the ith set, for i = 1, 2, …, k).
- The above Steps (1)–(3) can be repeated r times (cycles) if necessary to have an RSS of size .
The obtained RSS units are indicated by , where is the ith smallest ranked unit at the jth cycle in a set of size k.
Due to the importance of the RSS scheme, some new variations of the RSS are developed in the literature, as the median ranked set design is proposed by [2,3] who introduced the double RSS design, the L RSS is suggested by [4,5] who suggested neoteric RSS, and the varied L RSS scheme is offered by [6].
In statical analysis and lifetime data, the GFT is an important process for choosing the best probability distribution function that can fit the observed data. Let X be a random variable that adheres to a distribution function , and assume the following hypothesis test:
An efficient method for testing (1) is the goodness of fit test based on the empirical distribution function (EDF) which is defined for a SRS of size n, as
where is an indicator function. In practical cases, the parameters of the distribution function are unknown and hence may be estimated by using several techniques, including maximum likelihood and moments methods. The EDF-based tests are useful in cases of unknown population parameters, and hence they can be estimated from the data, because they can provide good power in some scenarios. For more details on the goodness-of-fit and entropy, one can refer to [7] for an entropy estimate by random sampling and some developed measures of sample entropy of continuous random variables are proposed by [8]. For goodness of-fit-tests (GFTs) for Laplace distribution in RSS, see [9,10]. For GFTs for logistic distribution based on phi divergence, see reference [11] for measures of sample entropy, and [12] for functionals’ estimation by class of statistics based on spacings. See reference [13] for GFT and entropy estimation for the inverse Gaussian and Laplace distributions using pair RSS, and [14] for Bayesian estimation of GFT and extropy.
In the current paper, we investigate some well-known GFTs based on RSS and SRS schemes for the weighted generalized quasi-Lindley distribution with unknown parameters. To the best of the authors’ knowledge, this problem has been not considered before. The rest of this paper is structured as follows. In Section 2, a description of the WGQLD and some of its main properties are presented. The maximum likelihood estimators (MLE) based on RSS and SRS methods are included in Section 3. In Section 4, some GFTs based on SRS and RSS designs are presented theoretically in detail. In Section 5, a simulation study is done to look at the efficacy of the suggested tests. Section 6 provides an application of actual data. Section 7 provides a few conclusions and recommendations for the future.
2. The WGQLD Model Description
In the last few decades, many researchers suggested various probability distributions based on different methods to fit real data in various fields. Some of them studied the concept of the weighted distributions, which is useful in modeling lifetime data and survival analysis. The WGQLD is a two-parameter continuous probability distribution proposed by [15]. Let X be a random variable that follows the WGQLD with parameters and . The probability density function (pdf) of X is given by
and its corresponding cumulative distribution function (cdf) is
Figure 1 displays the WGQLD pdf plots for various values of the distribution parameters. It is clear that the WGQLD pdf is right-skewed in general, and the shape of the distribution depends on the parameters values with coefficient of skewness ([15]) given by
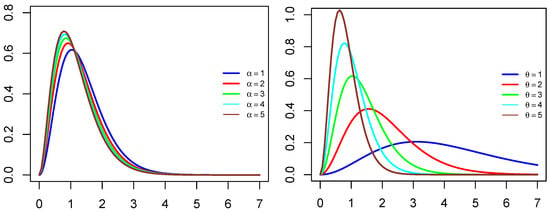
Figure 1.
Plots of the WGQLD PDF with (left) and (right) for some parameters’ values.
3. Maximum Likelihood Estimation
3.1. Under SRS
Assume that are random variables of size n follow the WGQLD. The likelihood function based on this sample is
The log of the likelihood function, say, , is
Taking the derivatives of relative to and yields
Because these equations have no closed forms, then the MLEs and of and respectively, can be obtained by using any numerical method.
3.2. Under RSS
Let be RSS data for X with a sample size , denoted by the ith-order statistics from the ith set of size k at the jth cycle assuming that the ranking is perfect. Similarly, the likelihood function using RSS is given by
where
The log-likelihood function is
We take the derivatives of (10) with respect to and , respectively, and equate the resulting quantities to zero and then solve numerically to find the MLE and of and , respectively.
4. Goodness-of-Fit Tests
Here, the GFT is considered to investigate whether a specific data set is consistent with a hypothesized null distribution. Hence, different EDF tests are considered to study the null hypothesis . The random sample follows the WGQLD with unknown parameters. The GFT for different distributions with unknown parameters has been studied by many researchers. For example about these studies, the GFTs for generalized Rayleigh distribution by [16,17] studied GFT of generalized exponential distribution, and reference [18] investigated Cramér–von Mises, Kolmogorov–Smirnov, and Watson and Liao and Shimokawa statistics, and Anderson–Darling who study GFTs for the generalized Frechet distribution. Here, the suggested GFTs are investigated based on both sampling methods.
4.1. GFT Using SRS
Let be a random sample from WGQLD with PDF and CDF . In addition, let and be the MLE of and , respectively. We proposed the following test statistics:
- The Kullback–Leibler distance (KL) between and suggested by Kullback and Leibler [19] aswhere is the entropy defined by [20] aswhich is estimated later by [21] bywhere m is an integer less than , known as window size, if and if . The estimator converges in probability to as and . Therefore, the KL test is defined by [22] is.
- The Kolmogorov–Smirnov test statistic (KS) is offered by [23,24] with the form
- The Anderson–Darling test statistic (AD) which is suggested by [25] by
- The Cramér–von Mises (CV) test statistic [26] and [27] is given by
- The Zhang test statistic [28] is defined as
- The Liao and Shimokawa (LS) test statistic [29] has the form
- The Watson test statistic [30,31] is defined by
4.2. Using RSS
Let be an RSS of size from the WGQLD with corresponding ordered values . Moreover, let and be the RSS maximum likelihood estimators of and , respectively. Thus, the abovementioned GFT based on the SRS method can be studied using RSS and described as follows.
- The test based on RSS KL is defined as.
- The Kolmogorov–Smirnov test statistic in RSS is
- The Anderson–Darling test statistic based on RSS is
- The Cramér–von Mises test statistic in terms of RSS is
- The Zhang [28] test statistic using RSS is
- The Liao and Shimokawa (LS) test statistic with RSS is
- The Watson test statistic in RSS is defined as
where and is the distribution function of WGQLD distribution.
5. Simulation Study
To determine how well the aforementioned GFT performed, a simulation study is conducted. A total of 100,000 samples are generated from the WGQLD with various sample sizes by using SRS and RSS methods. The powers of tests based on and depend on the window size m. Therefore, we use the method of [32] by Vexler and Gurevich (2010) for choosing the optimal m and we proposed the following modifications:
and
5.1. Critical Values
By generating 100,000 samples from the WGQLD of parameters and , we compute the critical values of the tests for the WGQLD in RSS design for significance level of 0.01, 0.05, 0.1. The values of n and k are chosen to be 2, 3, …, 9 and the set size 2, 3, …, 5. Table 1, Table 2 and Table 3 present the obtained results of critical values.

Table 1.
The CV values of different tests of WGQLD for some values of in RSS, at significance level of .

Table 2.
The CV values of different tests of WGQLD for some values of in RSS, at significance level of .

Table 3.
The CV values of different tests of WGQLD for some values of in RSS, at significance level of .
5.2. Power Comparison
In order to assess the powers of various GFT in SRS and RSS for the WGQLD, a simulation study for the power of each test is conducted. The probability of rejecting the null hypothesis correctly with a true alternative hypothesis is known as the power of a hypothesis test. We calculated the power of the tests for the WGQLD by simulating data from the alternative distributions in and computing the MLE estimators of and ; then we applied our test. The process is repeated 10,000 times by using SRS and RSS for , and 40. In order to discuss the effects of increasing the sample size for a given set size and subsequently the effects of increasing set size with a fixed sample size, the values of the set size k based on RSS are 2 and 5. Table 4, Table 5 and Table 6 present the findings for significance level of for the following alternative distributions:

Table 4.
Power estimates of different GFT in SRS and RSS for and = 0.05. Rounded numbers of four digits greater than zero.

Table 5.
Power estimates of different GFT in RSS and SRS for and = 0.05.

Table 6.
Power estimates of different GFT in RSS and SRS for and = 0.05.
- The generalized quasi-Lindley distribution with scale parameter (SP) 1 and shape parameter (ShP) 1 denoted by GQLD(1,1).
- The generalized quasi-Lindley distribution with SP 1 and ShP 2 denoted by GQLD(1,2).
- The log-logistic distribution with SP 3 and ShP 1 denoted by Llogis(3,1).
- The log-logistic distribution with SP 2 and ShP 1 denoted by Llogis(2,1).
- The Pareto distribution with SP 1.6 and ShP 2 denoted by Pareto(1.6,2).
- The Pareto distribution with SP 1 and ShP 2 denoted by Pareto(1,2).
- The Weibull distribution with SP 3 and ShP 1 denoted by Weibull(3,1).
- The Weibull distribution with SP 4 and ShP 1 denoted by Weibull(4,1).
- The power Lindley distribution with SP 3 and ShP 3 denoted by Plindley(3,3).
- The power Lindley distribution with SP 1 and ShP 2 denoted by Plindley(1,2).
- The generalized Rayleigh distribution with SP 1 and ShP 2 denoted by Genray(1,2).
With reference to the results in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, the following remarks can be made.
- The power values for the suggested tests based on RSS and SRS techniques are greater than zero for all cases considered in this section.
- In general, based on the SRS and RSS techniques the power reaches 1 for the alternatives Pareto, Weibull, and Lindley distributions with samples of size 40 or greater.
- The suggested RSS GFT for the WGQLD are more powerful than their SRS rivals for most cases investigated in this study. As an example, consider the case when and the Pareto(1.6, 2) as an alternative, the power values of the tests KS, , using RSS are 0.381, 0.281, and 0.311 compared to 0.327, 0.194, and 0.219 using SRS, respectively.
- The power of the GFT increases as the set size k increases. As an illustration, when for the generalized Rayleigh distribution, it is observed that , , and for , whereas for , they are , , and .
- By using RSS, the power of the GFT increases as the sample size increases. As an example, with for the power of the Lindley distribution (1,2), the power values of the Watson test are 0.097, 0.146, and 0.250 for , 20, and 40, respectively.
- For the fixed test, the power values of the suggested GFT depend on the distribution parameters values assuming a comparable sample size. As an example, the power of the Anderson–Darling test are 0.074 and 0.108, for generalized quasi-Lindley distribution with parameters (1,1) and (1,2), respectively, when and .
6. Real Data Example
In this section, three real datasets are used to show the importance of the WGQLD in modeling real-life data. The parameters of the considered models have been estimated through the MLE method. We consider the Akaike information criterion (AIC), Bayesian information criterion (BIC), consistent Akaike information criterion (AICc), Kolmogorov–Smirnov (KS), where AIC = CAIC = , HQIC = , BIC = , K-S = , and the p-value of the corresponding K-S test, where , k is the number of parameters, n is the sample size, and L is the value of maximum log-likelihood function.
The best model is the one with the smallest values of the AIC, BIC, HQIC, CAIC, and K-S, and the greatest value for the p-value of the K-S test. Now, based on the real datasets, the null and alternative hypothesis will be
The first data is from the rain dataset considered by [33]. The data consists of the annual maximum precipitation (inches) for one rain gauge in Fort Collins, Colorado from 1900 to 1999 and are given by 239, 232, 434, 85, 302, 174, 170, 121, 193, 168, 148, 116, 132, 132, 144, 183, 223, 96, 298, 97, 116, 146, 84, 230, 138, 170, 117, 115, 132, 125, 156, 124, 189, 193, 71, 176, 105, 93, 354, 60, 151, 160, 219, 142, 117, 87, 223, 215, 108, 354, 213, 306, 169, 184, 71, 98, 96, 218, 176, 121, 161, 321, 102, 269, 98, 271, 95, 212, 151, 136, 240, 162, 71, 110, 285, 215, 103, 443, 185, 199, 115, 134, 297, 187, 203, 146, 94, 129, 162, 112, 348, 95, 249, 103, 181, 152, 135, 463, 183, 241.
The second set of data represents the lifetime data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by [34], and it is given by 1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.2, 1.4, 3, 1.7, 2.3, 1.6, 2.
The third set of data on failure times for a particular model of windshield are given in [35]. These data were recently studied by [36]. The failure times of 84 aircraft windshields are 0.040, 1.866, 2.385, 3.443, 0.301, 1.876, 2.481, 3.467, 0.309, 1.899, 2.610, 3.478, 0.557, 1.911, 2.625, 3.578, 0.943, 1.912, 2.632, 3.595, 1.070, 1.914, 2.646, 3.699, 1.124, 1.981, 2.661, 3.779,1.248, 2.010, 2.688, 3.924, 1.281, 2.038, 2.82,3, 4.035, 1.281, 2.085, 2.890, 4.121, 1.303, 2.089, 2.902, 4.167, 1.432, 2.097, 2.934, 4.240, 1.480, 2.135, 2.962, 4.255, 1.505, 2.154, 2.964, 4.278, 1.506, 2.190, 3.000, 4.305, 1.568, 2.194, 3.103, 4.376, 1.615, 2.223, 3.114, 4.449, 1.619, 2.224, 3.117, 4.485, 1.652, 2.229, 3.166, 4.570, 1.652, 2.300, 3.344, 4.602, 1.757, 2.324, 3.376, 4.663.
To show the potential of the WGQLD with three other well-known competitive models, including the quasi-Lindley distribution (QLD) proposed by [37], the Pareto distribution (PD), and the two-parameter Sujatha distribution (TSPD) given by [38].
The PDFs of these competitive models are as follows.
- The PDF of the QLD distribution is
- The PDF of the PD distribution is
- The PDF of the TSPD distribution is
The values of the AIC, AICc, BIC, HQIC, and K-S with the corresponding p-value based on the rain data, patient data, and aircraft windshield data are reported in Table 7, Table 8 and Table 9, respectively. Moreover, Figure 2, Figure 3 and Figure 4 show the plots of estimated probability density functions and cumulative distribution functions for the three datasets, respectively.

Table 7.
The measures AIC, AICc, BIC, HQIC, and K-S with the corresponding p-value for rain data.

Table 8.
The measures AIC, AICc, BIC, HQIC, and K-S with the corresponding p-value for patient data.

Table 9.
The measures AIC, AICc, BIC, HQIC, and K-S with the corresponding p-value for aircraft windshield data.
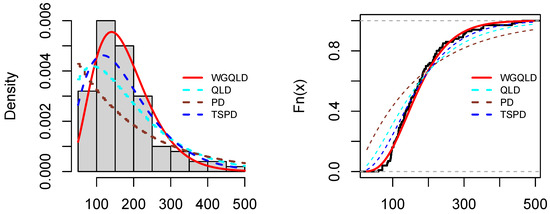
Figure 2.
Plots of estimated probability density functions and cumulative distribution functions for rain data.
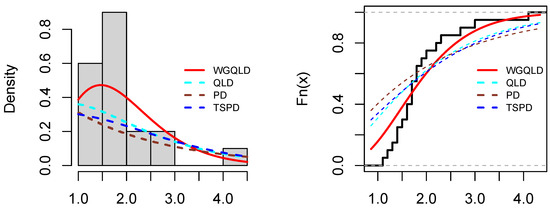
Figure 3.
Plots of estimated probability density functions and cumulative distribution functions for patient data.
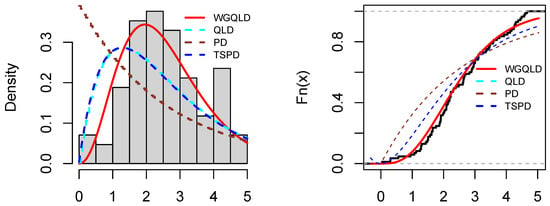
Figure 4.
Plots of estimated probability density functions and cumulative distribution functions for aircraft windshield data.
With reference to Table 7, Table 8 and Table 9, we observe that the WGQLD have the lowest values for all AIC, AICc, BIC, HQIC, and K-S with greatest p-values for the rain data, for the patients data, and for the aircraft data among all other competitive models, and Figure 2, Figure 3 and Figure 4 support our claim. Therefore, the WGQLD outperformed the other models for the three real datasets.
Now, we used the rain dataset to examine the applicability of the proposed SRS and RSS goodness of fit tests. The P-P and Q-Q plots for the WGQLD for the rain data are given in Figure 5. The TTT, box, and density plots for the data are presented in Figure 6.
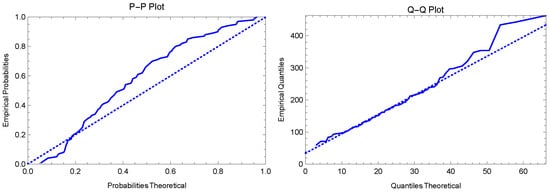
Figure 5.
P-P and Q-Q plots of the WGQLD for the rain data.
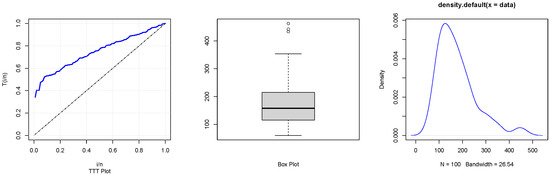
Figure 6.
The TTT, box, and density plots of the WGQLD for the rain data.
We extracted a ranked set sample of size using a set size and from the data assuming that the ranking is perfect and applied the different GFT considered in this study. The sampled values based on RSS are shown in Table 10.

Table 10.
The sample values using RSS.
The MLE of the parameters are and . The values of the test statistics given above are computed and provided in Table 11.

Table 11.
Values of different test statistics in RSS.
By comparing the values of different test statistics in RSS with the corresponding critical values, it is found that the null hypothesis that assumed that the data is from the WGQLD is not rejected by the , , , and at of significance level.
7. Conclusions
In this paper, various GFTs are presented for the WGQLD using SRS and RSS methods. The suggested tests are compared based on a simulation study for different sample sizes and alternative distributions to study their applicability. The empirical distribution function and sample entropy are considered for the tests involving the Kullback–Leibler, Kolomogorov–Sminrov, Anderson–Darling, Cramér–von Mises, Zhang, Liao, and Shimokawa, and Watson tests. Applications to three real datasets are considered to illustrate the flexibility of the proposed GFT for the WGQLD. It is found that the offered GFT tests based on SRS and RSS perform well, and the tests using the RSS are more efficient than their SRS competitors based on the same number of quantified units. For future research, the authors may investigate the same GFTs proposed in this study to other probability distributions based on perfect and imperfect ranking by using some variations of the RSS as the median RSS design, L RSS, and neoteric RSS methods.
Author Contributions
Conceptualization, A.I.A.-O.; methodology, A.I.A.-O. and S.B.; software, S.B. and A.I.A.-O.; validation, A.I.A.-O., S.B., and G.A.; investigation, G.A.; resources, S.B. and A.I.A.-O.; data curation, S.B.; writing—original draft preparation, S.B., A.I.A.-O., and G.A.; writing—review and editing, S.B., A.I.A.-O., and G.A.; supervision, A.I.A.-O.; funding acquisition, G.A. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R226), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare that they have no conflict of interest to report regarding the present study.
References
- McIntyre, G.A. A method of unbiased selective sampling using ranked set. Aust. J. Agric. Res. 1952, 3, 385–390. [Google Scholar] [CrossRef]
- Mutllak, H.A. Median ranked set sampling. J. Appl. Stat. Sci. 1997, 6, 245–255. [Google Scholar]
- Al-Saleh, M.F.; Al-Kadiri, M.A. Double-ranked set sampling. Stat. Probab. Lett. 2000, 48, 205–212. [Google Scholar] [CrossRef]
- Al-Nasser, A.D. L-Ranked set sampling: A generalization procedure for robust visual sampling. Commun. Stat. 2007, 6, 33–43. [Google Scholar] [CrossRef]
- Zamanzade, E.; Al-Omari, A.I. New ranked set sampling for estimating the population mean and variance. Hacettepe J. Math. Stat. 2016, 45, 1891–1905. [Google Scholar]
- Haq, A.; Brown, J.; Moltchanova, E.; Al-Omari, A.I. Varied L ranked set sampling scheme. J. Stat. Theory Pract. 2015, 9, 741–767. [Google Scholar] [CrossRef]
- Al-Omari, A.I. Estimation of entropy using random sampling. J. Comput. Appl. Math. 2014, 261, 95–102. [Google Scholar] [CrossRef]
- Al-Omari, A.I. A new measure of sample entropy of continuous random variable. J. Stat. Theory Pract. 2016, 10, 721–735. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Zamanzade, E. Goodness of-fit-tests for Laplace distribution in ranked set sampling. Investig. Oper. 2017, 38, 366–376. [Google Scholar]
- Al-Omari, A.I.; Zamanzade, E. Goodness of fit tests for logistic distribution based on Phi-divergence. Electron. J. Appl. Stat. Anal. 2018, 11, 185–195. [Google Scholar]
- Ebrahimi, N.; Pflughoeft, K.; Soofi, E. Two measures of sample entropy. Stat. Probab. Lett. 1994, 20, 225–234. [Google Scholar] [CrossRef]
- Van Es, B. Estimating functionals related to a density by class of statistics based on spacings. Scand. J. Stat. 1994, 19, 61–72. [Google Scholar]
- Al-Omari, A.I.; Haq, A. Entropy estimation and goodness-of-fit tests for the inverse Gaussian and Laplace distributions using pair ranked set sampling. J. Stat. Comput. Simul. 2016, 86, 2262–2272. [Google Scholar] [CrossRef]
- Al-Labadi, L.; Berry, S. Bayesian estimation of extropy and goodness of fit tests. J. Appl. Stat. 2022, 49, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Benchiha, S.; Al-Omari, A.I.; Alotaibi, N.; Shrahili, M. Weighted Generalized Quasi Lindley Distribution: Different Methods of Estimation, Applications for Covid-19 and Engineering data. AIMS Math. 2021, 6, 11850–11878. [Google Scholar] [CrossRef]
- Abd-Elfattah, A. Goodness of fit test for the generalized rayleigh distribution with unknown parameters. J. Stat. Comput. Simul. 2011, 81, 357–366. [Google Scholar] [CrossRef]
- Hassan, A.S. Goodness-of-fit for the generalized exponential distribution. Interstat Electron. J. 2011, 1–15. [Google Scholar]
- Abd-Elfattah, A.; Hala, A.F.; Omima, A. Goodness of fit tests for generalized frechet distribution. Aust. J. Basic Appl. Sci. 2010, 4, 286–301. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Vasicek, O. A test for normality based on sample entropy. J. R. Stat. Soc. Ser. B 1976, 38, 54–59. [Google Scholar] [CrossRef]
- Song, K.S. Goodness of fit tests based on Kullback-Leibler discrimination. IEEE Trans. Inf. Theory 2002, 48, 11031117. [Google Scholar]
- Kolmogorov, A.N. Sulla determinazione empirica di una legge di distribuzione. G. Dell’ Ist. Ital. Degli Attuari 1933, 4, 83–91. [Google Scholar]
- Smirnov, N.V. Estimate of deviation between empirical distribution functions in two independent samples. Bull. Mosc. Univ. 1933, 2, 3–16. [Google Scholar]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Cramer, H. On the Composition of Elementary Errors. Scand. Actuar. J. 1928, 1, 13–74. [Google Scholar] [CrossRef]
- Von Mises, R.E. Wahrscheinlichkeit, Statistik und Wahrheit; Springer: Julius, Japan, 1928. [Google Scholar]
- Zhang, J. Powerful goodness of fit tests based on the likelihood ratio. J. R. Stat. Soc. Ser. B 2002, 64, 281–294. [Google Scholar] [CrossRef]
- Liao, M.; Shimokawa, T. A new goodness-of-fit test for Type-I extreme-value and 2-parameter Weibull distributions with estimated parameters. J. Stat. Comput. Simul. 1999, 64, 23–48. [Google Scholar] [CrossRef]
- Watson, G.S. Goodness-of-Fit Tests on a Circle. I. Biometrika 1961, 48, 109–114. [Google Scholar] [CrossRef]
- Watson, G.S. Goodness-of-Fit Tests on a Circle. II. Biometrika 1962, 49, 57–63. [Google Scholar] [CrossRef]
- Vexler, A.; Gurevich, G. Empirical likelihood ratios applied to goodness-of-fit tests based on sample entropy. Comput. Stat. Data Anal. 2010, 54, 531–545. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Res. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Gross, A.J.; Clark, V. Survival Distributions: Reliability Applications in the Biomedical Sciences; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ramos, M.W.A.; Marinho, P.R.D.; da Silva, R.V.; Cordeiro, G.M. The exponentiated Lomax Poisson distribution with an application to lifetime data. Adv. Appl. Stat. 2013, 34, 107. [Google Scholar]
- Rama, S. A quasi Lindley distribution. Afr. J. Math. Comput. Sci. Res. 2013, 6, 64–71. [Google Scholar]
- Tesfay, M.; Shanker, R. A two–parameter Sujatha distribution. Biom. Biostat. Int. J. 2018, 7, 188–197. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).