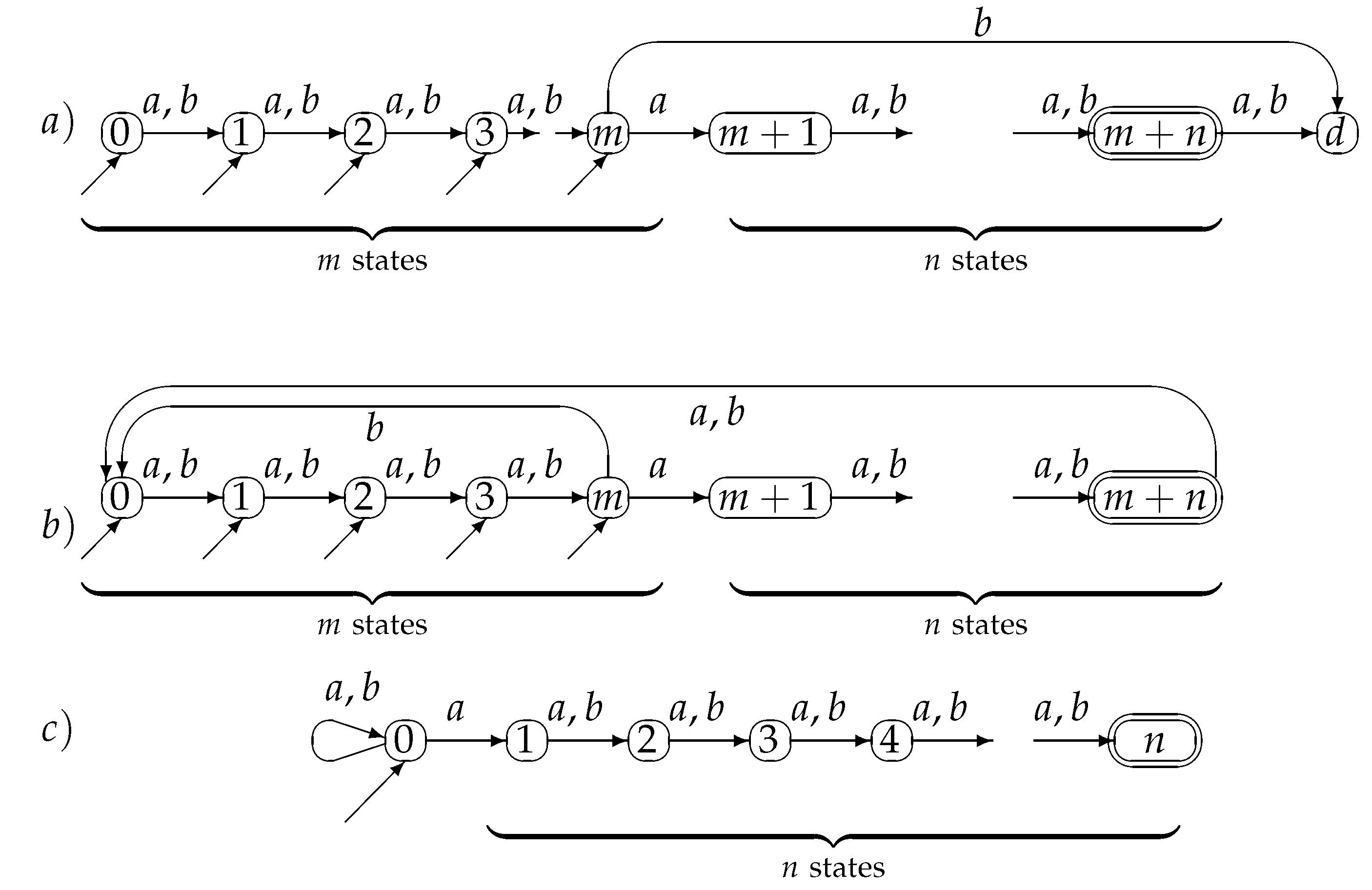1. Introduction
The concept of Cover Automata was first presented at a conference paper of Câmpeanu et al. at the Workshop on Implementations and Applications of Automata (WIAA) in Rouen (1999) [
1,
2] when the authors introduced a formal definition of a Deterministic Finite Cover Automaton (DFCA) and a minimization algorithm. A cover language for a language
L is a superset
of
L. If
L is a finite non-empty language, then the length of the longest word in
L exists, and we can denote it with a natural number,
l. A DFCA for a finite language
L is a deterministic finite automaton (DFA) accepting a cover language for
L, such that the accepted words that are not in
L have their length greater than
l.
During the last two decades, several papers used DCFAs for compact representation of finite languages. Other efficient minimization algorithms were also published, for example [
3,
4,
5,
6,
7,
8]. The concept of DFCA was also generalized to the nondeterministic version in a paper presented at AFL 2014 in Szeged by Câmpeanu [
9], followed by the journal version [
10].
Using nondeterminism, we can reduce the size of the automata recognizing some languages, but minimizing such automata is known to be PSPACE-complete. Therefore, several other intermediate representations of languages that maintain deterministic transitions were proposed. That is why it is a must to study these extensions in case they are applied to cover automata, which we are doing in
Section 2. The first extension considered here is to enhance DFCAs with
“do not care” symbols, thus obtaining finite cover automata with “do not care” symbols, denoted by ⋄-DFCAs, in other words, finite cover automata accepting partial words. Fischer and Paterson introduced partial words in [
11] in 1974, and the authors in [
12,
13] prove that the minimization of finite automata with “do not care” symbols is NP-hard. As emphasized by Professor Solomon Marcus in [
14], many researches from other areas studied the same concept, but in a different theoretical setup with different notations. An example of such a paper related to partial words is [
15], where the authors show strong connections between graph problems and pattern matching with some of the symbols in the patterns not known. In that paper, the “do not care” symbol denoted here by ⋄ is denoted by
. We will prefer the ⋄ notation because most references use this notation and using a symbol that is not part of any alphabet is easier to identify. Holzer et al. in [
16,
17] prove that “almost all problems related to partial word automata, such as equivalence and universality, are already PSPACE-complete”. Some of their proofs link non-deterministic automata problems with graph theory problems in a similar fashion as it is done in [
15]. As such, because the minimization of ⋄-DFAs is hard, only the simplification algorithms were developed for these types of finite machines, and an example is presented in [
13]. A simplification algorithm will eventually produce an equivalent automaton with less states than the input automaton, but it is not guaranteed to be minimal. In
Section 3, we show that the same difficulties found for NFCA’s simplification are also present for ⋄-DFCAs, even though ⋄-DFCAs can be considered a particular simpler class of NFCAs. We show a simplification algorithm for ⋄-DFCAs that has a better time complexity than the one presented for ⋄-DFAs in [
13].
In [
12], the authors give an example of automaton having limited nondeterminism—there is only one transition with degree 2 for the same letter—which is hard to minimize. The same argument can be used to prove that finding the minimal finite cover automaton with
“do not care” symbols is also a hard problem. We already know that NFCA minimization is NP-hard, and details of why the previous proofs work as well for ⋄-DFCAs are presented in
Section 3. In the same paper [
12], the example of an automaton that is hard to minimize accepts a finite language having all the accepted words of length at most 3. This example is used to show that minimizing multiple entry deterministic automata (MEFA) (When the number
k of entries is known, we use the term
k-DFA instead of MEFA) is hard. In
Section 4, we show that the method with exactly the same construction will also work for Multiple Entry Finite Cover Automata (MEFCA), or
k-entry DFCAs (
k-DFCA), adding the results on
k-entry FA to the previous ones obtained in [
18,
19,
20,
21]. In
Section 4, we show that for binary alphabets, by transforming a
k-DFCA into a minimal DFCA we can reach the upper bound for NFA to DFCA transformation. Moreover, we show that the general bound is reached for the state complexity of this transformation.
Section 5 includes future work and a list of open problems, and the conclusions are drawn in
Section 6.
2. Cover Automata Extensions
2.1. Notations
The number of elements of a set T is , an alphabet is usually denoted by , and the set of words over is . The length of a word is the number of letters of w, and it is denoted by . Thus, if , where , for all , then . In particular, when , we have a word with no letters, denoted by , and . We also use the following notations: , , , , and .
A Deterministic Finite Automaton (DFA) is a quintuple
, where
Q is a finite non-empty set, the set of states,
is the alphabet,
is the initial state,
is the set of final states, and
is the transition function. In case the transition function
is a partial function, denoted as
, we have a partial DFA. In case
is defined for all values of
and
, the DFA is complete. If we do not emphasize that the DFA is partial, then we understand that the DFA is complete. The transition function
can be extended in a natural way to
as follows:
,
. For the rest of the paper we denote the extension
, by
. If the transition function
is a partial function, then the automaton is incomplete; otherwise, it is a complete one. A Nondeterministic Finite Automaton (NFA) is a quintuple
, where all the elements are the same as for a DFA except,
is the set of initial states and the transition function
, which is now defined as
. In case of an NFA, for the transition function we have that for
,
, and
. In what follows, we will use the NFA’s with only one initial state as it is defined in [
22]. For any NFA
there is an equivalent NFA
, where
,
, for all
and
, and
. Using the form for NFA with only one initial state, or initially connected NFAs, simplify most of the definitions and results and the state complexity will differ from the general case by just one state.
For multiple entry automata, we have a quintuple
, where
. In some cases [
23], all the states are considered initial states, thus
, while in most other cases, we consider
k-entry DFA so the transition function
is deterministic and
[
19].
A state s in a finite automaton A is reachable if there is a word such that . In case of a k-entry DFA or an NFA, the state must be one of the initial states. A state s is useful if there exists such that . In case of a deterministic , we have that . A sink state or a dead state is a reachable state with all its transitions being self-loops. All states that are not reachable and not useful can be eliminated without changing the language accepted by the automaton. A deterministic automaton with all states reachable and useful, except one sink state, is called a reduced automaton. In the case of nondeterministic automata, an automaton is considered reduced if all its states are both reachable and useful. In what follows, all automata are reduced automata, so they do not have unreachable or unuseful states.
For an alphabet , we can consider a new symbol ⋄, called “do not care symbol”, which can replace any letter of . Thus, a word w over the alphabet , will be a partial word if . We say that the word is weaker than , denoted , if and for all positions i, , if then .
Let be a regular language over the alphabet }, with a substitution such that for all , and . The regular language is recognized by ⋄-DFA, , if . Accordingly, a ⋄-DFA associated with some substitution is defined as a DFA that recognizes a partial language , and it is also associated with the total language .
A cover automaton for a finite language
L is a DFA recognizing a cover language
such that
, for
l being the length of the longest word in
L. An
l-NFCA
A is a cover automaton for the language
, [
10,
24]. Any DFA
A accepting a finite language is a DFCA for
with
.
Two words, x and y, are similar with respect to the finite language L, written , if for every , , whenever . In this definition, l is the length of the longest words in L. The similarity relation on words is not an equivalence relation, as it is only reflexive, symmetric, and semi-transitive.
If A is a DFCA for the finite language L, we can also define the level of a state as the length of the shortest path from the initial state to that state, that is . In case of multiple entry DFCAs, a state will have k levels, i.e., , for all , and , where .
The following definition is in [
10] (Definition 2):
Definition 1. In a NFCA , two states are similar, written , if if , for all .
In case the NFCA A is understood, we may omit the subscript A, i.e., we write instead of , also we can write instead of .
We consider only non-trivial NFCAs for L, i.e., NFCAs such that for all states p, and with all the states useful and reachable.
We define deterministic and nondeterministic state complexity of a language as:
and
In case of a finite language
L, we can also define the cover complexity variants:
and
We have that , and .
For an automaton A, we say that it is minimal if the number of states of A is equal to its corresponding complexity; therefore, we can have minimal DFAs, NFAs, DFCAs, NFCAs, ⋄-DFAs, MEFAs, and MEFCAs. An algorithm which takes an automaton of one of the above types as input and produces a minimal automaton of the same type as output is called a minimization algorithm. In some cases, minimization algorithms are exponential. Therefore, it is worth designing algorithms that will reduce the number of states, but they may not produce a minimal automaton. In that case, we have simplification algorithms that may reduce the number of states of the automaton used as input and produce an equivalent one with possibly fewer states. Simplification algorithms are preferred for cases when their computational complexity is significantly lower than the complexity of a minimization algorithm.
For either minimization or simplification algorithms, the method that is used the most is to merge two or more states into one state in such a way that the recognized language does not change. By merging state
p into state
q we redirect all incoming transitions to state
p to incoming transitions to state
q. For outgoing transitions in case of deterministic automata, outgoing transitions from
p are lost, but outgoing transitions from
q are preserved. In case of nondeterministic automata merging can be done in many different ways. For example, the following definition is in [
10] (Definition 3):
Definition 2. Let be an NFCA for the finite language L.
- (1)
We say that the state q is weakly mergeable
in state p if the automaton , where , , and is also an NFCA for L. In this case, we write .
- (2)
We say that the state q is strongly mergeable
in state p, if the automaton , where , , and is also an NFCA for L. In this case, we write .
By Theorem 3 of [
10], if two states are similar, they are also strongly mergeable; therefore, we can reduce the size of that automaton.
Next, we analyze two possible extensions of cover automata. One of them is to allow “do not care” symbols, while the other is to add multiple initial states. For these two types of automata, first, we give the new definitions, then we analyze which results hold and which ones need to be adapted to the new concepts.
2.2. Cover Automata for Partial Words
A DFCA with “do not care” symbols, written ⋄-DFCA, is a cover automaton for the finite language . Please note that in a ⋄-DFA or ⋄-DFCA, it is not required to have for every state transitions with “do not-care” symbol ⋄. Thus, partial automata are usually presented as incomplete automata, namely, the transitions of “do not care” symbol to a dead state are omitted.
The language recognized by a ⋄-DFCA, A, over the extended alphabet is , where l is the length of the longest accepted word. We need to find the language over the original alphabet , thus we apply a substitution to get as the -language over , accepted by the ⋄-DFCA.
In [
13], as well as in [
25], for the substitution
we can have
. In this paper, we only consider the case where
, although most results are valid even if
.
By replacing the “do not care” symbols in a ⋄-DFCA with all letters in , the ⋄-DFCA becomes a NFCA. Thus, if L is a language accepted by a minimal ⋄-DFCA with n states, then the “do not care” state complexity of L is . Since any DFCA can be also considered a ⋄-DFCA, we have that .
3. Cover Automata with “Do Not Care” Symbols
In our study, we only need to see how “do not care” symbols influence state similarity and mergeability of two states, because everything that would be valid for NFCAs would then apply to ⋄-DFCAs. For strong mergeability, we always obtain deterministic transitions because we remove some of the states’ transitions.
For a transition , , , and a substitution , we consider , i.e., the set of all transitions that can be obtained by substituting the letter with . If is a DFCA for L, we can denote by , i.e., the set of all transitions in the automaton A and , the set of all transitions obtained from the original ones by applying the substitution .
We now define the compatibility of two states in a ⋄-DFCA.
Definition 3. Let be a ⋄-DFCA. Two states are σ-compatible for the substitution σ, denoted by , if the set .
Two states are σ-strongly compatible, denoted , if they are σ-compatible, , and if there are and such that , we either have , or , for all , or , for all .
When the substitution σ is understood or in case , it can be omitted and we say that p and q are compatible, respectively, strongly compatible.
In other words, two states are compatible if by applying the substitution of “do not care” symbols for the ⋄-transitions, we obtain the same destination states from p and q using the same letters in . A weak merge, in the sense of Definition 2 can be used in case p and q are compatible, but we need to check that this procedure won’t change the language.
At the same time, two states are strongly compatible if we can take a destination state s and all transitions with all letters to s can be replaced by only one transition using a “do not care” symbol, and all other destinations can be reached by at most one symbol from for all the other transitions originating in p and q.
Thus, by merging state p with state q and considering the set T of consolidated transitions, we can replace transitions in T with transitions such that
- (1)
we will have only one transition for each symbol in and
- (2)
by applying the substitution , we get the same consolidating transitions, i.e., .
This new procedure can be defined for partial DFAs and it corresponds to the strongly merging procedure in Definition 2.
Let us check the time complexity required to:
- (1)
Decide if two states are strongly compatible, and
- (2)
Define a method to merge two strongly compatible states.
To decide if two states are strongly compatible, we need to check the following:
- (1)
Check if . If no, then the states are not strongly compatible, so we do not attempt to strongly merge them (Consolidate the outgoing transitions and modify them to get deterministic transitions only).
- (2)
The number of destinations can be at most . If not, the states are not strongly compatible.
- (3)
If for a letter , there are at least three distinct states , such that , for all , then the states are not strongly compatible.
- (4)
If there exists a letter , such that if there are two states with , then we must have either for all , , , or for all , , , but not both.
If this condition is not satisfied, we cannot replace all the transitions on to only one of the states , or with the “do not care” symbol, and we do not obtain determinism for the transitions in the merged state.
Because , all these steps, 1 to 4, take time. Of course, for step 4, we may have two choices for the resulting automaton, but either one we choose, it takes constant time to do the merging. In step 4, if we have a transition from state p to state s with a letter and a transition from state p to state s with “do not care” symbol ⋄, the transition from state p to state s with a letter can be absorbed into transition from state p to state s with “do not care” symbol ⋄, as it is a redundant transition.
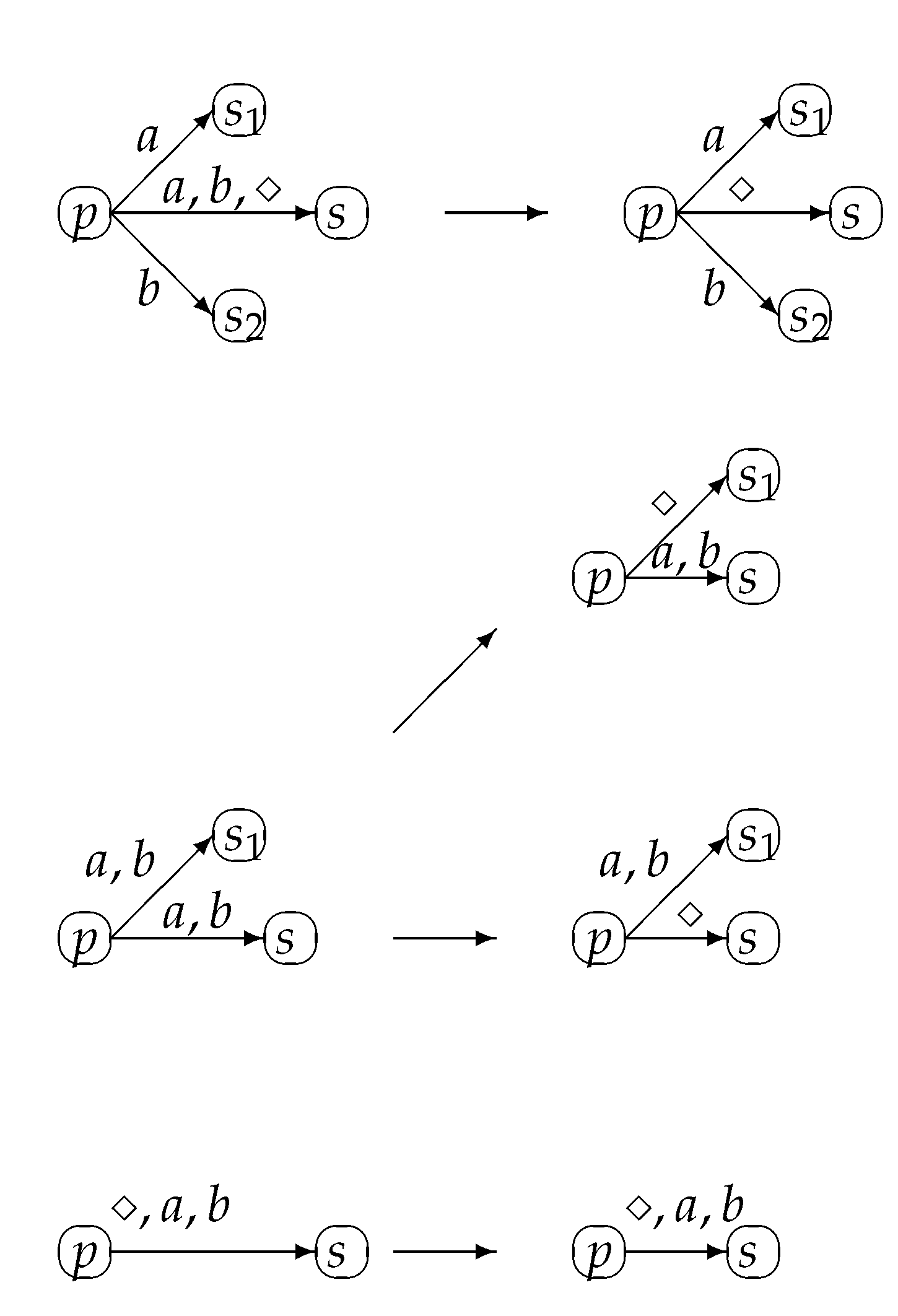
In
Figure 1 are depicted all possible cases of merging two strongly compatible states, in case the alphabet is
.
Remark 1. By strongly merging two states, we may obtain nondeterministic transitions. However, in the case of strongly compatible states, redundant transitions can be absorbed into the do not care symbol obtaining only deterministic ones.
For defining the similarity relation in a ⋄-DFCA for two states
p and
q, we need the states to be similar in the corresponding NFCA, as in Definition 2 of [
10].
Hence, we get the following:
Definition 4. For a ⋄-DFCA two states p and q are similar, denoted , if for all and a partial word u such that , there is a partial word v, such that , and we also have that if .
Lemma 1. Let ⋄-DFCA be a ⋄-DFCA. If two states p and q are similar, then they can be either strongly merged eliminating redundant transitions, if they are strongly compatible, or weakly merged otherwise.
Proof. Let be the language of partial words accepted by A, the associated finite language, and l the length of the longest words in L. Without any loss of generality, we may assume that . Let such that , , . It follows that for every word and any such that and , we have that . We also have that .
There is a partial word u, such that and because . Thus, by redirecting all transitions from q to p (the weakly merging method), we obtain a new automaton for which is in the associated language of .
If we have a word w in the associated language of , it means that there is a partial word z accepted by such that . If for every prefix of of z, , then , and z is accepted by A, therefore .
We have that because in case for some with . Since , for , there is a partial word u, such that and . We have either , or because is obtained from A by weakly merging q into state p. In both cases, , and either , or , so .
Hence, the language associated with the automaton does not change in case we do a weak merging of similar states.
If p and q are strongly compatible, let , . Thus, either , or . Consequently, the word is also in the language associated with the automaton .
If w is in the associated language of , then there is a partial word z such that . In case for some with , because , then and , .
Since , for , there is a partial word u, such that , and .
Because is obtained from A by strongly merging q into state p, we have either , or . In both cases, , and either , or , so . □
Let us see how we can use the above results to minimize ⋄-DFCAs.
In
Section 2 of [
12], the authors show that NFA minimization is NP-hard even in the case when the NFAs recognize finite languages, and they have limited non-determinism, i.e., the automata have at most one non-deterministic transition. Moreover, Corollary 7 on page 208 of [
12], states that the minimization problem is NP-hard even if the input is given as a DFA. Their proof is based on the fact that the normal set cover problem is NP-complete [
26,
27]. Hence, if you consider these sets as paths, which corresponds to words, in an NFA, finding a minimal NFA is equivalent to finding a minimal set cover. For proving it in case of limited nondeterminism, they need a normal set cover
B of a set
C, i.e., for each
, there is a subset
of
B such that
the elements in
are pairwise disjoint. The partition
B is separable normal set basis for
C if
B can be written as a disjoint union of two other non-empty sets
and
such that for each
, the subcollection
contains at most one element of
and at most one element of
. To do that, they use a modified version of a known reduction from vertex cover to normal set basis (Lemma 4 in [
28]), showing that the second problem is NP-hard. Using this result, they show that some instances of normal set basis sets in the partition will be pairwise disjoint and you can have just one state with two
a-transitions. For
, a separable normal set basis they consider, the language considered is
, over a growing alphabet
.
All accepted words are of length 3.
Therefore, for our case, we can use the same proof in two ways:
- (1)
Either showing that ⋄-DFAs satisfy the conditions of Definition 1 page 201 of [
12] and asking that the minimum length of the longest accepted string is at least 3, or
- (2)
Use the same input as they use and replace the a symbol, that generates the nondeterministic transition, with a “do not care” symbol, so we get a ⋄-DFA. In this case, the only change would be that , and we would get several instances of the same problem, only with the first letter changed. Finding a minimal a normal set cover will only involve letters 2 and 3 for all paths from the start state to the final state, therefore, we can follow the same proof, but ignoring the part where they need to show that the minimal finite automaton is not ambiguous—in our case, that’s not necessary. One can check that the proof works without any other change for ⋄-DFCAs, considering that the length of the longest accepted word is at least l, with .
It follows that:
Theorem 1. Minimizing ⋄-DFCAs is NP-hard.
Therefore, we need to seek simplification algorithms rather than minimization algorithms for ⋄-DFCAs. We already know [
1,
7,
24,
29] that all minimization algorithms for DFCAs are based on determining all similar states and merge them. For testing the similarity, one method [
24,
29], is to compute the gap function for two states
p and
q, where
is the length of the shortest word that will distinguish between the states
p and
q. For ⋄-DFCAs, this means that we need to determine the length of the shortest word
w such that:
if , , and , then for any partial word , such that , we have that .
if , , and , then for any partial word , such that , we have that .
It follows that:
if and and , then , and
if and , and , then .
Hence, we deduce that the gap function can be recursively computed as follows:
.
Because the number of transitions from p and q is bounded by , computing the gap function for a DFCA can be done in constant time for any pair , if we know the gap function for all pairs , such that , , .
Two state would be then similar if
. With these observations and the fact that all known minimization algorithms for DFCAs are based on computing the similarity relation, we can modify any of the known minimizing algorithms for DFCAs [
1,
4,
7,
29] or
l-DFCAs [
24], to obtain a simplification algorithm for ⋄-DFCAs, without changing their computational complexity. Since the minimization algorithms for DFCAs are at most
[
1,
10], for all these simplification algorithms the time complexity will be at most
as well, which is better than the time complexity of the simplification algorithm proposed in [
13]. Accordingly, we have obtained the following result:
Theorem 2. For every DFCA minimization algorithm based on merging similar states having the run time complexity of , there is a simplification ⋄-DFCA algorithm having the same complexity of .
A language is -minimal partial language for L if for any other language such that , there is no word such we can find with x is weaker than w and .
For example, is -minimal partial language for . Indeed, if is -partial language for L, and are such that , then we either have or . In the first case, and in the second case is false. Therefore, is a -minimal partial language for L.
It must be noted that the simplification algorithm proposed in [
13] obtains an approximation of the
-minimal partial language
for the regular language
L, and obtaining this
-minimal partial language is NP-hard [
13]. The cover language
, for the finite language
L that we obtain by applying the simplification algorithm, may not be a cover language for the
-minimal partial language
, i.e.,
, but it is a
-partial language that may have a lower state complexity than the original DFCA for
L and
is a cover language for
L, i.e.,
. Please note that
is the weakest partial language such that
.
In
Figure 2 for the language
,
, we have the partial language
, recognized by the ⋄-automaton
, with useful transitions
,
,
,
,
,
,
, that is a
-minimal partial cover language for
L, i.e.,
, and the words in
are the weakest possible with this property. We have that the
.
The language recognized by the ⋄-automaton , with useful transitions , is a -partial cover language for L, i.e., , and . and it contains 6 words, but has only 5 words.
The example above shows that it is impossible to obtain a cover language for the -partial minimal language that has, at the same time, the minimal cover state complexity.
4. Multiple Entry DFCAs
For multiple entry DFCAs, we can have two possible flavors of extensions. The first one and the easiest to consider is the same maximum length for all words accepted by the m-DFCA. The second approach is to consider for each initial state a different maximum length. Therefore, we can use the following definition:
Definition 5. A multiple entry DFCA with m initial states, i.e., an m-DFCA, is a structure , such that Q, Σ, δ, and F are the same as for usual DFCAs, is the set of initial states, , and is a sequence of m integers representing the maximum accepted length for each initial state. If and , the language accepted by the m-DFCA A is We have the condition , where , . The automata are subautomata induced by the m-DFCA A.
We observe from the above definition that the set of initial states has the size m. Thus, by replacing the set with an m-tuple , if we assign two possible lengths to an initial state, it does not change the accepted language. Assume that the initial states and are the same, i.e., . The automaton will then accept all the words of length less than , meaning that we can eliminate the one with the lowest maximum length, getting an -DFCA.
In the example given by Björklund and Martens [
12], they prove that minimizing
m-DFAs is NP-hard, using a construction with a finite language. Because any
m-DFA for a finite language is also an
m-DFCA, by setting
to be the length of the longest accepting walk starting at
, it follows that
Theorem 3. Minimizing m-DFCA is an NP-hard problem.
We can reduce the size of m-DFCA efficiently in a similar way to the previous case for partial automata, obtaining a simplified m-DFCA by merging states. To avoid changing the language recognized by an m-DFCA A, the simplest solution is to merge similar states in all the subautomata with the corresponding maximum length . Any other merge of states will modify at least one of the languages involved, which will not guarantee that their union stays the same as before. Therefore, we can obtain the following definition for similarity in m-DFCAs:
Definition 6. Let be an m-DFCA for the finite language L. Two states p and q are similar if p and q are similar in all cover automata , .
The simplification algorithms for m-DFCAs can be obtained as before by modifying existing DFA-minimization algorithms, therefore in what follows we will focus on state complexity problem, namely, on constructing a minimal DFCA for the same language, and evaluating the state complexity of this transformation.
It is known that for NFA to DFA transformation for finite languages, [
30], in case of a binary alphabet, the upperbound is
if
n is even, and
, if
n is odd,
n being the number of states of the NFA. Moreover, it is reached by the language
when
, or
, so
, and
.
Because the length of the longest word is
, the minimal nondeterministic finite automaton recognizing this language will have at least
states, while the minimal DFA will have at least
states, [
30], Theorem 2. A minimal
-DFA for
has the same number of states as the NFA, plus the sink state, therefore, is minimal as a
m-DFA. A minimal
-DFCA for
has the same number of states as the NFA minus one, because the sink state is similar with state 0, and that is the only possible similarity. We can see that the minimal nondeterministic cover automaton for
has only
states. For this NFCA for
, the initial state is obtained by merging all the
-entries into one, so a minimal
-DFCA must have
m states more than the NFCA, that is
.
Starting from an m-DFA for a finite language, we can construct an equivalent NFA by observing that there is one initial state with no incoming transition, and for each initial state , if , we can add the transitions from with a in , and we delete the sink state. This way, for the m-DFA to DFA transformation, we obtain the limits for NFA to DFA transformation, but we need to consider the extra sink state for m-DFAs.
Therefore, we just proved the following result:
Theorem 4. In case of a binary alphabet, the upperbound for a n-state m-DFCA to DFCA transformation is if n is odd, and , if n is even, and the bound is reached.
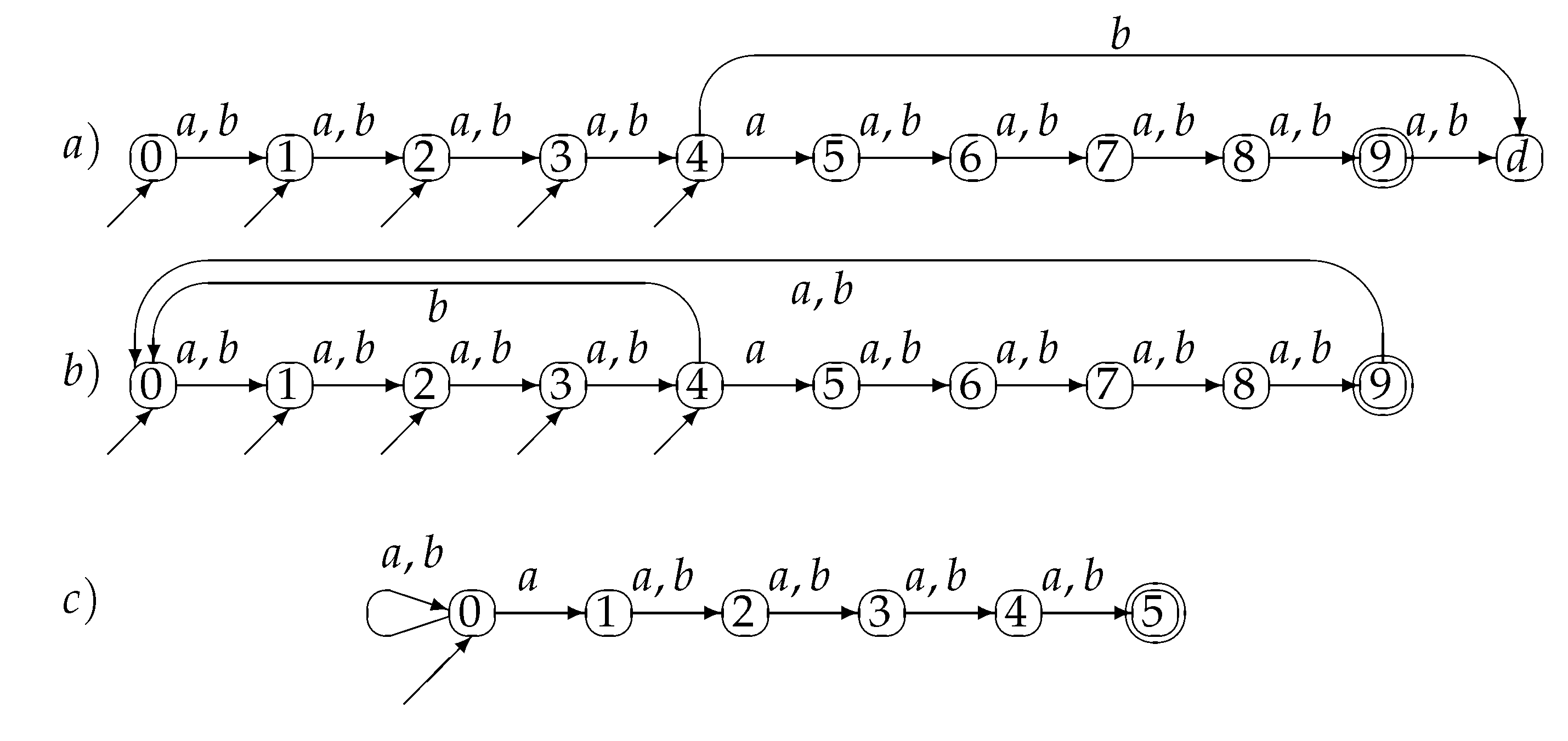
Figure 3 shows a 5-DFA with 11 states for the language
. This 5-DFA is a minimal multi-entry DFA. Any nondeterministic finite automaton recognizing
must have at least 11 states which is the length of the longest word in
plus 1. A DFA, multi-entry or not must have a sink state, because the language is finite, therefore the automaton depicted in
Figure 3a is minimal. The corresponding multi-entry DFCA,
Figure 3b has the dead state
d similar with state 0, so we can reduce the size by one state. The NFCA in
Figure 3c recognizes
, and it has only 6 states. The general case for
is depicted in
Figure 4.
The upperbound for m-DFA to DFCA transformation is the same as the NFA to DFCA transformation, but there is one difference. We have to consider that in the m-DFA, we must have one more state as dead state because the language is finite, while in the NFA that state can be eliminated, as it is not useful.