Global Stability Condition for the Disease-Free Equilibrium Point of Fractional Epidemiological Models †
Abstract
:1. Introduction
2. Preliminaries
- if , then ;
- if there exists a non-singular matrix P such that , then .
3. Main Results
- 1.
- For , the vector is globally asymptotically stable;
- 2.
- Function G can be written as , where for all , and can be written as , where and is a diagonal matrix;
- 3.
- Matrix A is diagonalizable, the real parts of the eigenvalues of A are nonpositive, and ;
- 4.
- for all (nonnegativity of solutions).
4. Examples
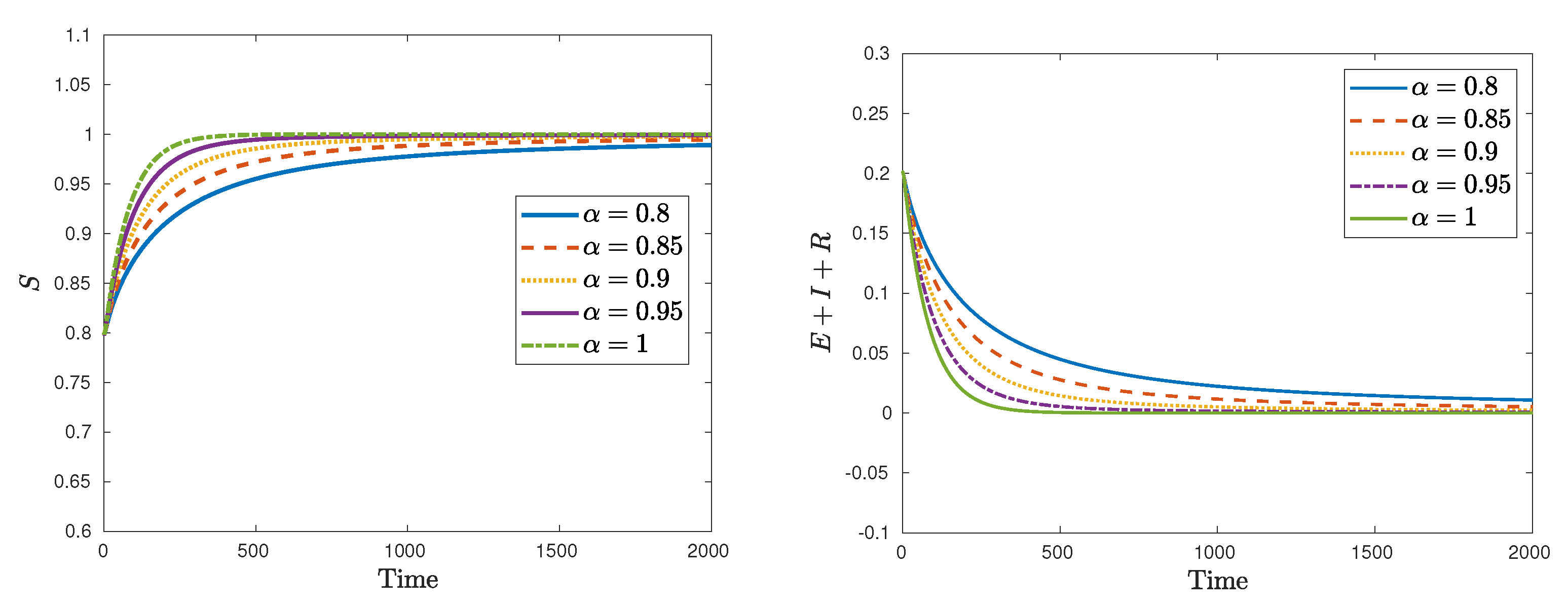
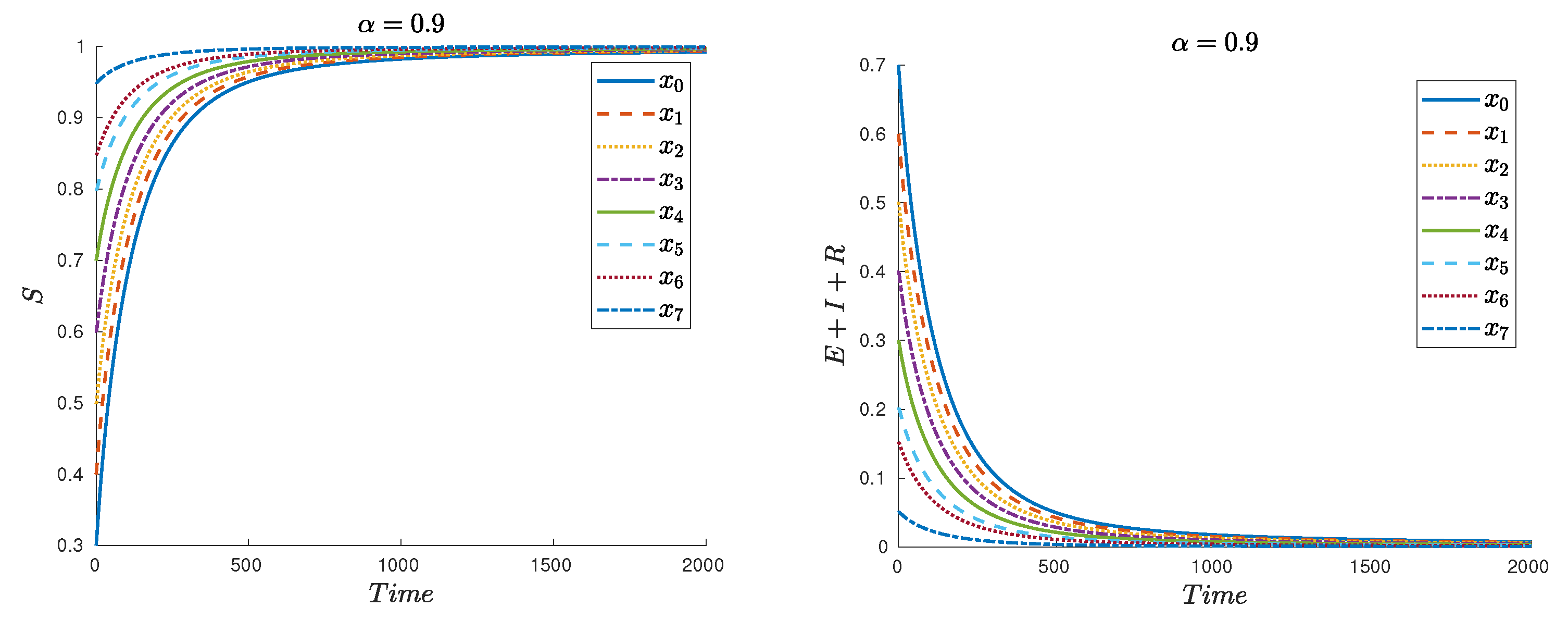
4.1. A Fractional SEIR Model with Traditional Incidence Rate
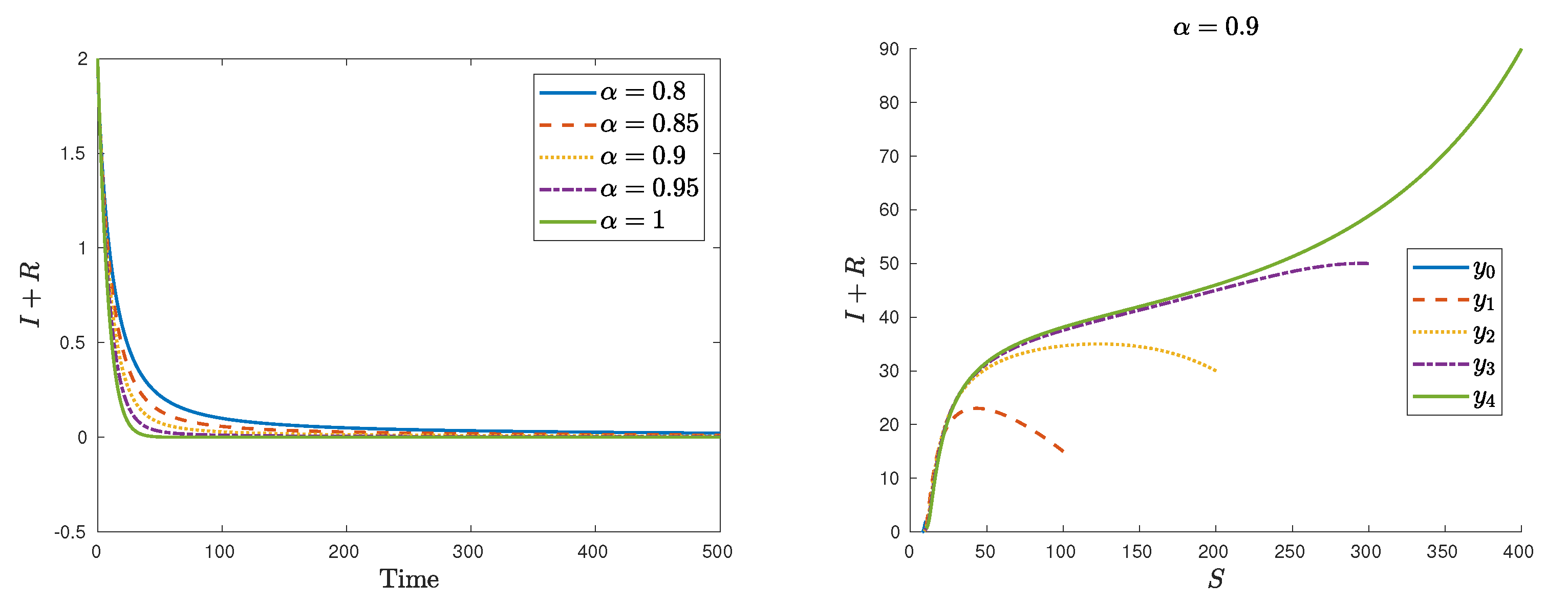
4.2. A Fractional SIRS Model with General Incidence Rate
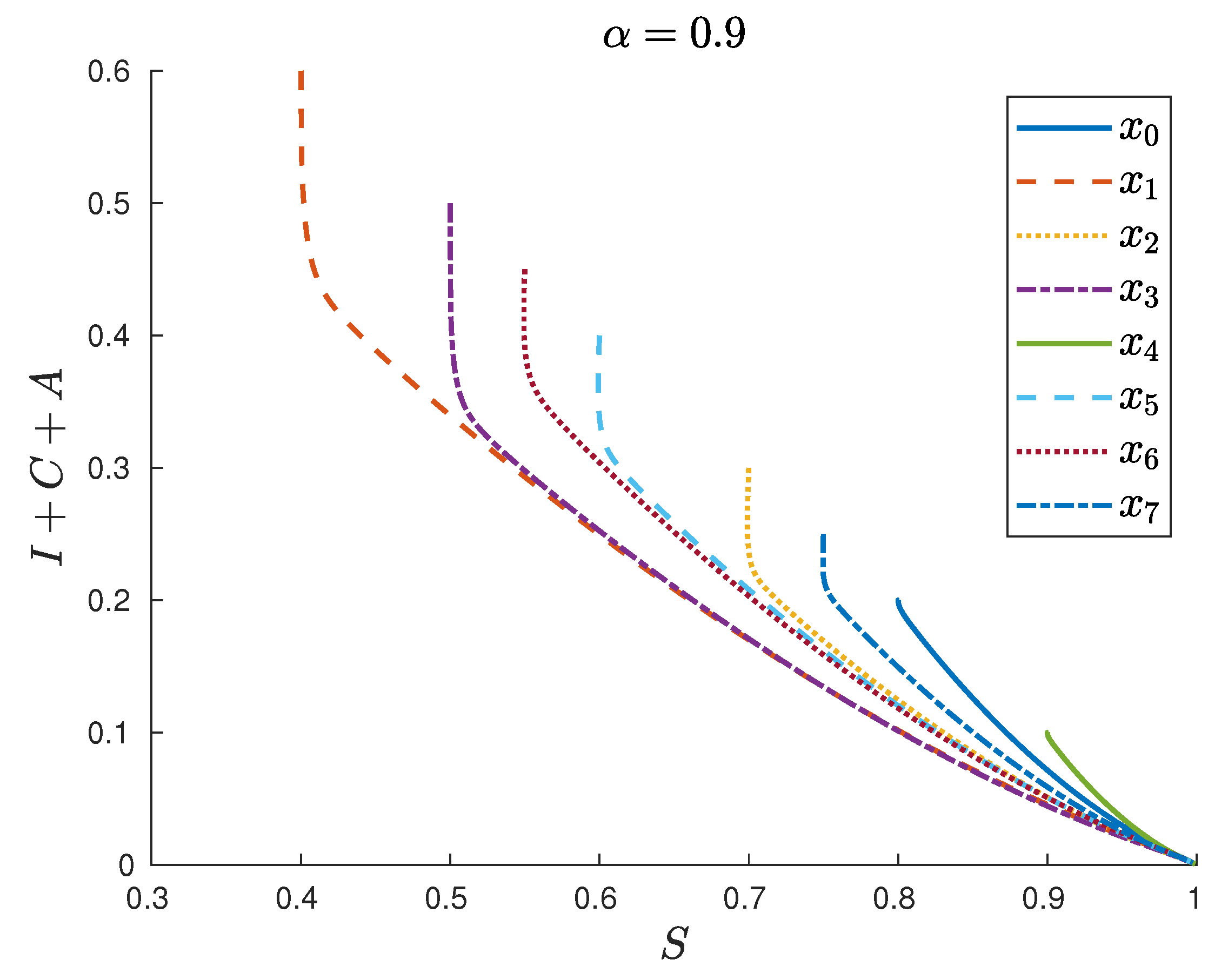
4.3. A Modified Fractional SICA Model for HIV/AIDS
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Jesus, I.S.; Machado, J.A.T.; Cunha, J.B. Fractional electrical impedances in botanical elements. J. Vib. Control 2008, 14, 1389–1402. [Google Scholar] [CrossRef] [Green Version]
- Boukhouima, A.; Hattaf, K.; Lotfi, E.M.; Mahrouf, M.; Torres, D.F.M.; Yousfi, N. Lyapunov functions for fractional-order systems in biology: Methods and applications. Chaos Solitons Fractals 2020, 140, 110224. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Stanislavsky, A.A. Fractional oscillator. Phys. Rev. E 2004, 70, 051103. [Google Scholar] [CrossRef] [Green Version]
- Skovranek, T. The Mittag–Leffler fitting of the Phillips curve. Mathematics 2019, 7, 589. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, Z.; Meng, B. Stability and bifurcation of a delayed time-fractional order business cycle model with a general liquidity preference function and investment function. Mathematics 2019, 7, 846. [Google Scholar] [CrossRef] [Green Version]
- Maalej, B.; Khlif, R.J.; Mhiri, C.; Elleuch, M.H.; Derbel, N. Adaptive fractional control optimized by genetic algorithms with application to polyarticulated robotic systems. Math. Probl. Eng. 2021, 2021, 5579541. [Google Scholar] [CrossRef]
- Paola, M.; Pinnola, F.P.; Zingales, M. Fractional differential equations and related exact mechanical models. Comput. Math. Appl. 2013, 66, 608–620. [Google Scholar] [CrossRef] [Green Version]
- Barros, L.C.; Lopes, M.M.; Pedro, F.S.; Esmi, E.; Santos, J.P.C.; Sánchez, D.E. The memory effect on fractional calculus: An application in the spread of COVID-19. Comput. Appl. Math. 2021, 40, 72. [Google Scholar] [CrossRef]
- Bushnaq, S.; Saeed, T.; Torres, D.F.M.; Zeb, A. Control of COVID-19 dynamics through a fractional-order model. Alex. Eng. J. 2021, 60, 3587–3592. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Fractional model of COVID-19 applied to Galicia, Spain and Portugal. Chaos Solitons Fractals 2021, 144, 110652. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lu, P. Stability analysis for HIV infection of CD4+ T-cells by a fractional differential time-delay model with cure rate. Adv. Differ. Equ. 2014, 2014, 298. [Google Scholar] [CrossRef]
- Silva, C.J.; Torres, D.F.M. Stability of a fractional HIV/AIDS model. Math. Comput. Simul. 2019, 164, 180–190. [Google Scholar] [CrossRef] [Green Version]
- Almeida, R.; Cruz, A.M.C.B.; Martins, N.; Monteiro, M.T.T. An epidemiological MSEIR model described by the Caputo fractional derivative. Int. J. Dyn. Control 2019, 7, 776–784. [Google Scholar] [CrossRef] [Green Version]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- Qureshi, S.; Jan, R. Modeling of measles epidemic with optimized fractional order under Caputo differential operator. Chaos Solitons Fractals 2021, 145, 110766. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Maritz, R.; Munganga, J. Some properties of the Kermack-McKendrick epidemic model with fractional derivative and nonlinear incidence. Adv. Differ. Equ. 2014, 2014, 278. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Ullah, S.; Ullah, S.; Farhan, M. Fractional order SEIR model with generalized incidence rate. AIMS Math. 2020, 5, 2843–2857. [Google Scholar] [CrossRef]
- Özalp, N.; Demirci, E. A fractional order SEIR model with vertical transmission. Appl. Math. Model. 2011, 54, 1–6. [Google Scholar] [CrossRef]
- Ammi, M.R.S.; Tahiri, M.; Torres, D.F.M. Global Stability of a Caputo Fractional SIRS Model with General Incidence Rate. Math. Comput. Sci. 2021, 15, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Günay, B.; Agarwal, P.; Guirao, J.L.G.; Momani, S. A fractional approach to a computational eco-epidemiological model with holling type-II functional response. Symmetry 2021, 13, 1159. [Google Scholar] [CrossRef]
- Hassouna, M.; Ouhadan, A.; Kinani, E.H.E. On the solution of fractional order SIS epidemic model. Chaos Solitons Fractals 2018, 117, 168–174. [Google Scholar] [CrossRef] [PubMed]
- Seo, Y.; Zeb, A.; Zaman, G.; Jung, I. Square-root dynamics of a SIR-model in fractional order. Appl. Math. 2012, 3, 1882–1887. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. Global stability for fractional diffusion equations in biological systems. Complexity 2020, 2020, 5476842. [Google Scholar] [CrossRef]
- Nabti, A.; Ghanbari, B. Global stability analysis of a fractional SVEIR epidemic model. Math. Methods Appl. Sci. 2021, 44, 8577–8597. [Google Scholar] [CrossRef]
- Salahshour, S.; Ahmadian, A.; Salimi, M.; Pansera, B.A.; Ferrara, M. A new Lyapunov stability analysis of fractional-order systems with nonsingular kernel derivative. Alex. Eng. J. 2020, 59, 2985–2990. [Google Scholar] [CrossRef]
- Xu, Q.; Zhuang, S.; Xu, X.; Che, C.; Xia, Y. Stabilization of a class of fractional-order nonautonomous systems using quadratic Lyapunov functions. Adv. Differ. Equ. 2018, 2018, 14. [Google Scholar] [CrossRef] [Green Version]
- Castillo–Chavez, C.; Feng, Z.; Huang, W. On the computation of R0 and its role in global stability. IMA Vol. Math. Its Appl. 2002, 125, 229–250. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering, 198; Academic Press Inc.: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Translated from the 1987 Russian Original; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag–Leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef] [Green Version]
- Hilfer, R.; Seybold, H.J. Computation of the generalized Mittag–Leffler function and its inverse in the complex plane. Integral Transform. Spec. Funct. 2006, 17, 637–652. [Google Scholar] [CrossRef]
- Popolizio, M. On the Matrix Mittag–Leffler Function: Theoretical Properties and Numerical Computation. Mathematics 2019, 7, 1140. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, A.; Cardoso, J.R. Some notes on properties of the matrix Mittag–Leffler function. Appl. Math. Comput. 2018, 338, 733–738. [Google Scholar] [CrossRef]
- Cong, N.D.; Doan, T.S.; Tuan, H.T. Asymptotic stability of linear fractional systems with constant coefficients and small time-dependent perturbations. Vietnam J. Math. 2018, 46, 665–680. [Google Scholar] [CrossRef] [Green Version]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous population. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.S.; Samko, S.G. A note on the complete monotonicity of the generalized Mittag–Leffler function. Real Anal. Exch. 1997, 23, 753–755. [Google Scholar] [CrossRef]
- Pollard, H. The completely monotonic character of the Mittag-Leffer function Eα(-x). Bull. Am. Math. Soc. 1948, 54, 1115–1116. [Google Scholar] [CrossRef] [Green Version]
- Diethelm, K. The Analysis of Fractional Differential Equations, An Application-Oriented Exposition Using Differential Operators of Caputo Type; LNM Springer: Berlin, Germany, 2010; Volume 2004. [Google Scholar]
- LaSalle, J.P. The Stability of Dynamical Systems, Regional Conferences Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Garrappa, R. Predictor-Corrector PECE Method for Fractional Differential Equations, MATLAB Central File Exchange, File ID: 32918. 2012. Available online: https://www.mathworks.com/matlabcentral/fileexchange/32918-predictor-corrector-pece-method-for-fractional-differential-equations (accessed on 13 July 2021).
- Diethelm, K.; Freed, A.D. The Frac PECE subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen 1998; Heinzel, S., Plesser, T., Eds.; Gessellschaft fur Wissenschaftliche Datenverarbeitung: Gottingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef]
- Lavault, C. Integral representations and asymptotic behaviour of a Mittag–Leffler type function of two variables. Adv. Oper. Theory 2018, 3, 365–373. [Google Scholar] [CrossRef]
- Silva, C.J.; Torres, D.F.M. A SICA compartmental model in epidemiology with application to HIV/AIDS in Cape Verde. Ecol. Complex. 2017, 30, 70–75. [Google Scholar] [CrossRef] [Green Version]
- Pebody, R. Undetectable Viral Load and Transmission–Information for People with HIV. November 2020. Available online: https://www.aidsmap.com/about-hiv/undetectable-viral-load-and-transmission-information-people-hiv (accessed on 13 July 2021).

| Symbol | Description | Value |
|---|---|---|
| μ | Recruitment rate/natural death rate | 1/69.54 |
| β | HIV transmission rate | 0.05 |
| ηA | Modification parameter | 1.3 |
| ϕ | HIV treatment rate for I individuals | 1 |
| ρ | Default treatment rate for I individuals | 0.1 |
| γ | AIDS treatment rate | 0.33 |
| ω | Default treatment rate for C individuals | 0.09 |
| d | AIDS induced death rate | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, R.; Martins, N.; Silva, C.J. Global Stability Condition for the Disease-Free Equilibrium Point of Fractional Epidemiological Models. Axioms 2021, 10, 238. https://doi.org/10.3390/axioms10040238
Almeida R, Martins N, Silva CJ. Global Stability Condition for the Disease-Free Equilibrium Point of Fractional Epidemiological Models. Axioms. 2021; 10(4):238. https://doi.org/10.3390/axioms10040238
Chicago/Turabian StyleAlmeida, Ricardo, Natália Martins, and Cristiana J. Silva. 2021. "Global Stability Condition for the Disease-Free Equilibrium Point of Fractional Epidemiological Models" Axioms 10, no. 4: 238. https://doi.org/10.3390/axioms10040238
APA StyleAlmeida, R., Martins, N., & Silva, C. J. (2021). Global Stability Condition for the Disease-Free Equilibrium Point of Fractional Epidemiological Models. Axioms, 10(4), 238. https://doi.org/10.3390/axioms10040238








