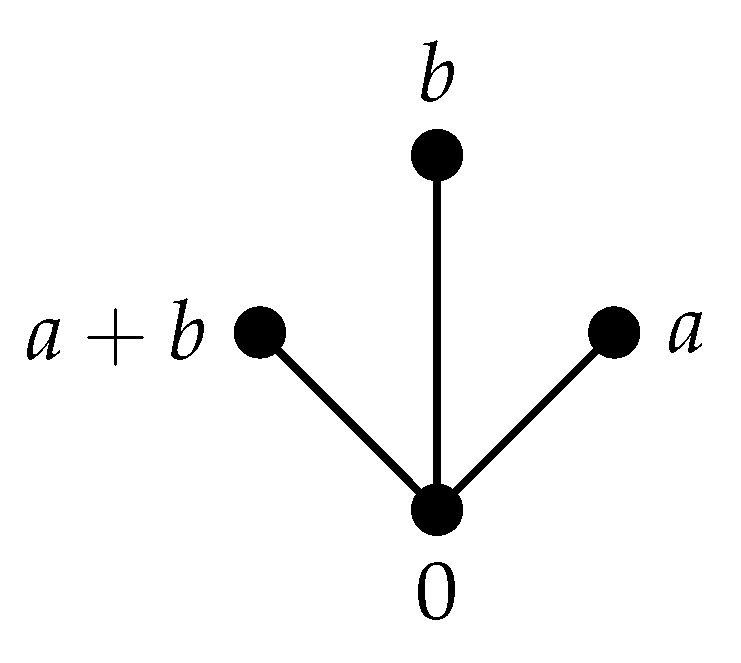1. Introduction
Throughout the paper, R denotes a finite ring and . Let be the center of R. For any element , the centralizer of x in R is a subring given by . Clearly, . For any two elements x and y of R, is called the additive commutator of x and y. Let and and for denote the additive subgroups of generated by the sets and , respectively.
The study of graphs defined on algebraic structures has been an active topic of research in the last few decades. The main question in this area is to recognize finite groups/rings through the properties of various graphs defined on it. In 2015, Erfanian, Khashyarmanesh and Nafar [
1] considered noncommuting graphs of finite rings. Recall that the noncommuting graph of a finite noncommutative ring
R is a simple undirected graph whose vertex set is
and two vertices
x and
y are adjacent if and only if
. The complement of noncommuting graph, called commuting graph, of a finite noncommutative ring is considered in [
2,
3,
4,
5]. The motivation for studying commuting/noncommuting graphs of finite rings comes from the study of commuting/noncommuting graphs of finite groups. Many interesting results on commuting/noncommuting graphs of finite groups can be found in [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. There are many generalizations of noncommuting graphs of finite groups. The
g-noncommuting graph of a finite group, studied extensively in [
17,
18,
19,
20], is a kind of generalization of noncommuting graph of a finite group. It is worth mentioning that commuting/noncommuting graphs and their generalizations for finite rings are not much studied. Some people want to know whether commuting/noncommuting graphs and their generalizations for finite rings possess results analogous to the results for finite groups.
In this paper, we introduce and study the r-noncommuting graph of a finite ring R for any given element analogous to g-noncommuting graph of a finite group. The r-noncommuting graph of R, denoted by , is a simple undirected graph whose vertex set is R and two vertices x and y are adjacent if and only if and . Clearly, . If , then the induced subgraph of with vertex set , denoted by , is nothing but the noncommuting graph of R. Note that is a 0-regular graph if and R is commutative. In addition, is complete if . Thus, for , is n-regular if and only if R is of order . Therefore throughout the paper we shall consider .
In
Section 2, we first compute degree of any vertex of
in terms of its centralizers. Then we characterize
R if
is a tree, in particular a star graph. We further show that
is not a regular graph (if
) or a lollipop graph for any noncommutative ring
R. We conclude this section by showing that
is isomorphic to
if
is an isoclinism between two finite rings
and
such that
. In
Section 3, we consider the induced subgraph
of
, induced by
, and obtain results on clique number and diameter of
along with certain characterizations of finite noncommutative rings such that
is
n-regular for some positive integer
n. As applications of our results, we characterize certain finite noncommutative rings such that their noncommuting graphs are
n-regular for
.
It was shown in [
21] that there are only two noncommutative rings (up to isomorphism) having order
, where
p is a prime, and the rings are given by
It is worth noting here that the graphs and are isomorphic to and , respectively.
2. Some Properties
In this section, we characterize R when is a tree or a star graph. We also show the non-existence of finite noncommutative rings R whose r-noncommuting graph is a regular graph (if ), a lollipop graph or a complete bipartite graph. However, we first compute degree of any vertex in the graph . For any two given elements x and r of R, we write to denote the generalized centralizer of x. The following proposition gives the degree of any vertex of in terms of its generalized centralizers.
Proposition 1. Let x be any vertex in . Then
- (a)
if .
- (b)
If then
Proof. (a) If , then is the number of such that . Note that gives the number of elements that commute with x. Hence, .
(b) Consider the case when . If then . Note that is not adjacent to x if and only if or . Therefore, . If then . It is easy to see that and if and only if . Therefore, . Note that is not adjacent to x if and only if or or . Therefore, . Hence the result follows. □
The following corollary gives degree of any vertex of in terms of its centralizers.
Corollary 1. Let x be any vertex in .
- (a)
If and then
- (b)
If and then
Proof. Notice that if and only if . Suppose that . Let and . Then and so . Therefore, . Again, if then and so . Therefore, . Thus, if . Hence, the result follows from Proposition 1. □
We now present some results regarding realization of the graph and characterization of R through certain properties of as applications of Proposition 1.
Proposition 2. Let R be a ring with unity. The r-noncommuting graph is a tree if and only if and .
Proof. If then, by Proposition 1(a), we have . Hence, is not a tree. Suppose that . If R is commutative, then . Hence, is a complete graph. Therefore is a tree if and only if . If R is noncommutative, then and for any . Therefore for all . Hence, is not a tree. □
Proposition 3. Let R be a noncommutative ring. If has an end vertex then and is a star graph if and only if R is isomorphic to or . Hence, is not a lollipop graph.
Proof. Let
be an end vertex in
. Then
. If
then
and so
. In addition, by Proposition 1(a), we have
. These give
. Hence,
, a contradiction. Therefore,
. By Corollary 1, we have
or
. These give
or
. Clearly,
and so
. Therefore, if
, then
. If
, then
is even and
. Therefore,
. Since
R is noncommutative, we have
, and so
R is isomorphic to either
or
. In
Figure 2, it is shown that
is a star graph if
. Furthermore,
is isomorphic to
. Hence, the result follows. □
It follows that if R is noncommutative, having more than four elements, then there is no vertex of degree one in .
It is observed that is -regular if . Additionally, if and R is commutative, then is 0-regular. In the following proposition, we show that is not regular if .
Proposition 4. Let R be a noncommutative ring and . Then is not regular.
Proof. If
, then, by Proposition 1(a), we have
. Let
be a non-central element. Then
. Therefore, by Proposition 1(a),
. This shows that
is not regular. If
then
. Therefore, by Corollary 1, we have
. Since
, there exists
such that
. Therefore, by Corollary 1, we have
or
. If
is regular, then
. Therefore,
which gives
, a contradiction. Hence,
is not regular. This completes the proof. □
The following result shows that is not complete bipartite if and .
Proposition 5. Let R be a finite ring.
- (a)
If then, is not complete bipartite.
- (b)
If then, is not complete bipartite for with .
Proof. Let be complete bipartite. Then there exist subsets and of R such that and if and then x and y are adjacent.
(a) If , then for and , we have . Therefore, , which implies . Again , which implies . Thus, , a contradiction. Hence is not complete bipartite.
(b) If and , then for any , and are adjacent. Let us take and . Since we have such that and . Furthermore, . Therefore, x is adjacent to both and . Therefore, , a contradiction. Hence is not complete bipartite. □
In 1940, Hall [
22] introduced isoclinism between two groups. Recently, Buckley et al. [
23] introduced isoclinism between two rings. Let
and
be two rings. A pair of additive group isomorphisms
where
and
is called an isoclinism between
to
if
whenever
and
. Two rings are called isoclinic if there exists an isoclinism between them. If
and
are two isomorphic rings and
is an isomorphism, then it is easy to see that
. In the following proposition, we show that
if
and
are two isoclinic rings with isoclinism
.
Proposition 6. Let and be two finite rings such that . If is an isoclinism between and , then Proof. Since is an isomorphism, and have the same number of elements. Let . Again, since , there exists a bijection . Let and be two transversals of and , respectively. Let and be defined as and for some , and .
Let us define a map
such that
for
. Clearly,
is a bijection. We claim that
preserves adjacency. Let
x and
y be two elements of
such that
x and
y are adjacent. Then
. We have
and
where
and
. Therefore,
This shows that and are adjacent. Hence the result follows. □
3. An Induced Subgraph
We write to denote the induced subgraph of with vertex set . It is worth mentioning that is the noncommuting graph of R. If , then it is easy to see that the commuting graph of R is a spanning subgraph of . The following result gives a condition such that is the commuting graph of R.
Proposition 7. Let R be a noncommutative ring and . If then is the commuting graph of R.
Proof. The result follows from the fact that two vertices in are adjacent if and only if . □
Let be the clique number of . The following result gives a lower bound for .
Proposition 8. Let R be a noncommutative ring and . If S is a commutative subring of R with maximal order, then .
Proof. The result follows from the fact that the subset of is a clique of . □
By ([
1] Theorem 2.1), it follows that the diameter of
is less than or equal to 2. The next result gives some information regarding diameter of
when
. We write
and
to denote the diameter of
and the distance between
x and
y in
, respectively. For any two vertices
x and
y, we write
to denote
x and
y are adjacent; otherwise
.
Theorem 1. Let R be a noncommutative ring and such that .
- (a)
If , then .
- (b)
If , and , then .
Proof. (a) If
for all
such that
, then it is easy to see that
. Suppose there exists a vertex
such that
. Then
or
. We have
Since , we have , and hence . Furthermore, . Therefore, , and so . Let such that . If , then , noting that . If , then (as shown above). In this case, . Hence, .
(b) If for all such that , then it is easy to see that . Suppose there exists a vertex such that . Let such that . We consider the following two cases.
Case 1: and .
If
, then
; note that
. Therefore,
. If
but
, then
. Consider the case when
as well as
. Therefore
or
. If
, then
; otherwise
, a contradiction. Let
such that
(such an element exists, since
). Clearly
. Suppose
. Then
, and so
. Suppose
. Then
or
. If
, then
Note that
; otherwise
, a contradiction. Therefore,
. Furthermore,
That is,
. Thus,
. Therefore,
. If
, then
Note that
; otherwise
, a contradiction. Therefore,
. Furthermore,
That is, . Thus, . Therefore, .
If
then
; otherwise
, a contradiction. Let
such that
. Suppose
. Then
and so
. Suppose
. Then
or
. If
then
Note that
; otherwise
, a contradiction. Therefore,
. Furthermore,
That is,
. Thus,
. Therefore,
. If
then
Note that
; otherwise
, a contradiction. Therefore,
. Furthermore,
That is, . Thus, . Therefore, , and hence .
Case 2: and .
Let such that .
Subcase 2.1:
If , then . Therefore, . If but , then . Therefore, . Consider the case when as well as . Therefore or . If , then ; otherwise , a contradiction. Suppose . Then and so . Suppose . Then or . If then . Therefore, . Therefore, . If , then . Therefore, and so .
If , then ; otherwise , a contradiction. Suppose . Then and so . Suppose . Then or . If then . Therefore, . Therefore, . If , then . Therefore, and so . Hence, .
Subcase 2.2:
In this case we have and . It can be seen that implies , and implies .
Suppose and . Then . Hence, . Now, we have the following cases.
- (i)
if .
- (ii)
if but .
Suppose as well as . Then, proceeding as in Subcase 2.1, we get the following cases:
- (iii)
if and but .
- (iv)
if and .
- (v)
if and .
- (vi)
if and .
- (vii)
if and .
Therefore, .
Suppose
and
. Then
Hence, . Now, proceeding as above, we get the following cases:
- (i)
if .
- (ii)
if but .
- (iii)
if and but .
- (iv)
if and .
- (v)
if and .
- (vi)
if and .
- (vii)
if and .
Therefore, .
Suppose
and
. Then
Hence, . Proceeding as above, we get the following similar cases:
- (i)
if .
- (ii)
if but .
- (iii)
if and but .
- (iv)
if and .
- (v)
if and .
- (vi)
if and .
- (vii)
if and .
Therefore, .
Suppose
and
. Then
Hence, , so we get the the following similar cases:
- (i)
if .
- (ii)
if but .
- (iii)
if and but .
- (iv)
if and .
- (v)
if and .
- (vi)
if and .
- (vii)
if and .
Therefore, . Hence, in all the cases, . This completes the proof. □
As a consequence of Proposition 1(a) and Corollary 1, we get the following result.
Corollary 2. Let x be any vertex in .
- (a)
If then .
- (b)
If and then - (c)
If and then
Some applications of Corollary 2 are given below.
Theorem 2. Let R be a noncommutative ring such that and let be the complete graph on n-vertices. If has an end vertex then and if and only if R is isomorphic to or . Hence, is neither a tree nor a lollipop graph.
Proof. Let be an end vertex in . Then . If then, by Corollary 2(a), we have . Therefore, , and hence , a contradiction. Therefore, . Now, we consider the following cases.
Case 1: and .
By Corollary 2(b), we have or . Hence or .
Subcase 1.1:.
In this case, we have or 2. If then , a contradiction. If then . Therefore, the additive quotient group is cyclic. Hence, R is commutative; a contradiction.
Subcase 1.2:.
In this case, or 2. If , then . Therefore, and hence . Therefore, R is commutative; a contradiction. If , then . Therefore, and so , a contradiction.
Case 2: and .
By Corollary 2(c), we have or . Hence, or . If , then, as shown in subcase 2.1, we get a contradiction. If then or 2.
Subcase 2.1:.
In this case,
. Therefore,
and so
. Hence,
R is isomorphic to either
or
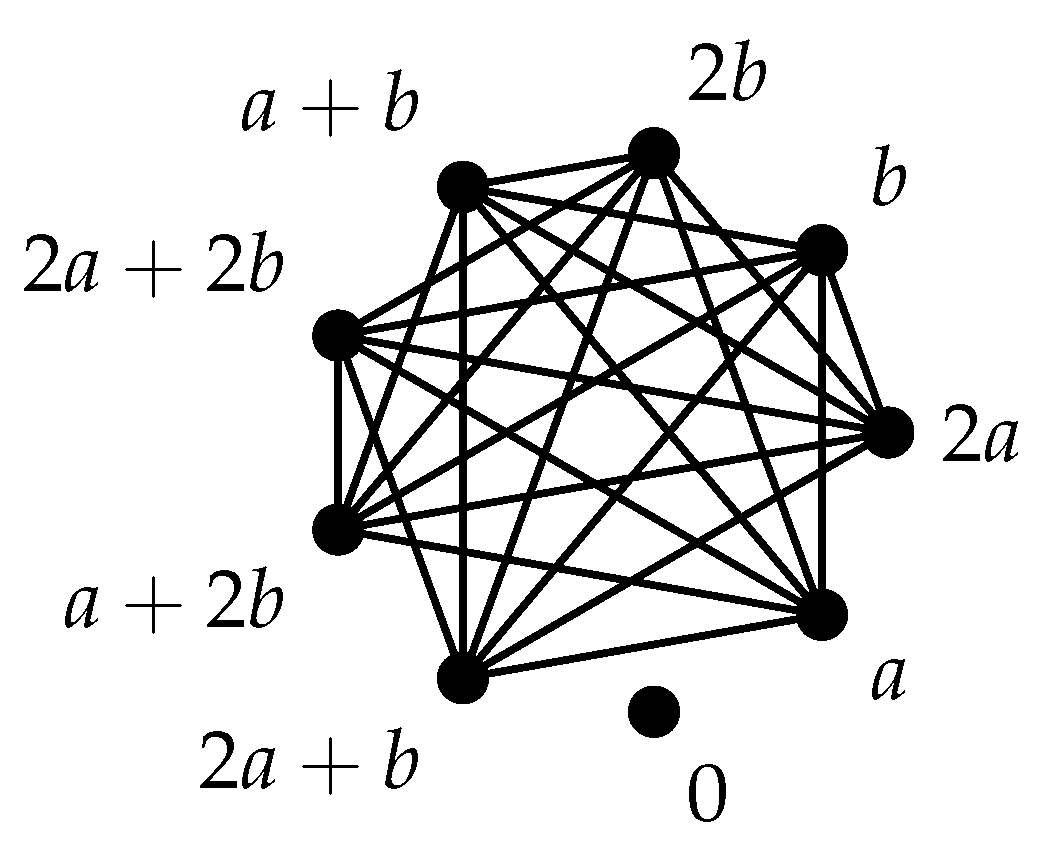
. It follows from
Figure 4 that
, noting that
and
are isomorphic.
Subcase 2.2:.
In this case, . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. Hence, the result follows. □
We have the following corollary to Theorem 2.
Corollary 3. Let R be a noncommutative ring such that . Then
- (a)
is 1-regular if and only if and R is isomorphic to or .
- (b)
The noncommuting graph of R does not have any end vertex. In particular, noncommuting graph of such ring is neither a tree nor a lollipop graph.
Proof. The results follow from Theorem 2; note that any 1-regular graph has end vertices and noncommuting graph of R is the graph . □
Theorem 3. Let R be a noncommutative ring such that . If has a vertex of degree 2 then and is a triangle if and only if R is isomorphic to or .
Proof. Suppose has a vertex x of degree 2. Consider the following cases.
Case 1:.
By Corollary 2(a), we have
. Therefore,
, and hence
. Therefore,
and so
R is isomorphic to
or
. Hence,
is a triangle (as shown in
Figure 1; note that
and
are isomorphic).
Case 2: and .
By Corollary 2(b), we have or . Therefore, or .
Subcase 2.1:.
In this case we have
or 3. If
, then
. As shown in
Figure 2,
is a null graph on three vertices. Therefore, it has no vertex of degree 2, which is a contradiction. If
then
. Therefore,
R is commutative; a contradiction.
Subcase 2.2:.
In this case, or 3. If , then . Therefore, or 4 and hence or 8; a contradiction. If , then . Therefore, and so , which contradicts our assumption.
Case 3: and .
By Corollary 2(c), we have or . Hence, or .
If , then, as shown in Subcase 2.1, we get a contradiction. If , then or 3.
Subcase 3.1:.
In this case, . Therefore, or 4 and hence or 12, which is a contradiction.
Subcase 3.2:.
In this case, . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. Hence, the result follows. □
We have the following corollary to Theorem 3.
Corollary 4. Let R be a noncommutative ring such that . Then
- (a)
is 2-regular if and only if and R is isomorphic to or .
- (b)
The noncommuting graph of R is 2-regular if and only if R is isomorphic to or .
Proof. The results follow from Theorem 3 noting the facts that any 2-regular graph has vertices of degree 2 and noncommuting graph of R is the graph . □
Theorem 4. Let R be a noncommutative ring such that . Then the graph has no vertex of degree 3.
Proof. Suppose has a vertex x of degree 3.
Case 1:.
By Corollary 2(a), we have . Therefore, and hence . Therefore, and hence R is commutative; a contradiction.
Case 2: and .
By Corollary 2(b), we have or . Therefore, or .
Subcase 2.1:.
In this case, we have or 2 or 4. If or 2, then or 6 and hence R is commutative; a contradiction. If , then . Therefore, the additive quotient group is cyclic. Hence, R is commutative; a contradiction.
Subcase 2.2:.
In this case, or 2 or 4. If , then . Therefore, and hence . Therefore, R is commutative; a contradiction. If , then . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. If , then . Therefore, and so ; a contradiction.
Case 3: and .
By Corollary 2(c), we have or . Hence, or .
If , then, as shown in Subcase 2.1, we get a contradiction. If , then or 2 or 4.
Subcase 3.1:.
In this case, . Therefore, then . Therefore, R is commutative; a contradiction.
Subcase 3.2:.
In this case, . Therefore, and so ; a contradiction.
Subcase 3.3:.
In this case, . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. This completes the proof. □
Corollary 5. Let R be a noncommutative ring such that . Then is not 3-regular. In particular, the noncommuting graph of such R is not 3-regular.
Theorem 5. Let R be a noncommutative ring such that . Then has no vertex of degree 4.
Proof. Suppose has a vertex x of degree 4.
Case 1:.
By Corollary 2(a), we have . Therefore, and hence or 4. If , then and hence R is commutative; a contradiction. If , then ; a contradiction.
Case 2: and .
By Corollary 2(b), we have or . Therefore, or .
Subcase 2.1:.
In this case we have or 5. Then or 10 and hence R is commutative; a contradiction.
Subcase 2.2:.
In this case,
or 5. If
, then
. Therefore,
or 3 or 6. If
, then
; a contradiction. If
, then
. It follows from
Figure 4 that
, which is a contradiction. If
, then
; a contradiction. If
, then
. Therefore,
and so
; a contradiction.
Case 3: and .
By Corollary 2(c), we have or . Hence, or .
If , then, as shown in Subcase 2.1, we get a contradiction. If , then or 5.
Subcase 3.1:.
In this case, . Therefore, or 3 or 6. If , then . Therefore R is commutative; a contradiction. If or 6, then or 18; a contradiction.
Subcase 3.2:.
In this case, . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. This completes the proof. □
Corollary 6. Let R be a noncommutative ring such that . Then is not 4-regular. In particular, the noncommuting graph of such R is not 4-regular.
Theorem 6. Let R be a noncommutative ring such that . Then has no vertex of degree 5.
Proof. Suppose has a vertex x of degree 5.
Case 1:.
By Corollary 2(a), we have . Therefore, , and hence . Then and hence R is commutative; a contradiction.
Case 2: and .
By Corollary 2(b), we have or . Therefore, or .
Subcase 2.1:.
In this case we have
or 2 or 3 or 6. If
, then
and hence
R is commutative; a contradiction. If
, then
; a contradiction. If
, then
. It follows from
Figure 4 that
, which is a contradiction. If
, then
. Therefore, the additive quotient group
is cyclic. Hence,
R is commutative; a contradiction.
Subcase 2.2:.
In this case, or 2 or 3 or 6. If , then . Therefore, then , and hence R is commutative; a contradiction. If , then . Therefore, or 8. If , then . Therefore, the additive quotient group is cyclic. Hence, R is commutative; a contradiction. If , then ; a contradiction. If , then . Therefore, , so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. If , then . Therefore, , so ; a contradiction.
Case 3: and .
By Corollary 2(c), we have or . Hence, or .
If , then, as shown in Subcase 2.1, we get a contradiction. If , then or 2 or 3 or 6.
Subcase 3.1:.
Here we have, . Therefore, then and hence R is commutative; a contradiction.
Subcase 3.2:.
In this case, . Therefore, or 8. If or 8, then or 24; a contradiction.
Subcase 3.3:.
In this case, . Therefore, and so ; a contradiction.
Subcase 3.4:.
In this case, . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. This completes the proof. □
Corollary 7. Let R be a noncommutative ring such that . Then is not 5-regular. In particular, the noncommuting graph of this R is not 5-regular.
We conclude this section with the following characterization of R.
Theorem 7. Let R be a noncommutative ring such that , . Then has a vertex of degree 6 if and only if and R is isomorphic to or .
Proof. Suppose has a vertex x of degree 6.
Case 1:.
By Corollary 2(a), we have
. Therefore,
and hence
or 3 or 6. If
, then
; a contradiction. If
, then
. Therefore,
is a 6-regular graph (as shown in
Figure 3). If
, then
; a contradiction.
Case 2: and .
By Corollary 2(b), we have or . Therefore or .
Subcase 2.1:.
In this case we have or 7. If , then ; a contradiction. If , then and hence R is commutative; a contradiction.
Subcase 2.2:.
In this case, or 7. If , then . Therefore, or 4 or 8. If , then . Thus, R is commutative; a contradiction. If or 8, then or 16; which are contradictions. If , then . Therefore, and so ; a contradiction.
Case 3: and .
By Corollary 2(c), we have or . Hence, or .
If , then as shown in Subcase 2.1, we get a contradiction. If , then or 7.
Subcase 3.1:.
In this case, . Therefore, or 4 or 8, and then or 16 or 24; all are contradictions to the order of R.
Subcase 3.2:.
In this case, . Therefore, and so . It follows that the additive quotient group is cyclic. Hence, R is commutative; a contradiction. This completes the proof. □
Corollary 8. Let R be a noncommutative ring such that , . Then is 6-regular if and only if and R is isomorphic to or . In particular, the noncommuting graph of such R is 6-regular if and only if R is isomorphic to or .