About the Normal Projectivity and Injectivity of Krasner Hypermodules

Abstract

Inspired by the concepts of projective and injective modules in classical algebraic structure theory, in this paper we initiate the study of the chains of hypermodules over a Krasner hyperring R, endowing first the set $Ho{m}_R^n(M,N)$ of all normal homomorphisms between two R-hypermodules M and N with a structure of R-hypermodule. Then, our study focuses on the concepts of normal injectivity and projectivity of hypermodules over a Krasner hyperring R, characterizing them by the mean of chains of R-hypermodules.

1. Introduction

Hypercompositional algebra is the modern theory of hypercompositional structures, which are algebraic structures having at least one hyperoperation. The output of a hyperoperation on a set H is not just an element, as the result of classical operation, but a subset of H. The firstly introduced hypercompositional structure was the hypergroup, defined by F. Marty in 1934, as a natural generalization of group, proving that the quotient of a group by any of its subgroups (not necessarily normal) is a hypergroup.

In 1956, Krasner [1] solved a problem in the approximation of a complete valued field by a sequence of such fields by a using a new hypercompositional structure, which he called hyperfield. Many years later, the same Krasner [2] introduced the notion of hyperring, as the hypercompositional structure that we now call Krasner hyperring. In the same paper, he also gave the definition of a hypermodule over a hyperring, now called Krasner hypermodule. The additive part of all these structures is a canonical hypergroup, with many applications in hypercompositional algebra. At the beginning, Krasner hyperrings, hyperfields, and hypermodules were studied by Krasner himself and their students Mittas and Stratigopoulos, mostly for their applications in the classical algebra. The theoretical basis of hypermodules has been settled by Massouros [3], when he gave important examples of hypermodules and introduced free and cyclic hypermodules. In 2008, Anvariyeh et al. [4,5] studied the fundamental relation $\theta$ defined on a hypermodule, in the same way that Vougiouklis [6] defined fundamental relations on hyperrings and Koskas [7] on hypergroups. Details about fundamental relations in hypercompositional structures can be read in [8], while new aspects of this theory are collected in [9,10,11]. The study of the categorial aspects of the theory of Krasner hypermodules was initiated by Madanshekaf [12] and deepened by Shojaei and Ameri [13,14,15]. The latter authors have recently defined [16] several types of projective and injective hypermodules based on different kinds of epimorphisms and monomorphisms that exist in Krasner hypermodule category. We explain them in the next section.

In this paper, we focus our study on a particular type of homomorphisms between hypermodules, called normal homomorphisms, and consequently on the normal projective and normal injective hypermodules. The main aim of the manuscript is to give an equivalent definition of these hypermodules by using exact chains of Krasner hypermodules and normal homomorphisms. This new approach will permit us to also obtain new results in other categories, because the injectivity plays a fundamental role not only in Krasner hypermodule category, but also in other categories. For example, in the category of Boolean algebras, a complete Boolean algebra is injective [17]. In the category of posets, the injective objects are the Dedekind-MacNeille completions [18], while the field of real numbers is injective in the category of Banach spaces.

The rest of the paper is organized as follows. In Section 2, we fix the notation and explain the terminology, as well as we provide the basic definitions and results concerning Krasner hypermodules. Section 3 is dedicated to the study of various chains of Krasner hypermodules. This is based on the family $Ho{m}_R^n(M,N)$ of all normal homomorphisms between two R-hypermodules M and N over a Krasner hyperring R, which we first endow with an R- hypermodule structure. Then we establish a relationship between the exactness of a chain of R-hypermodules and the corresponding chain of the sets of all normal R-homomorphisms obtained by a fixed R-hypermodule. In Section 4, we re-define the normal injective and projective Krasner R-hypermodules by using exact chains of Krasner hypermodules, showing that the new definitions are equivalent to those given in [16]. Moreover, we present a new characterization of normal injective R-hypermodules by considering an arbitrary hyperideal of R as a Krasner hypermodule. Concluding remarks and future works are gathered in the last section of the paper.

2. Preliminaries

Throughout this paper, unless stated otherwise, R denotes a Krasner hyperring, which we call here, for short, hyperring, and ${\mathcal{P}}^{\ast }\left(R\right)$ the family of all non-empty subsets of R.

Definition 1

([1]). A (Krasner) hyperring is a hyperstructure $(R,+,·)$ where

• $(R,+)$ is a canonical hypergroup, i.e.,

  (a)

  $(a,b\in R\Rightarrow a+b\subseteq R),$

  (b)

  $(\forall a,b,c\in R)(a+(b+c)=(a+b)+c),$

  (c)

  $(\forall a,b\in R)(a+b=b+a),$

  (d)

  $(\exists 0\in R)(\forall a\in R)(a+0=\{a\left\}\right),$

  (e)

  $(\forall a\in R)(\exists -a\in R)(0\in a+x\iff x=-a),$

  (f)

  $(\forall a,b,c\in R)(c\in a+b\Rightarrow a\in c+(-b\left)\right).$

• $(R,·)$ is a semigroup with a bilaterally absorbing element 0, i.e.,

  (a)

  $(a,b\in R\Rightarrow a·b\in R),$

  (b)

  $(\forall a,b,c\in R)(a·(b·c)=(a·b)·c),$

  (c)

  $(\forall a\in R)(0·a=a·0=0).$

• The product distributes from both sides over the hyperaddition, i.e.,

  (a)

  $(\forall a,b,c\in R)(a·(b+c)=a·b+a·cand(b+c)·a=b·a+c·a).$

Moreover, a hyperring is called commutative if $(R,·)$ is commutative, i.e.,

4.

$(\forall a,b\in R)(a·b=b·a)$.

Finally, if $(R,·)$ is a monoid, i.e.,

5.

$(\exists 1\in R)(\forall a\in R)(a·1=a=1·a)$, then we say that R is with a unit element, or a unitary hyperring.

Definition 2.

A hyperring homomorphism is a mapping f from a hyperring $(R_1,{+}_{R_1},{·}_{R_1})$ to a hyperring $(R_2,{+}_{R_2},{·}_{R_2})$ with the unit elements $1_{R_1}$ and $1_{R_2}$ such that

• $(\forall a,b\in R_1)(f\left(a{+}_{R_1}b\right)=f\left(a\right){+}_{R_2}f\left(b\right)).$
• $(\forall a,b\in R_1)(f\left(a{·}_{R_1}b\right)=f\left(a\right){·}_{R_2}f\left(b\right)).$
• $f\left(1_{R_1}\right)=1_{R_2}.$

The concept of hypermodule over a Krasner hyperring was introduced by Krasner himself and studied later more in detail for their algebraic properties in [3,19]. In 2016, Shojeai et al. [13] named this hypermodule a Krasner hypermodule and started their categorical study.

Definition 3.

Let R be a hyperring with the unit element 1. A canonical hypergroup $(M,+)$ together with a left external map $R\times M⟶M$ defined by

$$(a,m)\mapsto a·m=am\in M$$

(1)

such that for all $a,b\in R$ and $m_1,m_2\in M$, we have

• $(a+b)m_1=a{m}_1+b{m}_1.$
• $a(m_1+m_2)=a{m}_1+a{m}_2.$
• $\left(ab\right)m_1=a\left(b{m}_1\right).$
• $a{0}_M=0_R{m}_1=0_M$.
• $1m_1=m_1$,

which is called a left Krasner hypermodule over R, or for short, a left R-hypermodule. Similarly, one may define a right R-hypermodule. For simplicity, in this paper, we consider only left R-hypermodules, which we call R-hypermodules.

Definition 4.

A subhypermodule N of Mis a subhypergroup of M that is also closed under multiplication by elements of R.

As already mentioned by Krasner and then very clearly explained by Massouros [3], we may define more types of homomorphisms between R-hypermodules.

Definition 5

([3]). Let M and N be two R-hypermodules. A multivalued function $f:M⟶{\mathcal{P}}^{\ast }\left(N\right)$ is called an R-homomorphism if:

(i)

$(\forall m_1,m_2\in M)(f\left(m_1{+}_M{m}_2\right)\subseteq f\left(m_1\right){+}_{N}f\left(m_2\right)),$

(ii)

$(\forall m\in M)(\forall r\in R)(f\left(r{·}_{M}m\right)=r{·}_{N}f\left(m\right)),$

while f is called strong homomorphism if instead of $\left(i\right)$ we have

(i′)

$(\forall m_1,m_2\in M)(f\left(m_1{+}_M{m}_2\right)=f\left(m_1\right){+}_{N}f\left(m_2\right)).$

A singlevalued function $f:M⟶N$ is called a strict R-homomorphism if the axioms $\left(i\right)$ and $\left(ii\right)$ are valid, and it is called a normal R-homomorphism if $\left(i^{\prime }\right)$ and $\left(ii\right)$ are valid.

Notice that in the more recently published papers [13,14,16], a similar terminology is used, but here we want to keep the original one. This is why the next definitions are slightly changed with respect to their form in [16].

Definition 6.

Let R be a hyperring and M and N be R-hypermodules. The family of all normal R-homomorphisms from M to N is denoted by $Ho{m}_R^n(M,N)$, while the family of all strict homomorphisms from M to N is denoted by $Ho{m}_R(M,N)$.

Definition 7.

Let $f\in Ho{m}_R(M,N)$ (respectively $f\in Ho{m}_R^n(M,N)$). Then, f is called

(i)

a surjective (normal) R-homomorphism if $Im\left(f\right)=N$;

(ii)

an injective (normal) R-homomorphism if for all $m_1,m_2\in M$, $f\left(m_1\right)=f\left(m_2\right)$ implies $m_1=m_2$;

(iii)

(normal) R-isomorphism if it is a bijective (normal) R-homomorphism.

Definition 8.

For a normal homomorphism $f\in Ho{m}_R^n(M,N)$, the set $\{m\in M\mid f(m)=0\}$ is called the kernel of f and denoted by $Ker\left(f\right)$.

Then, it is easy to see that the R-normal homomorphism f is injective if and only if $Ker\left(f\right)=0$, so the zero subhypermodule of M.

Inspired by the similar notions defined in the category of modules, in [16], the authors introduced different types of projectivity and injectivity for Krasner hypermodules. Herein, we recall with our notations those connected with normal R-homomorphisms, consequently called normal projectivity and injectivity, which we will use in Section 4.

Definition 9

([16]). Let R be a hyperring.

(i)

An R-hypermodule P is called normal projective if for every surjective $g\in Ho{m}_R^n(M,N)$ and every $f\in Ho{m}_R^n(P,N)$, there exist $\overline{f}\in Ho{m}_R^n(P,M)$ such that $g\circ \overline{f}=f$.

(ii)

An R-hypermodule E is called normal injective if for every injective $g\in Ho{m}_R^n(M,N)$ and every $f\in Ho{m}_R^n(M,E)$, there exists $\overline{f}\in Ho{m}_R^n(N,E)$ such that $\overline{f}\circ g=f.$

3. Chains of R-Hypermodules

In this section, we first introduce the notion of exact chain of R-hypermodules and normal R-homomorphisms. Then, we prove that the set of all normal R-homomorphisms between two R-hypermodules M and N, denoted by $Ho{m}_R^n(M,N)$, is an R-hypermodule only when R is commutative. Finally, we study the relationship between the exactness of the chains of R-hypermodules and the corresponding sets of all normal R-homomorphisms obtained by a fixed R-hypermodule.

Note that the hyperring R needs not to be a commutative one, unless this is stated.

Proposition 1.

Let R be a hyperring and $f:M⟶M^{\prime }$ an injective normal R-homomorphism. Then, there exists an R-hypermodule $M^{″}$ that is an extension of M (i.e., there exists an inclusion mapping from M to $M^{″}$) and a normal R-isomorphism $g:M^{″}⟶M^{\prime }$ such that for every $m\in M$, $g\left(m\right)=f\left(m\right)$.

Proof. 

Set $N=M^{\prime }\setminus f\left(M\right)$. Define $M^{″}=M\cup N$, and for each $m^{″}\in M^{″}$, consider the map

$$g:M^{″}\to M^{\prime },m^{″}\mapsto \left\{\begin{array}{cc}f\left(m^{″}\right)\hfill & \mathrm{if}{\mathrm{m}}^{″}\in \mathrm{M},\hfill \\ m^{″}\hfill & \mathrm{if}{\mathrm{m}}^{″}\in \mathrm{N}.\hfill \end{array}\right.$$

(2)

Then g is a bijective map and an extension of f, meaning that for every $m\in M$, $g\left(m\right)=f\left(m\right)$.

By the help of g, we show that $M^{″}$ has an R-hypermodule structure. Suppose that $m_1^{″},m_2^{″}\in M^{″}$, and $r\in R$ are arbitrary elements. Then $g\left(m_1^{″}\right),g\left(m_2^{″}\right)\in M^{\prime }$. Since $M^{\prime }$ is an R-hypermodule, it follows that $g\left(m_1^{″}\right)+g\left(m_2^{″}\right)\subseteq M^{\prime }$ and $r·g\left(m_1^{″}\right)\in M^{\prime }$. Now we define

$$m_1^{″}+m_2^{″}=g^{-1}\left(g\left(m_1^{″}\right){+}_{M^{\prime }}g\left(m_2^{″}\right)\right),r·m_1^{″}=g^{-1}\left(r{·}_{M^{\prime }}g\left(m_1^{″}\right)\right)$$

(3)

Using these definitions for + and ·, the set $M^{″}$ has the structure of an R-hypermodule and clearly it is an extension of M.

Furthermore, from (3), we have

$$g(m_1^{″}+m_2^{″})=g\left(g^{-1}\left(g\left(m_1^{″}\right){+}_{M^{\prime }}g\left(m_2^{″}\right)\right)\right)=g\left(m_1^{″}\right)+g\left(m_2^{″}\right),$$

$$g(r·m_1^{″})=g\left(g^{-1}\left(r{·}_{M^{\prime }}g\left(m_1^{″}\right)\right)\right)=r{·}_{M^{\prime }}g\left(m_1^{″}\right).$$

Thus, g is a normal R-homomorphism and a bijective map. Therefore g is a normal R-isomorphism and the proof is complete. □

Definition 10.

Let $M_1$, $M_2$, and $M_3$ be R-hypermodules and consider the following chain of normal R-homomorphisms

$$M_1\stackrel{f}{⟶}{M}_2\stackrel{g}{⟶}{M}_3.$$

(4)

If $Im\left(f\right)\subseteq Ker\left(g\right)$, then the chain in (4) is said to be a zero chain.

Moreover, if $Im\left(f\right)=Ker\left(g\right)$, then the chain in (4) is said to be an exact chain.

Lemma 1.

The chain

$$0⟶M_1\stackrel{f}{⟶}{M}_2$$

(5)

is an exact chain of R-hypermodules if f is an injective normal R-homomorphism, while the chain

$$M_2\stackrel{g}{⟶}{M}_3⟶0$$

(6)

is an exact chain of R-hypermodules if g is a surjective normal R-homomorphism.

Proof. 

The proof is straightforward. □

Based on Lemma 1, the following result is obvious.

Corollary 1.

The chain of R-hypermodules

$$0⟶M_1\stackrel{f}{⟶}{M}_2\stackrel{g}{⟶}{M}_3⟶0$$

(7)

is an exact chain if f is an injective normal R-homomorphism, g is a surjective normal R-homomorphism, and $Im\left(f\right)=Ker\left(g\right)$.

Example 1.

Suppose that M is an R-hypermodule and N is a subhypermodule of M. Then, the following chain

$$0⟶N\stackrel{i}{⟶}M\stackrel{\rho }{⟶}\frac{M}{N}⟶0$$

(8)

is an exact one, where i is the inclusion function and ρ is the projection function, i.e., $\rho \left(m\right)=m+N$.

Example 2.

Let R be a hyperring, M be an R-hypermodule and ${\left\{M_i\right\}}_{i\in I}$ be a family of subhypermodules of M. Then, the sum of this family is denoted by ${\sum }_{i\in I}{M}_i$, and it is the family of the sets ${\sum }_{i\in I}{m}_i$, where for every $i\in I$, $m_i\in M_i$. More specifically,

$$M_1+M_2=\{m_1+m_2\mid m_1\in M_1,m_2\in M_2\},$$

(9)

where $m_1+m_2$ is a set (in particular a subset of M) and not only an element, since + is a hyperoperation on M, while

$$M_1+M_2+M_3=\{m_1+m_2+m_3\mid m_1\in M_1,m_2\in M_2,m_3\in M_3\},$$

where the set $m_1+m_2+m_3$ can be written as the union ${\bigcup }_{m\in m_1+m_2}m+m_3$.

Clearly, the structure ${\sum }_{i\in I}{M}_i$ is a subhypermodule of M, and it is the smallest subhypermodule of M containing every $M_i$. Moreover, the intersection of the family ${\left\{M_i\right\}}_{i\in I}$, denoted by ${\cap }_{i\in I}{M}_i$, is the largest subhypermodule of M, which is contained in every $M_i$.

Suppose now that $M_1$ and $M_2$ are R-hypermodules and $M_1+M_2$ is their sum as defined by (9). Then the following chain

$$0⟶M_1\stackrel{i}{⟶}{M}_1+M_2\stackrel{p}{⟶}{M}_2⟶0$$

(10)

is an exact one, where i is the injection function defined as $i\left(m_1\right)=m_1+0$, i.e., the set containing only the element $m_1$, and p is the projection function, such that $p(m_1+m_2)=m_2$.

In the following, we endow the set $Ho{m}_R^n(M,N)$ of all normal R-homomorphisms between two R-hypermodules M and N with an R-hypermodule structure.

Definition 11.

Let M and N be R-hypermodules. For any two normal R-homomorphisms $f_1,f_2\in Ho{m}_R^n(M,N)$ and $m\in M$, define

$$f_1\oplus f_2=\{g\in Ho{m}_R^n(M,N)\mid g\left(m\right)\in f_1\left(m\right){+}_N{f}_2\left(m\right),\forall m\in M\},$$

(11)

where ${+}_N$ is the hyperaddition on the R-hypermodule N. This means that

$$\oplus :Ho{m}_R^n(M,N)\times Ho{m}_R^n(M,N)⟶{\mathcal{P}}^{\ast }\left(Ho{m}_R^n(M,N)\right),$$

(12)

thus, ⊕ is a hyperoperation on the set $Ho{m}_R^n(M,N)$. Using the associativity, commutativity, and reproduction axiom of the hypergroup $(N,{+}_N)$, we can easily verify that the hypergroupoid ($Ho{m}_R^n(M,N),\oplus$) is a canonical hypergroup.

Remark 1.

The zero mapping $0:M⟶N$ is the identity element of this hypergroup, i.e., for $f\in Ho{m}_R^n(M,N)$, $f\oplus 0=f$. If either $M=0$ or $N=0$, then $Ho{m}_R^n(M,N)$ is a trivial hypergroup and clearly $Ho{m}_R^n(M,N)=0$.

Theorem 1.

Let R be a commutative hyperring and M, N be R-hypermodules. Then, $Ho{m}_R^n(M,N)$ is also an R-hypermodule.

Proof. 

Using Definition 11, it follows that $Ho{m}_R^n(M,N),\oplus )$ is a canonical hypergroup. Now, for any $r\in R$ and $f\in Ho{m}_R^n(M,N)$, define the R-multiplication ⊗ as follows:

$$\otimes :R\times Ho{m}_R^n(M,N)⟶Ho{m}_R^n(M,N)$$

(13)

$$(r\otimes f)\left(m\right)=r{·}_{N}f\left(m\right).$$

Then $r\otimes f\in Ho{m}_R^n(M,N)$ since for $m_1,m_2\in M$, and $s\in R$, we have

(i)

$$\begin{gathered} (r\otimes f)\left(m_1{+}_M{m}_2\right)=r{·}_{N}f(m_1+m_2)=r{·}_N\left(f\left(m_1\right){+}_{N}f\left(m_2\right)\right) \\ =\left(r{·}_{N}f\left(m_1\right)\right){+}_N\left(r{·}_{N}f\left(m_2\right)\right)=(r\otimes f)\left(m_1\right)+(r\otimes f)\left(m_2\right). \end{gathered}$$

(ii)

$$(r\otimes f)\left(s{·}_M{m}_1\right)=r{·}_{N}f\left(s{·}_M{m}_1\right)=r{·}_R\left(s{·}_{N}f\left(m_1\right)\right)=\left(r{·}_{R}s\right){·}_{N}f\left(m_1\right)$$

since R is a commutative hyperring,

$$\left(r{·}_{R}s\right){·}_{N}f\left(m_1\right)=\left(s{·}_{R}r\right){·}_{N}f\left(m_1\right)=s{·}_R\left(r{·}_{N}f\left(m_1\right)\right)=s{·}_R\left((r\otimes f)\left(m_1\right)\right).$$

It remains to prove that $Ho{m}_R^n(M,N)$ is an R-hypermodule. For $r_1,r_2\in R$ and $f_1,f_2\in Ho{m}_R^n(M,N)$, we have the following assertions, for an arbitrary element $m\in M$:

(i)

$$((r_1+r_2)\otimes f_1)\left(m\right)=(r_1+r_2){·}_N{f}_1\left(m\right)=r_1{·}_N{f}_1\left(m\right){+}_N{r}_2{·}_N{f}_1\left(m\right)$$

$$=(r_1\otimes f_1)\left(m\right){+}_N(r_2\otimes f_1)\left(m\right)=\left((r_1\otimes f_1){+}_N(r_2\otimes f_1)\right)\left(m\right).$$

(ii)

$$(r_1\otimes (f_1\oplus f_2))\left(m\right)=\{(r_1\otimes g)\left(m\right)\mid g\in Ho{m}_R^n(M,N),g\left(m\right)\in f_1\left(m\right){+}_N{f}_2\left(m\right)\}$$

$$=\{r_1{·}_{N}g\left(m\right)\mid g\in Ho{m}_R^n(M,N),g\left(m\right)\in f_1\left(m\right){+}_N{f}_2\left(m\right)\}=\left\{r_1{·}_N\left(f_1{+}_N{f}_2\right)\left(m\right)\right\}.$$

Similarly,

$$((r_1\otimes f_1)\oplus (r_1\otimes f_2))\left(m\right)=\{g\in Ho{m}_R^n(M,N)\mid g\left(m\right)\in (r_1\otimes f_1)\left(m\right){+}_N(r_1\otimes f_2)\left(m\right)\}$$

$$=\{g\in Ho{m}_R^n(M,N)\mid g\left(m\right)\in r_1{·}_N{f}_1\left(m\right){+}_N{r}_1{·}_N{f}_2\left(m\right)\}=\left\{r_1{·}_N\left(f_1{+}_N{f}_2\right)\left(m\right)\right\}.$$

Therefore, for $m\in M$,

$$(r_1\otimes (f_1\oplus f_2))\left(m\right)=((r_1\otimes f_1)\oplus (r_1\otimes f_2))\left(m\right).$$

(iii)

$$((r_1·r_2)\otimes f_1)\left(m\right)=(r_1·r_2){·}_N{f}_1\left(m\right)=r_1{·}_N\left(r_2{·}_N{f}_1\left(m\right)\right)=$$

$$=r_1{·}_N(r_2\otimes f_1)\left(m\right)=r_1\otimes (r_2\otimes f_1)\left(m\right).$$

(iv)

For the zero element 0 of $Ho{m}_R^n(M,N)$, there is

$$(r_1\otimes 0)\left(m\right)=r_1{·}_{N}0\left(m\right)=0,(0_R\otimes f_1)\left(m\right)=0{·}_N{f}_1\left(m\right)=0.$$

(v)

Clearly,

$$(1_R\otimes f)\left(m\right)=1_R{·}_{N}f\left(m\right)=f\left(m\right).$$

We can conclude now that $Ho{m}_R^n(M,N)$ is an R-hypermodule. □

Suppose that R is a hyperring and M is an R-hypermodule. Every element of the R-hypermodule $Ho{m}_R^n(M,N)$ is called a normal R-endomorphism of M and it is a normal R-homomorphism from M into itself. Accordingly, we denote $Ho{m}_R^n(M,M)$ by $En{d}_R\left(M\right)$. For an arbitrary element $m\in M$ and $f_1,f_2\in En{d}_R\left(M\right)$, define the multiplication on $En{d}_R\left(M\right)$ by

$$(f_1·f_2)\left(m\right)=f_1\left(f_2\left(m\right)\right).$$

(14)

With this operation, we endow $En{d}_R\left(M\right)$ with a hyperring structure, as explained in the following result.

Lemma 2.

Let R be a commutative hyperring and M be an R-hypermodule. Then, $En{d}_R\left(M\right)$ is a hyperring with the hyperoperation ⊕ defined in (11) and the operation · defined by (14).

Proof. 

Using Definition 11, it follows that $(En{d}_R\left(M\right),\oplus )$ is a commutative hypergroup. It is a routine to check that the multiplication operation is associative and distributive over the hyperoperation ⊕. Additionally, the hyperring $En{d}_R\left(M\right)$ has a unit element. This is the identity mapping $I:M⟶M$. □

Definition 12.

$En{d}_R\left(M\right)$ is called the hyperring of R-endomorphisms of M.

We shall now define a normal R-homomorphism between two R-hyper-modules $Ho{m}_R^n(M,N_1)$ and $Ho{m}_R^n(M,N_2)$. Thus, let $N_1$, $N_2$ and M be R-hypermodules and $f:N_1⟶N_2$ be a normal R-homomorphism. Define the map F as follows:

$$F:Ho{m}_R^n(M,N_1)⟶Ho{m}_R^n(M,N_2),F\left(g\right)=fg,foranyg\in Ho{m}_R^n(M,N_1)$$

where $fg\in Ho{m}_R^n(M,N_2)$ is defined by $fg\left(m\right)=f\left(g\right(m\left)\right)$ for any $m\in M$. Since R is a commutative hyperring, using Theorem 1, we conclude that $Ho{m}_R^n(M,N_1)$ and $Ho{m}_R^n(M,N_2)$ are R-hypermodules. In addition, we get

$$F(g_1\oplus g_2)=F\left(\{g\in Ho{m}_R^n(M,N_1)\mid g\left(m\right)\in g_1\left(m\right){+}_{N_1}{g}_2\left(m\right),\forall m\in M\}\right)=$$

$$\{F\left(g\right)\mid g\in Ho{m}_R^n(M,N_1),g\left(m\right)\in g_1\left(m\right){+}_{N_1}{g}_2\left(m\right),\forall m\in M\}=$$

$$\{fg\mid g\in Ho{m}_R^n(M,N_1),g\left(m\right)\in g_1\left(m\right){+}_{N_1}{g}_2\left(m\right),\forall m\in M\}.$$

When $g\left(m\right)\in g_1\left(m\right)+g_2\left(m\right)$, we conclude that for any $m\in M$, there is

$$fg\left(m\right)=f\left(g\left(m\right)\right)\in f\left(g_1\left(m\right){+}_{N_1}{g}_2\left(m\right)\right)=f\left(g_1\left(m\right)\right){+}_{N_2}f\left(g_2\left(m\right)\right)=$$

$$f{g}_1\left(m\right){+}_{N_2}f{g}_2\left(m\right)=\left(F\left(g_1\right){+}_{N_2}F\left(g_2\right)\right)\left(m\right).$$

Thus, we have,

$$F(g_1\oplus g_2)=\{fg\mid g\in Ho{m}_R^n(M,N_1),g\left(m\right)\in g_1\left(m\right){+}_{N_1}{g}_2\left(m\right),\forall m\in M\}=$$

$$\{fg\mid g\in Ho{m}_R^n(M,N_1),fg\left(m\right)\in F\left(g_1\right)\left(m\right){+}_{N_2}F\left(g_2\right)\left(m\right),\forall m\in M\}=F\left(g_1\right)\oplus F\left(g_2\right).$$

Clearly, for any $r\in R$, $F(r\otimes g_1)=r\otimes F\left(g_1\right)$. Therefore, F is a normal R-homomorphism.

The next step in our study is to define chains of R-hypermodules of normal R-homomorphisms. Therefore, from the chain of R-hypermodules $N_1,N_2$, $N_3$, and normal R-homomorphisms f and g

$$0⟶N_1\stackrel{f}{⟶}{N}_2\stackrel{g}{⟶}{N}_3,$$

(15)

we can derive the following chain of R-hypermodules and normal R-homomorphisms F and G

$$0⟶Ho{m}_R^n(M,N_1)\stackrel{F}{⟶}Ho{m}_R^n(M,N_2)\stackrel{G}{⟶}Ho{m}_R^n(M,N_3),$$

(16)

where for every $\varphi \in Ho{m}_R^n(M,N_1)$, we have $F\left(\varphi \right)=f\varphi$ and for every $\psi \in Ho{m}_R^n(M,N_2)$, it holds that $G\left(\psi \right)=g\psi$.

The next result states a relationship between the exactness of the chains defined in (15) and (16).

Proposition 2.

If the chain defined by (15) is an exact one, then the chain in (16) is exact, too.

Proof. 

Suppose that the chain defined by (15) is exact. Then, using Lemma 1, it follows that $Im\left(f\right)=Ker\left(g\right)$ and f is a normal monomorphism. In order to show that the chain in (16) is exact, it is enough to prove that the homomorphism F is a normal monomorphism (i.e., $Ker\left(F\right)=0$) and then that $Ker\left(G\right)=Im\left(F\right)$.

Suppose that $\varphi \in Ho{m}_R^n(M,N_1)$ such that $F\left(\varphi \right)=0$, i.e., $\varphi \in Ker\left(F\right)$. Then $f\varphi =0$,meaning that that, for any element $m\in M$, $f\left(\varphi \right(m\left)\right)=0$. Since the chain defined in (15) is exact, the results show that f is a normal monomorphism, so $Ker\left(f\right)=0$ and then $\varphi \left(m\right)=0$, for every element $m\in M$. Thereby, $\varphi =0$ and thus F is a normal monomorphism.

Let us prove now that $Ker\left(G\right)=Im\left(F\right)$. Take $\psi \in Ker\left(G\right)$. Then $G\left(\psi \right)=0$ and $\psi :M⟶N_2$. So, for every $m\in M$, we have $G\left(\psi \right(m\left)\right)=g\psi \left(m\right)=0$. Thus, $\psi \left(m\right)\in Ker\left(g\right)=Im\left(f\right)$. Hence, there exists $n_1\in N_1$ such that $f\left(n_1\right)=\psi \left(m\right)$. Since f is a normal monomorphism, it follows that there is only one $n_1\in N_1$ with the property that $f\left(n_1\right)=\psi \left(m\right)$. Now define $\varphi :M⟶N_1$ such that $\varphi \left(m\right)=n_1$. Clearly, $\varphi$ is a normal homomorphism, i.e., $\varphi \in Ho{m}_R^n(M,N_1)$. Then for any element $m\in M$,

$$F\left(\varphi \left(m\right)\right)=f\varphi \left(m\right)=f\left(\varphi \left(m\right)\right)=f\left(n_1\right)=\psi \left(m\right).$$

Thus, $\psi \in Im\left(F\right)$. Hence, $Ker\left(G\right)\subseteq Im\left(F\right)$.

Conversely, suppose that $\psi \in Im\left(F\right)$. Then there exists $\varphi \in Ho{m}_R^n(M,N_1)$ such that $F\left(\varphi \right)=\psi$. Hence, $f\varphi =\psi$. Now consider $G\left(\psi \right)=G\left(f\varphi \right)=gf\varphi$, and since the chain in (15) is exact, it follows that $G\left(\psi \right)=0$ and $\psi \in Ker\left(G\right)$. This implies that the chain defined by (16) is exact as well. □

We continue by defining another type of chains of R-hypermodules. Suppose that $M_1$, $M_2$, and N are R-hypermodules and $\gamma :M_1⟶M_2$ is a normal R-homomorphism. Define the map $\Gamma$ as follows:

$$\Gamma :Ho{m}_R^n(M_2,N)⟶Ho{m}_R^n(M_1,N),\Gamma \left(h\right)=h\gamma ,\forall h\in Ho{m}_R^n(M_2,N),$$

where $h\gamma \in Ho{m}_R^n(M_1,N)$ and for $m_1\in M_1$, $h\gamma \left(m_1\right)=h\left(\gamma \left(m_1\right)\right)$. Since R is a commutative hyperring, using Theorem 1, it follows that $Ho{m}_R^n(M_1,N)$ and $Ho{m}_R^n(M_2,N)$ are hypermodules and $\Gamma$ is a normal homomorphism.

Now consider the following chain of R-hypermodules $M_1$, $M_2$ and $M_3$, and normal R-homomorphisms $\gamma$ and $\delta$,

$$M_1\stackrel{\gamma }{⟶}{M}_2\stackrel{\delta }{⟶}{M}_3⟶0.$$

(17)

From this chain and based on the above discussion, we can derive the following chain of R-hypermodules and normal R-homomorphisms:

$$0⟶Ho{m}_R^n(M_3,N)\stackrel{\Delta }{⟶}Ho{m}_R^n(M_2,N)\stackrel{\Gamma }{⟶}Ho{m}_R^n(M_1,N),$$

(18)

where for every $k\in Ho{m}_R^n(M_3,N)$, $\Delta \left(k\right)=k\delta$ and for every $h\in Ho{m}_R^n(M_2,N)$, $\Gamma \left(h\right)=h\gamma$.

Similarly to Proposition 2, we obtain the following result.

Proposition 3.

If the chain defined by (17) is exact, then the chain in (18) is also exact.

Proof. 

Suppose that the chain defined by (17) is exact. Then, by Lemma 1, the results show that $Im\left(\gamma \right)=Ker\left(\delta \right)$ and $\delta$ is a surjective normal R-homomorphism.

Let k be an arbitrary element in $Ho{m}_R^n(M_3,N)$ and $\Delta \left(k\right)=0$. Then $k\delta =0$. Now suppose that $m_3\in M_3$ is an arbitrary element. Since $\delta$ is a surjective normal R-homomorphism, there exists $m_2\in M_2$ such that $\delta \left(m_2\right)=m_3$. Hence, $k\left(\delta \left(m_2\right)\right)=k\left(m_3\right)=0$. Thus, for every element $m_3\in M_3$, we have $k\left(m_3\right)=0$, which means that $k=0$ and $\Delta$ is an injective normal R-homomorphism.

Suppose that $h\in Ker(\Gamma )$. Then $\Gamma \left(h\right)=h\gamma =0$. We should find $k\in Ho{m}_R^n(M_3,N)$ such that $\Delta \left(k\right)=k\delta =h$. Suppose that $m_3\in M_3$ is an arbitrary element. Then, since $\delta$ is a normal R-homomorphism, there exists $m_2\in M_2$ such that $\delta \left(m_2\right)=m_3$. Now, define k as follows:

$$k:M_3⟶N,k\left(m_3\right)=h\left(m_2\right).$$

(19)

Then clearly $k\in Ho{m}_R^n(M_3,N)$, and for any element $m_2\in M_2$ we have

$$\Delta \left(k\right)\left(m_2\right)=k\delta \left(m_2\right)=k\left(\delta \left(m_2\right)\right)=k\left(m_3\right)=h\left(m_2\right).$$

Thus, $\Delta \left(k\right)=h$.

It remains to show that the function in (19) is well defined. For doing this, suppose that $\delta \left(m_2\right)=m_3$ and $\delta \left(m_2^{\prime }\right)=m_3$. Then

$$\delta \left(m_2\right)-\delta \left(m_2^{\prime }\right)=\delta (m_2-m_2^{\prime })=m_3-m_3.$$

We know that $0_{M_3}\in m_3-m_3$. Thus, $0_{M_3}\in \delta (m_2-m_2^{\prime })$. Therefore, there exists $m\in m_2-m_2^{\prime }$ such that $\delta \left(m\right)=0_{M_3}$. Therefore, $m\in ker\left(\delta \right)=Im\left(\gamma \right)$ and thus there exists $m_1\in M_1$ such that $\gamma \left(m_1\right)=m$. Hence,

$$0_N=h\left(\gamma \left(m_1\right)\right)=h\left(m\right)\in h(m_2-m_2^{\prime })=h\left(m_2\right)-h\left(m_2^{\prime }\right).$$

Therefore, $0\in h\left(m_2\right)-h\left(m_2^{\prime }\right)$, and since $(N,+)$ is a canonical hypergroup, using Definition 1 part (e) of 1, we conclude that $h\left(m_2\right)=h\left(m_2^{\prime }\right)$. Therefore, the relation (19) is well defined and $\Delta \left(k\right)=h$. This means that $h\in Im(\Delta )$ and $Ker(\Gamma )\subseteq Im(\Delta )$.

Now we have to prove that $Im(\Delta )\subseteq Ker(\Gamma )$. Suppose that $h\in Im(\Delta )$. Then, there exists $k\in Ho{m}_R^n(M_3,N)$ such that $\Delta \left(k\right)=k\delta =h$. So, for $m_1\in M_1$ we have

$$\Gamma \left(h\right)\left(m_1\right)=\Gamma \left(k\delta \right)\left(m_1\right)=\left(k\delta \gamma \right)\left(m_1\right)=k\left(\delta \left(\gamma \left(m_1\right)\right)\right)=0.$$

The last equation follows because the chain in (17) is exact and so $Im\left(\gamma \right)=Ker\left(\delta \right)$. Thus, $h\in Ker(\Gamma )$. Therefore,

$$Im(\Delta )=Ker(\Gamma )$$

and the chain defined in (18) is exact as requested. □

4. Normal Injective and Projective R-Hypermodules

The aim of this section is to provide an alternative definition of the normal injective and projective R-hypermodules introduced in [16], based on the notion of exact chains, which will permit us to better understand their relationships with the hyperring R and the hyperideals of R.

Consider the chain

$$0⟶N_1\stackrel{f}{⟶}{N}_2\stackrel{g}{⟶}{N}_3$$

of R-hypermodules $N_1,N_2$, $N_3$ and normal R-homomorphisms f and g. In Proposition 2, we proved that the exactness of the above chain implies the exactness of the following chain

$$0⟶Ho{m}_R^n(M,N_1)\stackrel{F}{⟶}Ho{m}_R^n(M,N_2)\stackrel{G}{⟶}Ho{m}_R^n(M,N_3).$$

It is worth noticing that, generally, the exactness of the chain of R-hypermodules $N_2$ and $N_3$

$$N_2⟶N_3⟶0$$

(20)

does not imply the exactness of the chain

$$Ho{m}_R^n(M,N_2)⟶Ho{m}_R^n(M,N_3)⟶0.$$

(21)

In order to give a positive answer to this general problem, we introduce a particular class of R-hypermodules.

Definition 13.

Let R be a hyperring and M be an R-hypermodule. If the exactness of the chain defined by (20), for two arbitrary R-hypermodules $N_1$ and $N_2$, implies the exactness of the chain defined in (21), then the R-hypermodule M is called a normal projective R-hypermodule.

Similarly, a dual concept can be defined, by reversing all the arrows. Consider the chain

$$M_1\stackrel{\gamma }{⟶}{M}_2\stackrel{\delta }{⟶}{M}_3⟶0$$

of R-hypermodules $M_1,M_2$, $M_3$, and normal R-homomorphisms $\gamma$ and $\delta$. According to Proposition 3, the exactness of the above chain implies the exactness of the following chain

$$0⟶Ho{m}_R^n(M_3,N)\stackrel{\Delta }{⟶}Ho{m}_R^n(M_2,N)\stackrel{\Gamma }{⟶}Ho{m}_R^n(M_1,N),$$

while generally, the exactness of the chain

$$0⟶M_1⟶M_2$$

(22)

of R-hypermodules $M_1$ and $M_2$ does not imply the exactness of the chain

$$Ho{m}_R^n(M_2,N)⟶Ho{m}_R^n(M_1,N)⟶0.$$

(23)

Definition 14.

Let R be a hyperring and N be an R-hypermodule. If the exactness of the chain defined in (22) for any R-hypermodules $M_1$ and $M_2$ implies the exactness of the chain defined in (23), then the R-hypermodule N is called a normal injective R-hypermodule.

The notions of normal injective and projective R-hypermodules have been recently introduced in [16], as we recalled them in Definition 9. Here, we re-define them by the mean of exact chains of R-hypermodules and we show that these definitions are equivalent.

Theorem 2.

Let R be a hyperring and N be an R-hypermodule. Then, the following statements are equivalent:

(i)

For any exact chain

$$0⟶M_1\stackrel{\gamma }{⟶}{M}_2\stackrel{\delta }{⟶}{M}_3⟶0$$

(24)

of R-hypermodules and normal R-homomorphisms, the chain

$$0⟶Ho{m}_R^n(M_3,N)\stackrel{\Delta }{⟶}Ho{m}_R^n(M_2,N)\stackrel{\Gamma }{⟶}Ho{m}_R^n(M_1,N)⟶0$$

(25)

is also exact.

(ii)

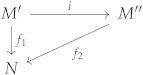
For any R-hypermodules $M_1,M_2,N$, and normal R-homomorphisms $\gamma :M_1⟶M_2$ and $k:M_1⟶N$ such that the chain $0⟶M_1\stackrel{\gamma }{⟶}{M}_2$ is exact, there exists a normal R-homomorphism $h:M_2⟶N$ such that the diagram in Figure 1 has the composition structure, i.e., $h\gamma =k$.

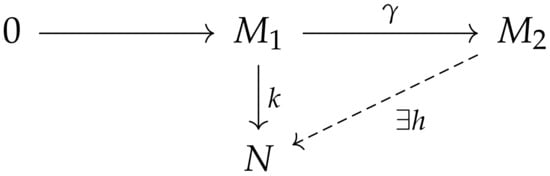Figure 1. Composition structure of a diagram for a normal injective R-hypermodule.

Proof. 

Suppose that assertion $\left(i\right)$ holds. Using Proposition 3 and Definition 14, we conclude that assertion $\left(i\right)$ is equivalent to the fact that, if the chain

$$0⟶M_1\stackrel{\gamma }{⟶}{M}_2$$

is exact, then the chain

$$Ho{m}_R^n(M_2,N)\stackrel{\Gamma }{⟶}Ho{m}_R^n(M_1,N)⟶0$$

(26)

is exact too, where the mapping $\Gamma$ is defined as follows

$$\forall h\in Ho{m}_R^n(M_2,N),\Gamma \left(h\right)=h\gamma .$$

Since the chain (24) is exact, we have

$$Im(\Gamma )=Ho{m}_R^n(M_1,N).$$

This means that if we have the diagram in Figure 1 with the exact row and $k\in Ho{m}_R^n(M_1,N)$; then, there exists $h\in Ho{m}_R^n(M_2,N)$ such that

$$\Gamma \left(h\right)=h\gamma =k,$$

equivalently, the diagram has the composition structure.

Now suppose that assertion $\left(ii\right)$ holds. Since $k:M_1⟶N$ is an arbitrary element of $Ho{m}_R^n(M_1,N)$, we conclude that for any $k\in Ho{m}_R^n(M_1,N)$, if the chain $0⟶M_1\stackrel{\gamma }{⟶}{M}_2$ is exact, then there exists $h\in Ho{m}_R^n(M_2,N)$ such that $\Gamma \left(h\right)=k$. This means that the normal R-homomorphism

$$\Gamma :Ho{m}_R^n(M_2,N)⟶Ho{m}_R^n(M_1,N)$$

is surjective, and thus, using Proposition 3, assertion $\left(i\right)$ also holds. □

Remark 2.

By Lemma 1, it follows that assertion $\left(ii\right)$ in Theorem 2 is equivalent with the definition of normal injectivity introduced in [16] (and recalled here in Definition 9), while assertion $\left(i\right)$ is equivalent with the same notion introduced in Definition 14. Therefore, we say that an R-hypermodule N is normal injective if it satisfies the equivalent conditions $\left(i\right)$ and $\left(ii\right)$ in Theorem 2.

We may provide a similar characterization for normal projective R-hypermodules.

Theorem 3.

Let R be a hyperring and M be an R-hypermodule. Then, the following statements are equivalent:

(i)

For any exact chain

$$0⟶N_1\stackrel{f}{⟶}{N}_2\stackrel{g}{⟶}{N}_3⟶0$$

of R-hypermodules and normal R-homomorphisms, the chain

$$0⟶Ho{m}_R^n(M,N_1)\stackrel{F}{⟶}Ho{m}_R^n(M,N_2)\stackrel{G}{⟶}Ho{m}_R^n(M,N_3)⟶0$$

is also exact.

(ii)

For any R-hypermodules $N_2,N_3,M$ and normal R-homomorphisms $g:N_2⟶N_3$ and $\phi :M⟶N_3$ such that the chain $N_2\stackrel{g}{⟶}{N}_3⟶0$ is exact, there exists a normal R-homomorphism $\psi :M⟶N_2$ such that the diagram in Figure 2 has the composition structure, i.e., $g\psi =\phi$.

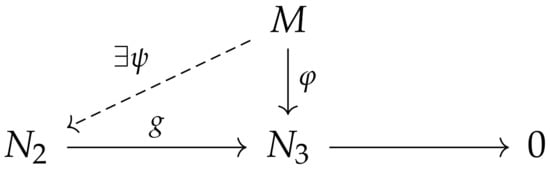Figure 2. Composition structure of a diagram for a normal projective R-hypermodule.

Proof. 

Similar to the proof of Theorem 2. □

Remark 3.

An R-hypermodule M is called normal projective if it satisfies the equivalent conditions $\left(i\right)$ and $\left(ii\right)$ of Theorem 3, where the first one is equivalent with the notion defined in Definition 13, while the second one is exactly the definition given in [16] (see Definition 9).

We conclude this section with a different characterization of normal injective R-hypermodules. One of the most commonly used equivalents of the axiom of choice is Zorn’s lemma. For a partially ordered set (also called a poset) P, a $chain$ in P is a nonempty subset S of P such that S is totally ordered, meaning that any two elements of S are comparable.

Lemma 3.

(Zorn’s lemma) If a poset P has the property that every chain in P has an upper bound, then P has a maximal element.

Based on Zorn’s lemma, the following theorem provides another equivalent definition of a normal injective R-hypermodule by considering R and an arbitrary hyperideal I of R as R-hypermodules (for further details, refer to [11]).

Theorem 4.

Let R be a hyperring and N be an R-hypermodule. Then, the following statements are equivalent:

(1)

N is a normal injective R-hypermodule.

(2)

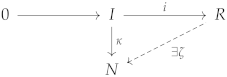
For any hyperideal I of R, an inclusion hyperring homomorphism $i:I⟶R$, and a normal R-homomorphism $k:I⟶N$, there exists a normal R-homomorphism $h:R⟶N$ such that the diagram in Figure 3 has the composition structure, i.e., $hi=k$.

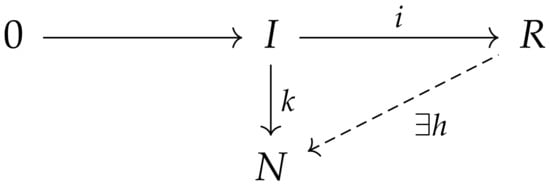Figure 3. Composition structure of a diagram for a normal injective R-hypermodule using hyperideals.

Proof.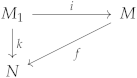 

Using Remark 2, it is enough to show that the assertion $\left(ii\right)$ in Theorem 2 and the statement $\left(2\right)$ of this theorem are equivalent.

Assume that N is a normal injective R-hypermodule. Thus, the assertion $\left(ii\right)$ in Theorem 2 holds. Since the hyperideal I can be considered as an R-hypermodule, statement $\left(2\right)$ is also true.

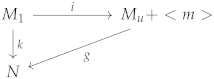
Now suppose that statement $\left(2\right)$ holds. Moreover, let $M_1$, $M_2$ and N be arbitrary R-hypermodules and $\gamma :M_1⟶M_2$ and $k:M_1⟶N$ be normal R-homomorphisms such that the chain $0⟶M_1\stackrel{\gamma }{⟶}{M}_2$ is exact. Denote by ∑ the set of all pairs $(M,f)$, where M is an R-hypermodule that contains $M_1$ and has the property that there exists an injective normal R-homomorphism from M to $M_2$ and $f:M⟶N$ is a normal R-homomorphism such that the following diagram has the composition structure, i.e., $fi=k$:

Then, ∑ is not empty, because $(M_1,k)\in \sum$. Define an order ≤ on ∑ such that $(M^{\prime },f_1)\le (M^{″},f_2)$ if and only if $M^{\prime }$ is a subhypermodule of $M^{″}$ and $f_2$ is an extension of $f_1$. This means that following diagram has the composition structure, i.e., $f_{2}i=f_1$.

Then $(\sum ,\le )$ is a partially ordered set. Suppose that ${\{M_i,f_i\}}_{i\in I}$ is a totally ordered subset of ∑. Let $\check{M}={\cup }_{i\in I}{M}_i$ and define $\check{f}:\check{M}⟶N$ by $\check{f}\left(\check{m}\right)=f_i\left(\check{m}\right)$, where $\check{m}\in M_i$. Clearly, $\{\check{M},\check{f}\}\in \sum$ and it is an upper bound for an arbitrary chain ${\{M_i,f_i\}}_{i\in I}$. Thus, using Lemma 3, we conclude that ∑ has a maximal element $(M_u,f_u)$. Now it is enough to show that $M_u=M_2$.

If $M_u\ne M_2$, then there is an element m such that $m\in M_2$ and $m\notin M_u$. Consider I the set of all elements $r\in R$ such that $r·m\in M_u$, i.e., $I=\{r\in R\mid r·m\in M_u\}.$ By a routine verification, we can check that I is a hyperideal. Now, define $\kappa :I⟶N$ such that for $r\in I$, $\kappa \left(r\right)=f_u(r·m).$ Then $\kappa$ is a normal R-homomorphism of R-hypermodules because, for $j_1,j_2\in I$ and $s\in R$, we have

$$\kappa (j_1+j_2)=f_u((j_1+j_2)·m)=f_u(j_1·m+j_2·m)=f_u(j_1·m)+f_u(j_2·m)=\kappa \left(j_1\right)+\kappa \left(j_2\right)$$

and

$$\kappa (s·j_1)=f_u((s·j_1)·m)=f_u(s·(j_1·m))=s·f_u(j_1·m)=s·\kappa \left(j_1\right).$$

By statement $\left(2\right)$, there exists a normal R-homomorphism $\zeta :R⟶N$ such that the following diagram has the composition structure, i.e., $\zeta i=\kappa$.

Consider the R-hypermodule $M_u+<m>$ and define the normal R-homomorphism $g:M_u+<m>⟶N$ such that, for $m_u\in M_u$ and $r\in R$,

$$g(m_u+r·m)=f_u\left(m_u\right)+\zeta \left(r\right).$$

Since $M_u\in \sum$, we conclude that $M_1\subseteq M_u+<m>$ and there exists an injective normal R-homomorphism from $M_u+<m>$ to $M_2$. Moreover, for $m_1\in M_1$

$$gi\left(m_1\right)=g\left(i\left(m_1\right)\right)=g(m_1+0·m)=f_u\left(m_1\right)+\zeta \left(0\right)=$$

$$f_u\left(m_1\right)+0_N=f_u\left(m_1\right)=f_u\left(i\left(m_1\right)\right)=f_{u}i\left(m_1\right)=k\left(m_1\right).$$

Thus, $gi=k$. Therefore, we have the following diagram with the composition structure.

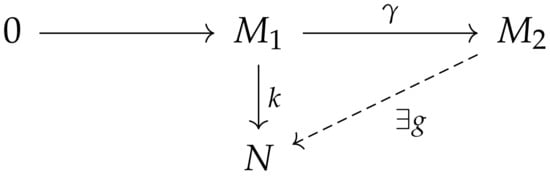
This means that $(M_u+<m>,g)\in \sum$, which is a contradiction because $(M_u,f_u)$ is the maximal element of ∑. So, $M_u=M_2$. Hence, we proved that $M_u+<m>=M_2$ and there exists the function $g:M_2⟶N$ such that the diagram in Figure 4 has a compositional structure.

Figure 4. The diagram for a normal injective R-hypermodule.

Using Theorem 2, we conclude that N is a normal injective R-hypermodule. □

Finally, we may summarize the characterization of a normal injective R-hypermodule as follows.

Theorem 5.

An R-hypermodule N is normal injective if it satisfies the following equivalent conditions.

(i)

For any exact chain

$$0⟶M_1\stackrel{\gamma }{⟶}{M}_2\stackrel{\delta }{⟶}{M}_3⟶0$$

(27)

of R-hypermodules and normal R-homomorphisms, the chain

$$0⟶Ho{m}_R^n(M_3,N)\stackrel{\Delta }{⟶}Ho{m}_R^n(M_2,N)\stackrel{\Gamma }{⟶}Ho{m}_R^n(M_1,N)⟶0$$

(28)

is also exact.

(ii)

For any R-hypermodules $M_1,M_2,N$, and normal R-homomorphisms $\gamma :M_1⟶M_2$ and $k:M_1⟶N$ such that the chain $0⟶M_1\stackrel{\gamma }{⟶}{M}_2$ is exact, there exists a normal R-homomorphism $h:M_2⟶N$ such that $h\gamma =k$.

(iii)

For any hyperideal I of R, any inclusion hyperring homomorphism $i:I⟶R$, and normal R-homomorphism $k:I⟶N$, there exists a normal R-homomorphism $h:R⟶N$ such that $hi=k$.

5. Conclusions and Future Work

In this article, we have studied the structure of the set of all normal R-homomorphisms between two arbitrary R-hypermodules M and N, namely $Ho{m}_R^n(M,N)$, and proved that it is an R-hypermodule when R is a commutative hyperring. After investigating the main properties of the R-hypermodule $Ho{m}_R^n(M,N)$, we proposed an alternative definition for the normal projective and injective R-hypermodules based on the notion of exact chains of R-hypermodules, and then involving also hyperideals of R.

In future work, we intend to apply these results to obtain new algebraic properties of normal injective and projective R-hypermodules, for example, those related to their sum and intersection as defined in Example 2. It is interesting to find out if they keep the property of normal injectivity and projectivity.