Simulink Implementation of a Hydrologic Model: A Tank Model Case Study
Abstract
1. Introduction
2. Materials and Methods
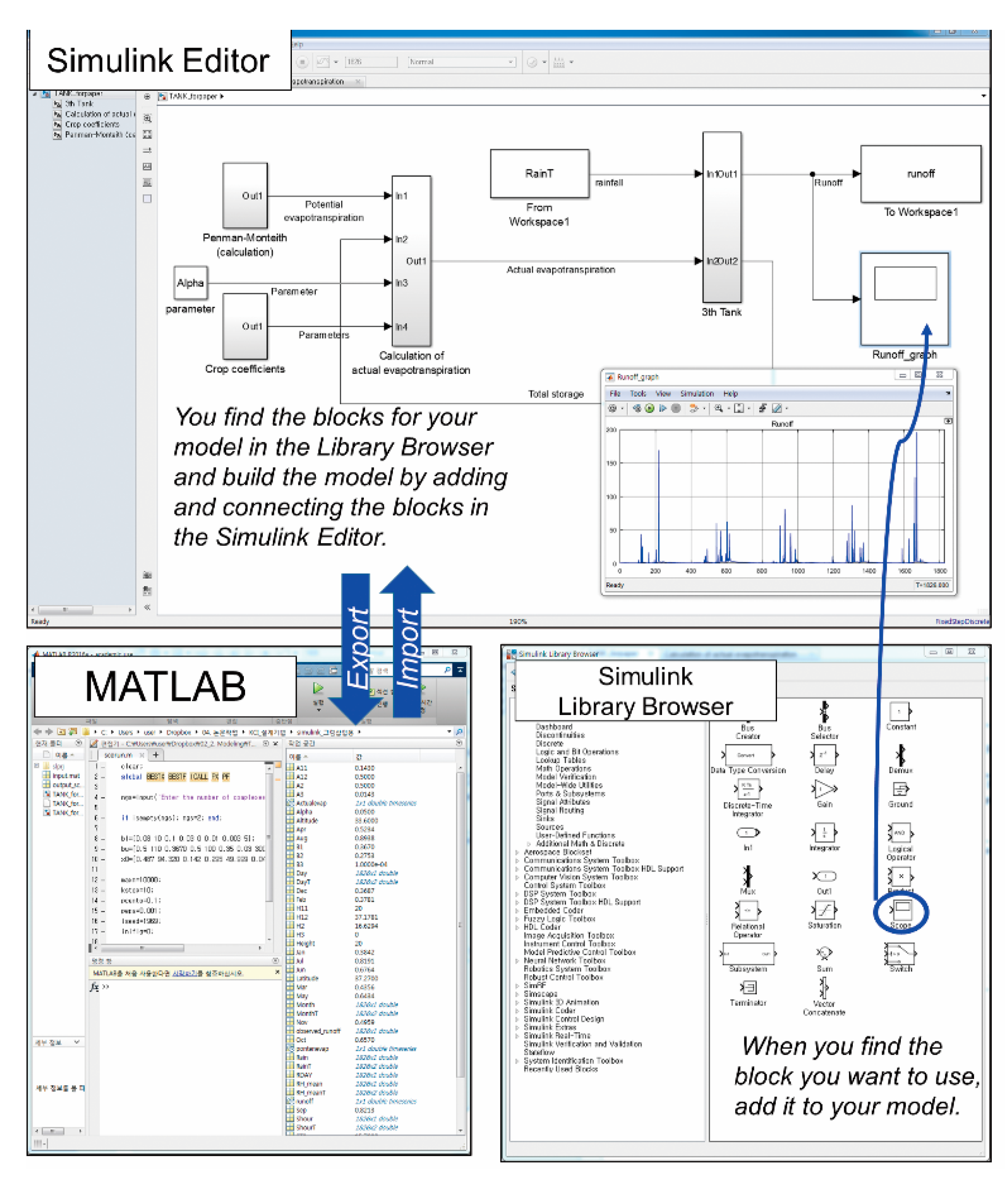
2.1. Simulink Modeling Framework
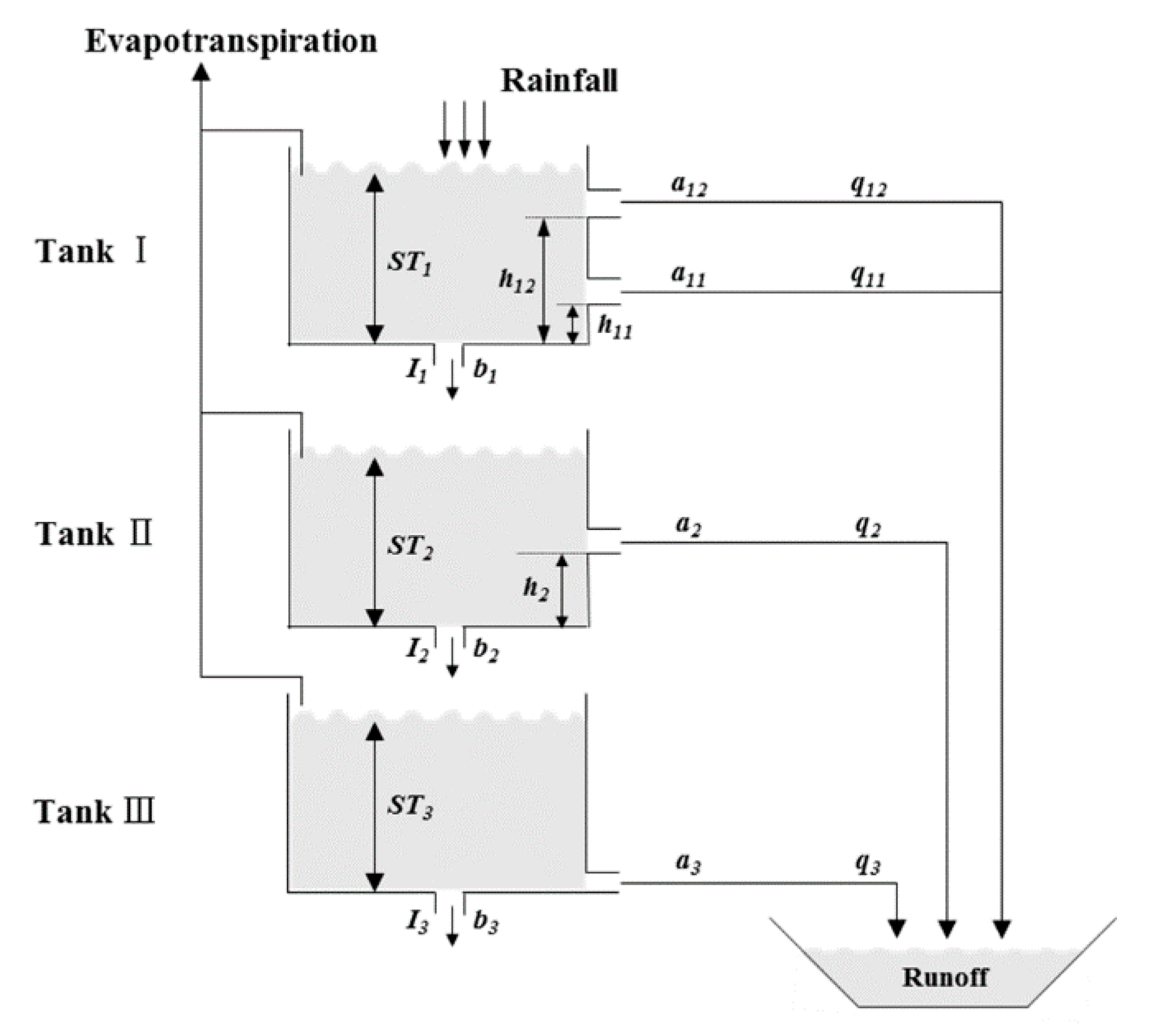
2.2. The Tank Model
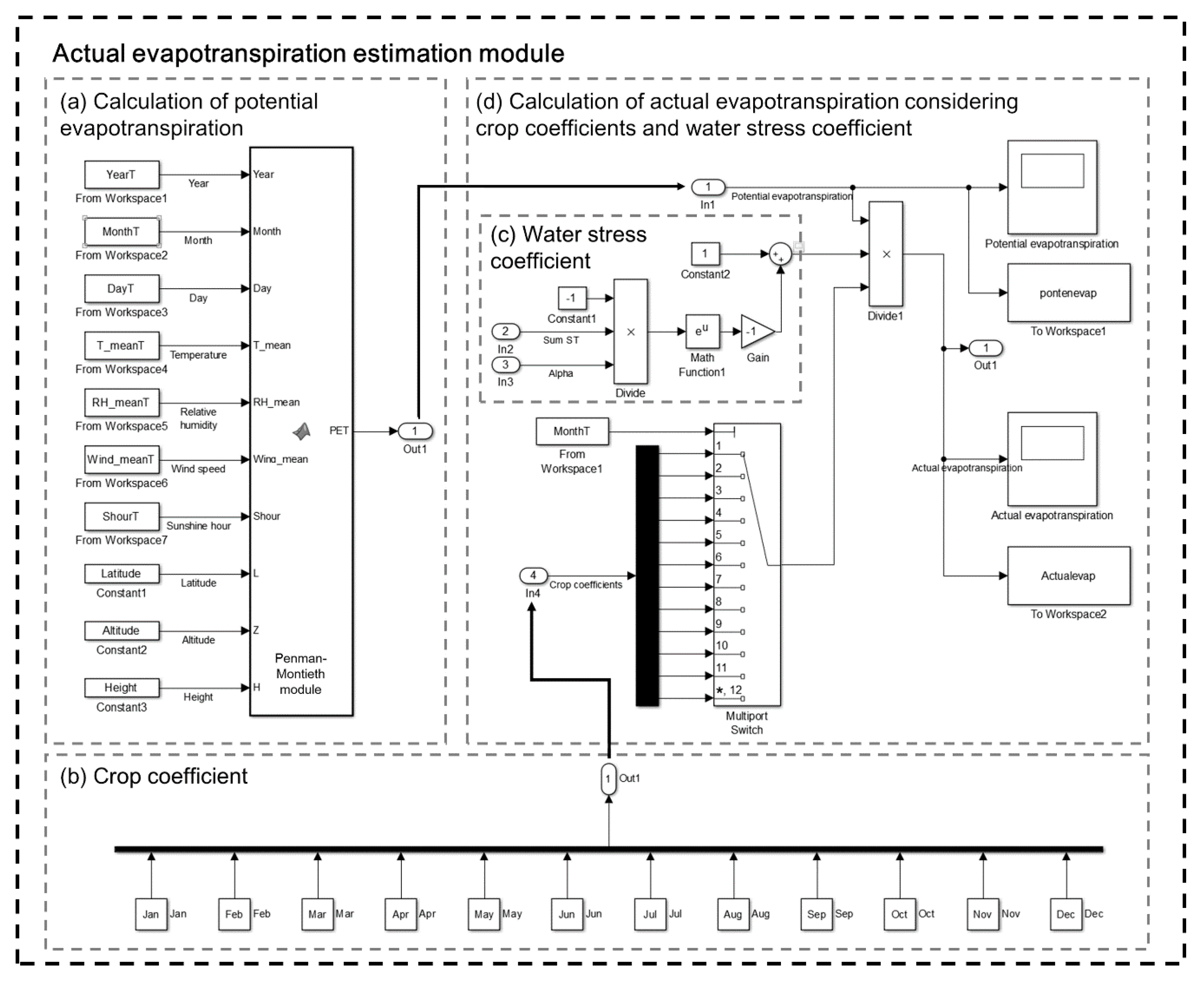
2.3. Watershed Evapotranspiration
2.3.1. Potential Evapotranspiration
2.3.2. Crop Coefficient
2.3.3. Soil Water Stress Coefficient
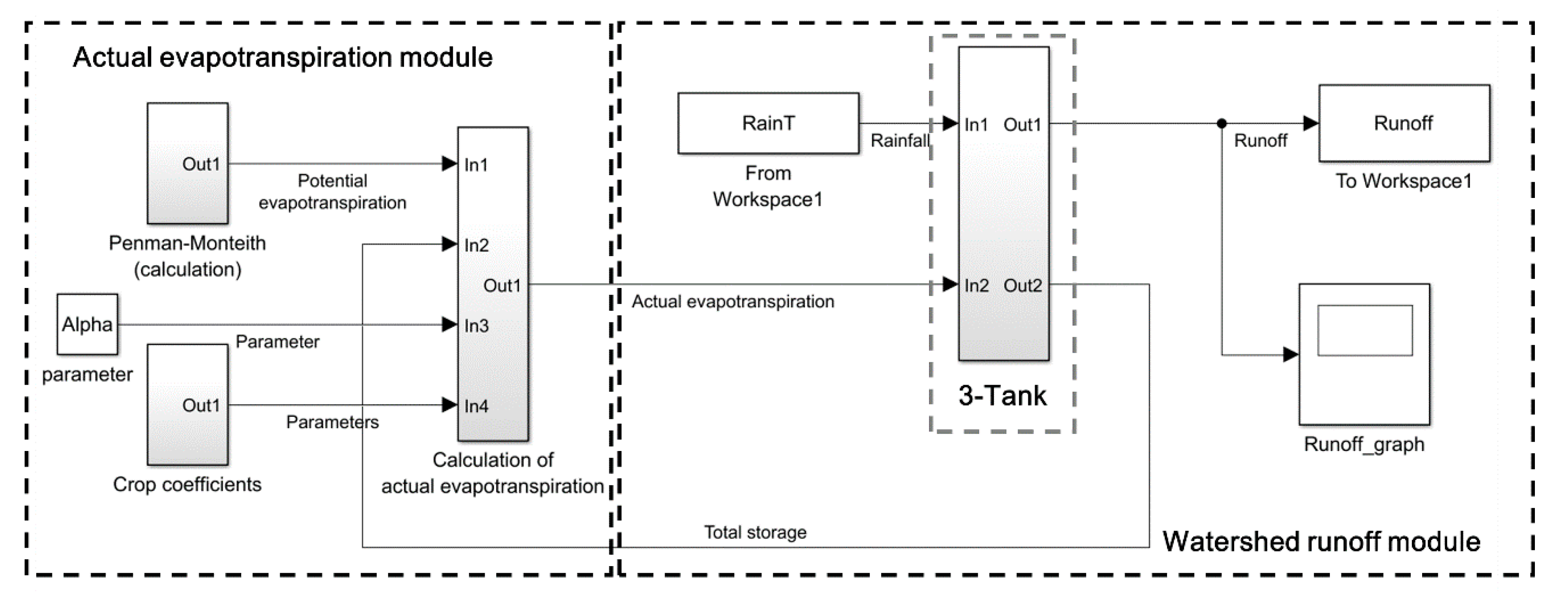
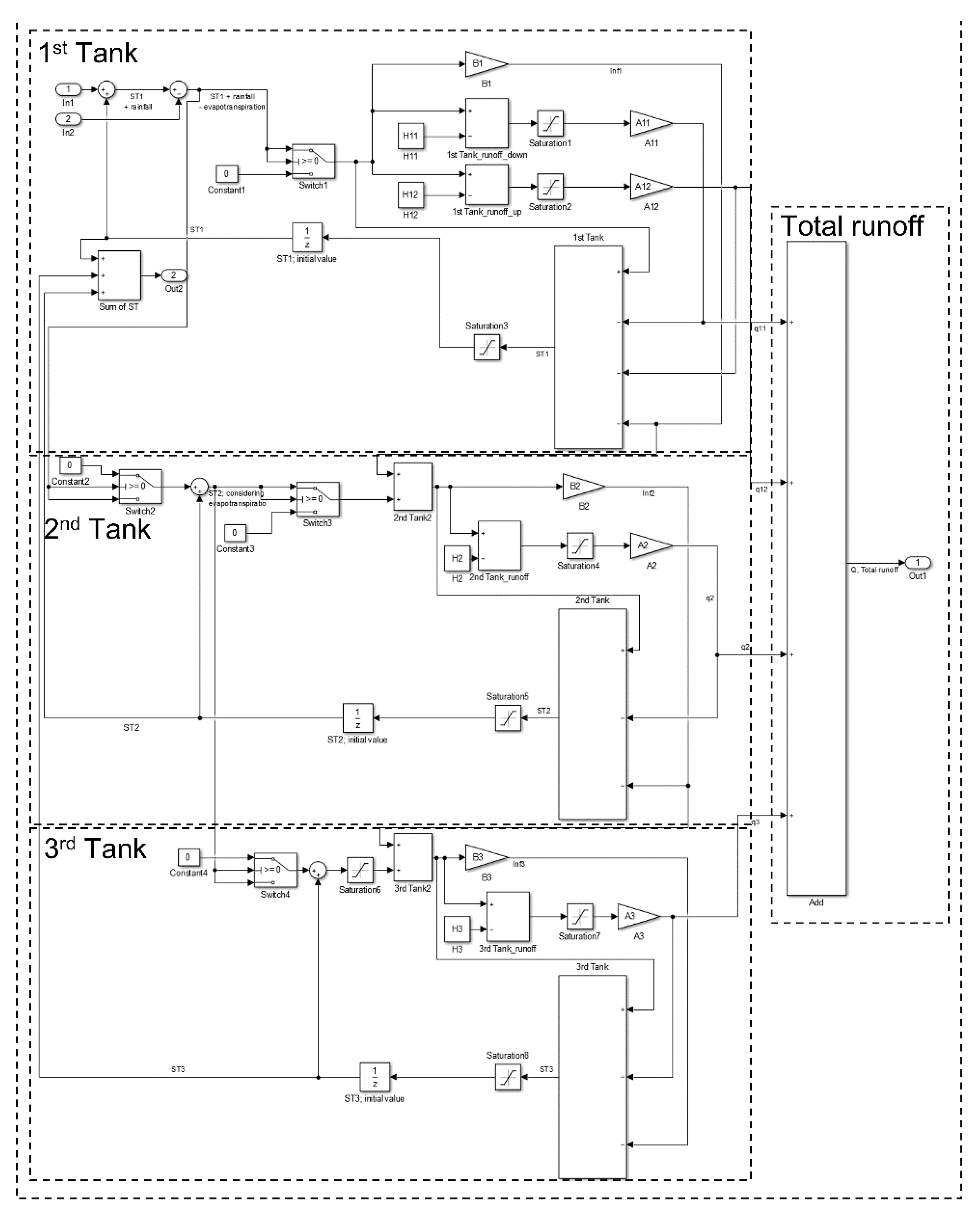
3. Simulink-Tank Model Structure
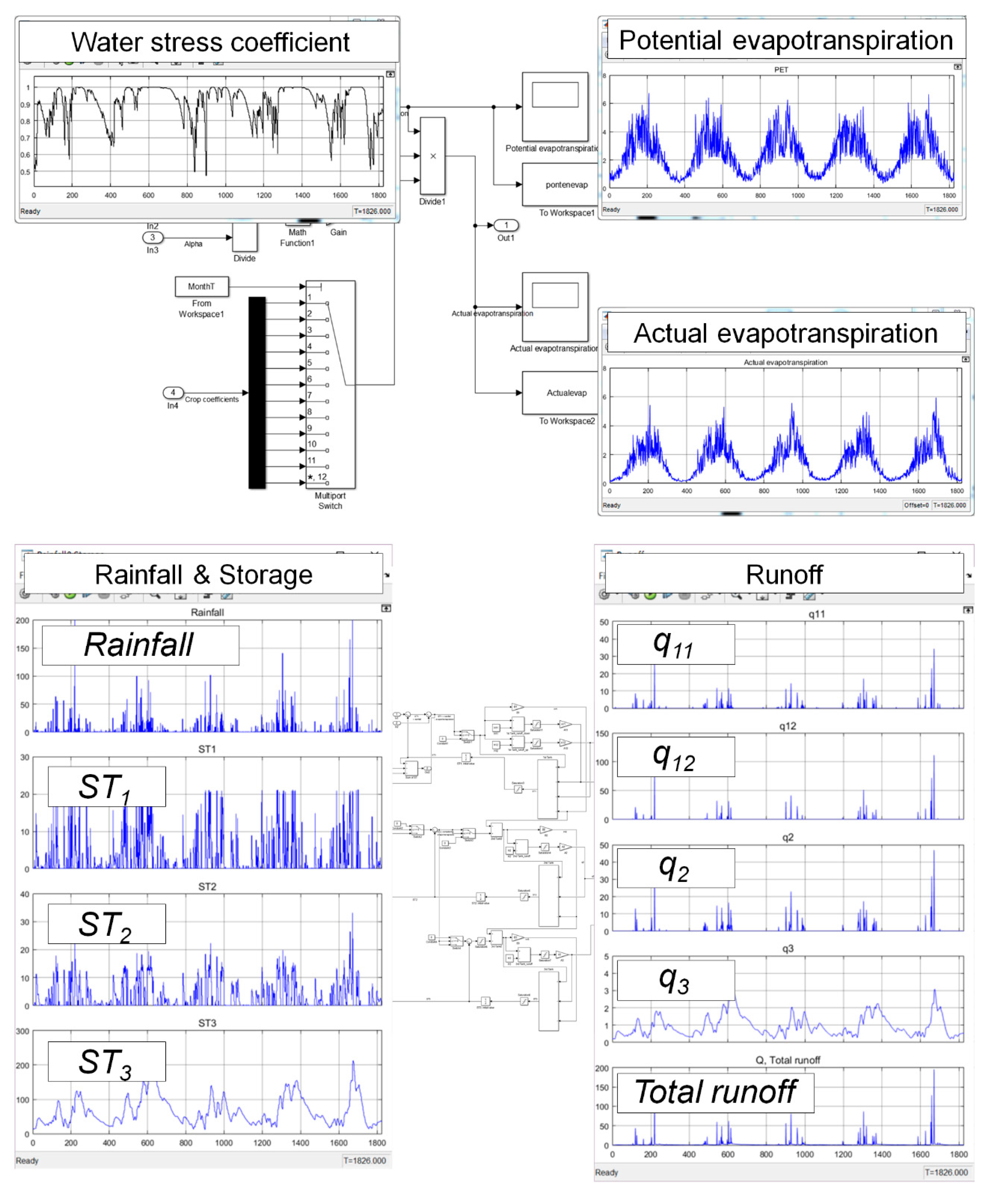
3.1. Watershed Evapotranspiration Module
3.2. 3-Tank Module
4. Case Study
5. Application and Discussion of the Simulink-Tank Model
5.1. Dynamic Description of a Hydrologic System
5.2. Parameter Calibration for the Simulink-Tank Model Using Optimization Techniques within MATLAB
5.2.1. Objective Function
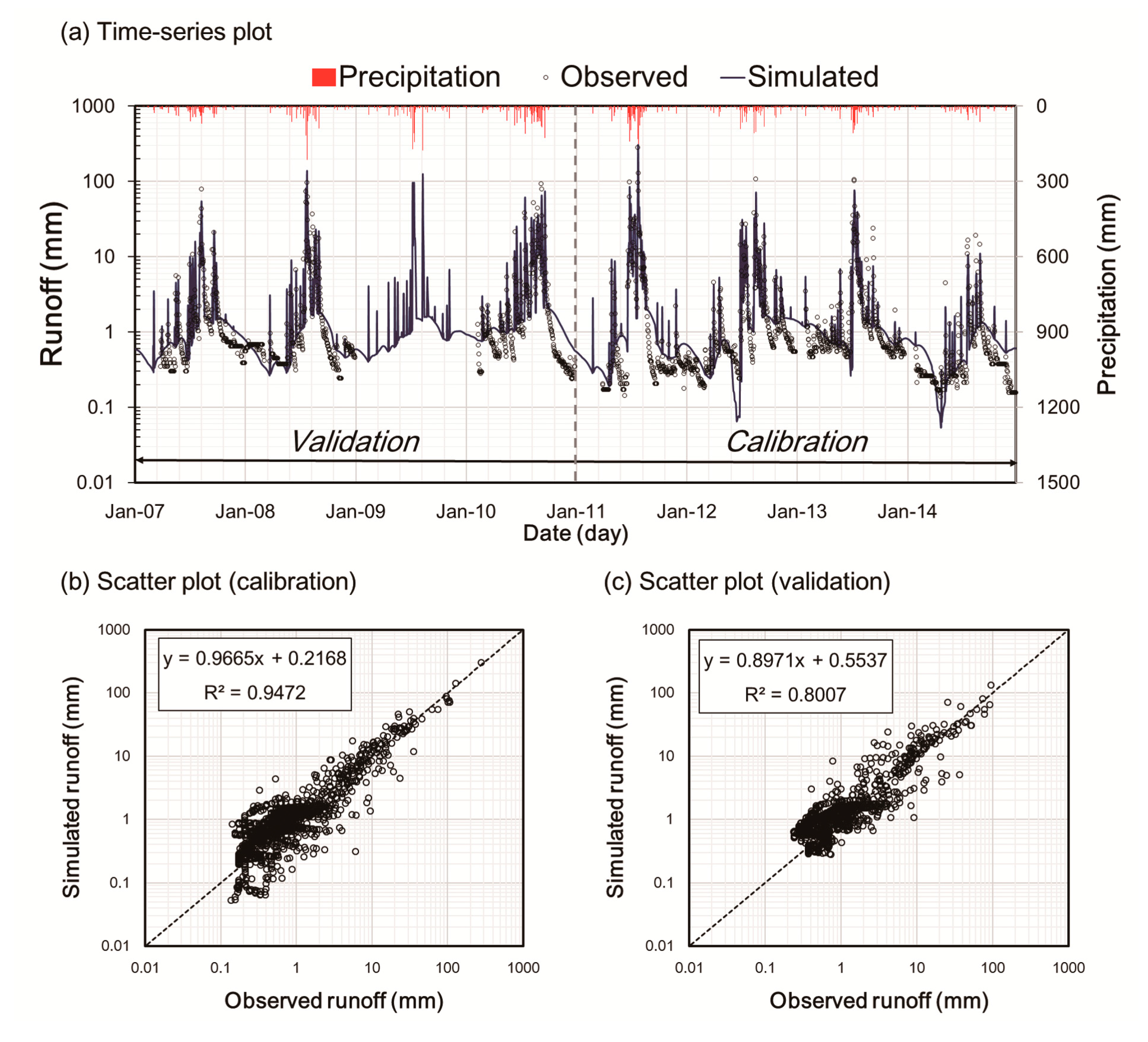
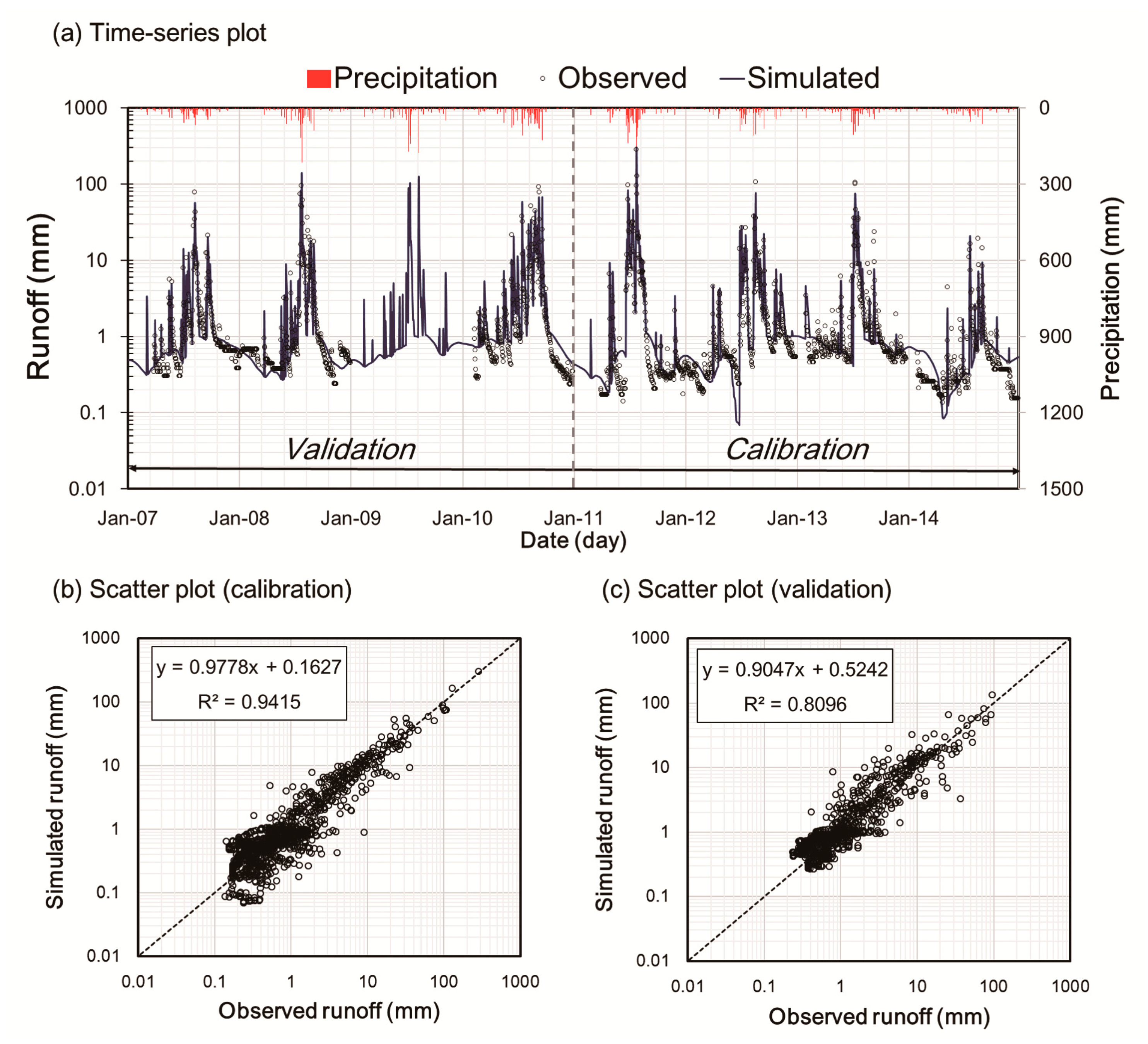
5.2.2. Optimization Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Singh, V.P.; Woolhiser, D.A. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Kang, M.S.; Srivastava, P.; Song, J.H.; Park, J.; Her, Y.; Kim, S.M.; Song, I. Development of a Component-Based Modeling Framework for Agricultural Water-Resource Management. Water 2016, 8, 351. [Google Scholar] [CrossRef]
- Sugawara, M. Automatic calibration of the tank model. Hydrol. Sci. J. 1979, 24, 375–388. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Moore, R.J. The probability-distributed principle and runoff production at point and basin scales. Hydrol. Sci. J. 1985, 30, 273–297. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS: A nonpoint-source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Beasley, D.B.; Huggins, L.F.; Monke, A. ANSWERS: A model for watershed planning. Trans. ASAE 1980, 23, 938–0944. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- Gurtz, J.; Zappa, M.; Jasper, K.; Lang, H.; Verbunt, M.; Badoux, A.; Vitvar, T. A comparative study in modelling runoff and its components in two mountainous catchments. Hydrol. Process. 2003, 17, 297–311. [Google Scholar] [CrossRef]
- Kobierska, F.; Jonas, T.; Zappa, M.; Bavay, M.; Magnusson, J.; Bernasconi, S.M. Future runoff from a partly glacierized watershed in Central Switzerland: A two-model approach. Adv. Water Resour. 2013, 55, 204–214. [Google Scholar] [CrossRef]
- Khakbaz, B.; Imam, B.; Hsu, K.; Sorooshian, S. From lumped to distributed via semi-distributed: Calibration strategies for semi-distributed hydrologic models. J. Hydrol. 2012, 418, 61–77. [Google Scholar] [CrossRef]
- Rumbaugh, J.; Blaha, M.; Premerlani, W.; Eddy, F.; Lorensen, W. Object-Oriented Modeling and Design; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Argent, R.M.; Voinov, A.; Maxwell, T.; Cuddy, S.M.; Rahman, J.M.; Seaton, S.; Vertessy, R.A.; Braddock, R.D. Comparing modelling frameworks—A workshop approach. Environ. Model. Softw. 2006, 21, 895–910. [Google Scholar] [CrossRef]
- Clements, P.C. From subroutines to subsystems: Component-based software development. Am. Program. 1995, 8, 1–8. [Google Scholar]
- Zeigler, B.P. Object-Oriented Simulation with Hierarchical Modular Models; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Maxwell, T. A parsi-model approach to modular simulation. Environ. Model. Softw. 1999, 14, 511–517. [Google Scholar] [CrossRef]
- Muhanna, W.A. SYMMS: A model management system that supports model reuse, sharing, and integration. Eur. J. Oper. Res. 1994, 72, 214–243. [Google Scholar] [CrossRef]
- Guariso, G.; Hitz, M.; Werthner, H. An integrated simulation and optimization modelling environment for decision support. Decis. Support Syst. 1996, 16, 103–117. [Google Scholar] [CrossRef]
- Bennett, D.A. A framework for the integration of geographical information systems and model base management. Int. J. Geogr. Inf. Sci. 1997, 11, 337–357. [Google Scholar] [CrossRef]
- Reed, M.; Cuddy, S.M.; Rizzoli, A.E. A framework for modelling multiple resource management issues—An open modelling approach. Environ. Model. Softw. 1999, 14, 503–509. [Google Scholar] [CrossRef]
- Mantecón, J.A.; Gómez, M.; Rodellar, J. A Simulink-based scheme for simulation of irrigation canal control systems. Simulation 2002, 78, 485–493. [Google Scholar] [CrossRef]
- Kinnucan, P.; Mosterman, P.J. A graphical variant approach to object-oriented modeling of dynamic systems. In Proceedings of the 2007 Summer Computer Simulation Conference, Society for Computer Simulation International, San Diego, CA, USA, 16–19 July 2007. [Google Scholar]
- Bowen, J.D.; Perry, D.N.; Bell, C.D. Hydrologic and Water Quality Model Development Using Simulink. J. Mar. Sci. Eng. 2014, 2, 616–632. [Google Scholar] [CrossRef]
- Romanowicz, R. A Matlab implementation of TOPMODEL. Hydrol. Process. 1997, 11, 1115–1129. [Google Scholar] [CrossRef]
- Lanini, S.; Courtois, N.; Giraud, F.; Petit, V.; Rinaudo, J.D. Socio-hydrosystem modelling for integrated water-resources management-the Hėrault catchment case study, southern France. Environ. Model. Softw. 2004, 19, 1011–1019. [Google Scholar] [CrossRef]
- Chappell, N.A.; Tych, W.; Bonell, M. Development of the forSIM model to quantify positive and negative hydrological impacts of tropical reforestation. For. Ecol. Manag. 2007, 251, 52–64. [Google Scholar] [CrossRef]
- Wolfs, V.; Meert, P.; Willems, P. Modular conceptual modelling approach and software for river hydraulic simulations. Environ. Model. Softw. 2015, 71, 60–77. [Google Scholar] [CrossRef]
- MATLAB Documentation. Available online: mathworks.com/help (accessed on 9 March 2017).
- Paik, K.; Kim, J.H.; Kim, H.S.; Lee, D.R. A conceptual rainfall-runoff model considering seasonal variation. Hydrol. Process. 2005, 19, 3837–3850. [Google Scholar] [CrossRef]
- Jang, T.; Kim, H.; Kim, S.; Seong, C.; Park, S. Assessing irrigation water capacity of land use change in a data-scarce watershed of Korea. J. Irrig. Drain. Eng. 2011, 138, 445–454. [Google Scholar] [CrossRef]
- Fumikazu, N.; Toshisuke, M.; Yoshio, H.; Hiroshi, T.; Kimihito, N. Evaluation of water resources by snow storage using water balance and tank model method in the Tedori River basin of Japan. Paddy Water Environ. 2013, 11, 113–121. [Google Scholar] [CrossRef]
- Song, J.H.; Kang, M.S.; Song, I.; Jun, S.M. Water balance in irrigation reservoirs considering flood control and irrigation efficiency variation. J. Irrig. Drain Eng. 2016, 142, 04016003. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.H.; Baetz, B.W.; Ancell, B.C. Towards robust quantification and reduction of uncertainty in hydrologic predictions: Integration of particle Markov chain Monte Carlo and factorial polynomial chaos expansion. J. Hydrol. 2017, 548, 484–497. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y.H.; Kim, J.H. Multiobjective Automatic Parameter Calibration of a Hydrological Model. Water 2017, 9, 187. [Google Scholar] [CrossRef]
- Kim, H.Y.; Park, S.W. Simulating daily inflow and release rates for irrigation reservoirs. J. Korean Soc. Agric. Eng. 1988, 30, 50–62. (In Korean) [Google Scholar]
- Huh, Y.M. A Streamflow Network Model for Daily Water Supply and Demands on Small Watershed. Ph.D. Thesis, Seoul National University, Seoul, Korea, 1992. [Google Scholar]
- Schrader, F.; Durner, W.; Fank, J.; Gebler, S.; Pütz, T.; Hannes, M.; Wollschläger, U. Estimating precipitation and actual evapotranspiration from precision lysimeter measurements. Procedia Environ. Sci. 2013, 19, 543–552. [Google Scholar] [CrossRef]
- Rahimi, S.; Gholami, S.M.A.; Raeini-Sarjaz, M.; Valipour, M. Estimation of actual evapotranspiration by using MODIS images (a case study: Tajan catchment). Arch. Agron. Soil Sci. 2015, 61, 695–709. [Google Scholar] [CrossRef]
- Valipour, M. Comparative evaluation of radiation-based methods for estimation of potential evapotranspiration. J. Hydrol. Eng. 2014, 20, 04014068. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements; No. 1275; US Department of Agriculture: Washington, DC, USA, 1962.
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. In Proceedings of the Royal Society of London, A: Mathematical, Physical, and Engineering Sciences, London, UK, 22 April 1948. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Chou, C.C. Effects of climate change on evapotranspiration from paddy fields in southern Taiwan. Clim. Chang. 2002, 54, 165–179. [Google Scholar] [CrossRef]
- Sung, S.H. Determination of Evapotranspiration Ratio to Estimate Actual Evapotranspiration in Small Forested-Watersheds. Master’s Thesis, Seoul National University, Seoul, Korea, 1997. (In Korean). [Google Scholar]
- Yoo, S.H.; Choi, J.Y.; Jang, M.W. Estimation of paddy rice crop coefficients for FAO Penman-Monteith and Modified Penman method. J. Korean Soc. Agric. Eng. 2006, 48, 13–23. (In Korean) [Google Scholar]
- Nonsaro. Available online: nongsaro.go.kr (accessed on 24 August 2017).
- Park, S.W. A Tank model shell program for simulating daily streamflow from small watershed. J. Korea Water Resour. Assoc. 1993, 26, 47–61. (In Korean) [Google Scholar]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Clark, M.P.; Kavetski, D.; Fenicia, F. Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour. Res. 2011, 47, 9. [Google Scholar] [CrossRef]
- Van Esse, W.; Perrin, C.; Booij, M.; Augustijn, D.; Fenicia, F.; Kavetski, D.; Lobligeois, F. The influence of conceptual model structure on model performance: A comparative study for 237 French catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4227–4239. [Google Scholar] [CrossRef]
- Gan, T.Y.; Dlamini, E.M.; Biftu, G.F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Chapman, S.J. MATLAB Programming for Engineers; Nelson Education: Scarborough, ON, Canada, 2015. [Google Scholar]
- Engel, B.; Storm, D.; White, M.; Arnold, J.; Arabi, M. A hydrologic/water quality model application protocol. J. Am. Water Resour. Assoc. 2007, 43, 1223–1236. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Oudin, L.; Andreassian, V.; Mathevet, T.; Perrin, C.; Michel, C. Dynamic averaging of rainfall-runoff model simulations from complementary model parameterizations. Water Resour. Res. 2006, 42, 7. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andreassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420, 171–182. [Google Scholar] [CrossRef]

| Parameter | Alpha | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | 0 | 0.08 | 0.08 | 5 | 20 | 0.1 | 0.03 | 0 | 0.01 | 0.003 | 0 | 0 |
| Max. | 0.5 | 0.5 | 0.5 | 60 | 110 | 0.5 | 0.5 | 100 | 0.35 | 0.03 | 0 | 0.11 |
| Crop Coeff. | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forest | 0.47 | 0.46 | 0.55 | 0.59 | 0.74 | 0.72 | 0.87 | 1.01 | 0.98 | 0.87 | 0.64 | 0.45 |
| Paddy | 0.20 | 0.20 | 0.20 | 0.65 | 0.70 | 0.99 | 1.30 | 1.17 | 0.83 | 0.20 | 0.20 | 0.20 |
| Upland | 0.36 | 0.36 | 0.37 | 0.37 | 0.58 | 0.78 | 0.82 | 0.82 | 0.76 | 0.57 | 0.37 | 0.36 |
| Others | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 |
| Year | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
|---|---|---|---|---|---|---|---|---|
| Rainfall (mm) | 1260 | 1458 | 1541 | 1977 | 2211 | 1481 | 1448 | 767 |
| Case | Period | (%) | |||
|---|---|---|---|---|---|
| 1 | Calibration | 0.95 | 0.95 | −0.15 | −4.4 |
| Validation | 0.80 | 0.79 | 0.34 | −7.5 | |
| 2 | Calibration | 0.94 | 0.94 | 0.07 | −3.6 |
| Validation | 0.81 | 0.80 | 0.57 | −7.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.-H.; Her, Y.; Park, J.; Lee, K.-D.; Kang, M.-S. Simulink Implementation of a Hydrologic Model: A Tank Model Case Study. Water 2017, 9, 639. https://doi.org/10.3390/w9090639
Song J-H, Her Y, Park J, Lee K-D, Kang M-S. Simulink Implementation of a Hydrologic Model: A Tank Model Case Study. Water. 2017; 9(9):639. https://doi.org/10.3390/w9090639
Chicago/Turabian StyleSong, Jung-Hun, Younggu Her, Jihoon Park, Kyung-Do Lee, and Moon-Seong Kang. 2017. "Simulink Implementation of a Hydrologic Model: A Tank Model Case Study" Water 9, no. 9: 639. https://doi.org/10.3390/w9090639
APA StyleSong, J.-H., Her, Y., Park, J., Lee, K.-D., & Kang, M.-S. (2017). Simulink Implementation of a Hydrologic Model: A Tank Model Case Study. Water, 9(9), 639. https://doi.org/10.3390/w9090639





