Uncertainty of Hydrological Drought Characteristics with Copula Functions and Probability Distributions: A Case Study of Weihe River, China
Abstract
:1. Introduction
2. Materials and Methods
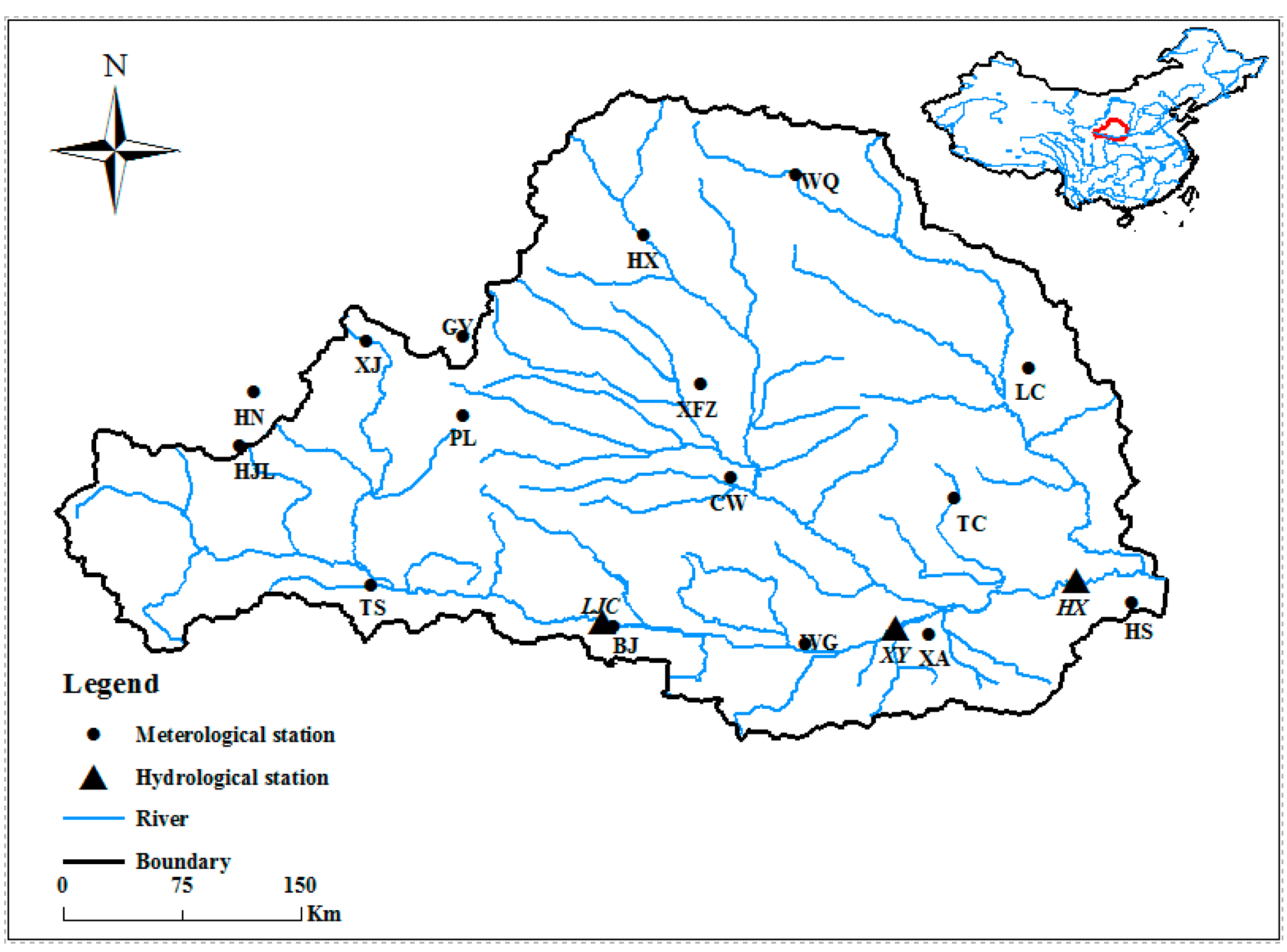
2.1. Weihe River Basin and Data
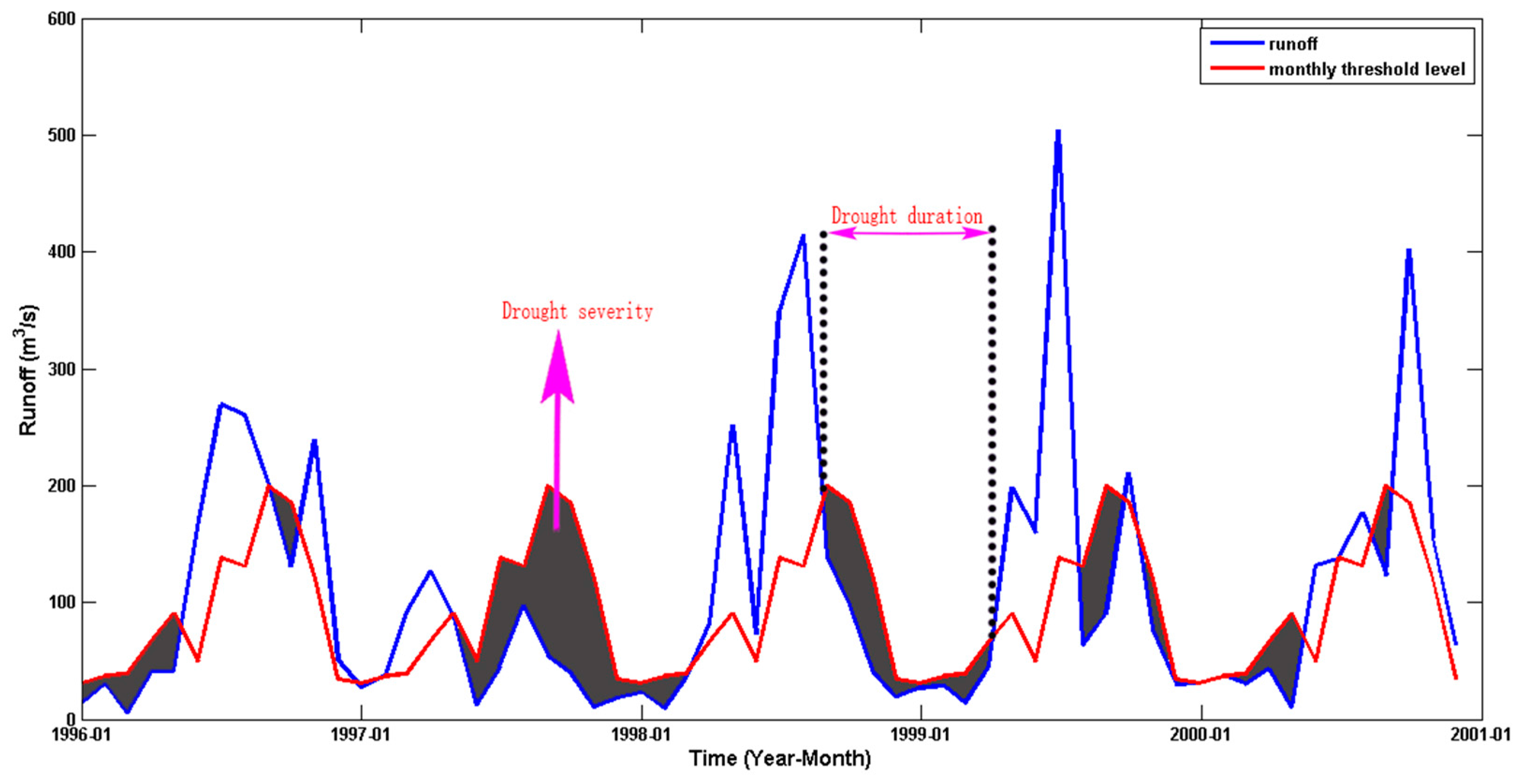
2.2. Defining Drought Duration and Severity
2.3. Marginal Distribution Model and Copula-Based Models
2.4. Return Period of Droughts
3. Results
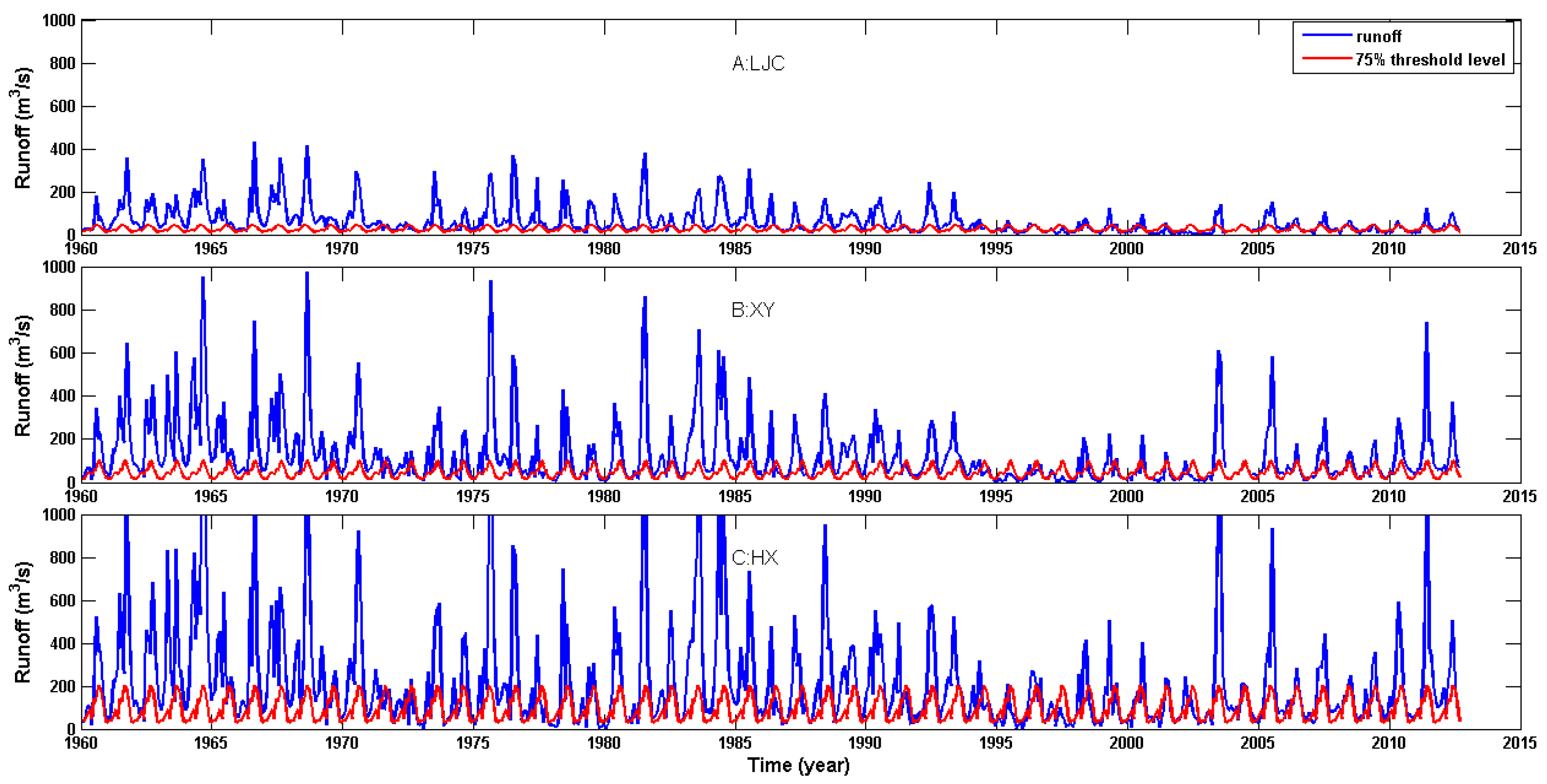
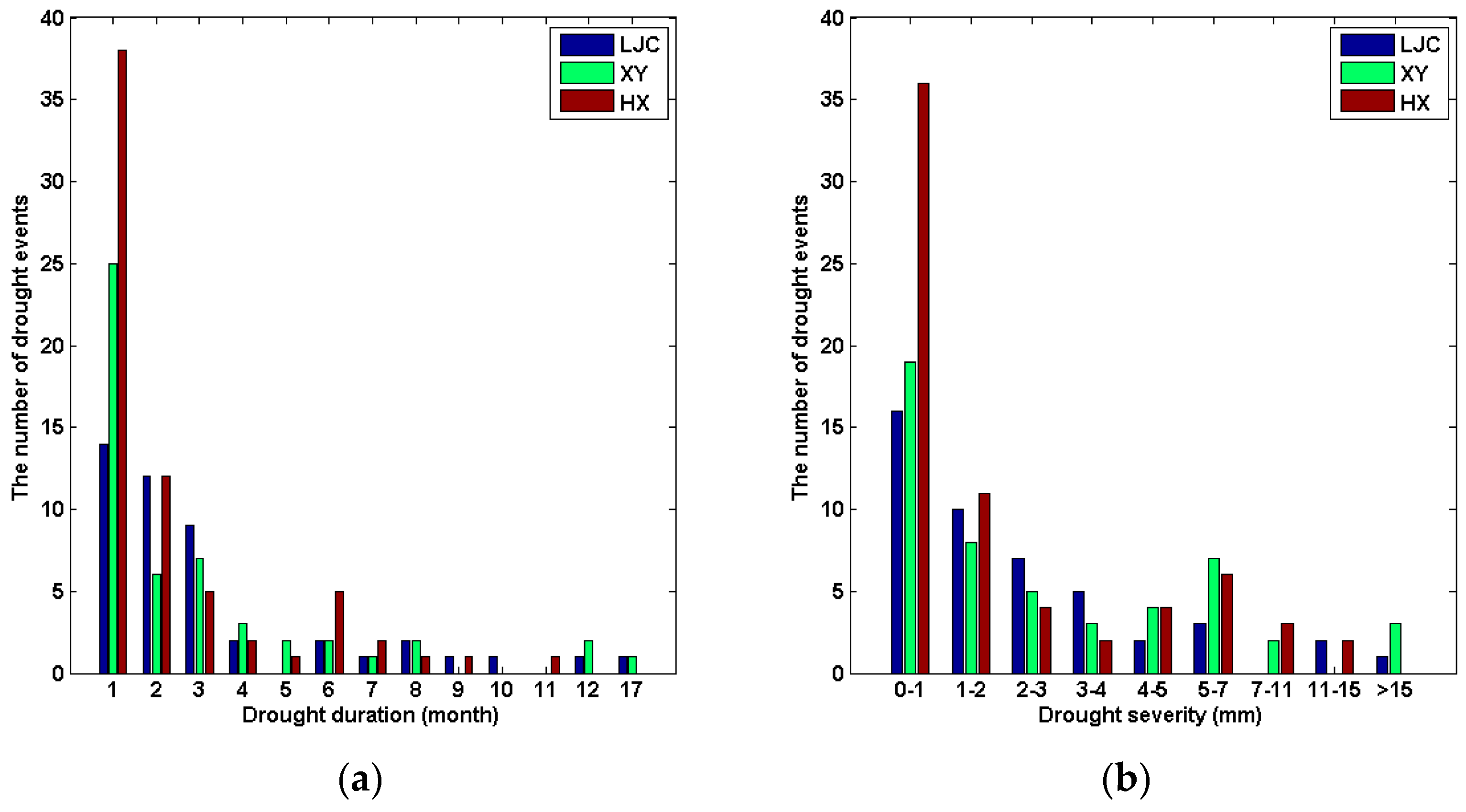
3.1. Drought Duration and Severity Characteristics
3.2. Marginal Distributions and Copula Functions
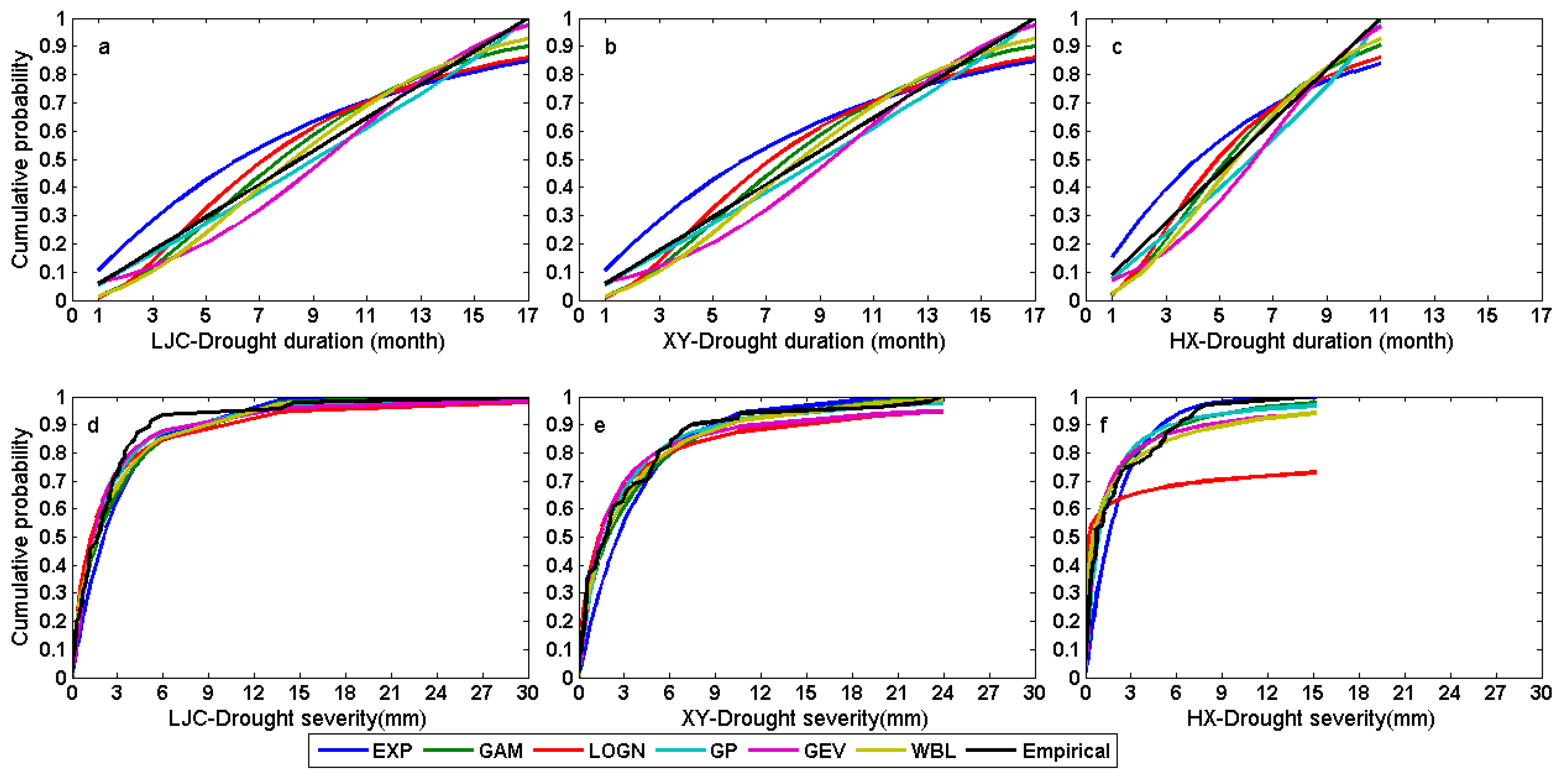
3.2.1. Selected Marginal Distributions
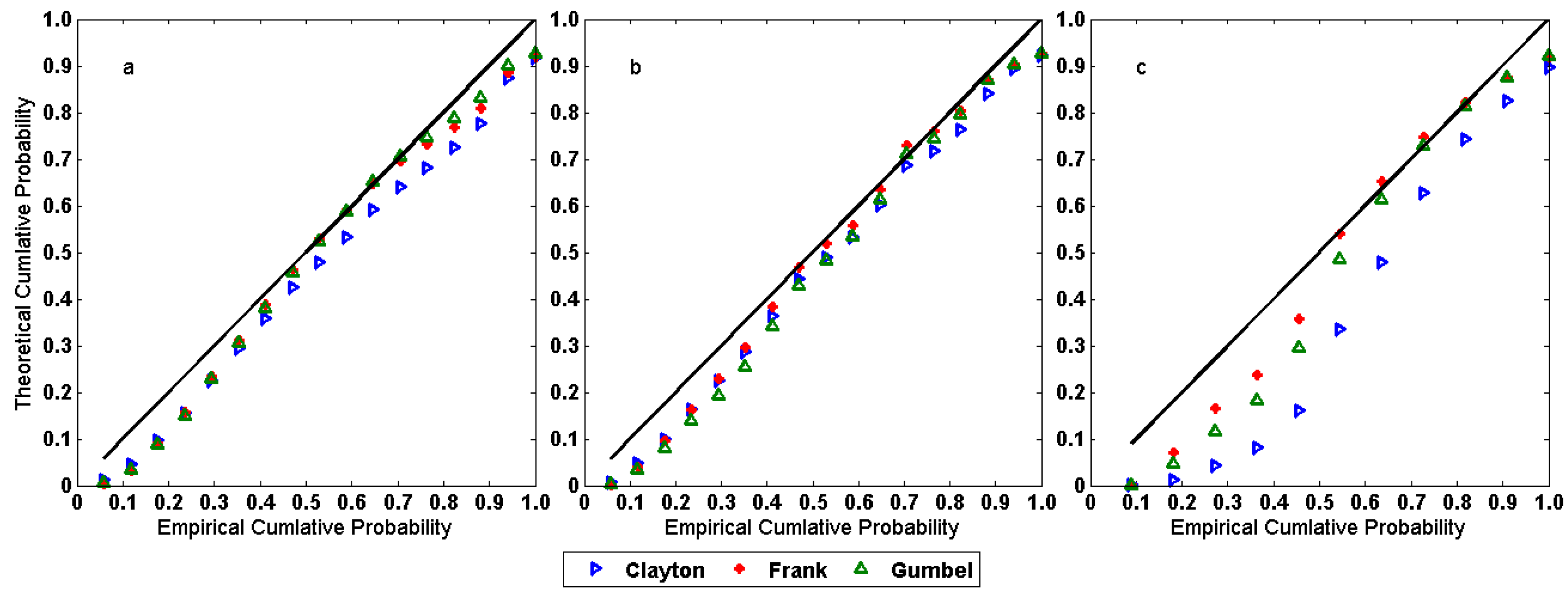
3.2.2. Selected Copula Functions
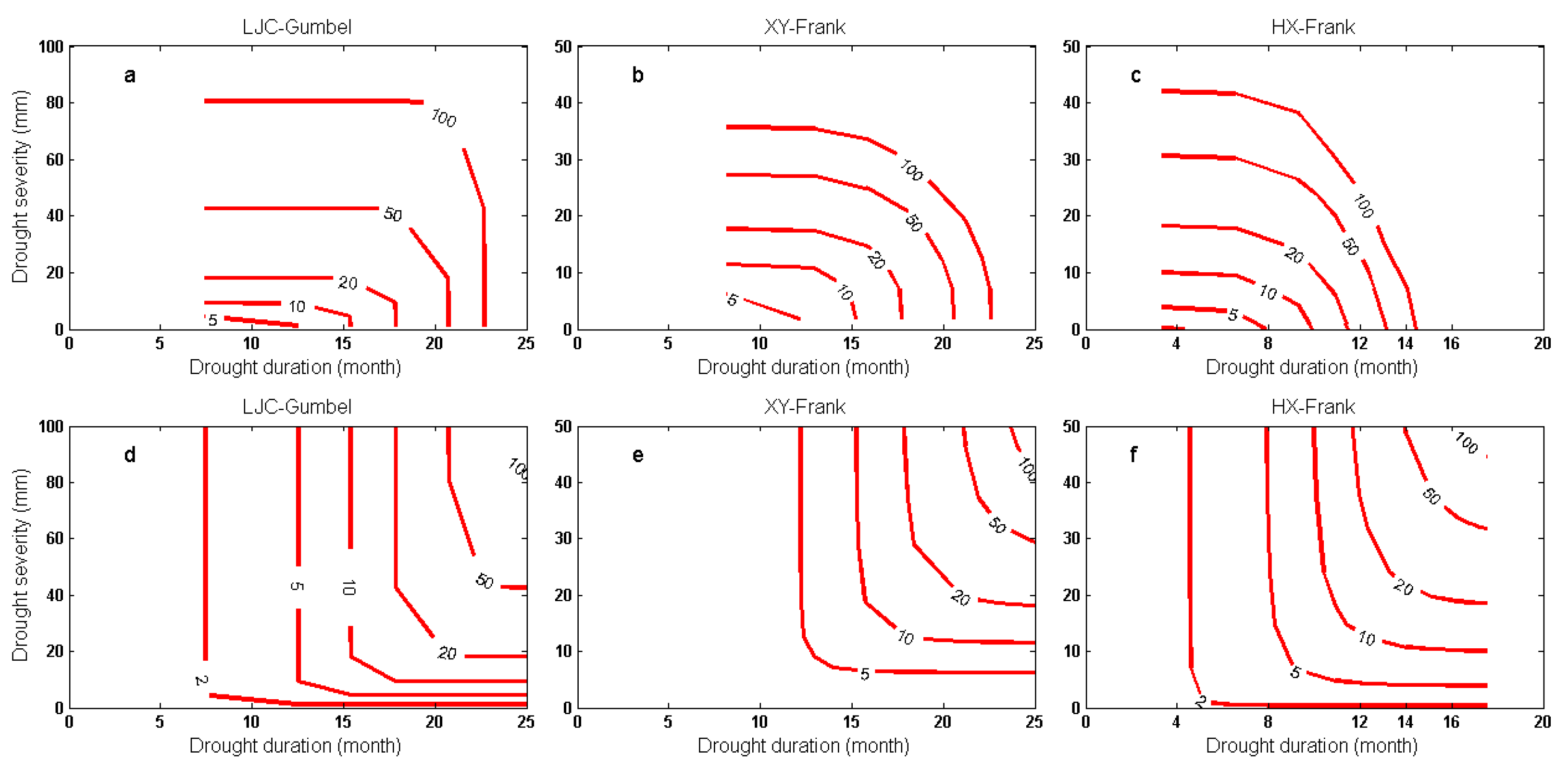
3.3. Return Period of Droughts
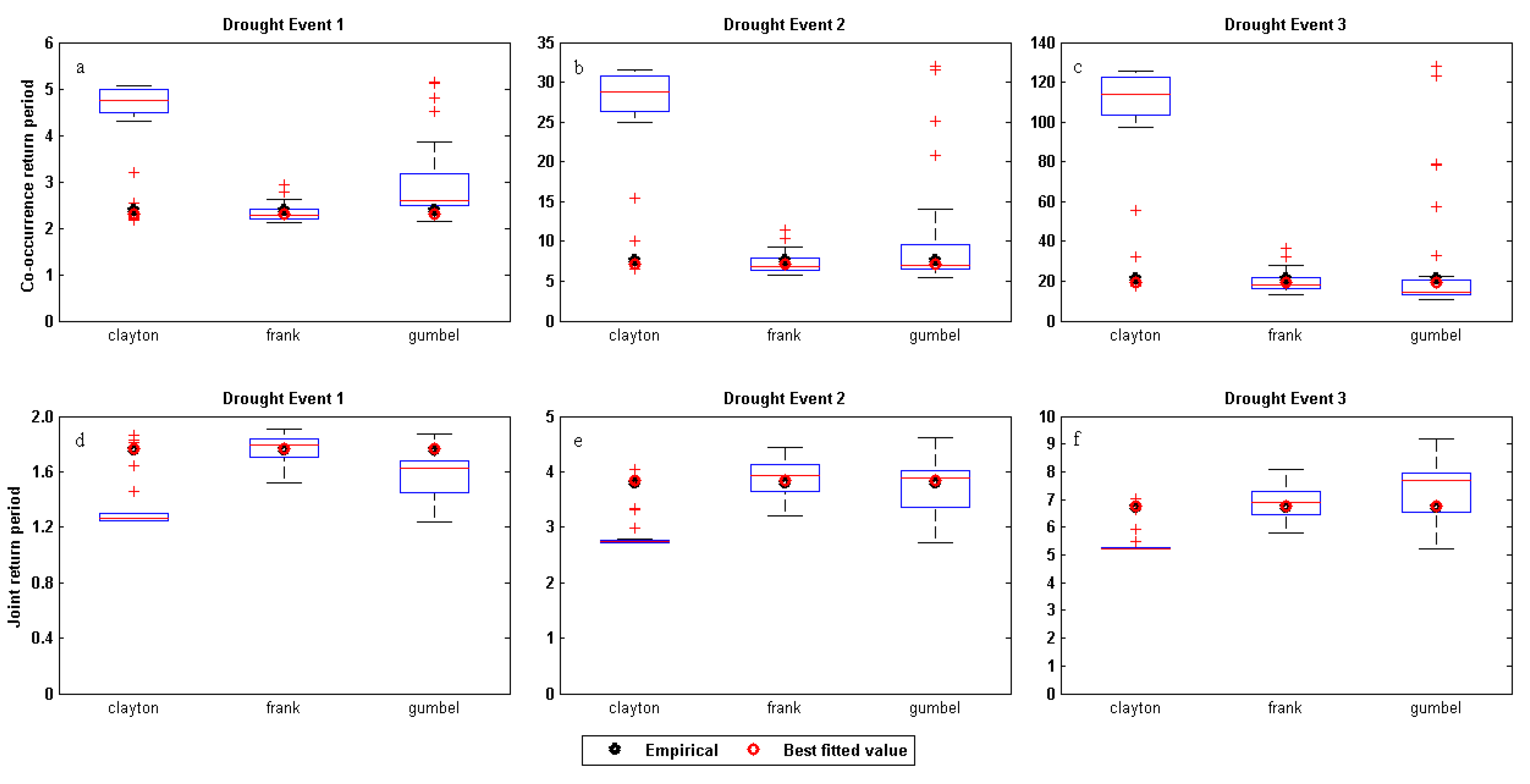
4. Sensitivity and Uncertainty of the Drought Frequency
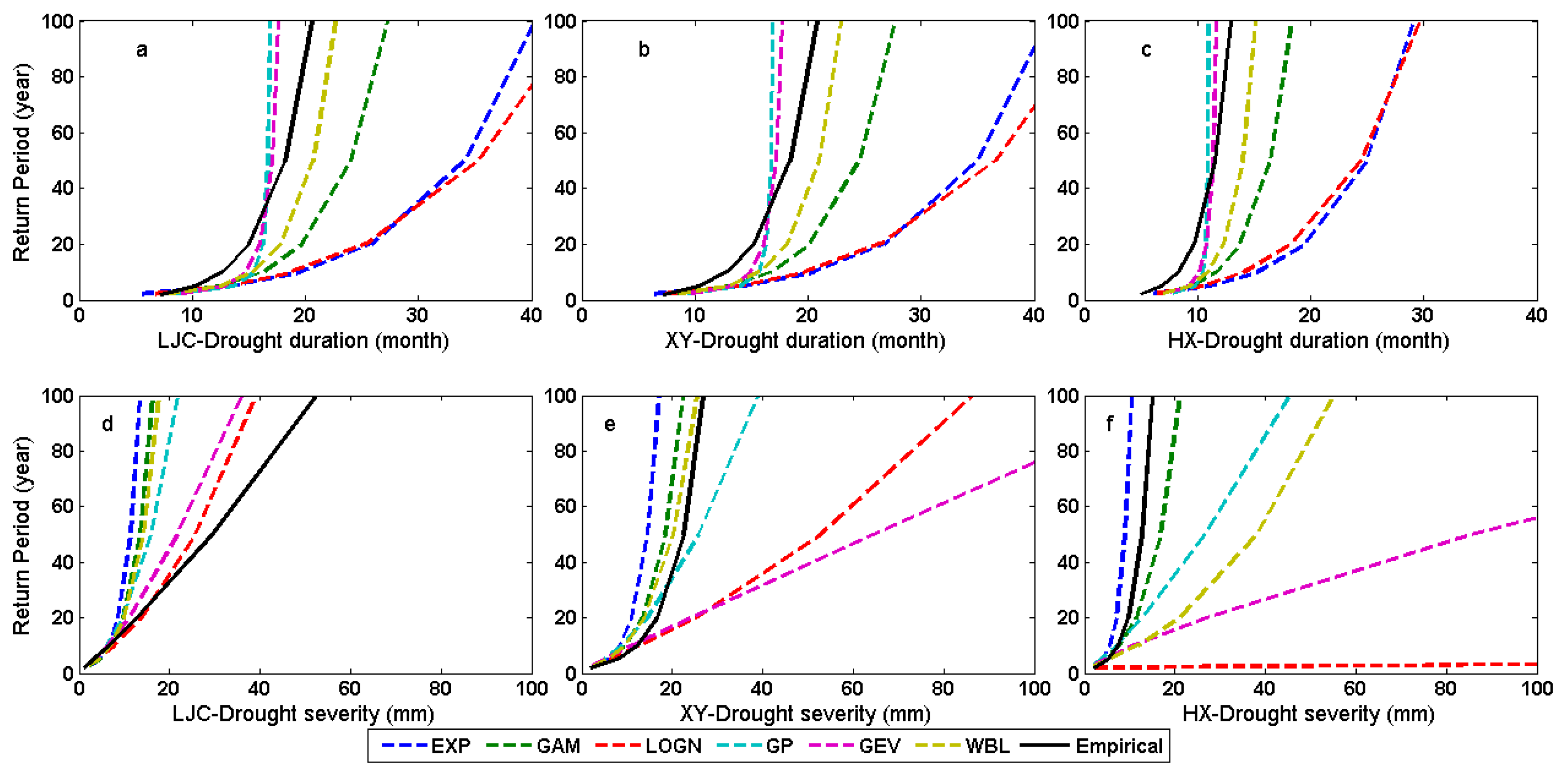
4.1. Effects of the Selection of Margin Distributions to the Return Period
4.2. Effects of the Selection of Copula Functions to the Return Period
4.3. Effects of Human Activities on Drought Frequency
5. Conclusions
- (1)
- There are more drought events at Huaxian station (lower basin) than at Linjiacun station (upper basin), but there are longer drought durations and greater severity at Linjiacun station.
- (2)
- Based on the AD test, five models (EXP, GAM, LOGN, GEV, WBL) are acceptable for the fit of the drought duration and drought severity at LJC and XY stations. The GP model is not acceptable for the goodness-of-fit of drought duration and drought severity at three stations, the EXP model is rejected for the fit of drought severity at Huaxian station.
- (3)
- Based on ordinary least squares (OLS) and Akaike information criterion (AIC), the Frank copula is the best joint distribution function at Linjiacun and Huaxian stations, while the Clayton copula is the best-fitted model at Huaxian station.
- (4)
- The co-occurrence return period is greater than both the return periods defined by drought duration and drought severity separately, while the joint return period is shorter than both of the return periods. This shows that these two kinds of combination return periods can be regarded as two extreme conditions of the marginal distribution return period. It is possible to estimate the interval of the actual return period according to the co-occurrence return period and the joint return period.
- (5)
- The drought return period is sensitive to the selected marginal distribution and different copula functions. Therefore, it is important to select proper marginal distributions and copula functions, and the sensitivity and uncertainty of hydrological droughts should be paid more attention on the modeling and designing of drought models with consideration to the condition of water resources and the requirement of water management.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tallaksen, L.M.; Van Lanen, H.A. Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 2004; Volume 48. [Google Scholar]
- Tallaksen, L.M.; Hisdal, H.; Van Lanen, H.A. Space–time modelling of catchment scale drought characteristics. J. Hydrol. 2009, 375, 363–372. [Google Scholar] [CrossRef]
- Van Loon, A.; Van Lanen, H. A process-based typology of hydrological drought. Hydrol. Earth Syst. Sci. 2012, 16, 1915. [Google Scholar] [CrossRef]
- Nyabeze, W.R. Estimating and interpreting hydrological drought indices using a selected catchment in Zimbabwe. Phys. Chem. Earth A/B/C 2004, 29, 1173–1180. [Google Scholar] [CrossRef]
- Byzedi, M.; Saghafian, B. Analysis of hydrological drought based on daily flow series. Proc. World Acad. Sci. Eng. Technol. 2010, 70, 249–252. [Google Scholar]
- Jaranilla-Sanchez, P.A.; Wang, L.; Koike, T. Modeling the hydrologic responses of the pampanga river basin, philippines: A quantitative approach for identifying droughts. Water Resour. Res. 2011, 47, W03514. [Google Scholar] [CrossRef]
- Ren, L.; Shen, H.; Yuan, F.; Zhao, C.; Yang, X. Hydrological drought characteristics in the Weihe catchment in a changing environment. Adv. Water Sci. 2016, 27, 492–500. [Google Scholar]
- Yue, S. Applying bivariate normal distribution to flood frequency analysis. Water Int. 1999, 24, 248–254. [Google Scholar] [CrossRef]
- Bacchi, B.; Becciu, G.; Kottegoda, N.T. Bivariate exponential model applied to intensities and durations of extreme rainfall. J. Hydrol. 1994, 155, 225–236. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.; Bobee, B. A review of bivariate gamma distributions for hydrological application. J. Hydrol. 2001, 246, 1–18. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Evaluation of trends and multivariate frequency analysis of droughts in three meteorological subdivisions of western India. Int. J. Climatol. 2014, 34, 911–928. [Google Scholar] [CrossRef]
- Shiau, J. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de Répartition à n Dimensions et Leurs Marges; Université Paris 8: Saint-Denis, France, 1959. [Google Scholar]
- Hürlimann, W. Fitting bivariate cumulative returns with copulas. Comput. Stat. Data Anal. 2004, 45, 355–372. [Google Scholar] [CrossRef]
- Michele, C.; Salvadori, G.; Vezzoli, R.; Pecora, S. Multivariate assessment of droughts: Frequency analysis and dynamic return period. Water Resour. Res. 2013, 49, 6985–6994. [Google Scholar] [CrossRef]
- Khedun, C.P.; Mishra, A.K.; Singh, V.P.; Giardino, J.R. A copula-based precipitation forecasting model: Investigating the interdecadal modulation of ENSO’s impacts on monthly precipitation. Water Resour. Res. 2014, 50, 580–600. [Google Scholar] [CrossRef]
- Nazemi, A.A.; Wheater, H.S. Assessing the vulnerability of water supply to changing streamflow conditions. Eos Trans. Am. Geophys. Union 2014, 95, 288. [Google Scholar] [CrossRef]
- Tu, X.; Singh, V.P.; Chen, X.; Ma, M.; Zhang, Q.; Zhao, Y. Uncertainty and variability in bivariate modeling of hydrological droughts. Stoch. Environ. Res. Risk Assess. 2016, 30, 1317–1334. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Marsaglia, G.; Marsaglia, J. Evaluating the Anderson-Darling distribution. J. Stat. Softw. 2004, 9, 1–5. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z. Regulation on runoff and sediment discharge of main branches located in wei river valley and benefits of runoff and sediment decrease under control measures of soil and water conservation. Bull. Soil Water Conversat. 1995, 15, 55–59. [Google Scholar]
- Song, J.; Xu, Z.; Liu, C.; Li, H. Ecological and environmental instream flow requirements for the Wei river—The largest tributary of the yellow river. Hydrol. Process. 2007, 21, 1066–1073. [Google Scholar] [CrossRef]
- Yuan, F.; Ma, M.; Ren, L.; Shen, H.; Li, Y.; Jiang, S.; Yang, X.; Zhao, C.; Kong, H. Possible future climate change impacts on the hydrological drought events in the weihe river basin, China. Adv. Meteorol. 2016. [Google Scholar] [CrossRef]
- Van Loon, A. On the Propagation of Drought: How Climate and Catchment Characteristics Influence Hydrological Drought Development and Recovery; Wageningen University: Wageningen, The Netherlands, 2013. [Google Scholar]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A global evaluation of streamflow drought characteristics. Hydrol. Earth Syst. Sci. 2006, 10, 535–552. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. A bivariate mixed distribution with a heavy-tailed component and its application to single-site daily rainfall simulation. Water Resour. Res. 2013, 49, 767–789. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Haan, C.T. Statistical Methods in Hydrology; The Iowa State University Press: Ames, IA, USA, 2002. [Google Scholar]
- Bonaccorso, B.; Bordi, I.; Cancelliere, A.; Rossi, G.; Sutera, A. Spatial variability of drought: An analysis of the SPI in Sicily. Water Resour. Manag. 2003, 17, 273–296. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; De Michele, C. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef]
- Fu, G.; Chen, S.; Liu, C.; Shepard, D. Hydro-climatic trends of the Yellow river basin for the last 50 years. Clim. Chang. 2004, 65, 149–178. [Google Scholar] [CrossRef]
- Jin, H.; Liang, R.; Wang, Y.; Tumula, P. Flood-runoff in semi-arid and sub-humid regions, a case study: A simulation of jianghe watershed in northern China. Water 2015, 7, 5155–5172. [Google Scholar] [CrossRef]
| Distribution | CDF | Parameters |
|---|---|---|
| Exponential (EXP) | : scale | |
| Gamma (GAM) | : shape | |
| : scale | ||
| Log-normal (LOGN) | : mean | |
| : standard deviation | ||
| Generalized Pareto (GP) | : shape | |
| : scale | ||
| : location | ||
| Generalized extreme value (GEV) | : shape | |
| : scale | ||
| : location | ||
| Weibull (WBL) | : scale | |
| : shape |
| Copulas | CDF | Parameters |
|---|---|---|
| Clayton | ||
| Frank | ||
| Gumel |
| Mean | Std.dev. | Max | Min | Cv | SK | ||
|---|---|---|---|---|---|---|---|
| Drought duration (month) | LJC | 3.391 | 3.363 | 17 | 1 | 0.992 | 2.172 |
| XY | 3.059 | 3.343 | 17 | 1 | 1.093 | 2.316 | |
| HX | 2.382 | 2.273 | 11 | 1 | 0.954 | 1.879 | |
| Drought Severity (mm) | LJC | 3.009 | 5.081 | 30.436 | 0.019 | 1.689 | 3.964 |
| XY | 3.726 | 5.387 | 23.946 | 0.002 | 1.446 | 2.513 | |
| HX | 2.175 | 2.959 | 15.169 | 0.001 | 1.360 | 2.074 | |
| Correlation Coefficient | LJC () | XY () | HX () |
|---|---|---|---|
| 0.883 | 0.916 | 0.885 | |
| 0.705 | 0.644 | 0.639 | |
| 0.827 | 0.803 | 0.776 |
| Margin | Parameter | LJC | XY | HX | |
|---|---|---|---|---|---|
| Duration | EXP | 3.391 | 3.059 | 2.382 | |
| GAM | 1.612 | 1.399 | 1.743 | ||
| 2.103 | 2.186 | 1.366 | |||
| LOGN | 0.880 | 0.720 | 0.555 | ||
| 0.789 | 0.838 | 0.731 | |||
| GP | −0.017 | 0.072 | −0.056 | ||
| 3.449 | 2.838 | 2.515 | |||
| GEV | 5.062 | 3.783 | 4.958 | ||
| 0.330 | 0.011 | 0.159 | |||
| 1.065 | 1.003 | 1.032 | |||
| WBL | 3.637 | 3.197 | 2.580 | ||
| 1.196 | 1.105 | 1.234 | |||
| Severity | EXP | 35.600 | 67.316 | 89.357 | |
| GAM | 0.691 | 0.594 | 0.287 | ||
| 51.513 | 113.247 | 311.259 | |||
| LOGN | 2.696 | 3.169 | 2.073 | ||
| 1.510 | 1.805 | 7.138 | |||
| GP | 0.381 | 0.529 | 0.747 | ||
| 21.939 | 36.178 | 38.080 | |||
| GEV | 0.706 | 1.042 | 1.239 | ||
| 12.958 | 21.278 | 25.334 | |||
| 11.151 | 15.605 | 16.587 | |||
| WBL | 29.791 | 53.411 | 51.179 | ||
| 0.768 | 0.706 | 0.417 | |||
| LJC | XY | HX | |||||
|---|---|---|---|---|---|---|---|
| AIC | AD | AIC | AD | AIC | AD | ||
| p-Value | p-Value | p-Value | |||||
| Duration | EXP | −76.856 | 0.243 | −76.856 | 0.243 | −39.335 | 0.393 |
| GAM | −98.198 | 0.945 | −98.198 | 0.945 | −50.448 | 0.962 | |
| LOGN | −88.137 | 0.635 | −88.137 | 0.635 | −46.052 | 0.857 | |
| GP | −90.31 | 0.000 | −90.31 | 0.000 | −52.657 | 0.000 | |
| GEV | −93.289 | 0.873 | −93.289 | 0.873 | −53.595 | 0.982 | |
| WBL | −100.749 | 0.975 | −100.749 | 0.975 | −59.937 | 0.986 | |
| Severity | EXP | −207.934 | 0.0295 | −230.471 | 0.021 | −307.066 | 0.0068 |
| GAM | −263.939 | 0.3543 | −291.92 | 0.3002 | −425.32 | 0.479 | |
| LOGN | −232.344 | 0.1144 | −256.857 | 0.0866 | −339.99 | 0.0348 | |
| GP | −427.811 | 0 | −475.892 | 0 | −676.391 | 0 | |
| GEV | −282.934 | 0.6941 | −312.324 | 0.4499 | −386.761 | 0.174 | |
| WBL | −281.932 | 0.5106 | −315.351 | 0.6396 | −415.183 | 0.2938 | |
| Copula | Parameters and Goodness of Fit Index | LJC | XY | HX |
|---|---|---|---|---|
| Clayton | 2.098 | 7.132 | 0.050 | |
| OLS | 0.071 | 0.057 | 0.181 | |
| AIC | −86.783 | −94.304 | −34.542 | |
| Frank | 9.829 | 40.229 | 28.017 | |
| OLS | 0.054 | 0.047 | 0.077 | |
| AIC | −96.422 | −100.643 | −53.330 | |
| Gumbel | 2.887 | 4.299 | 2.687 | |
| OLS | 0.050 | 0.063 | 0.104 | |
| AIC | −98.522 | −90.740 | −46.728 | |
| Best Function | Gumbel | Frank | Frank | |
| Drought Duration (month) | Drought Severity (mm) | ||||||
|---|---|---|---|---|---|---|---|
| LJC | XY | HX | LJC | XY | HX | ||
| Return period (year) | 2 | 7.452 | 8.152 | 6.551 | 1.156 | 1.690 | 1.041 |
| 5 | 12.500 | 12.962 | 9.272 | 3.449 | 5.702 | 4.357 | |
| 10 | 15.370 | 15.759 | 10.903 | 6.327 | 9.520 | 7.711 | |
| 20 | 17.841 | 18.184 | 12.329 | 10.954 | 13.859 | 11.483 | |
| 50 | 20.718 | 21.021 | 14.001 | 21.752 | 20.269 | 16.877 | |
| 100 | 22.685 | 22.966 | 15.149 | 36.024 | 25.564 | 21.168 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Lü, H.; Fu, G.; Zhu, Y.; Su, J.; Wang, J. Uncertainty of Hydrological Drought Characteristics with Copula Functions and Probability Distributions: A Case Study of Weihe River, China. Water 2017, 9, 334. https://doi.org/10.3390/w9050334
Zhao P, Lü H, Fu G, Zhu Y, Su J, Wang J. Uncertainty of Hydrological Drought Characteristics with Copula Functions and Probability Distributions: A Case Study of Weihe River, China. Water. 2017; 9(5):334. https://doi.org/10.3390/w9050334
Chicago/Turabian StyleZhao, Panpan, Haishen Lü, Guobin Fu, Yonghua Zhu, Jianbin Su, and Jianqun Wang. 2017. "Uncertainty of Hydrological Drought Characteristics with Copula Functions and Probability Distributions: A Case Study of Weihe River, China" Water 9, no. 5: 334. https://doi.org/10.3390/w9050334
APA StyleZhao, P., Lü, H., Fu, G., Zhu, Y., Su, J., & Wang, J. (2017). Uncertainty of Hydrological Drought Characteristics with Copula Functions and Probability Distributions: A Case Study of Weihe River, China. Water, 9(5), 334. https://doi.org/10.3390/w9050334







