Dynamics of Water Vapor Content around Isolated Sprinklers: Description and Validation of Model
Abstract
:1. Introduction
2. Theoretical Considerations
2.1. Vapor Pressure Deficit
2.2. Water Vapor Dynamics during Irrigation
2.3. Water Vapor Dynamics after Irrigation
2.4. Overall Water Vapor Dynamics
3. Materials and Methods
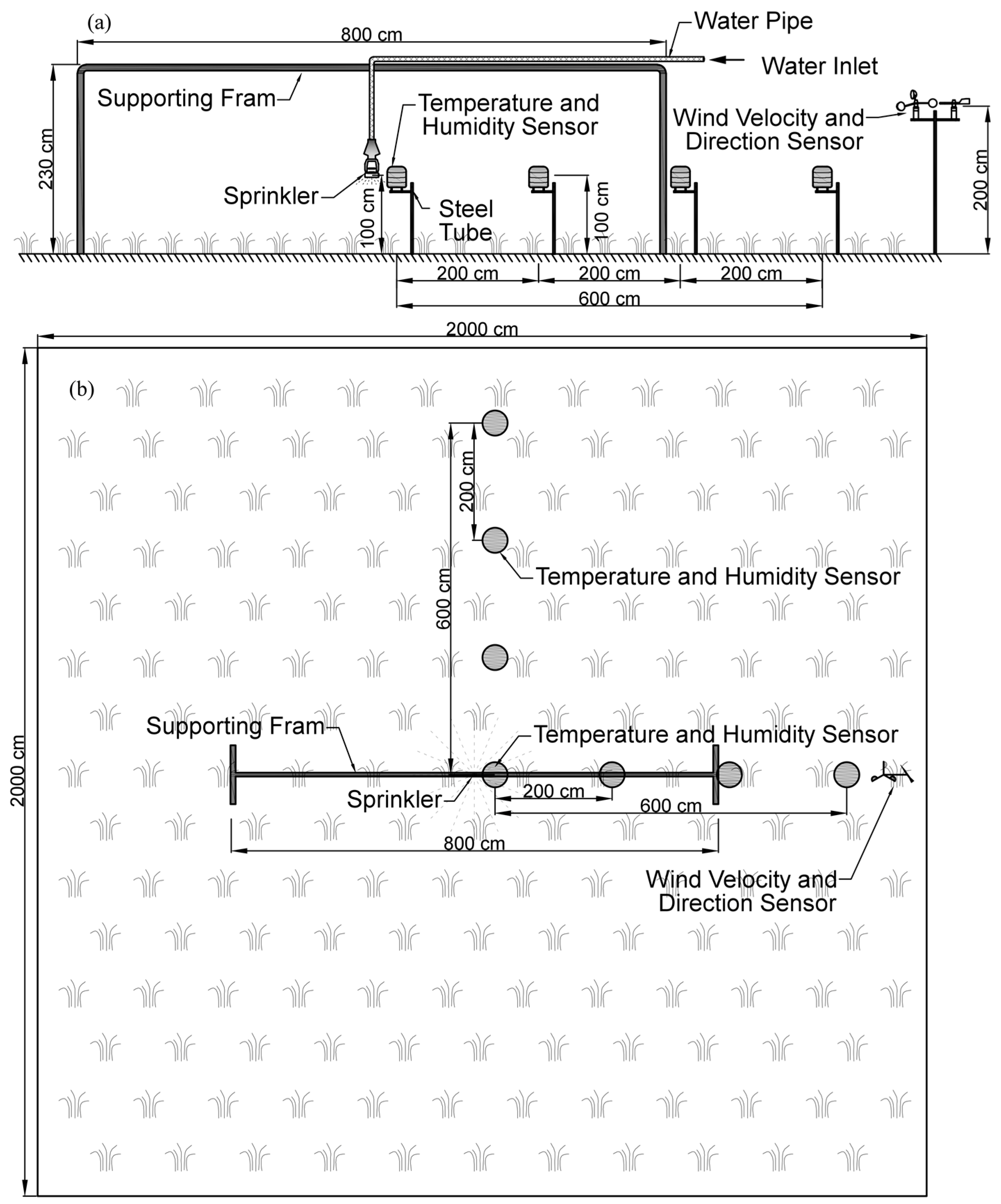
3.1. Experimental Site
3.2. Simulator for Single Sprinkler
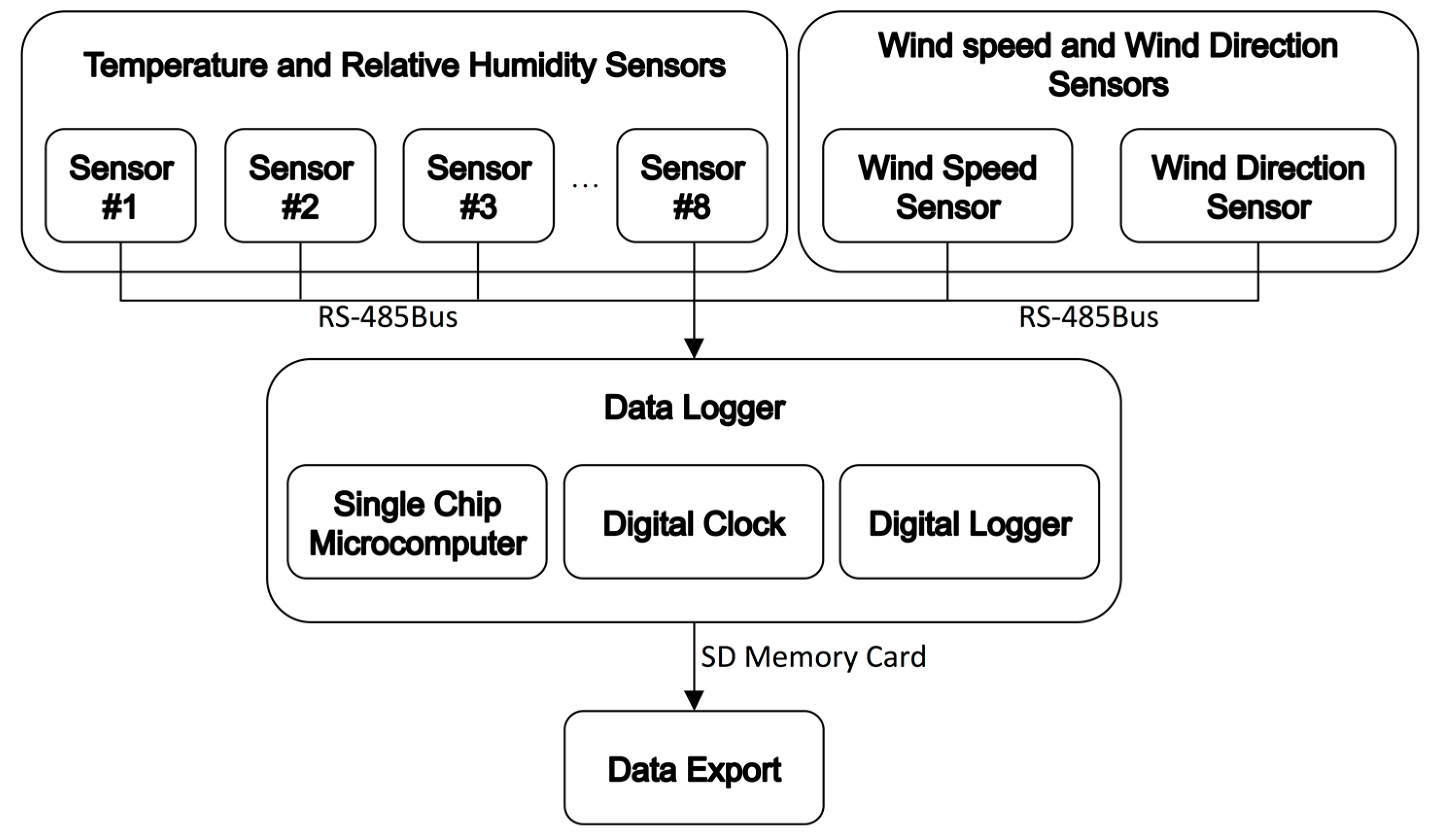
3.3. Water Vapor Measuring System
3.4. Statistics Processing and Analysis
3.5. General Characteristics of the Experiments
4. Results and Discussion
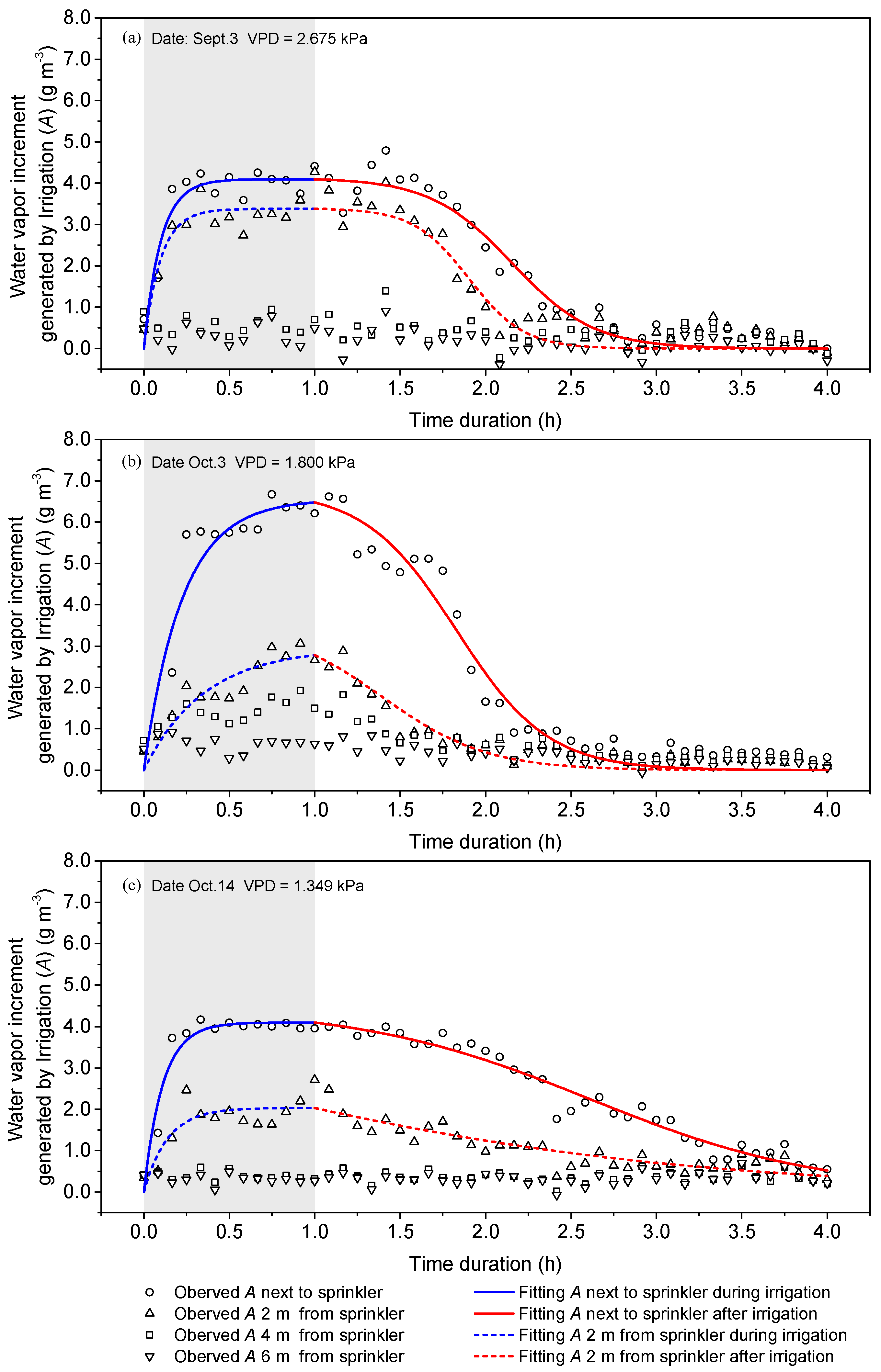
4.1. Water Vapor Dynamics
4.2. Water Vapor Dynamics and Meterorology
4.3. Water Vapor Increment
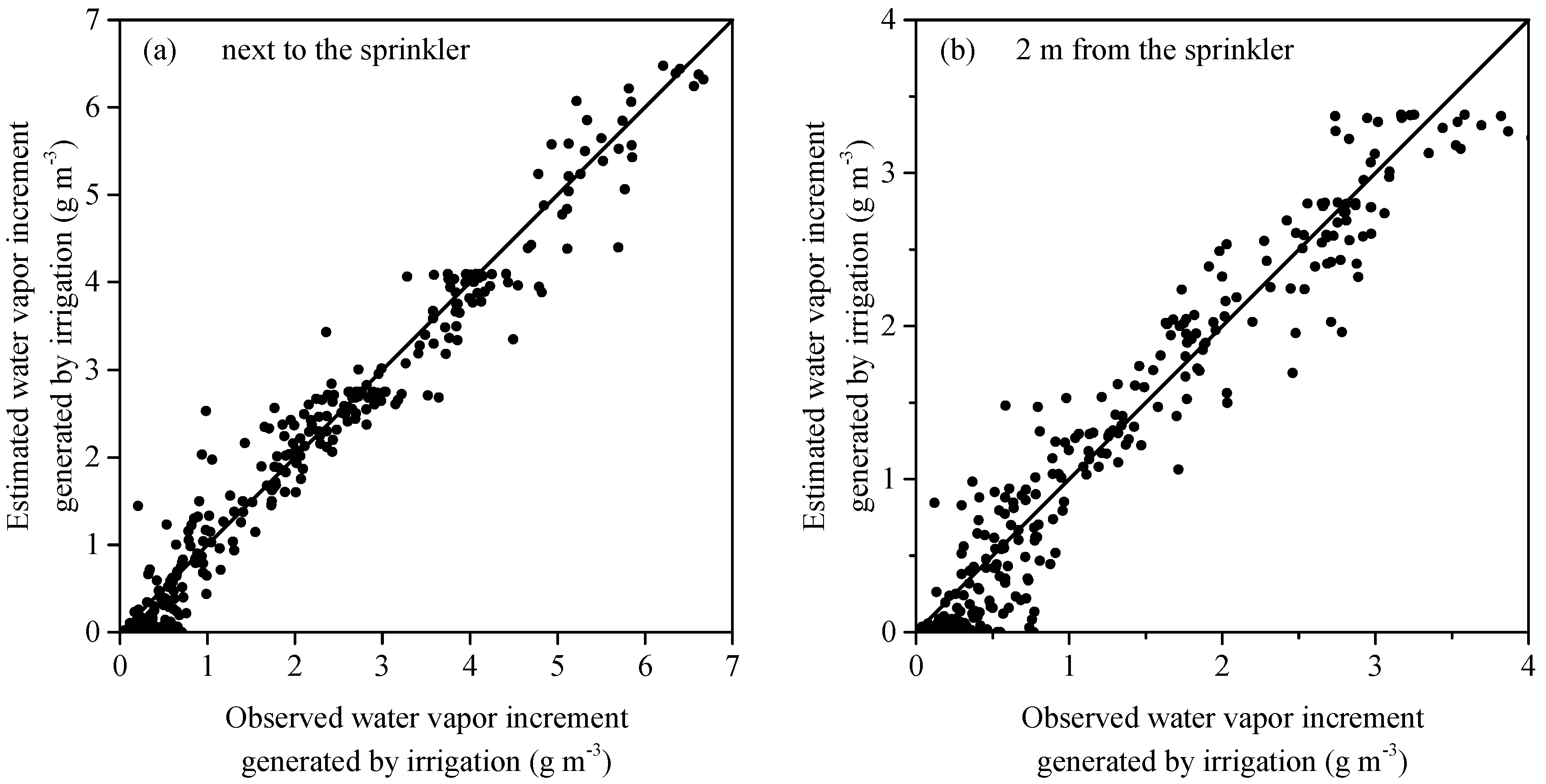
4.4. Model Validation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Boucher, O.; Myhre, G.; Myhre, A. Direct human influence of irrigation on atmospheric water vapour and climate. Clim. Dyn. 2004, 22, 597–603. [Google Scholar] [CrossRef]
- Douglas, E.M.; Niyogi, D.; Frolking, S.; Yeluripati, J.B.; Pielke, R.A.; Niyogi, N.; Vörösmarty, C.J.; Mohanty, U.C. Changes in moisture and energy fluxes due to agricultural land use and irrigation in the Indian Monsoon Belt. Geophys. Res. Lett. 2006, 33, 70–84. [Google Scholar] [CrossRef]
- Jaramillo, F.; Destouni, G. Local flow regulation and irrigation raise global human water consumption and footprint. Science 2015, 350, 1248–1251. [Google Scholar] [CrossRef] [PubMed]
- Rost, S.; Gerten, D.; Bondeau, A.; Lucht, W.; Rohwer, J.; Schaphoff, S. Agricultural green and blue water consumption and its influence on the global water system. Water Resour. Res. 2008, 44, 137–148. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.; Wanders, N.; Bierkens, M.F. Human water consumption intensifies hydrological drought worldwide. Environ. Res. Lett. 2013, 8, 034036. [Google Scholar] [CrossRef]
- Sun, Q.Z.; Yu, Z.; Ma, C.H.; Xu, C.C. Achievements of the alfalfa industry in last decade and priorities in next decade in China. Pratacult. Sci. 2013, 30, 471–477. [Google Scholar]
- Li, L.; Li, N.; Sheng, J.D.; Wang, H. Effects of nitrogen fertilizer and planting density on alfalfa growth and seed yield. Acta Agrestia Sin. 2012, 20, 54–57. [Google Scholar]
- Urrego-Pereira, Y.; Cavero, J.; Medina, E.; Martínez-Cob, A. Role of transpiration reduction during center-pivot sprinkler irrigation in application efficiency. J. Irrig. Drain. Eng. 2013, 139, 221–232. [Google Scholar] [CrossRef]
- Ouazaa, S.; Latorre, B.; Burguete, J.; Serreta, A.; Playán, E.; Salvador, R.; Paniagua, P.; Zapata, N. Effect of the start-stop cycle of center-pivot towers on irrigation performance: Experiments and simulations. Agric. Water Manag. 2015, 147, 163–174. [Google Scholar] [CrossRef]
- Foley, J.P. Centre pivot and lateral move machines. In WATERpak A Guide for Irrigation Management in Cotton; Cotton Research and Development Corporation: Narrabri, Australia, 2008; pp. 195–220. [Google Scholar]
- Chalfant, R.B.; Young, J.R. Chemigation, or application of insecticide through overhead sprinkler irrigation systems, to manage insect pests infesting vegetable and agronomic crops. J. Econ. Entomol. 1982, 75, 237–241. [Google Scholar] [CrossRef]
- Omary, M.; Camp, C.R.; Sadler, E.J. Center pivot irrigation system modification to provide variable water application depths. Trans. ASAE 1997, 13, 235–239. [Google Scholar]
- Faci, J.; Salvador, R.; Playán, E.; Sourell, H. Comparison of fixed and rotating spray plate sprinklers. J. Irrig. Drain. Eng. 2001, 127, 224–233. [Google Scholar] [CrossRef]
- Smajstrla, A.G.; Zazueta, F. Evaporation Loss during Sprinkler Irrigation; University of Florida Cooperative Extension Service, Institute of Food and Agriculture Sciences; EDIS: Gainesville, FL, USA, 1994. [Google Scholar]
- Uddin, J.; Smith, R.; Hancock, N.; Foley, J.P. Droplet evaporation losses during sprinkler irrigation: An overview. In Proceedings of the Australian Irrigation Conference and Exibition, Sydney, Australia; Irrigation Australia Ltd.: Sydney, Australia, 2010; pp. 1–10. [Google Scholar]
- Stambouli, T.; Martinez-Cob, A.; Faci, J.M.; Howell, T.; Zapata, N. Sprinkler evaporation losses in alfalfa during solid-set sprinkler irrigation in semiarid areas. Irrig. Sci. 2013, 31, 1075–1089. [Google Scholar] [CrossRef]
- Kohl, R.; Wright, J. Air temperature and vapor pressure changes caused by sprinkler irrigation. Agron. J. 1974, 66, 85–88. [Google Scholar] [CrossRef]
- Steiner, J.L.; Kanemasu, E.T.; Clark, R.N. Spray losses and partitioning of water under a center pivot sprinkler system. Trans. ASAE 1983, 26, 1128–1134. [Google Scholar] [CrossRef]
- ASAE Standards. Test Procedure for Determining the Uniformity of Water Distribution of Centre Pivot, Corner Pivot and Moving Lateral Irrigation Machines Equipped with Spray or Sprinkler Nozzles; ASAE: St. Joseph, MI, USA, 1995; Volume ANSI/ASAE S436.1. [Google Scholar]
- ISO 11545:2009. Agricultural Irrigation Equipment—Centre-Pivot and Moving Lateral Irrigation Machines with Sprayer or Sprinkler Nozzles—Determination of Uniformity of Water Distribution; ISO: Geneva, Switzerland, 2009; Volume ISO-11545. [Google Scholar]
- Tarjuelo, J.M.; Ortega, J.F.; Montero, J.; de Juan, J.A. Modelling evaporation and drift losses in irrigation with medium size impact sprinklers under semi-arid conditions. Agric. Water Manag. 2000, 43, 263–284. [Google Scholar] [CrossRef]
- Dechmi, F.; Playán, E.; Cavero, J.; Faci, J.; Martínez-Cob, A. Wind effects on solid set sprinkler irrigation depth and yield of maize (Zea mays). Irrig. Sci. 2003, 22, 67–77. [Google Scholar] [CrossRef]
- Playán, E.; Salvador, R.; Faci, J.M.; Zapata, N.; Martínez-Cob, A.; Sánchez, I. Day and night wind drift and evaporation losses in sprinkler solid-sets and moving laterals. Agric. Water Manag. 2005, 76, 139–159. [Google Scholar] [CrossRef]
- Ortíz, J.N.; Tarjuelo, J.M.; de Juan, J.A. Characterisation of evaporation and drift losses with centre pivots. Agric. Water Manag. 2009, 96, 1541–1546. [Google Scholar] [CrossRef]
- Sanchez, I.; Zapata, N.; Faci, J.M. Combined effect of technical, meteorological and agronomical factors on solid-set sprinkler irrigation: II. Modifications of the wind velocity and of the water interception plane by the crop canopy. Agric. Water Manag. 2010, 97, 1591–1601. [Google Scholar] [CrossRef]
- Martínez-Cob, A.; Playán, E.; Zapata, N.; Cavero, J.; Medina, E.; Puig, M. Contribution of evapotranspiration reduction during sprinkler irrigation to application efficiency. J. Irrig. Drain. Eng. 2008, 134, 745–756. [Google Scholar] [CrossRef]
- Sanchez, I.; Faci, J.M.; Zapata, N. The effects of pressure, nozzle diameter and meteorological conditions on the performance of agricultural impact sprinklers. Agric. Water Manag. 2011, 102, 13–24. [Google Scholar] [CrossRef]
- Playán, E.; Garrido, S.; Faci, J.M.; Galán, A. Characterizing pivot sprinklers using an experimental irrigation machine. Agric. Water Manag. 2004, 70, 177–193. [Google Scholar] [CrossRef]
- Sadeghi, S.-H.; Peters, T.R.; Amini, M.Z.; Malone, S.L.; Loescher, H.W. Novel approach to evaluate the dynamic variation of wind drift and evaporation losses under moving irrigation systems. Biosyst. Eng. 2015, 135, 44–53. [Google Scholar] [CrossRef]
- George, T.J. Evaporation from Irrigation Sprinkler Sprays as Determined by an Electrical Conductivity Method. Master’s Thesis, University of California, Davis, CA, USA, 1955. [Google Scholar]
- Kohl, K.D.; Kohl, R.A.; Deboer, D.W. Measurement of low pressure sprinkler evaporation loss. Trans. ASAE 1987, 30, 1071–1074. [Google Scholar] [CrossRef]
- Uddin, J.; Smith, R.J.; Hancock, N.H.; Foley, J.P. Evaporation and sapflow dynamics during sprinkler irrigation of cotton. Agric. Water Manag. 2013, 125, 35–45. [Google Scholar] [CrossRef]
- Faci, J.; Bercero, A. Wind effect on irrigation uniformity and on evaporation and wind drift losses in sprinkler systems. Investig. Agrar. Prod. Prot. Veg. 1991, 6, 171–182. [Google Scholar]
- Colombo, A.; Faria, L.C.; Silva, J.J.D.S.J.; Sant Ana, J.A.D.V.S.A.; Beskow, S.; Nörenberg, B.G.N. Modeling of evaporation and wind drift losses in rotating spray plate sprinklers. Rev. Bras. Eng. Agric. Ambient 2015, 19, 719–726. [Google Scholar] [CrossRef]
- Dechmi, F.; Playan, E.; Faci, J.; Tejero, M.; Bercero, A. Analysis of an irrigation district in northeastern spain: II. Irrigation evaluation, simulation and scheduling. Agric. Water Manag. 2003, 61, 93–109. [Google Scholar] [CrossRef]
- Beskow, S.; Faria, L.C.; Colombo, A.; Moura, D.C.M. Modeling of evaporation and wind drift losses in medium-pressure sprinklers. Rev. Bras. Eng. Agric. Ambient. 2011, 15, 221–228. [Google Scholar] [CrossRef]
- Yan, H.J.; Bai, G.; He, J.Q.; Li, Y.J. Model of droplet dynamics and evaporation for sprinkler irrigation. Biosyst. Eng. 2010, 106, 440–447. [Google Scholar] [CrossRef]
- De Wrachien, D.; Lorenzini, G. Modelling jet flow and losses in sprinkler irrigation: Overview and perspective of a new approach. Biosyst. Eng. 2006, 94, 297–309. [Google Scholar] [CrossRef]
- Liu, H.J.; Kang, Y.H. Effect of sprinkler irrigation on microclimate in the winter wheat field in the North China Plain. Agric. Water Manag. 2006, 84, 3–19. [Google Scholar] [CrossRef]
- Wang, D.; Li, J.; Rao, M. Estimation of net interception loss by crop canopy under sprinkler irrigation based on energy balance. Trans. Chin. Soc. Agric. Eng. 2007, 23, 27–33. [Google Scholar]
- Vaisala, O. Humidity Conversion Formulas; Vaisala Oyj: Helsinki, Finland, 2012. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef]
- Verhulst, P.F. Notice sur la loi que la population suit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–121. [Google Scholar]
- Andrewartha, H.G.; Birch, L.C. The Distribution and Abundance of Animals; University of Chicago Press: Chicago, IL, USA, 1954. [Google Scholar]
- Cavero, J.; Jiménez, L.; Puig, M.; Faci, J.M.; Martínez-Cob, A. Maize growth and yield under daytime and nighttime solid-set sprinkler irrigation. Agron. J. 2008, 100, 1573–1579. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- OriginPro Originlab Originpro Version 9.2, OriginPro Corp.: Northampton, MA, USA, 2014.
- Argus. Understanding and Using vpd. Argus Application Note. Available online: http://www.arguscontrols.com/resources/VPD_Application_Note.pdf (accessed on 9 November 2016).
- Leonardi, C.; Guichard, S.; Bertin, N. High vapour pressure deficit influences growth, transpiration and quality of tomato fruits. Sci. Hortic. 2000, 84, 285–296. [Google Scholar] [CrossRef]
- Urrego-Pereira, Y.; Cavero, J.; Medina, E.T.; Martínez-Cob, A. Microclimatic and physiological changes under a center pivot system irrigating maize. Agric. Water Manag. 2013, 119, 19–31. [Google Scholar] [CrossRef]
- Sayyadi, H.; Nazemi, A.H.; Sadraddini, A.A.; Delirhasannia, R. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler. Biosyst. Eng. 2014, 119, 13–24. [Google Scholar] [CrossRef]
- Raviv, M. Soilless Culture: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Stambouli, T.; Zapata, N.; Faci, J.M. Performance of new agricultural impact sprinkler fitted with plastic nozzles. Biosyst. Eng. 2014, 118, 39–51. [Google Scholar] [CrossRef]
- Yazar, A. Evaporation and drift losses from sprinkler irrigation systems under various operating conditions. Agric. Water Manag. 1984, 8, 439–449. [Google Scholar] [CrossRef]
- Cavero, J.; Medina, E.; Puig, M.; Martínez-Cob, A. Sprinkler irrigation changes maize canopy microclimate and crop water status, transpiration, and temperature. Agron. J. 2009, 101, 854–864. [Google Scholar] [CrossRef]
- Zhao, W.X.; Li, J.S.; Li, Y.F. Modeling sprinkler efficiency with consideration of microclimate modification effects. Agric. For. Meteorol. 2012, 161, 116–122. [Google Scholar] [CrossRef]
- Weaver, H.L. Temperature and humidity flux-variance relations determined by one-dimensional eddy correlation. Bound. Lay. Meteorol. 1990, 53, 77–91. [Google Scholar] [CrossRef]
- Kinoshita, N. Nonuniform distribution of high-frequency turbulence in the unstable boundary layer. Bound. Lay. Meteorol. 2003, 106, 61–91. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and nse performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Suleiman, A.A.; Tojo Soler, C.M.; Hoogenboom, G. Evaluation of FAO-56 crop coefficient procedures for deficit irrigation management of cotton in a humid climate. Agric. Water Manag. 2007, 91, 33–42. [Google Scholar] [CrossRef]
- Fan, J.; Oestergaard, K.T.; Guyot, A.; Lockington, D.A. Measuring and modeling rainfall interception losses by a native banksia woodland and an exotic pine plantation in subtropical coastal Australia. J. Hydrol. 2014, 515, 156–165. [Google Scholar] [CrossRef]
- Fang, Q.; Ma, L.; Yu, Q.; Ahuja, L.R.; Malone, R.W.; Hoogenboom, G. Irrigation strategies to improve the water use efficiency of wheat–maize double cropping systems in north china plain. Agric. Water Manag. 2010, 97, 1165–1174. [Google Scholar] [CrossRef]
- Joshi, S.N.; Pate, M.B.; Nelson, R.M.; House, J.M.; Klaassen, C.J. An experimental evaluation of duct-mounted relative humidity sensors: Part 2-accuracy results. ASHRAE Trans. 2005, 111, 167–176. [Google Scholar]
- Sensirion, A.G. Data Sheet SHT7x (SHT 71, SHT 75)-Humidity and Temperature Sensor IC. Available online: https://www.sensirion.com/fileadmin/user_upload/customers/sensirion/Dokumente/2_Humidity_Sensors/Sensirion_Humidity_Sensors_SHT7x_Datasheet_V5.pdf (accessed on 30 December 2014).
- Urrego-Pereira, Y.F.; Martínez-Cob, A.; Fernández, V.; Cavero, J. Daytime sprinkler irrigation effects on net photosynthesis of maize and alfalfa. Agron. J. 2013, 105, 1515–1528. [Google Scholar] [CrossRef]


| Tests | Date | RH (%) | T (°C) | W (m s−1) | VPD (kPa) |
|---|---|---|---|---|---|
| 1 | 29 August | 44.18 | 31.09 | 0.70 | 2.521 |
| 2 | 3 September | 43.10 | 31.80 | 0.81 | 2.675 |
| 3 | 21 September | 42.59 | 28.05 | 0.52 | 2.176 |
| 4 | 3 October | 41.75 | 24.58 | 0.89 | 1.800 |
| 5 | 9 October | 20.81 | 19.70 | 0.90 | 1.818 |
| 6 | 14 October | 48.21 | 21.75 | 0.80 | 1.349 |
| 7 | 1 November | 31.07 | 17.29 | 0.84 | 1.360 |
| Date | Distance (m) | Model: During Irrigation 0 < t ≤ ts | Model: After Irrigation t ≥ ts | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Am1 (g m−3) | k (h−1) | Ra2 | p | Am2 (g m−3) | As (g m−3) | r (h−1) | ts (h) | Ra2 | p | ||
| 29 August | 0 | 2.746 | 17.675 | 0.894 | <0.001 | 2.769 | 2.746 | 4.015 | 1 | 0.960 | <0.001 |
| 2 | 2.808 | 7.599 | 0.944 | <0.001 | 3.430 | 2.806 | 2.593 | 1 | 0.971 | <0.001 | |
| 3 September | 0 | 4.096 | 10.103 | 0.858 | <0.001 | 4.129 | 4.096 | 4.174 | 1 | 0.956 | <0.001 |
| 2 | 3.380 | 10.320 | 0.790 | <0.001 | 3.393 | 3.380 | 6.176 | 1 | 0.901 | <0.001 | |
| 21 September | 0 | 2.682 | 7.957 | 0.673 | <0.001 | 2.921 | 2.681 | 1.902 | 1 | 0.974 | <0.001 |
| 2 | 2.609 | 5.300 | 0.756 | <0.001 | 4.868 | 2.596 | 1.765 | 1 | 0.935 | <0.001 | |
| 3 October | 0 | 6.552 | 4.449 | 0.898 | <0.001 | 6.769 | 6.476 | 3.731 | 1 | 0.966 | <0.001 |
| 2 | 2.958 | 2.822 | 0.808 | <0.001 | 3.545 | 2.782 | 3.271 | 1 | 0.912 | <0.001 | |
| 9 October | 0 | 5.842 | 3.403 | 0.868 | <0.001 | 5.768 | 5.648 | 6.460 | 1 | 0.980 | <0.001 |
| 2 | 3.426 | 3.394 | 0.817 | <0.001 | 3.672 | 3.311 | 4.206 | 1 | 0.952 | <0.001 | |
| 14 October | 0 | 4.094 | 9.010 | 0.925 | <0.001 | 4.474 | 4.094 | 1.471 | 1 | 0.966 | <0.001 |
| 2 | 2.029 | 7.209 | 0.644 | <0.001 | 6.106 | 2.028 | 0.672 | 1 | 0.759 | <0.001 | |
| 1 November | 0 | 2.557 | 3.930 | 0.862 | <0.001 | 2.778 | 2.506 | 1.883 | 1 | 0.969 | <0.001 |
| 2 | 1.322 | 3.370 | 0.947 | <0.001 | 1.357 | 1.277 | 2.334 | 1 | 0.957 | <0.001 | |
| Coefficients | Model Performance | |
|---|---|---|
| Next to the Sprinkler | 2 m from Sprinkler | |
| SD | 1.72 | 1.04 |
| RMSE | 0.34 | 0.27 |
| ni | 4.05 | 2.91 |
| Nash—Sutcliffe model efficiency coefficient | 0.961 | 0.934 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, J.; Su, D.; Wang, Y. Dynamics of Water Vapor Content around Isolated Sprinklers: Description and Validation of Model. Water 2017, 9, 307. https://doi.org/10.3390/w9050307
Jiao J, Su D, Wang Y. Dynamics of Water Vapor Content around Isolated Sprinklers: Description and Validation of Model. Water. 2017; 9(5):307. https://doi.org/10.3390/w9050307
Chicago/Turabian StyleJiao, Jian, Derong Su, and Yadong Wang. 2017. "Dynamics of Water Vapor Content around Isolated Sprinklers: Description and Validation of Model" Water 9, no. 5: 307. https://doi.org/10.3390/w9050307
APA StyleJiao, J., Su, D., & Wang, Y. (2017). Dynamics of Water Vapor Content around Isolated Sprinklers: Description and Validation of Model. Water, 9(5), 307. https://doi.org/10.3390/w9050307





