Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution
Abstract
:1. Introduction
2. Materials and Methods
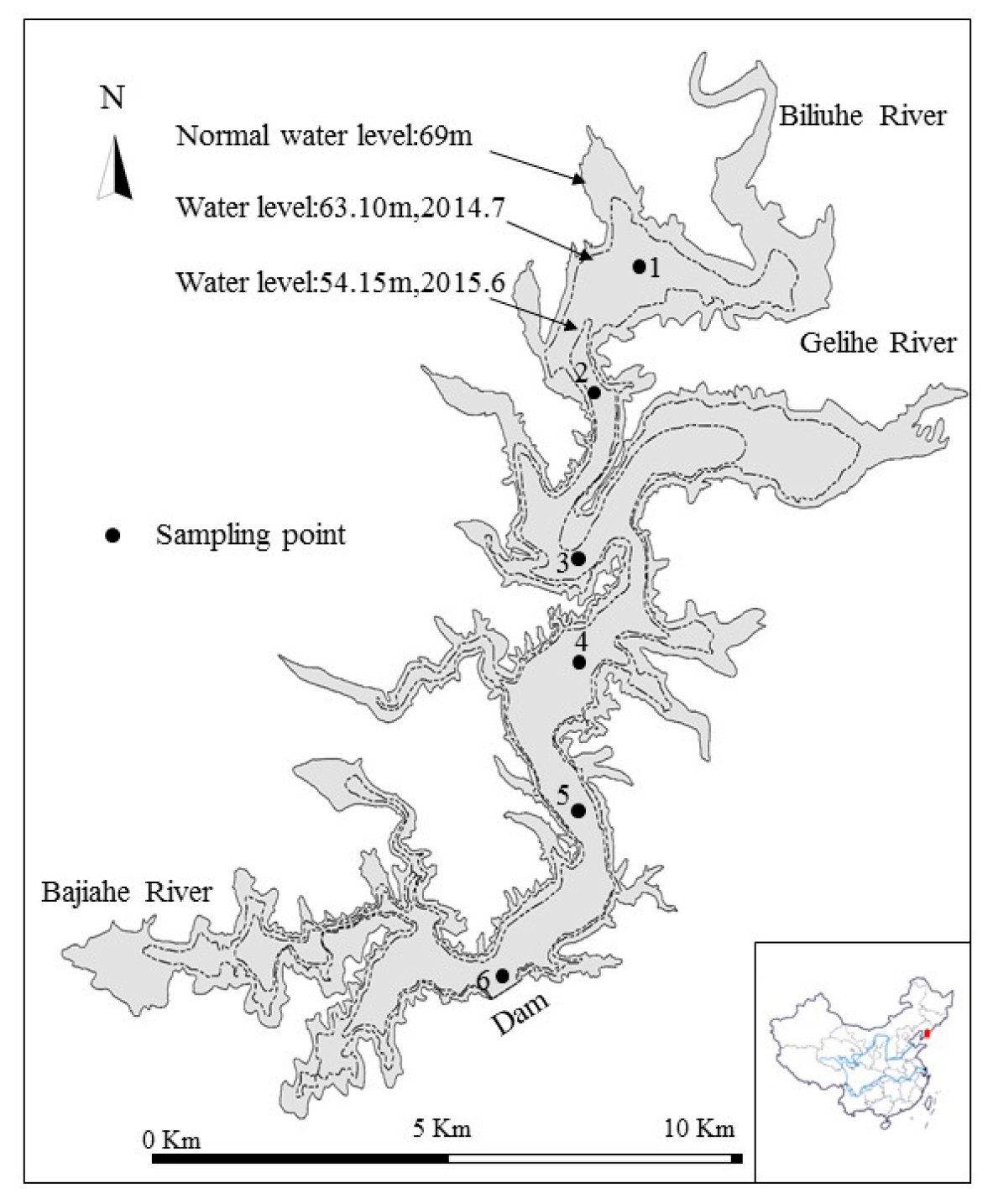
2.1. Study Area and Sampling
2.2. Experiment on Sediment Pollutant Release
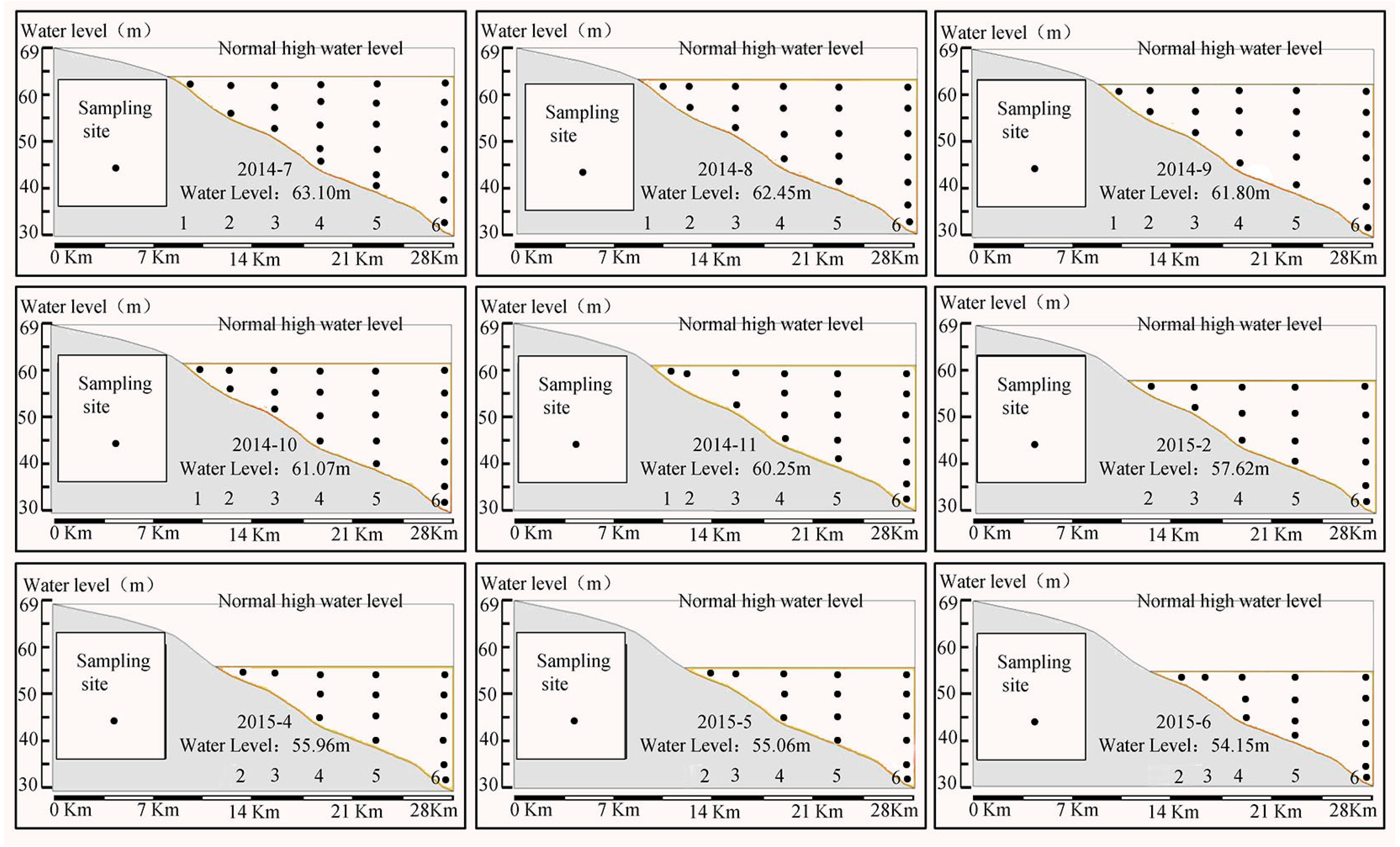
2.3. Dynamic Display of Water Quality Elements (Assessment Results)
- (1)
- Generate the DEM map of the study area based on the 1:5000 topographic map
- (2)
- Extract the dynamic boundaries according to the water level
- (3)
- Import the positions of the sampling points
- (4)
- Import the water quality elements (assessment results) of each sample
- (5)
- Generate the distribution of water quality, overall, by the inverse distance weighting method
- (6)
- Export the dynamic distribution diagram of the water quality after inserting a legend
2.4. Assessment Model of Water Quality
2.5. Steps of Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution
3. Results and Discussion
3.1. Analysis of the Reasonability of Assessment Model
3.2. Analysis of Release Ability of Nitrogen and Phosphorus in Sediment
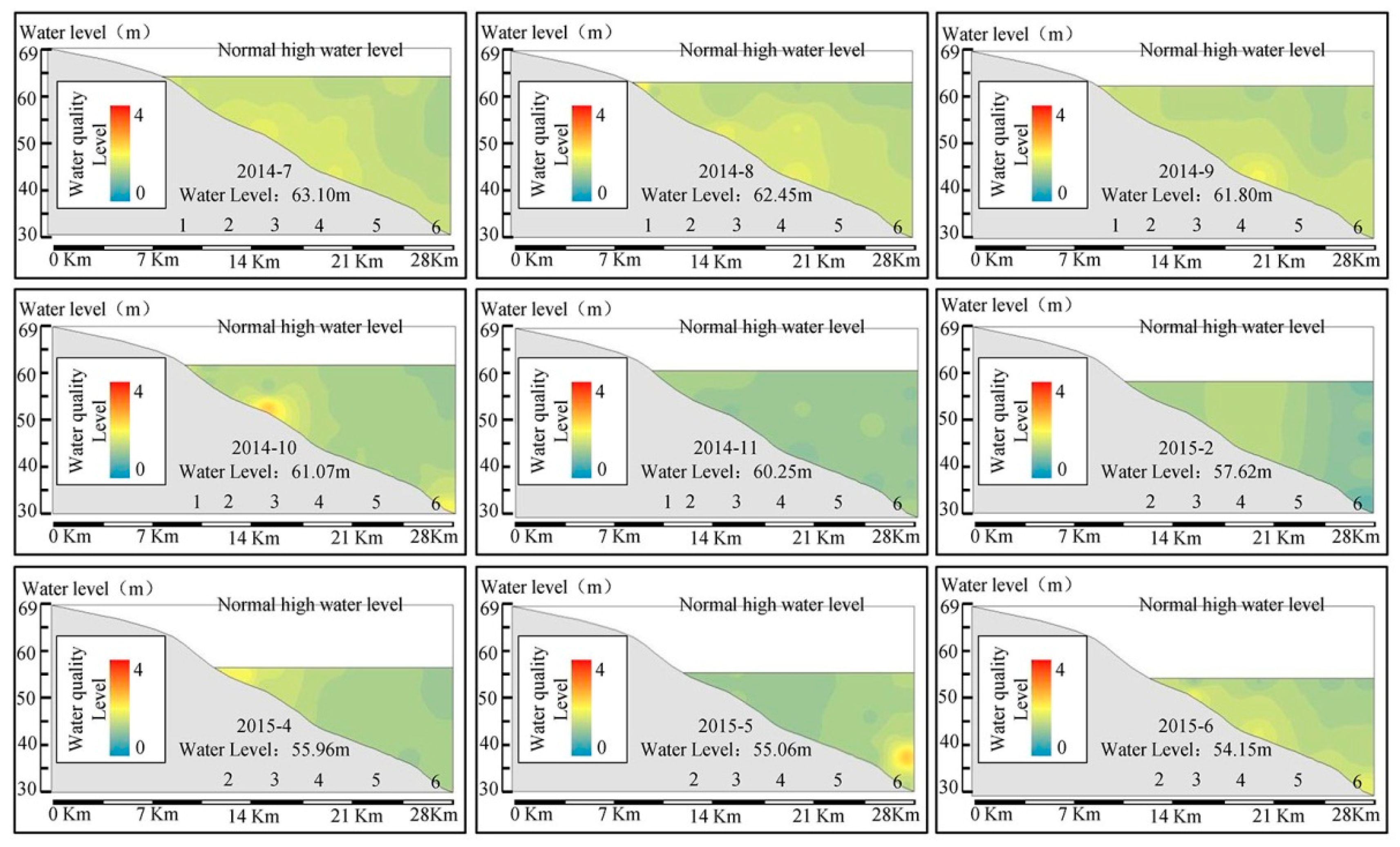
3.3. Results of Comprehensive Water Quality Assessment
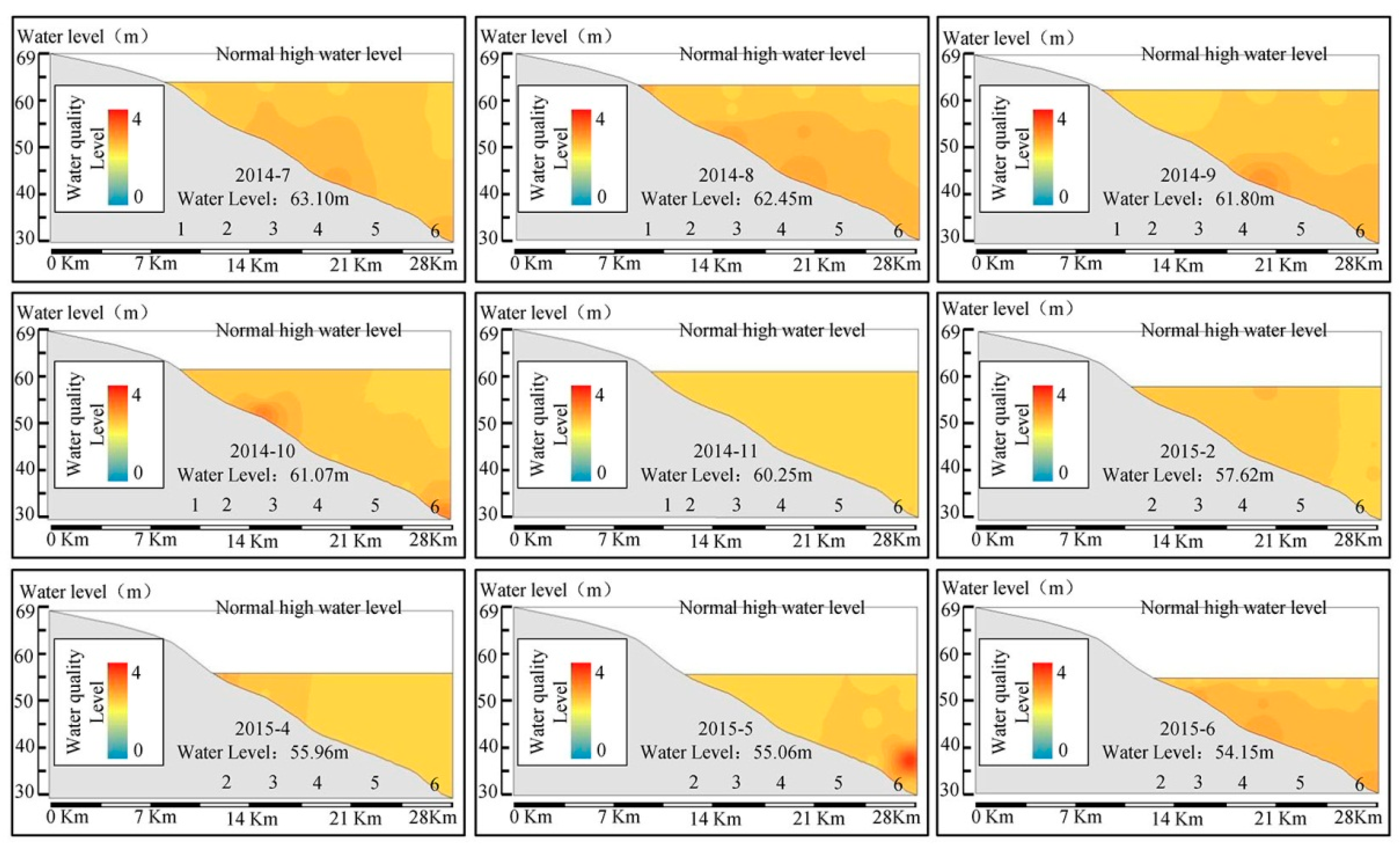
3.4. Assessment Results of Comprehensive Water Quality Considering Release of Sediment Pollution
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tan, X.; Sheldon, F.; Bunn, S.E.; Zhang, Q.F. Using diatom indices for water quality assessment in a subtropical river, China. Environ. Sci. Pollut. Res. 2013, 20, 4164–4175. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.G.; Wang, T.X. Review of research on accumulation process and effect of internal pollution of reservoir. Adv. Sci. Technol. Water Resour. 2015, 35, 162–167. (In Chinese) [Google Scholar] [CrossRef]
- Jin, X.C.; Wang, S.R.; Jiang, X. Preliminary study of the three dimension model of the lake water sediment interface. Res. Environ. Sci. 2004, 17, 1–6. (In Chinese) [Google Scholar]
- Cheng, H.M.; Hua, Z.L. Effects of hydrodynamic disturbances and resuspension characteristics on the release of tetrabromobisphenol A from sediment. Environ. Pollut. 2016, 219, 785–793. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; He, F.; Liu, Z.S.; Liu, B.Y.; Zhou, Q.H.; Wu, Z.B. Release characteristics of sediment phosphorus in all fractions of West Lake, Hang Zhou, China. Ecol. Eng. 2016, 95, 645–651. [Google Scholar] [CrossRef]
- Puttonen, I.; Kohonen, T.; Mattila, J. Factors controlling phosphorus release from sediments in coastal archipelago areas. Mar. Pollut. Bull. 2016, 108, 77–86. [Google Scholar] [CrossRef] [PubMed]
- Hongthanat, N.; Kovar, J.L.; Thompson, M.L. Phosphorus source-sink relationships of stream sediments in the Rathbun Lake watershed in southern Iowa, USA. Environ Monit. Assess. 2016, 188, 453. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhou, Y.Y.; Wang, X. Transport dynamics of Cr and Zn between deposited sediment and overlying water. Clean Soil Air Water 2016, 44, 1453–1460. [Google Scholar] [CrossRef]
- Yang, Q.Z.; Zhao, H.Z.; Zhao, N.N.; Ni, J.R.; Gu, X.J. Enhanced phosphorus flux from overlying water to sediment in a bioelectrochemical system. Bioresour. Technol. 2016, 216, 182–187. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhao, Y.J.; Wang, X.; Liang, D.F. Fluctuations in Cd release from surface-deposited sediment in a river-connected lake following dredging. J. Geochem. Explor. 2017, 172, 184–194. [Google Scholar] [CrossRef]
- Wu, Y.H.; Wen, Y.J.; Zhou, J.X. Phosphorus Release from Lake Sediments: Effects of pH, Temperature and Dissolved Oxygen. Ksce J. Civ. Eng. 2014, 18, 323–329. [Google Scholar] [CrossRef]
- Liu, C.; Zhong, J.C.; Wang, J.J.; Zhang, L.; Fan, C.X. Fifteen-year study of environmental dredging effect on variation of nitrogen and phosphorus exchange across the sediment-water interface of an urban lake. Environ. Pollut. 2016, 219, 639–648. [Google Scholar] [CrossRef] [PubMed]
- National Service Center for Environmental Publications (USEPA). EPA’s Contaminated Sediment Management Strategy; National Service Center for Environmental Publications: Washington, DC, USA, 1998.
- Zhang, X.H. Water Environment Restoration Engineering Principle and Its Application; Chemical Industry Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Wu, G.D.; Wei, Z.; Su, R.X. Distribution, accumulation and mobility of mercury in superficial sediment samples from Tianjin, northern China. J. Environ. Monitor. 2011, 13, 2488–2495. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.H.; Qin, Y.W.; Zhang, L.; Ma, Y.Q.; Zhao, Y.M.; Wen, Q. Sixty-year sedimentary records of polymetallic contamination (Cu, Zn, Cd, Pb, As) in the Dahuofang Reservoir in Northeast China. Environ. Earth Sci. 2016, 75, 486. [Google Scholar] [CrossRef]
- Ji, D.B.; Wells, S.A.; Yang, Z.J.; Liu, D.F.; Huang, Y.L.; Ma, J.; Berger, C.J. Impacts of water level rise on algal bloom prevention in the tributary of Three Gorges Reservoir, China. Ecol. Eng. 2017, 98, 70–81. [Google Scholar] [CrossRef]
- Lamastra, L.; Balderacchi, M.; Di, G.A.; Monchiero, M.; Trevisan, M. A novel fuzzy expert system to assess the sustainability of the viticulture at the wine-estate scale. Sci. Total Environ. 2016, 572, 724–733. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Zhang, L.G.; Zeng, Y.; Zuo, C.Y.; Li, J. Water Quality Comprehensive Index Method of Eltrix River in Xin Jiang Province using SPSS. Procedia Earth Plantetary Sci. 2012, 5, 314–321. [Google Scholar] [CrossRef]
- Lopez-Doval, J.C.; Montagner, C.C.; de Alburquerque, A.F.; Moschini-Carlos, V.; Umbuzeiro, G.; Pompeo, M. Nutrients, emerging pollutants and pesticides in a tropical urban reservoir: Spatial distributions and risk assessment. Sci. Total Environ. 2017, 575, 1307–1324. [Google Scholar] [CrossRef] [PubMed]
- Sinha, K.; Das, P. Assessment of water quality index using cluster analysis and artificial neural network modeling: A case study of Hooghly river basin, west Bengal, India. Desalin. Water Treat. 2015, 54, 28–36. [Google Scholar] [CrossRef]
- Chu, H.B.; Lu, W.X.; Zhang, L. Application of artificial neural network in environmental water quality assessment. J. Agric. Sci. Technol. 2013, 2, 343–356. [Google Scholar]
- Yan, F.; Liu, L.; Zhang, Y.; Chen, M.S.; Chen, N. The research of dynamic variable fuzzy set assessment model in water quality evaluation. Water Resour. Manag. 2016, 30, 63–78. [Google Scholar] [CrossRef]
- Logez, M.; Roy, R.; Tissot, L.; Argillier, C. Effects of water-level fluctuations on the environmental characteristics and fish-environment relationships in the littoral zone of a reservoir. Fund. Appl. Limnol. 2016, 189, 37–49. [Google Scholar] [CrossRef]
- Easton, Z.M. Defining Spatial Heterogeneity of Hillslope Infiltration Characteristics Using Geostatistics, Error Modeling, and Autocorrelation Analysis. J. Irrig. Drain-ASCE 2013, 139, 718–727. [Google Scholar] [CrossRef]
- Deshmukh, K.K.; Aher, S.P. Assessment of the Impact of Municipal Solid Waste on Groundwater Quality near the Sangamner City using GIS Approach. Water Resour. Manag. 2016, 30, 2425–2443. [Google Scholar] [CrossRef]
- Peng, H.; Zhou, H.C.; Li, M. Assessing water renewal of the northern coastal zone in China using a variable fuzzy pattern recognition model. J. Hydroinform. 2010, 12, 339–350. [Google Scholar] [CrossRef]
- Xu, S.G.; Wang, T.X.; Hu, S.D. Dynamic Assessment of Water Quality Based on a Variable Fuzzy Pattern Recognition Model. Int. J. Environ. Res. Public Health 2015, 12, 2230–2248. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Kumar, R.N. Assessment of groundwater quality at a MSW landfill site using standard and AHP based water quality index: A case study from Ranchi, Jharkhand, India. Environ. Monit. Assess. 2016, 188, 335. [Google Scholar] [CrossRef] [PubMed]
- Bozdag, A. Combining AHP with GIS for assessment of irrigation water quality in Cumra irrigation district (Konya), Central Anatolia, Turkey. Environ. Earth Sci. 2015, 73, 8217–8236. [Google Scholar] [CrossRef]
- Ou, C.P.; St-Hilaire, A.; Ouarda, T.B.M.J.; Conly, F.M.; Armstrong, N.; Khalil, B.; Proulx-Mclnnis, S. Coupling geostatistical approaches with PCA and fuzzy optimal model (FOM) for the integrated assessment of sampling locations of water quality monitoring networks (WQMNs). J. Environ. Monit. 2012, 14, 3118–3128. [Google Scholar] [CrossRef] [PubMed]
- Dalal, S.G.; Shirodkar, P.V.; Jagtap, T.G.; Naik, B.G.; Rao, G.S. Evaluation of significant sources influencing the variation of water quality of Kandla creek, Gulf of Katchchh, using PCA. Environ. Monit. Assess. 2010, 163, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.W.; Li, L.Y.; Lei, K.; Wang, L.J.; Zhai, Y.X.; Zhai, M. Water quality assessment of Wei River, China using fuzzy synthetic evaluation. Environ. Earth Sci. 2010, 60, 1693–1699. [Google Scholar] [CrossRef]
- Flores, P.E.D.; Geronimo, F.K.F.; Alihan, J.C.P.; Kim, L.H. Transport of nonpoint source pollutants and stormwater runoff in a hybrid rain garden system. J. Wetl. Res. 2016, 18, 481–487. [Google Scholar] [CrossRef]
- Nemirovskaya, I.A. Variations in different compounds in Volga water, suspension, and bottom sediments in the summer of 2009. Water Resour. 2012, 39, 533–545. [Google Scholar] [CrossRef]
- Stefanovic, D.L.; Stefan, H.G. Two-dimensional temperature and dissolved oxygen dynamics in the littoral region of an ice-covered lake. Cold Reg. Sci. Technol. 2002, 34, 159–178. [Google Scholar] [CrossRef]
- Reagan, M.T.; Moridis, G.J.; Keen, N.D.; Johnson, J.N. Numerical simulation of the environmental impact of hydraulic fracturing of tight/shale gas reservoirs on near-surface groundwater: Background, base cases, shallow reservoirs, short-term gas, and water transport. Water Resour. Res. 2015, 51, 2543–2573. [Google Scholar] [CrossRef] [PubMed]
- Doig, L.E.; North, R.L.; Hudson, J.J.; Hewlett, C.; Lindenschmidt, K.E.; Liber, K. Phosphorus release from sediments in a river-valley reservoir in the northern Great Plains of North America. Hydrobiologia 2017, 787, 323–339. [Google Scholar] [CrossRef]
| Indicators | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 (mg/L) | X2 (mg/L) | X3 (mg/L) | X4 (mg/L) | X5 (mg/L) | X6 (-) | X7 (mg/L) | X8 (mg/L) | ||
| Virtual water samples | 1 | 7.6 | 0.005 | 0.1 | 0.1 | 1 | 7 | 0.05 | 0.005 |
| 2 | 6.2 | 0.005 | 0.1 | 0.1 | 1 | 7 | 0.05 | 0.005 | |
| 3 | 7.6 | 0.02 | 0.1 | 0.1 | 1 | 7 | 0.05 | 0.005 | |
| 4 | 6.75 | 0.0175 | 0.35 | 0.325 | 3 | 7.5 | 0.15 | 0.03 | |
| 5 | 5.5 | 0.0375 | 0.75 | 0.75 | 5 | 8.5 | 0.25 | 0.075 | |
| 6 | 4 | 0.075 | 1.25 | 1.25 | 8 | 9.5 | 0.4 | 0.15 | |
| 7 | 2.5 | 0.15 | 1.75 | 1.75 | 12.5 | 12 | 0.75 | 0.3 | |
| 8 | 1 | 0.4 | 3 | 3 | 16 | 14 | 2 | 0.5 | |
| Water quality standards | 1 | 7.5 | 0.01 | 0.2 | 0.15 | 2 | 6–9 | <0.3 | <0.1 |
| 2 | 6 | 0.025 | 0.5 | 0.5 | 4 | ||||
| 3 | 5 | 0.05 | 1 | 1 | 6 | ||||
| 4 | 3 | 0.1 | 1.5 | 1.5 | 10 | >9 or <6 | >0.3 | >0.1 | |
| 5 | 2 | 0.2 | 2 | 2 | 15 | ||||
| Component | Initial Eigenvalues | ||
|---|---|---|---|
| Total | % of Variance | Cumulative % | |
| 1 | 7.666 | 95.829 | 95.829 |
| 2 | 0.248 | 3.101 | 98.930 |
| 3 | 0.063 | 0.790 | 99.721 |
| 4 | 0.017 | 0.206 | 99.927 |
| 5 | 0.003 | 0.043 | 99.970 |
| 6 | 0.002 | 0.026 | 99.996 |
| 7 | 0.000 | 0.003 | 99.999 |
| 8 | 4.423 × 10−5 | 0.001 | 100.000 |
| Judgment Matrix | ||||||||
|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | |
| X1 | 1 | 1 | 2 | 4 | 4 | 4 | 3 | 3 |
| X2 | 1 | 1 | 2 | 4 | 4 | 4 | 3 | 3 |
| X3 | 0.5 | 0.5 | 1 | 2 | 2 | 2 | 2 | 2 |
| X4 | 0.25 | 0.25 | 0.5 | 1 | 1 | 1 | 0.5 | 0.5 |
| X5 | 0.25 | 0.25 | 0.5 | 1 | 1 | 1 | 0.5 | 0.5 |
| X6 | 0.25 | 0.25 | 0.5 | 1 | 1 | 1 | 0.5 | 0.5 |
| X7 | 0.33 | 0.33 | 0.5 | 2 | 2 | 2 | 1 | 1 |
| X8 | 0.33 | 0.33 | 0.5 | 2 | 2 | 2 | 1 | 1 |
| The consistency ratio is 0.0078 < 0.1 | ||||||||
| Serial Number | Indicators | Weight | |||
|---|---|---|---|---|---|
| AHP | PCA | AHP-PCA | EW | ||
| 1 | DO, X1 | 0.251 | 0.124 | 0.249 | 0.125 |
| 2 | Total phosphorus, X2 | 0.251 | 0.123 | 0.247 | 0.125 |
| 3 | Total nitrogen, X3 | 0.137 | 0.127 | 0.140 | 0.125 |
| 4 | Ammonia nitrogen, X4 | 0.057 | 0.127 | 0.058 | 0.125 |
| 5 | CODMn, X5 | 0.057 | 0.125 | 0.057 | 0.125 |
| 6 | Ph, X6 | 0.057 | 0.125 | 0.057 | 0.125 |
| 7 | Iron, X7 | 0.095 | 0.123 | 0.094 | 0.125 |
| 8 | Manganese, X8 | 0.095 | 0.127 | 0.097 | 0.125 |
| Samples | Methods | ||||||
|---|---|---|---|---|---|---|---|
| WQI | EW-VFPR | PCA-VFPR | AHP-VFPR | PCA/AHP-VFPR | I-PCA/AHP-FCA | PCA/AHP-FCA | |
| 1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 2 | 1.00 | 1.23 | 1.22 | 1.49 | 1.48 | 1.21 | 1.00 |
| 3 | 1.00 | 1.05 | 1.04 | 1.08 | 1.07 | 1.16 | 1.00 |
| 4 | 2.00 | 1.50 | 1.50 | 1.50 | 1.50 | 1.50 | 1~2 |
| 5 | 3.00 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2~3 |
| 6 | 4.00 | 3.50 | 3.50 | 3.50 | 3.50 | 3.50 | 3~4 |
| 7 | 5.00 | 4.50 | 4.50 | 4.50 | 4.50 | 4.50 | 4~5 |
| 8 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 |
| Sampling Sites | TN | TP | ||
|---|---|---|---|---|
| Q (mg/kg) | △x (mg/L) | Q (mg/kg) | △x (mg/L) | |
| 1 | 41.97 | 1.13 | 17.28 | 0.47 |
| 2 | 67.32 | 1.81 | 11.85 | 0.32 |
| 3 | 88.00 | 2.37 | 10.13 | 0.27 |
| 4 | 56.22 | 1.52 | 17.68 | 0.48 |
| 5 | 45.68 | 1.23 | 8.22 | 0.22 |
| 6 | 52.25 | 1.41 | 9.67 | 0.26 |
| Average values | 58.57 | 1.58 | 12.47 | 0.34 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Xu, S.; Liu, J. Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution. Water 2017, 9, 275. https://doi.org/10.3390/w9040275
Wang T, Xu S, Liu J. Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution. Water. 2017; 9(4):275. https://doi.org/10.3390/w9040275
Chicago/Turabian StyleWang, Tianxiang, Shiguo Xu, and Jianwei Liu. 2017. "Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution" Water 9, no. 4: 275. https://doi.org/10.3390/w9040275
APA StyleWang, T., Xu, S., & Liu, J. (2017). Dynamic Assessment of Comprehensive Water Quality Considering the Release of Sediment Pollution. Water, 9(4), 275. https://doi.org/10.3390/w9040275






