Effect of Water Quality Sampling Approaches on Nitrate Load Predictions of a Prominent Regression-Based Model
Abstract
:1. Introduction
2. Materials and Methods
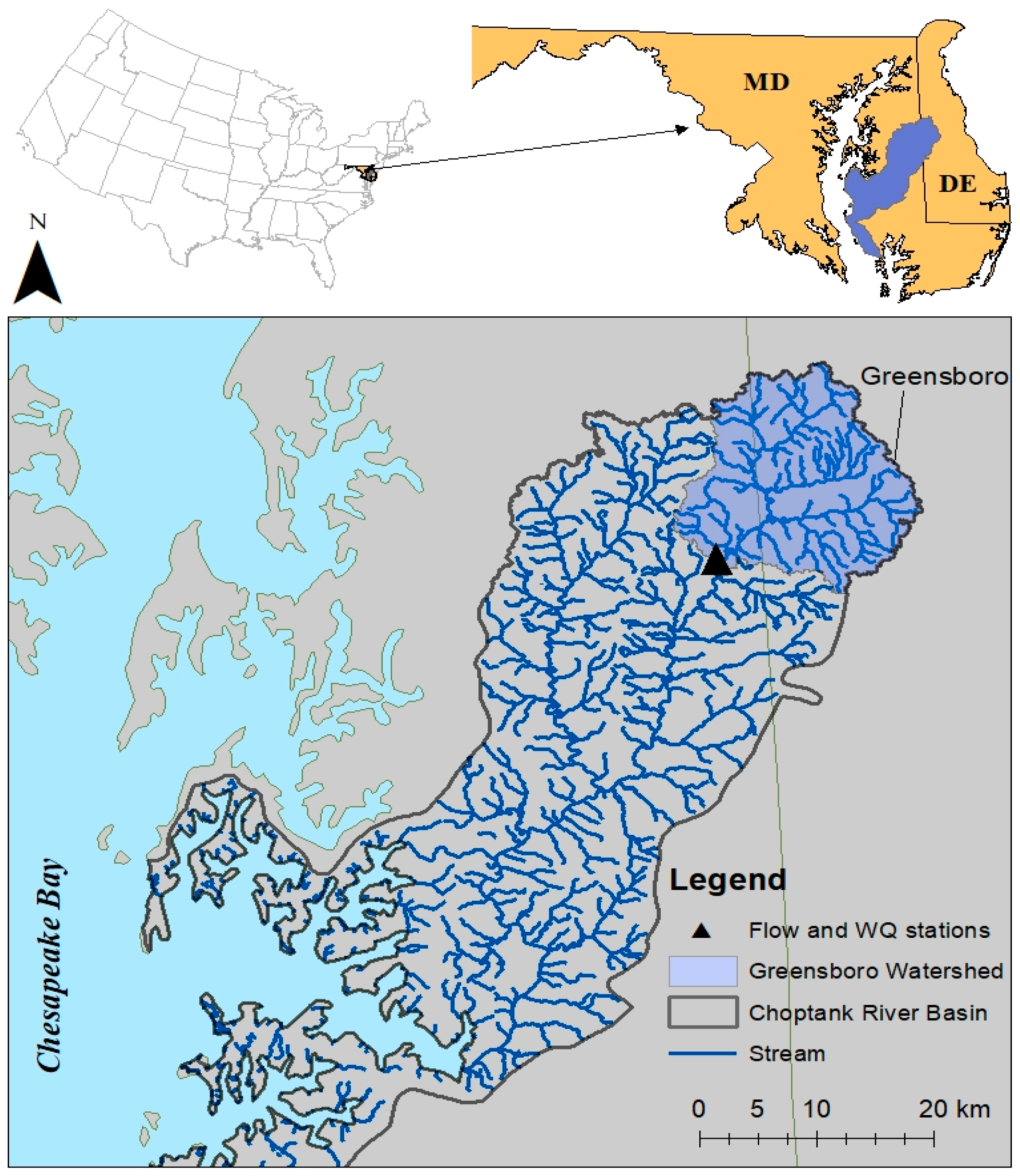
2.1. Study Area
2.2. Historic Discharge and Water Quality Sampling Data
2.3. Real-Time Nitrate Data Processing
2.4. USGS LOAD ESTimator
2.5. Prediction Intervals for Regression Relationships
3. Results
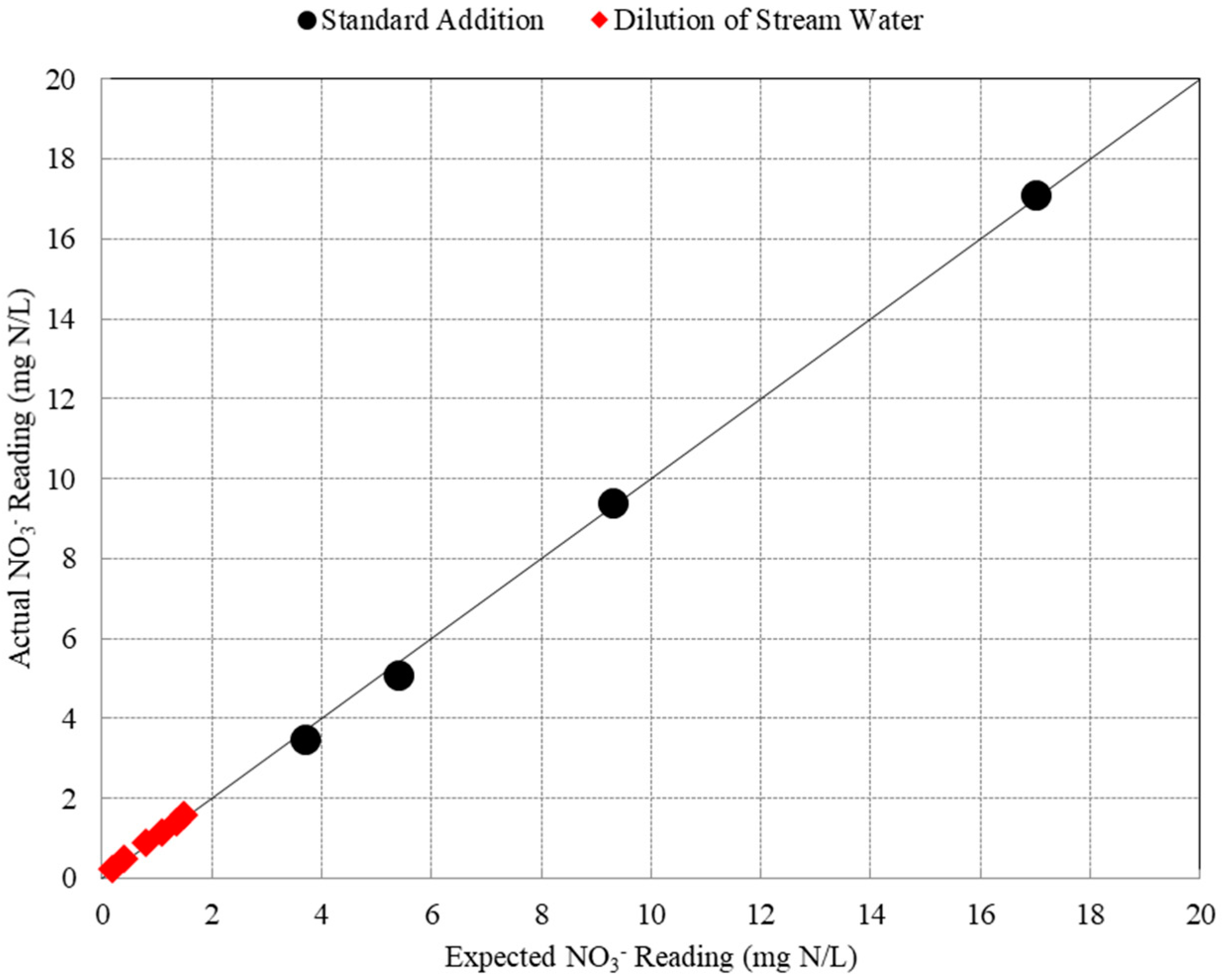
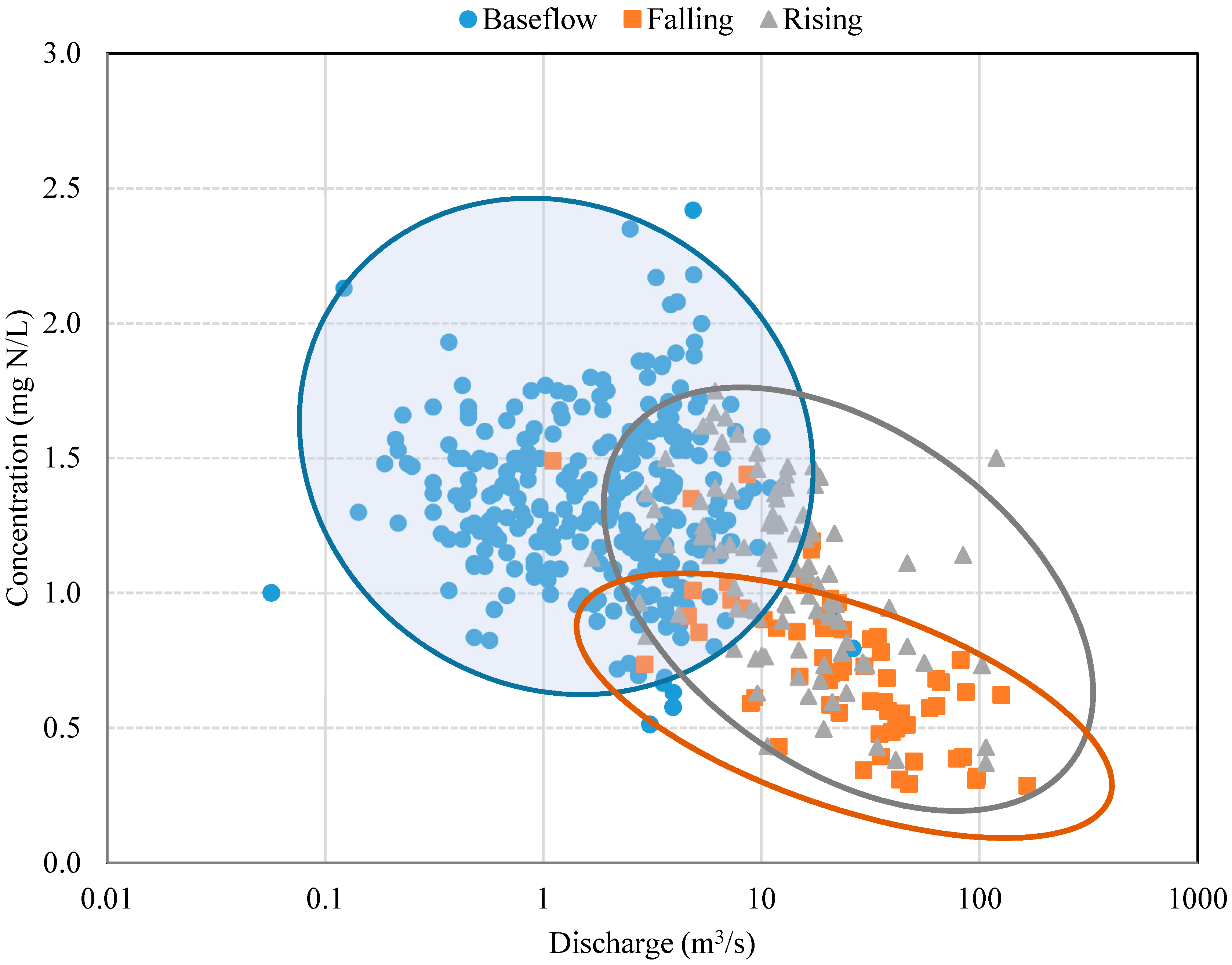
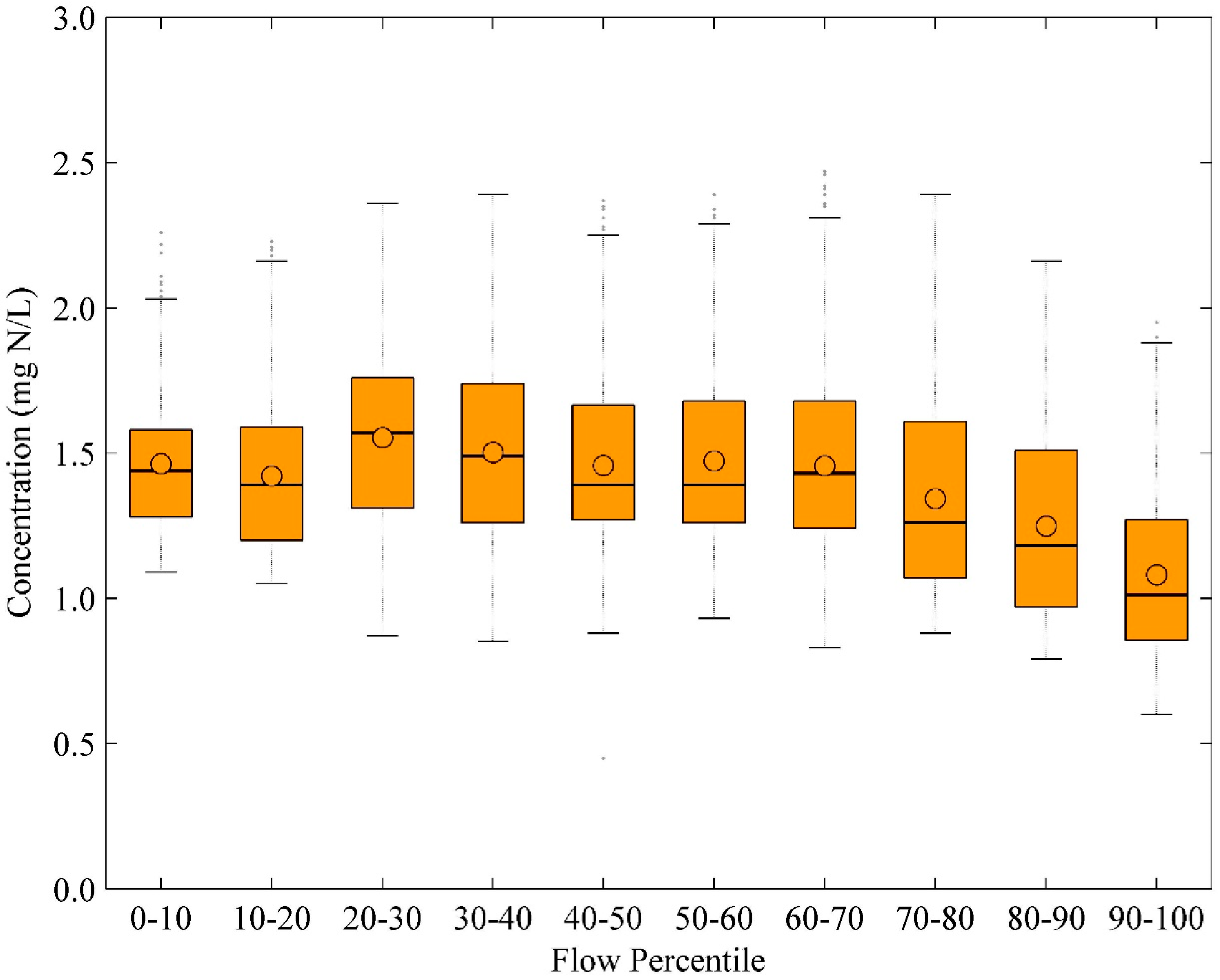
3.1. Analysis of Nitrate Grab Samples
3.2. Analysis of Real-Time Nitrate Data
3.3. LOADEST Regression Analysis
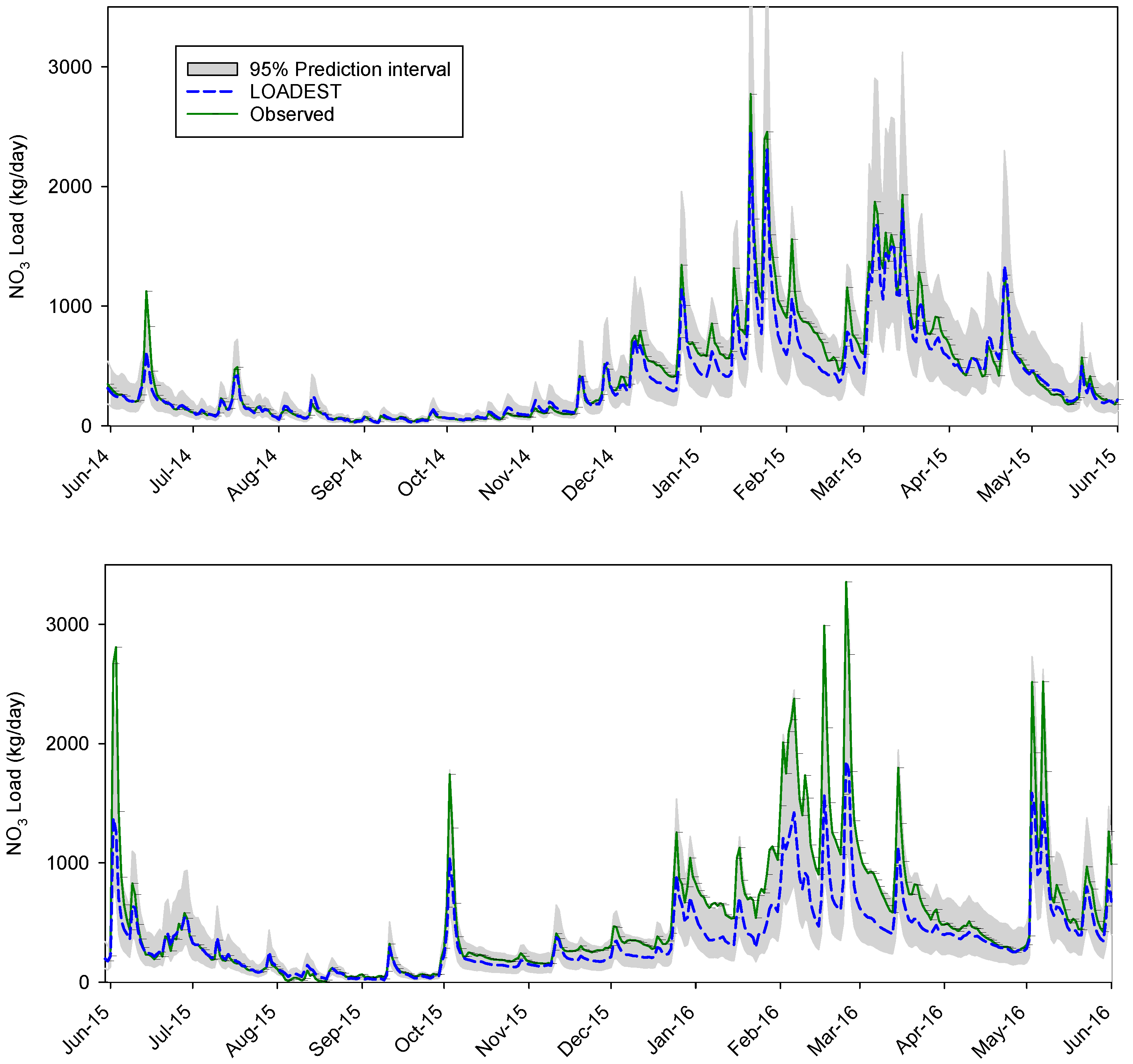
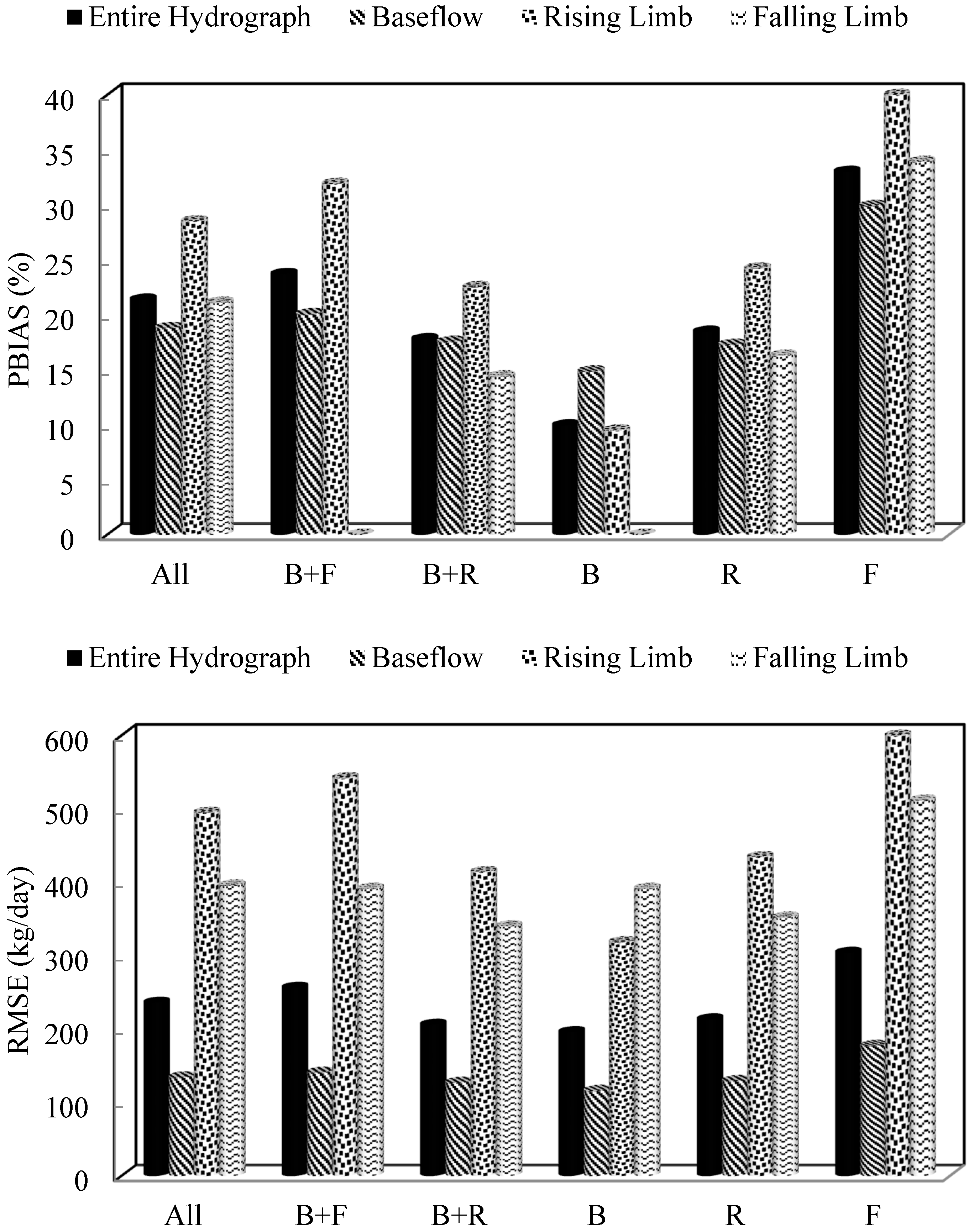
3.4. Validation of Regression Analysis
4. Discussion
4.1. Effect of Sampling Time on Storm Load Prediction
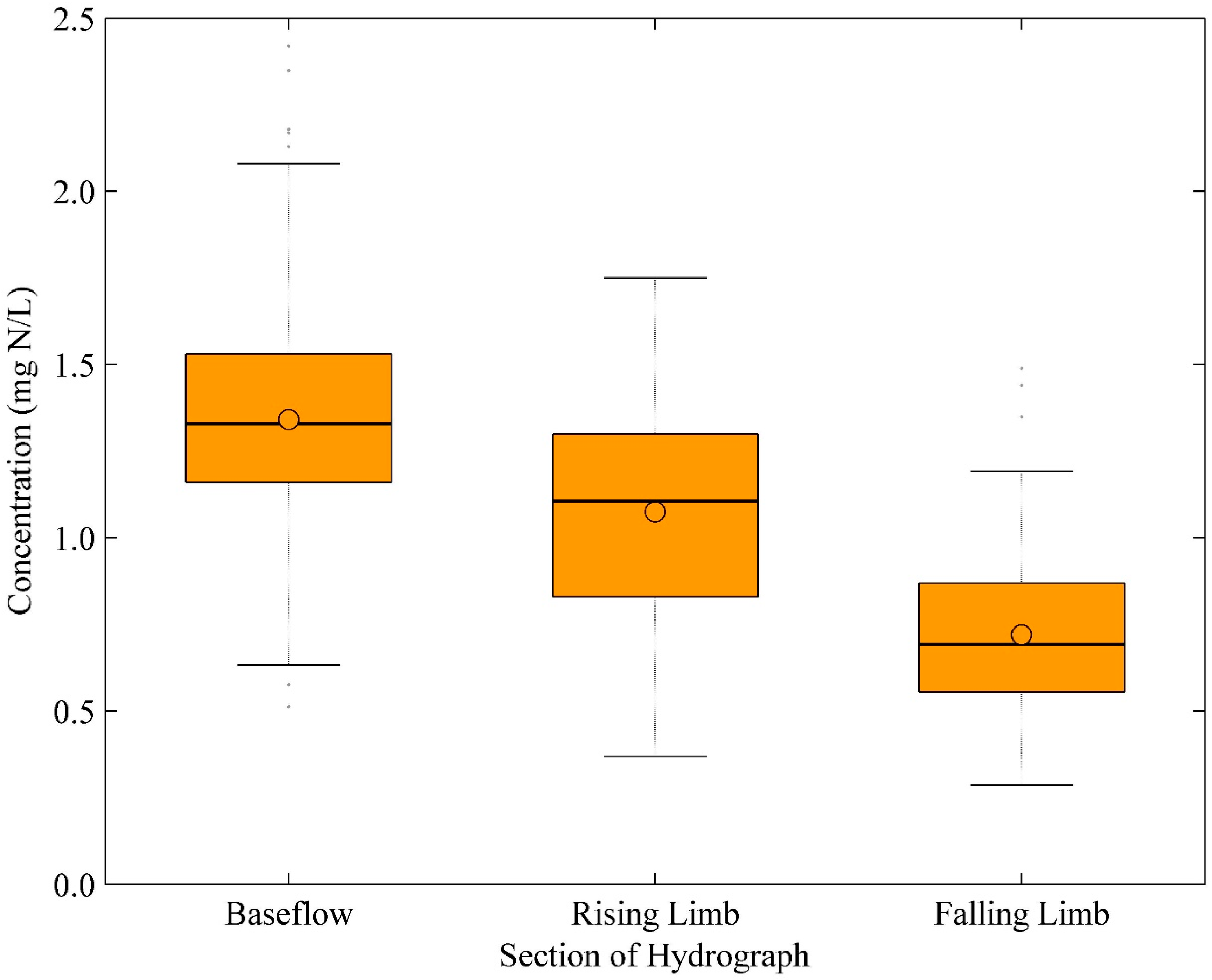
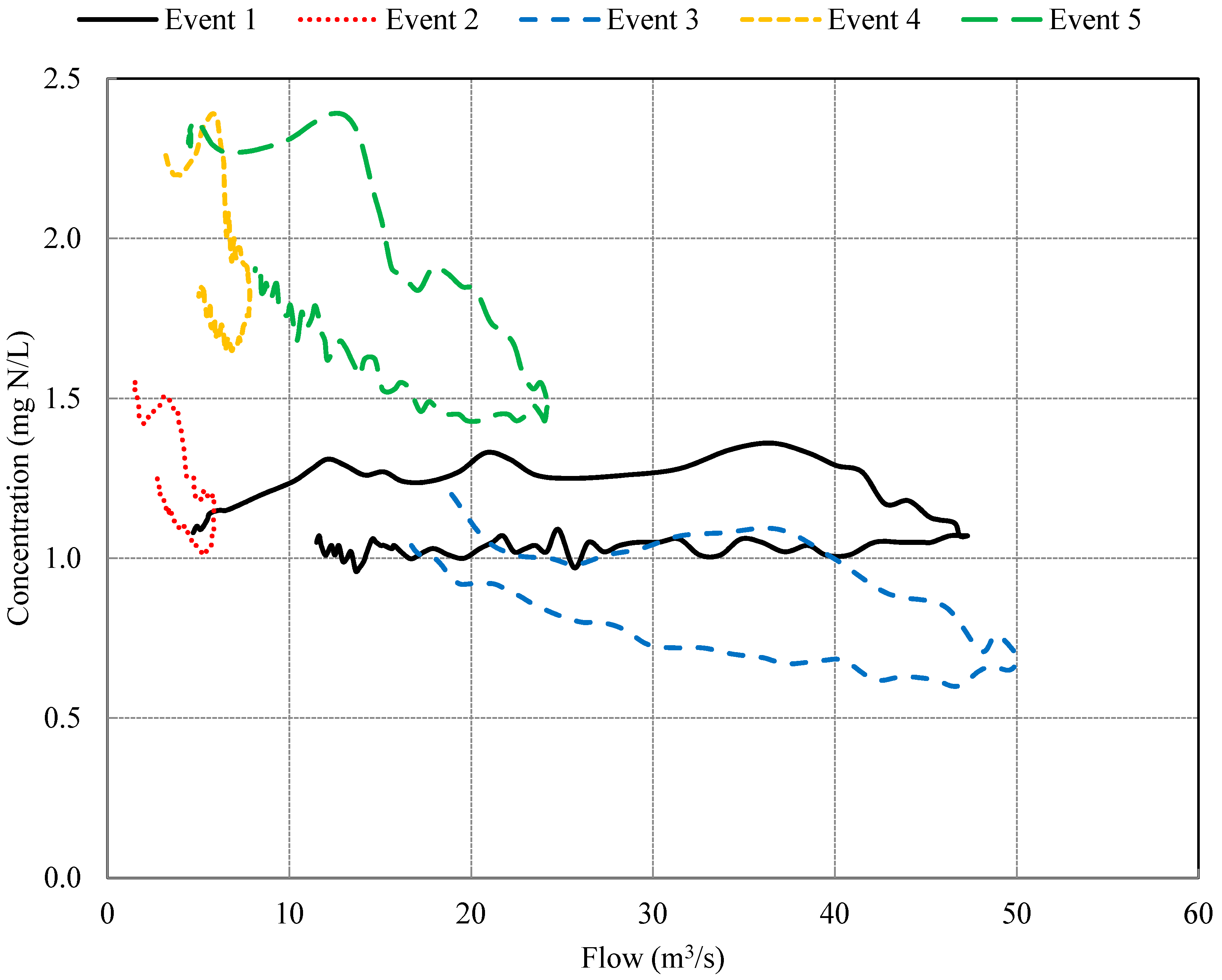
4.2. Effect of Hysteresis on Nitrate Load Estimation
4.3. Potential Impact on Correlated Applications
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; de Marinis, G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (Loadest): A Fortran Program. for Estimating Constituent Loads in Streams and Rivers; Science for the Changing World: Reston, VA, USA, 2004; Chapter A5. [Google Scholar]
- Park, Y.; Engel, B.; Frankenberger, J.; Hwang, H. A web-based tool to estimate pollutant loading using loadest. Water 2015, 7, 4858–4868. [Google Scholar] [CrossRef]
- Maier, H.; Dandy, G. The use of artificial neural networks for the prediction of water quality parameters. Water Resour. Res. 1996, 32, 1013–1022. [Google Scholar] [CrossRef]
- Maier, H.; Dandy, G. Reply [to “Comment on ‘The use of artificial neural networks for the prediction of water quality parameters’ by H. R. Maier and G. C. Dandy”]. Water Resour. Res. 1997, 33, 2425–2427. [Google Scholar] [CrossRef]
- Han, H.; Chen, Q.; Qiao, J. An efficient self-organizing rbf neural network for water quality prediction. Neural Netw. 2011, 24, 717–725. [Google Scholar] [CrossRef] [PubMed]
- Partalas, I.; Tsoumakas, G.; Hatzikos, E.; Vlahavas, I. Greedy regression ensemble selection: Theory and an application to water quality prediction. Inf. Sci. 2008, 178, 3867–3879. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, J.; Yu, H.; Zhen, Z.; Li, D. Three-dimensional short-term prediction model of dissolved oxygen content based on pso-bpann algorithm coupled with kriging interpolation. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Xu, L.; Liu, S. Study of short-term water quality prediction model based on wavelet neural network. Math. Comput. Model. 2013, 58, 801–807. [Google Scholar] [CrossRef]
- Cerro, I.; Antiguedad, I.; Srinavasan, R.; Sauvage, S.; Volk, M.; Sanchez-Perez, J. Simulating land management options to reduce nitrate pollution in an agricultural watershed dominated by an alluvial aquifer. J. Environ. Qual. 2014, 43, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Jha, M.; Gassman, P.; Arnold, J. Water quality modeling for the raccoon river watershed using swat. Trans. ASABE 2007, 50, 479–493. [Google Scholar] [CrossRef]
- Duan, S.; Kaushal, S.S.; Groffman, P.M.; Band, L.E.; Belt, K.T. Phosphorus export across an urban to rural gradient in the chesapeake bay watershed. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Brigham, M.E.; Wentz, D.A.; Aiken, G.R.; Krabbenhoft, D.P. Mercury cycling in stream ecosystems. 1. Water column chemistry and transport. Environ. Sci. Technol. 2009, 43, 2720–2725. [Google Scholar] [CrossRef] [PubMed]
- Dornblaser, M.M.; Striegl, R.G. Suspended sediment and carbonate transport in the yukon river basin, alaska: Fluxes and potential future responses to climate change. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Park, Y.S.; Engel, B.A. Use of pollutant load regression models with various sampling frequencies for annual load estimation. Water 2014, 6, 1685–1697. [Google Scholar] [CrossRef]
- Walling, D.E.; Foster, I.D.L. Variations in natural chemical concentration of river water during flood flows, and lag effect—Some further comments. J. Hydrol. 1975, 26, 237–244. [Google Scholar] [CrossRef]
- Evans, C.; Davies, T.D. Causes of concentration/discharge hysteresis and its potential as a tool for analysis of episode hydrochemistry. Water Resour. Res. 1998, 34, 129–137. [Google Scholar] [CrossRef]
- House, W.A.; Warwick, M.S. Hysteresis of the solute concentration/discharge relationship in rivers during storms. Water Res. 1998, 32, 2279–2290. [Google Scholar] [CrossRef]
- Beck, M. Water-quality modeling—A review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. [Google Scholar] [CrossRef]
- King, K.W.; Harmel, R.D. Comparison of time-based sampling strategies to determine nitrogen loading in plot-scale runoff. Trans. ASAE 2004, 47, 1457–1463. [Google Scholar] [CrossRef]
- Meals, D.W.; Richards, R.P.; Dressing, S.A. Pollutant Load Estimation for Water Quality Monitoring Projects; Tech Notes 8; Developed for U.S. Environmental Protection Agency by Tetra Tech, Inc.: Fairfax, VA, USA, 2013; p. 21. [Google Scholar]
- Yen, H.; Wang, X.; Fontane, D.; Harmel, R.; Arabi, M. A framework for propagation of uncertainty contributed by parameterization, input data, model structure, and calibration/validation data in watershed modeling. Environ. Model. Softw. 2014, 54, 211–221. [Google Scholar] [CrossRef]
- Yen, H.; Hoque, Y.; Wang, X.; Harmel, R. Applications of explicitly incorporated/post-processing measurement uncertainty in watershed modeling. J. Am. Water Resour. Assoc. 2016, 52, 523–540. [Google Scholar] [CrossRef]
- Pellerin, B.A.; Bergamaschi, B.A.; Gilliom, R.J.; Crawford, C.G.; Saraceno, J.; Frederick, C.P.; Downing, B.D.; Murphy, J.C. Mississippi river nitrate loads from high frequency sensor measurements and regression-based load estimation. Environ. Sci. Technol. 2014, 48, 12612–12619. [Google Scholar] [CrossRef] [PubMed]
- Pellerin, B.A.; Saraceno, J.F.; Shanley, J.B.; Sebestyen, S.D.; Aiken, G.R.; Wollheim, W.M.; Bergamaschi, B.A. Taking the pulse of snowmelt: In-situ sensors reveal seasonal, event and diurnal patterns of nitrate and dissolved organic matter variability in an upland forest stream. Biogeochemistry 2012, 108, 183–198. [Google Scholar] [CrossRef]
- Heffernan, J.B.; Cohen, M.J. Direct and indirect coupling of primary production and diel nitrate dynamics in a subtropical spring-fed river. Limnol. Oceanogr. 2010, 55, 677–688. [Google Scholar] [CrossRef] [Green Version]
- Sprague, L.A.; Langland, M.; Yochum, S.; Edwards, R.; Blomquist, J.; Phillips, S.; Shenk, G.; Preston, S. Factors Affecting Nutrient Trends in Major Rivers of the Chesapeake bay Watershed; Water Resources Investigations Report 00-4218; U.S. Geological Survey: Richmond, VA, USA, 2000.
- Ator, S.W.; Denver, J.M. Estimating contributions of nitrate and herbicides from groundwater to headwater streams, northern atlantsdic coastal plain, United States. J. Am. Water Resour. Assoc. 2012, 48, 1075–1090. [Google Scholar] [CrossRef]
- McCarty, G.W.; McConnell, L.L.; Hapernan, C.J.; Sadeghi, A.; Graff, C.; Hively, W.D.; Lang, M.W.; Fisher, T.R.; Jordan, T.; Rice, C.P.; et al. Water quality and conservation practice effects in the choptank river watershed. J. Soil Water Conserv. 2008, 63, 461–474. [Google Scholar] [CrossRef]
- McCarty, G.W.; Hapeman, C.J.; Rice, C.P.; Hively, W.D.; McConnell, L.L.; Sadeghi, A.M.; Lang, M.W.; Whitall, D.R.; Bialek, K.; Downey, P. Metolachlor metabolite (MESA) reveals agricultural nitrate-n fate and transport in choptank river watershed. Sci. Total Environ. 2014, 473, 473–482. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.J.; Engel, B.A.; Tang, Z.X.; Choi, J.; Kim, K.S.; Muthukrishnan, S.; Tripathy, D. Automated web gis based hydrograph analysis tool, what. J. Am. Water Resour. Assoc. 2005, 41, 1407–1416. [Google Scholar] [CrossRef]
- Evaldi, R.D.; Moore, B.L. Techniques for Estimating the Quantity and Quality of Storm Runoff from Urban Watersheds of Jefferson County, Kentucky; Water-Resources Investigations Report 94-4023; U.S. Geological Survey: Louisville, KY, USA, 1994.
- Cohn, T.A.; Gilroy, E.J.; Baier, W.G. Estimating Fluvial Transport of Trace Constituents Using a Regression Model with Data Subject to Censoring; U.S. Geological Survey: Reston, VA, USA, 1992.
- Kutner, M.H.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill/Irwin: New York, NY, USA, 2005; pp. 214–247. ISBN 0-07-238688-6. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Lloyd, C.; Freer, J.; Johnes, P.; Collins, A. Using hysteresis analysis of high-resolution water quality monitoring data, including uncertainty, to infer controls on nutrient and sediment transfer in catchments. Sci. Total Environ. 2016, 543, 388–404. [Google Scholar] [CrossRef] [PubMed]
- Webb, B.W.; Walling, D.E. Nitrate behavior in streamflow from a grassland catchment in Devon, UK. Water Res. 1985, 19, 1005–1016. [Google Scholar] [CrossRef]
- Yates, C.; Johnes, P. Nitrogen speciation and phosphorus fractionation dynamics in a lowland chalk catchment. Sci. Total Environ. 2013, 444, 466–479. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Wu, J.; Hong, H. Effect of storm events on riverine nitrogen dynamics in a subtropical watershed, southeastern china. Sci. Total Environ. 2012, 431, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Davis, C.A.; Ward, A.S.; Burgin, A.J.; Loecke, T.D.; Riveros-Iregui, D.A.; Schnoebelen, D.J.; Just, C.L.; Thomas, S.A.; Weber, L.J.; St Clair, M.A. Antecedent moisture controls on stream nitrate flux in an agricultural watershed. J. Environ. Qual. 2014, 43, 1494–1503. [Google Scholar] [CrossRef] [PubMed]
- Macrae, M.; English, M.; Schiff, S.; Stone, M. Influence of antecedent hydrologic conditions on patterns of hydrochemical export from a first-order agricultural watershed in Southern Ontario, Canada. J. Hydrol. 2010, 389, 101–110. [Google Scholar] [CrossRef]
- Biron, P.; Roy, A.; Courschesne, F.; Hendershot, W.; Cote, B.; Fyles, J. The effects of antecedent moisture conditions on the relationship of hydrology to hydrochemistry in a small forested watershed. Hydrol. Process. 1999, 13, 1541–1555. [Google Scholar] [CrossRef]
- Lloyd, C.E.M.; Freer, J.E.; Johnes, P.J.; Collins, A.L. Technical Note: Testing an improved index for analysing storm discharge-concentration hysteresis. Hydrol. Earth Syst. Sci. 2016, 20, 625–632. [Google Scholar] [CrossRef]
- Bowes, M.J.; Jarvie, H.P.; Halliday, S.J.; Skeffington, R.A.; Wade, A.J.; Loewenthal, M.; Gozzard, E.; Newman, J.R.; Palmer-Felgate, E.J. Characterising phosphorus and nitrate inputs to a rural river using high-frequency concentration-flow relationships. Sci. Total Environ. 2015, 511, 608–620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferrant, S.; Laplanche, C.; Durbe, G.; Probst, A.; Dugast, P.; Durand, P.; Sanchez-Perez, J.M.; Probst, J.L. Continuous measurement of nitrate concentration in a highly event-responsive agricultural catchment in south-west of france: Is the gain of information useful? Hydrol. Process. 2013, 27, 1751–1763. [Google Scholar] [CrossRef] [Green Version]
- Daggupati, P.; Yen, H.; White, M.; Srinivasan, R.; Arnold, J.; Keitzer, C.; Sowa, S. Impact of model development, calibration and validation decisions on hydrological simulations in west lake erie basin. Hydrol. Process. 2015, 29, 5307–5320. [Google Scholar] [CrossRef]
- Keitzer, S.; Ludsin, S.; Sowa, S.; Annis, G.; Arnold, J.; Daggupati, P.; Froehlich, A.; Herbert, M.; Johnson, M.; Sasson, A.; et al. Thinking outside of the lake: Can controls on nutrient inputs into lake erie benefit stream conservation in its watershed? J. Great Lakes Res. 2016, 42, 1322–1331. [Google Scholar] [CrossRef]
- Yen, H.; White, M.; Arnold, J.; Keitzer, S.; Johnson, M.; Atwood, J.; Daggupati, P.; Herbert, M.; Sowa, S.; Ludsin, S.; et al. Western lake erie basin: Soft-data-constrained, nhdpius resolution watershed modeling and exploration of applicable conservation scenarios. Sci. Total Environ. 2016, 569, 1265–1281. [Google Scholar] [CrossRef] [PubMed]
- Scavia, D.; Kalcic, M.; Muenich, R.; Read, J.; Aloysius, N.; Bertani, I.; Boles, C.; Confesor, R.; DePinto, J.; Gildow, M.; et al. Multiple models guide strategies for agricultural nutrient reductions. Front. Ecol. Environ. 2017, 15, 126–132. [Google Scholar] [CrossRef]
- Ajami, N.; Duan, Q.; Sorooshian, S. An integrated hydrologic bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
| Calibration Dataset | ||||||
|---|---|---|---|---|---|---|
| All | 455 | 6.1043 | 0.8492 | −0.0459 | 0.95 | 0.0766 |
| Base + Rising | 391 | 5.8298 | 0.9125 | −0.0295 | 0.95 | 0.0669 |
| Base + Falling | 354 | 6.0002 | 0.8357 | −0.0524 | 0.95 | 0.0684 |
| Baseflow | 291 | 5.0926 | 0.9765 | −0.0006 | 0.94 | 0.0568 |
| Rising | 100 | 7.1893 | 0.8060 | −0.0240 ₦ | 0.82 | 0.0929 |
| Falling | 63 | 7.0563 | 0.7218 | −0.0313 ₦ | 0.85 | 0.0880 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharifi, A.; Yen, H.; Wallace, C.W.; McCarty, G.; Crow, W.; Momen, B.; Lang, M.W.; Sadeghi, A.; Lee, S.; Denver, J.; et al. Effect of Water Quality Sampling Approaches on Nitrate Load Predictions of a Prominent Regression-Based Model. Water 2017, 9, 895. https://doi.org/10.3390/w9110895
Sharifi A, Yen H, Wallace CW, McCarty G, Crow W, Momen B, Lang MW, Sadeghi A, Lee S, Denver J, et al. Effect of Water Quality Sampling Approaches on Nitrate Load Predictions of a Prominent Regression-Based Model. Water. 2017; 9(11):895. https://doi.org/10.3390/w9110895
Chicago/Turabian StyleSharifi, Amirreza, Haw Yen, Carlington W. Wallace, Gregory McCarty, Wade Crow, Bahram Momen, Megan W. Lang, Ali Sadeghi, Sangchul Lee, Judith Denver, and et al. 2017. "Effect of Water Quality Sampling Approaches on Nitrate Load Predictions of a Prominent Regression-Based Model" Water 9, no. 11: 895. https://doi.org/10.3390/w9110895
APA StyleSharifi, A., Yen, H., Wallace, C. W., McCarty, G., Crow, W., Momen, B., Lang, M. W., Sadeghi, A., Lee, S., Denver, J., & Rabenhorst, M. C. (2017). Effect of Water Quality Sampling Approaches on Nitrate Load Predictions of a Prominent Regression-Based Model. Water, 9(11), 895. https://doi.org/10.3390/w9110895






