1. Introduction
Breaking waves are rarely adopted as a flow field for modelling turbulence due to the unsteadiness and to the complexity of the phenomena taking place, enhanced by vorticity and turbulence generation and evolution during breaking and near the bottom. While the phenomena at the bottom are relevant in shallow water, the phenomena near the free surface are always relevant, even though with different level of importance depending on the stage of breaking evolution. Vorticity injection is addressed (i) to surface curvature plus the effects of boundary conditions at the interface (Longuet-Higgins, 1992 [
1]); (ii) to the sharp curvature of the interface (Lin and Rockwell, 1994 [
2]); (iii) to deceleration of the free surface before breaking (Dabiri and Gharib, 1997 [
3]). Vorticity is often accompanied by turbulence even in cases where the classical air entrapment of the breaker is not observed. Turbulence is the final stage of energy transfer in sea gravity waves and marks the evolution of a low entropy system (gravity waves in non breaking conditions) to a high entropy system (broken waves). This evolution is accompanied by several phenomena of practical interest, like enhanced diffusion of heat, chemicals, gases, pollutants, currents generation, action on the sand bottom to activate sediment transport, or spray diffusion in the atmosphere. We notice that the energy budget of the incoming waves is generally not dominated by dissipation at viscous level (the final stage of turbulence action at a molecular scale, with the generation of heat), but is also based on transfer toward large scale features as long-shore and cross-shore currents, free (unbounded) long waves escaping offshore, edge waves trapped in the nearshore, and macro eddies at the wave length scale. In this respect, the analysis of turbulence structure in breaking waves helps the comprehension of all these new flow field structures, but at the same time it is more complex with respect to many other turbulence fields. Very recent contributions to the description of the flow field structure in waves and breaking waves are due to Grue and Kolaas, (2017) [
4], who applied particle tracking velocimetry (in two-dimensional space, 2D) in non-breaking periodic laboratory waves to estimate the Lagrangian drift velocity, and to Smith et al., (2017) [
5], who studied plunging breakers on a sloping beach (in 2D) with Particle Image Velocimetry, paying attention to air bubbles geometry and dynamics. The threshold of onset of breaking is still under scrutiny, since there are numerous phenomena affecting the process. In this respect, the analysis by Barthelemy et al., (2015) [
6], has been recently extended by Saket et al., (2017) [
7] to include deep water wave groups with or without wind action.
The models of turbulence generation and evolution are based on observations, detailed measurements, and direct numerical simulation (DNS) (see also Deike et al., 2016 [
8] and the recent paper by Deike et al., 2017 [
9]). The dissipation in unsteady breaking waves has been parametrized by Drazen et al., (2008) [
10], who found a dissipation per unit length of breaking crest proportional to
, being
the mass density of water,
g the gravity acceleration, and
c the phase speed. A huge effort in measuring the flow field characteristics in breaking surface waves and in analysing the turbulence characteristics (in 2D) is documented in Drazen and Melville, (2009) [
11]. In particular, many models for turbulence have been developed by analysing the structure of the Reynolds stress tensor and of the dissipation tensors, which can be obtained only with DNS. These tensors carry information about the “componentality” of turbulence, i.e., the strength of turbulence with direction, and are local estimators. Other tensors are non–local estimators and depict the “dimensionality” of turbulence and account for the space structure of fluctuations (Reynolds, 1989 [
12], Stilyanou et al., 2015 [
13]). The study of the invariants of these tensors is of interest since their relative strength can be adopted to develop models based on a functional dependence.
The availability of three-dimensional measurements of fluid velocity with particle tracking methodology allows for the first time a direct evaluation of these tensors. The aim of the present work is (i) the identification of the level of isotropy/anisotropy in the turbulence by analysing the Reynolds stress tensor and the dissipation tensor; and (ii) the individuation of the functional dependence between the components of these tensors. A feature of anisotropic Reynolds stress flows is the presence of organized flow structures. It is true in wall boundary layers (Robinson, 1991 [
14]) and in free surface boundary layers (Longo, 2010 [
15]), and is expected to be true also in the region beneath the free surface in breaking waves.
In the present work we focus on the structure of turbulence. The experimental layout, the experiments, and the data analysis are detailed in Clavero et al., (2016) [
16], and are shortly described herein. The vorticity dynamics has been analysed in depth in Chiapponi et al., (2017) [
17].
The paper is structured as follows.
Section 2 briefly describes the experimental layout and the experiments,
Section 3 explains the methodology for data analysis.
Section 4 is devoted to the analysis of the Reynolds stress and dissipation tensors.
Section 5 gives the Conclusions.
2. Experimental Set-Up and Experiments
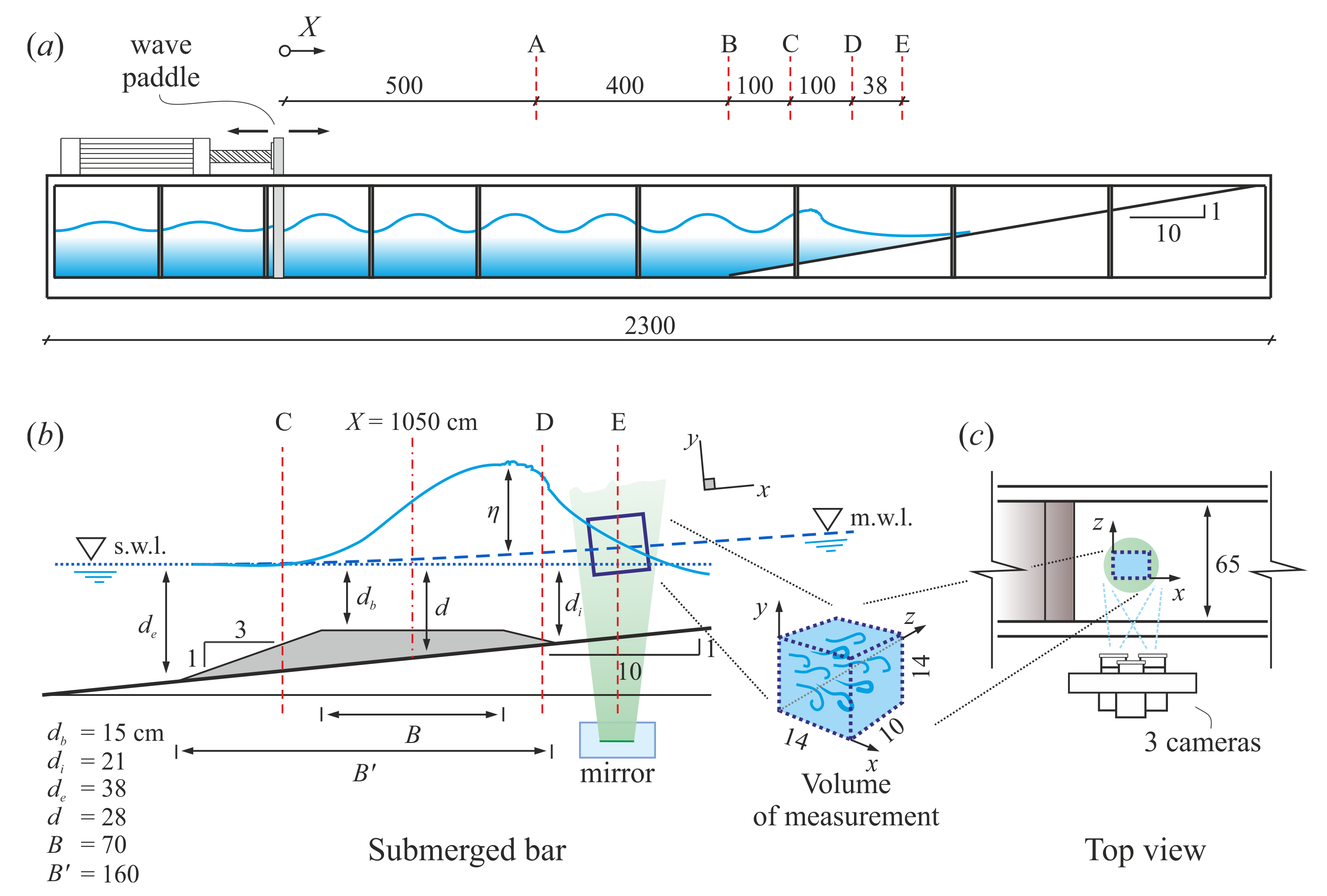
A series of experiments were planned in the wave flume of the Andalusian Institute for Earth System Research (IISTA), Universities of Granada and Cordoba, in Granada. An artificial slope of 1:10 with a berm of stones and plastic blocks was realized in order to force the breaking section, see
Figure 1, with a still-water depth in front of the paddle of
. Reflection was controlled with an active absorption system (AWACS).
A three-dimensional (3D) Particle Tracking Velocimetry system (V3V by TSI Inc., USA) was used for measuring the velocity in a volume of ≈14 . The volume of measurement was enlightened by a laser, and three cameras ( pixels) generated three pairs of 12-bit images, with a time delay between two images of each pair of . The frequency of V3V was , with 10 or 13 shots per each period for waves with and , respectively. Each experiment contained 10 cycles, with a total of 100 and 130 shots. The overall accuracy in velocity measurements is 0.1 cm/s for the cross-shore and the vertical direction, and 0.4 cm/s for the alongshore velocity component.
The surface elevation during tests was measured in several sections using Ultrasonic probes (UltraLab® USL 80D by General Acoustics, Kiel, Germany, sensor model USS635), with an accuracy on the instantaneous water level measurements equal to mm.
The main parameters of the experiments are listed in
Table 1.
3. Data Analysis and Visualization
The raw signal was elaborated by applying operators expressing different kind of averages. The phase-average for the variable
a is
where
T is the period of the signal and
N is the number of cycles. The time-average is defined as
and the phasic-average is defined as
where
and
if water is present or absent, respectively. The relative volume of water is
and
below the (minimum) trough level, and
above the (maximum) crest level. The phasic-average is always greater than and equal to the time average if
and
, respectively.
The phasic-phase-average is also defined as
For simplicity and for more consistency, in the present analysis we refer to “vertically integrated” data, meaning data phasic-averaged in the vertical, and “cycle integrated” equivalent to a time-average or a phasic-average according to the indications.
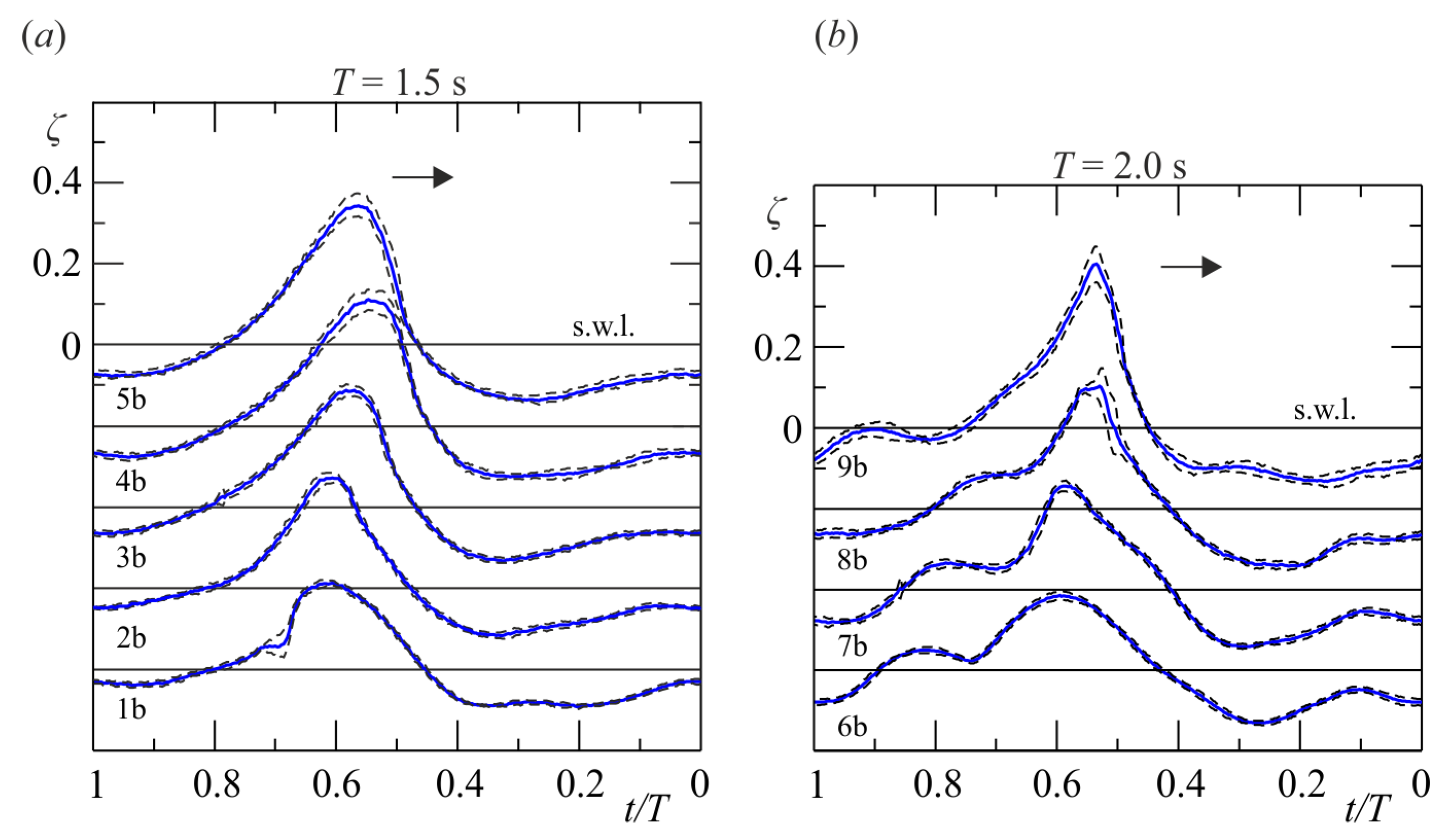
Figure 2 shows the shape of the wave at the breaking section for all the experiments.
The first problem is the separation of periodic (organized) components and fluctuating (turbulent) components. First (i) a principal orthogonal decomposition (POD) is applied to the time series of the spatial measured velocity in order to detect the most energetic contributions; (ii) then a cut-off number of components is chosen in order to eliminate disturbances and the reconstructed time series with a limited number of modes is used for the computations. The details are reported in Clavero et al., (2016) [
16]. The results are presented as average in the cross-shore and alongshore directions, obtaining a single profile in the vertical per shot as average of ≈800 profiles. If the results are further phase averaged over 10 and 13 cycles, each profile in the vertical is the average of ≈8000 and ≈10,500 profiles, a very large sample which guarantees an adequate accuracy of the statistical estimators.
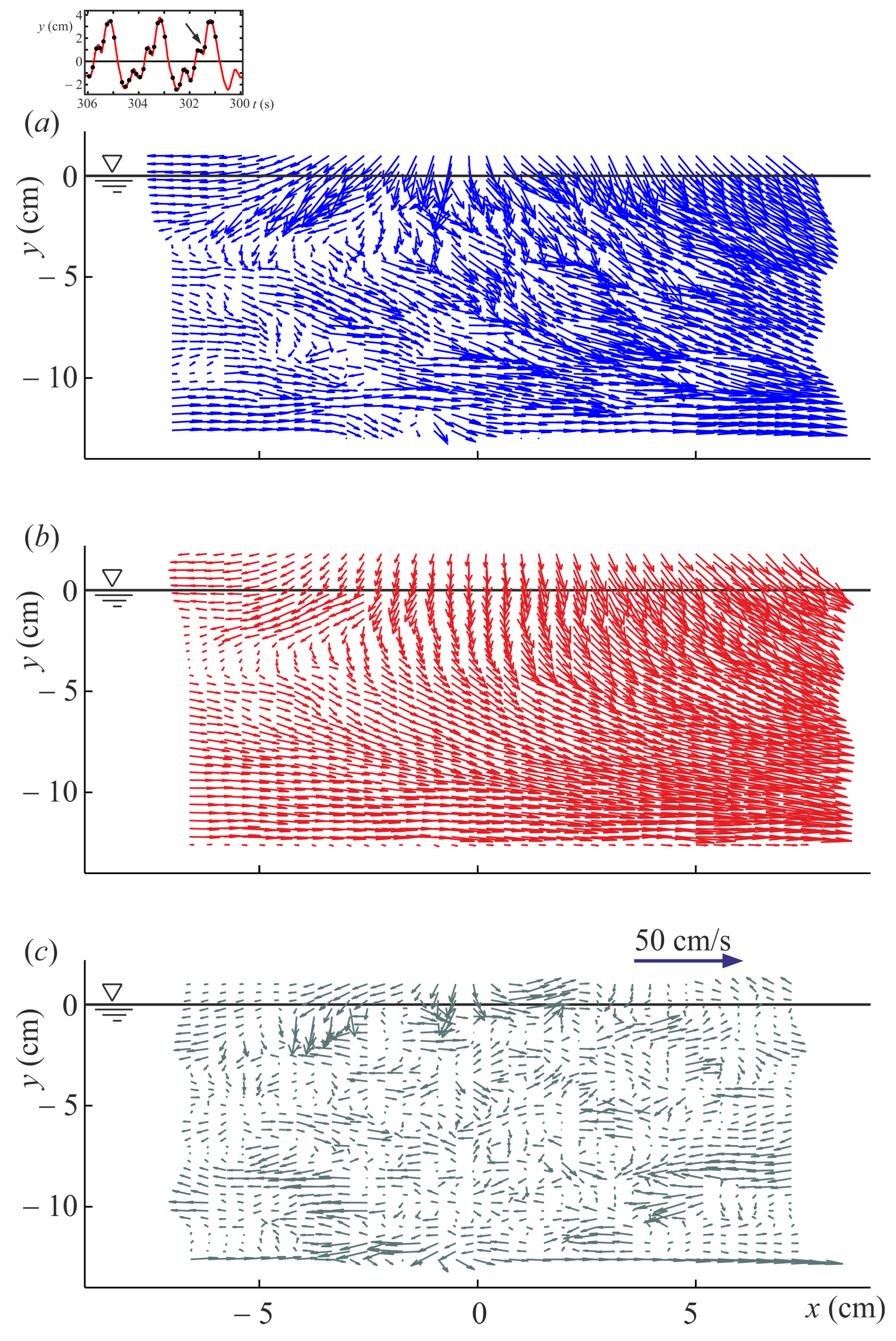
Figure 3 shows the instantaneous measured velocity, the phase-averaged and the fluctuating velocity for a single snapshot of Experiment 6b.
4. Turbulent Stress Invariants Analysis and Relation with the Dissipation Tensor
The anisotropy Reynolds stress tensor is defined as
where
is the turbulent kinetic energy,
are the spatial components and
if
,
if
is the Kronecker delta. Perfect isotropy gives a tensor with null diagonal elements.
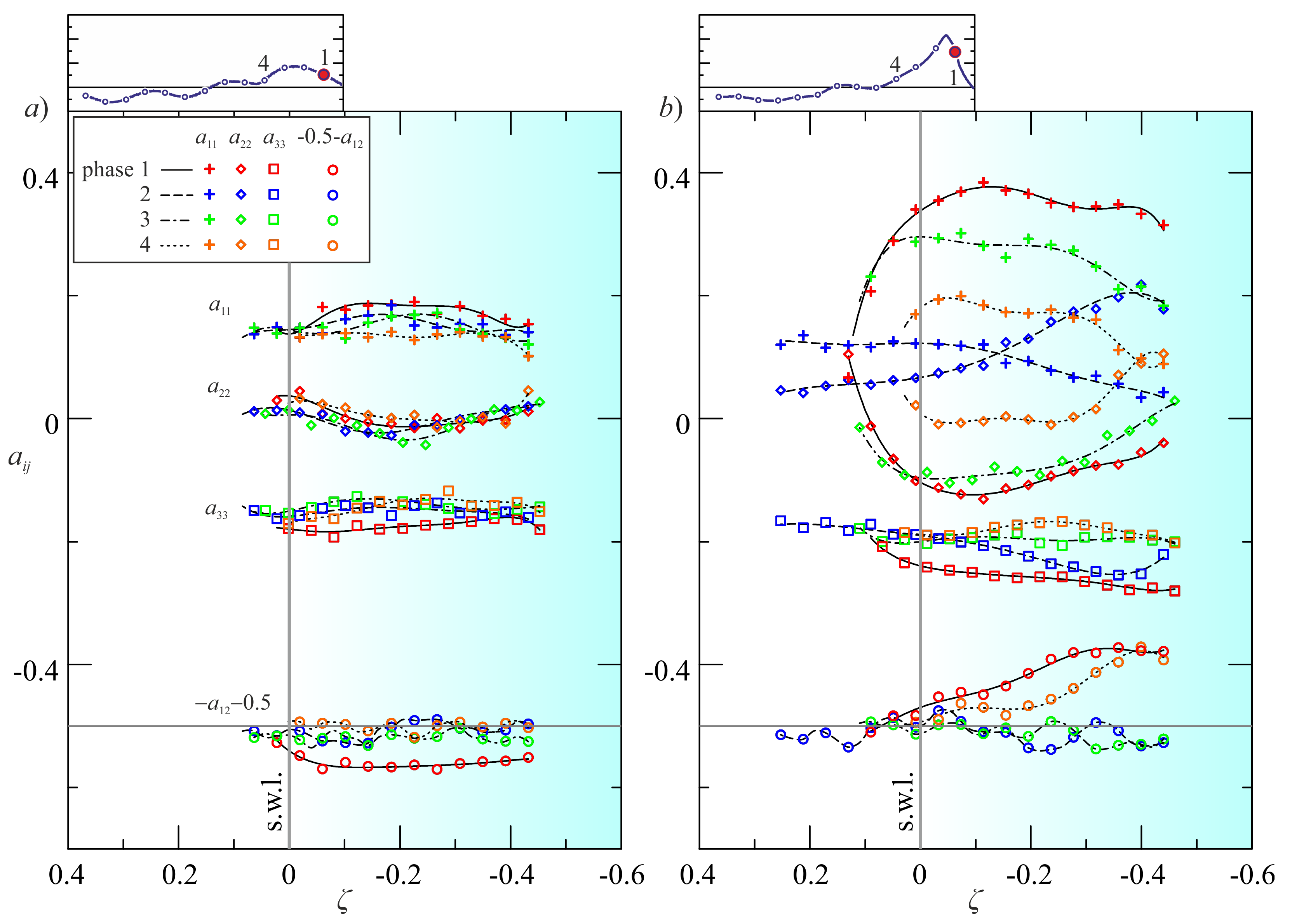
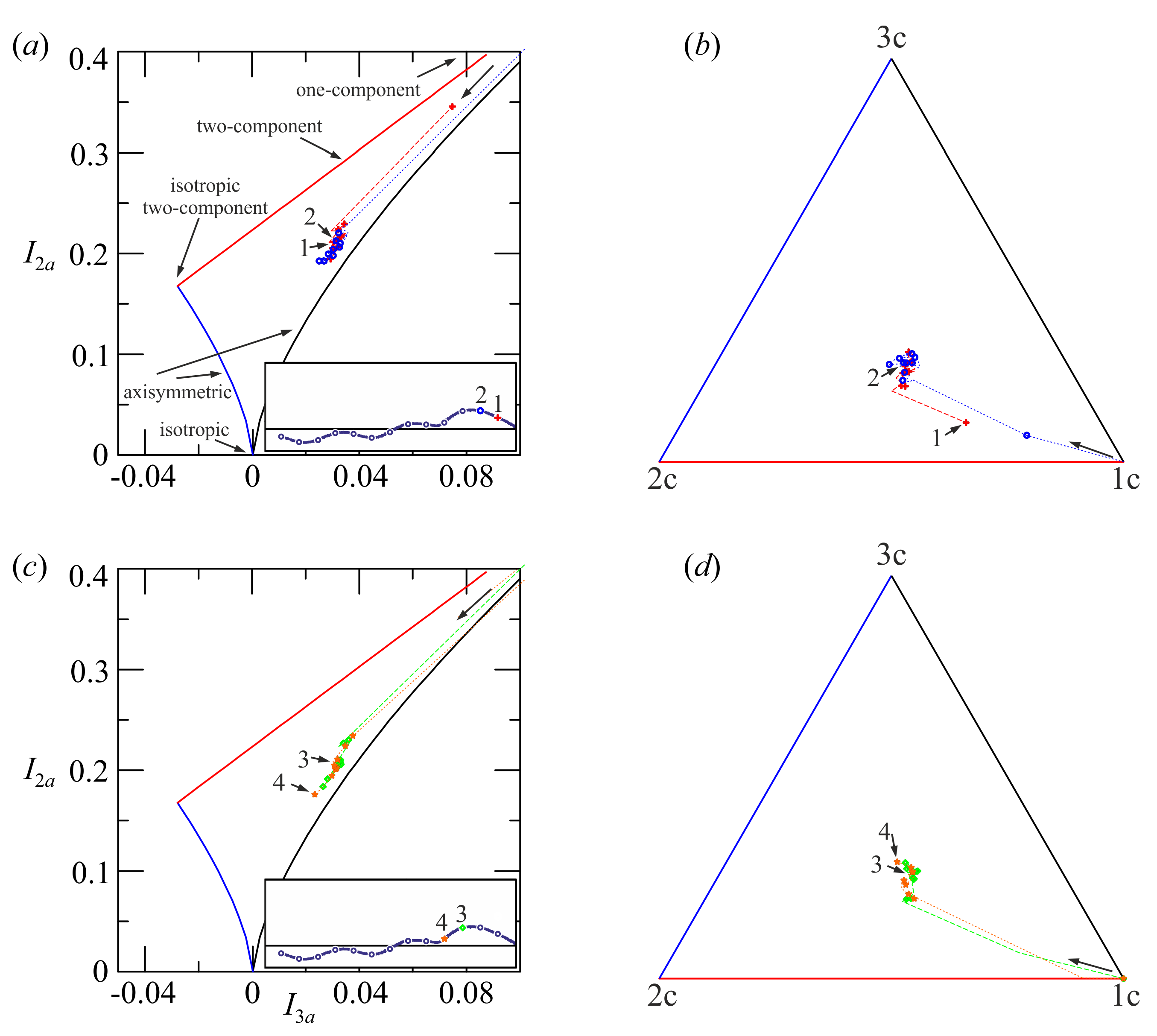
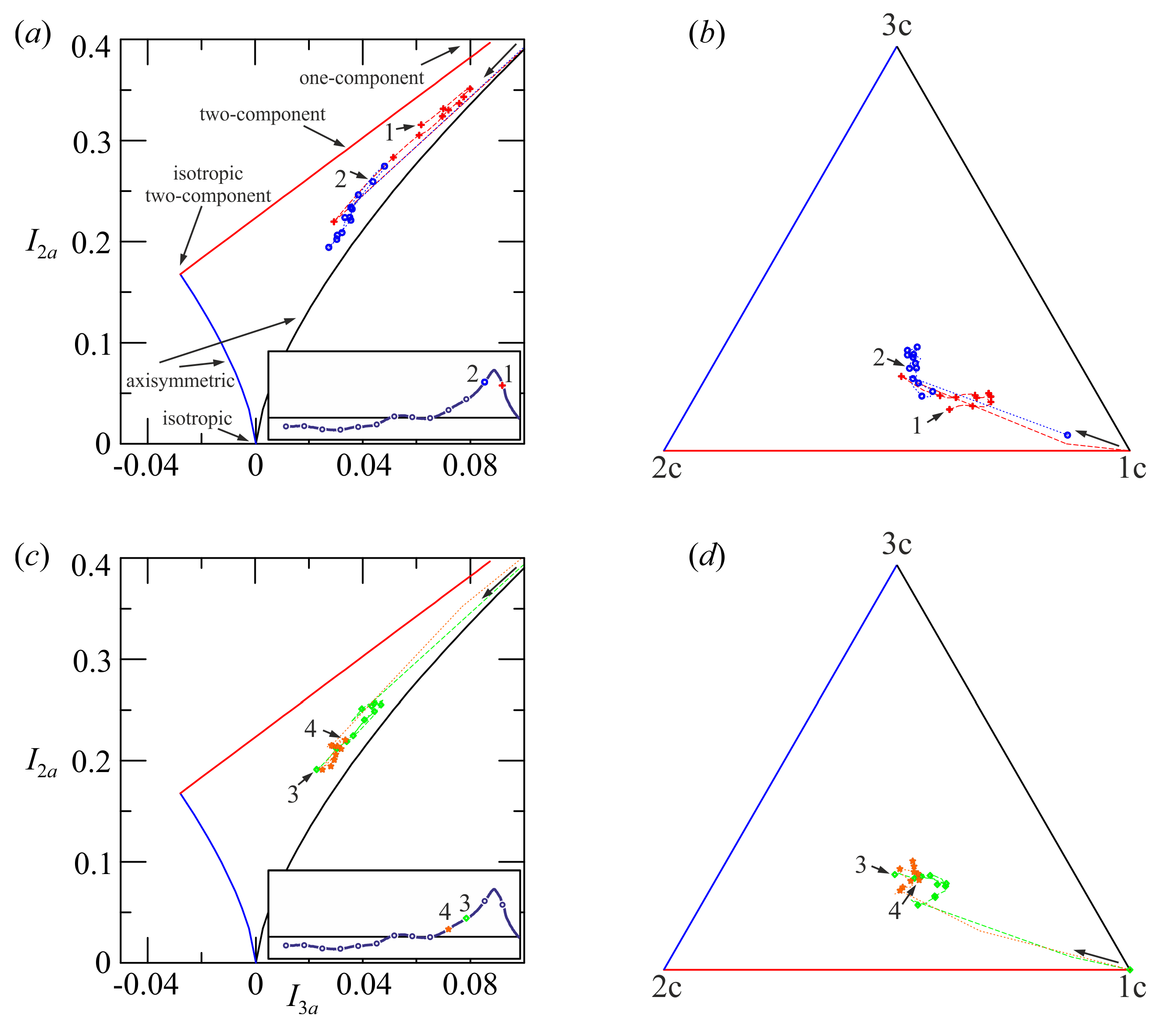
Figure 4a,b show the most representative elements
for the four phases across breaking, for Experiment 6b and Experiment 9b, respectively (the less and the most energetic breaking conditions).
In Experiment 6b, turbulence is largely oriented in plane 1–2 (cross-shore-vertical), with the 3rd component (longshore) carrying a modest fraction of the total kinetic energy. The changes of the structure due to breaking are modest and mainly limited to an increment of turbulent kinetic energy (TKE) in the 3-direction. In Experiment 9b there is a clear evolution of the tensor before and after breaking. In phase 2 a significant axisymmetric structure develop with axis along the 3-direction.
A useful tool to analyse the structure of turbulence is given by the Lumley triangle, which contours all the Reynolds anisotropy stress tensor invariants (Lumley, 1978 [
18]). For an incompressible flow, the three invariants of the anisotropy tensor are
and they are bounded by limits related to the state of turbulence. For instance,
is the definition of isotropic turbulence; while
represents one-component turbulence, and
represents two-component turbulence. In most cases the modified expressions for the invariants,
and
, are adopted.
A different synthetic representation of the level of anisotropy of turbulence is obtained through the eigenvalues of the anisotropy Reynolds tensor. Let
, and
be the three eigenvalues in descending order, the tensor can be expressed as a linear combination of the three tensors of a basis (see Banerjee et al., 2007 [
19]) with coefficients given by
and satisfying the normalizing condition
. These coefficients are used to plot a barycentric map according to the following transformation (see Banerjee et al., 2007 [
19])
where
are the coordinates of three arbitrary basis points. Usually the barycentric map is an equilateral triangle.
Figure 5 shows the structure of turbulence in Experiment 6b represented in a Lumley map and in a barycentric map, with data averaged in horizontal layers 0.4-cm thick, for the first four phases of the first wave cycle. Breaking appears between phase 2 and phase 3. In all of the analysed phases, turbulence has three different components and is anisotropic. At the wave crest and near the free surface, the turbulence is almost one-component turbulence, with only the cross-shore component.
Figure 6 shows the structure of turbulence in Experiment 9b, with breaking between phase 1 and phase 2. Again, turbulence is three-component and in general the distance from isotropy is smaller for the deepest levels, toward the bottom. An exception is phase 3, after breaking, in which the levels near the free surface have a degree of isotropy larger than that of the levels toward the bottom. The scenario is coherent with the turbulence in the breaker being mainly one dimensional (in the
x direction) and with a fast return to isotropy. This fast return can be attributed partially to the fluctuating pressure acting to redistribute the energy amongst the three components, and partially to the transport toward the bottom of the most energetic components, which in turn are responsible of the increase in anisotropy in the deep layers. This mechanism of exchange of anisotropy between different vertical layers can be observed only for the highest waves of the set of experiments (Experiment 5b -not shown- and Experiment 9b) and is much less evident for the less energetic breakers.
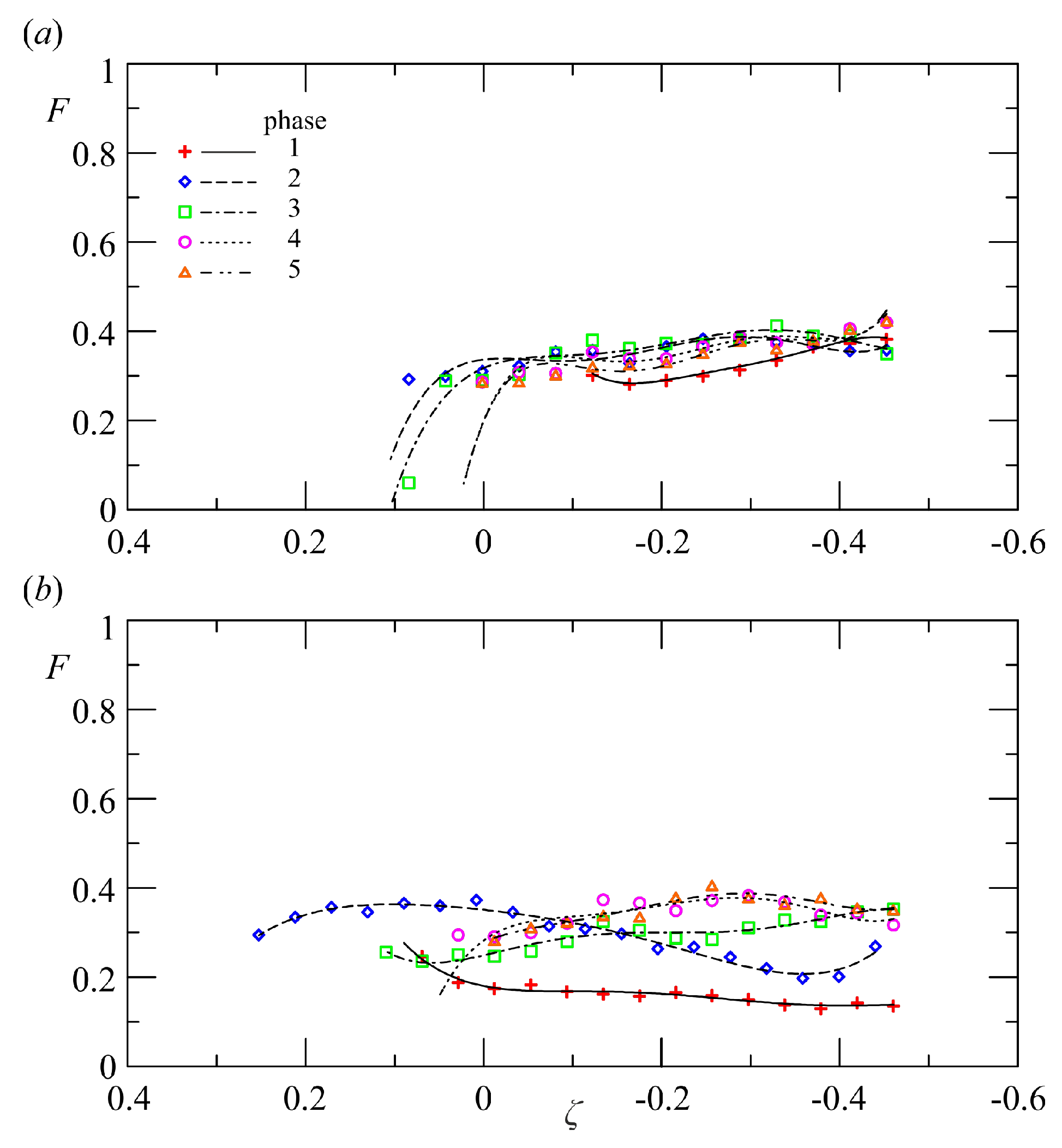
An anisotropy measurement suggested by Lumley and Newman (1977) [
20] is
, which varies between
for a two-component turbulence, and
for the three-component isotropic turbulence.
Figure 7 shows the invariant function
F for two experiments, five phases across breaking, first cycle.
The flow organization reasonably influences the small scale turbulence structures, inducing isotropy or anisotropy in the dissipation rate (Antonia et al., 1994 [
21], Mansour et al., 1988 [
22]). The structure of dissipation rate is depicted by the following tensor
with its anisotropic form
where
is the kinematic viscosity and
is the average dissipation rate of TKE.
This tensor has been considered as a significant element in the attempts to model Reynolds stresses, since
and
are likely to be related at least in some categories of flow.
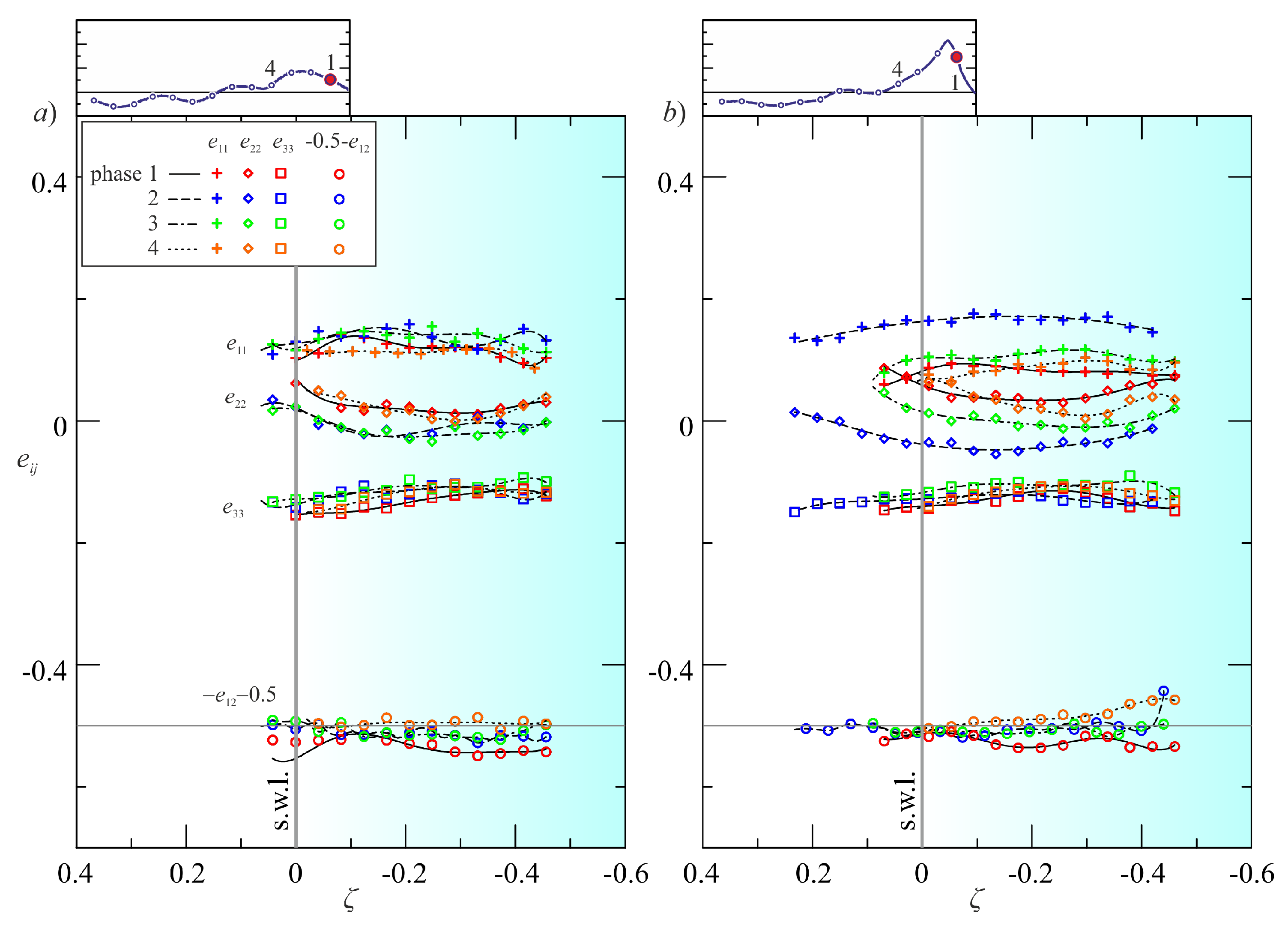
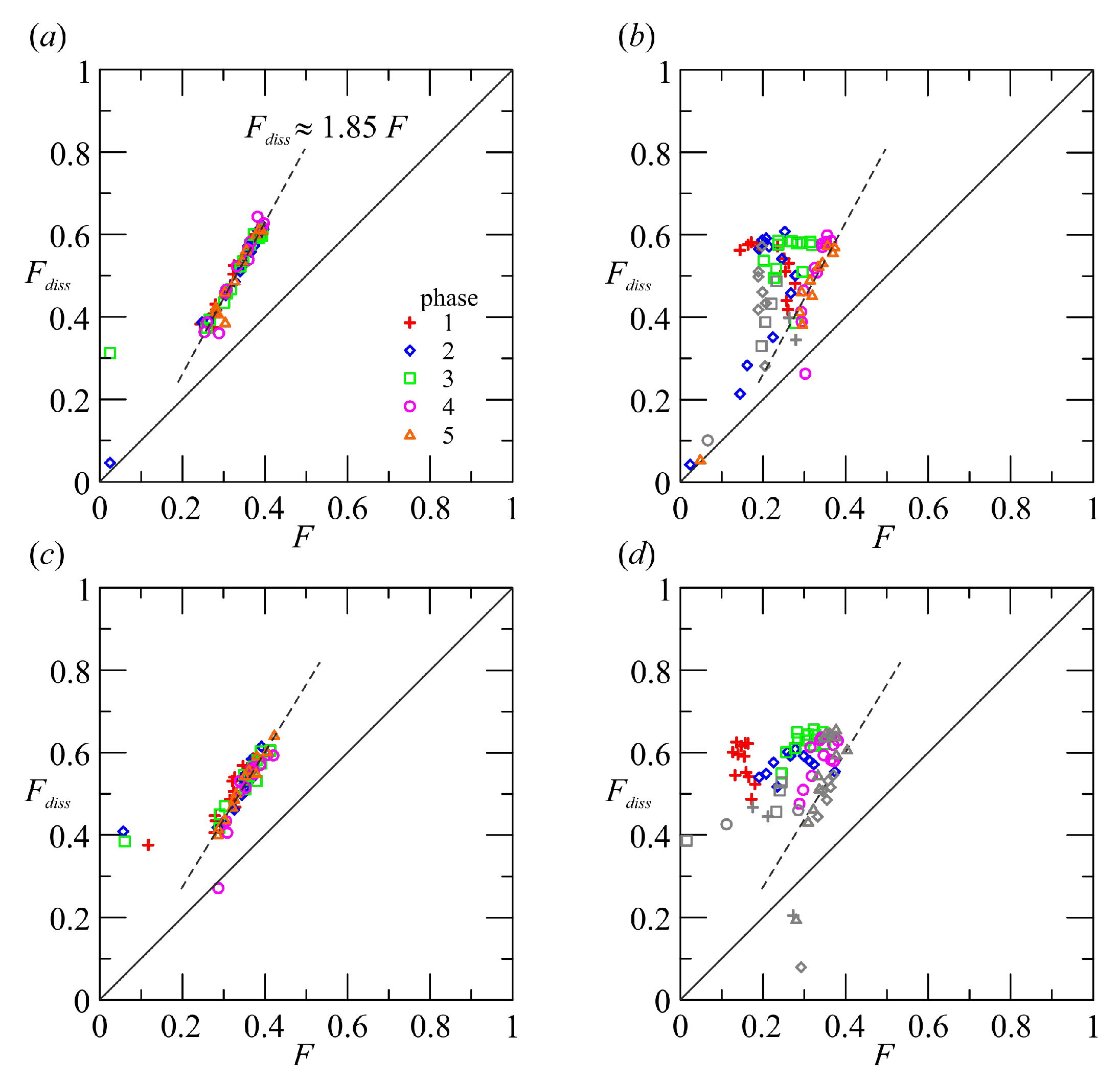
Figure 8 show the main components of the anisotropic dissipation tensor for two experiments. Again for the most intense breaking wave the dissipation tensor is largely anisotropic, with the main term in the cross shore direction immediately after breaking. The overall relation between the two tensors is depicted in
Figure 9, where the invariant function
F for the anisotropy Reynolds tensor
is compared with the corresponding invariant
for the anisotropy dissipation tensor
. For Experiment 1b–6b (low energy breaking) there is a proportionality between
F and
, with dissipation more isotropic (
) than turbulence, and with
. For Experiments 5b–9b (high energy breaking) the data are much more dispersed. The dissipation tensor is still more isotropic than turbulence, but there is no evident correlation with the level of isotropy of turbulence tensor. Surprisingly, the coherence is still present only for data measured above the still water, in the breaker crest. All these analyses refer to macroturbulence, since the data resolution in space and time of the measurements does not allow an in-depth analysis of the behaviour at the microscales.
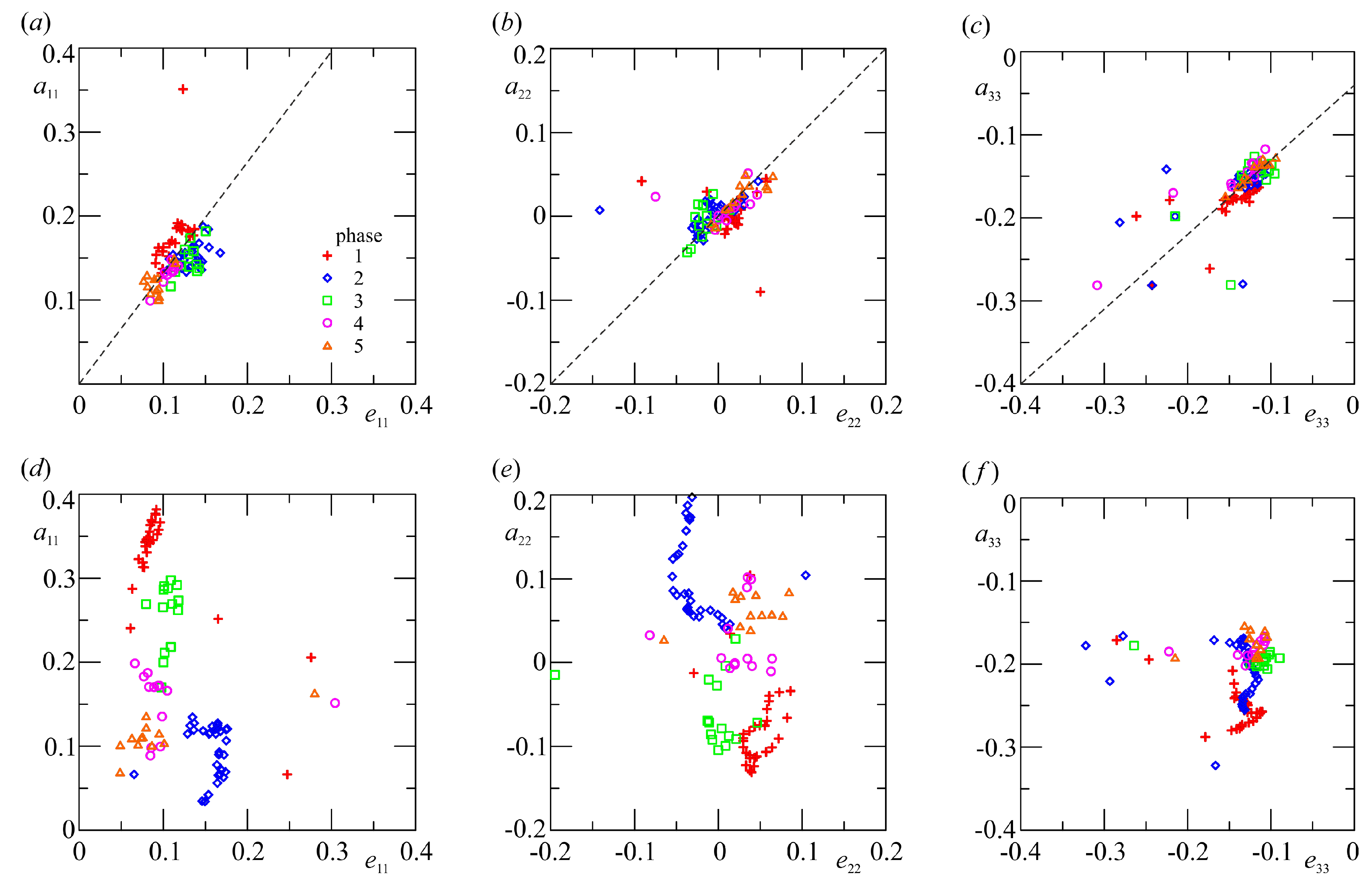
Several data in literature show that a relationship holds between the components of the anisotropy Reynolds tensor and of the anisotropy dissipation tensor. The shape of the relation is strictly dependent on the flow field and has been described as linear in wall boundary layer (see Antonia et al., 1994 [
21]). Also in the present experiments a linear function is forecast for the low energy breaker in
Figure 10a–c, with a coefficient of proportionality almost equal for the three main components. We expect that the coefficient is function of the ratio between the turbulence microscale
and the integral macroscale
(see, e.g., Tennekes and Lumley, 1972 [
23], Longo, 2010 [
15]), which in the present experiments is related to the intensity of the breaker. However, very energetic breakers show a poor coherence between the components of the two tensors, see
Figure 10d–f.
5. Conclusions
We have analysed the anisotropy of the Reynolds stress and of the dissipation tensors with a unique dataset of measurements in breaking waves. The anisotropy is quantified by the invariants and is relatively high during all phases and more evident for the most energetic breakers. For low energy breakers, anisotropy is minor in the dissipation tensor than in the Reynolds stress tensor, with ( means perfect isotropy). For high energy breakers, the dissipation tensor still has an adequate level of isotropy, the Reynolds stress tensor is biased toward anisotropy.
The relationship between the main components of the two tensors is a simple proportionality for low energy breaker. That means that some classical models of turbulence are still applicable. For high energy breakers the relationship looks much more complex, and no simple model can be suggested.
The unique availability of these experimental data has allowed an in depth analysis following the same path adopted for DNS data. However, we expect that the dissipation tensor is affected by the limited space resolution of the data, and both tensors are affected by the limited time resolution, hence the presented results should be evaluated in the light of these limitations.
Beyond the application of well known models for turbulence estimation, there is the important novelty of huge experimental data set for calibrating these models. This data set are a step ahead toward the detailed interpretation of the fundamental mechanisms of turbulence generation, evolution and dissipation.
As a development of data analysis there is the evaluation of the “dimensionality” elements of turbulence. This is left to future work.