Updated Smoothed Particle Hydrodynamics for Simulating Bending and Compression Failure Progress of Ice
Abstract
1. Introduction
2. Governing Equations
2.1. Ice Elasto-Plastic Constitutive Model
3. Failure Model in the SPH Framework
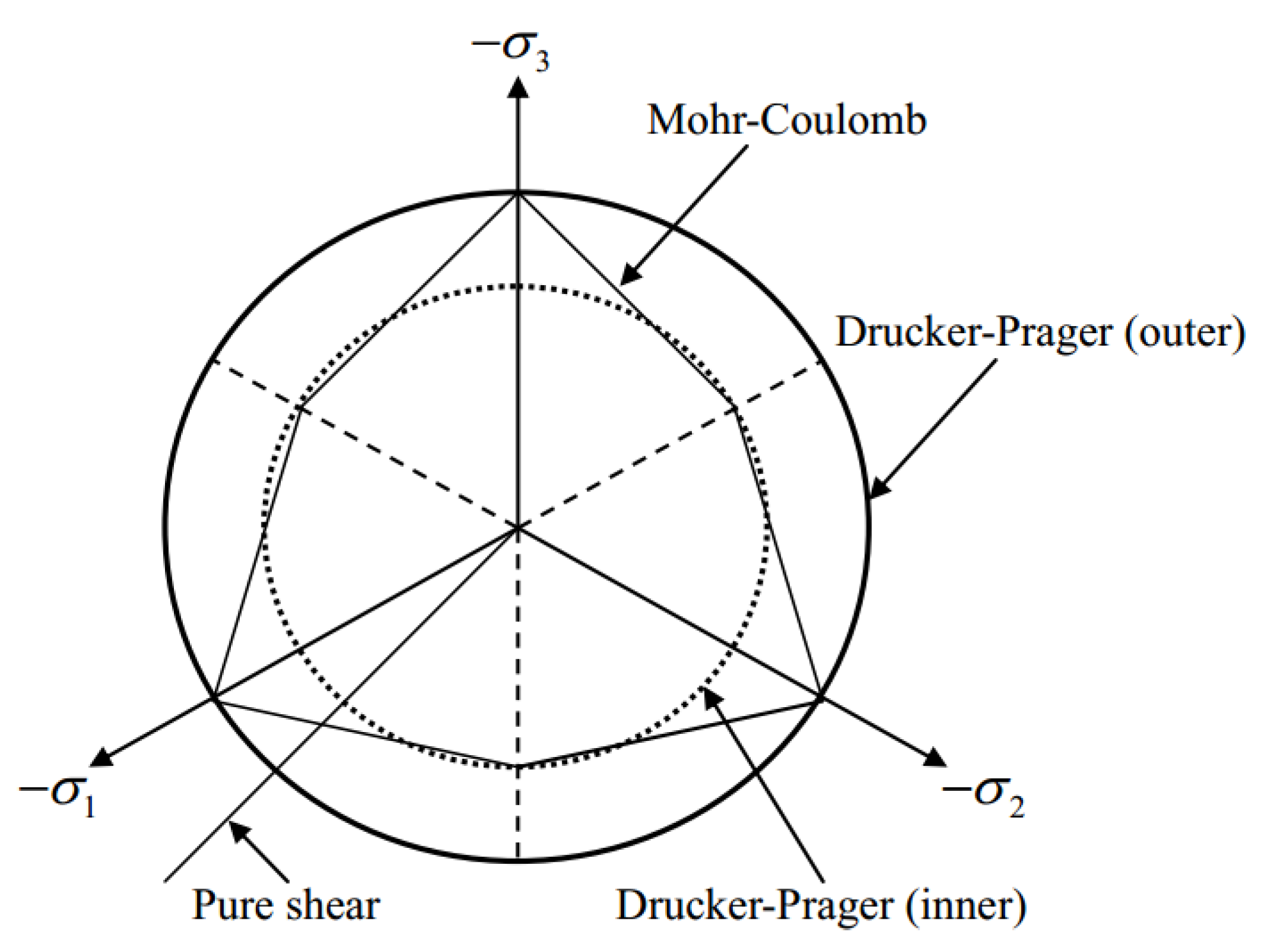
3.1. Drucker–Prager Model
3.2. Numerical Errors in Computational Plasticity
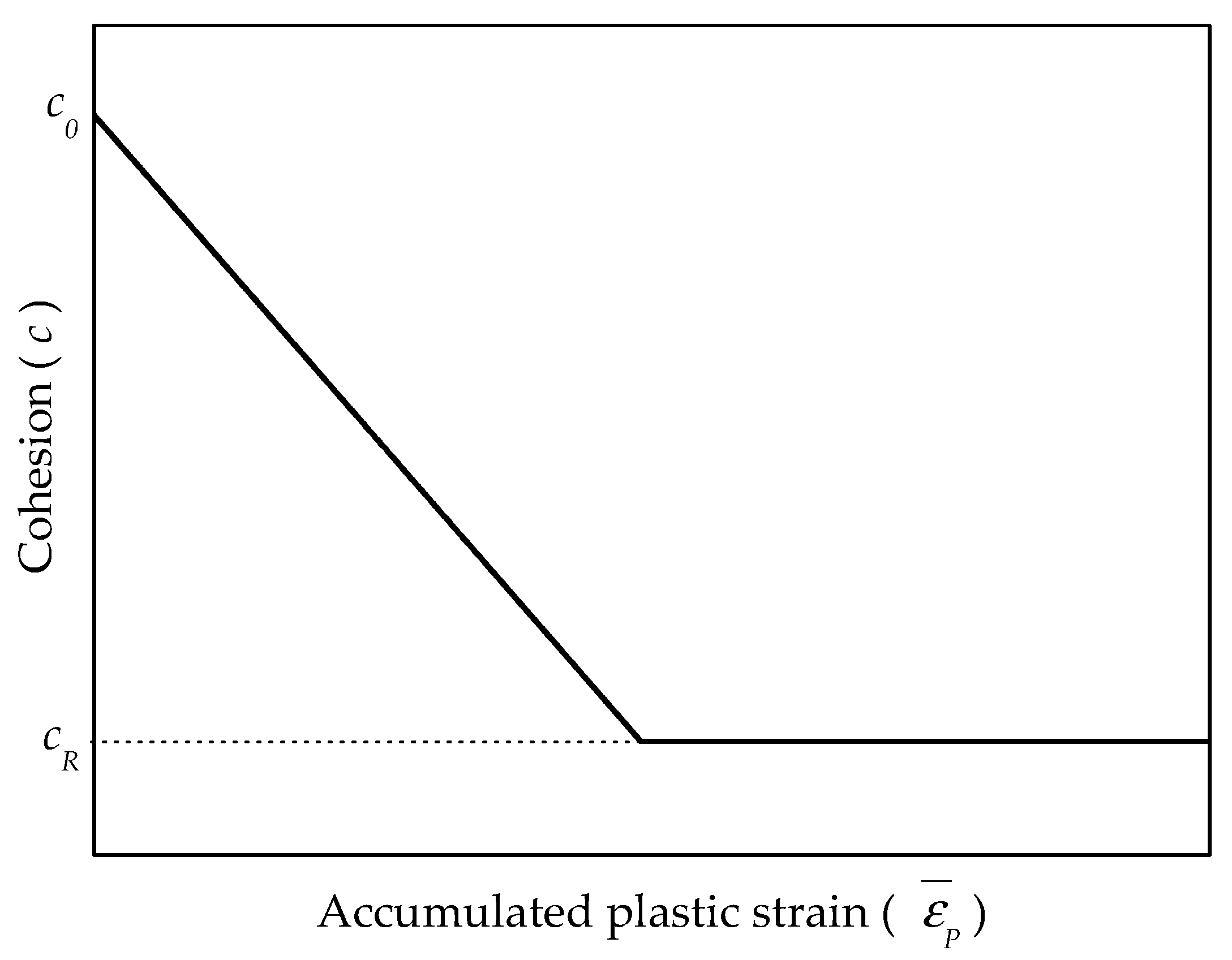
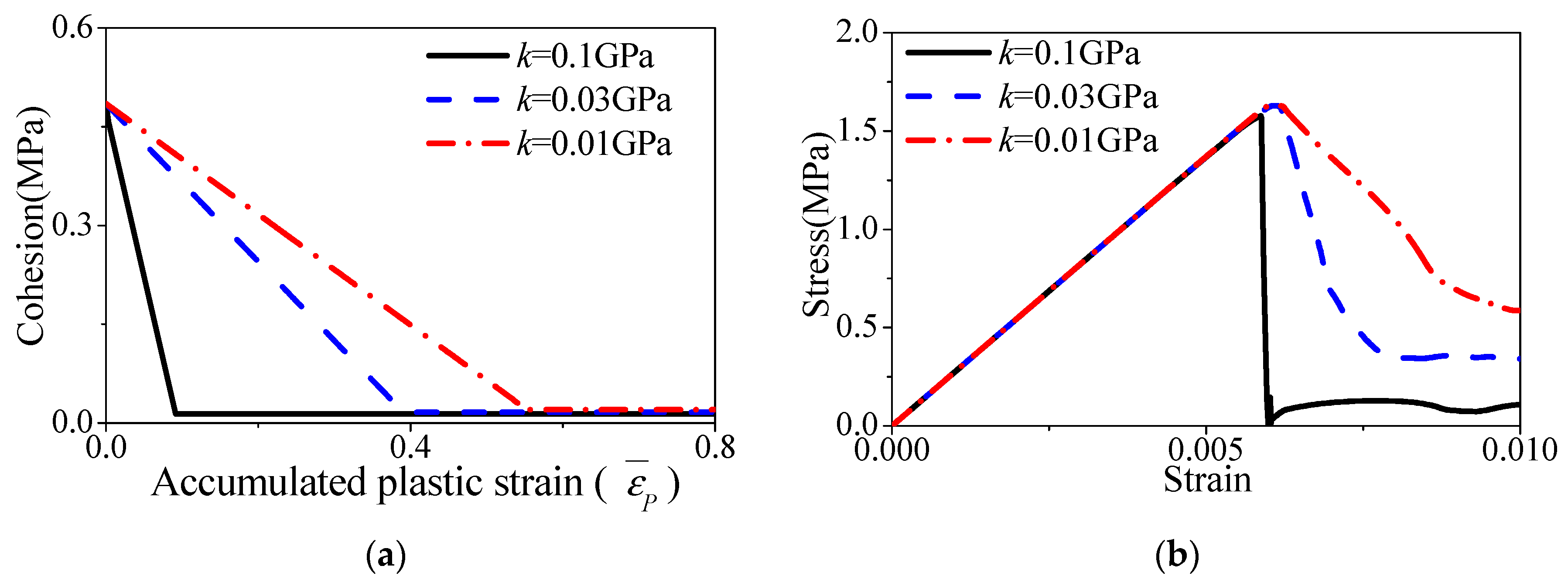
3.3. Cohesion Softening
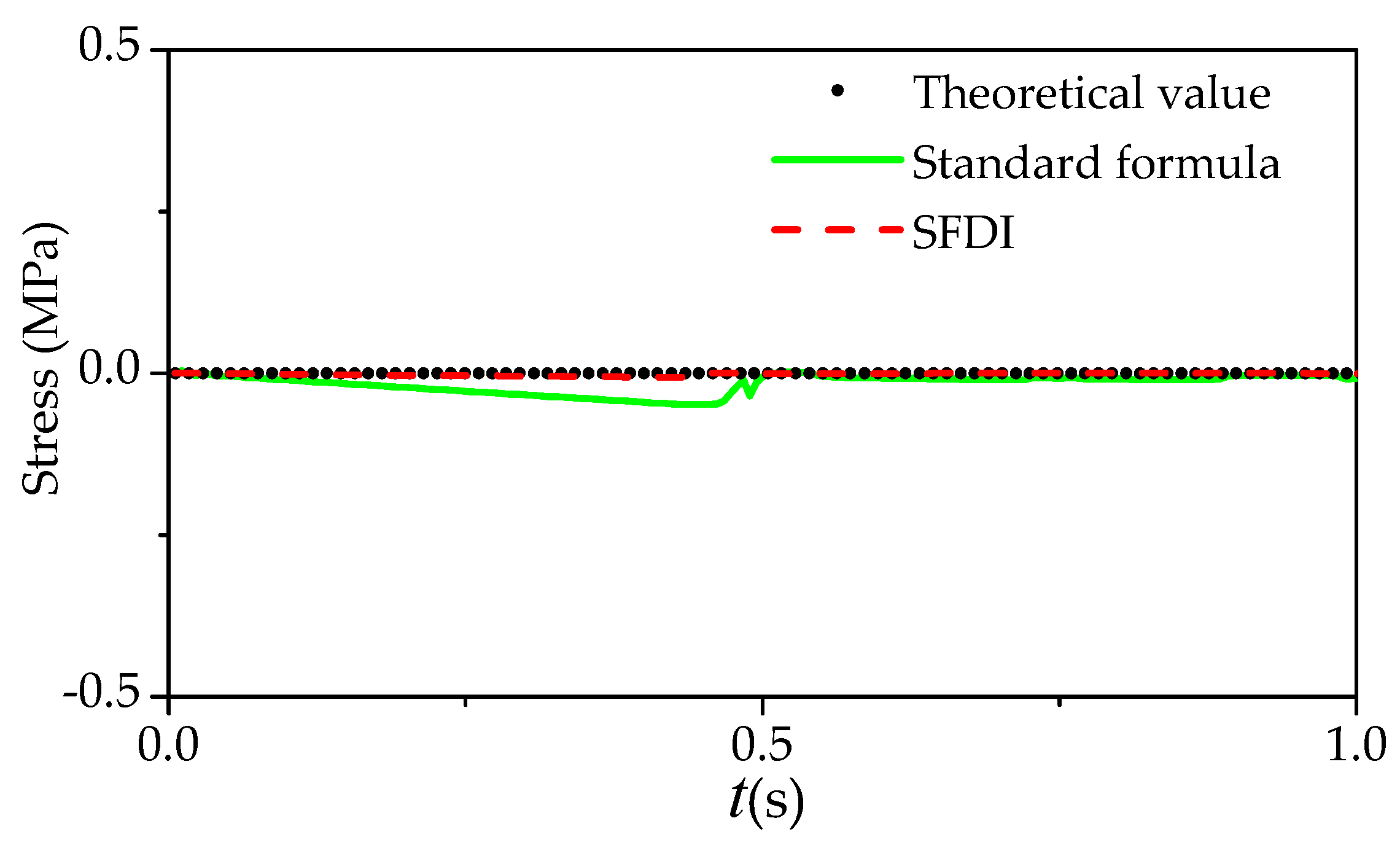
4. SPH Formulations and Corrective SPH Method
4.1. The Particle Approximation and Spatial Derivatives of SPH
4.2. Artificial Stress Method
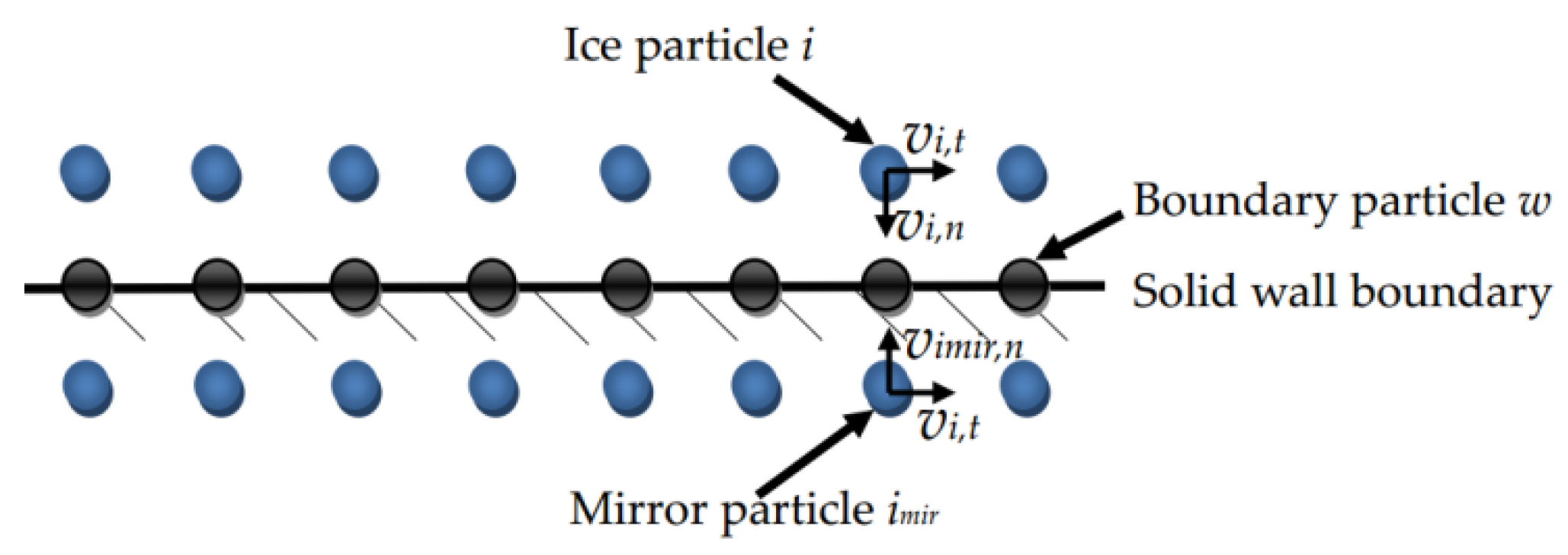
4.3. Boundary Conditions
4.4. Corrective SPH Method
- (1)
- Calculate the values of and from Equations (47), (17) or (19).
- (2)
- Calculate the stress components based on the obtained stress rate .
- (3)
- Check the stress state and judge whether the corresponding stress need to be corrected: if , the stress need to be modified by Equation (25).
- (4)
- Implement Cohesion softening model based on Equation (27).
5. Numerical Simulations
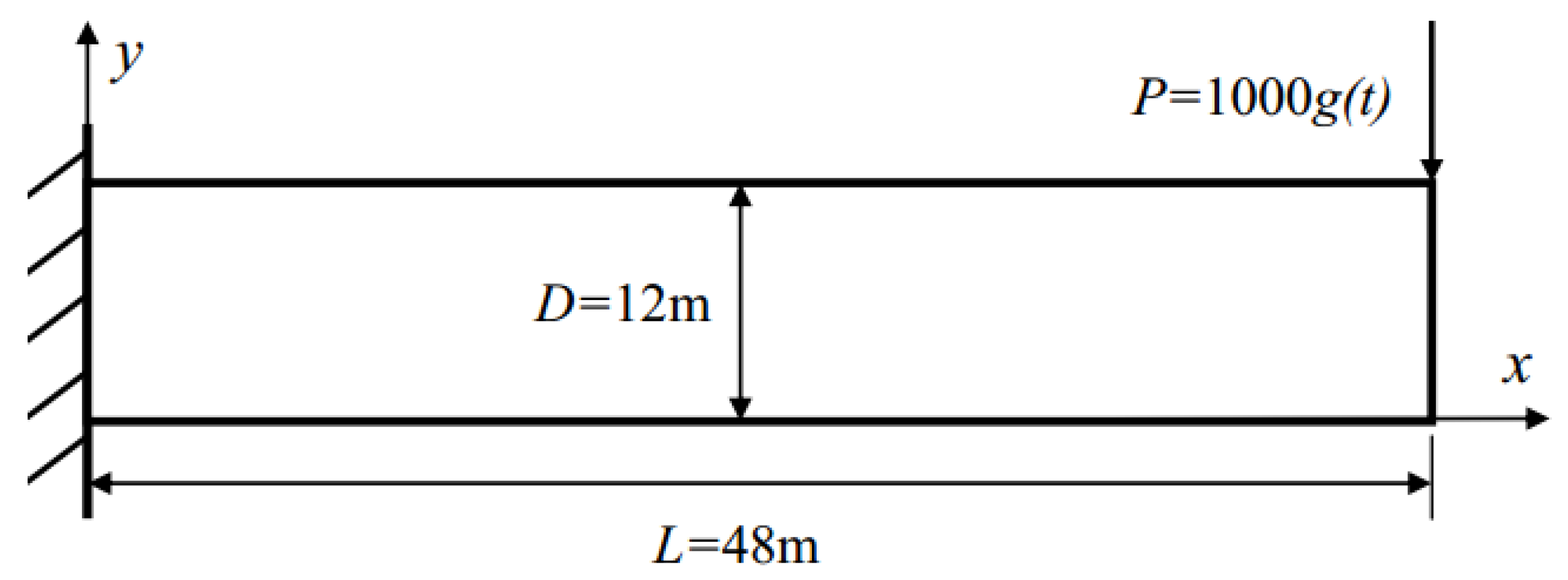
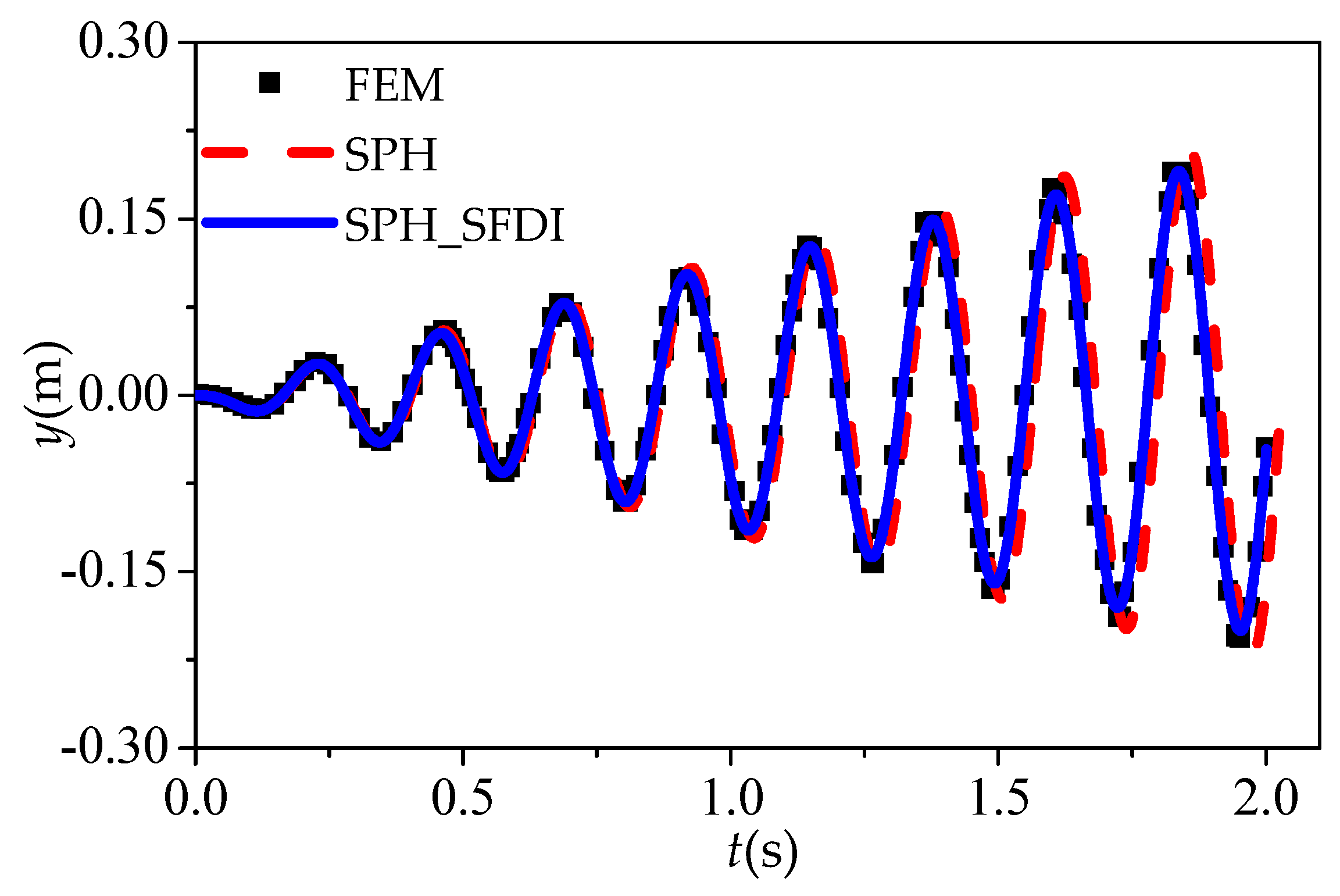
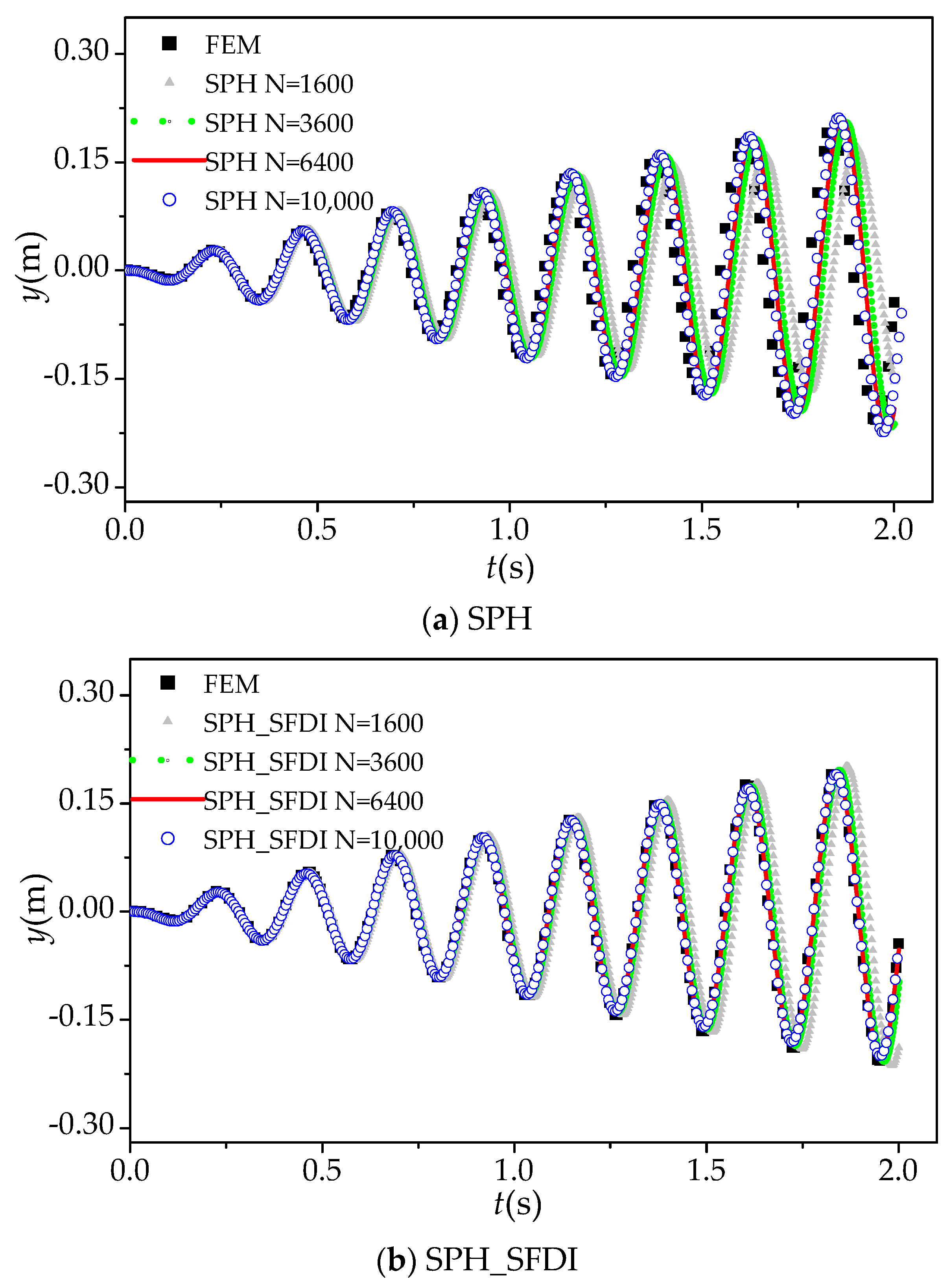
5.1. Elastic Vibration of a Cantilever Beam
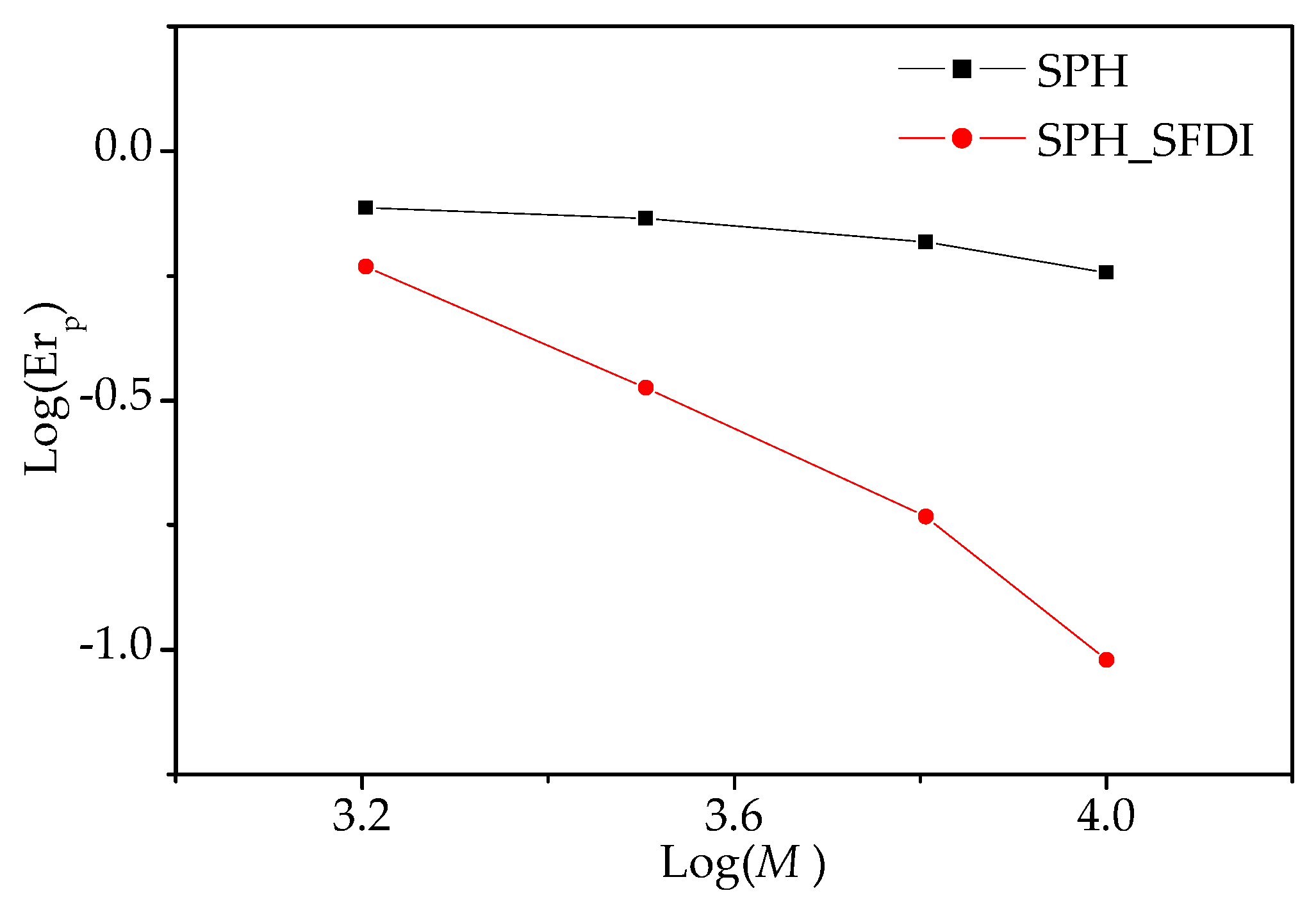
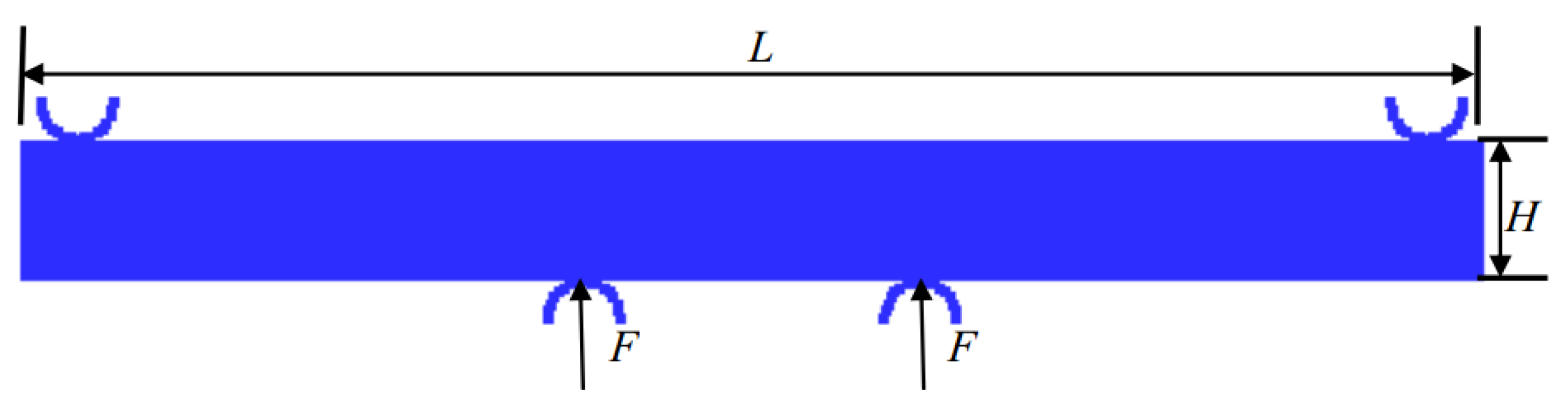
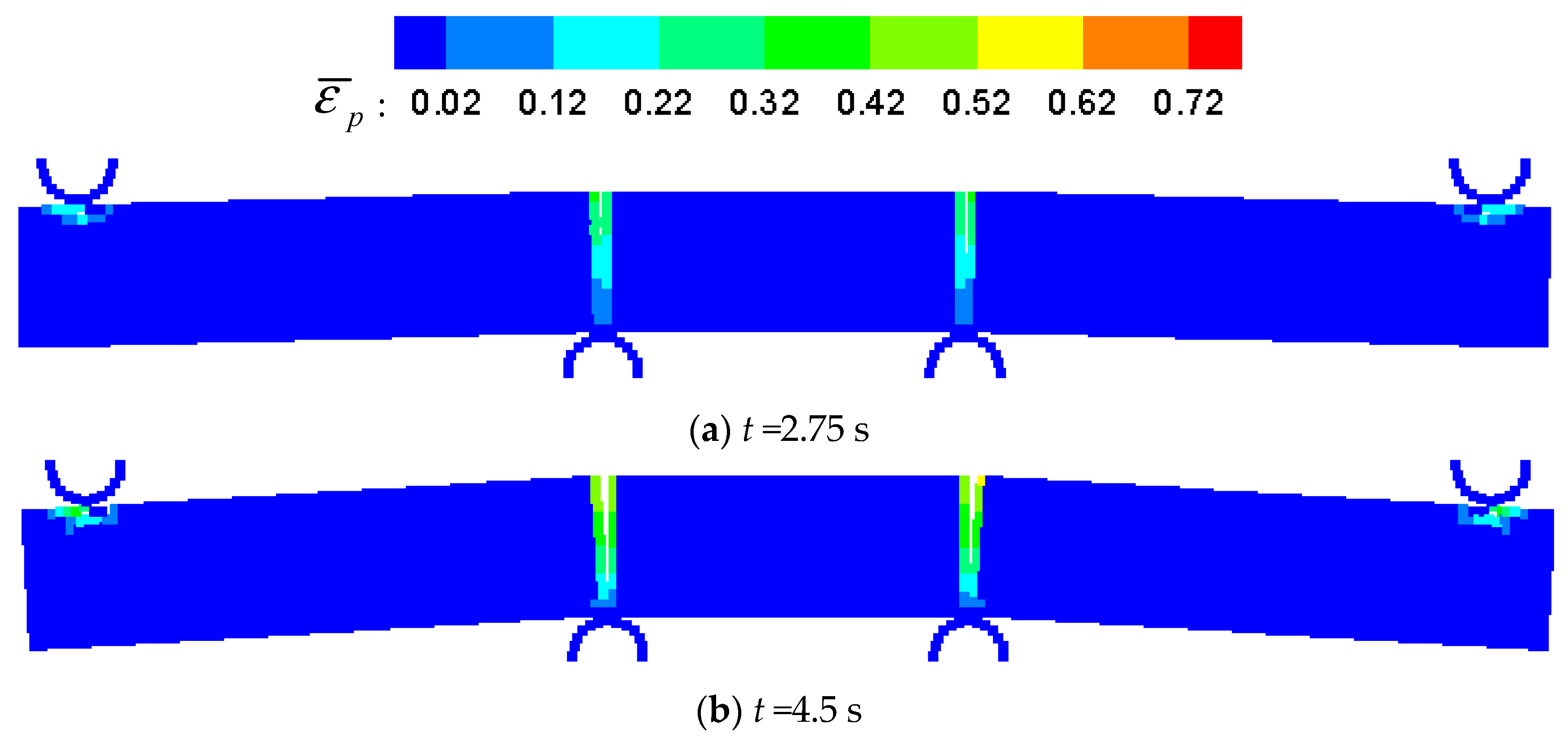
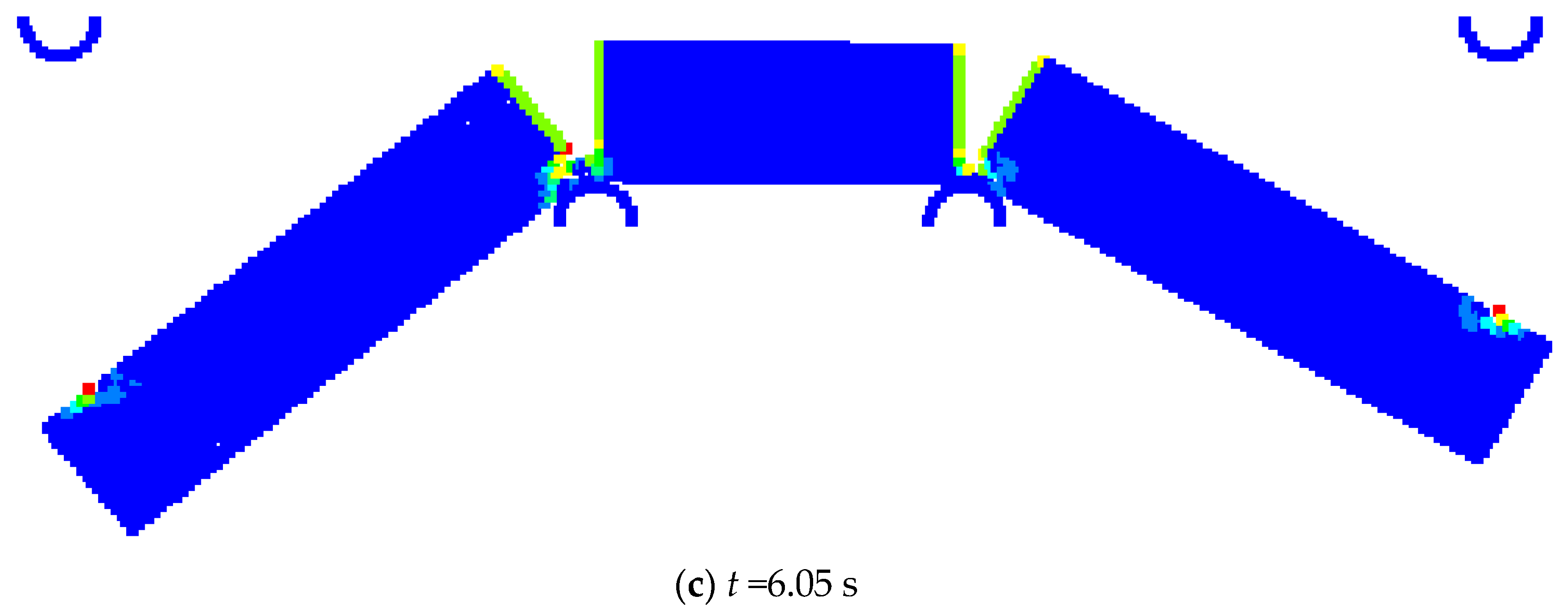
5.2. Four-Point Pending of Ice Beam
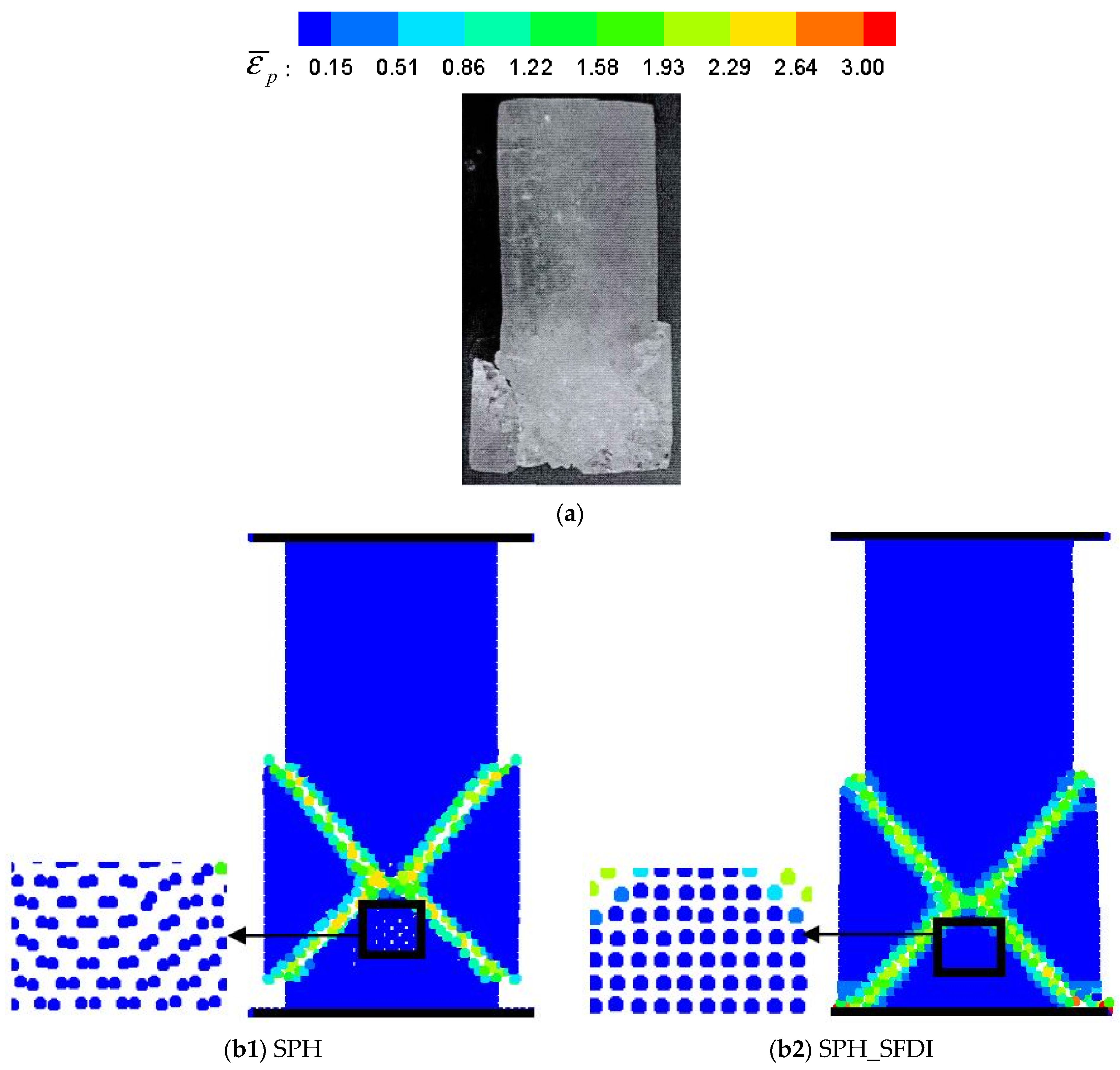
5.3. Uniaxial Compressive Test of Ice Specimen
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, L.; Riska, K.; Moan, T.; Su, B. Numerical modeling of ice loads on an icebreaking tanker: Comparing simulations with models tests. Cold Reg. Sci. Technol. 2013, 87, 33–46. [Google Scholar] [CrossRef]
- Lindqvist, G. A straightforward method for calculation of ice resistance of ships. In Proceedings of the 10th International Conference on Port and Ocean Engineering under Arctic Conditions, Luleaa, Sweden, 12–16 June 1989. [Google Scholar]
- Valanto, P. The resistance of ships in level ice. Trans. Soc. Nav. Archit. Mar. Eng. 2001, 119, 53–83. [Google Scholar]
- Kujala, P.; Riska, K.; Varsta, P. Results from in situ four point bending tests with Baltic Sea Ice. In Proceedings of the IAHR Symposium on Ice Problems, Helsinki, Finland, 19–23 August 1990; pp. 261–278. [Google Scholar]
- Schulson, E.M. Compressive shear faults within arctic sea ice: Fracture on scales large and small. J. Geophys. Res. Oceans 2004, 109, 101–111. [Google Scholar] [CrossRef]
- Schulson, E.M.; Fortt, A.L.; Iliescu, D.; Renshaw, C.E. Failure envelope of first-year arctic sea ice: The role of friction in compressive fracture. J. Geophys. Res. Oceans 2006, 111, 2209–2223. [Google Scholar] [CrossRef]
- Li, Z.J.; Zhang, L.M.; Lu, P.; Leppäranta, M. Experimental study on the effect of porosity on the uniaxial compressive strength of sea ice in bohai sea. Sci. China Technol. Sci. 2011, 54, 2429–2436. [Google Scholar] [CrossRef]
- Polach, R.V.B.U.; Ehlers, S.; Kujala, P. model-scale ice—Part A: Experiments. Cold Reg. Sci. Technol. 2013, 94, 74–81. [Google Scholar] [CrossRef]
- Corasdale, K. Platform shape and ice interaction: A review. In Proceedings of the 21st International Conference on Port and Ocean Engineering under Arctic Conditions, Montreal, QC, Canada, 10–14 July 2011. [Google Scholar]
- Lu, W.; Lubbad, R.; Hoyland, K.; Loset, S. Physical model and theoretical model study of level ice and wide sloping structure interactions. Cold Reg. Sci. Technol. 2014, 101, 40–72. [Google Scholar] [CrossRef]
- Zhou, L.; Su, B.; Riska, K.; Moan, T. Numerical simulation of moored structure station keeping in level ice. Cold Reg. Sci. Technol. 2012, 71, 54–66. [Google Scholar] [CrossRef]
- Kolari, K.; Kuutti, J.; Kurkela, J. FE-simulation of continuous ice failure based on model update technique. In Proceedings of the 20th International Conference on Port and Ocean Engineering under Arctic Conditions, Luleå, Sweden, 9–12 June 2009. [Google Scholar]
- Hopkins, M.A. On the mesoscale interaction of lead ice and floes. J. Geophys. Res. 1996, 101, 18315–18326. [Google Scholar] [CrossRef]
- Paavilainen, J.; Tuhkuri, J. Parameter effects on simulated ice rubbling forces on a wide sloping structure. Cold Reg. Sci. Technol. 2012, 81, 1–10. [Google Scholar] [CrossRef]
- Paavilainen, J.; Tuhkuri, J.; Polojarvi, A. 2D numerical simulation of ice rubble formation process against an inclined structure. Cold Reg. Sci. Technol. 2011, 68, 20–34. [Google Scholar] [CrossRef]
- Das, J. Modeling and validation of simulation results of an ice beam in four-point bending using smoothed particle hydrodynamics. Int. J. Offshore Polar Eng. 2017, 27, 82–89. [Google Scholar] [CrossRef]
- Deb, D.; Pramanik, R. Failure process of brittle rock using smoothed particle hydrodynamics. J. Eng. Mech. 2013, 139, 1551–1565. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of fusion process. Astron. J. 1977, 88, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics—Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Morris, J.; Fox, P.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Cleary, P.; Prakash, M. Discrete-element modelling and smoothed particle hydrodynamics: Potential in the environmental sciences. Philos. Trans. R. Soc. Lond. Ser. A 2004, 362, 2003–2030. [Google Scholar]
- Khayyer, A.; Gotoh, H.; Shao, S.D. Corrected incompressible SPH method for accurate water surface tracking in breaking waves. Coast. Eng. 2008, 55, 236–250. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S.D. Enhanced predictions of wave impact pressure by improved incompressible SPH methods. Appl. Ocean Res. 2009, 31, 111–131. [Google Scholar] [CrossRef]
- Zheng, X.; Ma, Q.W.; Duan, W.Y. Incompressible SPH method based on Rankine source solution for violent water wave simulation. J. Comput. Phys. 2014, 276, 291–314. [Google Scholar] [CrossRef]
- Shao, S.D. Incompressible SPH flow model for wave interactions with porous media. Coast. Eng. 2010, 57, 304–316. [Google Scholar] [CrossRef]
- Liu, X.; Xu, H.; Shao, S.; Lin, P. An improved incompressible SPH model for simulation of wave–structure interaction. Comput. Fluids 2013, 71, 113–123. [Google Scholar] [CrossRef]
- Shao, S.D.; Lo, E.Y.M. Incompressible SPH method for simulating newtonian and non-newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Xu, R.; Stansby, P.; Laurence, D.; Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Napoli, E.; Marchis, M.D.; Gianguzzi, C.; Milici, B.; Monteleone, A. A coupled finite volume–smoothed particle hydrodynamics method for incompressible flows. Comput. Methods Appl. Mech. Eng. 2016, 310, 674–693. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petschek, A.G. Smoothed particle hydrodynamics with strength of materials. In Proceedings of the Next Free Lagrange Conference, Moran, WY, USA, 3–7 June 1990; Trease, H., Friits, J., Crowley, W., Eds.; Springer: New York, NY, USA, 1991; Volume 395, pp. 248–257. [Google Scholar]
- Benz, W.; Asphaug, E. Simulations of brittle solids using smooth particle hydrodynamics. Comput. Phys. Commun. 1995, 87, 253–265. [Google Scholar] [CrossRef]
- Randles, P.; Libersky, L. Smoothed particle hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 375–408. [Google Scholar] [CrossRef]
- Bui, H.; Fukagawa, R.; Sako, K.; Ohno, S. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic–plastic soil constitutive model. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1537–1570. [Google Scholar] [CrossRef]
- Douillet-Grellier, T.; Jones, B.D.; Pramanik, R.; Pan, K.; Albaiz, A.; Williams, J.R. Mixed-mode fracture modeling with smoothed particle hydrodynamics. Comput. Geotech. 2016, 79, 73–85. [Google Scholar] [CrossRef]
- Zhang, N.B.; Zheng, X.; Ma, Q.W.; Hao, H.B. Numerical simulation of failure progress of ice using smoothed particle hydrodynamics. In Proceedings of the SOPE 2017, International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Whyatt, J.K.; Board, M.P. Numerical Exploration of Shear-Fracture-Related Rock Bursts Using a Strain-Softening Constitutive Law; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1991.
- Ma, Q.W. A new meshless interpolation scheme for MLPG_R method. CMES Comput. Model. Eng. Sci. 2008, 23, 75–89. [Google Scholar]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH without a tensile instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Gray, J.; Monaghan, J.; Swift, R. SPH elastic dynamics. Comput. Methods Appl. Mech. Eng. 2001, 190, 6641–6662. [Google Scholar] [CrossRef]
- Swegle, J.; Hicks, D.; Attaway, S. Smoothed particle hydrodynamics stability analysis. J. Comput. Phys. 1995, 116, 123–134. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petschek, A.G.; Carney, T.C.; Hipp, J.R.; Allahdadi, F.A. High strain Lagrangian hydrodynamics: A three-dimensional SPH code for dynamic material response. J. Comput. Phys. 1993, 109, 67–75. [Google Scholar] [CrossRef]
- Zheng, X.; Shao, S.D.; Khayyer, A.; Duan, W.Y.; Ma, Q.W.; Liao, K.P. Corrected first-order derivative ISPH in water wave simulations. Coast. Eng. J. 2017, 59, 1750010. [Google Scholar] [CrossRef]
- Long, S.Y. Meshless Methods and Their Applications in Solid Mechanics; Science Press: Beijing, China, 2014; pp. 235–238. [Google Scholar]
- Ehlers, S.; Kujala, P. Optimization-based material parameter identification for the numerical simulation of sea ice in four-point bending. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2013, 228, 70–80. [Google Scholar] [CrossRef]
- ITTC. Ice Property Measurements, 7.5-02-04-02. Available online: http://ittc.sname.org (accessed on 19 June 2017).
- Zhang, L.M. Experimental Study on Uniaxial Compressive Strength and Influencing Factors of Ice. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
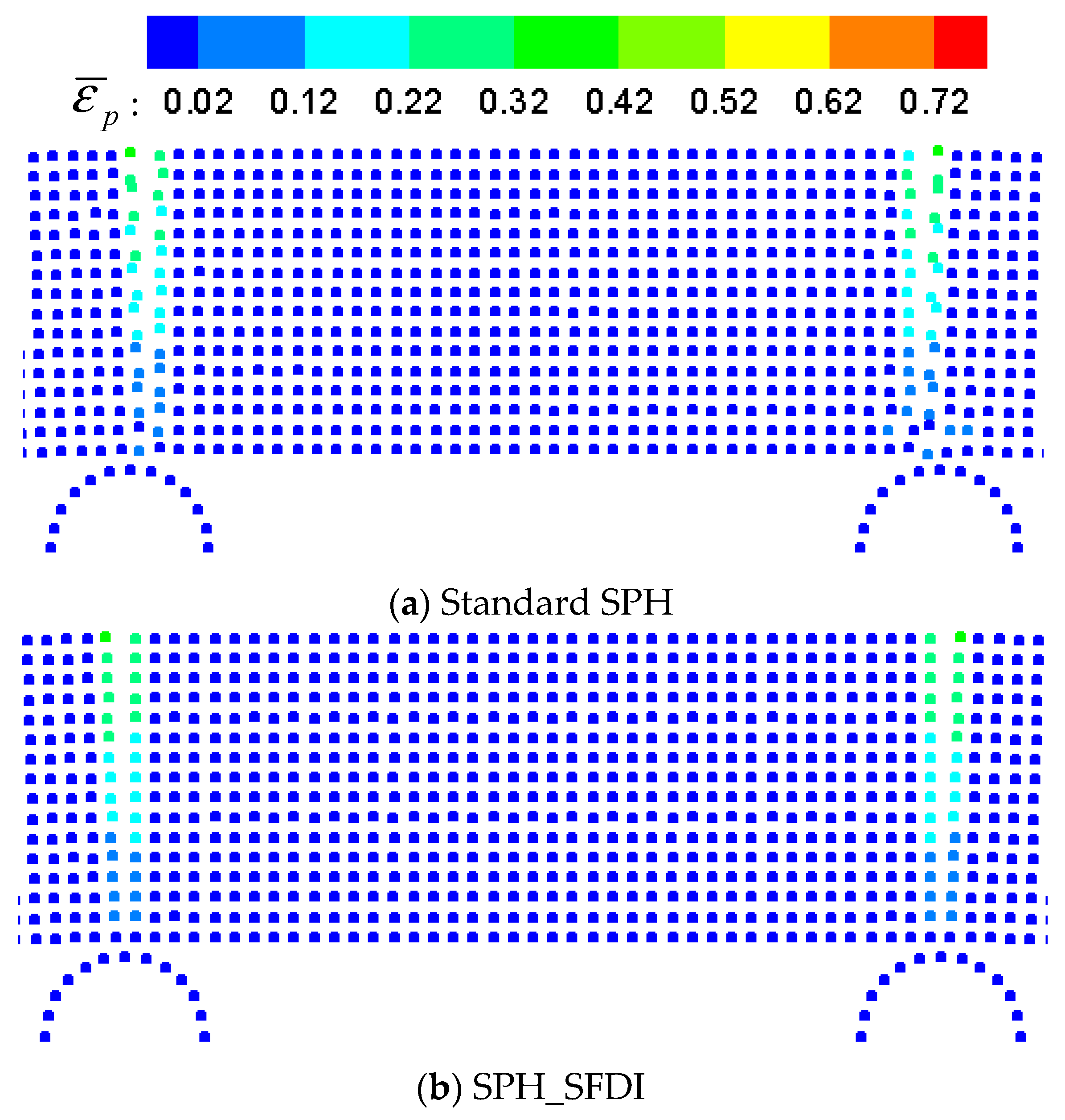
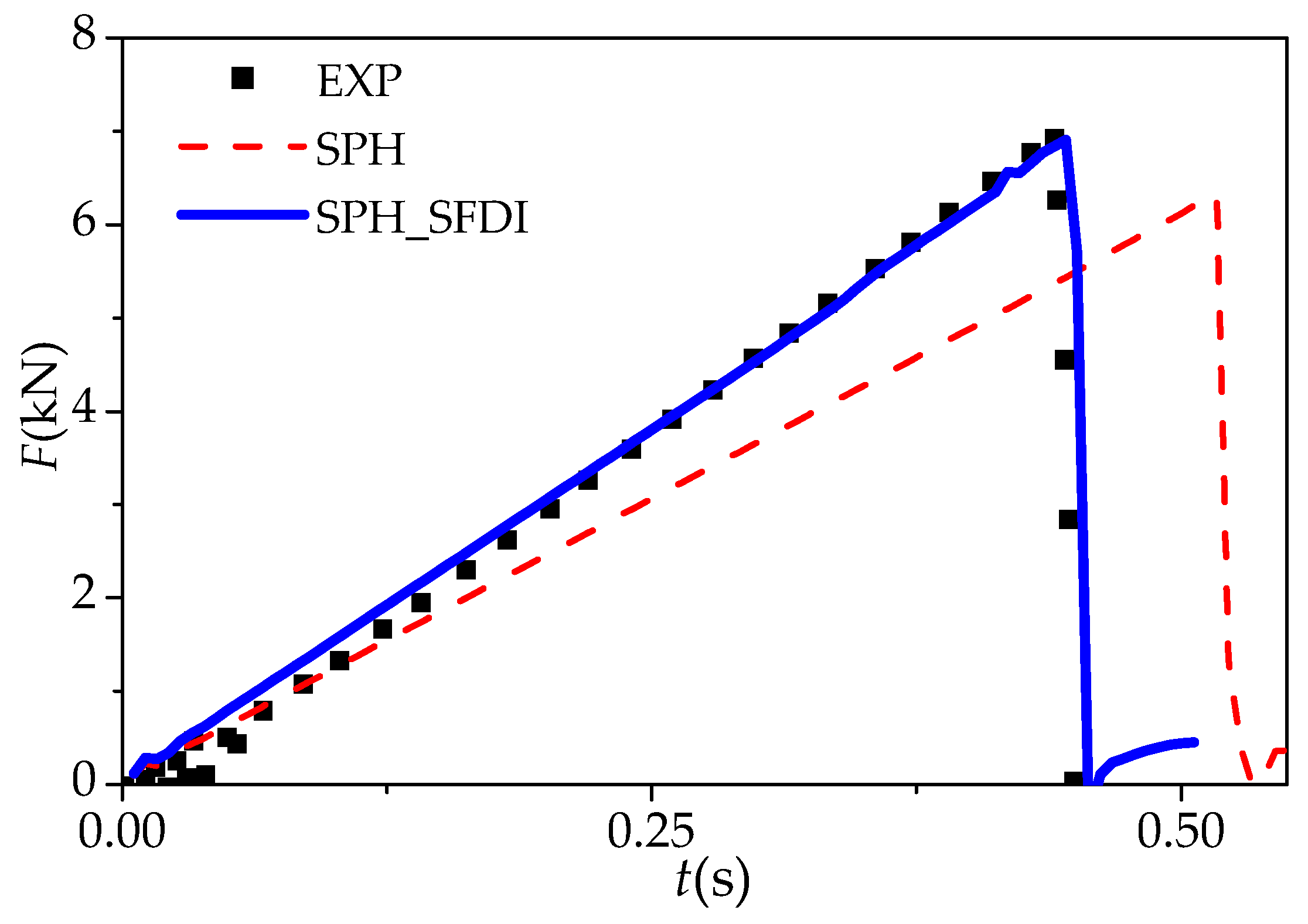
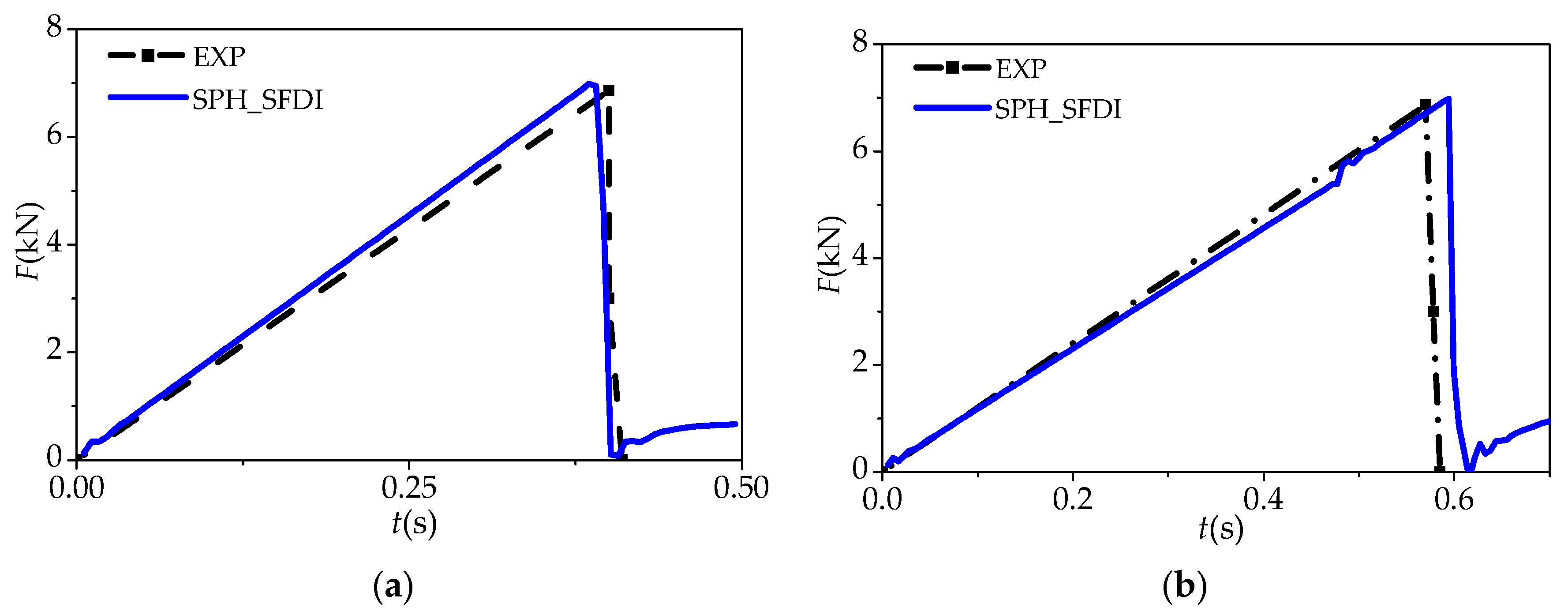
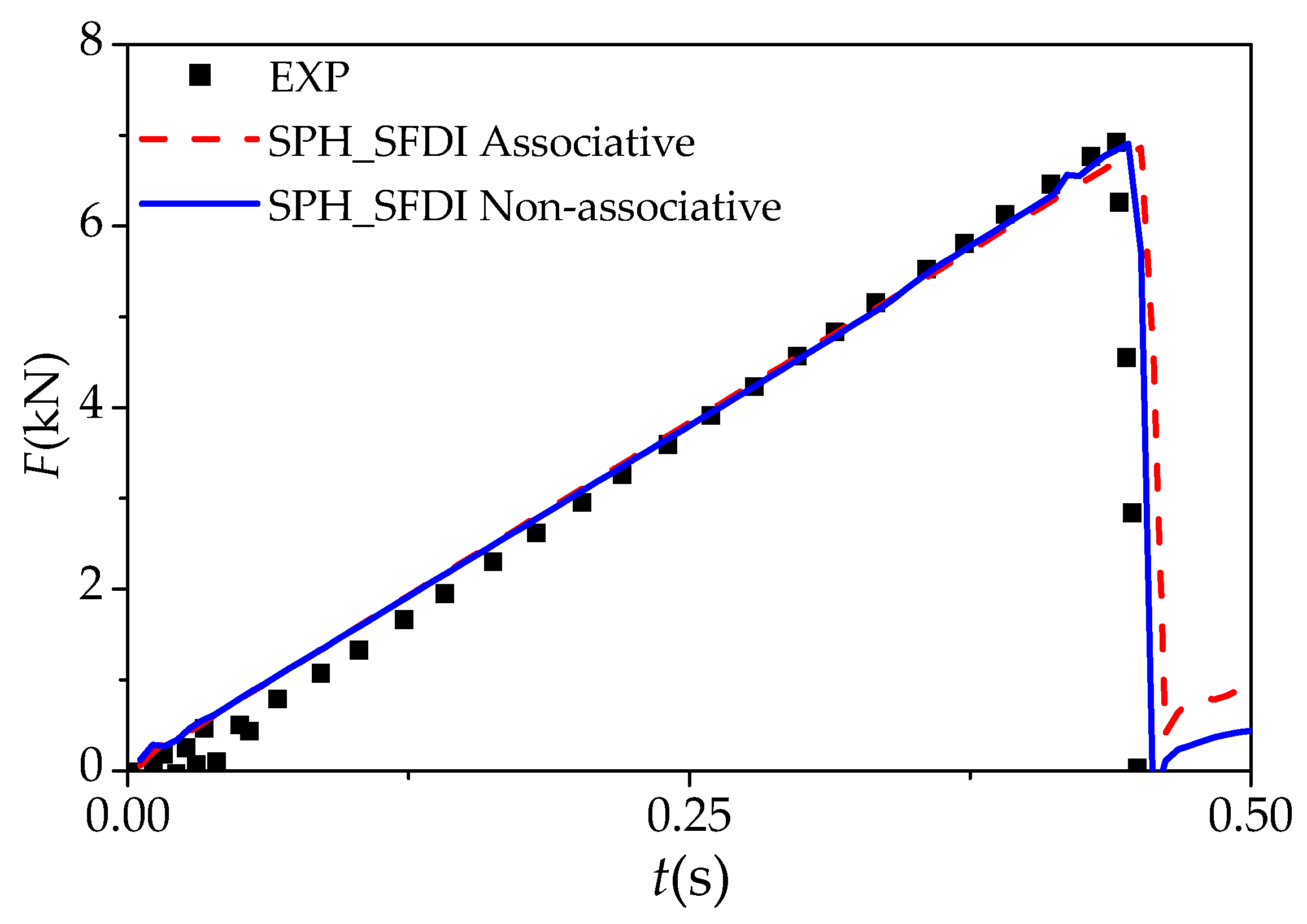
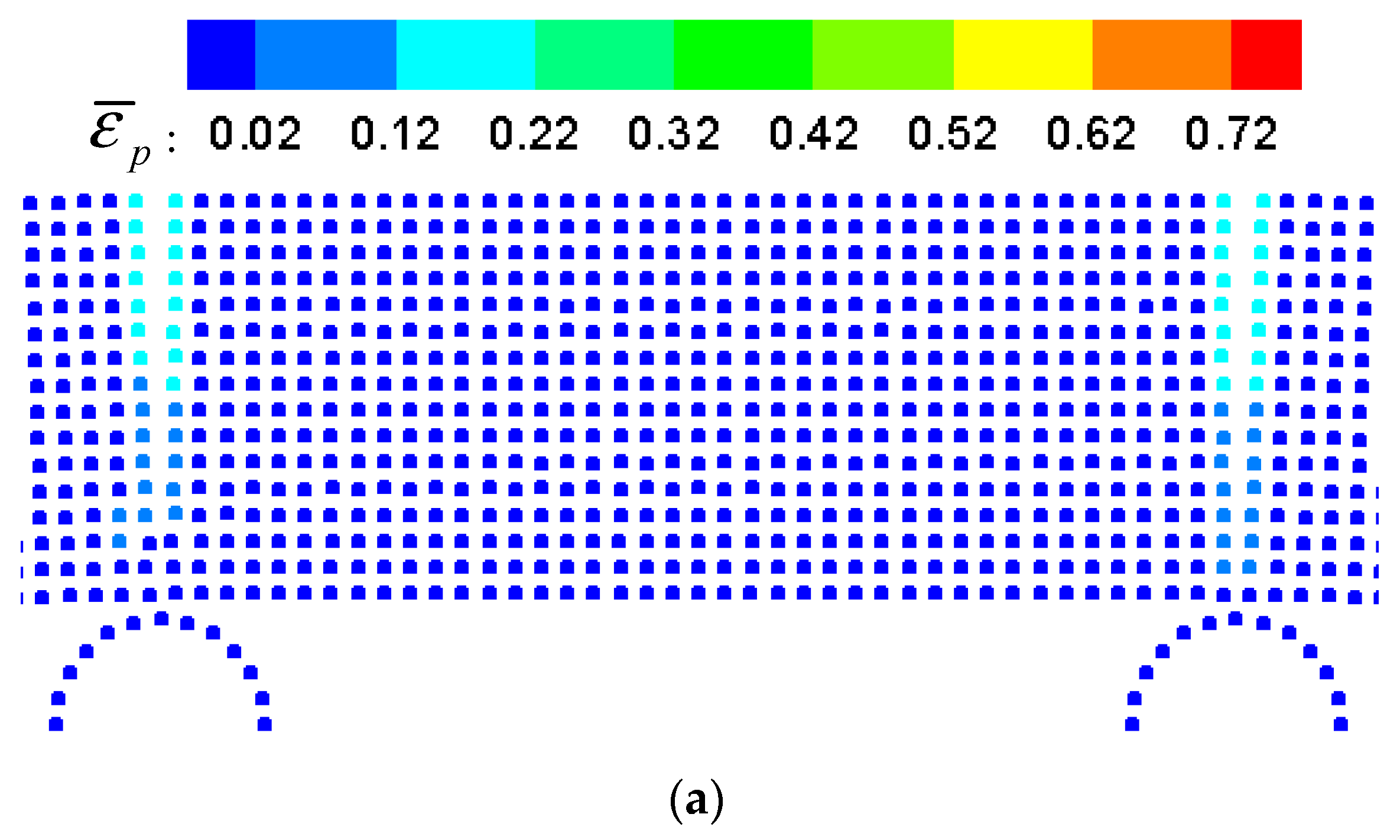

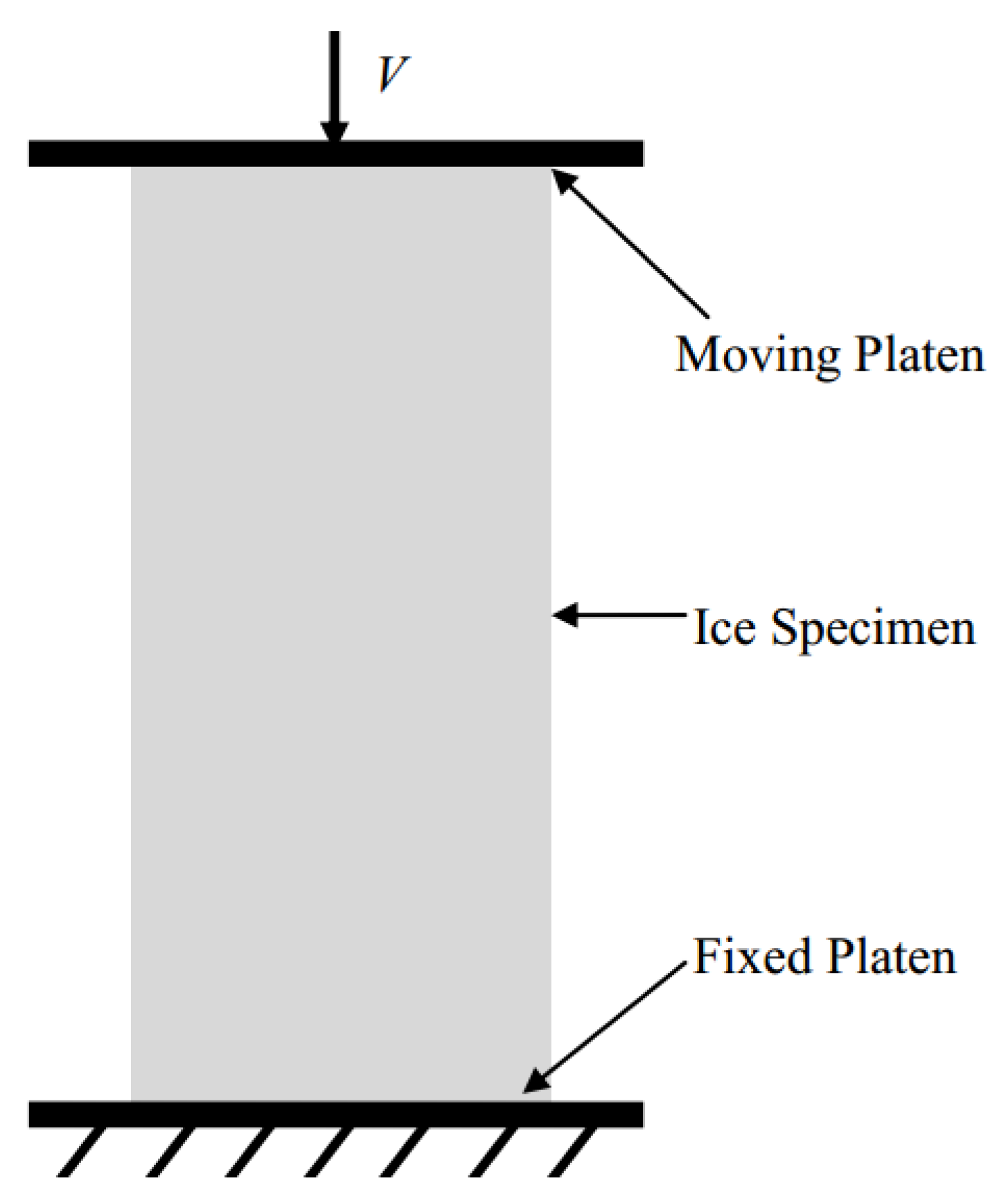


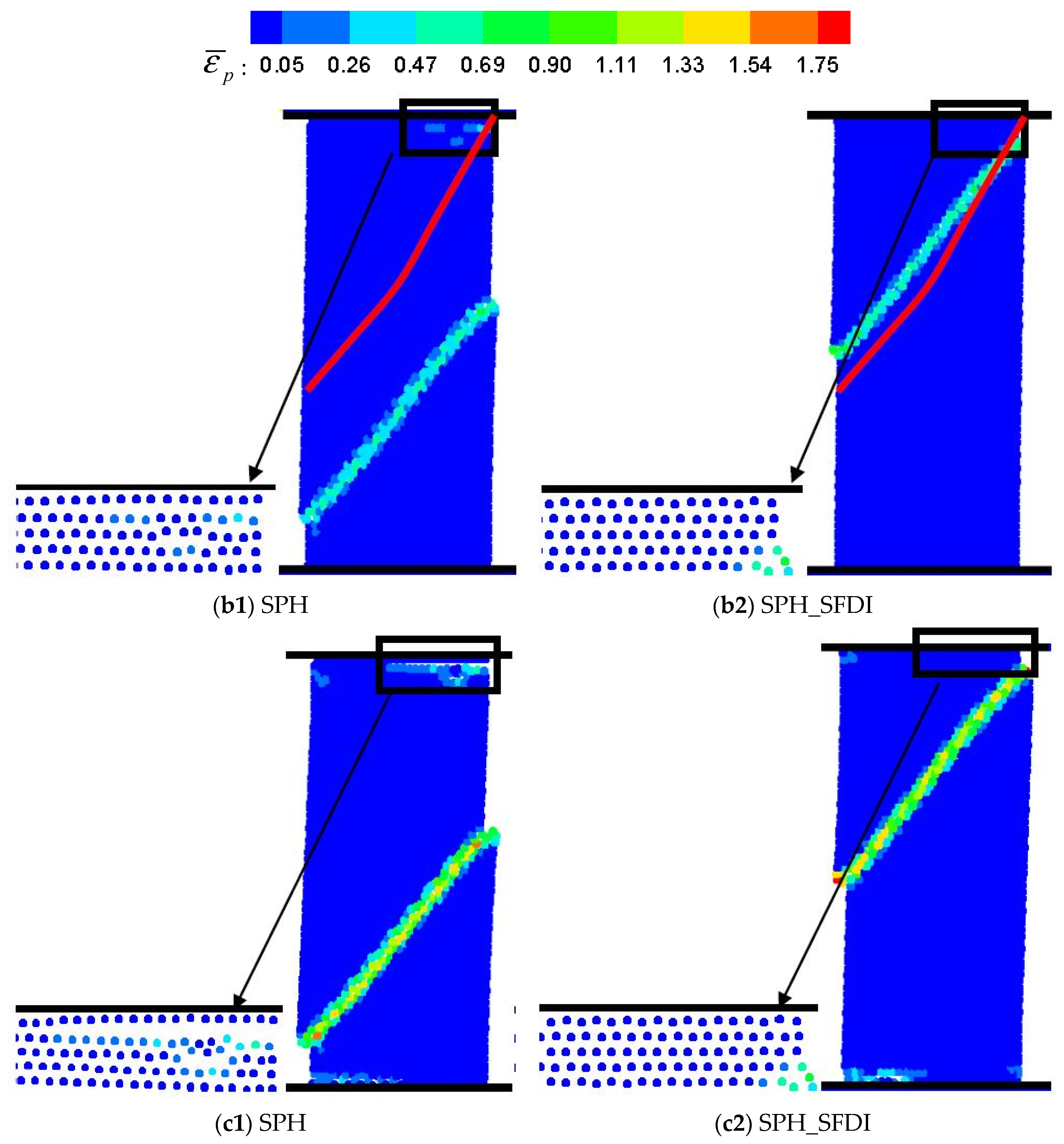
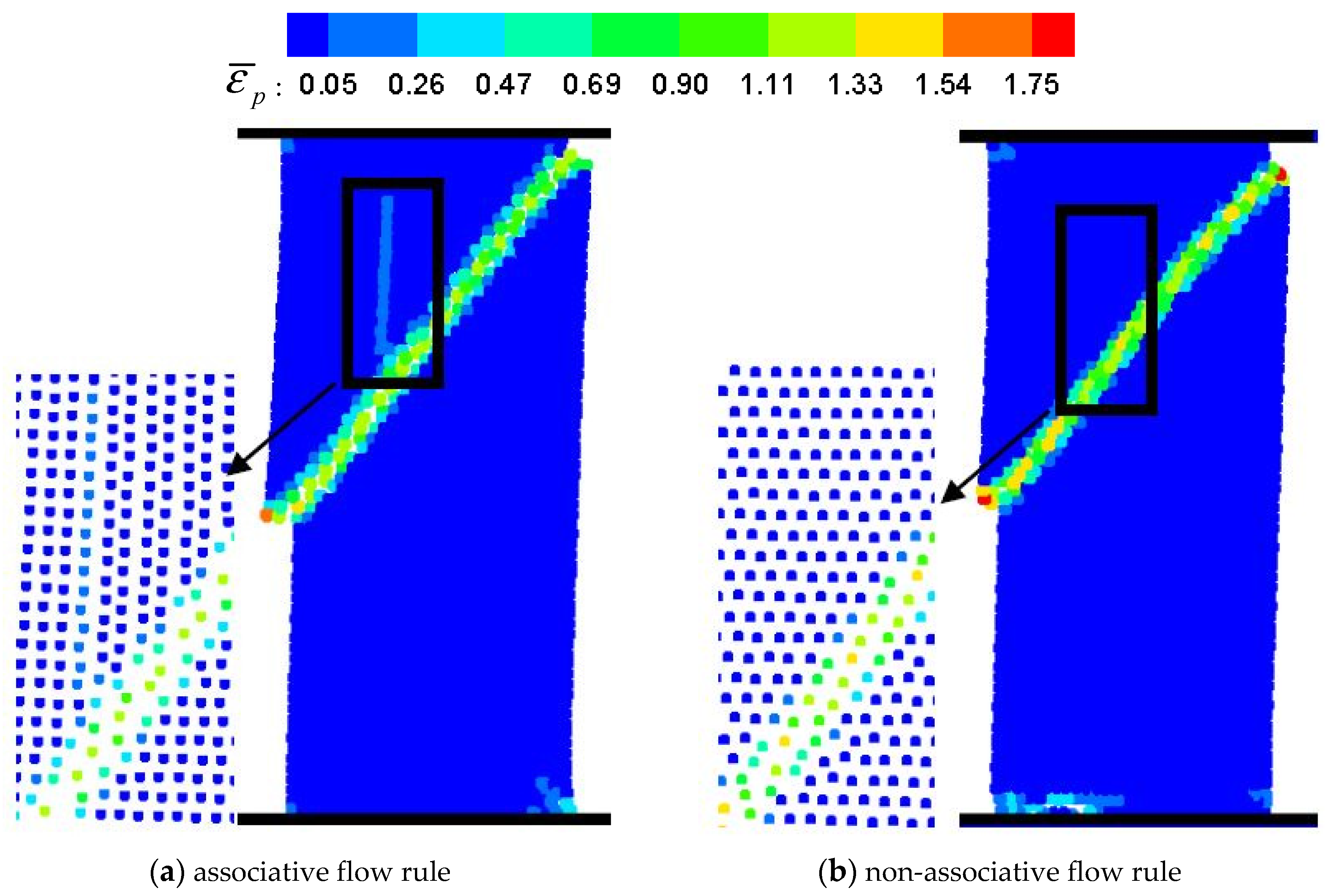
| Approach | () | () | () | () | () | () |
|---|---|---|---|---|---|---|
| EXP | 6.87 kN | 0.40 s | 1.29 mm | 6.87 kN | 0.57 s | 1.05 mm |
| SPH_SFDI | 6.95 kN | 0.39 s | 1.24 mm | 6.98 kN | 0.59 s | 1.15 mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Zheng, X.; Ma, Q. Updated Smoothed Particle Hydrodynamics for Simulating Bending and Compression Failure Progress of Ice. Water 2017, 9, 882. https://doi.org/10.3390/w9110882
Zhang N, Zheng X, Ma Q. Updated Smoothed Particle Hydrodynamics for Simulating Bending and Compression Failure Progress of Ice. Water. 2017; 9(11):882. https://doi.org/10.3390/w9110882
Chicago/Turabian StyleZhang, Ningbo, Xing Zheng, and Qingwei Ma. 2017. "Updated Smoothed Particle Hydrodynamics for Simulating Bending and Compression Failure Progress of Ice" Water 9, no. 11: 882. https://doi.org/10.3390/w9110882
APA StyleZhang, N., Zheng, X., & Ma, Q. (2017). Updated Smoothed Particle Hydrodynamics for Simulating Bending and Compression Failure Progress of Ice. Water, 9(11), 882. https://doi.org/10.3390/w9110882






