Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.3. Computational Methodology
2.3.1. FAO-56 Penman–Monteith Equation
2.3.2. Extreme-Learning Machine
2.3.3. Support Vector Regression
2.3.4. Model Development
2.3.5. Model Goodness-of-Fit Criteria
3. Results
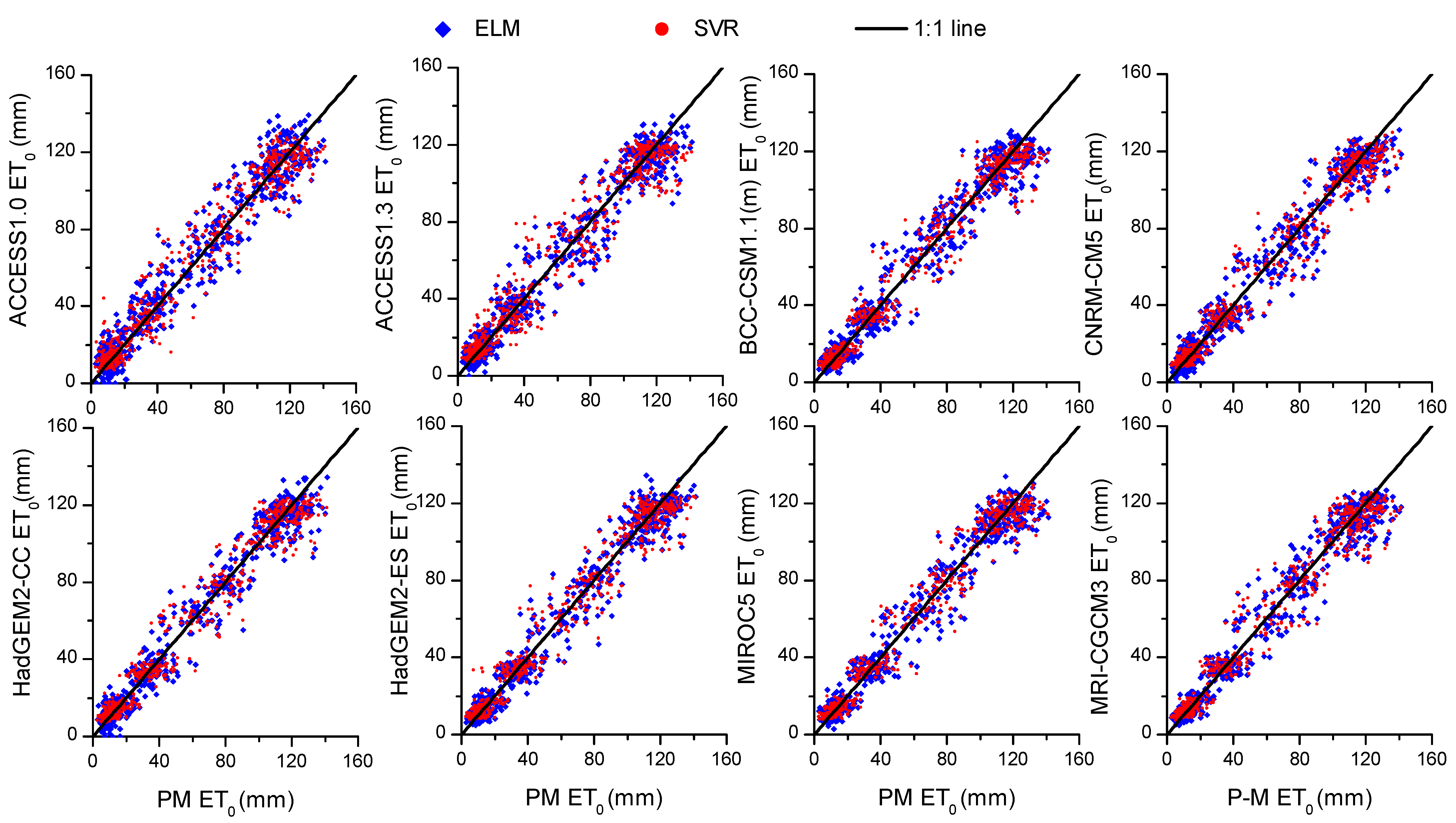
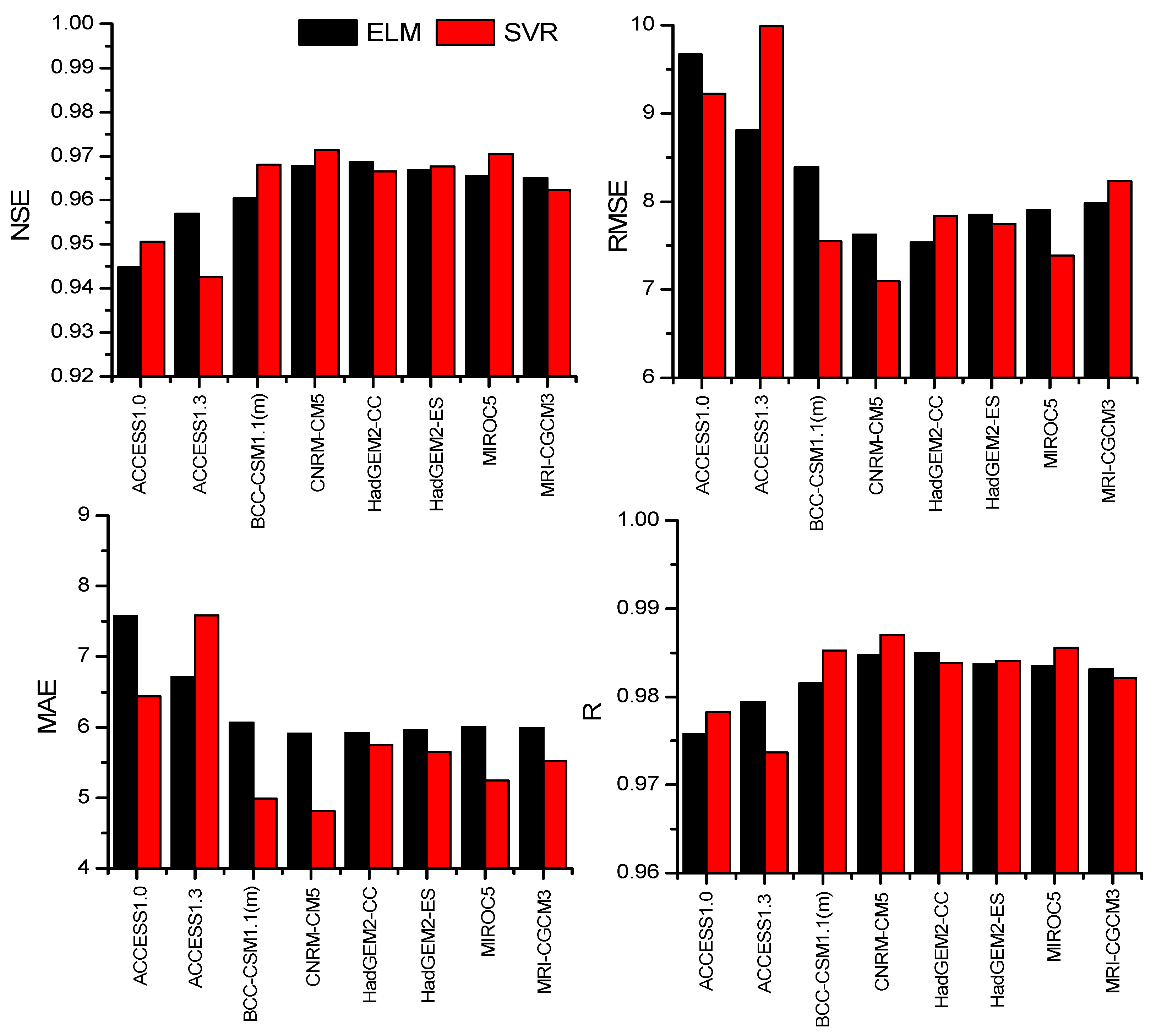
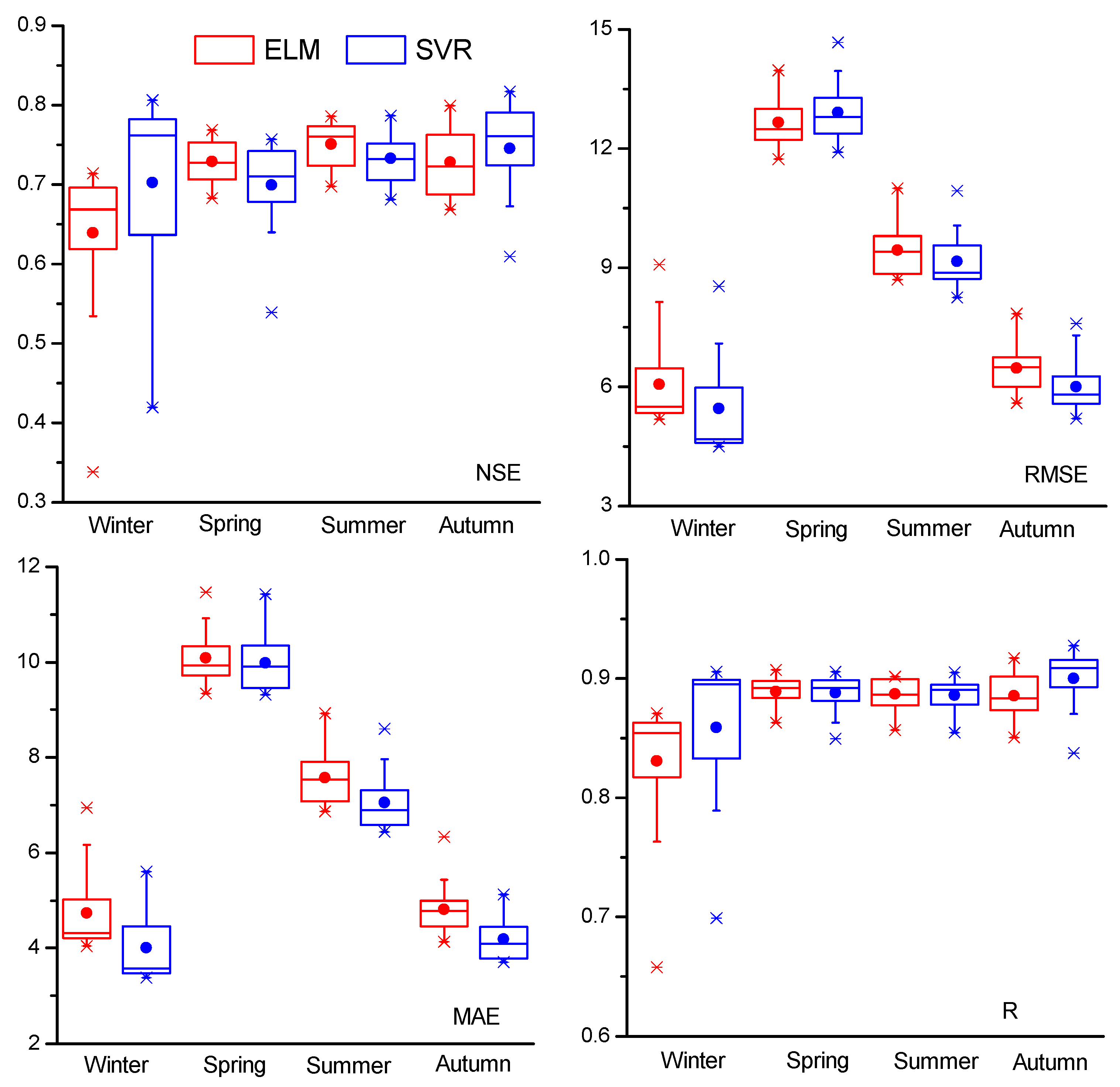
3.1. Model Verification and Comparison
3.2. Evaluation of Future ET0 Projections
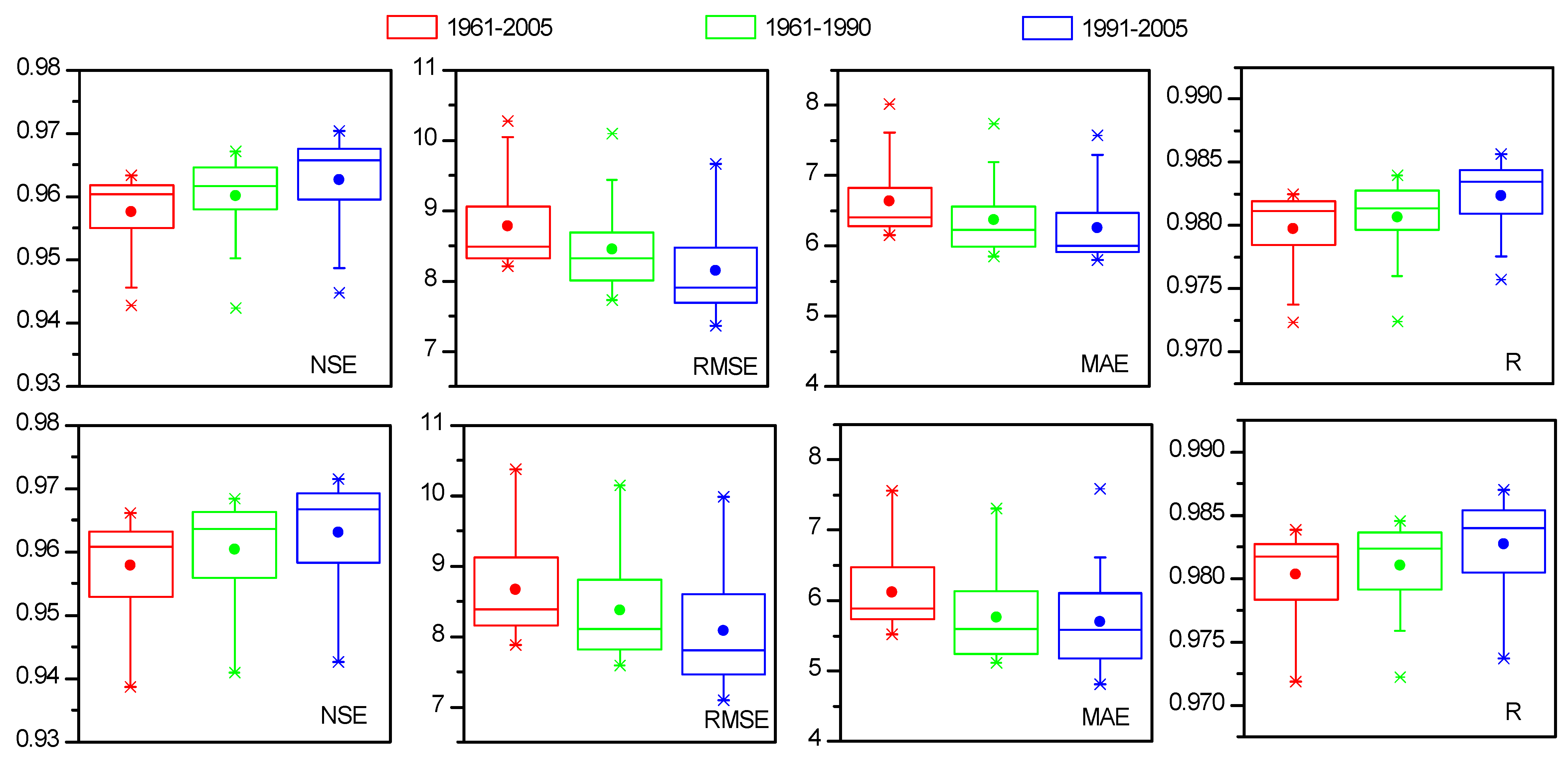
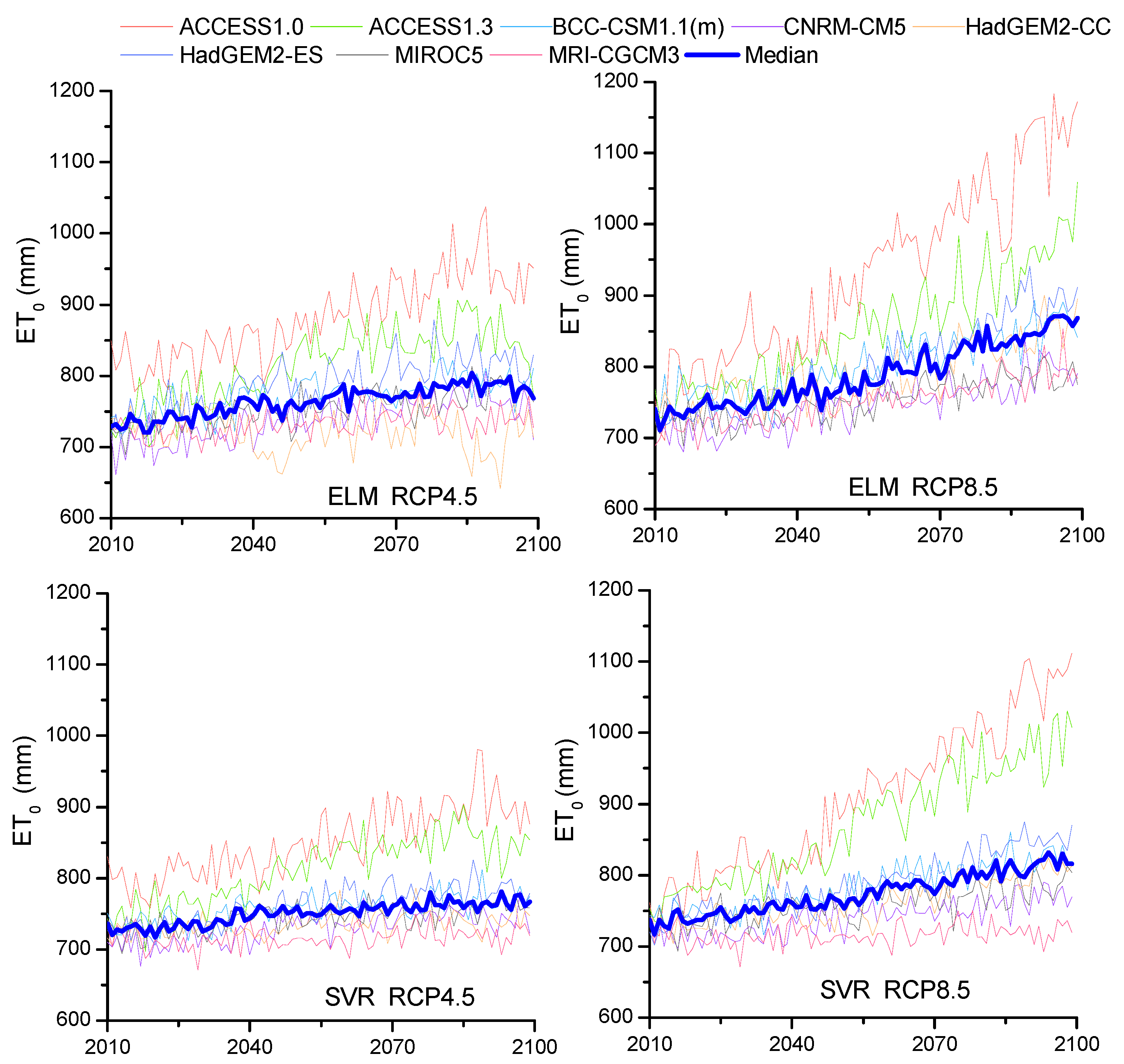
3.2.1. Annual Future ET0
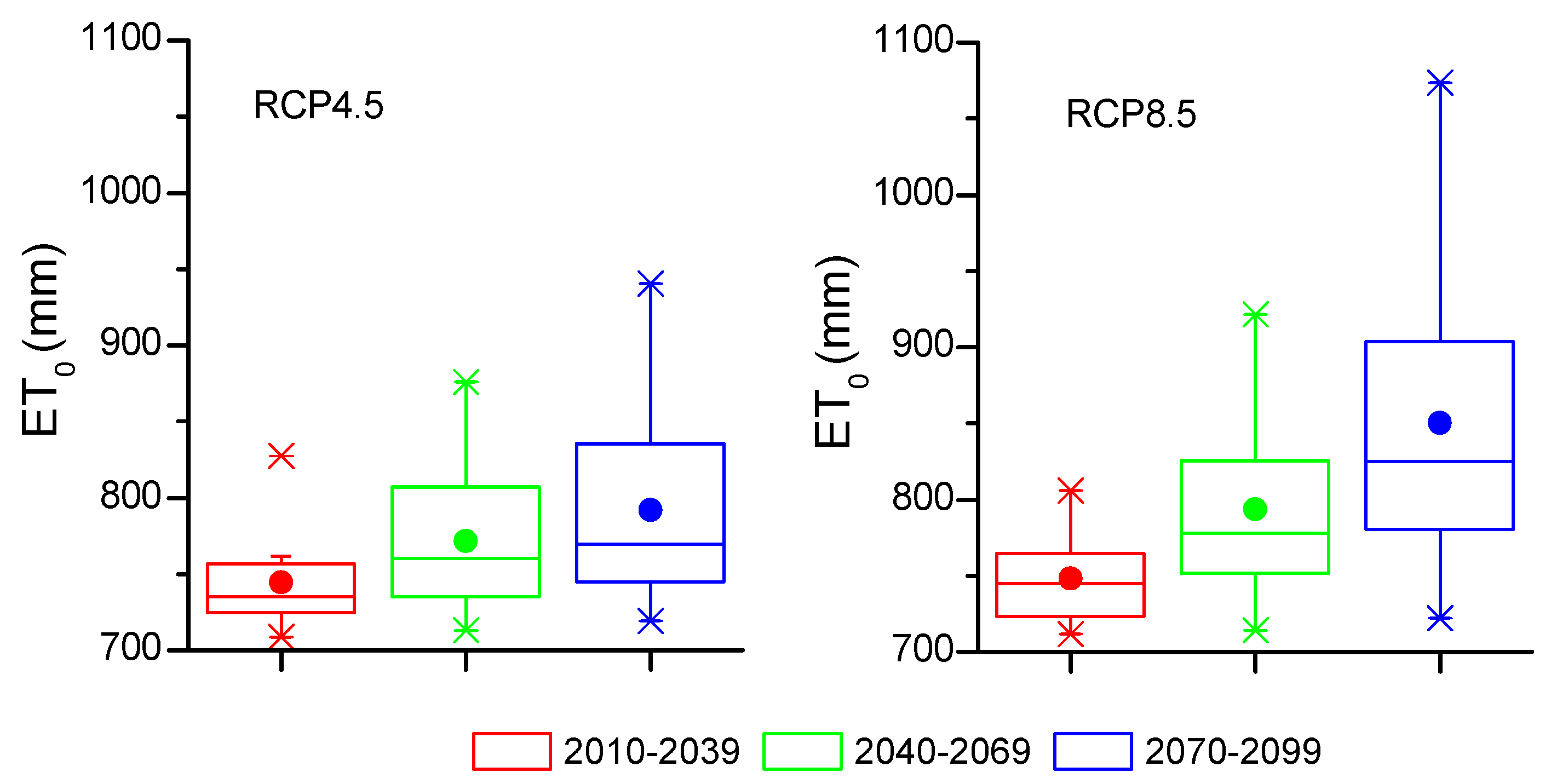
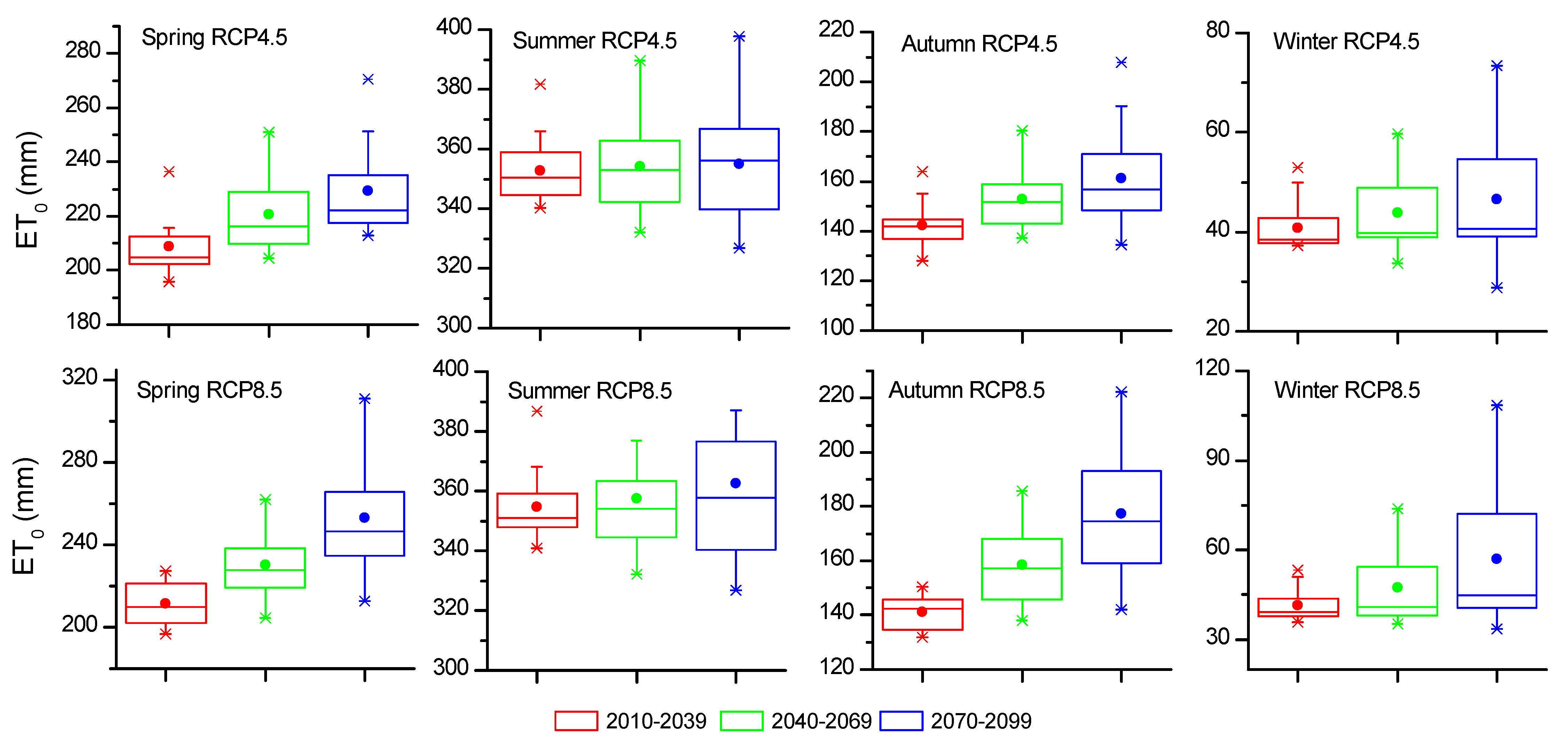
3.2.2. Decadal and Seasonal Future ET0 Projections
3.3. Projection of Future ET0 Variation
4. Discussion and Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Xiang, Y.; Zheng, J. Climate change effects on reference crop evapotranspiration across different climatic zones of china during 1956–2015. J. Hydrol. 2016, 542, 923–937. [Google Scholar] [CrossRef]
- Wang, W.; Xing, W.; Shao, Q. How large are uncertainties in future projection of reference evapotranspiration through different approaches? J. Hydrol. 2015, 524, 696–700. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme learning machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Shiri, J.; Kişi, Ö.; Landeras, G.; López, J.J.; Nazemi, A.H.; Stuyt, L.C.P.M. Daily reference evapotranspiration modeling by using genetic programming approach in the basque country (northern spain). J. Hydrol. 2012, 414–415, 302–316. [Google Scholar] [CrossRef]
- Li, Y.; Yao, N.; Chau, H.W. Influences of removing linear and nonlinear trends from climatic variables on temporal variations of annual reference crop evapotranspiration in xinjiang, china. Sci. Total Environ. 2017, 592, 680–692. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; He, J.; Dong, K.; Li, X. Trends in reference evapotranspiration and their causative factors in the west liao river basin, china. Agric. For. Meteorol. 2017, 232, 106–117. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; Mcnulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the southeastern united states. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Goyal, R.K. Sensitivity of evapotranspiration to global warming: A case study of arid zone of rajasthan (india). Agr. Water Manag. 2004, 69, 1–11. [Google Scholar] [CrossRef]
- Temesgen, B.; Eching, S.; Davidoff, B.; Frame, K. Comparison of some reference evapotranspiration equations for california. J. Irrig. Drain. Eng. 2005, 131, 73–84. [Google Scholar] [CrossRef]
- Liu, X.; Xu, C.; Zhong, X.; Li, Y.; Yuan, X.; Cao, J. Comparison of 16 models for reference crop evapotranspiration against weighing lysimeter measurement. Agric. Water Manag. 2017, 184, 145–155. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Peng, S.; Yu, Z.; Yong, B.; Taylor, J. Changes of reference evapotranspiration in the haihe river basin: Present observations and future projection from climatic variables through multi-model ensemble. Glob. Planet. Chang. 2014, 115, 1–15. [Google Scholar] [CrossRef]
- Kisi, O.; Sanikhani, H.; Zounemat-Kermani, M.; Niazi, F. Long-term monthly evapotranspiration modeling by several data-driven methods without climatic data. Comput. Electron. Agric. 2015, 115, 66–77. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in china during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Chau, K.W.; Wu, C.L. A hybrid model coupled with singular spectrum analysis for daily rainfall prediction. J. Hydroinf. 2010, 12, 458. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Fan, C. Prediction of rainfall time series using modular artificial neural networks coupled with data-preprocessing techniques. J. Hydrol. 2010, 389, 146–167. [Google Scholar] [CrossRef]
- Chen, X.Y.; Chau, K.W.; Busari, A.O. A comparative study of population-based optimization algorithms for downstream river flow forecasting by a hybrid neural network model. Eng. Appl. Artif. Intell. 2015, 46, 258–268. [Google Scholar] [CrossRef]
- Gholami, V.; Chau, K.W.; Fadaee, F.; Torkaman, J.; Ghaffari, A. Modeling of groundwater level fluctuations using dendrochronology in alluvial aquifers. J. Hydrol. 2015, 529, 1060–1069. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W. Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and extreme learning machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Wang, W.-c.; Chau, K.-w.; Xu, D.-m.; Chen, X.-Y. Improving forecasting accuracy of annual runoff time series using arima based on eemd decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R.; Wallender, W.W.; Pruitt, W.O. Estimating evapotranspiration using artificial neural network. J. Irrig. Drain. Eng. 2002, 128, 224–233. [Google Scholar] [CrossRef]
- Kisi, O. The potential of different ann techniques in evapotranspiration modelling. Hydrol. Process. 2008, 22, 2449–2460. [Google Scholar] [CrossRef]
- Kisi, O.; Cengiz, T.M. Fuzzy genetic approach for estimating reference evapotranspiration of turkey: Mediterranean region. Water Resour. Manag. 2013, 27, 3541–3553. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.S. Neural networks and genetic algorithm approach for nonlinear evaporation and evapotranspiration modeling. J. Hydrol. 2008, 351, 299–317. [Google Scholar] [CrossRef]
- Shiri, J.; Dierickx, W.; Pour-Ali Baba, A.; Neamati, S.; Ghorbani, M.A. Estimating daily pan evaporation from climatic data of the state of illinois, USA using adaptive neuro-fuzzy inference system (anfis) and artificial neural network (ann). Hydrol. Res. 2011, 42, 491. [Google Scholar] [CrossRef]
- Shiri, J.; Nazemi, A.H.; Sadraddini, A.A.; Landeras, G.; Kisi, O.; Fakheri Fard, A.; Marti, P. Comparison of heuristic and empirical approaches for estimating reference evapotranspiration from limited inputs in iran. Comput. Electron. Agric. 2014, 108, 230–241. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. Evapotranspiration modelling using support vector machines. Hydrol. Sci. J. 2009, 54, 918–928. [Google Scholar] [CrossRef]
- Kisi, O. Modeling reference evapotranspiration using three different heuristic regression approaches. Agric. Water Manag. 2016, 169, 162–172. [Google Scholar] [CrossRef]
- Rahimikhoob, A.; Asadi, M.; Mashal, M. A comparison between conventional and m5 model tree methods for converting pan evaporation to reference evapotranspiration for semi-arid region. Water Resour. Manag. 2013, 27, 4815–4826. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of elm, gann, wnn and empirical models for estimating reference evapotranspiration in humid region of southwest china. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the artificial neural network model for prediction of monthly standardized precipitation and evapotranspiration index using hydrometeorological parameters and climate indices in eastern australia. Atmos. Res. 2015, 161, 65–81. [Google Scholar] [CrossRef]
- Patil, A.P.; Deka, P.C. An extreme learning machine approach for modeling evapotranspiration using extrinsic inputs. Comput. Electron. Agric. 2016, 121, 385–392. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H. Support-vector-machine-based models for modeling daily reference evapotranspiration with limited climatic data in extreme arid regions. Water Resour. Manag. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Hosseinzadeh Talaee, P. Svm, anfis, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444–445, 78–89. [Google Scholar] [CrossRef]
- Yin, Z.; Wen, X.; Feng, Q.; He, Z.; Zou, S.; Yang, L. Integrating genetic algorithm and support vector machine for modeling daily reference evapotranspiration in a semi-arid mountain area. Hydrol. Res. 2017, 48, 1177–1191. [Google Scholar] [CrossRef]
- Kisi, O. Least squares support vector machine for modeling daily reference evapotranspiration. Irrig. Sci. 2013, 31, 611–619. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004. [Google Scholar]
- Wang, X.; Han, M. Online sequential extreme learning machine with kernels for nonstationary time series prediction. Neurocomputing 2014, 145, 90–97. [Google Scholar] [CrossRef]
- Cambria, E.; Huang, G.B.; Kasun, L.L.C.; Zhou, H.; Vong, C.M.; Lin, J.; Yin, J.; Cai, Z.; Liu, Q.; Li, K.; et al. Extreme learning machines [trends & controversies]. IEEE Intell. Syst. 2013, 28, 30–59. [Google Scholar]
- Deo, R.C.; Downs, N.; Parisi, A.; Adamowski, J.; Quilty, J. Very short-term reactive forecasting of the solar ultraviolet index using an extreme learning machine integrated with the solar zenith angle. Environ. Res. 2017, 155, 141–166. [Google Scholar] [CrossRef] [PubMed]
- Deo, R.C.; Şahin, M. Application of the extreme learning machine algorithm for the prediction of monthly effective drought index in eastern australia. Atmos. Res. 2015, 153, 512–525. [Google Scholar] [CrossRef]
- Deo, R.C.; Sahin, M. An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern queensland. Environ. Monit. Assess. 2016, 188, 90. [Google Scholar] [CrossRef] [PubMed]
- Deo, R.C.; Samui, P.; Kim, D. Estimation of monthly evaporative loss using relevance vector machine, extreme learning machine and multivariate adaptive regression spline models. Stoch. Environ. Res. Risk Assess. 2015, 1–16. [Google Scholar] [CrossRef]
- Deo, R.C.; Syktus, J.; McAlpine, C.; Lawrence, P.; McGowan, H.; Phinn, S.R. Impact of historical land cover change on daily indices of climate extremes including droughts in eastern australia. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Deo, R.C.; Tiwari, M.K.; Adamowski, J.F.; Quilty, M.J. Forecasting effective drought index using a wavelet extreme learning machine (w-elm) model. Stoch. Environ. Res. Risk Assess. 2016, 1–30. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in iraq. J. Hydrol. 2016. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Gocic, M.; Petković, D.; Shamshirband, S.; Kamsin, A. Comparative analysis of reference evapotranspiration equations modelling by extreme learning machine. Comput. Electron. Agric. 2016, 127, 56–63. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Chruch, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in china. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Irmak, S.; Kabenge, I.; Skaggs, K.E.; Mutiibwa, D. Trend and magnitude of changes in climate variables and reference evapotranspiration over 116-yr period in the platte river basin, central nebraska–USA. J. Hydrol. 2012, 420–421, 228–244. [Google Scholar] [CrossRef]
- Tabari, H.; Aghajanloo, M.-B. Temporal pattern of aridity index in iran with considering precipitation and evapotranspiration trends. Int. J. Climatol. 2013, 33, 396–409. [Google Scholar] [CrossRef]
- Palumbo, A.D.; Vitale, D.; Campi, P.; Mastrorilli, M. Time trend in reference evapotranspiration: Analysis of a long series of agrometeorological measurements in southern italy. Irrig. Drain. Syst. 2011, 25, 395–411. [Google Scholar] [CrossRef]
- Piticar, A.; Mihăilă, D.; Lazurca, L.G.; Bistricean, P.-I.; Puţuntică, A.; Briciu, A.-E. Spatiotemporal distribution of reference evapotranspiration in the republic of moldova. Theor. Appl. Climatol. 2016, 124, 1133–1144. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Bhadra, A.; Raghuwanshi, N.S.; Singh, R. Temporal trends in estimates of reference evapotranspiration over india. J. Hydrol. Eng. 2009, 14, 508–515. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.-L.; Liu, W.-Z. Spatiotemporal characteristics of reference evapotranspiration during 1961–2009 and its projected changes during 2011–2099 on the loess plateau of china. Agric. For. Meteorol. 2012, 154–155, 147–155. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, Q.; Zhao, X.; Wu, P.; Pan, W.; Gao, X.; Sun, M. Temporal and spatial evolution of the standardized precipitation evapotranspiration index (spei) in the loess plateau under climate change from 2001 to 2050. Sci. Total Environ. 2017, 595, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the loess plateau of china during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Kundu, S.; Khare, D.; Mondal, A. Future changes in rainfall, temperature and reference evapotranspiration in the central india by least square support vector machine. Geosci. Front. 2017, 8, 583–596. [Google Scholar] [CrossRef]
- Aksornsingchai, P.; Srinilta, C. Statistical downscaling for rainfall and temperature prediction in thailand. In Proceedings of the international multiconference of engineers and computer scientists, Hong Kong, China, 16–18 March 2011. [Google Scholar]
- Tripathi, S.; Srinivas, V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Sachindra, D.; Huang, F.; Barton, A.; Perera, B. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Climatol. 2013, 33, 1087–1106. [Google Scholar] [CrossRef]
- Kharin, V.; Scinocca, J. The impact of model fidelity on seasonal predictive skill. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Zou, S.; Yang, L. Assessing variation in water balance components in mountainous inland river basin experiencing climate change. Water 2016, 8, 472. [Google Scholar] [CrossRef]
- Cheng, G.; Li, X.; Zhao, W.; Xu, Z.; Feng, Q.; Xiao, S.; Xiao, H. Integrated study of the water–ecosystem–economy in the heihe river basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef]
- Marsland, S.; Bi, D.; Uotila, P.; Fiedler, R.; Griffies, S.; Lorbacher, K.; O'Farrell, S.; Sullivan, A.; Uhe, P.; Zhou, X.; et al. Evaluation of access climate model ocean diagnostics in cmip5 simulations. Aust. Meteorol. Oceanogr. J. 2013, 63, 101–119. [Google Scholar] [CrossRef]
- Ren, H.-L.; Wu, J.; Zhao, C.-B.; Cheng, Y.-J.; Liu, X.-W. Mjo ensemble prediction in bcc-csm1.1(m) using different initialization schemes. Atmos. Ocean. Sci. Lett. 2016, 9, 60–65. [Google Scholar] [CrossRef]
- Voldoire, A.; Sanchez-Gomez, E.; Salas y Mélia, D.; Decharme, B.; Cassou, C.; Sénési, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The cnrm-cm5.1 global climate model: Description and basic evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef]
- Martin, G.M.; Bellouin, N.; Collins, W.J.; Culverwell, I.D.; Halloran, P.R.; Hardiman, S.C.; Hinton, T.J.; Jones, C.D.; McDonald, R.E.; McLaren, A.J.; et al. The hadgem2 family of met office unified model climate configurations. Geosci. Model Dev. 2011, 4, 723–757. [Google Scholar]
- Watanabe, M.; Suzuki, T.; O’ishi, R.; Komuro, Y.; Watanabe, S.; Emori, S.; Takemura, T.; Chikira, M.; Ogura, T.; Sekiguchi, M.; et al. Improved climate simulation by miroc5: Mean states, variability, and climate sensitivity. J. Clim. 2010, 23, 6312–6335. [Google Scholar] [CrossRef]
- Yukimoto, S.; Adachi, Y.; Hosaka, M.; Sakami, T.; Yoshimura, H.; Hirabara, M.; Tanaka, T.Y.; Shindo, E.; Tsujino, H.; Deushi, M.; et al. A new global climate model of the meteorological research institute: Mri-cgcm3 —model description and basic performance&mdash. J. Meteorol. Soc. Jpn. Ser. II 2012, 90A, 23–64. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements Fao Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern queensland. Environ. Monit. Assess. 2016. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Tezel, G.; Buyukyildiz, M. Monthly evaporation forecasting using artificial neural networks and support vector machines. Theor. Appl. Climatol. 2016, 124, 69–80. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Li, C.; Si, J.; Wen, X.; Yin, Z. Detecting climate variability impacts on reference and actual evapotranspiration in the taohe river basin, nw china. Hydrol. Res. 2017, 48, 596–612. [Google Scholar] [CrossRef][Green Version]
- Chai, T.; Draxler, R.R. Root mean square error (rmse) or mean absolute error (mae)?–arguments against avoiding rmse in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part i—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Thompson, J.R.; Green, A.J.; Kingston, D.G. Potential evapotranspiration-related uncertainty in climate change impacts on river flow: An assessment for the mekong river basin. J. Hydrol. 2014, 510, 259–279. [Google Scholar] [CrossRef]
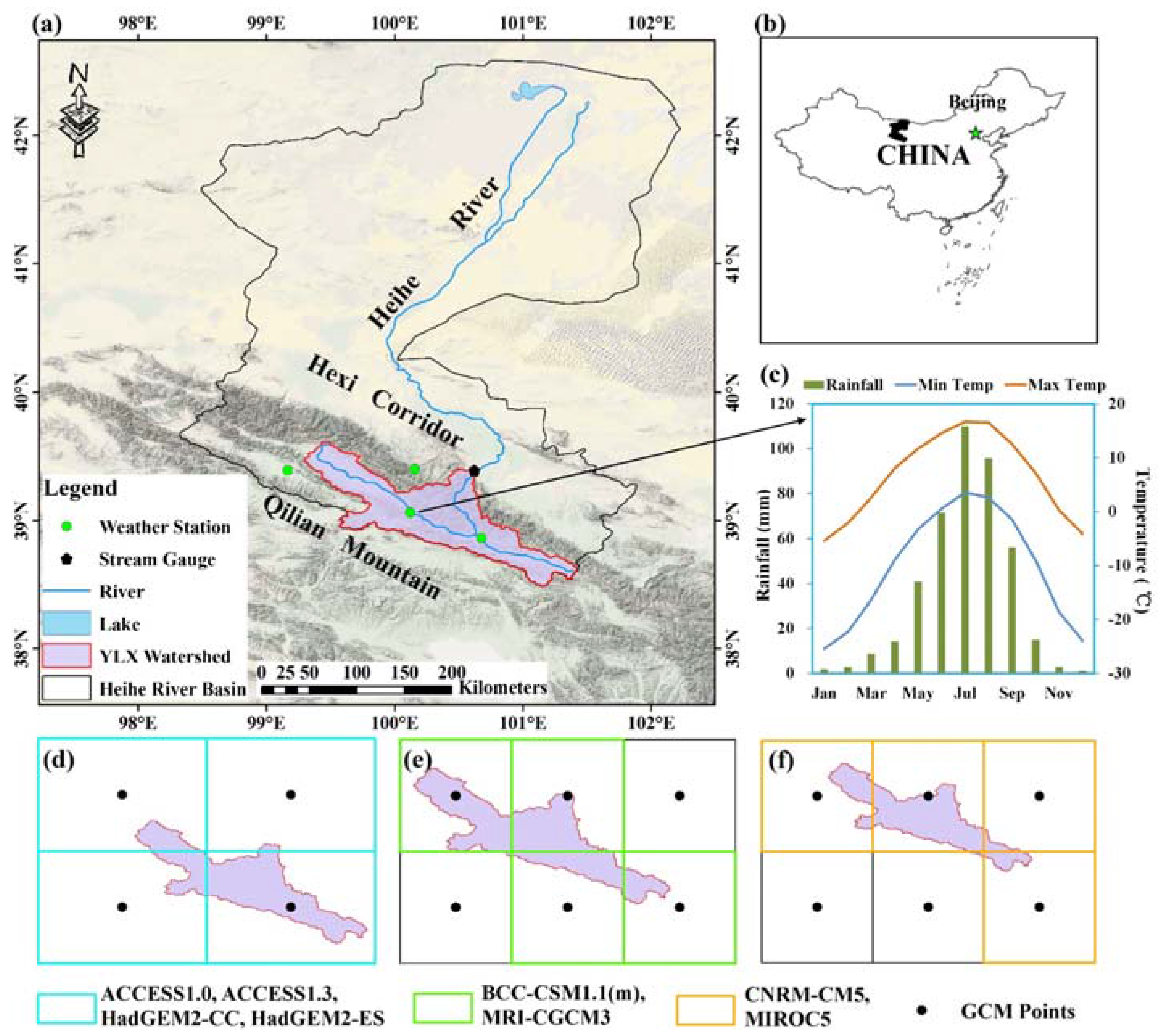

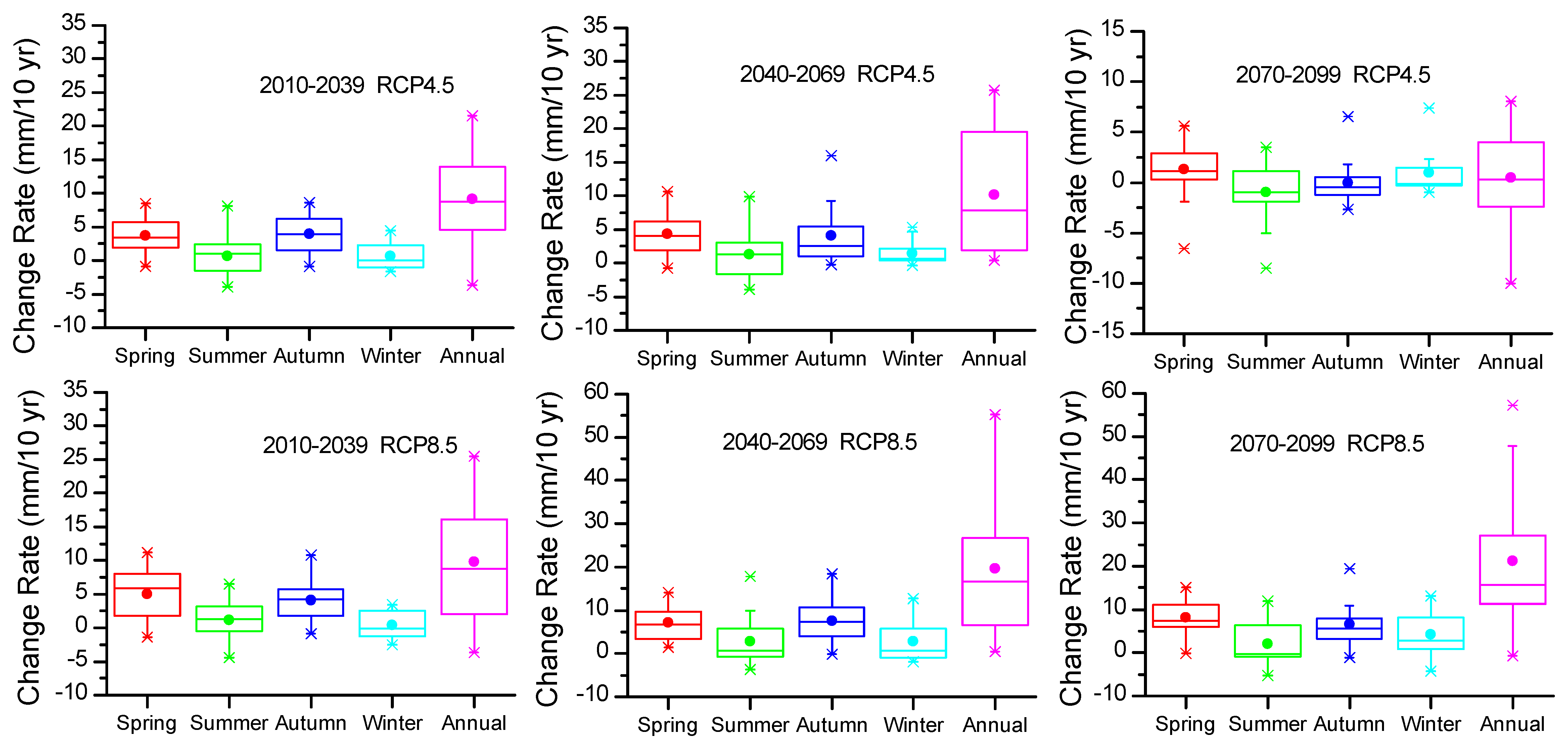
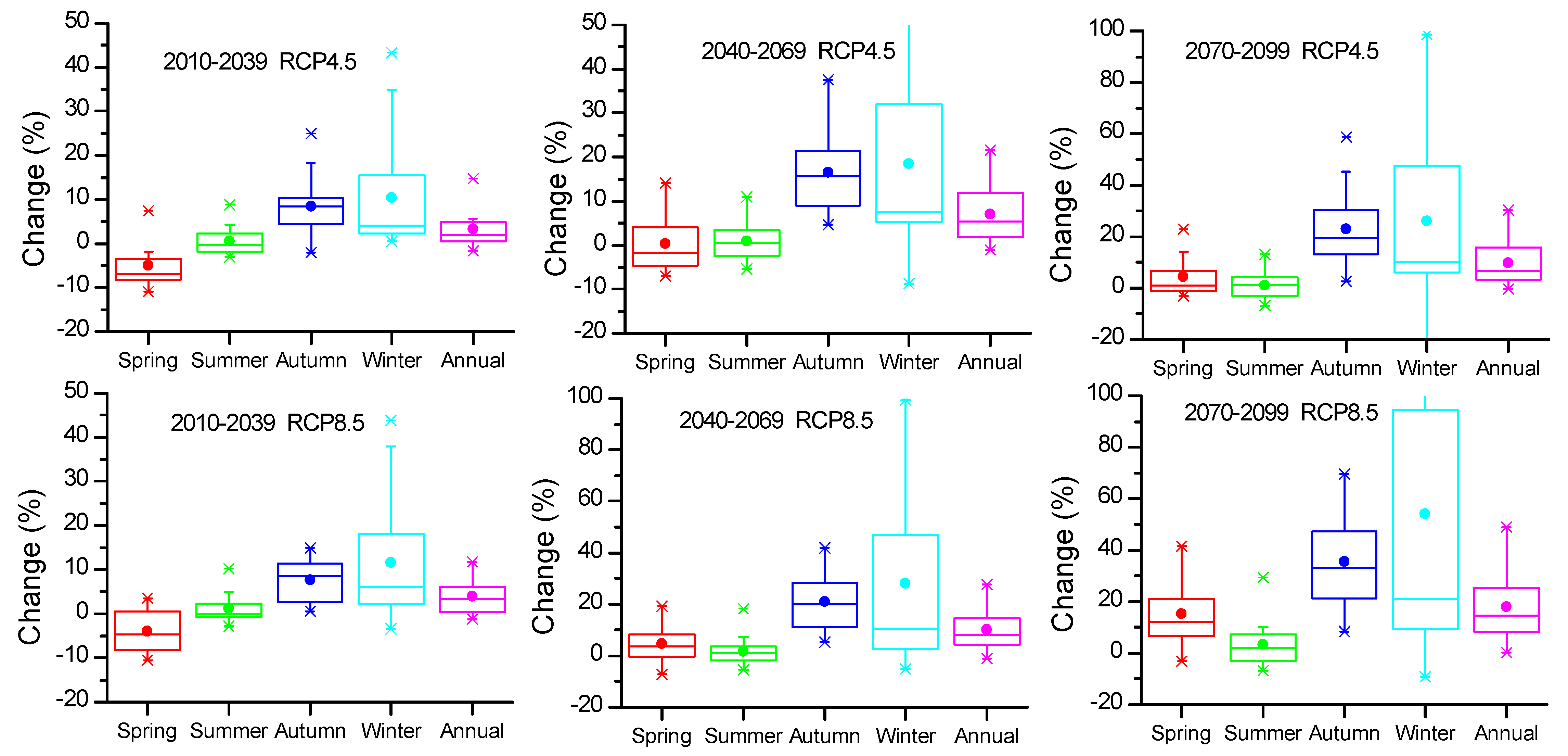
| Id | Model | Centre Acronym(s)/Country | Scenarios | Reference |
|---|---|---|---|---|
| 1 | ACCESS1.0 | CSIRO-BOM/Australia | Historical; RCP4.5; RCP8.5 | [67] |
| 2 | ACCESS1.3 | CSIRO-BOM/Australia | Historical; RCP4.5; RCP8.5 | [67] |
| 3 | BCC-CSM1.1(m) | BCC/China | Historical; RCP4.5; RCP8.5 | [68] |
| 4 | CNRM-CM5 | CNRM-CERFACS/France | Historical; RCP4.5; RCP8.5 | [69] |
| 5 | HadGEM2-CC | MOHC/UK | Historical; RCP4.5; RCP8.5 | [70] |
| 6 | HadGEM2-ES | MOHC/UK | Historical; RCP4.5; RCP8.5 | [70] |
| 7 | MIROC5 | MIROC/Japan | Historical; RCP4.5; RCP8.5 | [71] |
| 8 | MRI-CGCM3 | MRI/Japan | Historical; RCP4.5; RCP8.5 | [72] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Feng, Q.; Yang, L.; Deo, R.C.; Wen, X.; Si, J.; Xiao, S. Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China. Water 2017, 9, 880. https://doi.org/10.3390/w9110880
Yin Z, Feng Q, Yang L, Deo RC, Wen X, Si J, Xiao S. Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China. Water. 2017; 9(11):880. https://doi.org/10.3390/w9110880
Chicago/Turabian StyleYin, Zhenliang, Qi Feng, Linshan Yang, Ravinesh C. Deo, Xiaohu Wen, Jianhua Si, and Shengchun Xiao. 2017. "Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China" Water 9, no. 11: 880. https://doi.org/10.3390/w9110880
APA StyleYin, Z., Feng, Q., Yang, L., Deo, R. C., Wen, X., Si, J., & Xiao, S. (2017). Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China. Water, 9(11), 880. https://doi.org/10.3390/w9110880











