Evaluation of Sustainable Use of Water Resources in Beijing Based on Rough Set and Fuzzy Theory
Abstract
:1. Introduction
2. Methods
2.1. RSWRS System
2.1.1. Index Determination
2.1.2. Index Ideal Set Partition
2.2. Rough Set
2.2.1. Method Introduction
2.2.2. Calculation Procedure
- (1)
- Calculate the division of the conditional attribute set C on the domain U, that is .
- (2)
- Calculate , among which represents the cardinality of a knowledge particle, that is, the number of elements contained in a collection.
- (3)
- Calculate the division of the single attribute x on the domain U, that is , thus calculate .
- (4)
- In turn, after each condition attribute x is removed, require the classification of attribute set X on the domain U, and calculate .
- (5)
- Calculate the importance of attribute c, that is .
- (6)
- Calculate the weights .
2.3. Fuzzy Theory
- (1)
- Set an index in the system as , and compare the elements and of the index set. If is more important than , then . If is as important as , then . If is more important than , then . The binary comparison matrix E is finally obtained, and specific conversion relationships are shown in Table 4.
- (2)
- Add all rows of the comparison matrix E and arrange the results in descending order to obtain the order of importance of each index.
- (3)
- According to the importance of sorting, combining with relevant empirical knowledge, build the binary comparison judgment matrix .
- (4)
- Sum each row of the matrix (without the fuzzy scale value of self-comparison which is 0.5), the result vector is the relative importance of target set P to quantify the feature vector:
- (5)
- Normalize the vector to get the weight of the index set.
2.4. Other Methods
3. Analysis and Evaluation of Sustainable Use of Water Resources in Beijing
3.1. Data
3.2. Determination of the Index Weight
3.3. Determination of the Rule Layer Weight
3.4. Evaluation Results and Analysis
3.4.1. Evaluation Results
3.4.2. Interpretation of Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Step | Formula |
|---|---|
| |
| |
| |
| |
| |
| Step | Formula |
|---|---|
| Benefit index: Cost index: |
| In the formula: |
|
| Step | Formula |
|---|---|
| |
| |
| |
| |
| |
| |
|
| Step | Formula |
|---|---|
| In the formula: |
| |
|
| Step | Formula |
|---|---|
| Benefit index: Cost index: |
| Benefit index: Cost index: |
| |
| |
| |
| |
| |
|
| Step | Formula |
|---|---|
| Calculate the correlation coefficient. |
References
- Hoekstra, A.Y.; Chapagain, A.K.; Oel, P.R.V. Advancing water footprint assessment research: Challenges in monitoring progress towards sustainable development goal 6. Water 2017, 9. [Google Scholar] [CrossRef]
- Deng, L.; Chen, S.; Karney, B. Comprehensive evaluation method of urban water resources utilization based on dynamic reduct. Water Resour. Manag. 2012, 26, 2733–2745. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Weighted minimum and maximum operations in fuzzy set theory. Inform. Sci. 1986, 39, 205–210. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets and intelligent data analysis. Inform. Sci. 2002, 147. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron, A. Rough sets: Some extensions. Inform. Sci. 2007, 177, 28–40. [Google Scholar] [CrossRef]
- Yao, Y. The two sides of the theory of rough sets. Knowl. Based. Syst. 2015, 80, 67–77. [Google Scholar] [CrossRef]
- D’Eer, L.; Restrepo, M.; Cornelis, C.; Gómez, J. Neighborhood operators for covering-based rough sets. Inform. Sci. 2016, 336, 21–44. [Google Scholar] [CrossRef]
- An, A.; Shan, N.; Chan, C.; Cercone, N.; Ziarko, W. Discovering rules for water demand prediction: An enhanced rough-set approach. Eng. Appl. Artif. Intell. 1996, 9, 645–653. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst. 2003, 133, 227–235. [Google Scholar] [CrossRef]
- Zhao, J.; Li, M.; Guo, P.; Zhang, C.; Tan, Q. Agricultural water productivity oriented water resources allocation based on the coordination of multiple factors. Water 2017, 9. [Google Scholar] [CrossRef]
- Esogbue, A.O.; Theologidu, M.; Guo, K. On the application of fuzzy sets theory to the optimal flood control problem arising in water resources systems. Fuzzy Sets Syst. 1992, 48, 155–172. [Google Scholar] [CrossRef]
- Guan, J.; Aral, M.M. Optimal design of groundwater remediation systems using fuzzy set theory. Water Resour. Res. 2004, 40, 62–74. [Google Scholar] [CrossRef]
- Song, S.B.; Cai, H.J. Comprehensive assessment method for region sustainable water resources. Adv. Water Sci. 2005, 16, 244–249. (In Chinese) [Google Scholar]
- Beynon, M. Reducts within the variable precision rough sets model: A further investigation. Eur. J. Oper. Res. 2001, 134, 592–605. [Google Scholar] [CrossRef]
- Zou, Q.; Zhou, J.; Zhou, C.; Song, L.; Guo, J. Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP. Stoch. Environ. Res. Risk Assess. 2013, 27, 525–546. [Google Scholar] [CrossRef]
- Peng, S.H.; Tang, C. Blending the analytic hierarchy process and fuzzy logical systems in Scenic beauty assessment of check dams in streams. Water 2015, 7, 6983–6998. [Google Scholar] [CrossRef]
- Ding, X.; Chong, X.; Bao, Z.; Zhang, S. Fuzzy comprehensive assessment method based on the entropy weight method and its application in the water environmental safety evaluation of the Heshangshan drinking water source area, Three Gorges Reservoir area, China. Water 2017, 9. [Google Scholar] [CrossRef]
- Wu, Y.N.; Yang, Y.S.; Feng, T.T.; Kong, L.N.; Liu, W.; Fu, L.J. Macro-site selection of wind/solar hybrid power station based on Ideal Matter-Element Model. Int. J. Electr. Power Energy Syst. 2013, 50, 76–84. [Google Scholar]
- Zar, J.H. Significance testing of the spearman rank correlation coefficient. J. Am. Stat. Assoc. 1972, 67, 578–580. [Google Scholar] [CrossRef]
- Yang, G.; He, X.L.; Li, J.F.; Jia, X.J. The research of water resource sustainable utilization in Manas River. Acta Ecol. Sin. 2011, 9, 2407–2413. (In Chinese) [Google Scholar]
- Condon, A.G.; Richards, R.A.; Rebetzke, G.J.; Farquhar, G.D. Breeding for high water-use efficiency. J. Exp. Bot. 2004, 55, 2447–2460. [Google Scholar] [CrossRef] [PubMed]
- Gendron, C. Beyond environmental and ecological economics: Proposal for an economic sociology of the environment. Ecol. Econ. 2014, 105, 240–253. [Google Scholar] [CrossRef]
- Liu, Z.J.; Zhang, M.; Wang, Z.Y.; Li, X.Y. A comprehensive assessment of the sustainable utilization of water resources in Zhengzhou city based on the ANN evaluation method. China Rural Water Hydropower 2008, 12, 55–58, 62. (In Chinese) [Google Scholar]
- Zhou, N.Q.; Zhao, L.; Shen, X.P.; Li, Z.Z. A DPS1R model for vulnerability assessment of water resources system in ChangZhuTan area. J. Tongji Univ. Nat. Sci. 2013, 7, 1061–1066. (In Chinese) [Google Scholar]
- Cherp, A.; Jewell, J.; Vinichenko, V.; Bauer, N.; Cian, E. Global energy security under different climate policies, GDP growth rates and fossil resource availabilities. Clim. Chang. 2016, 136, 83–94. [Google Scholar] [CrossRef]
- Wang, H.S.; Yue, B.; Wang, J.; Lei, K.; Zong, Y.Y.; Wang, Y.W.; Hou, Y.N.; Tong, M.H. The study of the evaluation of water resources sustainable utilization in Beijing. Environ. Sustain. Dev. 2011, 36, 69–73. (In Chinese) [Google Scholar]
- Halkijevic, I.; Vukovic, Z.; Vouk, D. Indicators and a Neuro-Fuzzy based model for the evaluation of water supply sustainability. Water Res. Manag. 2017, 31, 3683–3693. [Google Scholar] [CrossRef]
- Eggers, S.; Griesser, M.; Ekman, J. Predator-induced reductions in nest visitation rates are modified by forest cover and food availability. Behav. Ecol. 2008, 19, 1056–1062. [Google Scholar] [CrossRef]
- Sellaro, R.; Crepy, M.; Trupkin, S.A.; Karayekov, E.; Buchovsky, A.S.; Rossi, C.; Casal, J.J. Cryptochrome as a sensor of the blue/green ratio of natural radiation in Arabidopsis. Plant Physiol. 2010, 154, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Xu, X.Y.; Wang, H.R.; Wang, W. The evaluation of water resources sustainable utilization in Beijing based on improved bank correlation analysis. J. Nat. Res. 2015, 30, 164–176. (In Chinese) [Google Scholar]
- Gallardo, B.; Gascón, S.; Quintana, X.; Comín, F.A. How to choose a biodiversity indicator—Redundancy and complementarity of biodiversity metrics in a freshwater ecosystem. Ecol. Indic. 2011, 11, 1177–1184. [Google Scholar] [CrossRef]
- Hu, T.; Lv, B.C.; Chen, G. Uncertainty knowledge representation method based on rough sets. Comput. Sci. 2000, 27, 90–92, 98. (In Chinese) [Google Scholar]
- Liu, S.Z. The Research on Attribute Weight Based on Rough Set in the Forest Ecosystem Health Evaluation. Master’s Thesis, CSUFT, Changsha, China, 2014. (In Chinese). [Google Scholar]
- Ke, L.N.; Wang, Q.M.; Geng, Y.D.; Zhang, L. The island sustainable development evaluation model and its application in Changhai County based on the non-structural decision fuzzy set theory. Trans. Oceanol. Limnol. 2013, 1, 159–166. (In Chinese) [Google Scholar]
- Yu, F.M.; Du, Z.C. Dynamic Analysis of Coupling Relationship between Economic Development and Ecological Environment Based on Entropy Method—A Case Study of Xi an City. Meteorol. Environ. Res. 2011, 9, 62–66. [Google Scholar]
- Chong, T.; Yi, S.; Che, H. Application of set pair analysis method on occupational hazard of coal mining. Saf. Sci. 2017, 92, 10–16. [Google Scholar] [CrossRef]
- Pan, G.; Xu, Y.; Yu, Z.; Song, S.; Zhang, Y. Analysis of river health variation under the background of urbanization based on entropy weight and matter-element model: A case study in Huzhou City in the Yangtze River Delta, China. Environ. Res. 2015, 139, 31–35. [Google Scholar] [CrossRef] [PubMed]
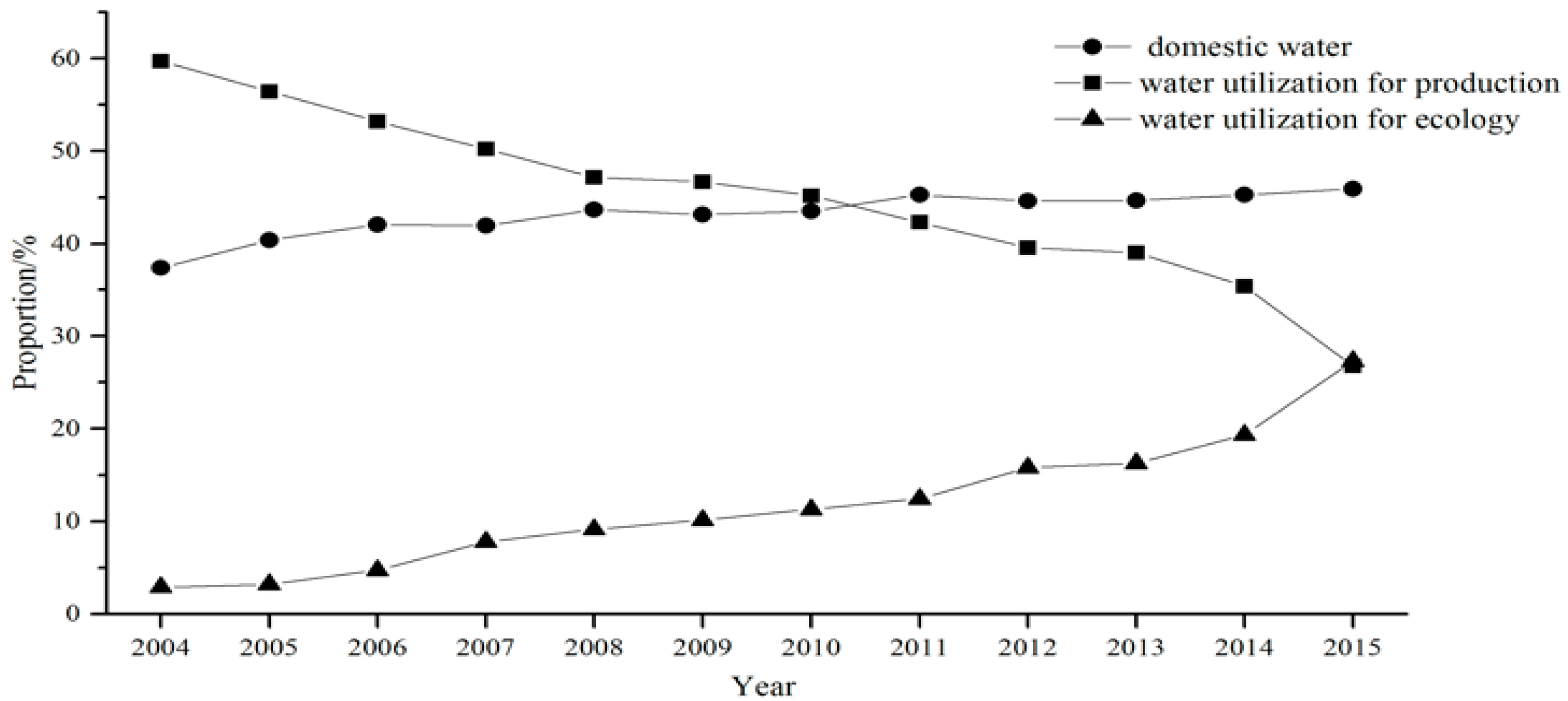
| Rule Layer | Criteria | Index |
|---|---|---|
| Economic subsystem | Agriculture | The grain yield per unit water [24] |
| Water efficiency of irrigation [25] | ||
| Industry | The value of industrial output per unit water [24] | |
| Repeated use rate of industrial water [25] | ||
| Industrial water quota [25] | ||
| Tertiary industry | Third industry accounted for the proportion of total GDP [26] | |
| Comprehensive index | Ten thousand Yuan GDP water consumption [24] | |
| GDP growth rate [26] | ||
| Environmental subsystem | Water quality | Water quality compliance rate in water function area [25] |
| Water pollution comprehensive index [24] | ||
| Reuse of water resources | Sewage disposal rate [27] | |
| The use of recycled water [28] | ||
| Plant | Forest cover rate [29] | |
| Green ratio [30] | ||
| The loss of soil and water | Soil erosion modulus of water loss and soil erosion in sloping land [25] | |
| The ratio of water and soil loss control [27] | ||
| Groundwater | Funnel area/whole area [24] | |
| Groundwater level change rate [25] | ||
| Social subsystem | Human | Density of population [27] |
| Natural growth rate of population [27] | ||
| Per capita water resources [27] | ||
| Daily water consumption per capita [25] | ||
| Consciousness of saving water [24] | ||
| City | Urbanization level [31] | |
| The popular rate of tap water [25] |
| Rule Layer | Index | Unit |
|---|---|---|
| Economic subsystem | The grain yield per unit water u11 | kg/m3 |
| The value of industrial output per unit water u12 | Yuan/m3 | |
| Ten thousand Yuan GDP water consumption u13 | m3/104 Yuan | |
| Third industry accounted for the proportion of total GDP u14 | % | |
| Environmental subsystem | Water quality compliance rate in water function area u21 | % |
| Forest cover rate u22 | % | |
| Sewage disposal rate u23 | % | |
| Soil erosion modulus of water loss and soil erosion in sloping land u24 | t/km2 | |
| Funnel area/whole area u25 | % | |
| Social subsystem | Density of population u31 | person/km2 |
| Urbanization level u32 | % | |
| Per capita water resources u33 | m3/(person and year) | |
| Daily water consumption per capita u34 | L/person |
| Index | I | II | III | IV | V |
|---|---|---|---|---|---|
| u11 | >1.8 | 1.5–1.8 | 1.2–1.5 | 0.8–1.2 | <0.8 |
| u12 | >800 | 600–800 | 400–600 | 200–400 | <200 |
| u13 | <50 | 50–150 | 150–250 | 250–350 | >350 |
| u14 | >75 | 75–60 | 60–50 | 50–40 | <40 |
| u21 | >80 | 70–80 | 60–70 | 45–60 | <45 |
| u22 | >60 | 50–60 | 30–50 | 10–30 | <10 |
| u23 | >95 | 85–95 | 75–85 | 65–75 | <65 |
| u24 | <100 | 100–200 | 200–500 | 500–1000 | >1000 |
| u25 | <1 | 1–5 | 5–10 | 10–15 | >15 |
| u31 | <200 | 200–500 | 500–800 | 800–1200 | >1200 |
| u32 | >85 | 75–85 | 65–75 | 55–65 | <55 |
| u33 | >4000 | 3000–4000 | 2000–3000 | 1000–2000 | <1000 |
| u34 | <160 | 160–180 | 180–200 | 200–220 | >220 |
| Fuzzy Mood | Equal | Slightly | Somewhat | Rather | Obvious | Remarkably |
| Fuzzy Scale | 0.5 | 0.55 | 0.6 | 0.65 | 0.7 | 0.75 |
| Fuzzy Mood | Very | Extra | Exceeding | Extreme | Incomparable | |
| Fuzzy Scale | 0.8 | 0.85 | 0.9 | 0.95 | 1 |
| Methods | Introduction |
|---|---|
| EW | The Entropy Weight (EW) method of objective weighting, according to the basic principle of information theory, can be interpreted that information is a measure of degree of order system. Entropy is a measure of the degree of disorder of the system. When the information entropy is very small, the amount of information provided by the index is larger, which plays the greater role in the comprehensive evaluation, and the weight is higher [36]. EW is implemented to determine weights in this study. |
| AHP | Analytic hierarchy process (AHP) is a subjective method that allows the user to visually assess the relative weight of more than one standard or multiple options according to the given standard. Even if the quantitative rating is not available, the decision-makers can still recognize that a standard is more important than another [17]. AHP is used to calculate weights in this study. |
| SPA | The set pair analysis (SPA) method is a set of system theory to deal with the uncertainty of analysis, it is not only a technical means, but also a decision-making system that reflects dialectical thinking. SPA is used widely since it turns the problem of uncertainty into mathematical problems by introducing the concept of the connection degree [37]. The confirmed weights are analyzed with SPA for evaluation in this study. |
| AR | The attribute recognition (AR) method is a qualitative measure of the relationship between the discussion questions and different methods of qualitative description and the relationship between the corresponding measure, which has the advantages of simple calculation and good operation. The results are more reliable. It has been applied quite extensive in the evaluation of soil and water resources and environment in the field of the gas system. The confirmed weights are analyzed with AR for evaluation in this study. |
| MEM | The matter-element model (MEM) is a method of solving the multiple indicators evaluation problem. It can be abstracted as a complex problem visualization model. It indicates the results that may completely reflect the comprehensive quality of things by establishing a quality evaluation model of multiple-index performance parameters and using quantitative results. Additionally, it is easy to use a computer to solve [38]. The confirmed weights are analyzed with MEM for evaluation in this study. |
| SRCC | The Spearman rank correlation coefficient (SRCC) method is used to describe the degree of correlation and direction between the two variables. Original variable distribution is not required in this method, which belongs to the non-parametric statistical method. In this study, this method was used to obtain the close degree of each evaluation results and other results of the evaluation, and the highest correlation coefficient is selected as the final evaluation result [20]. |
| Index | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| u11 | 0.54 | 0.75 | 0.91 | 0.87 | 1.11 | 1.1 | 1.07 | 1.19 | 1.22 | 1.06 | 0.78 | 0.98 |
| u12 | 203.2 | 251.0 | 293.8 | 362.2 | 409.9 | 442.9 | 546.2 | 608.5 | 673.7 | 696.6 | 736.1 | 976.6 |
| u13 | 57.27 | 49.5 | 42.25 | 35.35 | 31.56 | 29.21 | 24.94 | 22.12 | 20.07 | 18.92 | 17.08 | 16.6 |
| u14 | 68 | 70 | 72 | 73 | 75 | 76 | 75 | 76 | 77 | 78 | 76 | 80 |
| u21 | 57.9 | 54 | 58.7 | 49 | 47.5 | 46 | 48 | 51 | 48.5 | 46 | 47 | 53.4 |
| u22 | 35.4 | 35.5 | 35.9 | 36.5 | 36.5 | 36.7 | 37 | 37.6 | 38.6 | 40.1 | 41 | 41.6 |
| u23 | 53.9 | 62.4 | 73.2 | 76.2 | 78.9 | 80.3 | 81 | 82 | 83 | 84.6 | 86.1 | 87.9 |
| u24 | 117.2 | 151.3 | 145.3 | 139.4 | 219.7 | 65.8 | 94.9 | 103.4 | 747.9 | 294.4 | 194.4 | 238.5 |
| u25 | 5.95 | 5.95 | 6.23 | 6.26 | 6.27 | 6.38 | 6.44 | 6.45 | 6.39 | 6.44 | 6.45 | 6.43 |
| u31 | 910 | 937 | 976 | 1021 | 1079 | 1133 | 1196 | 1230 | 1261 | 1289 | 1311 | 1323 |
| u32 | 79 | 83.6 | 84.3 | 84.5 | 84.9 | 85 | 85.9 | 86.2 | 86.2 | 86.3 | 86.3 | 86.5 |
| u33 | 143.0 | 151.2 | 141.5 | 148.2 | 205.5 | 126.6 | 124.2 | 134.7 | 193.2 | 118.6 | 95.2 | 124.0 |
| u34 | 226.8 | 152.9 | 154.7 | 166.8 | 187.2 | 192.1 | 174.9 | 172.6 | 171.8 | 196.9 | 187.5 | 183.8 |
| Rule Layer | Index | Weight | |||
|---|---|---|---|---|---|
| Economic subsystem | u11 | 0.37 | 0.64 | 1.02 | 0.30 |
| u12 | 0.45 | 0.75 | 1.20 | 0.36 | |
| u13 | 0.07 | 0.48 | 0.55 | 0.16 | |
| u14 | 0.00 | 0.62 | 0.62 | 0.18 | |
| Environmental subsystem | u21 | 0.14 | 0.40 | 0.54 | 0.14 |
| u22 | 0.00 | 0.40 | 0.40 | 0.10 | |
| u23 | 0.55 | 0.70 | 1.24 | 0.32 | |
| u24 | 0.60 | 0.73 | 1.33 | 0.34 | |
| u25 | 0.00 | 0.40 | 0.40 | 0.10 | |
| Social subsystem | u31 | 0.27 | 0.64 | 0.91 | 0.27 |
| u32 | 0.13 | 0.64 | 0.77 | 0.23 | |
| u33 | 0.00 | 0.40 | 0.40 | 0.12 | |
| u34 | 0.54 | 0.74 | 1.28 | 0.38 |
| Index | I | II | III | IV | V |
|---|---|---|---|---|---|
| u11 | −1.00 | −1.00 | 0.10 | 1.00 | −0.10 |
| u12 | 1.00 | 0.64 | −1.00 | −1.00 | −1.00 |
| u13 | 1.00 | −0.34 | −1.00 | −1.00 | −1.00 |
| u14 | 1.00 | 0.88 | −1.00 | −1.00 | −1.00 |
| u21 | −1.00 | −1.00 | 0.26 | 1.00 | −0.26 |
| u22 | −1.00 | 0.39 | 1.00 | −0.39 | −1.00 |
| u23 | −0.37 | 1.00 | 0.37 | −1.00 | −1.00 |
| u24 | −1.00 | 0.74 | 1.00 | −0.74 | −1.00 |
| u25 | −1.00 | 0.43 | 1.00 | −0.43 | −1.00 |
| u31 | −1.00 | −1.00 | −1.00 | −0.23 | 1.00 |
| u32 | 1.00 | 0.97 | −1.00 | −1.00 | −1.00 |
| u33 | −1.00 | −1.00 | −1.00 | −0.40 | 1.00 |
| u34 | −1.00 | 0.62 | 1.00 | −0.62 | −1.00 |
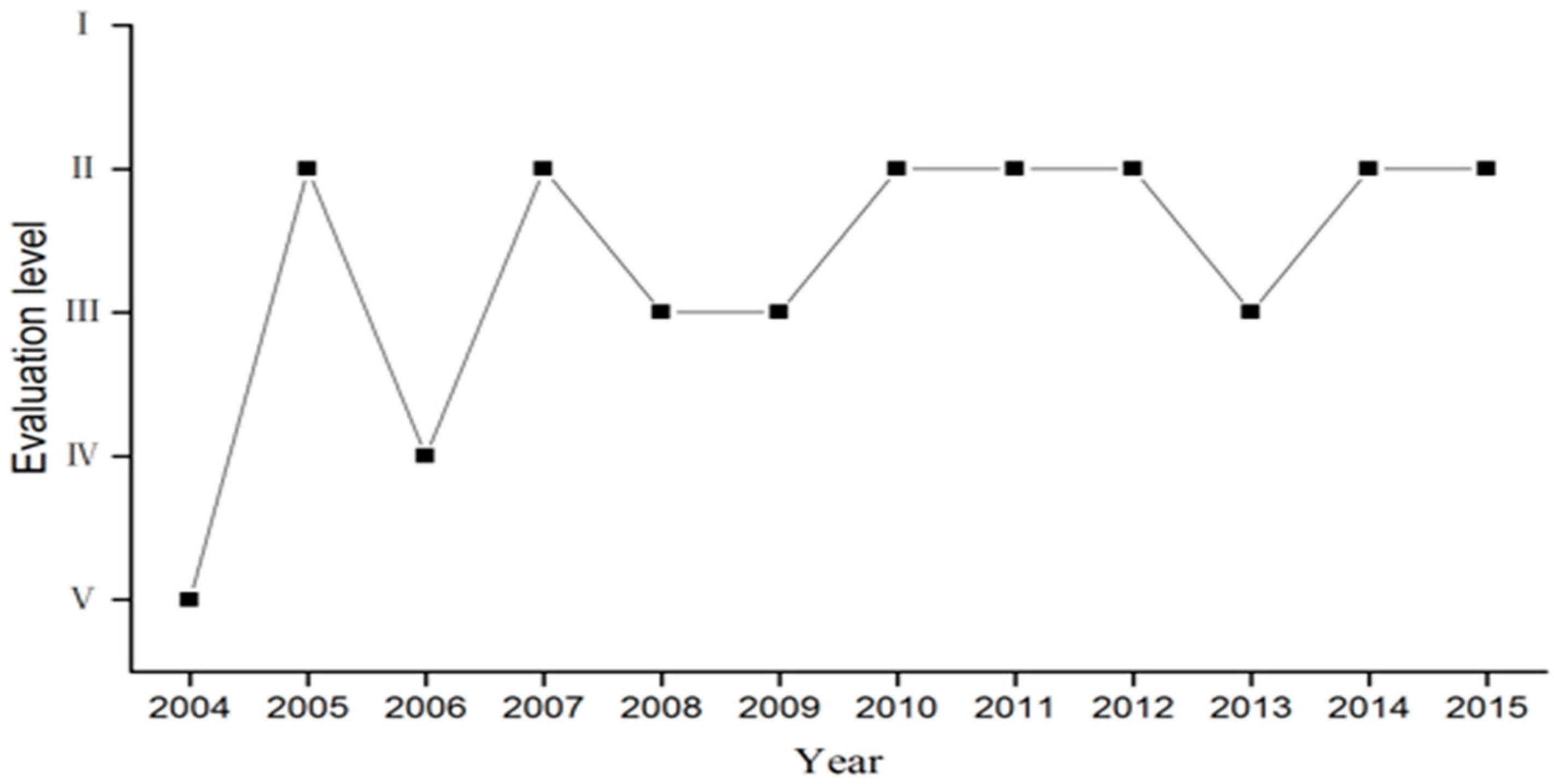
| Year | Weighted Connection Degrees | Evaluation Level | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| 2004 | −0.60 | −0.35 | −0.47 | −0.09 | 0.07 | V |
| 2005 | −0.24 | −0.05 | −0.46 | −0.07 | −0.30 | II |
| 2006 | −0.20 | −0.06 | −0.24 | −0.03 | −0.56 | IV |
| 2007 | −0.29 | −0.04 | −0.16 | −0.05 | −0.56 | II |
| 2008 | −0.58 | −0.11 | 0.24 | 0.03 | −0.66 | III |
| 2009 | −0.41 | −0.17 | 0.02 | 0.00 | −0.62 | III |
| 2010 | −0.33 | 0.20 | −0.09 | −0.33 | −0.58 | II |
| 2011 | −0.29 | 0.26 | −0.08 | −0.42 | −0.64 | II |
| 2012 | −0.35 | 0.12 | −0.11 | −0.29 | −0.54 | II |
| 2013 | −0.45 | −0.03 | 0.01 | −0.22 | −0.56 | III |
| 2014 | −0.38 | 0.18 | −0.20 | −0.48 | −0.42 | II |
| 2015 | −0.29 | 0.17 | −0.14 | −0.50 | −0.56 | II |
| Year | SPAro | ARro | SPAen | ARen | SPAan | ARan | MEM |
|---|---|---|---|---|---|---|---|
| 2004 | V | V | V | V | V | V | V |
| 2005 | II | IV | II | II | II | IV | IV |
| 2006 | IV | IV | IV | IV | II | IV | IV |
| 2007 | II | IV | II | IV | II | II | IV |
| 2008 | III | III | III | III | III | III | III |
| 2009 | III | III | III | III | III | III | III |
| 2010 | II | III | II | III | II | II | III |
| 2011 | II | II | II | III | II | II | II |
| 2012 | II | II | II | III | II | II | II |
| 2013 | III | III | II | III | III | III | III |
| 2014 | II | II | II | II | II | III | III |
| 2015 | II | I | II | I | II | I | I |
| Methods | SPAro | ARro | SPAen | ARen | SPAan | ARan | MEM | Average |
|---|---|---|---|---|---|---|---|---|
| SPAro | 1.000 | 0.965 | 0.965 | 0.972 | 0.986 | 0.979 | 0.962 | 0.976 |
| Arro | 0.965 | 1.000 | 0.930 | 0.979 | 0.951 | 0.979 | 0.997 | 0.972 |
| SPAen | 0.965 | 0.930 | 1.000 | 0.937 | 0.951 | 0.944 | 0.927 | 0.951 |
| Aren | 0.972 | 0.979 | 0.937 | 1.000 | 0.958 | 0.958 | 0.976 | 0.969 |
| SPAan | 0.986 | 0.951 | 0.951 | 0.958 | 1.000 | 0.965 | 0.948 | 0.966 |
| Aran | 0.979 | 0.979 | 0.944 | 0.958 | 0.965 | 1.000 | 0.983 | 0.973 |
| MEM | 0.962 | 0.997 | 0.927 | 0.976 | 0.948 | 0.983 | 1.000 | 0.970 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, B.; Liu, H.; Tian, W.; Liu, H. Evaluation of Sustainable Use of Water Resources in Beijing Based on Rough Set and Fuzzy Theory. Water 2017, 9, 852. https://doi.org/10.3390/w9110852
Men B, Liu H, Tian W, Liu H. Evaluation of Sustainable Use of Water Resources in Beijing Based on Rough Set and Fuzzy Theory. Water. 2017; 9(11):852. https://doi.org/10.3390/w9110852
Chicago/Turabian StyleMen, Baohui, Huanlong Liu, Wei Tian, and Haoyue Liu. 2017. "Evaluation of Sustainable Use of Water Resources in Beijing Based on Rough Set and Fuzzy Theory" Water 9, no. 11: 852. https://doi.org/10.3390/w9110852
APA StyleMen, B., Liu, H., Tian, W., & Liu, H. (2017). Evaluation of Sustainable Use of Water Resources in Beijing Based on Rough Set and Fuzzy Theory. Water, 9(11), 852. https://doi.org/10.3390/w9110852




