On the Direct Calculation of Snow Water Balances Using Snow Cover Information
Abstract
1. Introduction
2. Materials and Methods
2.1. The Degree-Day Method
2.2. Direct Estimation of the DDM Snowmelt Factor
2.3. Testing the Approach at Sites with Accurate Data
2.4. Testing the Approach Using Regional Information
2.4.1. Testing Modelled SWE at Snow Depth Measurement Stations
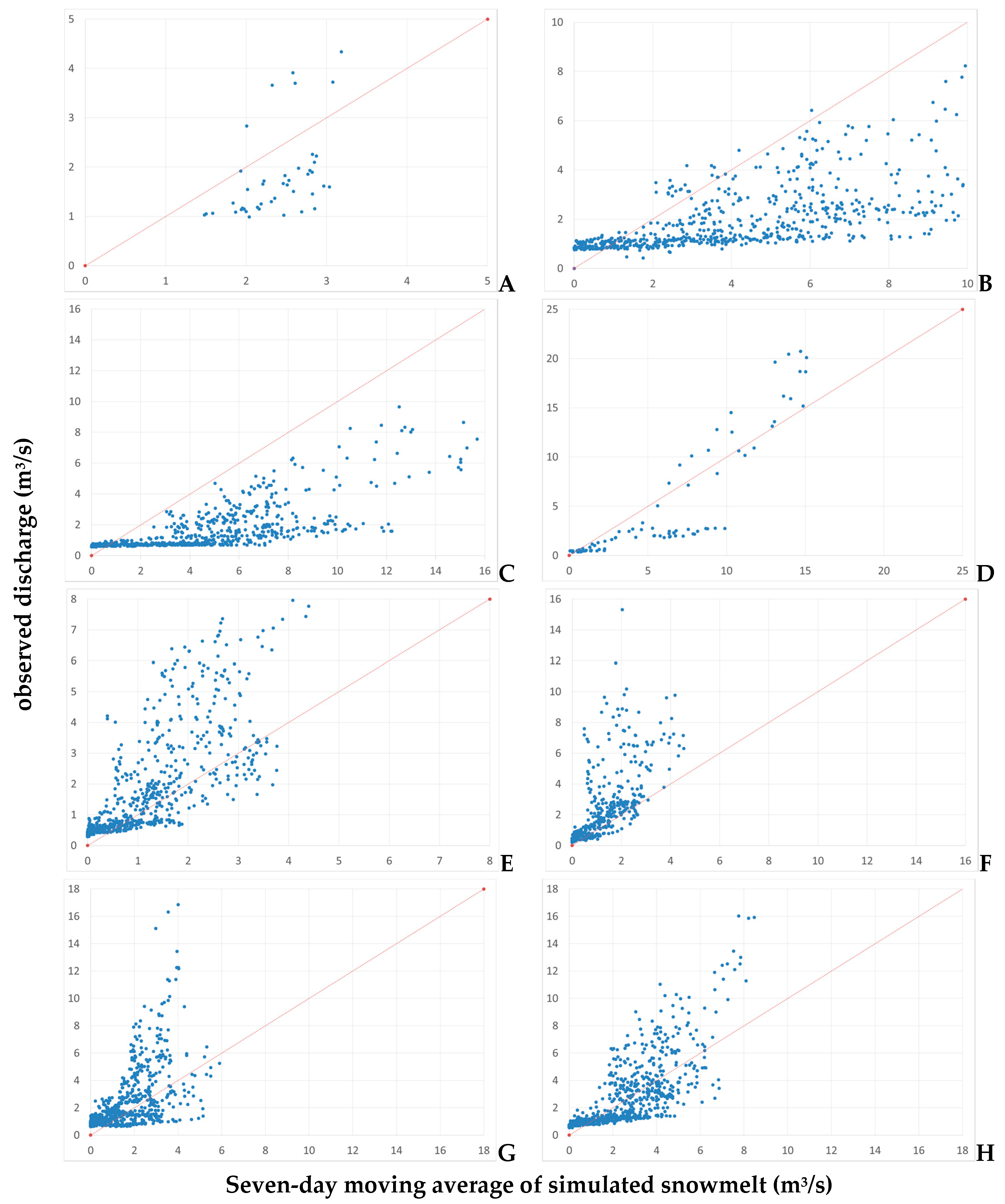
2.4.2. Testing Modelled Melt Flows at Headwater Discharge Measurement Stations
3. Results and Discussion
3.1. Snowmelt Coefficients and Snow Water Equivalents at SNOTEL Sites
3.2. Snowmelt Coefficients and Snow Water Equivalents at Snow Depth Measurement Stations
3.3. Simulated Snowmelt
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Dietz, A.J.; Wohner, C.; Kuenzer, C. European Snow Cover Characteristics between 2000 and 2011 Derived from Improved MODIS Daily Snow Cover Products. Remote Sens. 2012, 4, 2432–2454. [Google Scholar] [CrossRef]
- Pulliainen, J. Retrieval of Regional Snow Water Equivalent from Space-Borne Passive Microwave Observations. Remote Sens. Environ. 2001, 75, 76–85. [Google Scholar] [CrossRef]
- Derksen, C.; Walker, A.; Goodison, B. Evaluation of passive microwave snow water equivalent retrievals across the boreal forest/tundra transition of western Canada. Remote Sens. Environ. 2005, 96, 315–3279. [Google Scholar] [CrossRef]
- Bocchiola, D.; Groppelli, B. Spatial Estimation of snow water equivalent at different dates within the Adamello Park of Italy. Cold Reg. Sci. Technol. 2010, 63, 97–109. [Google Scholar] [CrossRef]
- Bocchiola, D.; Rosso, R. The distribution of daily snow water equivalent in the central Italian Alps. Adv. Water Resour. 2007, 30, 135–147. [Google Scholar] [CrossRef]
- Mizukami, N.; Perica, S.; Hatch, D. Regional Approach for mapping climatological snow water equivalent over the mountainous regions of the western United States. J. Hydrol. 2011, 400, 72–82. [Google Scholar] [CrossRef]
- Timilsena, J.; Piechota, T. Regionalization and reconstruction of snow water equivalent in the upper Colorado River basin. J. Hydrol. 2008, 352, 94–106. [Google Scholar] [CrossRef]
- USACE Snow Hydrology. Summary Report of the Snow Investigations. US Corps of Engineers: Portland, OR, USA, 1956. Available online: https://www.wcc.nrcs.usda.gov/ftpref/wntsc/H&H/snow/SnowHydrologyCOE1956thruCh6.pdf (accessed on 15 September 2017).
- Martinec, J. The degree-day factor for snowmelt-runoff forecasting. In General Assembly of Helsinki. Commission on Surface Areal Value of Degree-Day Factor: Waters; IAHS: Publication No. 51. 1960. Available online: https://iahs.info/uploads/dms/051058.pdf (accessed on 15 September 2017).
- United States Army Corps of Engineers (USACE). Engineering and Design—Runoff from Snowmelt; The Corps: Washington, DC, USA, 1998. [Google Scholar]
- Hock, R. Temperature index melt modeling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Ohara, N.; Kavvas, M.L. Field observations and numerical model experiments for the snowmelt process at a field site. Adv. Water Res. 2006, 29, 194–211. [Google Scholar] [CrossRef]
- Garen, D.C.; Marks, D. Spatially distributed energy balance snowmelt modeling in a mountainous river basin: estimation of meteorological inputs and verification of model results. J. Hydrol. 2005, 315, 126–153. [Google Scholar] [CrossRef]
- Rango, A.; Salmonson, V.V.; Foster, J.L. Seasonal stream flow estimation in the Himalayan region employing meteorological satellite snow cover observations. Water Resour. Res. 1977, 13, 109–112. [Google Scholar] [CrossRef]
- Callegari, M.; Mazzoli, P.; de Gregorio, L.; Notarnicola, C.; Pasolli, L.; Petitta, M.; Pistocchi, A. Seasonal River Discharge Forecasting Using Support Vector Regression: A Case Study in the Italian Alps. Water 2015, 7, 2494–2515. [Google Scholar] [CrossRef]
- Udnaes, H.C.; Engeset, R.V.; Andreassen, L.M. Use of Satellite-derived snow data in a HBV-type model. In Proceedings of the EARSeL-LISSIG Workshop Observing Our Cryosphere from Space, Bern, Switzerland, 11–13 March 2002; pp. 54–64. [Google Scholar]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images—Potential for snow cover mapping. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Duethmann, D.; Peters, J.; Blume, T.; Vorogushyn, S.; Güntner, A. The value of satellite-derived snow cover images for calibrating a hydrological model in snow-dominated catchments in Central Asia. Water Resour. Res. 2014, 50, 2002–2021. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G.; Barrett, A.P.; Hay, L.E.; McCabe, G.J.; Rajagopalan, B.; Leavesley, G.H. Assimilation of snow covered area information into hydrologic and land-surface models. Adv. Water Resour. 2006, 29, 1209–1221. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Turcotte, R. Improvement of springtime streamflow simulations in a boreal environment by incorporating snow-covered area derived from remote sensing data. J. Hydrol. 2010, 390, 35–44. [Google Scholar] [CrossRef]
- Yatheendradas, S.; Lidard, C.D.; Koren, V.; Cosgrove, B.A.; De Goncalves, L.G.G.; Smith, M.; Geiger, J.; Cui, Z.; Borak, J.; Kumar, S.V.; et al. Distributed assimilation of satellite-based snow extent for improving simulated streamflow in mountainous, dense forests: An example over the DMIP2 western basins. Water Resour. Res. 2012, 48, w09557. [Google Scholar] [CrossRef]
- Thirel, G.; Salamon, P.; Burek, P.; Kalas, M. Assimilation of MODIS snow cover area data in a distributed hydrological model using the particle filter. Remote Sens. 2013, 5, 5825–5850. [Google Scholar] [CrossRef]
- Tekeli, A.E.; Akyurek, Z.; Sorman, A.A.; Sensoy, A.; Unal Sorman, A. Using MODIS snow cover maps in modeling snowmelt runoff process in the eastern part of Turkey. Remote Sens. Environ. 2005, 97, 216–230. [Google Scholar] [CrossRef]
- Molotch, N.P.; Margulis, S.A. Estimating the distribution of snow water equivalent using remotely sensed snow cover data and a spatially distributed snowmelt model: a multi-resolution, multi-sensor comparison. Adv. Water Resour. 2008, 31, 1503–1514. [Google Scholar] [CrossRef]
- Slater, A.G.; Clark, M.P.; Barrett, A.P. Comment on “Estimating the distribution of snow water equivalent using remotely sensed snow cover data and a spatially distributed snowmelt model: A multi-resolution, multi-sensor comparison”. Adv. Water Resour. 2008, 31, 1503–1514. [Google Scholar]
- Molotch, N.P.; Margulis, S.A.; Jepsen, S. Response to comment by A.G. Slater, M.P. Clark and A.P. Barrett on ‘Estimating the distribution of snow water equivalent using remotely sensed snow cover data and a spatially distributed snowmelt model: A multi-resolution, multi-sensor comparison’. Adv. Water Resour. 2010, 33, 213–239. [Google Scholar]
- He, Z.H.; Parajka, J.; Tian, F.Q.; Blöschl, G. Estimating degree-day factors from MODIS for snowmelt runoff modeling. Hydrol. Earth Syst. Sci. 2014, 18, 4773–4789. [Google Scholar] [CrossRef]
- Walter, T.M.; Brooks, E.S.; McCool, D.K.; King, L.G.; Molnau, M.; Boll, J. Process-based snowmelt modeling: Does it require more input data than temperature-index modeling? J. Hydrol. 2005, 300, 65–75. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall—Runoff Modelling: The Primer; Wiley: Chichester, UK, 2001; p. 360. [Google Scholar]
- Bengtsson, L.; Singh, V.P. Model sophistication in relation to scales in snowmelt runoff modeling. Nord. Hydrol. 2000, 31, 267–286. [Google Scholar]
- Egli, L.; Jonas, T.; Meister, R. Comparison of different automatic methods for estimating snow water equivalent. Cold Reg. Sci. Technol. 2009, 57, 107–115. [Google Scholar] [CrossRef]
- Magnusson, J.; Wever, N.; Essery, R.; Helbig, N.; Winstral, A.; Jonas, T. Evaluating snow models with varying process representations for hydrological applications. Water Resour. Res. 2015, 51, 2707–2723. [Google Scholar] [CrossRef]
- Rango, A. Worldwide testing of the snowmelt runoff model with applications for predicting the effects of climate change. Nord. Hydrol. 1992, 23, 155–171. [Google Scholar]
- Singh, P.; Kumar, N. Impact assessment of climate change on the hydrological response of a snow and glacier melt runoff dominated Himalayan river. J. Hydrol. 1997, 193, 316–350. [Google Scholar] [CrossRef]
- Singh, P.; Bengtsson, L. Hydrological sensitivity of a large Himalayan basin to climate change. Hydrol. Process. 2004, 18, 2363–2385. [Google Scholar] [CrossRef]
- Arora, M.; Singh, P.; Goel, N.K.; Singh, R.D. Climate variability influences on hydrological responses of a large himalayan basin. Water Resour. Manag. 2008, 22, 1461–1475. [Google Scholar] [CrossRef]
- Singh, P.; Arora, M.; Goel, N.K. Effect of climate change on runoff of a glacierized Himalayan basin. Hydrol. Process. 2006, 20, 1979–1992. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, P.; Singh, V. Snow and glacier melt contribution in the Beas River at Pandoh Dam, Himachal Pradesh, India. Hydrol. Sci. J. 2007, 52, 376–388. [Google Scholar] [CrossRef]
- Singh, P.; Bengtsson, L.; Berndtsson, R. Relating air temperatures to the depletion of snow covered area in a Himalayan basin. Nord. Hydrol. 2003, 34, 267–280. [Google Scholar]
- Singh, P.; Bengtsson, L. Impact of warmer climate on melt and evaporation for the rainfed, snowfed and glacierfed basins in the Himalayan region. J. Hydrol. 2005, 300, 140–154. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N.; Arora, M. Degree-day factors for snow and ice for Dokriani glacier, Garhwal Himalayas. J. Hydrol. 2000, 235, 1–11. [Google Scholar] [CrossRef]
- Singh, P.R.; Gan, T.Y.; Gobena, A.K. Modified temperature index method using near-surface soil and air temperatures for modeling snowmelt in the Canadian Prairies. J. Hydrol. Eng. 2005, 10, 405–419. [Google Scholar] [CrossRef]
- Singh, P.R.; Gan, T.Y.; Gobena, A.K. Evaluating a hierarchy of snowmelt models at a watershed in the Canadian Prairies. J. Geophys. Res. Atmos. 2009, 114, D04109. [Google Scholar] [CrossRef]
- Brubaker, K.; Rango, A.; Kustas, W. Incorporating radiation inputs into the snowmelt runoff model. Hydrol. Process. 1996, 10, 1329–1343. [Google Scholar] [CrossRef]
- Hock, R. A distributed temperature-index ice-and snowmelt model including potential direct solar radiation. J. Glaciol. 1999, 45, 101–111. [Google Scholar] [CrossRef]
- Viviroli, D.; Gurtz, J.; Zappa, M. The Hydrological modeling system PREVAH. Part II—Physical model description. In Geographica Bernensia P40; Institute of Geography: Bern, Switzerland, 2007; p. 86. [Google Scholar]
- Burek, P.A.; Van Der Knijff, J.; de Roo, A.P.J. LisFlood—Distributed Water Balance and Flood Simulation Model—Revised User Manual 2013; EUR—Scientific and Technical Research Reports JRC78917; Publications Office of the European Union: Luxembourg, 2013; Available online: http://publications.jrc.ec.europa.eu/repository/handle/JRC78917 (accessed on 15 September 2017). [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool, Theoretical Documentation, Version 2005; GSWRL-ARS: Temple, TX, USA, 2005. [Google Scholar]
- Cazorzi, F.; Della Fontana, G. Snowmelt modeling by combining air temperature and a distributed radiation index. J. Hydrol. 1996, 181, 169–187. [Google Scholar] [CrossRef]
- Winstral, A.; Marks, D.; Gurney, R. Simulating wind-affected snow accumulations at catchment to basin scales. Adv. Water Resour. 2013, 55, 64–79. [Google Scholar] [CrossRef]
- Shulski, M.D.; Seeley, M.W. Application of snowfall and wind statistics to snow transport modeling for snowdrift control in Minnesota. J. App. Met. 2004, 43, 1711–1721. [Google Scholar] [CrossRef]
- Bowling, L.; Pomeroy, J.; Lettenmaier, D. Parameterization of Blowing-Snow Sublimation in a Macroscale Hydrology Model. J. Hydrometeorol. 2004, 5, 745–762. [Google Scholar] [CrossRef]
- Strasser, U.; Bernhardt, M.; Weber, M.; Liston, G.E.; Mauser, W. Is snow sublimation important in the alpine water balance? Cryosphere 2008, 2, 53–66. [Google Scholar] [CrossRef]
- Gustafson, J.R.; Brooks, P.D.; Molotch, N.P.; Veatch, W.C. Estimating snow sublimation using natural chemical and isotopic tracers across a gradient of solar radiation. Water Resour. Res. 2010, 46, W12511. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Clow, D.W.; Stannard, D.I.; Fassnacht, S.R. Comparison of methods for quantifying surface sublimation over seasonally snow-covered terrain. Hydrol. Process. 2016, 30, 3373–3389. [Google Scholar] [CrossRef]
- MacDonald, M.K.; Pomeroy, J.W.; Pietroniro, A. On the importance of sublimation to an alpine snow mass balance in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 2010, 14, 1401–1415. [Google Scholar] [CrossRef]
- Feiccabrino, J.; Gustaffson, D.; Lundberg, A. Surface-based precipitation phase determinaion methods in hydrological models. Hydrol. Res. 2013, 44, 44–57. [Google Scholar] [CrossRef]
- Feiccabrino, J.; Lundberg, A.; Gustaffson, D. Improving surface-based precipitation phase determination through air mass boundary identification. Hydrol. Res. 2012, 43, 179–190. [Google Scholar]
- López-Burgos, V.; Gupta, H.V.; Clark, M. Reducing cloud obscuration of MODIS snow cover area products by combining spatio-temporal techniques with a probability of snow approach. Hydrol. Earth Syst. Sci. 2013, 17, 1809–1823. [Google Scholar] [CrossRef]
- Snow Telemetry (SNOTEL) Network. Available online: https://www.wcc.nrcs.usda.gov/snow/ (accessed on 15 September 2017).
- DeWalle, D.R.; Henderson, Z.; Rango, A. Spatial and temporal variations in snowmelt degree-day factors computed from SNOTEL data in the upper Rio Grande Basin. In Proceedings of the 70th Annual Western Snow Conference, Granby, CO, USA, 20–23 May 2002. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- European Academy (EURAC). Operational Service of Snow Cover Maps for the Alps. Available online: http://webgis.eurac.edu/snowalps/ (accessed on 15 September 2017).
- Notarnicola, C.; Duguay, M.; Moelg, N.; Schellenberger, T.; Tetzlaff, A.; Monsorno, R.; Costa, A.; Steurer, C.; Zebisch, M. Snow Cover Maps from MODIS Images at 250 m Resolution, Part 1: Algorithm Description. Remote Sens. 2013, 5, 110–126. [Google Scholar] [CrossRef]
- Notarnicola, C.; Duguay, M.; Moelg, N.; Schellenberger, T.; Tetzlaff, A.; Monsorno, R.; Costa, A.; Steurer, C.; Zebisch, M. Snow Cover Maps from MODIS Images at 250 m Resolution, Part 2: Validation. Remote Sens. 2013, 5, 1568–1587. [Google Scholar] [CrossRef]
- Bagli, S.; Pistocchi, A.; Bertoldi, G.; Borga, M.; Brenner, J.; Mazzoli, P.; Luzzi, V.; Zanotelli, D. IASMHYN: An Open Source Web Mapping Tool for Soil Water Budget and Agro-Hydrological Assessment trough the Integration of Monitoring and Remote Sensing Data. Atti del XXXV Convegno Nazionale di Idraulica e Costruzioni Idrauliche Bologna. 14–16 September 2016, pp. 1373–1376. Available online: http://amsacta.unibo.it/5400/1/ATTI_IDRA16.pdf (accessed on 15 September 2017).
- Pistocchi, A. Simple estimation of snow density in an Alpine region. J. Hydrol. Reg. Stud. 2016, 6, 82–89. [Google Scholar] [CrossRef]
- Gafurov, A.; Bárdossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci. 2009, 13, 1361–1373. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. The value of MODIS snow cover data in validating and calibrating conceptual hydrologic models. J. Hydrol. 2008, 358, 240–258. [Google Scholar] [CrossRef]
- Dietz, A.J.; Conrad, C.; Kuenzer, C.; Gesell, G.; Dech, S. Identifying Changing Snow Cover Characteristics in Central Asia between 1986 and 2014 from Remote Sensing Data. Remote Sens. 2014, 6, 12752–12775. [Google Scholar] [CrossRef]
- Molotch, N.P.; Bales, R.C. Scaling snow observations from the point to the grid element: Implications for observation network design. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Artan, G.A.; Verdin, J.P.; Lietzow, R. Large scale snow water equivalent status monitoring: Comparison of different snow water products in the upper Colorado Basin. Hydrol. Earth Syst. Sci. 2013, 17, 5127–5139. [Google Scholar] [CrossRef]
- Wilmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Slater, A.G.; Barrett, A.P.; Clark, M.P.; Lundquist, J.D.; Raleigh, M.S. Uncertainty in seasonal snow reconstruction: Relative impacts of model forcing and image availability. Adv. Water Resour. 2013, 55, 165–177. [Google Scholar] [CrossRef]
- Herrnegger, M.; Senoner, T.; Nachtnebel, H.P. Adjustment of spatio-temporal precipitation patterns in a high Alpine environment. J. Hydrol. 2016, in press. [Google Scholar] [CrossRef]
- Dressler, K.A.; Leavesley, G.H.; Bales, R.C.; Fassnacht, S.R. Evaluation of gridded snow water equivalent and satellite snow cover products for mountain basins in a hydrologic model. Hydrol. Process. 2006, 20, 673–688. [Google Scholar] [CrossRef]
- Zaitchik, B.; Rodell, M. Forward-looking assimilation of MODIS-derived snow-covered area into a land surface model. J. Hydrometeorol. 2009, 10, 130–148. [Google Scholar] [CrossRef]
- Hood, J.L.; Hayashi, M. Characterization of snowmelt flux and groundwater storage in an Alpine headwater basin. J. Hydrol. 2015, 521, 482–497. [Google Scholar] [CrossRef]
- Clark, M.P.; Hendrikx, J.; Slater, A.G.; Kavetski, D.; Anderson, B.; Cullen, N.J.; Kerr, T.; Örn Hreinsson, E.; Woods, R.A. Representing spatial variability of snow water equivalent in hydrologic and land-surface models: A review. Water Resour. Res. 2011, 47, W07539. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]

| Station | C0 (mm/°C Day) | Average of Daily Snowmelt Coeff. in [62] (mm/°C Day) |
|---|---|---|
| Wolf Creek Summit | 1.79 | 2.9 |
| Beartown | 4.14 | 5.2 |
| Cumbres Trestle | 2.91 | 4.1 |
| Middle Creek | 2.82 | 4.0 |
| Lily pond | 2.87 | 5.9 |
| Culebra #2 | 3.33 | 4.9 |
| Trinchera | 2.03 | 3.2 |
| Code | Station Name | Z (m a.s.l.) | P (mm) | T (dd) | P × T (mm dd) | N | N (Meas.) |
|---|---|---|---|---|---|---|---|
| X136Y7 | Prettau | 1449 | 1386 | 248 | 1914 | 1121 | 1491 |
| X86Y37 | Pens | 1487 | 1068 | 527 | 858 | 818 | 1211 |
| X127Y14 | Klausberg-Steinhaus | 1590 | 1152 | 1456 | 2418 | 1107 | 1432 |
| X139Y5 | Kasern | 1590 | 1349 | 1132 | 2248 | 1039 | 1273 |
| X136Y17 | Rein in Taufers | 1600 | 738 | 660 | 630 | 617 | 1525 |
| X60Y36 | Pfelders | 1620 | 1567 | 1019 | 1845 | 1003 | 1283 |
| X14Y35 | Ausserrojen | 1833 | 1189 | 441 | 532 | 1038 | 1289 |
| X113Y18 | Stausee Neves | 1860 | 1670 | 2484 | 3686 | 1463 | 1351 |
| X96Y82 | Obereggen | 1872 | 1868 | 1125 | 2113 | 1225 | 1056 |
| X41Y71 | Weissbrunn-Ulten | 1890 | 2536 | 727 | 937 | 1273 | 1270 |
| X27Y32 | Melag | 1915 | 1139 | 899 | 1029 | 1050 | 1336 |
| X124Y59 | Piz la Ila | 1995 | 1209 | 2260 | 4480 | 1353 | 1366 |
| X106Y29 | Gitschberg-Meransen | 2010 | 770 | 3088 | 5551 | 1310 | 1554 |
| X75Y48 | Waidmannalm-Hafling | 2040 | 1996 | 2495 | 4462 | 1307 | 1436 |
| X112Y63 | Ciampinoi | 2150 | 2492 | 2048 | 5129 | 1445 | 1190 |
| X35Y41 | Lazauneralm-Schnals | 2450 | 1224 | 2654 | 3155 | 1616 | 1513 |
| Code | NSE | d | R2 | Slope | Intercept (mm) | MSEs% | MSEu% | RMSE (mm) | C0 (mm °C−1 Day −1) |
|---|---|---|---|---|---|---|---|---|---|
| X112Y63 | −3.80 | 0.38 | 0.04 | 0.41 | 98.67 | 9.3% | 90.7% | 201.76 | 1.19 |
| X106Y29 | −1.42 | 0.51 | 0.54 | 0.20 | 2.98 | 98.5% | 1.5% | 217.66 | 0.25 |
| X35Y41 | −0.97 | 0.55 | 0.84 | 0.27 | 4.14 | 99.3% | 0.7% | 216.75 | 0.46 |
| X124Y59 | −0.60 | 0.60 | 0.45 | 0.30 | −0.48 | 92.8% | 7.2% | 168.39 | 0.52 |
| X75Y48 | −0.59 | 0.61 | 0.28 | 0.37 | 35.71 | 77.6% | 22.4% | 157.07 | 0.79 |
| X86Y37 | −0.41 | 0.61 | 0.53 | 0.33 | 6.05 | 93.3% | 6.7% | 140.17 | 1.99 |
| X127Y14 | −0.27 | 0.53 | 0.24 | 0.15 | 41.20 | 94.6% | 5.4% | 163.10 | 0.78 |
| X136Y17 | −0.24 | 0.62 | 0.58 | 0.34 | 23.52 | 93.3% | 6.7% | 131.41 | 1.11 |
| X27Y32 | 0.02 | 0.72 | 0.74 | 0.49 | −4.26 | 91.0% | 9.0% | 94.20 | 1.25 |
| X113Y18 | 0.13 | 0.68 | 0.49 | 0.38 | 24.70 | 83.0% | 17.0% | 126.18 | 0.66 |
| X14Y35 | 0.13 | 0.72 | 0.74 | 0.46 | 9.36 | 91.5% | 8.5% | 87.25 | 2.67 |
| X41Y71 | 0.21 | 0.75 | 0.15 | 0.36 | 70.12 | 57.6% | 42.4% | 102.77 | 3.44 |
| X96Y82 | 0.31 | 0.73 | 0.33 | 0.39 | 56.91 | 56.6% | 43.4% | 78.56 | 1.71 |
| X136Y7 | 0.35 | 0.78 | 0.66 | 0.51 | 30.21 | 79.9% | 20.1% | 97.80 | 5.18 |
| X139Y5 | 0.42 | 0.78 | 0.42 | 0.45 | 52.48 | 52.0% | 48.0% | 71.76 | 1.17 |
| X60Y36 | 0.80 | 0.94 | 0.80 | 0.82 | 12.68 | 17.9% | 82.1% | 40.68 | 1.51 |
| Code | Name | Catchment Area km2 | Elevation m a.s.l. | r | Inflow (m3/s) | Outflow (m3/s) |
|---|---|---|---|---|---|---|
| 2075 | Rio Plan-Eschbaum | 49.6 | 1575 | 0.80 | 1.20 | 1.22 |
| 3195 | Rio Fleres a Colle Isarco | 72.4 | 1063.32 | 0.76 | 5.02 | 1.87 |
| 3355 | Rio Vizze a Novale | 109.7 | 1365.4 | 0.58 | 2.24 | 1.85 |
| 3415 | Vedretta Piana (*) | 23.1 | 2120 | 0.49 | 0.59 | 1.55 |
| 3585 | Rio Racines a Stange | 47.2 | 960 | 0.69 | 2.37 | 1.36 |
| 4575 | Rio Casies a Colle | 117.3 | 1196.07 | 0.71 | 10.74 | 1.65 |
| 4875 | Rio Anterselva a Bagni Salomone | 83.5 | 1095.95 | 0.73 | 8.70 | 1.20 |
| 5497 | Rio Riva a Caminata | 116.2 | 855 | 0.88 | 7.23 | 2.41 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pistocchi, A.; Bagli, S.; Callegari, M.; Notarnicola, C.; Mazzoli, P. On the Direct Calculation of Snow Water Balances Using Snow Cover Information. Water 2017, 9, 848. https://doi.org/10.3390/w9110848
Pistocchi A, Bagli S, Callegari M, Notarnicola C, Mazzoli P. On the Direct Calculation of Snow Water Balances Using Snow Cover Information. Water. 2017; 9(11):848. https://doi.org/10.3390/w9110848
Chicago/Turabian StylePistocchi, Alberto, Stefano Bagli, Mattia Callegari, Claudia Notarnicola, and Paolo Mazzoli. 2017. "On the Direct Calculation of Snow Water Balances Using Snow Cover Information" Water 9, no. 11: 848. https://doi.org/10.3390/w9110848
APA StylePistocchi, A., Bagli, S., Callegari, M., Notarnicola, C., & Mazzoli, P. (2017). On the Direct Calculation of Snow Water Balances Using Snow Cover Information. Water, 9(11), 848. https://doi.org/10.3390/w9110848





