1. Introduction
Evaporation, which is an overall term covering all processes in which liquid water is transferred as water vapour to the atmosphere—definition already provided by ancient Greek philosophers [
1]—is crucial element of multiple disciplines and an essential input of hydrological modelling, water resources management, irrigation planning, and climatological studies. Numerous efforts are reported in the literature, presenting different expressions of evaporation (including actual, potential, reference crop, and pan evaporation), based on different types of data. McMahon et al. [
2,
3] provide a major discussion of the background theory and definitions, as well as a critical assessment of the models developed so far.
Here, we emphasize the concept of potential evapotranspiration, PET, which is a theoretical quantity considered as “the rate at which evapotranspiration would occur from a large area completely and uniformly covered with growing vegetation, which has access to an unlimited supply of soil water, and without advection or heating effects” [
4]. Since PET depends on soil properties, a better defined term is the so-called reference crop evapotranspiration, introduced by Doorenbos and Pruitt [
5], and typically denoted as ET
0, which refers to the evapotranspiration from a standardized vegetated surface (i.e., actively growing and completely shading grass of 0.12 m height, surface resistance 70 s · m
−1, and albedo = 0.23). The globally accepted method for consistent estimation of PET is the Penman-Monteith (herein referred to as PM) equation, as formalized by the Food and Agriculture Organization (FAO), which is physically-based, and is therefore used as standard for comparisons with other, more simple approaches [
6]. The major drawback for the generalized application of the PM method worldwide is the need of simultaneous measurements of four meteorological variables (air temperature, wind speed, relative humidity, and net radiation or, alternatively, sunshine duration), at the desirable spatial and temporal resolution.
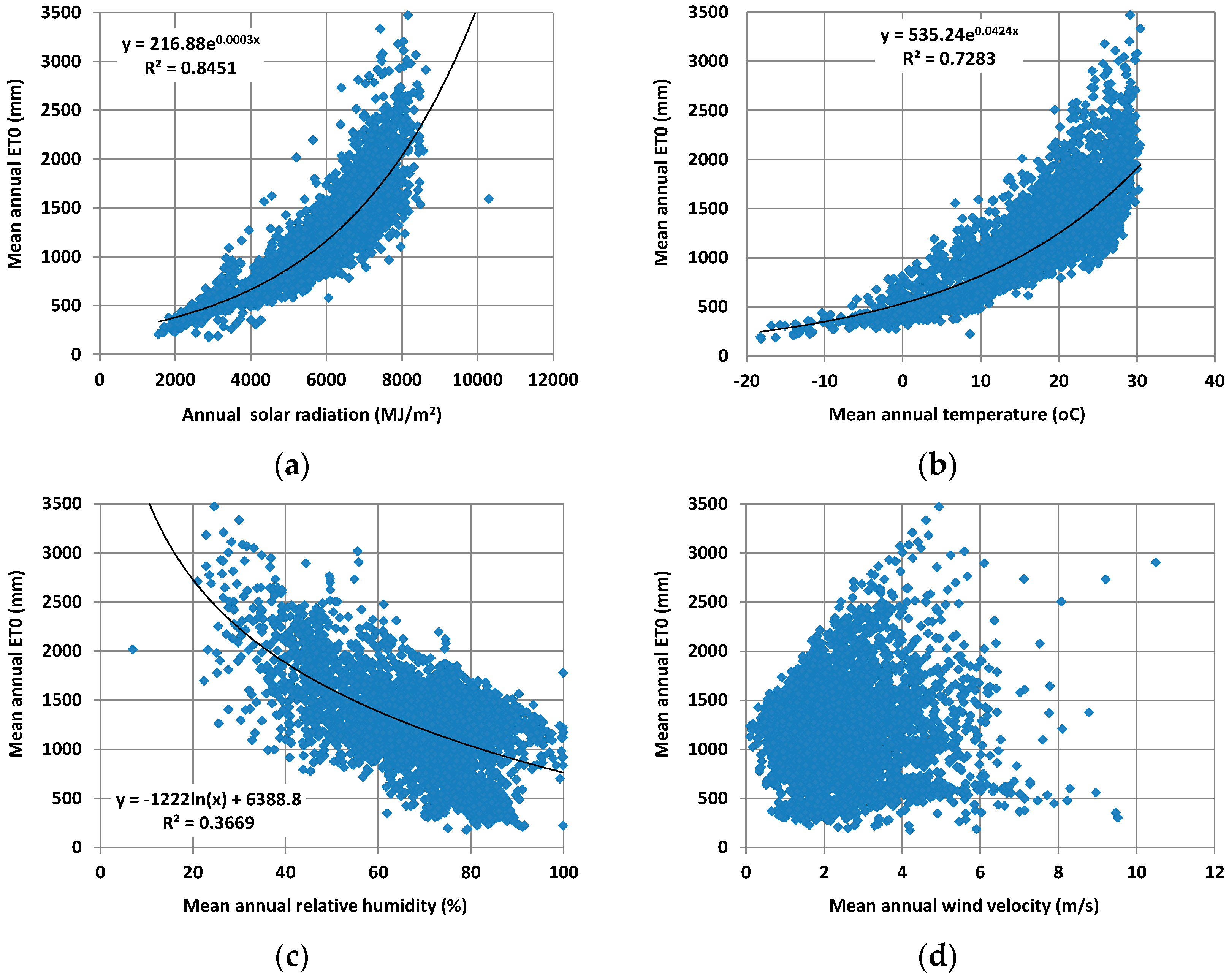
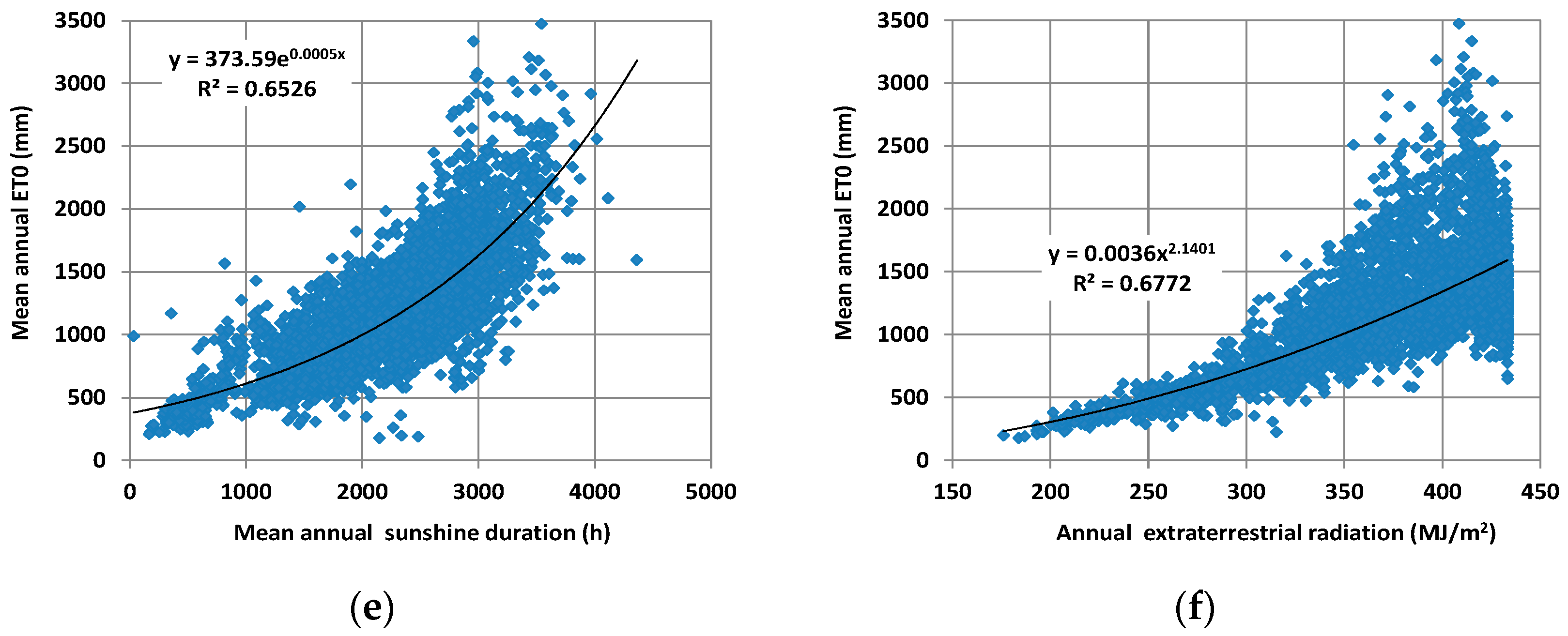
To overcome the data requirements of the PM formula, a number of alternative approaches have been developed, which are typically classified into temperature-based and radiation-based; the former use only temperature observations, which are dense and easily accessible, while the latter also use values of extraterrestrial radiation (which is, in fact, periodic function of latitude and time). For many decades, such approaches have been widely applied for PET modelling worldwide using the standard “literature” values of the parameters involved in their governing equations. However, since these have been developed for specific studies, locations, and climatic conditions [
7], their applicability outside of these distinct conditions usually result in unreliable predictions, introducing significant bias in PET estimations. For this reason, and particularly in the last years, significant attention is payed to local calibrations of empirical PET models, either by using direct PET observations at the field scale (e.g., lysimeter measurements) and/or against simulated PET data, provided by the PM formula. One of the first attempts is reported by Allen and Pruit [
8], who calibrated and validated the Blaney-Criddle model against PM data, using local wind function and taking advantage of daily lysimeter measurements of alfalfa evapotranspiration. Similar calibration approaches were employed for all of the widespread PET formulas, such as the Thornthwaite, Blaney-Criddle and Priestley-Taylor (e.g., [
9,
10,
11]), and other empirical expressions as well (e.g., [
12]). Many recent publications also focus on the re-evaluation of the sole parameter of the Hargreaves equation against regional data, for a range of climatic regimes [
13,
14,
15,
16,
17].
Although the spatial resolution and accuracy of meteorological data over the extended areas of the globe is not sufficient, current advances in remote sensing technologies allowed quite reliable estimations of PET by combining satellite and ground information [
18]. Since gridded data of meteorological inputs and canopy characteristics is now easily accessible, several researchers employed PET estimations at large spatial scales, up to global [
19,
20,
21,
22], by employing scaling and interpolation techniques of varying physical complexity [
23].
In two recent studies, Tegos et al. [
24,
25] calibrated a simplified radiation-based expression of the PM formula, using monthly meteorological data from a large number of stations over Greece and California, respectively. In both areas, the proposed formula, which contains either three or two free parameters, clearly outperformed other widely used methods, such as Hargreaves and Samani [
26], Oudin et al. [
12], and Jensen and Haise [
27], as modified by McGuinness and Bordne [
28]. Malamos et al. [
29] also employed the parametric model at the daily scale, in the context of PET mapping over the irrigated plain of Arta, Western Greece.
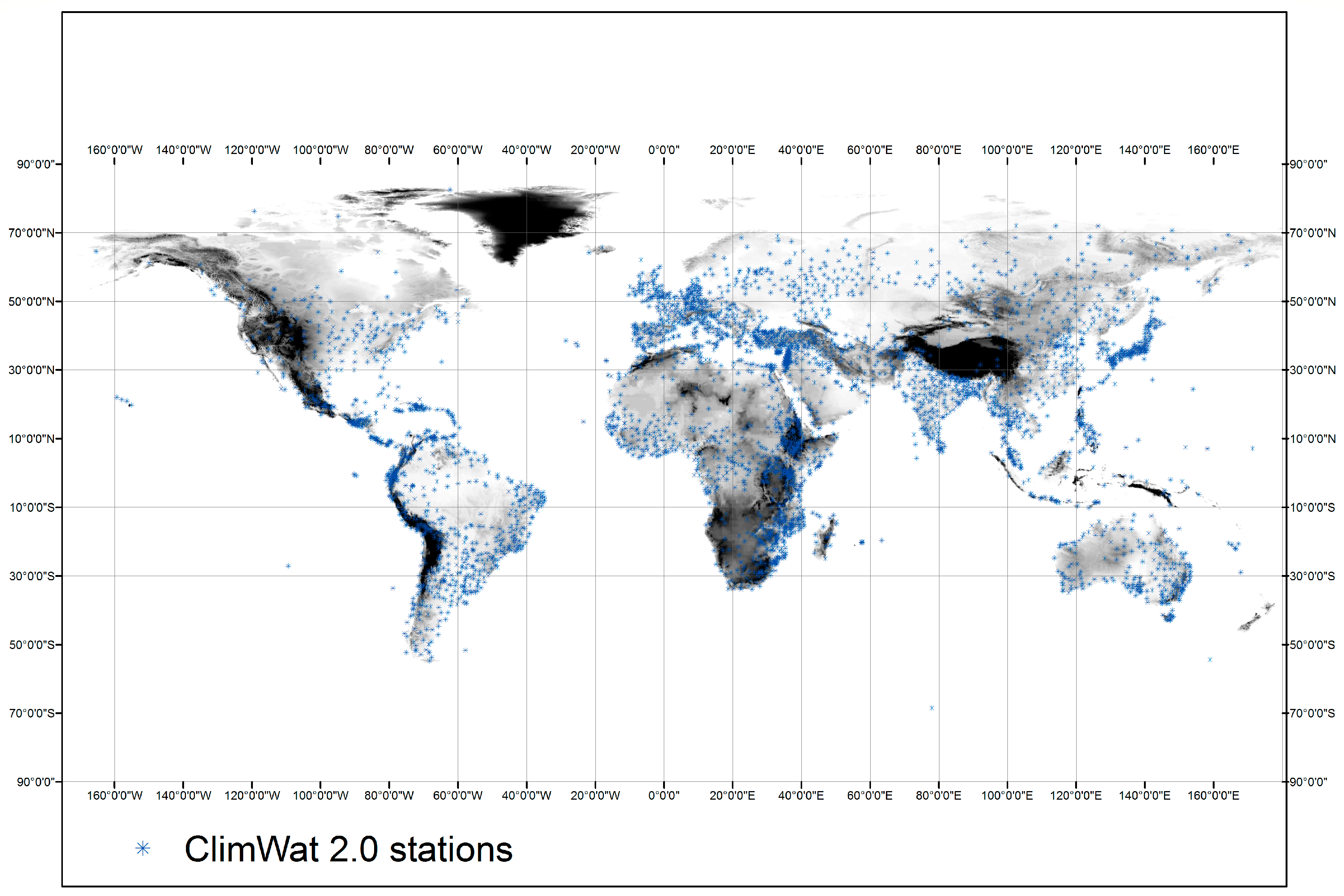
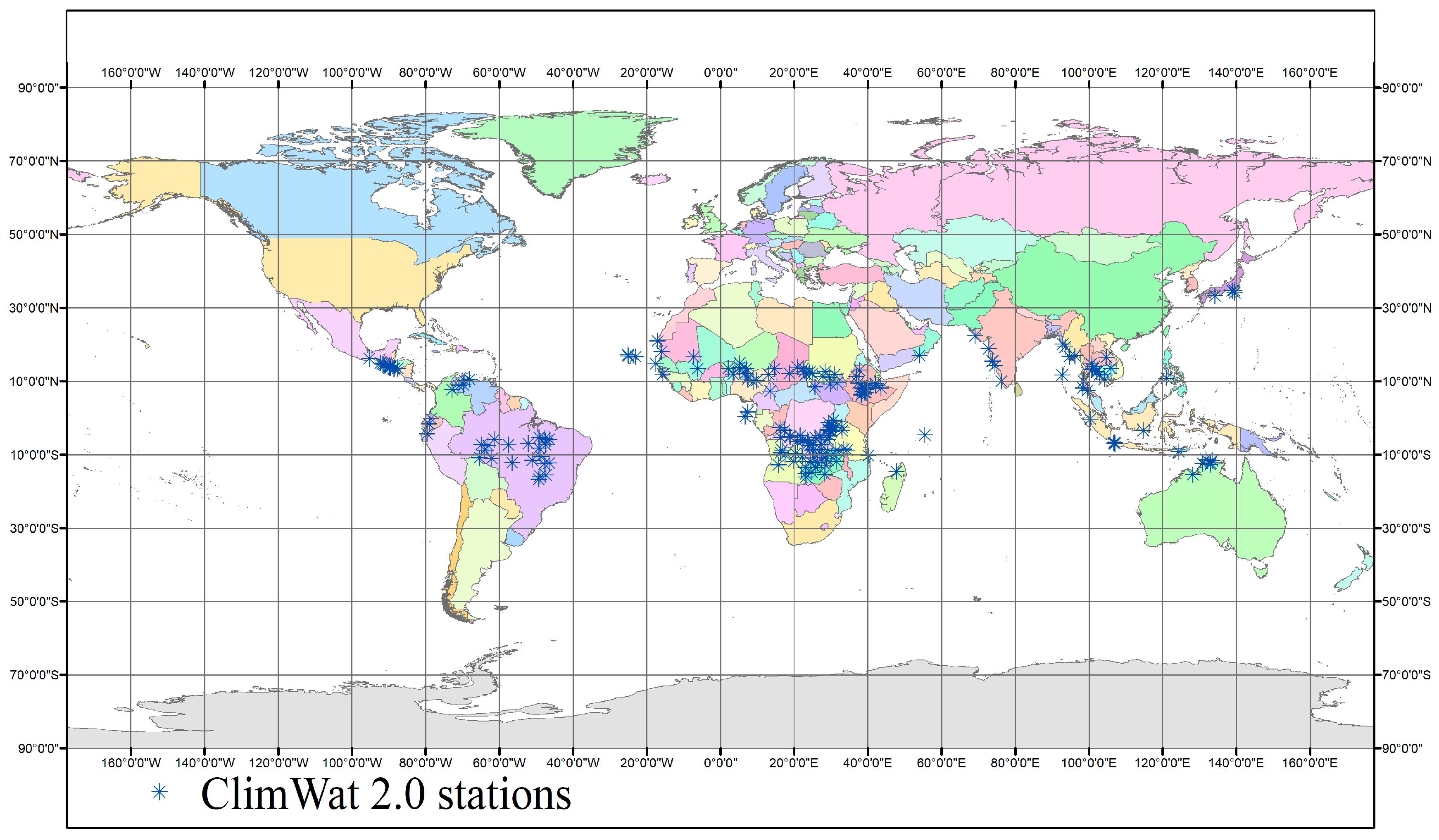
In the present study, we employ the simplified (i.e., with two parameters) expression of the aforementioned model over the globe, by inferring its parameters through calibration against given Penman-Monteith values (next referred to as reference PET or ET
0). The meteorological inputs and ET
0 data are retrieved by the FAO CLIMWAT database that provides monthly climatic information at 4300 locations worldwide. A preliminary analysis of these data allowed explaining the major drivers of PET over the globe and across seasons. We perform extended analysis of the model inputs and outputs, including the production of global maps of optimized model parameters and associated performance metrics, as well as comparisons with a widely known formula by Hargreaves and Samani [
26]. Finally, we use the interpolated values of the optimized parameter values to validate the predictive capacity of the model against detailed meteorological data, in terms of monthly time series, at several stations worldwide. The results are very encouraging, since even with the use of abstract climatic information for its calibration, the model generally ensures very reliable PET estimations. However, we have detected few cases where the model systematically fails to reproduce the reference PET, particularly across tropical areas. Except for these specific areas, the parameter estimations through the derived maps can be directly employed within the proposed formula, at both point and regional scales.
4. Model Calibration
4.1. Evaluation Criteria
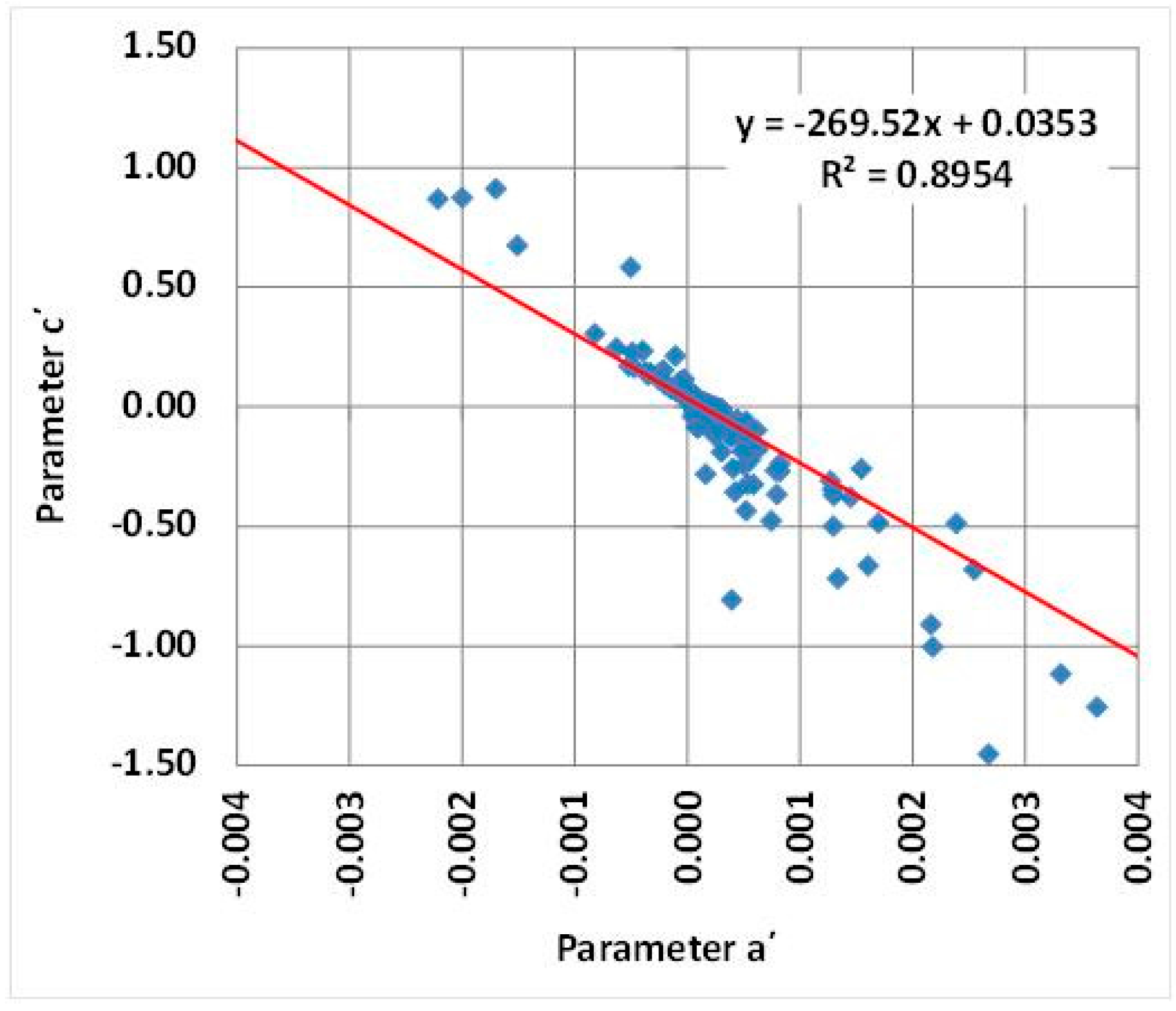
The large-scale PET information provided by FAO CLIMWAT database was used as reference data, for calibrating the parametric expression (Equation (5)), thus providing local estimations of parameters a′ and c′ at all station sites. For the evaluation of the model performance against reference PET (i.e., ET0) we used the following statistical criteria:
The coefficient of determination, most commonly referred to as efficiency or Nash-Sutcliffe efficiency:
where is the ET0 value, estimated by the PM formula at time step t, is the modeled value at time step t, is the monthly average value of the reference PET, and T is total number of time steps (in the particular case, T equals the number of months, i.e., 12).
In calibrations, we used as performance measure the NSE, while the two other statistical metrics have been used for further evaluation. It is well-known that NSE ranges between −∞ and 1, with NSE = 1 indicating perfect fitting of the modelled against the given reference values. Due to the generally high linear correlations of Ra and T against ET0, we only consider values greater than 0.70 as satisfying, whereas positive values less than 0.50 are only marginally accepted. On the other hand, negative NSE values are definitely unacceptable, since they indicate that the mean observed value is a better predictor than the simulated value. The mean absolute error and the bias are quite similar metrics, quantifying in absolute (i.e., mm/month) and relative (%) terms the deviation of the mean modelled ET0 from the corresponding mean reference value, .
4.2. Optimization Procedure
At each station, we formulated the associated global optimization problem, based on the given 12 monthly average values of ET
0, and using NSE as the objective function to maximize against parameters
a′ and
c′. Within calibration, we have considered a quite extended feasible space, by allowing
a′ and
c′ to vary within ranges [–0.02, 0.02] and [–5.0, 5.0], respectively. The global search was carried out with the evolutionary annealing-simplex algorithm, which is a heuristic technique that has been proved very effective on locating global optima in highly nonlinear spaces [
49,
50].
Due to the exceptionally large number of calibration problems to be solved at the full sample of 4300 stations, the computational procedure was automatized in a MATLAB environment.
4.3. Assessment against Linear Regression Estimations
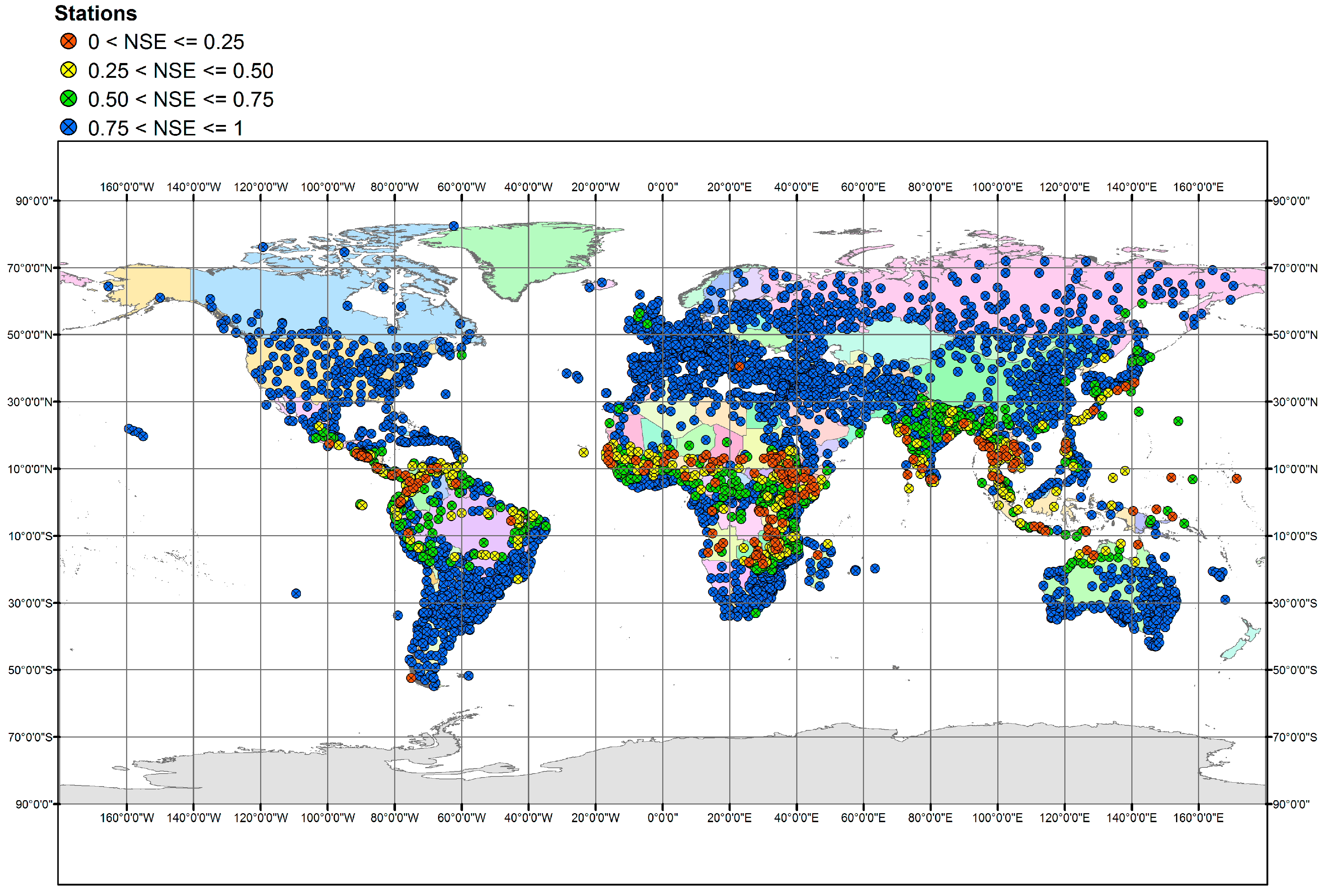
In order to assess the predictive capacity of the parametric model, we compare its performance against two benchmarks by means of linear regression models of reference PET against
T and
Ra. In
Figure 5 we contrast the ranges of coefficients of determination,
r2, achieved by the two linear regression models and the nonlinear parametric model, for the entire sample of 4300 stations. The parametric model ensures very satisfying efficiency (NSE > 0.90) in 58.8% of stations, while only 32.8% and 35.9% of stations exhibit such good performance, considering the linear regression models against
T and
Ra, respectively. In 2562 stations (59.6%), the parametric approach outperforms both regression models, while in 1327 stations (30.9%) it outperforms at least one model. Only in 411 stations (9.6%) the two benchmarks achieve a higher
r2 than the parametric approach. We remark that in linear regression theory,
r2 is mathematically equivalent to efficiency, which is the most widely used goodness-of-fitting measure for evaluating nonlinear models. However, while the coefficient of determination of a nonlinear model can take any value from −∞ to unity, in linear regression this metric is by definition non-negative (
r2). Moreover, linear regression models are by definition unbiased, given that the least-square line is forced to pass through the observed mean.
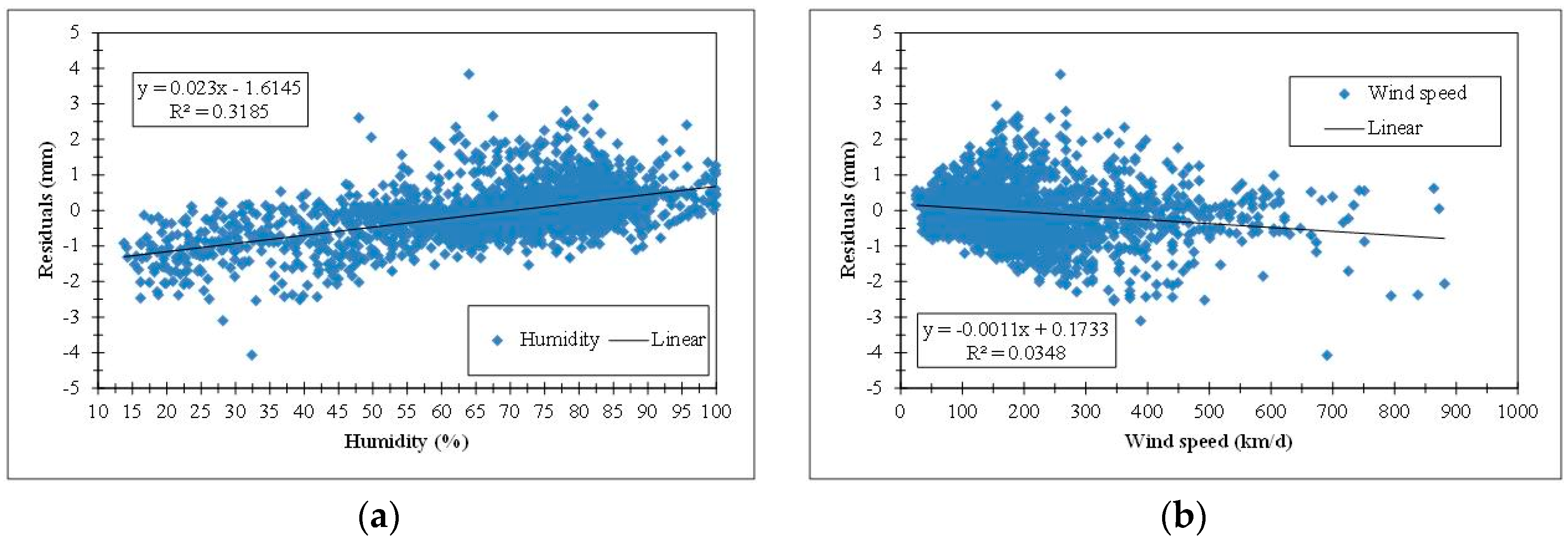
However, there are relatively few cases where the parametric model, even after calibration, does not ensure good predictive capacity. In particular, at 10.3% of stations, the model exhibits marginally accepted performance (0 < NSE < 0.50), while in 4.7% of stations the model predictions are definitely unacceptable (NSE < 0). In these cases, it is impossible to achieve acceptable predictions of mean monthly ET
0 through the parameterization implemented in Equation (5), because of the irregular relationship of ET
0 vs. the two explanatory variables, or due to the influence of additional meteorological drivers (relative humidity and wind speed) as rationalized in
Section 3.3.
4.4. Assessment against Hargreaves-Samani Estimations
The substantial advantage of a parametric approach, allowing calibration, over an empirical formula with given numerical constants, is further highlighted by contrasting our predictions with the ones provided by the well-known Hargraves-Samani equation, given by:
where
T is the mean monthly temperature.
As shown in
Table 2, providing abstract information on model efficiency in terms of quartiles, in the majority of stations the predictive capacity of Equation (9) is absolutely disappointing, mainly due to the existence of substantial bias in ET
0 estimations across stations. This bias is actually embedded in the coefficients that are embedded in Equation (9), which have been estimated on the basis of specific climatic regime, which cannot be representative of any conditions worldwide. On the other hand, Equation (5) with calibrated parameters ensures very satisfactory performance in an extended part of the station sample, since the model is adapted to local climatic conditions.
7. Conclusions
In the present study, the concept of parametric PET modelling was thoroughly analyzed, by performing a global survey of its applicability. The model has a very simple structure and uses easily retrieved information, by means of air temperature and extraterrestrial radiation. Therefore, the model is simultaneously simple and parsimonious, in terms of both parameterization and data requirements.
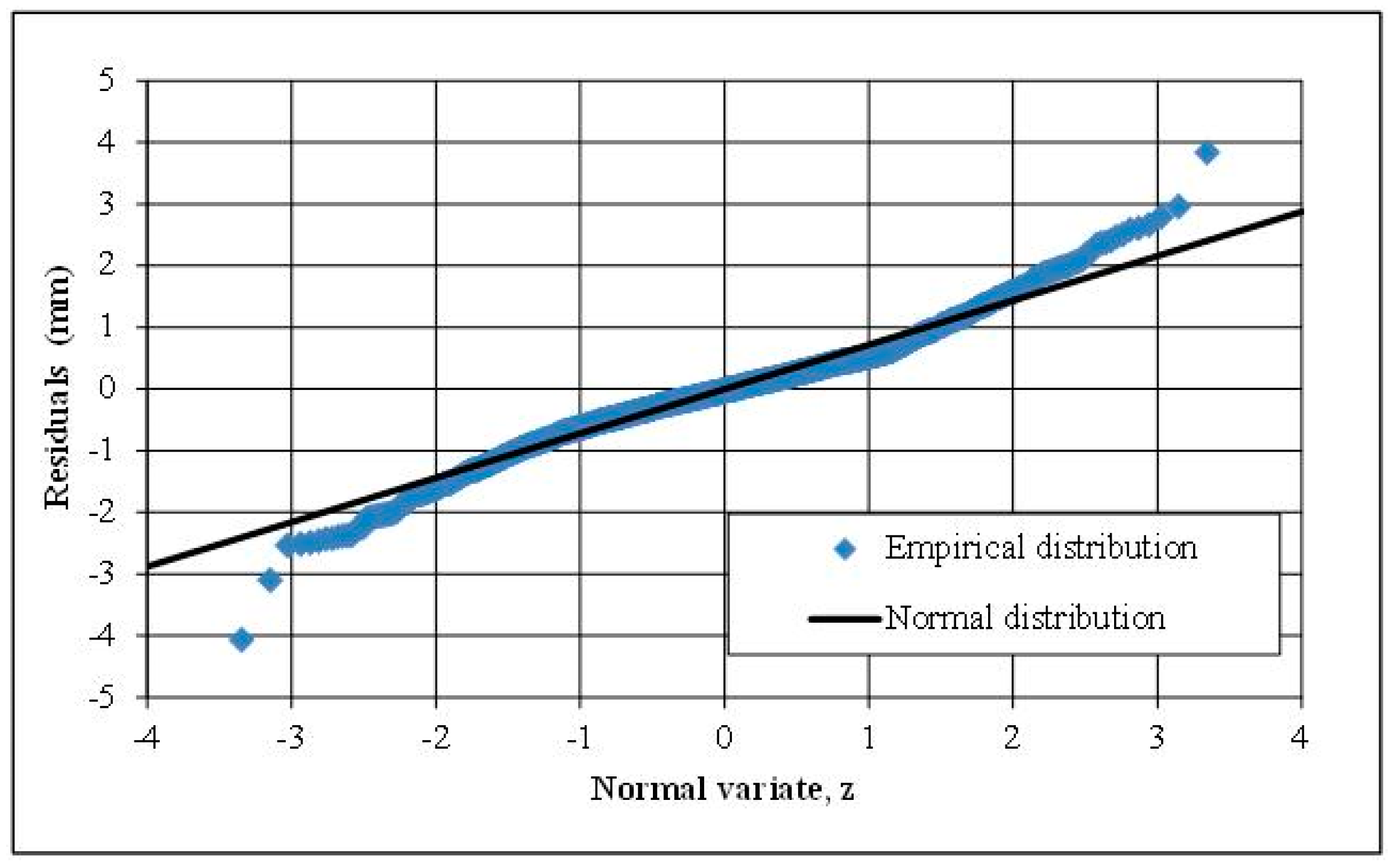
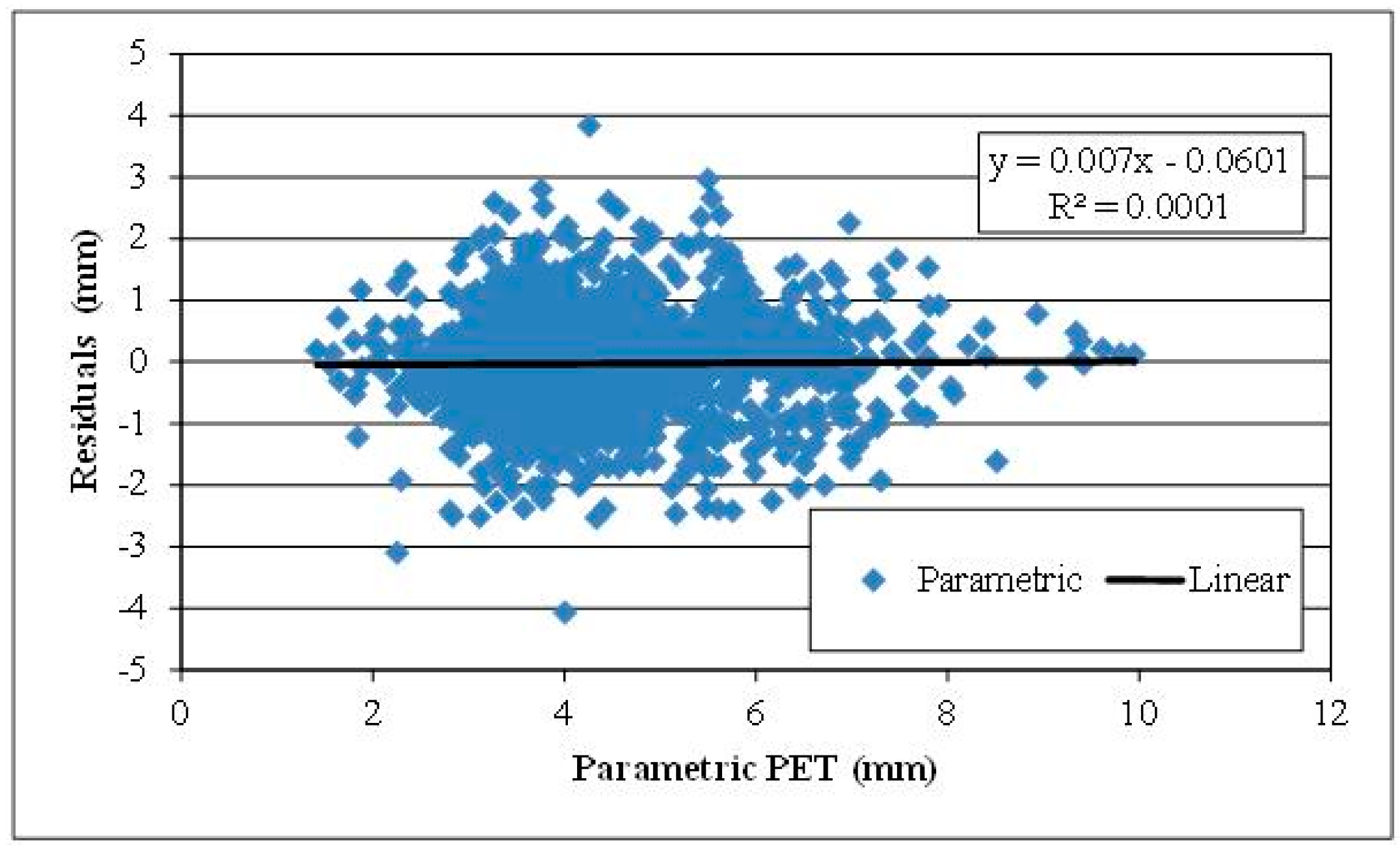
Preliminary analysis of the extended climatic data at 4300 stations worldwide, provided by the FAO CLIMWAT database, allowed for justifying the use of temperature and extraterrestrial radiation as key explanatory variables of reference PET over the globe. However, it also indicated that in few cases the two variables exhibit irregular seasonal patterns, which cannot be adequately represented through simple modelling structures. The statistical analysis of the residuals, in these cases, showed that the model is consistent in terms of parameters estimation and model validation.
At all CLIMWAT stations, we provided optimal estimations of model parameters c′ and a′, by calibrating them against given Penman-Monteith values at the mean monthly scale. Using typical goodness-of-fitting criteria (efficiency, mean absolute error, relative bias), we evaluated the model performance, which was generally very satisfying in a large portion of stations. However, in less than 10% of the data set the calibrated model exhibited negative efficiency. Further analysis across broader geographical regions showed that the model deviates from the Penman-Monteith PET estimates in some locations, which is rather expected due to the significant influence of relative humidity and wind speed, which are not accounted for in the parametric model.
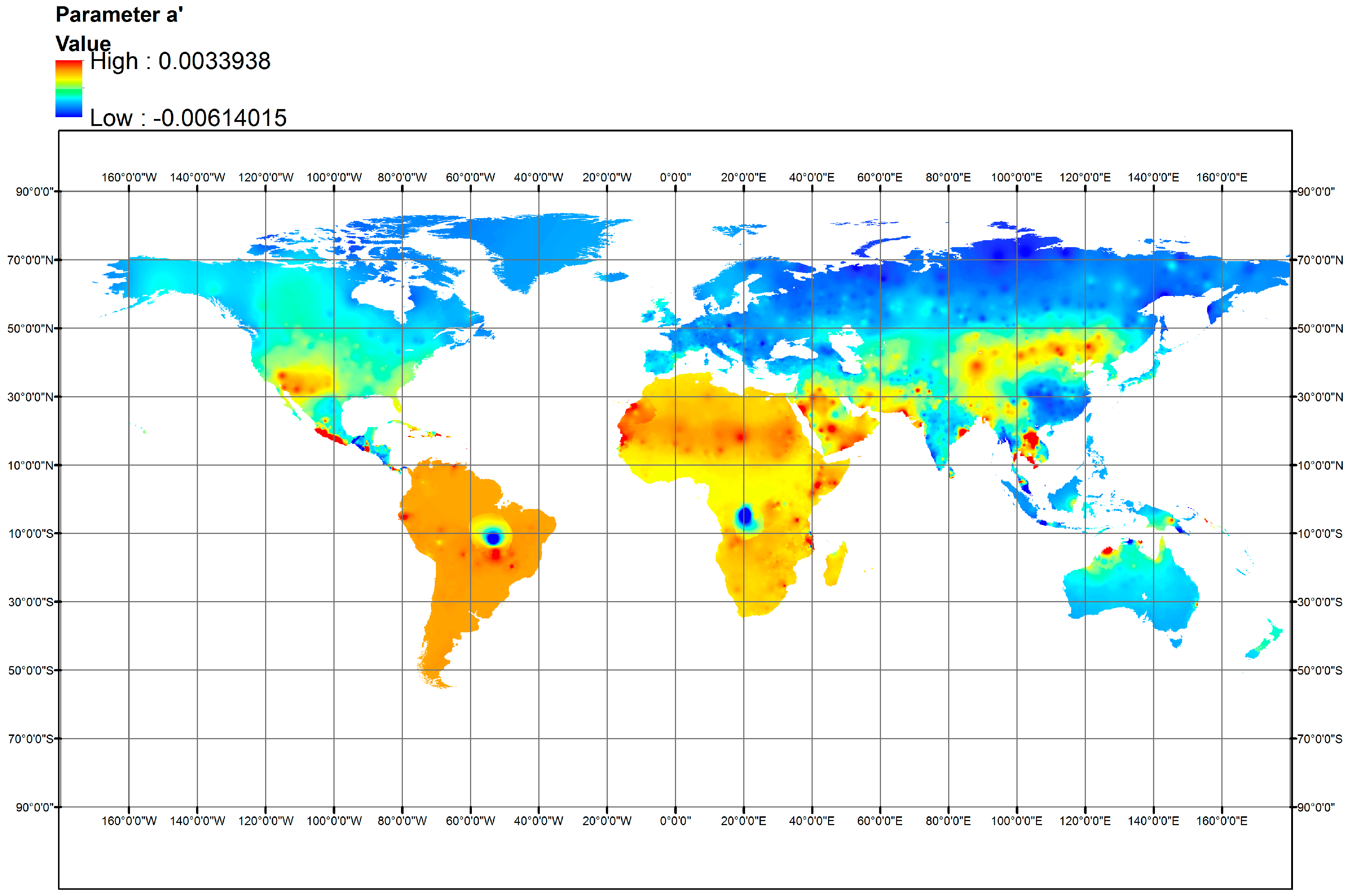
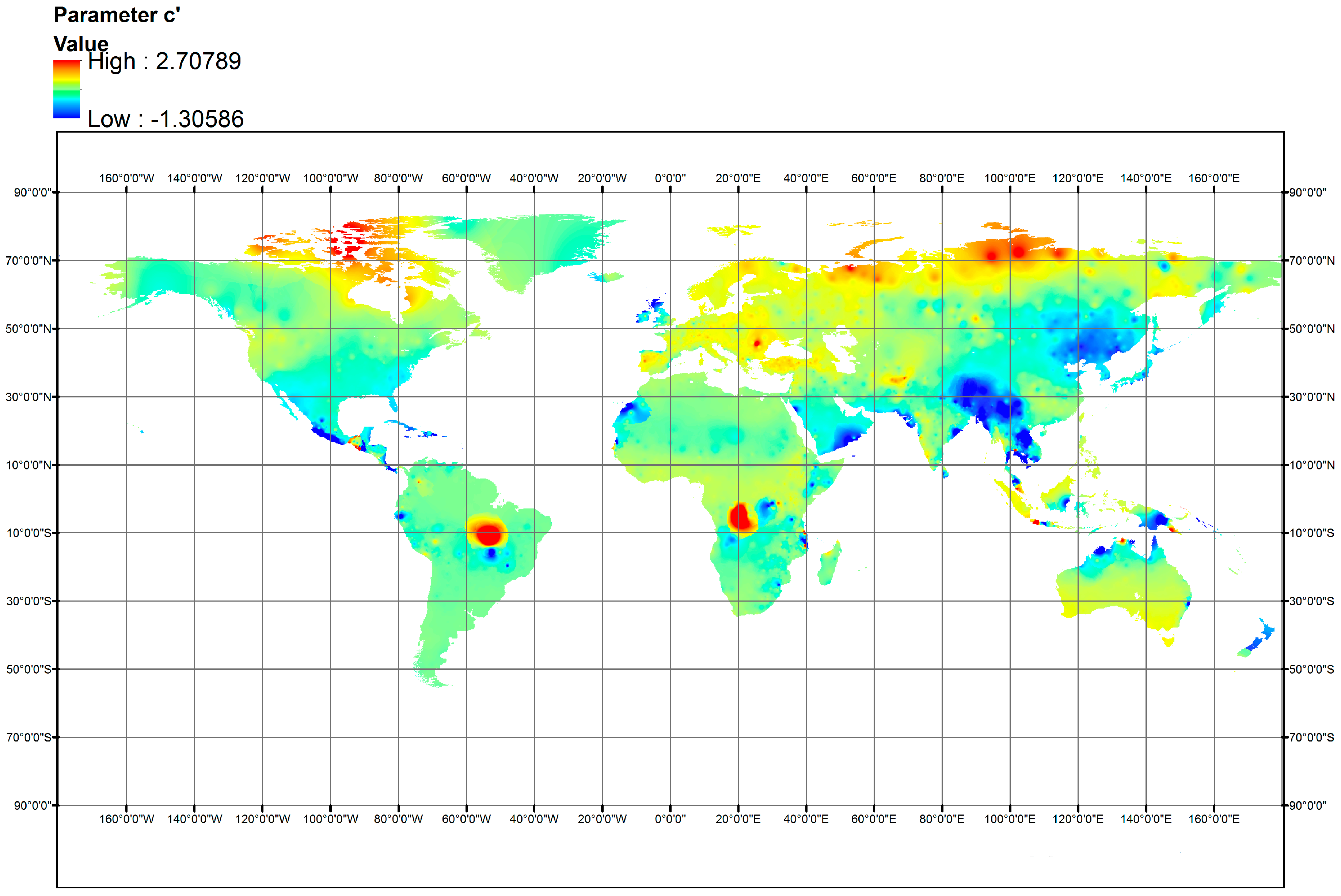
An important outcome of this research was the generation of spatially distributed maps of model parameters, by employing the IDW interpolation technique against their optimized values at 4088 out of 4300 stations, exhibiting non-negative efficiency (the dataset of point parameter estimations is available at
http://www.itia.ntua.gr/en/docinfo/1738/). The spatial pattern of both parameters over the globe is fully reasonable, which is a strong indicator of their physical consistency. These maps can be straightforwardly used to provide suitable parameter values at both the local and regional scale, thus allowing for the direct use of the parametric model wherever in the world.
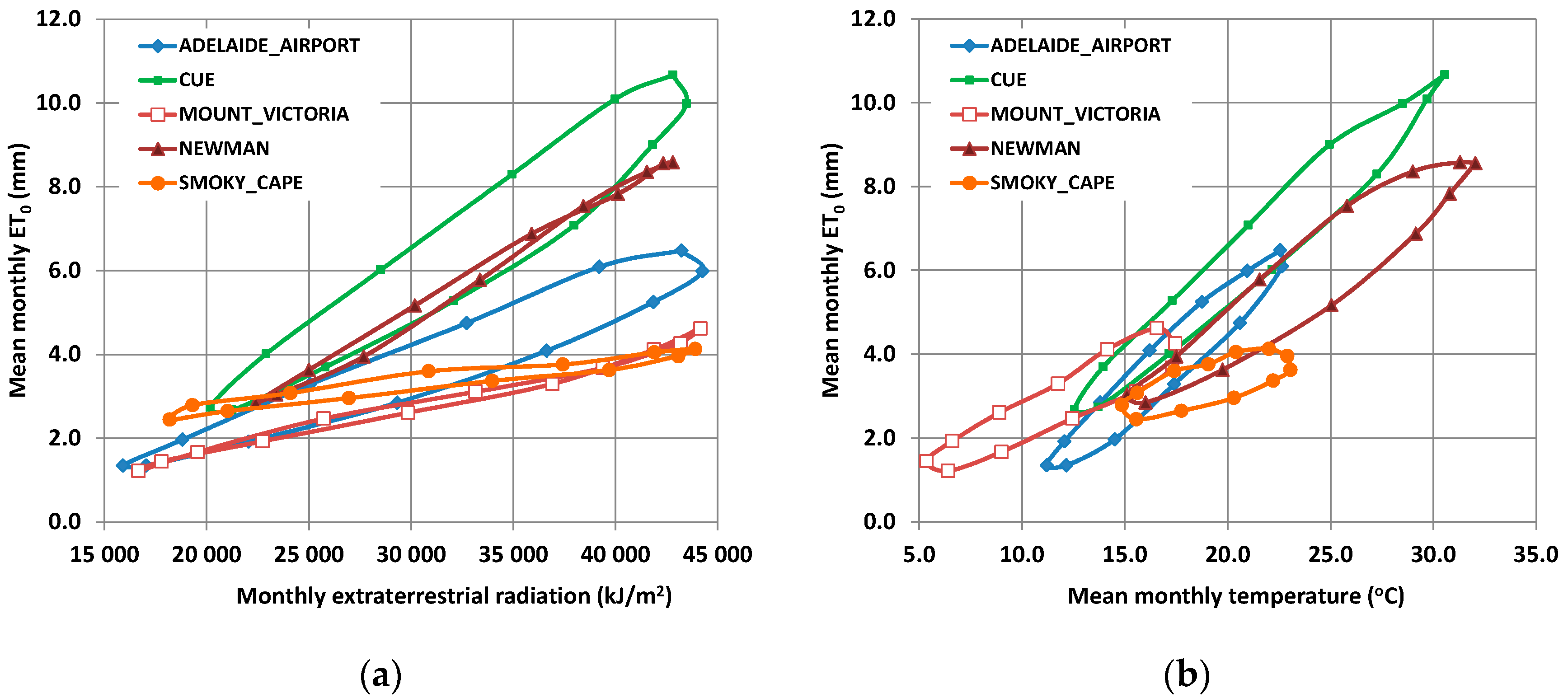
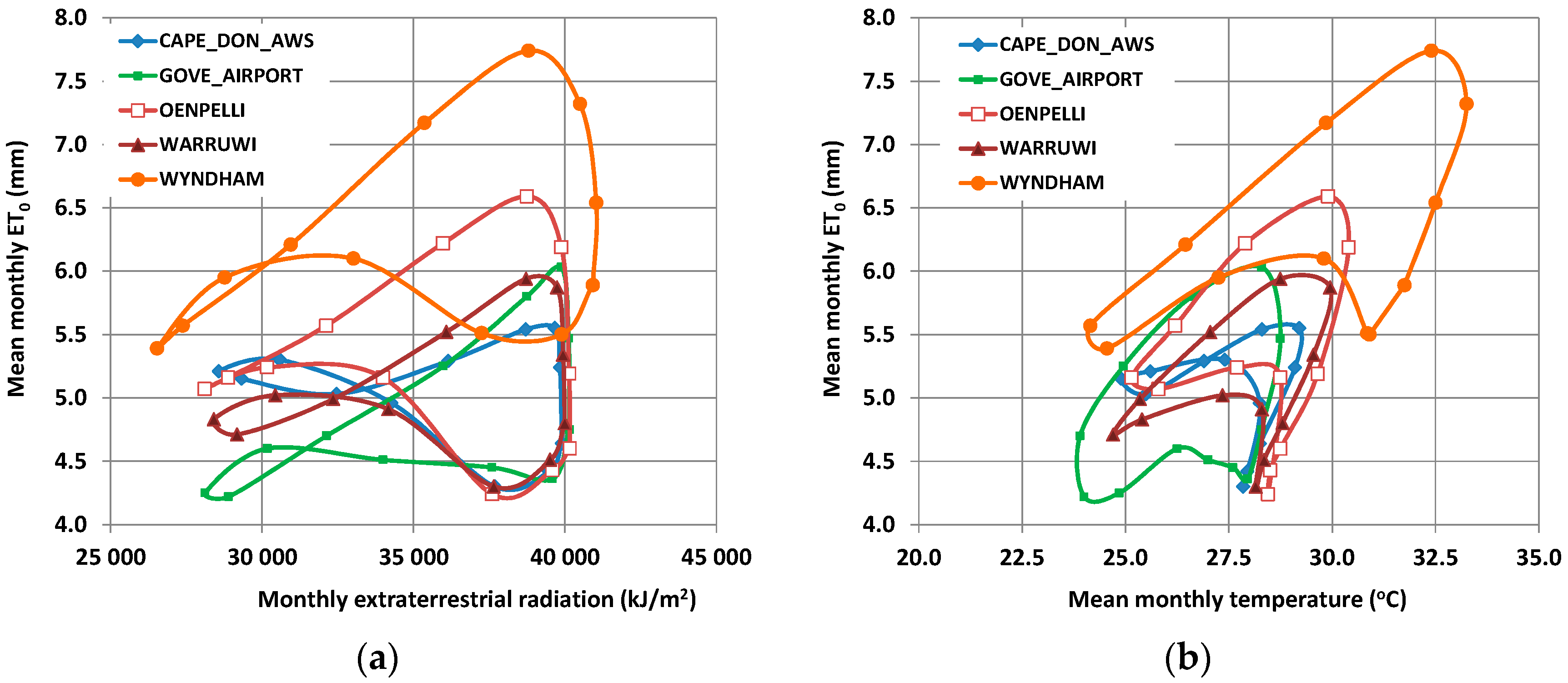
The validation procedure against PM estimates from detailed meteorological information (i.e., monthly time series) from 37 stations across California, as well as 17 independent stations across Europe, Asia, and Australia, proved that the application of the parametric model using spatially interpolated parameters provides reliable estimates, thus being a promising alternative of the widely recognized yet data demanding Penman-Monteith approach, when there is lack of the full data set that the latter requires.
Future research steps include a detailed investigation of the factors affecting the model poor performance in specific areas over the globe, in order to recognize whether these can be handled through a slightly different model structure or they do require the use of additional explanatory variables or parameters. Apparently, this will require the use of full meteorological time series instead of climatic data, which is a very challenging task at global scale. A survey of the calibration results against different climatic zones is another challenging task that will further highlight the model advantages, as well as potential shortcomings.