A Novel SWMM Based Algorithm Application to Storm Sewer Network Design
Abstract
:1. Introduction
2. Literature Review
3. Governing Equations
3.1. Governing Equations in Hydrologic and Hydraulic Simulations
3.2. Determination of Pipe Diameter and Slope
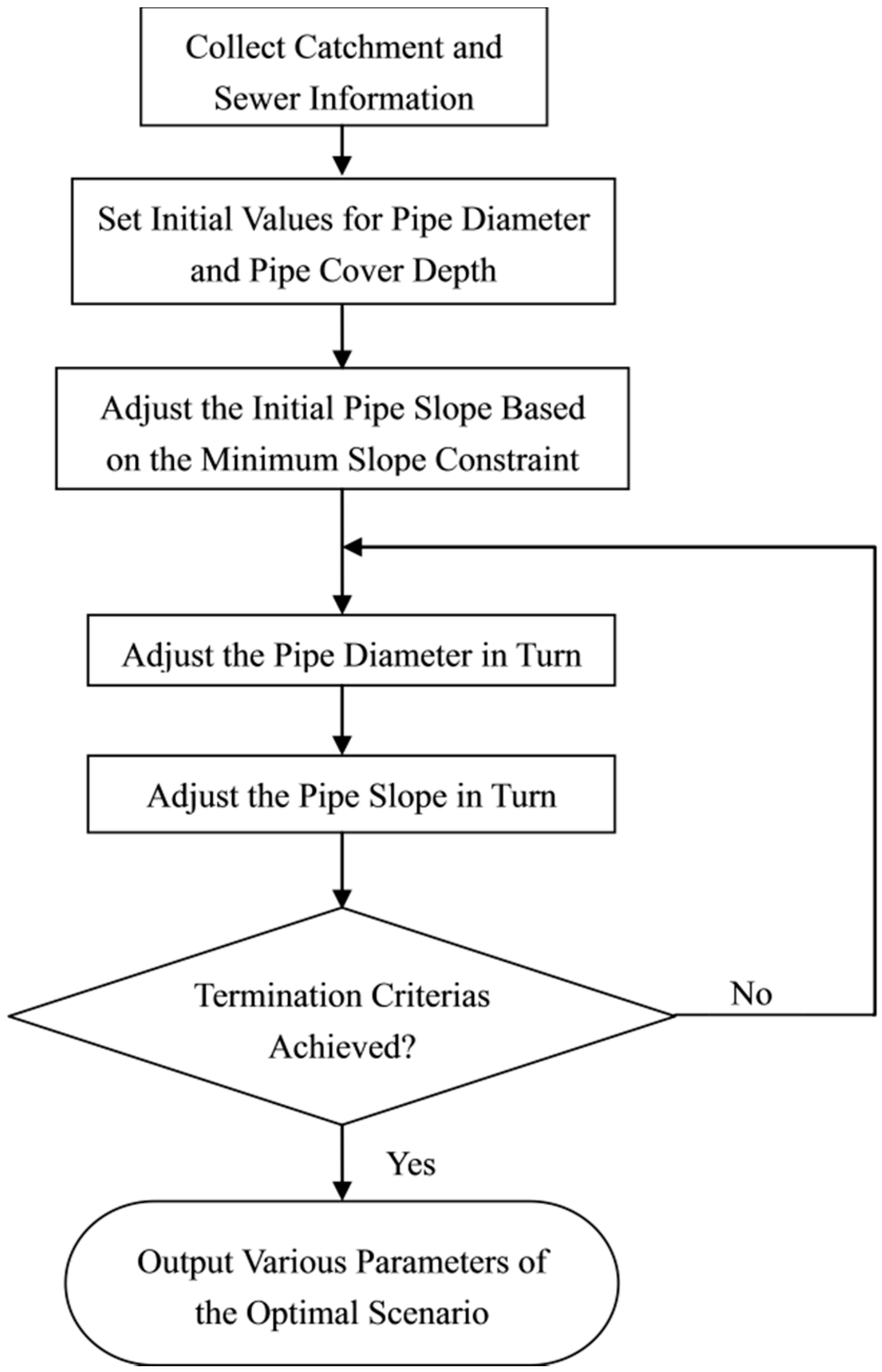
4. Model Development
- vmin < vi < vmax
- hmin < hi < hmax
- Di+1 > Di
- Hi > Hmin
4.1. Initial Value Computation
- Pipe slope that is less than the minimum slope is increased to a minimum grade and the elevation of the pipe invert at the downstream, correspondingly, is decreased. After that, if the adjusted elevation of the pipe invert is less than the elevation of the manhole invert at the downstream, the elevation of the manhole invert and outlet offset at the downstream is updated, otherwise, only the outlet offset is updated.
- After adjusting the parameters of this pipe segment, if the adjusted elevation of the pipe invert is greater than the adjacent downstream pipe invert elevation at the upstream, only the outlet offset of the pipe segment is decreased. Otherwise, the adjacent downstream pipe crown elevation at the upstream node is kept the same as the pipe at the downstream node while the inlet offset and slope of the adjacent downstream pipe segment is updated.
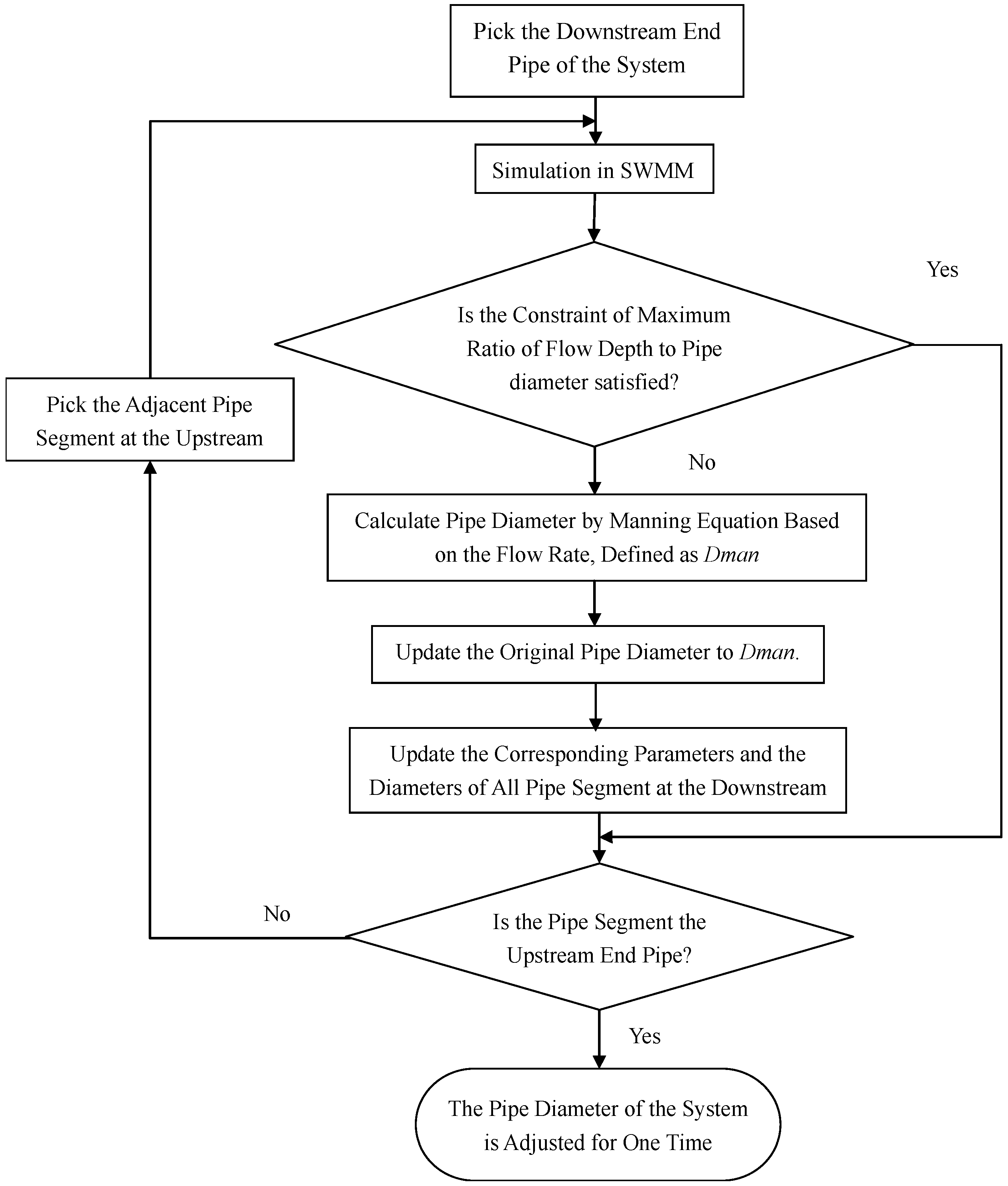
4.2. First Stage Iteration
- Based on the maximum flow rate obtained by the hydrological and hydraulic simulation, the required diameter is calculated using Manning’s equation. The calculated diameter is rounded to the upper discrete diameter available and the original pipe diameter is updated to this value.
- After adjusting the pipe diameter, if the original inlet and outlet offset is greater than the increase of the pipe diameter, the original inlet and outlet offset will be updated. The elevation of the manhole invert at the upstream and downstream is kept unchanged for the next step, otherwise, all the parameters will be updated correspondingly.
- After adjusting the parameters of this pipe segment, the inlet and outlet offset of the adjacent upstream and downstream pipe segment are updated.
- Every time after the adjustment of the pipe diameter, all the downstream pipe diameters are updated to ensure there is no decrease in sewer pipe diameter in the downstream direction.
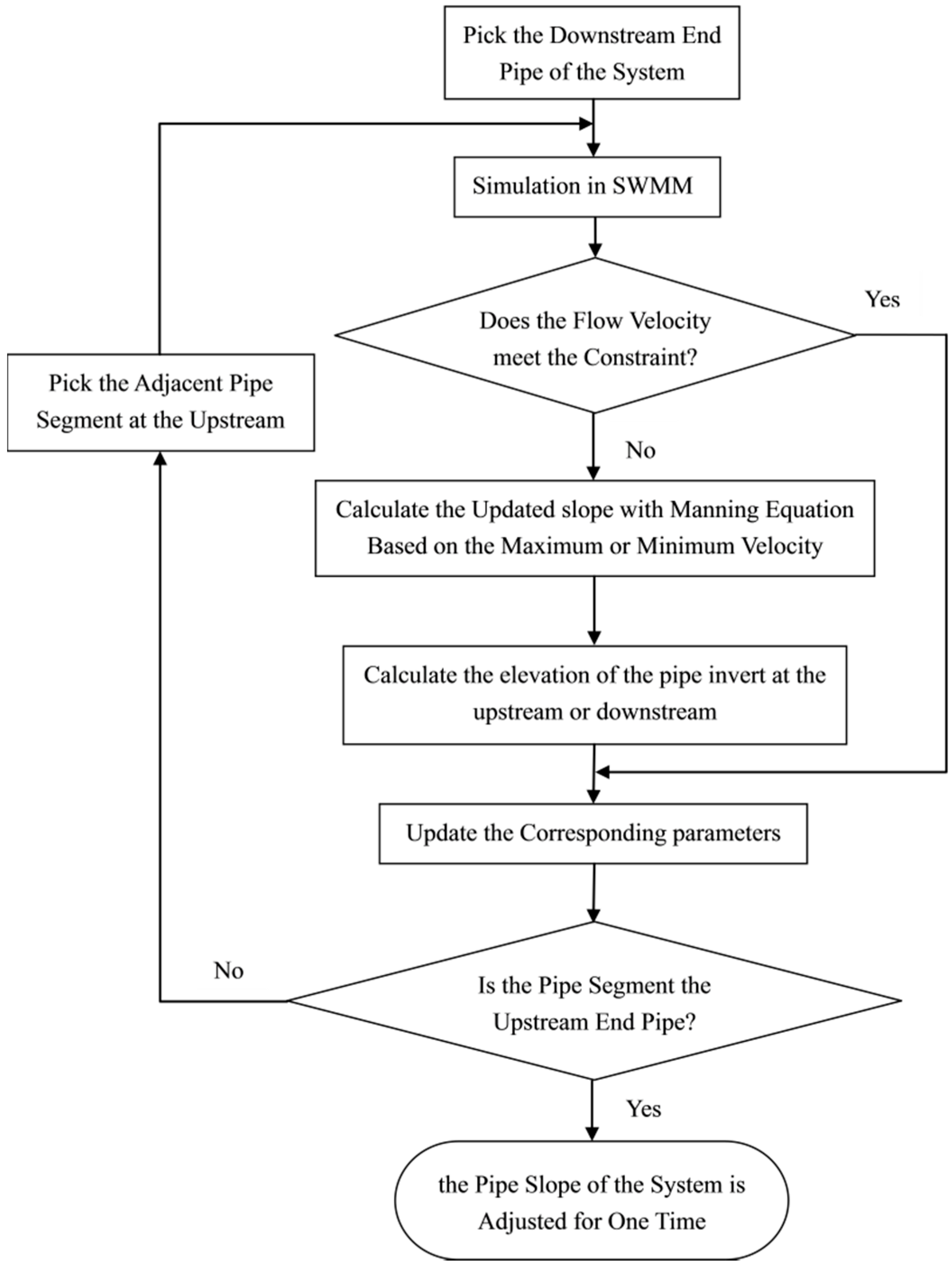
4.3. Second Stage Iteration
- If the flow velocity is greater than maximum flow velocity, the slope of the pipe is decreased to the slope calculated by Manning’s equation based on maximum flow velocity. In the meanwhile, the elevation of the pipe invert at the upstream is decreased.
- After the elevation of the pipe invert at the upstream is decreased, if the adjusted elevation of the pipe invert is greater than the elevation of the manhole invert at the upstream, the inlet offset is updated and the elevation of the manhole invert at the upstream is kept unchanged for the next step. Otherwise, both parameters need to be updated and the outlet offset of the adjacent upstream pipe segment is updated simultaneously with the slope keeps unchanged.
- If the flow velocity is less than minimum flow velocity, the slope of the pipe is increased to the slope calculated by Manning’s equation based on minimum flow velocity constraint and the elevation of the pipe invert at the downstream is decreased correspondingly.
- After the elevation of the pipe invert at the downstream is decreased, if the adjusted elevation of the pipe invert is greater than the adjacent pipe invert elevation at the downstream, only the outlet offset of the pipe segment is decreased. Otherwise, the adjacent downstream pipe crown elevation at the upstream node is kept the same as the pipe at the downstream node while the inlet offset and slope of the adjacent downstream pipe segment is updated.
5. Model Applications
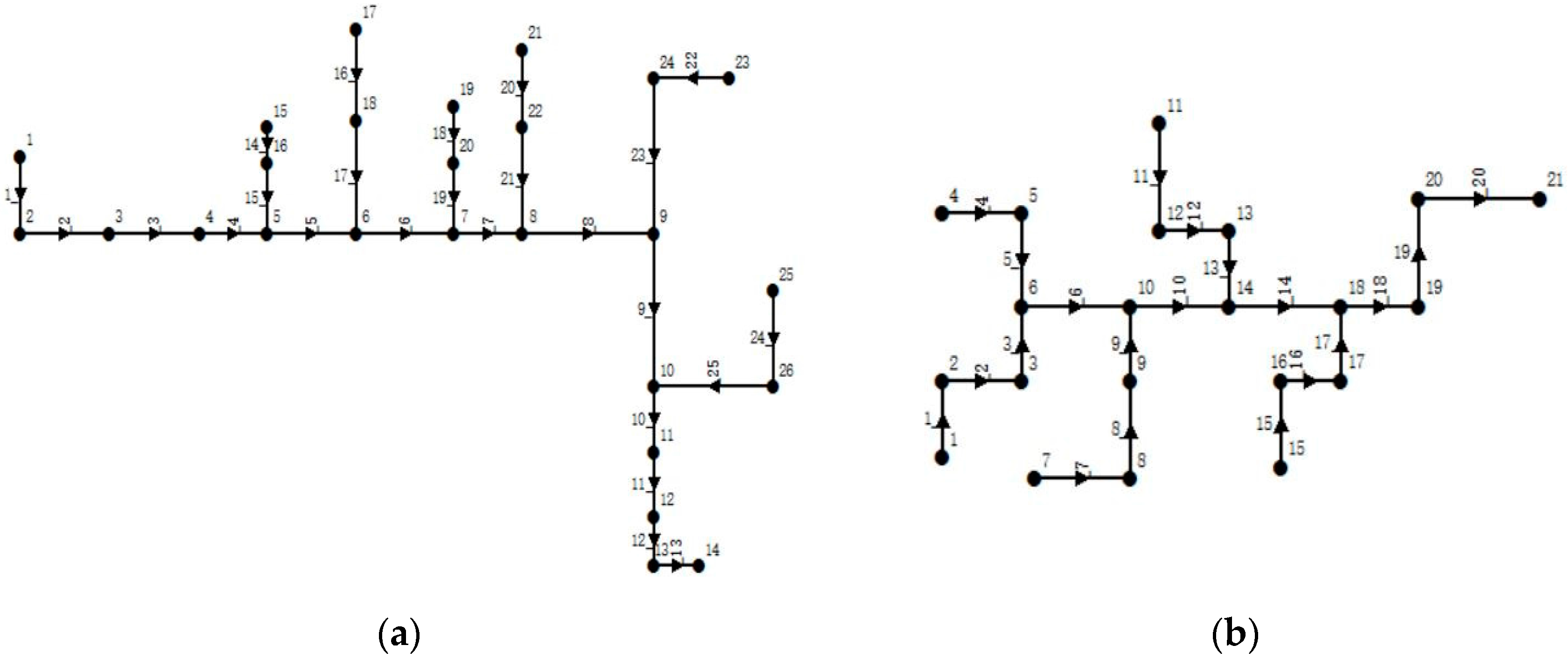
5.1. Description of Study Cases
5.2. Automated Design Procedure
- Assign value for the manhole ground elevation according to the collected catchment information.
- Assign initial value for the properties of the sewer networks, pipe diameters and minimum pipe cover depths.
- Adjust the initial pipe slopes to satisfy the minimum slope constraint.
- Determine the pipe diameter and slope calculated iteratively with two consecutive stages.
5.3. Discussion of Results
- In the conventional design procedure, flowrate calculation was carried out using Rational Method with a composite runoff coefficient. The hydraulic design was carried out based on manning equation and assuming a steady state open channel flow. The hydrologic and hydraulic processes occurring in the storm water system are greatly simplified in the conventional method. The proposed algorithm simulates a dynamic rainfall process and unsteady state flow which typically produce realistic hydrological and hydraulic results. This resulted a difference of the design discharge using the conventional process and the proposed algorithm. Hencefurther affects the designed pipe diameters and slopes.
- Except for pipe 1, the diameter of the remaining pipe segments obtained by the proposed algorithm are basically smaller than those by the conventional design method. This could be attributed to the nature of the proposed algorithm and the characteristics of the study area. The diameter of pipe 1 depends on the setting value of the initial pipe diameter. In the design process of the proposed algorithm, the pipe diameter with a minimum initial value increases gradually as the iteration progresses. The study area is steep and the pipe slope with large initial value decreases as the iteration progresses. The iteration terminates once the pipe flow velocity and depth meet the requirements. Therefore, while meeting the design requirements of the storm sewer system, a design scheme of storm sewer network with smaller diameter and pipe cover depth (i.e., a larger pipe slope) was obtained by the proposed algorithm.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kuichling, E. The relation between rainfall and the discharge of sewers in populous districts Trans. Am. Soc. Civ. Eng. 1889, 20, 1–56. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual (Version 5.1); U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2015.
- Peng, H.Q.; Liu, Y.; Wang, H.W. Urban storm water forecasting model and drainage optimization based on water environmental capacity. Environ. Earth Sci. 2016, 75, 1–11. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model Reference Manual Volume I—Hydrology (Revised); U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2016.
- Deininger, R.A. Computer aided design of waste collection and treatment systems. In Proceedings of the 2nd Annual Conference of American Water Resources, Chicago, IL, USA, 18 May 1966; pp. 247–258. [Google Scholar]
- Holland, M.E. Computer Models of Wastewater Collection Systems. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1966. [Google Scholar]
- Deininger, R.A. Systems Analysis for Water Supply and Pollution Control, Natural Resource Systems Models in Decision Making. 1970. Available online: http://scholar.google.com/scholar_lookup?title=Systems%20analysis%20for%20water%20supply%20and%20pollution%20control%2C%20natural%20resource%20systems%20models%20in%20decision%20making &author=RA.%20Deininger&publication_year=1970 (accessed on 28 September 2017).
- Dajani, J.S.; Hasit, Y. Capital cost minimization of drainage networks. J. Environ. Eng. Division 1974, 100, 325–337. [Google Scholar]
- Price, R.K. Design of storm water sewers for minimum construction cost. In Proceedings of the 1st International Conference on Urban Storm Drainage, Southampton, UK, January 1978; pp. 636–647. [Google Scholar]
- Kulkarni, V.S.; Khanna, P. Pumped wastewater collection systems optimization. J. Environ. Eng. 1985, 111, 589–601. [Google Scholar] [CrossRef]
- Miles, S.W.; Heaney, J.P. Better than optimal method for designing drainage systems. J. Water Resour. Plan. Manag. 1988, 114, 477–499. [Google Scholar] [CrossRef]
- Mays, L.W.; Wenzel, H.G. Optimal design of multi-level branching sewer systems. Water Resour. Res. 1976, 12, 913–917. [Google Scholar] [CrossRef]
- Walters, G.A.; Lohbeck, T. Optimal layout of tree networks using genetic algorithms. Eng. Optim. 1993, 22, 27–48. [Google Scholar] [CrossRef]
- Heaney, J.P.; Pitt, R.; Field, R. Innovative Urban Wet-Weather Flow Management Systems; EPA/600/R-99/029; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Afshar, M.H. Application of a genetic algorithm to storm sewer network optimization. Sci. Iran. 2006, 13, 234–244. [Google Scholar]
- Pan, T.C.; Kao, J.J. GA-QP model to optimize sewer system design. J. Environ. Eng. 2009, 135, 17–24. [Google Scholar] [CrossRef]
- Haghighi, A.; Bakhshipour, A.E. Optimization of sewer networks using an adaptive genetic algorithm. Water Resour. Manag. 2012, 26, 3441–3456. [Google Scholar] [CrossRef]
- Guo, Y.; Walters, G.A.; Khu, S.T.; Keedwell, E. A novel cellular automata based approach to storm sewer design. Eng. Optim. 2007, 39, 345–364. [Google Scholar] [CrossRef]
- Afshar, M.H.; Shahidi, M.; Rohani, M. Application of cellular automata to sewer network optimization problems. Sci. Iran. 2011, 18, 304–312. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rohani, M. Optimal design of sewer networks using cellular automata-based hybrid methods: Discrete and continuous approaches. Eng. Optim. 2012, 44, 1–22. [Google Scholar] [CrossRef]
- Afshar, M.H.; Zaheri, M.M.; Kim, J.H. Improving the efficiency of Cellular Automata for sewer network design optimization problems using Adaptive Refinement. Proc. Eng. 2016, 154, 1439–1447. [Google Scholar] [CrossRef]
- Afshar, M.H. Improving the efficiency of ant algorithms using adaptive refinement: Application to stormwater network design. Adv. Water Resour. 2006, 29, 1371–1382. [Google Scholar] [CrossRef]
- Afshar, M.H.; Moeini, R. Partially and fully constrained ant algorithms for the optimal solution of large scale reservoir operation problems. J. Water Resour. Manag. 2008, 22, 1835–1857. [Google Scholar] [CrossRef]
- Afshar, M.H. A parameter free continuous Ant colony optimization algorithm for the optimal design of storm sewer networks. Adv. Eng. Softw. 2010, 41, 188–195. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Constrained Ant Colony Optimisation Algorithm for the layout and size optimisation of sanitary sewer networks. Urban Water J. 2012, 10, 1–20. [Google Scholar] [CrossRef]
- Afshar, M.H. Rebirthing particle swarm optimization algorithm: Application to Storm Sewer Network design. Can. J. Civ. Eng. 2008, 35, 1120–1127. [Google Scholar] [CrossRef]
- Karovic, O.; Mays, L.W. Sewer system design using simulated annealing in excel. Water Resour. Manag. 2014, 28, 4551–4565. [Google Scholar] [CrossRef]
- Steele, J.C.; Mahoney, K.; Karovic, O. Heuristic Optimization Model for the Optimal Layout and Pipe Design of Sewer Systems. Water Resour. Manag. 2016, 30, 1605–1620. [Google Scholar] [CrossRef]
- Walters, G.A. A review of pipe network optimization techniques. In Pipeline Systems, Fluid Mechanics and Its Applications; Coulbeck, B., Evans, E., Eds.; Springer Science & Business Media: Dordrecht, The Netherlands, 1992; pp. 3–13. [Google Scholar]
- Liong, S.Y.; Chan, W.T.; ShreeRam, J. Peak-flow forecasting with genetic algorithm and SWMM. J. Hydraul. Eng. 1995, 121, 613–617. [Google Scholar] [CrossRef]
- Krebs, G.; Kokkonen, T.; Valtanen, M.; Koivusalo, H.; Setälä, H. A high resolution application of a stormwater management model (SWMM) using genetic parameter optimization. Urban Water J. 2013, 10, 394–410. [Google Scholar] [CrossRef]
- Martinez-Solano, F.J.; Iglesias-Rey, P.L.; Saldarriaga, J.G.; Vallejo, D. Creation of an SWMM Toolkit for Its Application in Urban Drainage Networks Optimization. Water 2016, 8, 259. [Google Scholar] [CrossRef]
- Wang, K.H.; Altunkaynak, A. Comparative case study of rainfall-runoff modeling between SWMM and fuzzy logic approach. J. Hydrol. Eng. 2011, 17, 283–291. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]

| Link | Ground Elevation (m) | Length (m) | |
|---|---|---|---|
| Upstream | Downstream | ||
| 1 | 341.95 | 335.02 | 108.50 |
| 2 | 335.02 | 325.11 | 145.20 |
| 3 | 325.11 | 315.89 | 145.50 |
| 4 | 315.89 | 308.10 | 109.10 |
| 5 | 308.10 | 298.14 | 145.20 |
| 6 | 298.14 | 297.90 | 158.90 |
| 7 | 297.90 | 278.10 | 110.90 |
| 8 | 278.10 | 264.31 | 212.40 |
| 9 | 264.31 | 257.90 | 217.60 |
| 10 | 257.90 | 251.50 | 92.00 |
| 11 | 251.50 | 245.00 | 91.30 |
| 12 | 245.00 | 240.50 | 70.20 |
| 13 | 240.50 | 235.00 | 30.30 |
| Link | Ground Elevation (m) | Length (m) | Design Discharge (m3/s) | |
|---|---|---|---|---|
| Upstream | Downstream | |||
| 1 | 152.40 | 150.88 | 106.68 | 0.11 |
| 2 | 150.88 | 148.49 | 121.92 | 0.20 |
| 3 | 148.49 | 146.30 | 106.68 | 0.25 |
| 4 | 149.35 | 147.83 | 121.92 | 0.11 |
| 5 | 147.83 | 146.30 | 131.08 | 0.23 |
| 6 | 146.30 | 143.26 | 167.68 | 0.62 |
| 7 | 149.35 | 147.83 | 147.64 | 0.23 |
| 8 | 147.83 | 147.83 | 137.16 | 0.34 |
| 9 | 144.78 | 143.26 | 106.68 | 0.45 |
| 10 | 143.26 | 141.73 | 152.40 | 1.25 |
| 11 | 147.83 | 144.78 | 152.40 | 0.25 |
| 12 | 144.78 | 143.26 | 106.68 | 0.45 |
| 13 | 143.26 | 141.73 | 106.68 | 0.57 |
| 14 | 141.73 | 138.65 | 172.21 | 2.01 |
| 15 | 142.65 | 141.43 | 121.92 | 0.11 |
| 16 | 141.43 | 140.21 | 91.44 | 0.17 |
| 17 | 140.21 | 138.65 | 105.23 | 0.25 |
| 18 | 138.65 | 137.46 | 121.92 | 2.46 |
| 19 | 137.46 | 136.55 | 152.40 | 2.52 |
| 20 | 136.55 | 135.64 | 186.54 | 2.66 |
| Link | Proposed Algorithm | Conventional Method | ||||||
|---|---|---|---|---|---|---|---|---|
| Crown Elevations (m) | Slope (‰) | Diameter (m) | Crown Elevation (m) | Slope (‰) | Diameter (m) | |||
| Upstream | Downstream | Upstream | Downstream | |||||
| 1 | 339.23 | 333.52 | 52.60 | 0.45 | 338.9 | 333.52 | 41.55 | 0.30 |
| 2 | 329.79 | 323.61 | 42.59 | 0.45 | 329.23 | 323.61 | 38.71 | 0.45 |
| 3 | 316.68 | 314.39 | 15.74 | 0.70 | 317.12 | 314.39 | 18.79 | 0.60 |
| 4 | 308.30 | 306.60 | 15.58 | 0.70 | 307.89 | 306.6 | 11.77 | 0.70 |
| 5 | 299.36 | 296.64 | 18.70 | 0.70 | 298.12 | 296.64 | 10.23 | 0.90 |
| 6 | 296.58 | 293.40 | 20.01 | 0.80 | 296.05 | 294.19 | 11.71 | 1.00 |
| 7 | 278.62 | 276.60 | 18.22 | 0.80 | 277.4 | 276.6 | 7.17 | 1.20 |
| 8 | 267.09 | 262.81 | 20.16 | 0.90 | 264.25 | 262.81 | 6.82 | 1.30 |
| 9 | 258.75 | 256.40 | 10.78 | 1.20 | 257.73 | 256.4 | 6.08 | 1.40 |
| 10 | 251.31 | 250.00 | 14.25 | 1.20 | 250.47 | 250 | 5.12 | 1.40 |
| 11 | 244.60 | 243.50 | 12.03 | 1.25 | 243.99 | 243.5 | 5.39 | 1.60 |
| 12 | 239.76 | 239.00 | 10.85 | 1.60 | 239.4 | 239 | 5.65 | 1.70 |
| 13 | 235.02 | 233.50 | 50.00 | 1.70 | 233.64 | 233.5 | 4.79 | 1.70 |
| Link | Proposed Algorithm | Adaptive CA | ||||
|---|---|---|---|---|---|---|
| Diameter (m) | Crown Elevations (m) | Diameter (m) | Crown Elevations (m) | |||
| Upstream | Downstream | Upstream | Downstream | |||
| 1 | 0.30 | 149.96 | 148.88 | 0.30 | 149.96 | 148.44 |
| 2 | 0.45 | 148.88 | 146.39 | 0.40 | 148.44 | 146.00 |
| 3 | 0.45 | 146.39 | 146.03 | 0.40 | 146.00 | 143.87 |
| 4 | 0.30 | 146.91 | 145.71 | 0.30 | 146.91 | 145.37 |
| 5 | 0.45 | 145.71 | 144.23 | 0.45 | 145.39 | 143.87 |
| 6 | 0.80 | 144.23 | 142.80 | 0.60 | 143.87 | 140.82 |
| 7 | 0.30 | 146.91 | 145.24 | 0.45 | 146.91 | 145.39 |
| 8 | 0.45 | 145.24 | 142.28 | 0.45 | 145.39 | 142.34 |
| 9 | 0.60 | 142.28 | 140.79 | 0.50 | 142.34 | 140.82 |
| 10 | 0.80 | 140.79 | 138.91 | 0.70 | 140.82 | 139.06 |
| 11 | 0.45 | 145.39 | 142.74 | 0.40 | 145.39 | 142.34 |
| 12 | 0.60 | 142.74 | 141.15 | 0.50 | 142.34 | 140.82 |
| 13 | 0.60 | 141.15 | 139.35 | 0.60 | 140.82 | 139.29 |
| 14 | 0.90 | 138.26 | 136.68 | 0.90 | 138.40 | 136.25 |
| 15 | 0.45 | 140.21 | 138.53 | 0.30 | 140.21 | 138.67 |
| 16 | 0.45 | 138.53 | 138.21 | 0.40 | 138.74 | 137.77 |
| 17 | 0.60 | 138.21 | 137.29 | 0.45 | 137.77 | 136.25 |
| 18 | 1.00 | 137.29 | 134.58 | 1.00 | 136.25 | 135.03 |
| 19 | 1.00 | 134.58 | 133.55 | 1.00 | 135.03 | 133.83 |
| 20 | 1.20 | 133.55 | 129.24 | 1.00 | 133.83 | 132.15 |
| Optmization Method | Case 1 | Case 2 | ||
|---|---|---|---|---|
| Total Cost ($) | Number of Iterations | Total Cost ($) | Number of Iterations | |
| Conventional Algorithm | 1,057,551 | - | - | - |
| Adaptive CA | - | - | 938,836 | 174–192 |
| Proposed Algorithm | 961,703 | - | 952,415 | 9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Z.; Zhang, X.; Li, S.; Deng, S.; Chai, H. A Novel SWMM Based Algorithm Application to Storm Sewer Network Design. Water 2017, 9, 747. https://doi.org/10.3390/w9100747
Shao Z, Zhang X, Li S, Deng S, Chai H. A Novel SWMM Based Algorithm Application to Storm Sewer Network Design. Water. 2017; 9(10):747. https://doi.org/10.3390/w9100747
Chicago/Turabian StyleShao, Zhiyu, Xiaoyuan Zhang, Shuang Li, Shihu Deng, and Hongxiang Chai. 2017. "A Novel SWMM Based Algorithm Application to Storm Sewer Network Design" Water 9, no. 10: 747. https://doi.org/10.3390/w9100747
APA StyleShao, Z., Zhang, X., Li, S., Deng, S., & Chai, H. (2017). A Novel SWMM Based Algorithm Application to Storm Sewer Network Design. Water, 9(10), 747. https://doi.org/10.3390/w9100747






