A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China
Abstract
:1. Introduction
2. Study Area, Data and Method
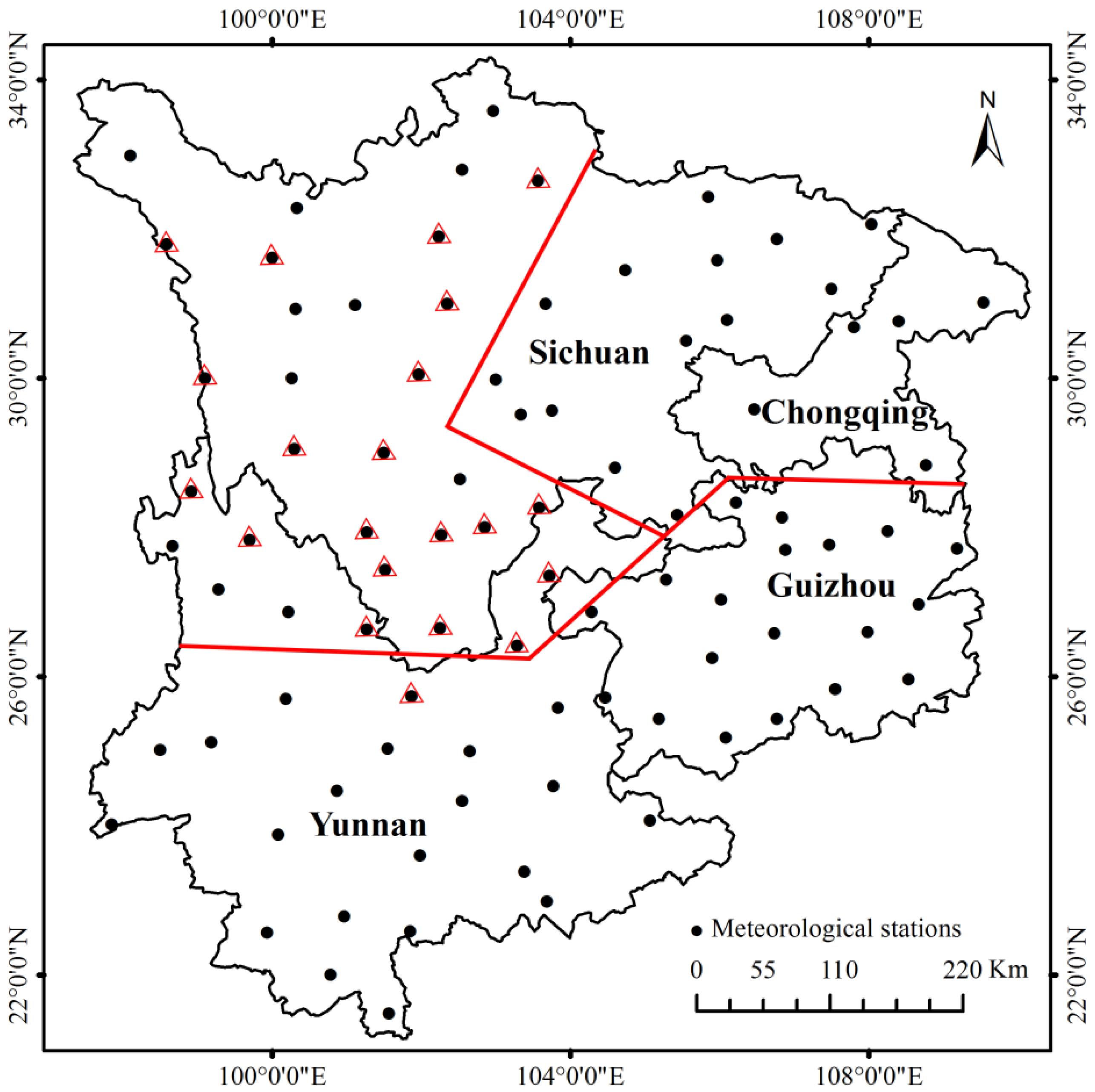
2.1. Study Area
2.2. Data Sources
2.3. PET Evaluation Methods
2.3.1. Daily Based methods
2.3.2. Monthly Based Methods
2.4 Statistical Analysis
3. Results
3.1. PET Estimated by FAO–PM Method in the Four Sub-Regions
3.2. Sichuan Basin
3.3. Yun-Gui Plateau
3.4. The Eastern Margin of the Tibetan Plateau
3.5. Arid River Valley Region
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Almorox, J.Y.; Hontoria, C. Global solar radiation estimation using sunshine duration in Spain. Energy Convers. Manag. 2004, 45, 1529–1535. [Google Scholar] [CrossRef]
- Khoob, A.R. Comparative study of Hargreaves’s and artificial neural network’s methodologies in estimating reference evapotranspiration in a semiarid environment. Irrig. Sci. 2008, 26, 253–259. [Google Scholar] [CrossRef]
- Singh, R.K.; Pawar, P.S. Comparative study of reference crop evapotranspiration (ETO) by different energy based method with FAO 56 Penman-Monteith method at New Delhi, India. Eng. Sci. Technol. 2011, 3, 7861–7868. [Google Scholar]
- Amatya, D.M.; Harrison, C.A.; Trettin, C.C. Comparison of potential evapotranspiration (PET) using three methods for a grass reference and a natural forest in Coastal Plain of South Carolina. Proceeding of the 2014 South Carolina Water Resources Conference, Columbia, SC, USA, 14–16 October 2014; Available online: http://tigerprints.clemson.edu/cgi/viewcontent.cgi?article=1298&context=scwrc (accessed on 25 September 2017).
- Bandyopadhyay, A.; Bhadra, A.; Swarnakar, R.K.; Raghuwanshi, N.S.; Singh, R. Estimation of reference evapotranspiration using a user-friendly decision support system: DSS_ET. Agric. For. Meteorol. 2012, 154–155, 19–29. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Li, F.; Zhang, Y.; Tong, L. Evapotranspiration measurement and estimation using modified Priestley–Taylor model in an irrigated maize field with mulching. Agric. For. Meteorol. 2013, 168, 140–148. [Google Scholar] [CrossRef]
- Allen, R.G.; Masahiro, T.; Ricardo, T. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Wagle, P.; Bhattarai, N.; Gowda, P.H.; Kakani, V.G. Performance of five surface energy balance models for estimating daily evapotranspiration in high biomass sorghum. ISPRS J. Photogramm. Remote Sens. 2017, 128, 192–203. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelinse for Computing Crop Water Requirements. Fao Irrigation and Drainage Paper 56; FAO-Food and Agriculture Organization of the United Nations Rome: Rome, Italy, 1998. [Google Scholar]
- Lu, J.; Sun, G.; Mcnulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Liu, X.; Lin, E. Performance of the Priestley–Taylor equation in the semiarid climate of North China. Agric. Water Manag. 2005, 71, 1–17. [Google Scholar]
- Chen, D.; Gao, G.; Xu, C.; Guo, J.; Ren, G. Comparison of the Thornthwaite method and pan data with the standard Penman–Monteith estimates of reference evapotranspiration in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman–Monteith formula. J. Hydrol. 2015, 524, 708–717. [Google Scholar] [CrossRef]
- McMahon, T.A.; Finlayson, B.L.; Peel, M.C. Historical developments of models for estimating evaporation using standard meteorological data. Wiley Interdiscip. Rev. Water 2016, 3, 788–818. [Google Scholar] [CrossRef]
- Allen, R.G.; Clemmens, A.J.; Burt, C.M.; Solomon, K.; O’Halloran, T. Prediction accuracy for projectwide evapotranspiration using crop coefficients and reference evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 24–36. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; et al. A recommendation on standardized surface resistance for hourly calculation of reference ETO by the FAO 56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.Y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Al-Ghobari, H.M. Estimation of reference evapotranspiration for southern region of Saudi Arabia. Irri Sci. 2000, 19, 81–86. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Stricker, J.N.M. Evaporation of grass under non-restricted soil moisture conditions. Hydrol. Sci. J. 2000, 45, 391–406. [Google Scholar] [CrossRef]
- Jacobs, J.M.; Satti, S.R. Evaluation of Reference Evapotranspiration Methodologies and Afsirs Crop Water Use Simulation Model: Final Report; University of Florida: Gainesville, FL, USA, 2001. [Google Scholar]
- Garcia, M.; Raes, D.; Allen, R.; Herbas, C. Dynamics of reference evapotranspiration in the Bolivian highlands (Altiplano). Agric. For. Meteorol. 2004, 125, 67–82. [Google Scholar] [CrossRef]
- Xu, C.; Chen, D. Comparison of seven models for estimation of evapotranspiration and groundwater recharge using lysimeter measurement data in Germany. Hydrol Process. 2005, 19, 3717–3734. [Google Scholar] [CrossRef]
- Xu, C.; Gong, L.; Jiang, T.; Chen, D.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves–Samani and FAO-PM temperature methods for a wide range of climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–89. [Google Scholar] [CrossRef]
- Abtew, W. Evapotranspiration measurements and modeling for three wetland systems in south Florida. J. Am. Water Resour. Assoc. 1996, 32, 465–473. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Brouwer, C.; Heibloem, M. Irrigation Water Management: Irrigation Water Needs: Training Manual No.3; FAO Land and Water Development Division: Rome, Italy, 1986. [Google Scholar]
- Hamon, W.R. Computation of direct runoff amounts from storm rainfall. Int. Assoc. Sci. Hydrol. Pub. 1963, 63, 52–62. [Google Scholar]
- Linacre, E.T. A simple formula for estimating evaporation rates in various climates, using temperature data alone. J. Agric. Meteorol. 1977, 18, 409–424. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Makkink, G.F. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Li, Y.; Xu, H.; Liu, D. Features of the extremely severe drought in the east of southwest China and anomalies of atmospheric circulation in summer 2006. Acta Meteorol. Sin. 2011, 25, 176–187. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, F.; Zhao, J.; Qi, L.; Ren, H. The possible influence of a nonconventional El Niño on the severe autumn drought of 2009 in Southwest China. J. Clim. 2013, 26, 8392–8405. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, J.; Li, J.; Wang, K.; Lei, L.; Guo, H. The 2010 spring drought reduced primary productivity in southwestern China. Environ. Res. lett. 2012, 7, 045706. [Google Scholar] [CrossRef]
- Lv, L. Geography of China; Science Press: Beijing, China, 2012; Available online: http://202.115.182.3:8080/opac/book/a2c2df0859a38b1e0b5544ac7a617e8a (accessed on 22 September 2017). (In Chinese)
- Zhao, J.; Chen, C. Geography of China; Higher Education Press: Beijing, China, 1999; Available online: http://book.ixueshu.com/book/3d20d9eb5a0768e2.html (accessed on 22 September 2017). (In Chinese)
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- National Science & Technology Infrastructure. Available online: http://data.cma.cn/ (accessed on 8 May 2014). (In Chinese).
- Li, Z.; He, Y.; An, W.; Song, L.; Zhang, W.; Catto, N.; Wang, Y.; Wang, S.; Liu, H.; Cao, W.; Theakstone, W.H.; Wang, S.; Du, J. Climate and glacier change in southwestern China during the past several decades. Environ. Res. Lett. 2011, 6, 045404. [Google Scholar] [CrossRef]
- Pang, X.; Bao, W.; Wu, N. Reasons of dry valley climate characteristic and its formation reason in upstream of Mingjiang river. Resour. Environ. Yangtze Basin 2008, 17, 48–55. [Google Scholar]
- China Meteorological Administration. Classification of Meteorological Drought; China Meteorological Press: Beijing, China, 2006. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part Ι–A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Daut, I.; Irwanto, M.; Irwan, Y.M.; Gomesh, N.; Ahmad, N.S. Combination of Hargreaves method and linear regression as a new method to estimate solar radiation in Perlis, Northern Malaysia. Sol. Energy 2011, 85, 2871–2880. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Tukimat, N.N.A.; Harun, S.; Shahid, S. Comparison of different methods in estimating potential evapotranspiration at Muda Irrigation Scheme of Malaysia. J. Agric. Rural Dev. Trop. Subtrop. 2012, 113, 77–85. [Google Scholar]
- Jadhav, P.B.; Kadam, S.A.; Gorantiwar, S.D. Comparison of methods for estimating reference evapotranspiration (ETO) for Rahuri region. J. Agrometeorol. 2015, 17, 204–207. [Google Scholar]
- Wei, M.; Menzel, L. A global comparison of four potential evapotranspiration equations and their relevance to stream flow modeling in semi-arid environments. Adv. Geosci. 2008, 18, 15–23. [Google Scholar]
- Nikam, B.; Kumar, P.; Garg, V.; Thakur, P.K.; Aggarwal, S.P. Comparative evaluation of different potential evapotranspiration estimation approaches. Int. J. Res. Eng. Technol. 2014, 3, 544–552. [Google Scholar]
- Mohd, E.T.; Mazlin, M.; Muhamad, B.G.; Sharifah, M.S.A.; Osman, J.; Nor, A.A.A. Water resources study and modeling at north Kedah: A case of Kubang Pasu and Padang Terap water supply schemes. Res. J. Earth Sci. 2009, 1, 35–42. [Google Scholar]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Base, F.B. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Sahi̇n, S.; Ci̇gi̇zoglu, H.K. Homogeneity analysis of Turkish meteorological data set. Hydrol. Process. 2010, 24, 981–992. [Google Scholar] [CrossRef]
- Chu, R.; Li, M.; Shen, S.; Islam, A.R.M.T.; Cao, W.; Tao, S.; Gao, P. Changes in reference evapotranspiration and its contributing factors in Jiangsu, a major economic and agricultural province of eastern China. Water 2017, 9, 486. [Google Scholar] [CrossRef]
| Regions | PET (mm) | ||||
|---|---|---|---|---|---|
| Annual | Spring | Summer | Autumn | Winter | |
| Sichuan basin | 2860.2 | 917.6 | 967.4 | 495.9 | 479.3 |
| Yun-Gui plateau | 3374.6 | 926.3 | 947.7 | 754.8 | 745.8 |
| The eastern margin of the Tibetan Plateau | 2993.4 | 956.1 | 864.4 | 569.0 | 603.9 |
| Arid river valley region | 3347.5 | 991.7 | 978.0 | 711.5 | 664.2 |
| Regions | Time | HS | Ham | PT | Lin | Mak | Abt | Tho | BC |
|---|---|---|---|---|---|---|---|---|---|
| SCB | Annual | −18.79 | 44.12 | −28.62 | 55.28 | 15.46 | −10.97 | 72.29 | 44.64 |
| Spring | −21.63 | 42.72 | −29.26 | 59.18 | 15.22 | −7.55 | 73.37 | 50.20 | |
| Summer | −18.09 | 33.20 | −28.46 | 57.05 | 15.97 | −0.68 | 67.02 | 48.76 | |
| Autumn | −15.54 | 53.94 | −27.74 | 46.85 | 15.52 | −19.46 | 70.87 | 32.70 | |
| Winter | −18.11 | 58.70 | −28.62 | 52.94 | 14.84 | −29.54 | 82.33 | 38.05 | |
| YGP | Annual | −15.62 | 40.28 | −29.46 | 58.31 | 13.64 | −11.04 | 76.65 | 53.22 |
| Spring | −18.48 | 42.28 | −29.66 | 60.03 | 14.02 | −9.28 | 77.31 | 54.81 | |
| Summer | −16.75 | 40.47 | −29.65 | 59.27 | 14.46 | −49.41 | 72.84 | 52.97 | |
| Autumn | −12.66 | 38.60 | −29.31 | 56.52 | 13.19 | −13.61 | 75.73 | 50.97 | |
| Winter | −13.67 | 39.31 | −29.10 | 56.81 | 12.58 | −18.46 | 81.72 | 53.93 | |
| ETP | Annual | −7.16 | 53.11 | −33.14 | 48.62 | 9.46 | −34.21 | 83.61 | 61.64 |
| Spring | −10.51 | 55.20 | −34.37 | 54.97 | 10.01 | −23.56 | 82.56 | 64.06 | |
| Summer | −13.30 | 54.34 | −31.86 | 53.40 | 12.32 | −18.57 | 79.02 | 59.24 | |
| Autumn | 0.37 | 49.35 | −30.26 | 40.57 | 9.88 | −47.73 | 83.83 | 60.01 | |
| Winter | 2.87 | 52.88 | −34.62 | 40.38 | 6.44 | −57.24 | 92.18 | 64.12 | |
| ARV | Annual | −9.14 | 45.09 | −29.46 | 48.95 | 11.96 | −20.60 | 81.90 | 59.99 |
| Spring | −11.40 | 44.97 | −30.16 | 52.44 | 11.70 | −18.00 | 83.05 | 63.48 | |
| Summer | −12.98 | 46.35 | −29.86 | 53.16 | 13.39 | −9.74 | 77.64 | 58.59 | |
| Autumn | −5.50 | 44.66 | −29.07 | 44.90 | 11.96 | −23.80 | 80.64 | 56.63 | |
| Winter | −3.44 | 44.13 | −28.12 | 41.71 | 10.70 | −36.50 | 87.90 | 60.65 |
| Time Scales | Equations | HS | Ham | PT | Lin | Mak | Abt | Tho | BC |
|---|---|---|---|---|---|---|---|---|---|
| Year | NSE | −3.578 | −21.338 | −8.363 | −34.177 | −1.857 | −1.040 | −58.724 | −22.051 |
| Re | 0.188 | −0.441 | 0.286 | −0.553 | −0.155 | 0.110 | −0.723 | −0.446 | |
| NRMSE | 0.201 | 0.444 | 0.288 | 0.557 | 0.159 | 0.134 | 0.726 | 0.451 | |
| Spring | NSE | −0.068 | −2.786 | −0.788 | −0.644 | 0.477 | 0.664 | −10.163 | −4.505 |
| Re | 0.216 | −0.427 | 0.293 | −0.592 | −0.152 | 0.075 | −0.734 | −0.502 | |
| NRMSE | 0.230 | 0.434 | 0.298 | 0.608 | 0.161 | 0.129 | 0.745 | 0.523 | |
| Summer | NSE | 0.560 | −0.304 | 0.039 | −3.030 | 0.691 | 0.937 | −4.290 | −2.063 |
| Re | 0.181 | −0.332 | 0.285 | −0.571 | −0.160 | 0.007 | −0.670 | −0.488 | |
| NRMSE | 0.202 | 0.348 | 0.299 | 0.613 | 0.170 | 0.076 | 0.702 | 0.534 | |
| Autumn | NSE | 0.552 | −3.148 | −0.162 | −2.361 | 0.630 | 0.295 | −6.142 | −0.788 |
| Re | 0.155 | −0.539 | 0.277 | −0.469 | -0.155 | 0.195 | −0.709 | −0.327 | |
| NRMSE | 0.181 | 0.550 | 0.291 | 0.495 | 0.164 | 0.227 | 0.722 | 0.361 | |
| Winter | NSE | 0.276 | −0.450 | 0.617 | −0.470 | 0.886 | 0.611 | −2.097 | −0.016 |
| Re | 0.181 | −0.587 | 0.286 | −0.529 | −0.148 | 0.295 | −0.823 | −0.381 | |
| NRMSE | 0.270 | 0.618 | 0.318 | 0.623 | 0.173 | 0.320 | 0.904 | 0.518 |
| Time Scales | Equations | HS | Ham | PT | Lin | Mak | Abt | Tho | BC |
|---|---|---|---|---|---|---|---|---|---|
| Annual | NSE | −0.316 | −6.200 | −2.861 | −14.326 | 0.138 | 0.334 | −25.391 | −12.099 |
| Re | 0.156 | −0.403 | 0.295 | −0.583 | −0.136 | 0.110 | −0.766 | −0.532 | |
| NRMSE | 0.174 | 0.406 | 0.297 | 0.592 | 0.140 | 0.123 | 0.777 | 0.548 | |
| Spring | NSE | 0.544 | −0.861 | 0.068 | −2.962 | 0.223 | 0.845 | −5.295 | −2.459 |
| Re | 0.185 | −0.423 | 0.297 | −0.600 | −0.140 | 0.093 | −0.773 | −0.548 | |
| NRMSE | 0.217 | 0.439 | 0.311 | 0.641 | 0.152 | 0.127 | 0.808 | 0.599 | |
| Summer | NSE | 0.116 | −3.219 | −1.242 | −8.108 | 0.432 | 0.805 | −12.520 | −6.432 |
| Re | 0.168 | −0.405 | 0.168 | −0.405 | 0.168 | −0.405 | 0.168 | −0.405 | |
| NRMSE | 0.190 | 0.415 | 0.302 | 0.609 | 0.152 | 0.089 | 0.742 | 0.550 | |
| Autumn | NSE | 0.667 | −1.061 | −0.203 | −3.633 | 0.735 | 0.585 | −6.824 | −2.813 |
| Re | 0.127 | −0.386 | 0.293 | −0.565 | −0.132 | 0.136 | −0.757 | −0.510 | |
| NRMSE | 0.161 | 0.400 | 0.306 | 0.600 | 0.144 | 0.180 | 0.780 | 0.545 | |
| Winter | NSE | 0.803 | −0.012 | 0.410 | −1.327 | 0.886 | 0.761 | −3.604 | −1.333 |
| Re | 0.137 | −0.393 | 0.291 | −0.568 | −0.126 | 0.185 | −0.817 | −0.539 | |
| NRMSE | 0.182 | 0.413 | 0.315 | 0.626 | 0.138 | 0.201 | 0.880 | 0.627 |
| Time Scales | Equations | HS | Ham | PT | Lin | Mak | Abt | Tho | BC |
|---|---|---|---|---|---|---|---|---|---|
| Annual | NSE | −0.454 | −14.142 | −4.988 | −12.064 | 0.238 | −6.409 | −36.528 | −19.630 |
| RE | 0.072 | −0.531 | 0.331 | −0.846 | −0.095 | 0.342 | −0.836 | −0.616 | |
| NRMSE | 0.166 | 0.536 | 0.337 | 0.498 | 0.120 | 0.375 | 0.844 | 0.626 | |
| Spring | NSE | −0.952 | −22.931 | −8.559 | −23.089 | 0.049 | −3.836 | −52.481 | −31.627 |
| RE | 0.105 | −0.552 | 0.344 | −0.550 | −0.100 | 0.236 | −0.826 | −0.641 | |
| NRMSE | 0.159 | 0.556 | 0.352 | 0.558 | 0.111 | 0.250 | 0.832 | 0.650 | |
| Summer | NSE | 0.351 | −3.006 | −0.356 | −3.156 | 0.747 | 0.240 | −7.347 | −3.764 |
| RE | 0.133 | −0.543 | 0.319 | −0.534 | −0.123 | 0.186 | −0.790 | −0.592 | |
| NRMSE | 0.227 | 0.563 | 0.328 | 0.574 | 0.142 | 0.245 | 0.813 | 0.614 | |
| Autumn | NSE | 0.665 | −1.228 | 0.141 | −0.912 | 0.849 | −1.485 | −5.319 | −2.283 |
| RE | −0.004 | −0.493 | 0.303 | −0.406 | −0.099 | 0.477 | −0.838 | −0.600 | |
| NRMSE | 0.201 | 0.518 | 0.322 | 0.480 | 0.135 | 0.547 | 0.872 | 0.629 | |
| Winter | NSE | 0.738 | −4.575 | −1.552 | −2.779 | 0.860 | −5.303 | −14.556 | −6.944 |
| RE | −0.029 | −0.529 | 0.346 | −0.404 | −0.064 | 0.572 | −0.922 | −0.641 | |
| NRMSE | 0.123 | 0.565 | 0.383 | 0.466 | 0.090 | 0.601 | 0.945 | 0.675 |
| Time Scales | Equations | HS | Ham | PT | Lin | Mak | Abt | Tho | BC |
|---|---|---|---|---|---|---|---|---|---|
| Annual | NSE | 0.433 | −7.018 | −2.389 | −8.634 | 0.344 | −0.992 | −25.358 | −13.328 |
| RE | 0.091 | −0.451 | 0.295 | −0.489 | −0.120 | 0.206 | −0.819 | −0.600 | |
| NRMSE | 0.121 | 0.457 | 0.297 | 0.501 | 0.131 | 0.228 | 0.828 | 0.611 | |
| Spring | NSE | 0.449 | −4.225 | −1.261 | −5.955 | 0.600 | −0.046 | −6.109 | −9.221 |
| RE | 0.114 | −0.450 | 0.302 | −0.524 | −0.117 | 0.180 | −0.831 | −0.635 | |
| NRMSE | 0.152 | 0.467 | 0.307 | 0.539 | 0.129 | 0.209 | 0.846 | 0.654 | |
| Summer | NSE | 0.548 | −3.116 | −0.721 | −4.758 | 0.628 | 0.677 | −10.384 | −5.641 |
| RE | 0.130 | −0.464 | 0.299 | −0.532 | −0.134 | 0.097 | −0.776 | −0.586 | |
| NRMSE | 0.158 | 0.478 | 0.309 | 0.565 | 0.144 | 0.134 | 0.795 | 0.607 | |
| Autumn | NSE | 0.829 | −1.092 | 0.072 | −1.610 | 0.808 | 0.241 | −5.829 | −2.542 |
| RE | 0.055 | −0.447 | 0.291 | −0.449 | −0.120 | 0.238 | −0.806 | −0.566 | |
| NRMSE | 0.132 | 0.462 | 0.308 | 0.517 | 0.140 | 0.279 | 0.835 | 0.602 | |
| Winter | NSE | 0.797 | −0.822 | 0.310 | −0.790 | 0.861 | −0.253 | −5.541 | −2.346 |
| RE | 0.034 | −0.441 | 0.281 | −0.417 | −0.107 | 0.365 | −0.879 | −0.607 | |
| NRMSE | 0.162 | 0.484 | 0.298 | 0.480 | 0.134 | 0.401 | 0.917 | 0.656 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water 2017, 9, 734. https://doi.org/10.3390/w9100734
Lang D, Zheng J, Shi J, Liao F, Ma X, Wang W, Chen X, Zhang M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water. 2017; 9(10):734. https://doi.org/10.3390/w9100734
Chicago/Turabian StyleLang, Dengxiao, Jiangkun Zheng, Jiaqi Shi, Feng Liao, Xing Ma, Wenwu Wang, Xuli Chen, and Mingfang Zhang. 2017. "A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China" Water 9, no. 10: 734. https://doi.org/10.3390/w9100734
APA StyleLang, D., Zheng, J., Shi, J., Liao, F., Ma, X., Wang, W., Chen, X., & Zhang, M. (2017). A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water, 9(10), 734. https://doi.org/10.3390/w9100734





