Energy Saving in a Water Supply Network by Coupling a Pump and a Pump As Turbine (PAT) in a Turbopump
Abstract
:1. Introduction
2. State-of-the-Art
2.1. Machine Behaviour
2.2. Energy Recovery in Water Systems
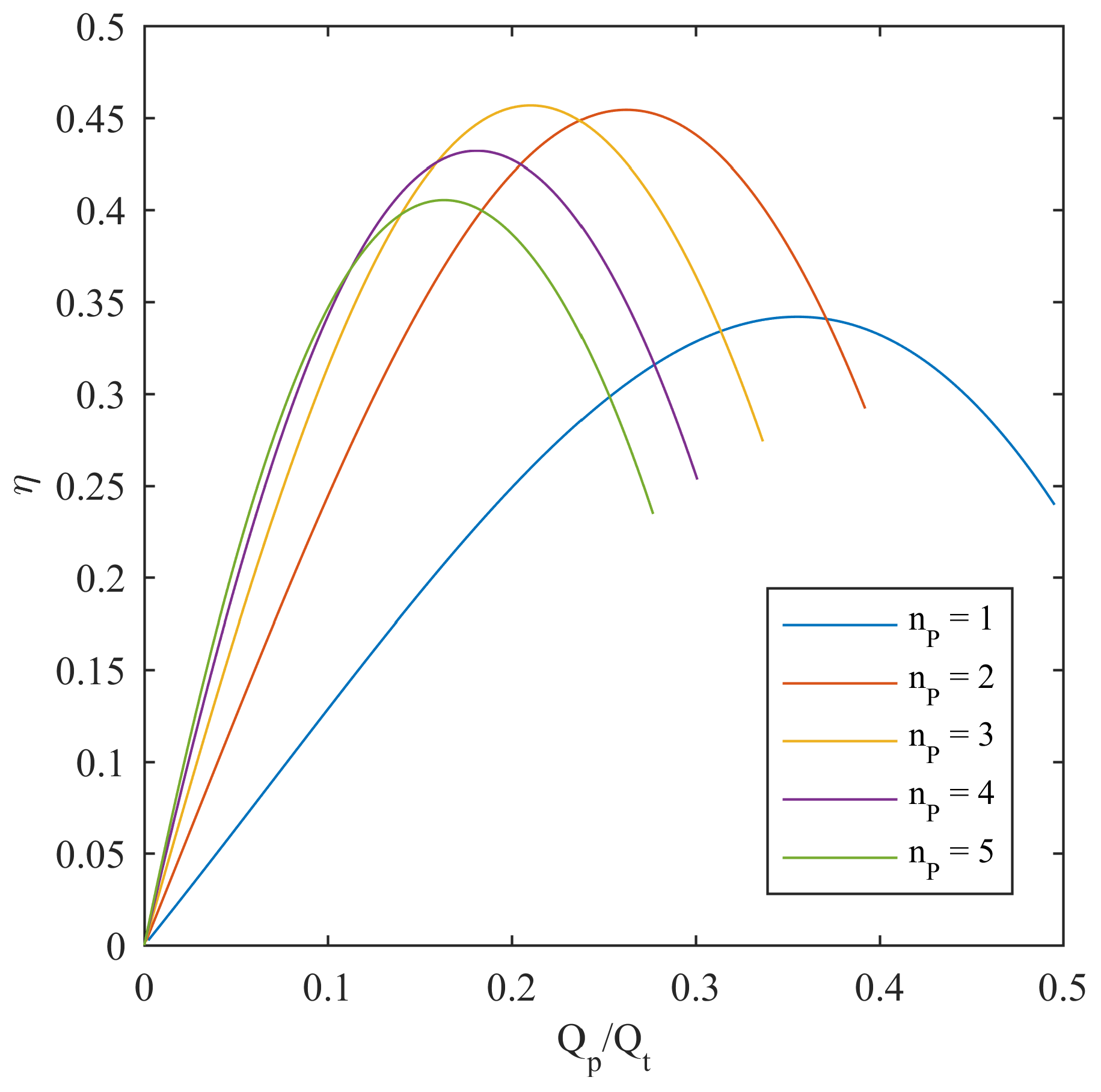
3. Pump and PAT Characteristic Curves
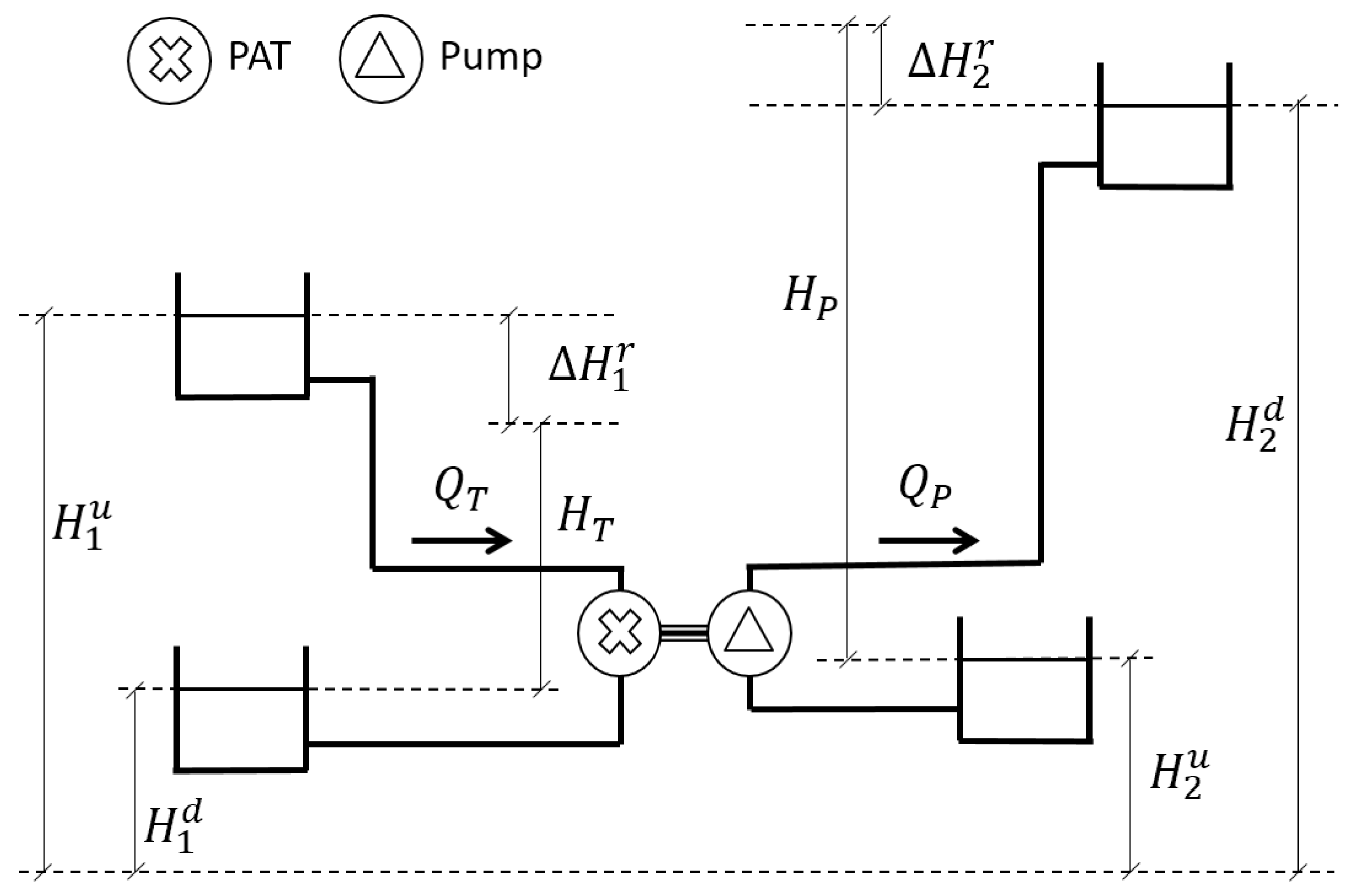
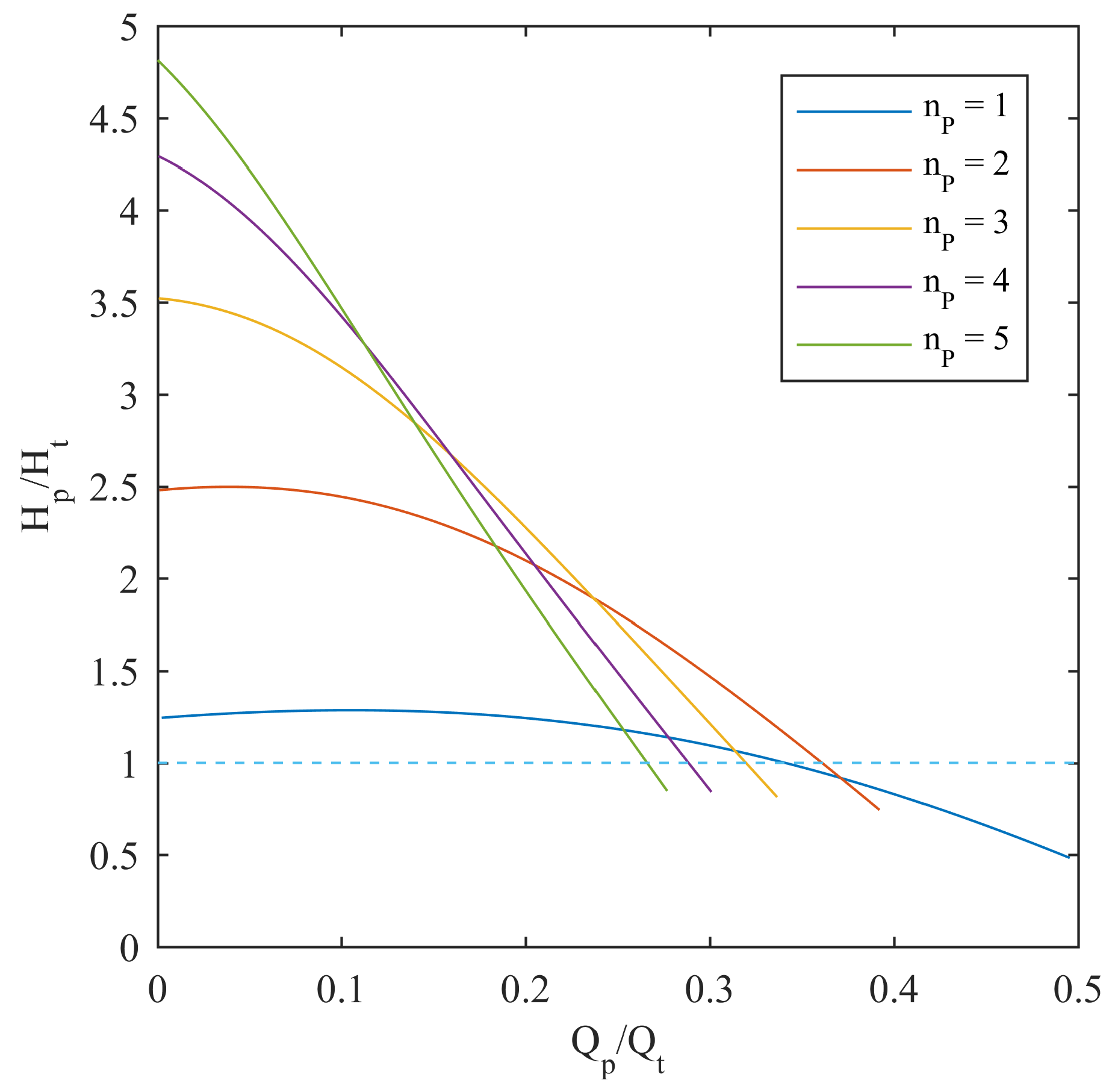
4. PAT and Pump System (P&P) Modelling
Behaviour of the P&P Plant
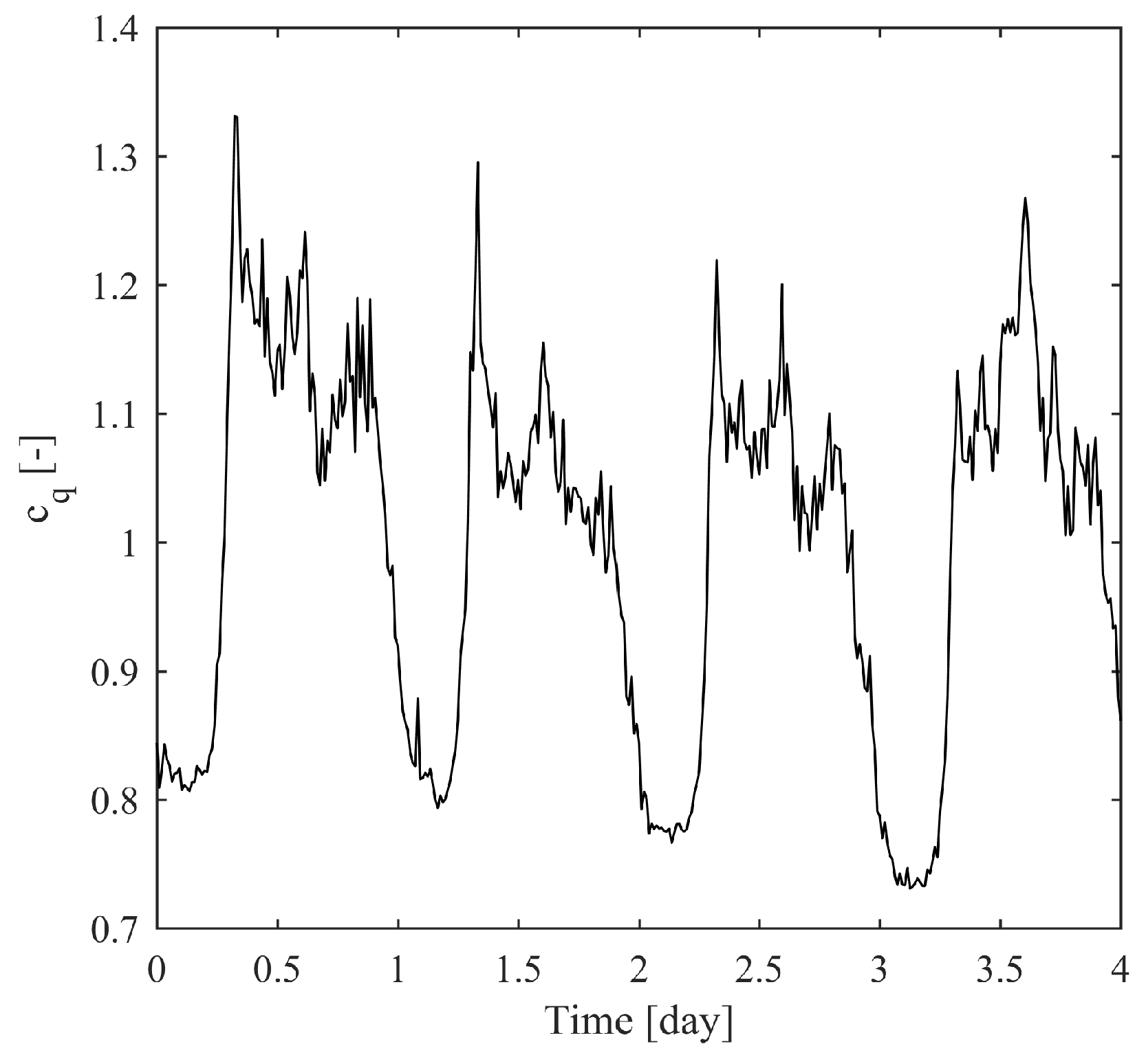
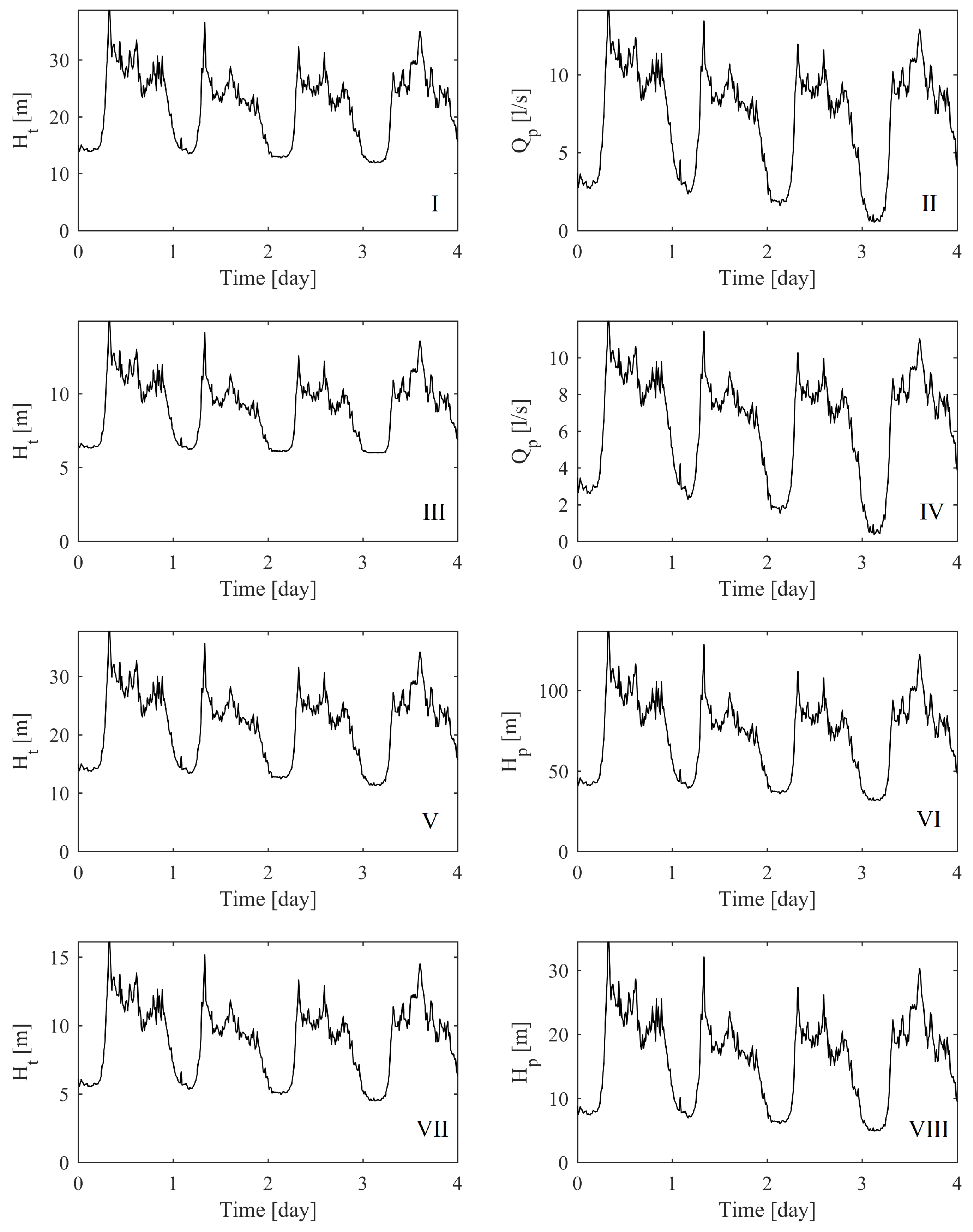
5. Case Study
- Elevated tank—Variable , constant
- Direct pumping—Variable , constant
- (a)
- A high difference in ground elevation between district 1 and district 2 and large turbined discharge
- (b)
- A low difference in ground elevation between district 1 and district 2 and small turbined discharge
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Pahl-Wostl, C. Transitions towards adaptive management of water facing climate and global change. Water Resour. Manag. 2007, 21, 49–62. [Google Scholar] [CrossRef]
- Ramos, H.; Covas, D.; Araujo, L.; Mello, M. Available energy assessment in water supply systems. In Proceedings of the XXXI IAHR Congress, Seoul, Korea, 11–16 September 2005.
- Gallagher, J.; Styles, D.; McNabola, A.; Williams, A.P. Life cycle environmental balance and greenhouse gas mitigation potential of micro-hydropower energy recovery in the water industry. J. Clean. Prod. 2015, 99, 152–159. [Google Scholar] [CrossRef]
- Almandoz, J.; Cabrera, E.; Arregui, F.; Cabrera, E.; Cobacho, R. Leakage Assessment through Water Distribution Network Simulation. J. Water Resour. Plan. Manag. 2005, 131, 458–466. [Google Scholar] [CrossRef]
- Xue, X.; Hawkins, T.R.; Schoen, M.E.; Garland, J.; Ashbolt, N.J. Comparing the Life Cycle Energy Consumption, Global Warming and Eutrophication Potentials of Several Water and Waste Service Options. Water 2016, 8, 154. [Google Scholar] [CrossRef]
- Abbott, M.; Cohen, B. Productivity and efficiency in the water industry. Util. Policy 2009, 17, 233–244. [Google Scholar] [CrossRef]
- Filion, Y.; MacLean, H.; Karney, B. Life Cycle Energy Analysis of a Water Distribution System. J. Infrastruct. Syst. 2004, 10, 120–130. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Sinagra, M.; Tucciarelli, T. Cost-benefit analysis for hydropower production in water distribution networks by a Pump As Turbine. J. Water Resour. Plan. Manag. 2013, 140, 04014002. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Lumbers, J. Leakage Reduction in Water Distribution Systems: Optimal Valve Control. J. Hydraul. Eng. 1998, 124, 1146–1154. [Google Scholar] [CrossRef]
- Tucciarelli, T.; Criminisi, A.; Termini, D. Leak Analysis in Pipeline Systems by Means of Optimal Valve Regulation. J. Hydraul. Eng. 1999, 125, 277–285. [Google Scholar] [CrossRef]
- Nicolini, M.; Zovatto, L. Optimal location and control of pressure reducing valves in water networks. J. Water Resour. Plan. Manag. 2009, 135, 178–187. [Google Scholar] [CrossRef]
- Liberatore, S.; Sechi, G. Location and Calibration of Valves in Water Distribution Networks Using a Scatter-Search Meta-heuristic Approach. Water Resour. Manag. 2009, 23, 1479–1495. [Google Scholar] [CrossRef]
- Ramos, H.; Mello, M.; De, P. Clean power in water supply systems as a sustainable solution: From planning to practical implementation. Water Sci. Technol. 2010, 10, 39–49. [Google Scholar] [CrossRef]
- Gallagher, J.; Harris, I.; Packwood, A.; McNabola, A.; Williams, A. A strategic assessment of micro-hydropower in the UK and Irish water industry: Identifying technical and economic constraints. Renew. Energy 2015, 81, 808–815. [Google Scholar] [CrossRef]
- Samora, I.; Manso, P.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Energy Recovery Using Micro-Hydropower Technology in Water Supply Systems: The Case Study of the City of Fribourg. Water 2016, 8, 344. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Lansey, K.E. Optimal control of water supply pumping systems. J. Water Resour. Plan. Manag. 1994, 120, 237–252. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, X.; Zhang, J. Optimal sizing and operation of pumping systems to achieve energy efficiency and load shifting. Electr. Power Syst. Res. 2012, 86, 41–50. [Google Scholar] [CrossRef]
- Punys, P.; Dumbrauskas, A.; Kvaraciejus, A.; Vyciene, G. Tools for Small Hydropower Plant Resource Planning and Development: A Review of Technology and Applications. Energies 2011, 4, 1258–1277. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H. Numerical simulation on Pump As Turbine: Mesh reliability and performance concerns. In Proceedings of the International Conference on Clean Electrical Power, Ischia, Italy, 14–16 June 2011; Franco Angeli: Milano, Italy, 2011. [Google Scholar]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G. Real Time Control of a Prototype for Pressure Regulation and Energy Production in Water Distribution Networks. J. Water Resour. Plan. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Theoretical, numerical and experimental investigation of centrifugal pumps in reverse operation. Exp. Therm. Fluid Sci. 2008, 32, 1620–1627. [Google Scholar] [CrossRef]
- Singh, P.; Nestmann, F. An optimization routine on a prediction and selection model for the turbine operation of centrifugal pumps. Exp. Therm. Fluid Sci. 2010, 34, 152–164. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two Pumps As Turbines for hydropower generation. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Golia, U.M.; La Rocca, M.; Martino, R.; Padulano, R.; Tucciarelli, T. Optimization of Osmotic Desalination Plants for Water Supply Networks. Water Resour. Manag. 2016, 30, 3965–3978. [Google Scholar] [CrossRef]
- Carravetta, A.; Conte, M.; Fecarotta, O.; Ramos, H. Evaluation of PAT Performances by Modified Affinity Law. Procedia Eng. 2014, 89, 581–587. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Martino, R.; Antipodi, L. PAT efficiency variation with design parameters. Procedia Eng. 2014, 70, 285–291. [Google Scholar] [CrossRef]
- Simpson, A.R.; Marchi, A. Evaluating the approximation of the affinity laws and improving the efficiency estimate for variable speed pumps. J. Hydraul. Eng. 2013, 139, 1314–1317. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 54. [Google Scholar] [CrossRef]
- Afshar, A.; Jemaa, F.; Marino, M. Optimization of hydropower plant integration in water supply system. J. Water Resour. Plan. Manag. 1990, 116, 665–675. [Google Scholar] [CrossRef]
- Dannier, A.; Del Pizzo, A.; Giugni, M.; Fontana, N.; Marini, G.; Proto, D. Efficiency evaluation of a micro-generation system for energy recovery in water distribution networks. In Proceedings of the 2015 IEEE International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 1, pp. 689–694. [Google Scholar]
- McNabola, A.; Coughlan, P.; Corcoran, L.; Power, C.; Williams, A.P.; Harris, I.; Gallagher, J.; Styles, D. Energy recovery in the water industry using micro-hydropower: An opportunity to improve sustainability. Water Policy 2014, 16, 168–183. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Energy Production in Water Distribution Networks: A PAT Design Strategy. Water Resour. Manag. 2012. [Google Scholar] [CrossRef]
- Rodrigues, A.; Singh, P.; Williams, A.; Nestmann, F.; Lai, E. Hydraulic analysis of a pump as a turbine with CFD and experimental data. In Proceedings of the IMechE Seminar Computational Fluid Dynamics for Fluid Machinery, London, UK, 18 November 2003.
- Ramos, H.M.; Borga, A.; Simão, M. New design solutions for low-power energy production in water pipe systems. Water Sci. Eng. 2009, 2, 69–84. [Google Scholar]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower potential in water distribution networks: Pressure control by PATs. Water Resour. Manag. 2015, 29, 699–714. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Pump As Turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Del Giudice, G.; Ramos, H. Energy recovery in water systems by PATs: A comparisons among the different installation schemes. Procedia Eng. 2014, 70, 275–284. [Google Scholar] [CrossRef]
- Corcoran, L.; McNabola, A.; Coughlan, P. Optimization of water distribution networks for combined hydropower energy recovery and leakage reduction. J. Water Resour. Plan. Manag. 2015, 142, 04015045. [Google Scholar] [CrossRef]
- Samora, I.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Simulated annealing in optimization of energy production in a water supply network. Water Resour. Manag. 2016, 30, 1533–1547. [Google Scholar] [CrossRef]

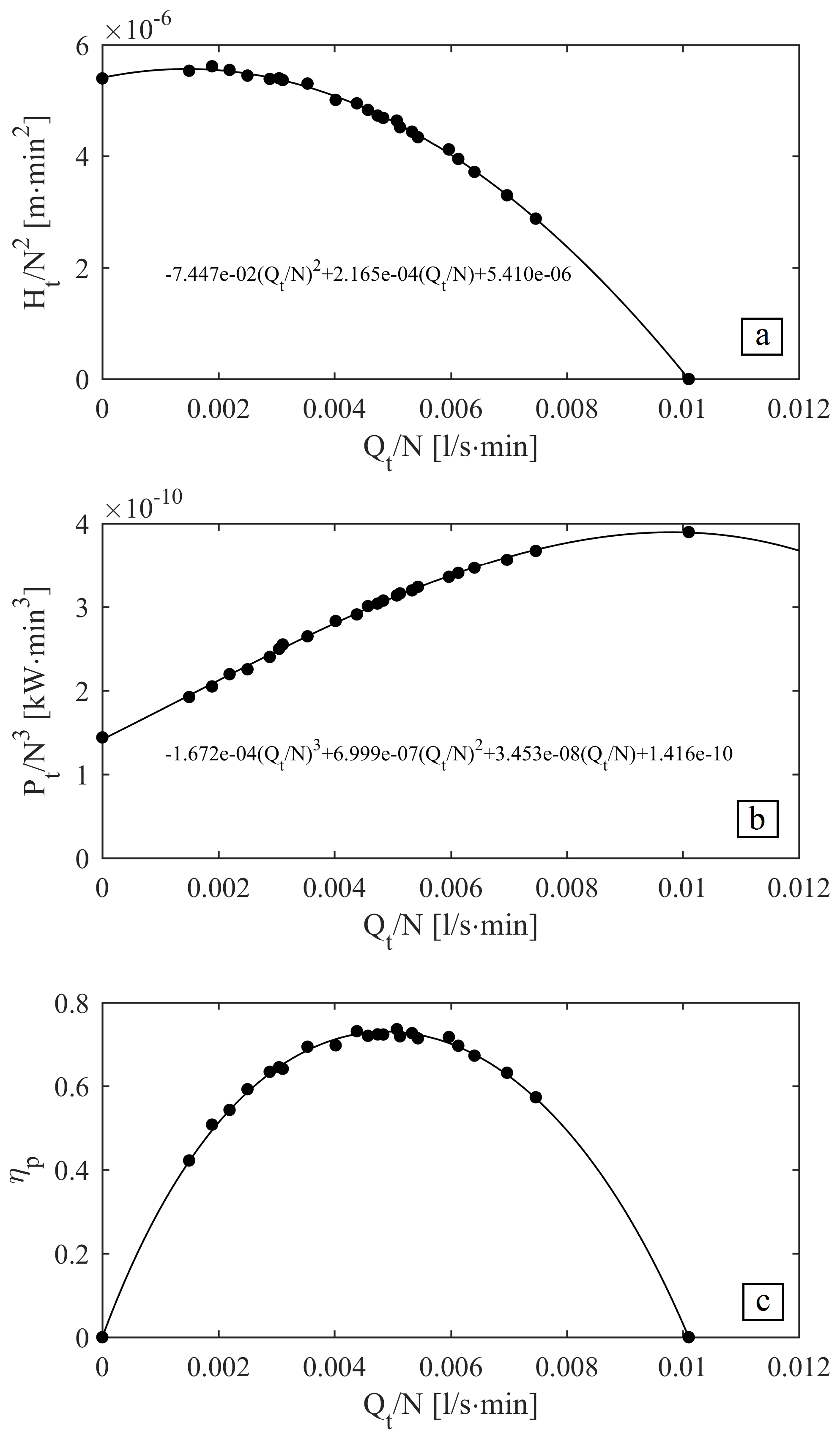
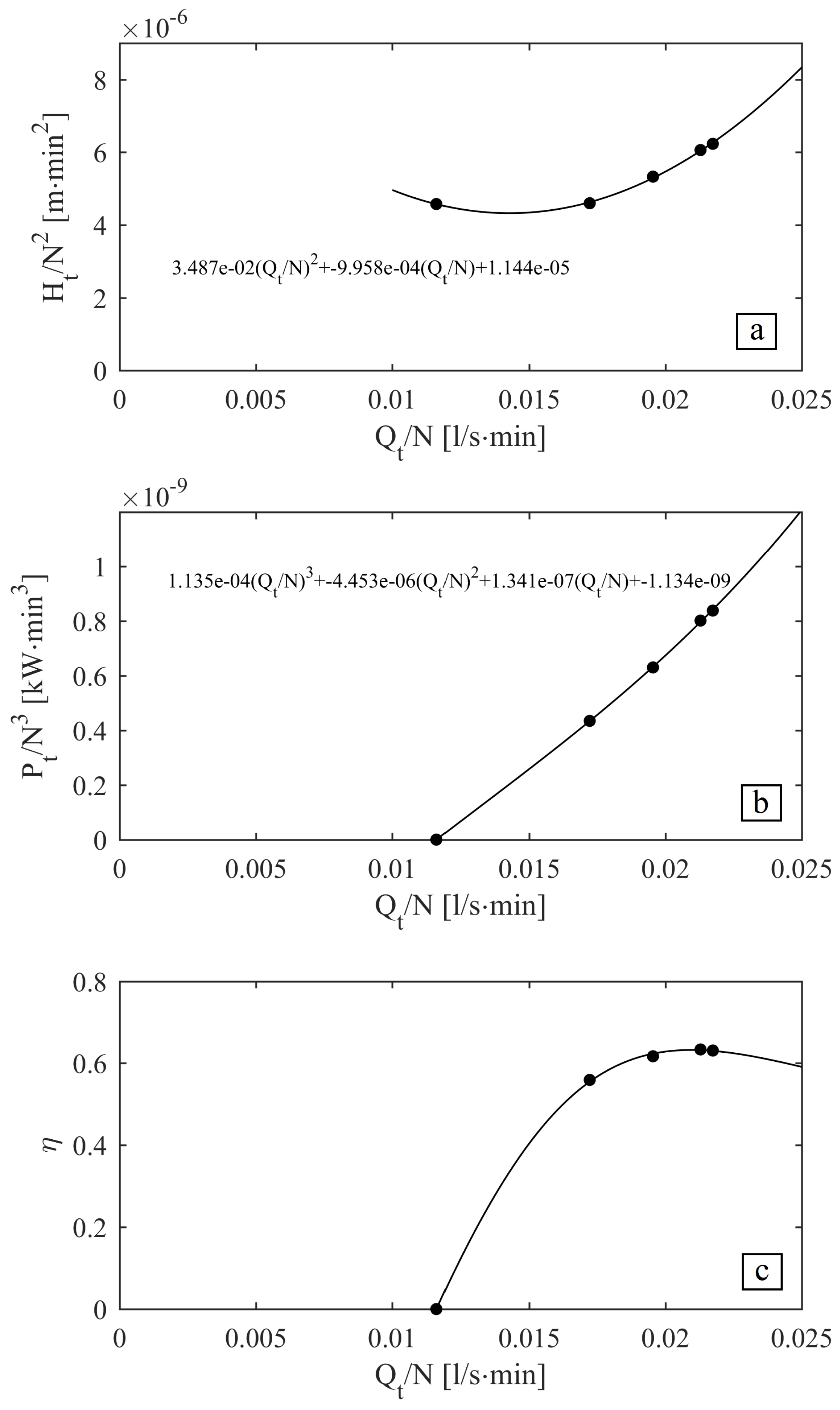
| Measured Quantity | Maximum Uncertainty Value |
|---|---|
| Q | |
| H | |
| P | |
| η |
| Specification | Value | Unit |
|---|---|---|
| Nominal speed | 2900 | rpm |
| m | ||
| % |
| Specification | Value | Unit |
|---|---|---|
| Nominal speed | 1550 | rpm |
| m | ||
| % |
| Casea | Caseb | |
|---|---|---|
| Supply condition 1 | Variable ( 40 ) | Variable ( 25 ) |
| Variable | Variable | |
| Variable | Variable | |
| m | m | |
| Supply condition 2 | Variable ( 40 ) | Variable ( 25 ) |
| Variable | Variable | |
| Variable | Variable | |
| Scenario | Turbined Average Power (kW) | Turbined Maximum Power (kW) | Pumped Average Power (kW | Pumped Maximum Power (kW) | Average Efficiency | Annual Energy Saving (MWh) |
|---|---|---|---|---|---|---|
| 48.1–77.0 | ||||||
| 12.7–20.3 | ||||||
| 42.5–68.0 | ||||||
| 13.8–22.0 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carravetta, A.; Antipodi, L.; Golia, U.; Fecarotta, O. Energy Saving in a Water Supply Network by Coupling a Pump and a Pump As Turbine (PAT) in a Turbopump. Water 2017, 9, 62. https://doi.org/10.3390/w9010062
Carravetta A, Antipodi L, Golia U, Fecarotta O. Energy Saving in a Water Supply Network by Coupling a Pump and a Pump As Turbine (PAT) in a Turbopump. Water. 2017; 9(1):62. https://doi.org/10.3390/w9010062
Chicago/Turabian StyleCarravetta, Armando, Lauro Antipodi, Umberto Golia, and Oreste Fecarotta. 2017. "Energy Saving in a Water Supply Network by Coupling a Pump and a Pump As Turbine (PAT) in a Turbopump" Water 9, no. 1: 62. https://doi.org/10.3390/w9010062
APA StyleCarravetta, A., Antipodi, L., Golia, U., & Fecarotta, O. (2017). Energy Saving in a Water Supply Network by Coupling a Pump and a Pump As Turbine (PAT) in a Turbopump. Water, 9(1), 62. https://doi.org/10.3390/w9010062








