A Deterministic Model for Predicting Hourly Dissolved Oxygen Change: Development and Application to a Shallow Eutrophic Lake
Abstract
:1. Introduction
2. Methodology
2.1. Site Description
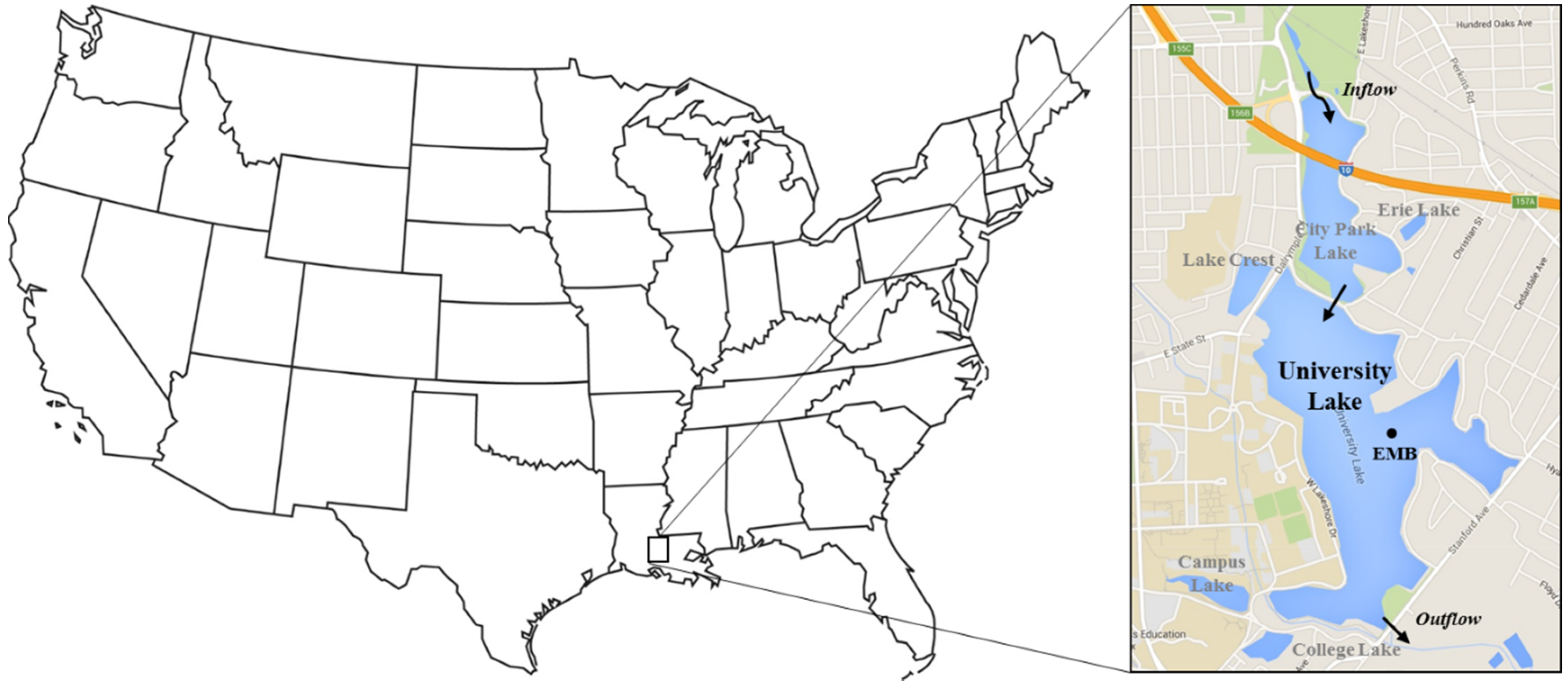
2.2. Water Quality Monitoring
2.3. Climatic Data Collection
3. Development of a Process-Based DO Model
3.1. Oxygen Production by Photosynthesis
3.2. Re-Aeration by Wind Regime
For U ≥ 3.7 m/s, KL = 4.33U – 13.3
3.3. Respiration
3.4. Sediment Oxygen Demand
3.5. Dissolved Oxygen Transport Equation
+ αj × (KL/H) × (Csat – Cs)
− αr × θr(T−20) × Chl-a
− SS20 × θs(T−20)/Z (11)
3.6. Model Limitations and Assumptions
3.7. DO Modeling
3.8. Model Evaluation
4. Results
4.1. Model Calibration
| Parameter | Calibrated Value | Uncertainty Analysis | |
|---|---|---|---|
| Value Range | Mean (Mg·L−1) ± Standard Deviation | ||
| αpar | 2 | [1,3] | 6.40 ± 0.06 |
| αj | 2.6 | [1.3,3.9] | 6.33 ± 0.57 |
| αr | 7 | [3.5,10.5] | 6.53 ± 0.73 |
| Ss20 | 0.083 | [0.042,0.125] | 6.45 ± 0.21 |
| Month | Calibration | Validation | ||||
|---|---|---|---|---|---|---|
| n | r-Squared | NSE | n | r-Squared | NSE | |
| Spring | 707 | 0.49 | 0.41 | 1223 | 0.50 | −0.42 |
| Summer | 365 | 0.60 | 0.48 | 177 | 0.59 | 0.46 |
| Fall | 332 | 0.61 | 0.57 | 384 | 0.42 | 0.32 |
| Winter | 708 | 0.60 | 0.58 | 822 | 0.51 | −0.43 |
| Year | 2112 | 0.66 | 0.66 | 2606 | 0.61 | 0.21 |
4.2. Uncertainty Analysis
4.3. Sensitivity Analysis
| Parameter a | Value | ΔDO (%) | ||||
|---|---|---|---|---|---|---|
| Year | Spring | Summer | Fall | Winter | ||
| αpar | 3 | −0.92 | −0.13 | −6.7 | 0.13 | 0.79 |
| αpar | 1 | −5.2 | −1.5 | −12.7 | −11.5 | −2.1 |
| αj | 3.9 | 21.8 | 5.3 | 73.7 | 35.0 | 5.4 |
| αj | 1.3 | −25.0 | −15.1 | −54.8 | −36.1 | −14.3 |
| αr | 10.5 | −19.9 | −8.9 | −49.7 | −30.3 | −10.6 |
| αr | 3.5 | 62.9 | 8.9 | 216.7 | 120.2 | 10.6 |
| Ss20 | 0.125 | −7.7 | −4.3 | −22.6 | −9.4 | −2.7 |
| Ss20 | 0.042 | 12.0 | 4.3 | 45.0 | 11.9 | 2.7 |
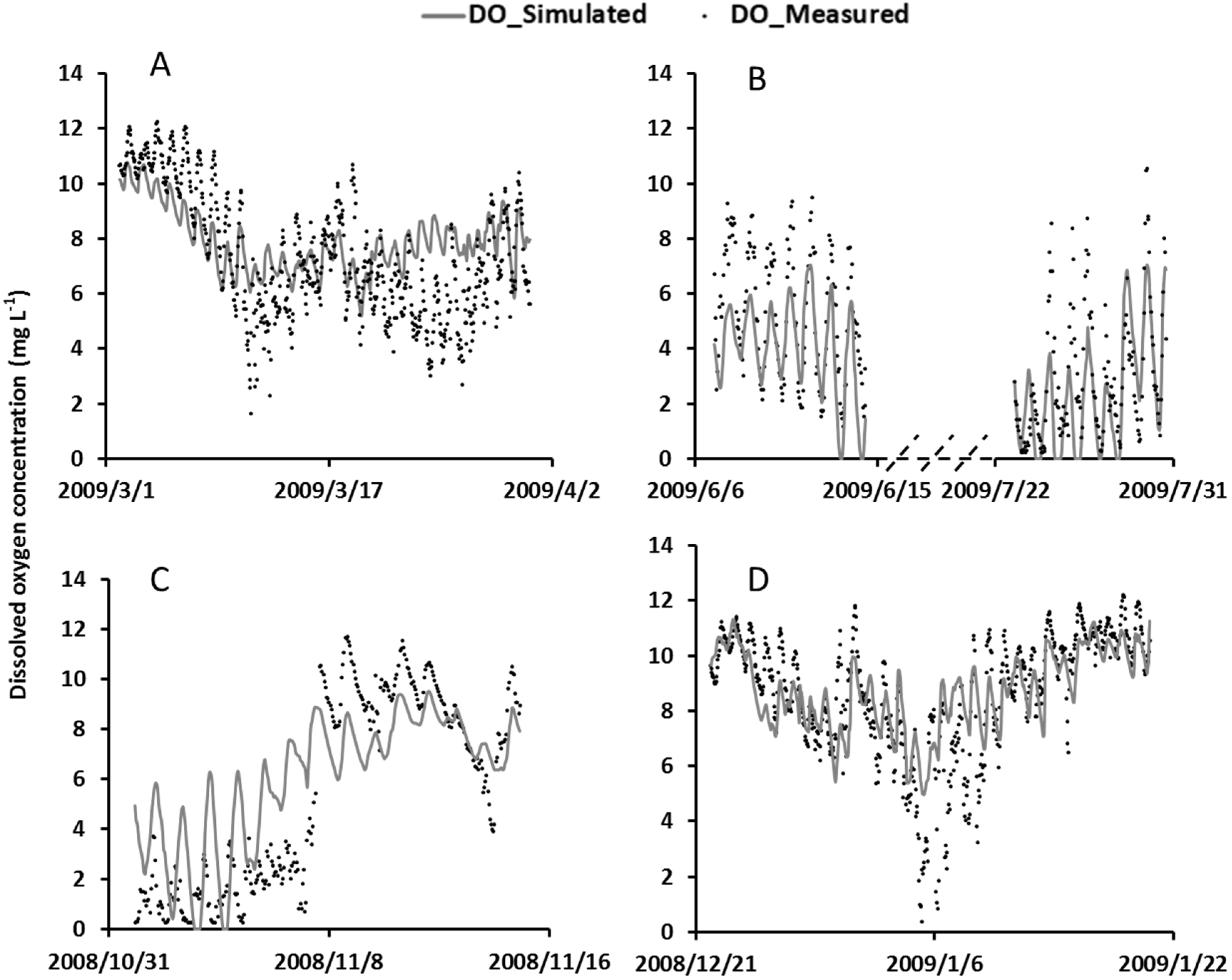
4.4. Model Validation
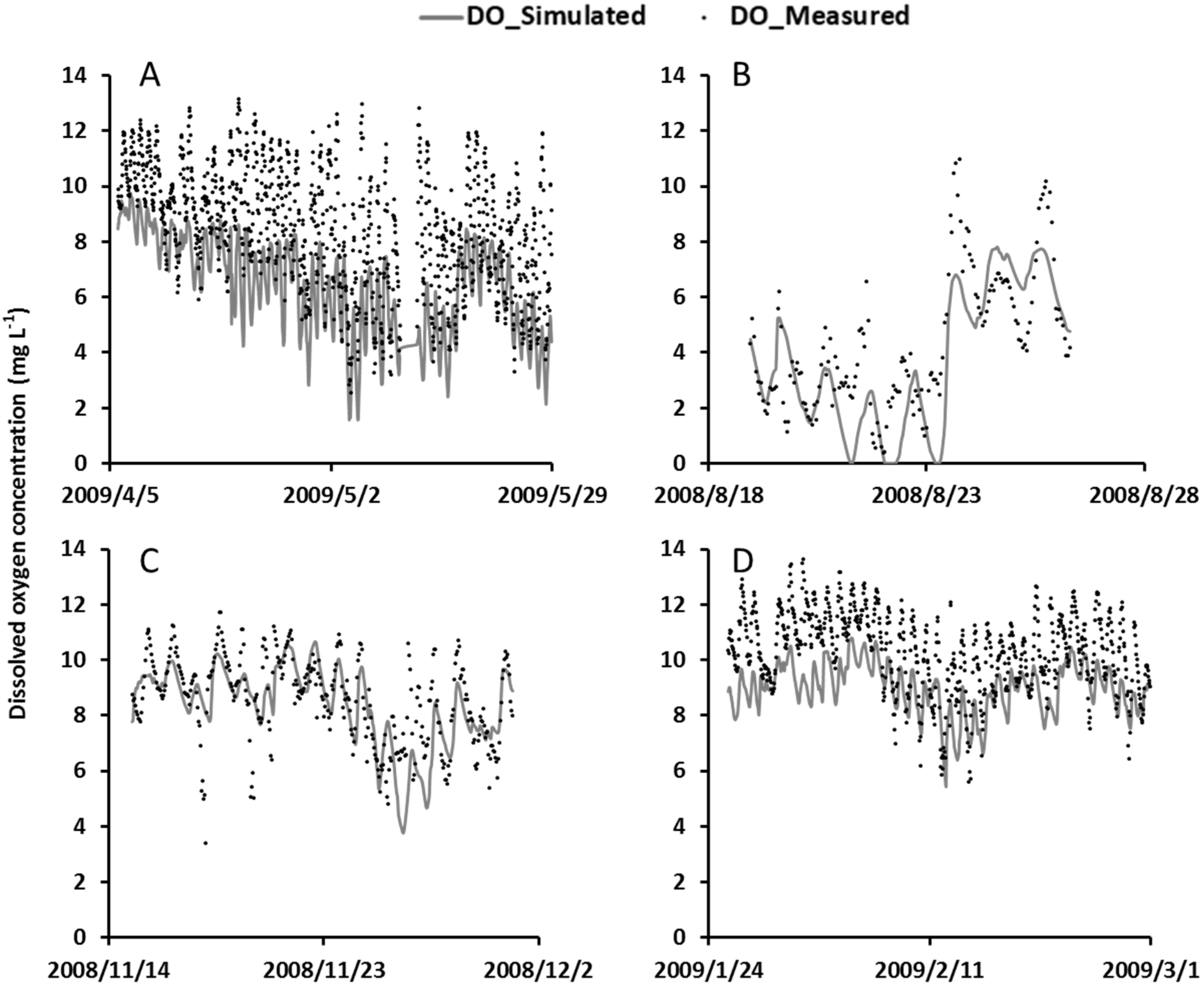
4.5. The Interplay among Model Processes and Weather Conditions
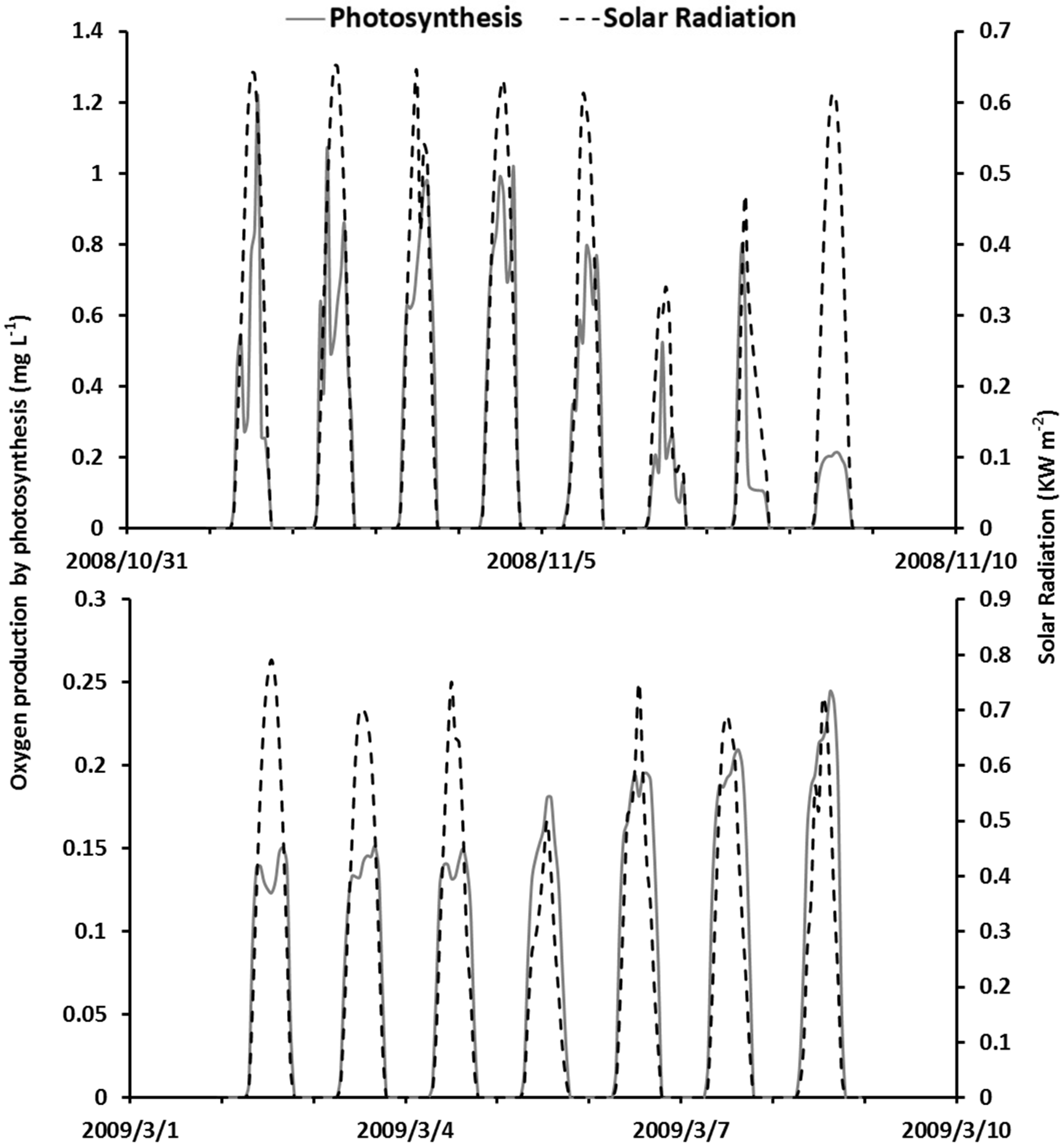
5. Discussions
5.1. Model Performance
5.2. Dynamic Interplay among Model Processes and Weather Conditions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Frodge, J.D.; Thomas, G.L.; Pauley, G.B. Effects of canopy formation by floating and submergent aquatic macrophytes on the water-quality of 2 shallow pacific-northwest lakes. Aquat. Bot. 1990, 38, 231–248. [Google Scholar] [CrossRef]
- Diaz, R.J.; Rosenberg, R. Spreading dead zones and consequences for marine ecosystems. Science 2008, 321, 926–929. [Google Scholar] [CrossRef] [PubMed]
- Kemp, W.M.; Sampou, P.; Caffrey, J.; Mayer, M.; Henriksen, K.; Boynton, W.R. Ammonium recycling versus denitrification in chesapeake bay sediments. Limnol. Oceanogr. 1990, 35, 1545–1563. [Google Scholar] [CrossRef]
- Breitburg, D.L. Episodic hyp oxia in Chesapeake Bay—Interacting effects of recruitment, behavior, and physical disturbance. Ecol. Monographs 1992, 62, 525–546. [Google Scholar] [CrossRef]
- Hamilton, S.K.; Sippel, S.J.; Calheiros, D.F.; Melack, J.M. An anoxic event and other biogeochemical effects of the pantanal wetland on the Paraguay River. Limnol. Oceanogr. 1997, 42, 257–272. [Google Scholar] [CrossRef]
- Gray, J.S.; Wu, R.S.S.; Or, Y.Y. Effects of hypoxia and organic enrichment on the coastal marine environment. Mar. Ecol. Prog. Ser. 2002, 238, 249–279. [Google Scholar] [CrossRef]
- Harrison, J.A.; Matson, P.A.; Fendorf, S.E. Effects of a diel oxygen cycle on nitrogen transformations and greenhouse gas emissions in a eutrophied subtropical stream. Aquat. Sci. 2005, 67, 308–315. [Google Scholar] [CrossRef]
- Stevens, P.W.; Blewett, D.A.; Casey, J.P. Short-term effects of a low dissolved oxygen event on estuarine fish assemblages following the passage of hurricane charley. Estuar. Coasts 2006, 29, 997–1003. [Google Scholar] [CrossRef]
- Holtgrieve, G.W.; Schindler, D.E.; Jankowski, K. Comment on Demars et al. 2015, “Stream metabolism and the open diel oxygen method: Principles, practice, and perspectives”. Limnol. Oceanogr. Methods 2015. [Google Scholar] [CrossRef]
- Stefan, H.G.; Fang, X. Dissolved-oxygen model for regional lake analysis. Ecol. Model. 1994, 71, 37–68. [Google Scholar] [CrossRef]
- Culberson, S.D.; Piedrahita, R.H. Aquaculture pond ecosystem model: Temperature and dissolved oxygen prediction—Mechanism and application. Ecol. Model. 1996, 89, 231–258. [Google Scholar] [CrossRef]
- Haider, H.; Ali, W.; Haydar, S. Evaluation of various relationships of reaeration rate coefficient for modeling dissolved oxygen in a river with extreme flow variations in Pakistan. Hydrol. Process. 2013, 27, 3949–3963. [Google Scholar] [CrossRef]
- Benson, A.; Zane, M.; Becker, T.E.; Visser, A.; Uriostegui, S.H.; DeRubeis, E.; Moran, J.E.; Esser, B.K.; Clark, J.F. Quantifying reaeration rates in alpine streams using deliberate gas tracer experiments. Water 2014, 6, 1013–1027. [Google Scholar]
- Haider, H.; Ali, W. Calibration and verification of a dissolved oxygen management model for a highly polluted river with extreme flow variations in Pakistan. Environ. Monit. Assess. 2013, 185, 4231–4244. [Google Scholar]
- Hull, V.; Parrella, L.; Falcucci, M. Modelling dissolved oxygen dynamics in coastal lagoons. Ecol. Model. 2008, 211, 468–480. [Google Scholar] [CrossRef]
- Rucinski, D.K.; Beletsky, D.; DePinto, J.V.; Schwab, D.J.; Scavia, D. A simple 1-dimensional, climate based dissolved oxygen model for the central basin of Lake Erie. J. Great Lakes Res. 2010, 36, 465–476. [Google Scholar] [CrossRef]
- Benoit, P.; Gratton, Y.; Mucci, A. Modeling of dissolved oxygen levels in the bottom waters of the lower St. Lawrence estuary: Coupling of benthic and pelagic processes. Mar. Chem. 2006, 102, 13–32. [Google Scholar] [CrossRef]
- Mooij, W.M.; Trolle, D.; Jeppesen, E.; Arhonditsis, G.; Belolipetsky, P.V.; Chitamwebwa, D.B.R.; Degermendzhy, A.G.; DeAngelis, D.L.; Domis, L.N.D.; Downing, A.S.; et al. Challenges and opportunities for integrating lake ecosystem modelling approaches. Aquat. Ecol. 2010, 44, 633–667. [Google Scholar] [CrossRef]
- James, R.T.; Martin, J.; Wool, T.; Wang, P.F. A sediment resuspension and water quality model of Lake Okeechobee. J. Am. Water Resour. Assoc. 1997, 33, 661–680. [Google Scholar] [CrossRef]
- Tundisi, J.G. Perspectives for ecological modeling of tropical and subtropical reservoirs in South-America. Ecol. Model. 1990, 52, 7–20. [Google Scholar] [CrossRef]
- D’Autilia, R.; Falcucci, M.; Hull, V.; Parrella, L. Short time dissolved oxygen dynamics in shallow water ecosystems. Ecol. Model. 2004, 179, 297–306. [Google Scholar] [CrossRef]
- Oren, A. Saltern evaporation ponds as model systems for the study of primary production processes under hypersaline conditions. Aquat. Microbial Ecol. 2009, 56, 193–204. [Google Scholar] [CrossRef]
- Wan, Y.S.; Ji, Z.G.; Shen, J.; Hu, G.D.; Sun, D.T. Three dimensional water quality modeling of a shallow subtropical estuary. Mar. Environ. Res. 2012, 82, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Blauw, A.N.; Los, H.F.J.; Bokhorst, M.; Erftemeijer, P.L.A. Gem: A generic ecological model for estuaries and coastal waters. Hydrobiologia 2009, 618, 175–198. [Google Scholar] [CrossRef]
- Pena, M.A.; Katsev, S.; Oguz, T.; Gilbert, D. Modeling dissolved oxygen dynamics and hypoxia. Biogeosciences 2010, 7, 933–957. [Google Scholar] [CrossRef]
- Rabalais, N.N.; Turner, R.E.; Wiseman, W.J. Hypoxia in the Gulf of Mexico. J. Environ. Qual. 2001, 30, 320–329. [Google Scholar] [CrossRef] [PubMed]
- Yin, K.D.; Lin, Z.F.; Ke, Z.Y. Temporal and spatial distribution of dissolved oxygen in the Pearl River estuary and adjacent coastal waters. Cont. Shelf Res. 2004, 24, 1935–1948. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, Y.J. Determination of trophic state changes with diel dissolved oxygen: A case study in a shallow lake. Water Environ. Res. 2015, 87, 1970–1979. [Google Scholar] [CrossRef] [PubMed]
- Reich Association. City Park/University Lakes Management Plan; Applied Technology Research Corporation: Baton Rouge, LA, USA, 1991. [Google Scholar]
- Xu, Y.J.; Mesmer, R. The dynamics of dissolved oxygen and metabolic rates in a shallow subtropical urban lake, Louisiana, USA. In Understanding Freshwater Quality Problems in a Changing World; Berit, A., Ed.; International Association of Hydrological Sciences (IAHS): Wallingford, UK, 2013; pp. 212–219. [Google Scholar]
- Mesmer, R. Impact of Urban Runoff of Phosphorus, Nitrogen and Dissolved Oxygen in a Shallow Subtropical Lake. Master’s Thesis, Louisiana State University and Agricultural and Mechanical College, Raton Rouge, LA, USA, 2010. [Google Scholar]
- Xu, Z.; Xu, Y.J. Rapid field estimation of biochemical oxygen demand in a subtropical eutrophic urban lake with chlorophyll a fluorescence. Environ. Monit. Assess. 2015, 187, 14. [Google Scholar] [CrossRef] [PubMed]
- Demars, B.O.L.; Thompson, J.; Manson, J.R. Stream metabolism and the open diel oxygen method: Principles, practice, and perspectives. Limnol. Oceanogr. Methods 2015, 13, 356–374. [Google Scholar] [CrossRef]
- Steele, J.H. Environmental control of photosynthesis in the sea. Limnol. Oceanogr. 1962, 7, 137–150. [Google Scholar] [CrossRef]
- Banniste, T.T. Production equations in terms of chlorophyll concentration, quantum yield, and upper limit to production. Limnol. Oceanogr. 1974, 19, 1–12. [Google Scholar] [CrossRef]
- Alados, I.; FoyoMoreno, I.; AladosArboledas, L. Photosynthetically active radiation: Measurements and modelling. Agric. Forest Meteorol. 1996, 78, 121–131. [Google Scholar] [CrossRef]
- Gregor, J.; Marsalek, B. Freshwater phytoplankton quantification by chlorophyll α: A comparative study of in vitro, in vivo and in situ methods. Water Res. 2004, 38, 517–522. [Google Scholar] [CrossRef] [PubMed]
- Megard, R.O.; Tonkyn, D.W.; Senft, W.H. Kinetics of oxygenic photosynthesis in planktonic algae. J. Plankton Res. 1984, 6, 325–337. [Google Scholar] [CrossRef]
- Gelda, R.K.; Auer, M.T.; Effler, S.W.; Chapra, S.C.; Storey, M.L. Determination of reaeration coefficients: Whole-lake approach. J. Environ. Eng. 1996, 122, 269–275. [Google Scholar] [CrossRef]
- Demars, B.O.L.; Manson, J.R. Temperature dependence of stream aeraion coefficients and the effect of water turbulence: A critival review. Water Res. 2013, 47, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Crusius, J.; Wanninkhof, R. Gas transfer velocities measured at low wind speed over a lake. Limnol. Oceanogr. 2003, 48, 1010–1017. [Google Scholar] [CrossRef]
- Ambrose, R.B.; Wool, T.A.; Connolly, J.P.; Schanz, R.W. WASP4 (EUTRO4), A Hydrodynamic and Water Quality Model—Model Theory, User′s Manual, and Programmer′s Guide; EPA/600/3–87/039; U.S. Environmental Protection Agency: Athens, GA, USA, 1988.
- Thomann, R.V.; Mueller, J.A. Principles of Surface Water Quality Modeling and Control; Harper & Row: New York, NY, USA, 1987. [Google Scholar]
- Zison, S.W.; Mills, W.B.; Diemer, D.; Chen, C.W. Rates, Constants and Kinetic Formulations in Surface Water Quality Modeling; EPA 600-3-78-105; Tetra Tech., Inc. for U.S. Environmental Protection Agency: Athens, GA, USA, 1978.
- Nash, J.E.; Sutcliffe, J.E. River flow forecasting through conceptual models, Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large river basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic simulation on agricultural watersheds: Choosing between two models. Trans. ASAE 2003, 46, 1539–1551. [Google Scholar] [CrossRef]
- Fernandez, G.P.; Chescheir, G.M.; Skaggs, R.W.; Amatya, D.M. Development and testing of watershed-scale models for poorly drained soils. Trans. ASAE 2005, 48, 639–652. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Wu, K.; Xu, Y.J. Evaluation of the applicability of the swat model for coastal watersheds in southeastern Louisiana. J. Am. Water Resour. Assoc. 2006, 42, 1247–1260. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Veith, T.L.; Bosch, D.D.; Arnold, J.G. Suitability of swat for the conservation effects assessment project: Comparison on USDA agricultural research service watersheds. J. Hydrol. Eng. 2007, 12, 173–189. [Google Scholar] [CrossRef]
- Motovilov, Y.G.; Gottschalk, L.; Engeland, K.; Rodhe, A. Validation of a distributed hydrological model against spatial observations. Agric. Forest Meteorol. 1999, 98–99, 257–277. [Google Scholar] [CrossRef]
- Portielje, R.; Kersting, K.; Lijklema, L. Primary production estimation from continuous oxygen measurements in relation to external nutrient input. Water Res. 1996, 30, 625–643. [Google Scholar] [CrossRef]
- Iriarte, A.; Daneri, G.; Garcia, V.M.T.; Purdie, D.A.; Crawford, D.W. Plankton community respiration and its relationship to chlorophyll a concentration in marine coastal waters. Oceanol. Acta 1991, 14, 379–388. [Google Scholar]
- Fourqurean, J.W.; Webb, K.L.; Hollibaugh, J.T.; Smith, S.V. Contributions of the plankton community to ecosystem respiration, Tomales Bay, California. Estuar. Coast. Shelf Sci. 1997, 44, 493–505. [Google Scholar] [CrossRef]
- Tyystjarvi, E.; Aro, E.M. The rate constant of photoinhibition, measured in lincomycin-treated leaves, is directly proportional to light intensity. Proc. Natl. Acad. Sci. USA 1996, 93, 2213–2218. [Google Scholar] [CrossRef] [PubMed]
- Beardall, J. Photosynthesis and photorespiration in marine-phytoplankton. Aquat. Bot. 1989, 34, 105–130. [Google Scholar] [CrossRef]
- Sharkey, T.D. Estimating the rate of photorespiration in leaves. Physiol. Plant. 1988, 73, 147–152. [Google Scholar] [CrossRef]
- Parkhill, K.L.; Gulliver, J.S. Application of photorespiration concepts to whole stream productivity. Hydrobiologia 1998, 389, 7–19. [Google Scholar] [CrossRef]
- Parkhill, K.L.; Gulliver, J.S. Modeling the effect of light on whole-stream respiration. Ecol. Model. 1999, 117, 333–342. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Xu, Y.J. A Deterministic Model for Predicting Hourly Dissolved Oxygen Change: Development and Application to a Shallow Eutrophic Lake. Water 2016, 8, 41. https://doi.org/10.3390/w8020041
Xu Z, Xu YJ. A Deterministic Model for Predicting Hourly Dissolved Oxygen Change: Development and Application to a Shallow Eutrophic Lake. Water. 2016; 8(2):41. https://doi.org/10.3390/w8020041
Chicago/Turabian StyleXu, Zhen, and Y. Jun Xu. 2016. "A Deterministic Model for Predicting Hourly Dissolved Oxygen Change: Development and Application to a Shallow Eutrophic Lake" Water 8, no. 2: 41. https://doi.org/10.3390/w8020041
APA StyleXu, Z., & Xu, Y. J. (2016). A Deterministic Model for Predicting Hourly Dissolved Oxygen Change: Development and Application to a Shallow Eutrophic Lake. Water, 8(2), 41. https://doi.org/10.3390/w8020041







