On the Modeling of Bank Storage in a Groundwater Model: The April, 1983, Flood Event in the Neuwieder Becken (Middle Rhine)
Abstract
: For predictive numerical simulations of subsurface floods (groundwater head rise due to high water in a contiguous river), it is important to know how to represent the bank storage process in a numerical groundwater model. Whilst leakage approaches are frequently used for modeling bank storage, another option is the application of a head boundary condition. In order to get a better understanding of the bank storage process, we analyze the bank storage event in the Neuwieder Becken (Middle Rhine) in April 1983, which has been reported by Ubell (1987). We found the leakage function to be nonlinear and hysteretic. The evaluation of different model variants for Ubell’s bank storage event shows that both a head boundary condition and a leakage boundary condition are appropriate modeling approaches. For practical reasons, the leakage boundary condition is preferred. A linear leakage function represents the bank storage process for the analyzed event sufficiently. A hysteretic course of the leakage function can be achieved in a three-dimensional groundwater model by layering the hydraulic soil properties in the vicinity of the bank.1. Introduction
The August 2002 flood was one of the most disastrous floods in Germany in recent years. Many cities and villages in the catchment of the River Elbe were affected. A special characteristic of this flood event was the severe groundwater head rise: at some locations, the groundwater rose up to six meters over a short period of time. This level had never been measured before [1]. In particular, the inhabitants of the City of Dresden were impacted by this type of subsurface flood. We define a “subsurface flood” (unterirdisches Hochwasser or Grund-Hochwasser; see [2,3]) as a groundwater head rise that is caused by high water in a river and distinguish it from groundwater flooding, which is related to heavy rainfall events (see, e.g., [4,5]). For the Dresden flood event, Huber et al. [6] and Kreibich and Thieken [7] quote that a significant percentage of the total economical losses due to the flood was related to groundwater.
Subsurface floods are mainly a problem of urban areas that are located in the vicinity of large rivers. Damage arises from groundwater that enters cellars and basements and destroys walls and interiors by wetting. When critical infrastructure, like power grid facilities, is affected [8], a power breakdown can be a consequence of a subsurface flood. Groundwater that enters sewage pipes can cause an overload of the sewage system [1,2]. Finally, rising groundwater levels can cause the failure of foundations due to uplift forces. This can affect apartment buildings and office buildings, but also road and railway tunnels.
A special problem of subsurface floods is that the groundwater rise is often unexpected. This is for two reasons: Firstly, the subsurface flood can propagate far away from the river. Therefore, subsurface floods can affect locations that are usually not affected by the visible surface inundations. Secondly, the subsurface flood follows the river flood with delay. Groundwater levels keep rising when the flood wave in the river is already decreasing. Beyer [8] reports the case of a low-lying sports hall in Dresden during the August flood 2002. The basement plate of this sports hall is located 3.6 m below the ground surface, and the building is located in an area that was not inundated. Not until the parquet floor bulged several decimeters due to groundwater entering the hall had the threat even been noticed. As an urgent measure, water tanks and sand bags were brought into the hall to prevent the ground plate from cracking.
Subsurface flood hazard maps help urban planners to prepare cities located in the vicinity of large rivers for protection against subsurface floods. Decision makers benefit from such maps during flood protection operations, and inhabitants can inform themselves if they live in areas that are at risk of subsurface floods. The essential information of such a subsurface flood hazard map is the minimal depth to the groundwater table that probably is reached during a flood. Groundwater models are a helpful tool to prepare such subsurface flood hazard maps [9].
Bank storage (see [10]) is one important mechanism of water exchange between a river and the neighboring aquifer and, consequently, an important mechanism to account for in studies related to subsurface floods. Bank storage events are reported in several studies [11–14]. Within the frame of predictive subsurface flood modeling, it is important to understand the corresponding interchange processes and to know how they can be represented in a numerical groundwater model. In groundwater models, the river-aquifer interaction is usually represented with a head boundary condition or a leakage boundary condition (see, e.g., [15–17]). The question we address in this article is which one of these two approaches is more suitable for large rivers that strongly interact with the adjacent aquifer. In Section 2, we summarize the mathematical background of these two options and discuss selected leakage functions from the literature.
Ubell [12] reports a bank storage event that occurred during the Rhine flood in April 1983, in the “Neuwieder Becken” (Middle Rhine). We review this bank storage event in Section 3. In Section 4, we describe a groundwater model that we set up for the Ubell bank storage event with the flow simulation program Feflow (see [18,19]). The water exchange between river and aquifer is modeled with a head boundary condition and a leakage boundary condition, which leads to two model variants. The groundwater model should reproduce the groundwater levels observed by Ubell [12]. Based on the simulation results of these two model variants, we discuss the two model approaches for modeling bank storage in a groundwater model. The article closes with a recommendation for modeling bank storage and an outlook on the further needs for research.
2. Modeling Bank Storage in a Groundwater Model
2.1. Introduction
Common approaches to represent river-aquifer interactions in a groundwater model are:
a head boundary condition (first order, Dirichlet type) and
a leakage boundary condition (third order, Cauchy type)
A second order boundary condition (q-boundary condition, Neumann-type) is usually not applicable, because the amount of water exchange per time step is unknown in most cases.
2.2. Head Boundary Condition
Modeling the river-aquifer interaction with a head boundary condition means setting hR for the unknown groundwater level h at the boundary condition node:
The boundary condition causes a withdrawal or an allocation of water at the boundary node according to the applied boundary condition value. The exchange flux also depends on the groundwater flow situation in the vicinity of the boundary condition node. Freeze [20] limits the applicability of head-boundary conditions to shallow rivers with non-varying depths and where steep groundwater gradients and large leakage areas are existent. For subsurface floods, these conditions will not apply in general. Cunningham and Sinclair [21] recommend head-boundary conditions for rivers that are fully penetrating the aquifer. This condition will apply to many of the large rivers where subsurface floods occur. Ubell [22] uses a head boundary condition in his modeling study. Modeling bank storage with a head boundary condition does not necessarily rely on the assumption of an interface layer between river and aquifer. If there is no interface, hR is the river stage. If a sediment layer separates the river and aquifer, the sediment layer must be modeled directly, i.e., with elements that comprise the hydraulic conductivity properties of the interface layer, or hR represents the groundwater level on the aquifer side of the interface layer. Boundary condition data for the latter case can be obtained by pre-model calculation.
2.3. Leakage Boundary Condition
2.3.1. Introduction
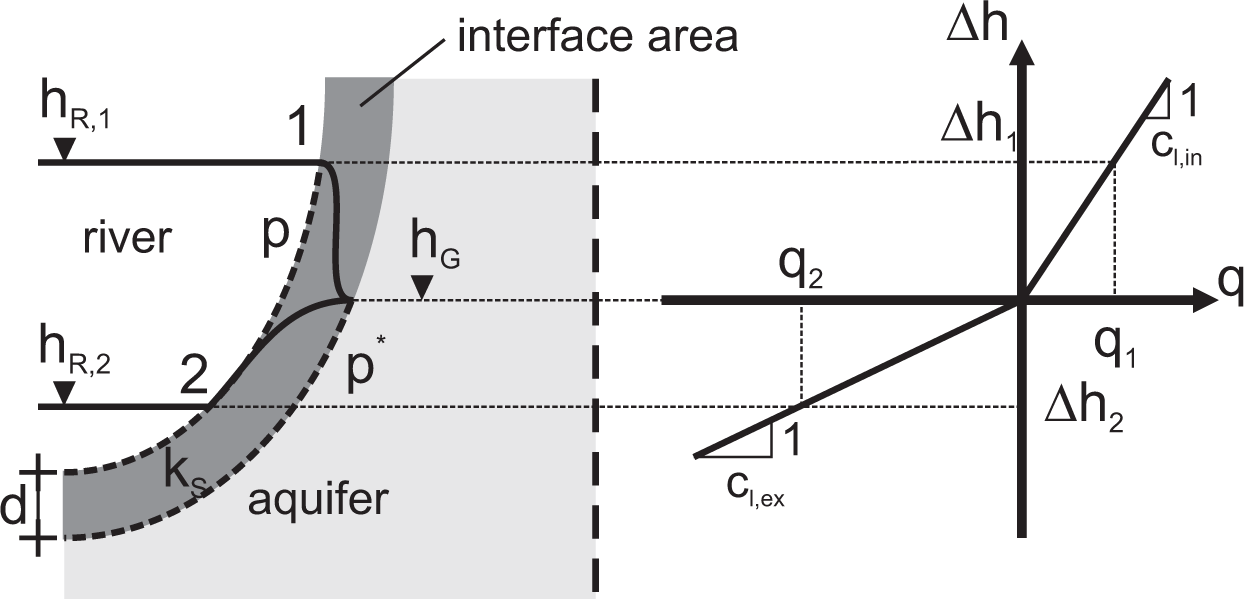
A leakage boundary condition uses a leakage function with the river stage hR as the boundary condition value. Figure 1 shows a schematic view of an idealized stream and the neighboring aquifer. The river stage hR,1 is higher than the groundwater level hG. In this case, the water infiltrates towards the aquifer. If the river stage is lower than the groundwater level, the hydraulic gradient points towards the stream, and water exfiltrates from the aquifer. Mathematical leakage models or leakage approaches relate the head difference between the river stage hR (m) and the groundwater level hG (m)
The groundwater level hG and the leakage rate q are initially unknown and obtained as model results. A time-variant groundwater level in a transient groundwater model accounts for the impact of storage on the interchange process. In this article, positive values of q and ∆h are defined as infiltration (inflow of river water into the aquifer), and negative values of q describe exfiltration.
2.3.2. Leakage Functions
Certainly, the leakage function that is most frequently used is given by the following equation:
Within this article, this approach is called the Darcy model, because the conceptional model assumes saturated Darcian flow through the interface layer. In Equation (4), cl (1/s) is a leakage coefficient. The leakage coefficient takes positive values and is defined as a ratio of hydraulic conductivity kS (m/s) and the thickness d (m) of an interface layer that is assumed to separate the river and the aquifer:
Often, data for d and kS are not available and highly spatially variable. Consequently, in many groundwater modeling studies, the leakage coefficient cl is treated as a model parameter and determined by calibration.
For many rivers in central Europe, water exfiltrates during normal or low flow conditions, while during high water conditions, water infiltrates into the aquifer. If Equation (4) is used both for infiltration and exfiltration, the flow resistance must be the same for both flow directions. Brunke and Gonser [27] point out that the stream bed can act like a mechanical filter. Depending on flow conditions and suspended load in the stream, colmation of the bed can reduce the infiltration rate [27–29]. In order to account for different resistance properties, different leakage coefficients are applied for infiltration (cl,in) and exfiltration (cl,ex) (see, e.g., [18,30]):
The diagram in Figure 1 shows the relationship between the leakage flux and the head difference according to the Darcy leakage approach. Different leakage coefficients are used for infiltration and exfiltration, respectively.
The total leakage flux Q (m3/s) is the product of the exchange rate q and the interface area A (m2):
With Equation (7), the Darcy approach describes a linear relationship between Q and ∆h if the interface area is assumed to be constant. The leakage function becomes nonlinear if the interface area A is calculated in dependence of the wetted perimeter of the river bed p (m) (see Figure 1), as proposed by Pinder and Sauer [10], Cunningham and Sinclair [21], Panday and Huyakorn [31], Krom and Graham [32] and Rushton [26]:
In this equation, l (m) stands for the length of the river section, which usually remains constant during the flow simulation. The wetted perimeter p depends on the river stage and the river morphology.
An empirical nonlinear relationship between exchange rate and head difference is presented by Rushton and Tomlinson [33] (see also [34]):
C1 (m2/s), C2 (1/m) and C3 (m2/s) are positive leakage parameters. For small changes in the head difference, a large increase of the exchange rate is achieved if the parameters C1 and C3 are adjusted appropriately. C2 limits the exchange rate for large values of ∆h.
The leakage rate is related to the length of the river section. Thus, the total leakage flux is obtained as:
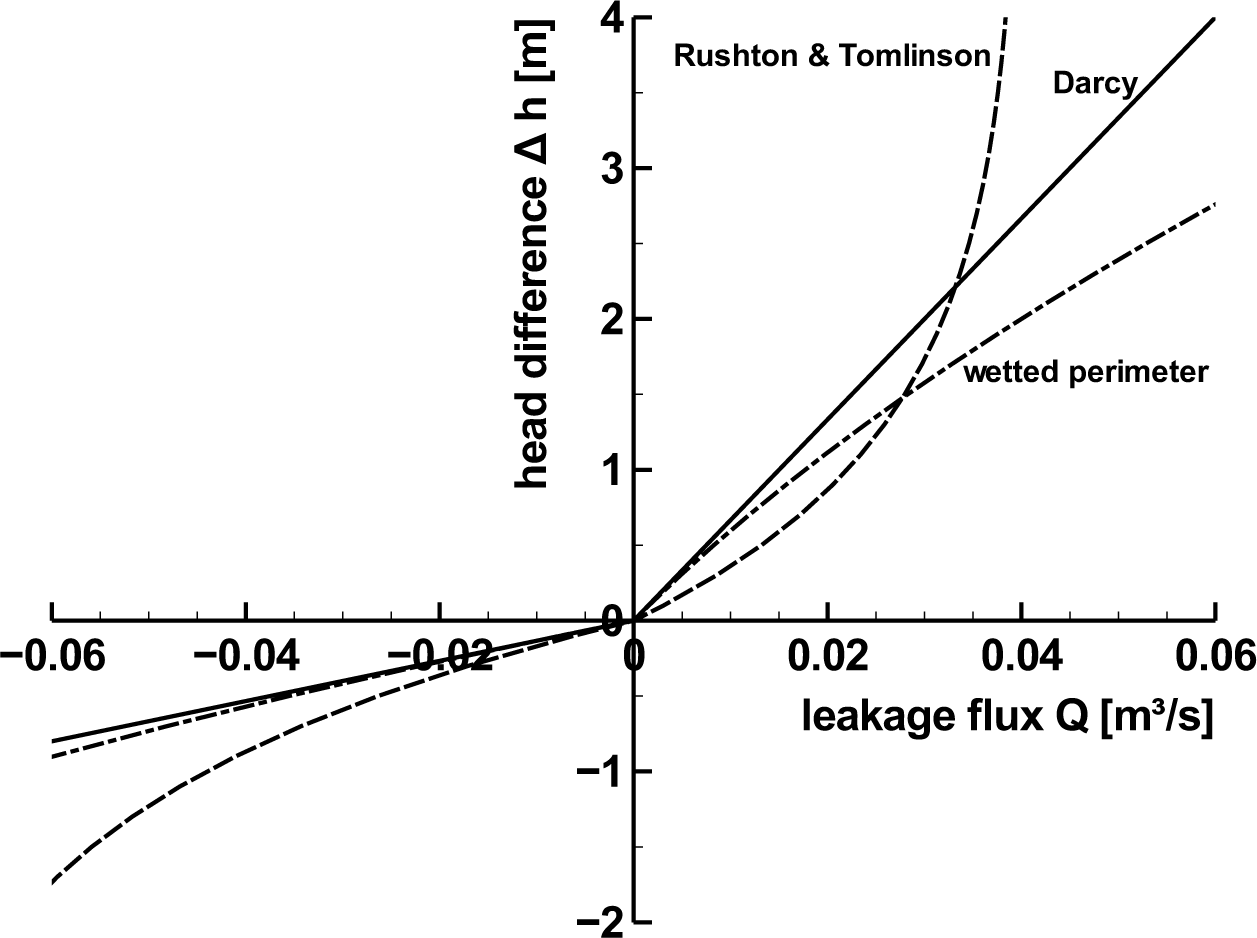
The diagram in Figure 2 shows example infiltration curves for the Darcy approach, the wetted perimeter approach and Rushton and Tomlinson’s empirical approach. For all curves, the groundwater level hG has been set constant to 4.5 m. The river stage hR varies between 2.5 m and 8.5 m. In order to show the different characters of the three approaches, the leakage parameters and the channel geometry (Table 1) have been chosen in such a way that all three leakage functions give flux values in the same order of magnitude for a given head difference. The approach presented by Rushton & Tomlinson [33] leads to disproportional small flux values in case of large head differences. The linear Darcy approach does not differentiate between large and small head differences, and the wetted perimeter approach gives disproportional high flux values for large head differences. For the wetted perimeter approach curve, a trapezoidal cross-section with a bed elevation of 0 m above the datum has been applied.
Subsurface flood events are characterized by high infiltration into the aquifer during a comparatively short period of time. High water in the river initially causes large head differences. Figure 2 shows that leakage flux values that correspond with high head differences can be very different, depending on which leakage approach is applied. Which leakage approach is suitable depends on the study area, the intensity of the surface water-groundwater interaction and the objectives of the study. For hydrological modeling studies that aim to estimate the runoff induced by a specific rainfall event, a simple approach can be sufficient, while for groundwater models that are bordered by large rivers and that are built in order to assess the impact of groundwater extractions on the groundwater balance, a more advanced approach can be necessary. The third order boundary condition feature of several groundwater flow simulation programs, like the MODFLOW river package [35], FESSim [36] or Feflow [23], is based on the Darcy approach, and several textbooks (e.g., [15–17]) recommend this approach for the stream-aquifer interaction; therefore, it is assumed that in many practical model applications, the Darcy approach is used both for small and large rivers and streams. The approach proposed by Rushton and Tomlinson [33] limits the infiltration for high water level differences, so this approach will apply for small rivers and streams with small variations in water levels. Krom and Graham [32] report an application case where they use the wetted-perimeter approach for a braided river with wide cross-sections, where a small increase of discharge is attended by a large increase of the wetted perimeter. In theory, the wetted perimeter approach is physically more accurate than the Darcy approach, because it takes the change of the interface area into account.
2.3.3. The Leakage Boundary Condition of the Groundwater Flow Simulation Program Feflow
The groundwater flow simulation program Feflow provides a leakage boundary condition based on Darcian flow; Equation (4). The leakage rate q = cl∆h depending on the river stage hR and the unknown groundwater level hG is set as a source or sink on the boundary condition node. Different parameters for infiltration and exfiltration can be set (Equation (6)). The total interface area A is calculated as:
3. Bank Storage during the Rhine Flood Event in the Neuwieder Becken in April, 1983
3.1. Study Area
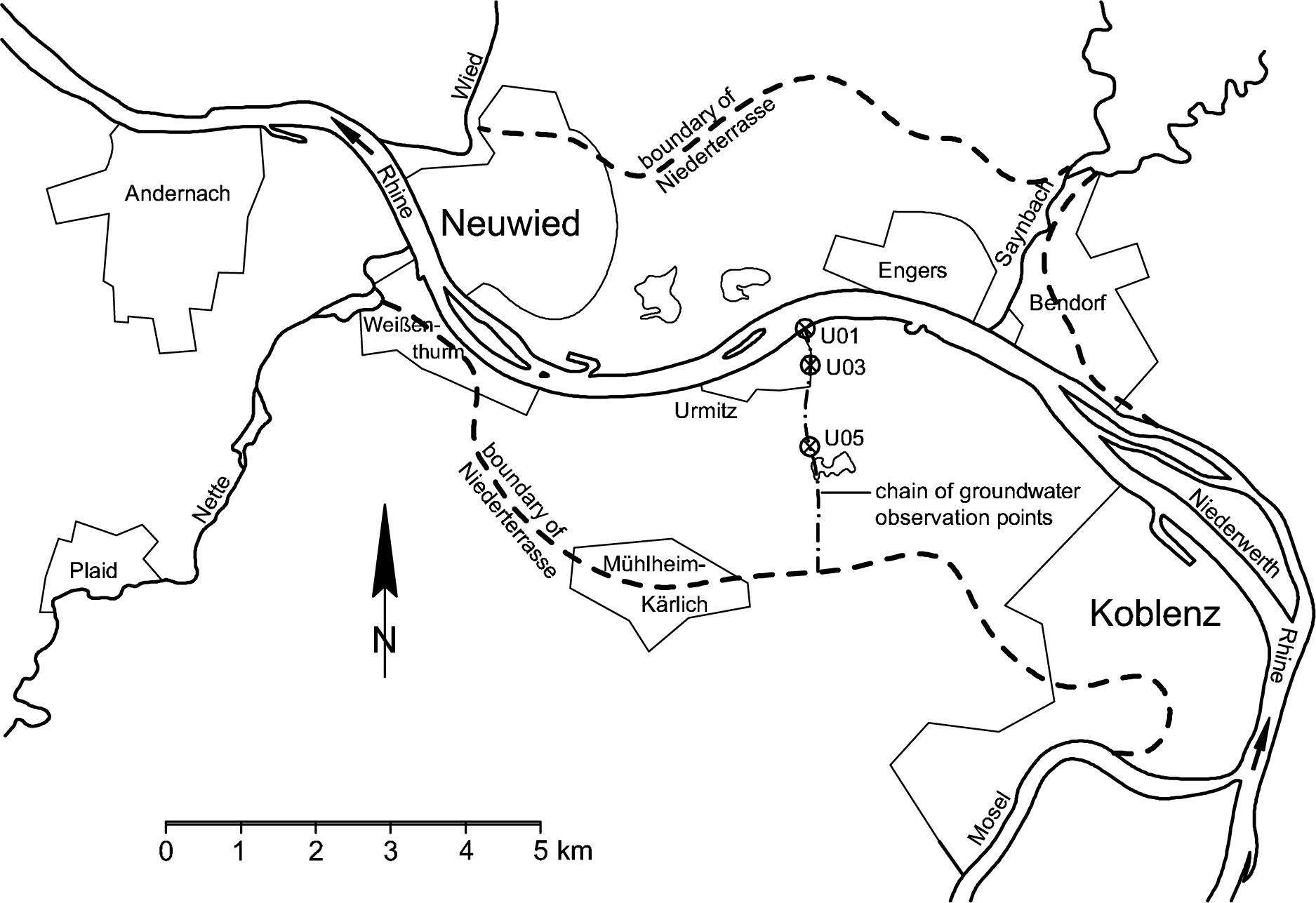
With a length of 1232 km, the Rhine is one of the largest European rivers. At the gauge in Emmerich, the average discharge is 2330 m3/s, and the Rhine is 730 m wide here [37]. The Neuwieder Becken is a broad valley at the Rhine located between the cities of Koblenz and Andernach (see Figure 4). Here, the Rhine is about 400 m wide. The Neuwieder Becken covers an area of 7 km in width and 15 km in length and is a result of tectonic settlement within the “Rheinisches Schiefergebirge”. Sedimentary and erosion processes generated several terraces (the two large ones are the Ältere Niederterrasse and the Jüngere Niederterrasse). This results in a localized groundwater system with minimal interaction with other groundwater systems [38]. Above the tertiary aquifer base of hard rock [12], there is a thick gravel aquifer with a high permeable material that is covered with layers of sand and sandy loam. Loose pumice stones originating from the Laacher See volcano [39] can also be found. In Figure 5, a cross-sectional hydrogeological profile is given.
Ubell [12] gives hydraulic conductivity values kf of between 2 · 10−2 m/s and 4 · 10−3 m/s for the Niederterrasse aquifer, the average saturated thickness being 10–15 m and the effective porosity neff 0.20. The groundwater in the Niederterrasse aquifer is primarily influenced by the Rhine water [12]. Groundwater recharge originates mainly from rainfall and base flow from the hillside. A water supply company extracts groundwater for water supply. However, due to the high permeability of the aquifer material, the influence of groundwater extractions on the groundwater table is limited locally.
Near the village of Urmitz at Rhine kilometer 602.4 (official chainage), a chain of seven observation points has been installed [12,40]. The location of the observation points is shown in Figures 4 and 5. These observation points are not located in the area of influence of the groundwater extractions [40].
3.2. Hydrographs during the Flood Event in April, 1983
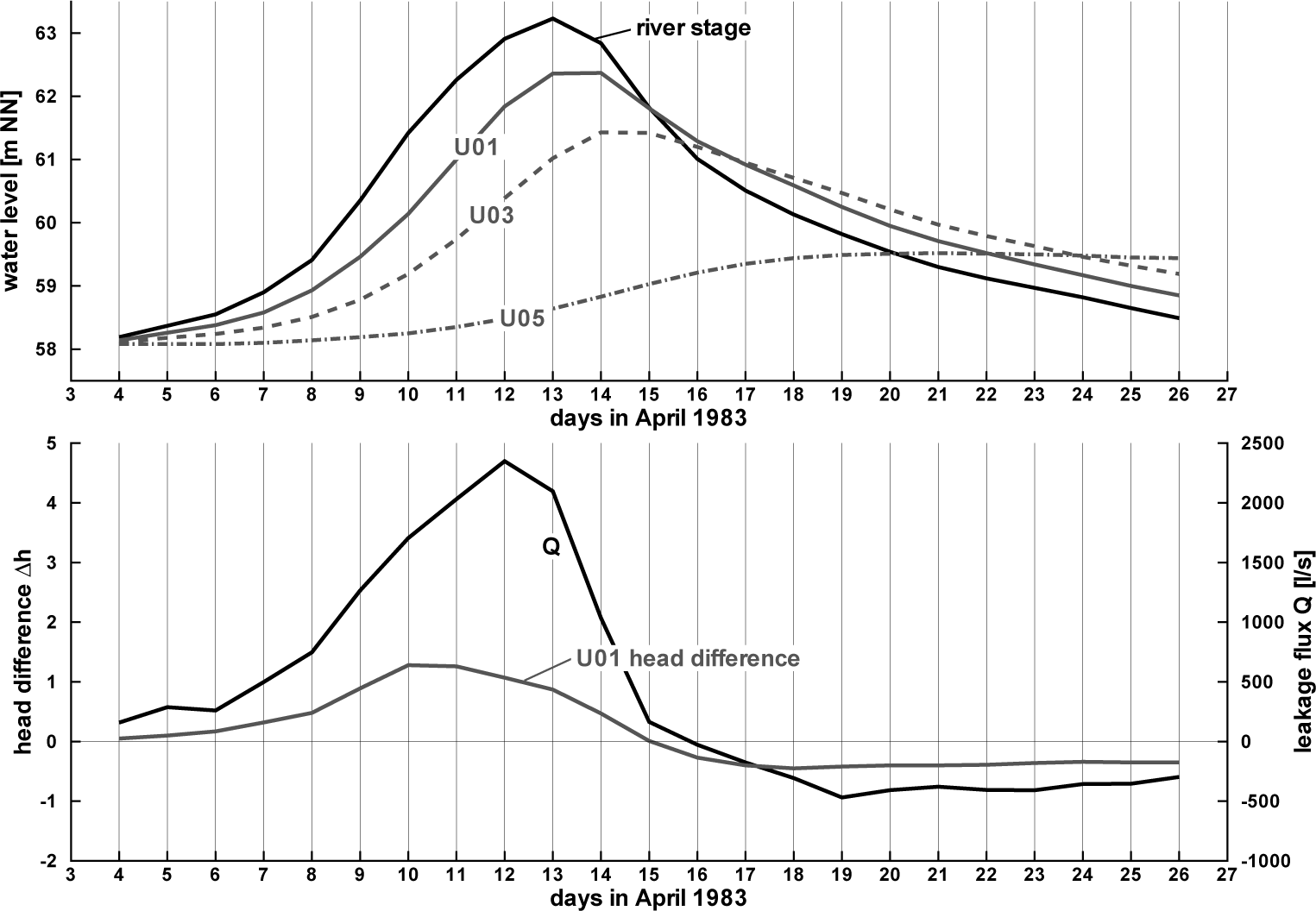
Figure 6 shows hydrographs of the Rhine river stage and groundwater levels at three groundwater observation points located in the profile “Urmitz” with different distances to the river bank (see Table 2). The hydrographs are related to the flood event in April, 1983. The diagrams give evidence for a strong interaction between the river and neighboring aquifer: according to the distance between the observation point and the river bank, the groundwater level hydrographs follow the river stage, damped and with delay. River and aquifer are always connected, because the groundwater level never falls below the river bed. The fact that the impact of rising river stage reaches that far into the hinterland is facilitated by the high conductivity property of the aquifer and the long duration of the flood event. Rushton [26] points out that the river coefficient or river conductance, which is defined as:
“depends primarily on the horizontal hydraulic conductivity of the aquifer system rather than the vertical hydraulic conductivity of the riverbed deposits”. A rapid increase of the groundwater level is attended by an increase of saturated thickness that, again, facilitates the entrance and spreading of river water towards the hinterland.
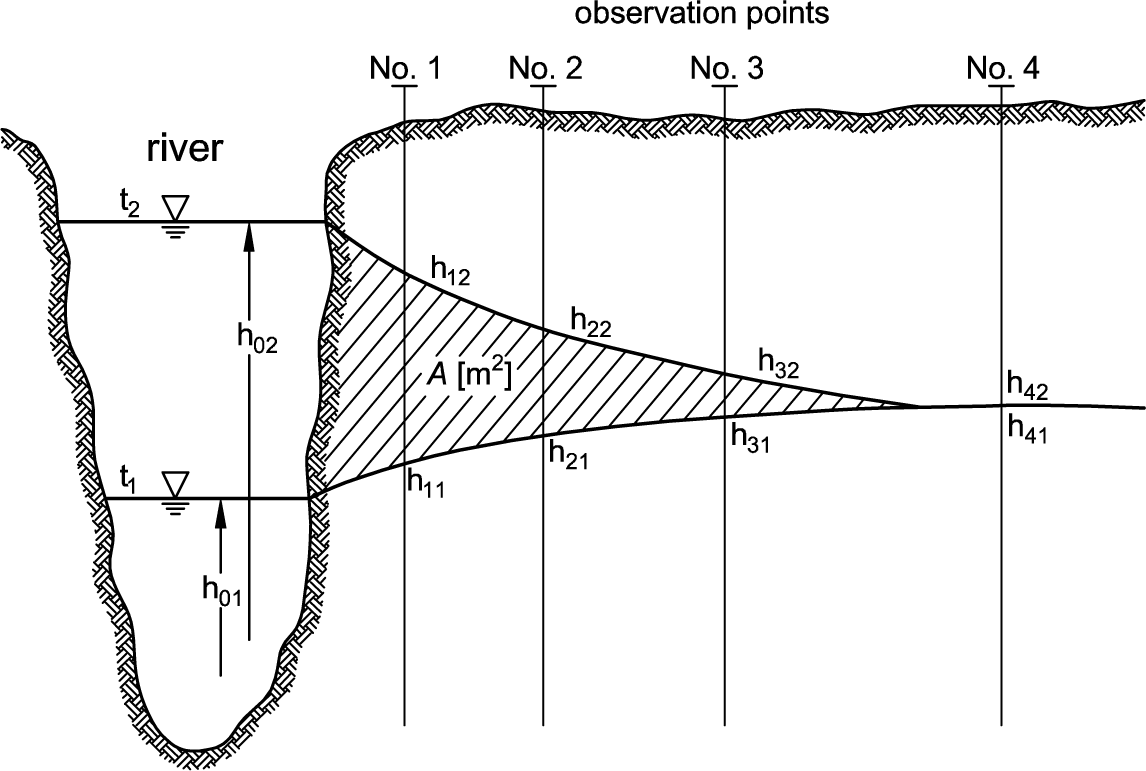
The leakage flux has been determined by Ubell [12] with his volume balance method (Volumenbilanzmethode, see [11,12,41,42] and Appendix). The course of leakage flux over time does neither coincide exactly with the Rhine water stage nor with any groundwater observation hydrograph: the maximum exchange flux occurs on Day 12, while the maximum water level in the river Rhine occurs later, on Day 13. The maximum groundwater level for groundwater observation point U01 reaches its maximum value one day later again.
3.3. A Leakage Function for Ubell’s Rhine Flood Event
In order to derive a leakage function for the flood event in April, 1983, head differences between the river stage and the groundwater level observed at observation point U01 have been calculated (Figure 6, bottom). Observation point U01 has been chosen, because this observation well is located directly at the bank and, thus, is the most feasible of all observation wells according to the leakage approach conceptual model, where the head difference ∆h is defined between both sides of the assumed interface layer. The head difference values mainly comprise two sources of inaccuracy: firstly, the river stage used for the head difference has been measured at a different location and has been transferred to the chain of observation points [12]. Secondly, the groundwater level is related to an observation well that does not necessarily represent the edge of the interface layer. If there is a distance between the aquifer side of the interface layer and the location the head difference ∆h is computed, the groundwater level hG reacts to the leakage flux q with delay (see [43]) and not directly. However, as observation point U01 is located at the river bank, we assume this effect to be small.
Leakage flux values were taken from Ubell [12]. It is generally difficult to obtain the amount of water exchanged between river and aquifer, because it is nearly impossible to measure the leakage flux directly (see Appendix). Ubell’s method requires that the flow direction must always be parallel to the chain of observation points. For the current example, this condition is violated for normal flow conditions when the groundwater flows parallel to the river [38]. However, the leakage function covers a time period of high water conditions, where the flow direction is oriented along the line of observation points [38]. For the calculation of the volume stored in the aquifer per period of time, the storage coefficient has been assumed to be spatially and temporarily constant. Finally, the method neither allows for the separation of groundwater recharge processes and backwater effects from base flow from the hillside, nor does it account for the influences of groundwater withdrawal and the effect of the gravel pits on the groundwater storage. However, the impact of those processes is assumed to be small in comparison to the impact of the infiltration of river water [40].
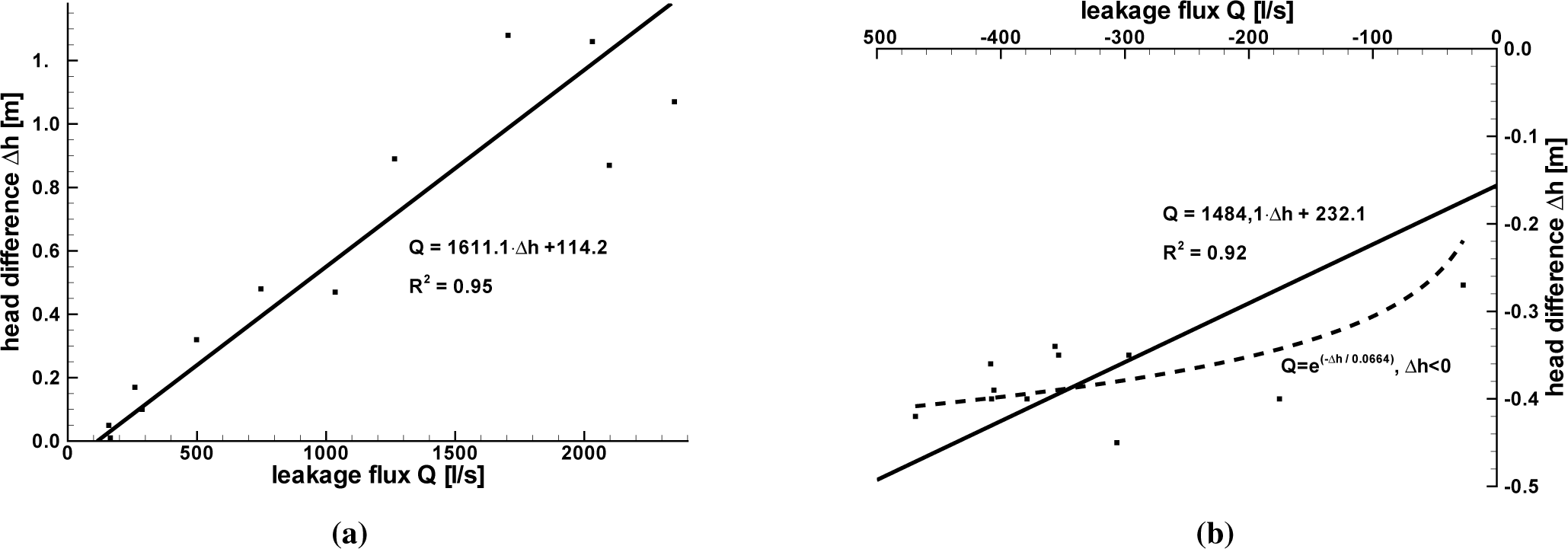
Figure 7 shows the pairs of values of Q and ∆h for infiltration and exfiltration and smoothing functions. For positive leakage flux, a linear leakage function seems to represent the infiltration process quite well. However, the curve does not hit the point of origin. This is not in accordance with the leakage model concept. Inaccuracies of the volume balance method that have been mentioned above can be one reason for this behavior. Another explanation is that the water exchange is governed by processes not covered by the leakage conceptual model. These processes are discussed at the end of this section.
For the exfiltration process, the slope of the regression line is slightly lower than the slope of the regression line for the infiltration process. The axis intercept is larger than in the case of infiltration, while the coefficient of determination R2 calculated for exfiltration is smaller than it is in the case of infiltration. An exponential function appears to match better with the observed data. However, the interpretation that the leakage flux is independent of the head difference seems also to be suitable here. In this case, the leakage model would not be appropriate to describe the interchange process. As mentioned in Section 2.3.2, it is often assumed that the leakage flux for a certain head difference is smaller for infiltration than for exfiltration, due to a river bed colmation (see, e.g., [27]). The leakage function presented here does not support this assumption for the current case.
In the case of infiltration, the absolute head differences range between zero and 1.28 m, while for exfiltration, the maximum absolute head difference is only 0.45 m. Large absolute head differences coincide with large leakage fluxes. This matches well with the view in which a groundwater level rise occurs within a short time period due to infiltration, but then decays very slowly (see, e.g., [1,2]).
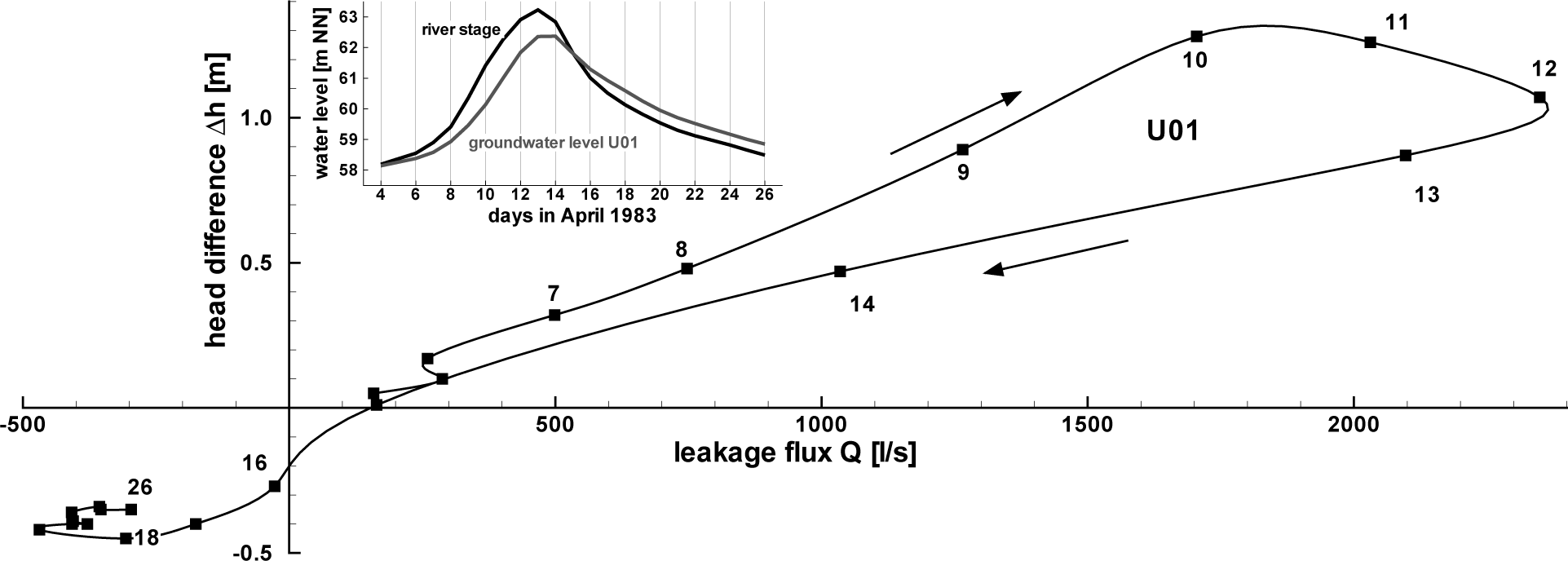
An evaluation of the Q-∆h relation with respect to the chronological sequence of the flood event is given in Figure 8. The curve has a hysteretic course: up to Day 10, the curve increases with an approximately linear course. From Day 10 to Day 11, the head difference rises only a little, while the leakage flux increases disproportionally high. On Day 12, the head difference already begins to decrease, but the leakage flux continues to rise. Therefore, a limitation of the leakage flux for large head differences ∆h, as given with Equation (9), seems less appropriate than a leakage function that returns disproportionally high values for large head differences, like the wetted perimeter approach.
There are several possible physical explanations for a hysteretic leakage function:
Both the groundwater level and the river stage change over time. Consequently, the wetted perimeter of the river cross-sectional profile changes as well. Therefore, for the same head difference, two different leakage fluxes are possible.
The properties of the interface layer between river and aquifer change during the flood event (see, e.g., [44]). Sedimentation of a suspended load or biogenous stabilization processes create a colmation layer on the river bed during normal or low flow conditions. A flood wave can destroy this colmation layer because of increased shear stress, and reduce the sediment layer’s thickness or even totally erode the sediment layer. In addition, the loosening of the river bed material may increase the hydraulic conductivity of the river bed, which increases the exchange of water between the river and the aquifer. With the decay of the flood event, the river bed is clogged again by sedimentation and stabilization processes and allows the leakage flux to decrease slowly [28,45–47]. Rushton [48] (Section 12.2) reports a hysteretic course of the river coefficient over river stage for the semi-arid River Yobe in northeastern Nigeria within a cycle of the hydrological year.
The temperature of infiltrating river water is higher than the temperature of the pre-event groundwater in the aquifer (see [25]). With an increasing temperature, the hydraulic conductivity increases, which again allows more river water enter the aquifer.
Preferential flow paths created by animals or ice crushes can be activated during the flood (see [49]).
4. A Numerical Groundwater Model for Ubell’s Case
4.1. Introduction
Within this section, we present a groundwater model for Ubell’s bank storage case. The objective is to reproduce the observed groundwater levels and the derived leakage flux from Ubell [12] with the groundwater model. The river-aquifer interaction is modeled in two different ways: as a leakage boundary condition and as a head boundary condition. By comparing the simulated leakage function of these two model variants with the one derived from observed values, we assess these two ways of modeling the river-aquifer interaction in a groundwater model.
4.2. The Groundwater Model
Ubell [22] already presents a groundwater model of the vertical cross-section through the aquifer along the chain of observation points near Urmitz (see Figures 4 and 5). He uses this model to quantify the impact of river-aquifer exchange processes on the water balance of the River Rhine.
Our groundwater model represents the same model area, and the conceptual model of the hydrogeological system follows Ubell [22] using the equations for saturated flow in porous media:
In this equation, h denotes the groundwater head at time t; ki the hydraulic conductivity; and x1, x2 and x3 are Cartesian space coordinates. The specific storage Ssp incorporates the specific yield or drainable porosity Sy and the specific storage (compressibility). For the current case, the specific storage is neglectable against the drainable porosity, because of unconfined conditions. Equation (15) is solved with the finite element method using the groundwater flow simulation program Feflow [18,19].
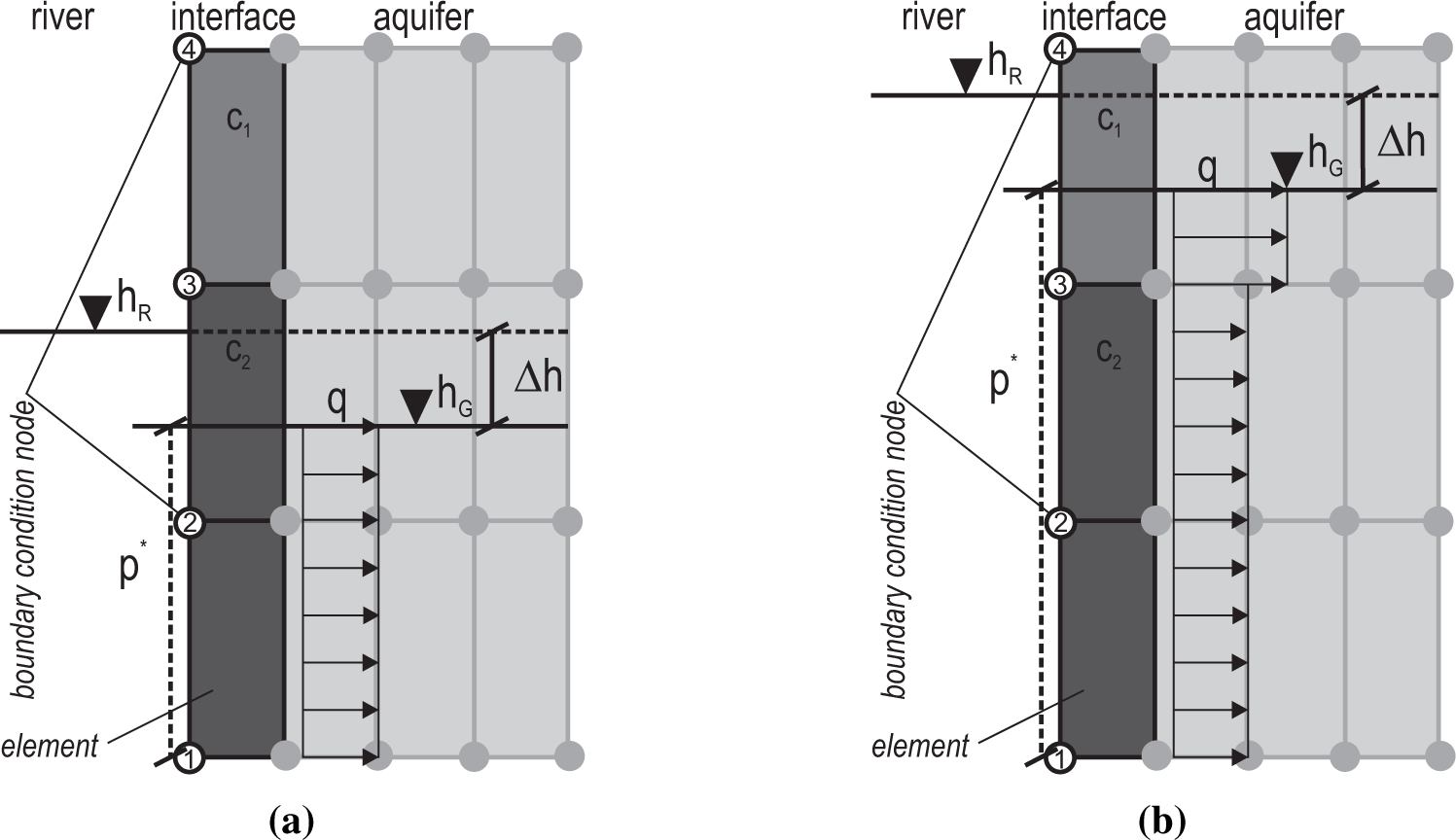
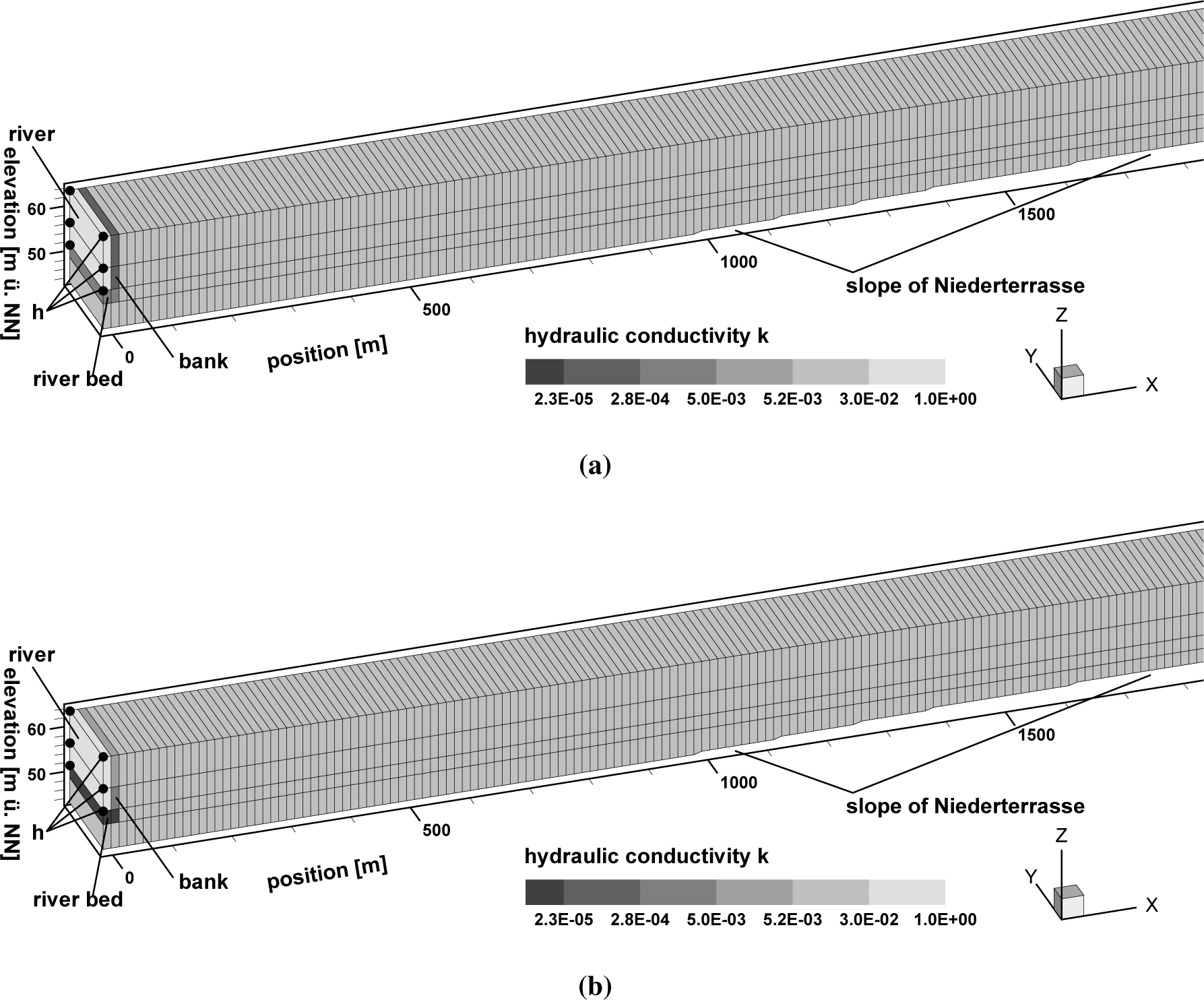
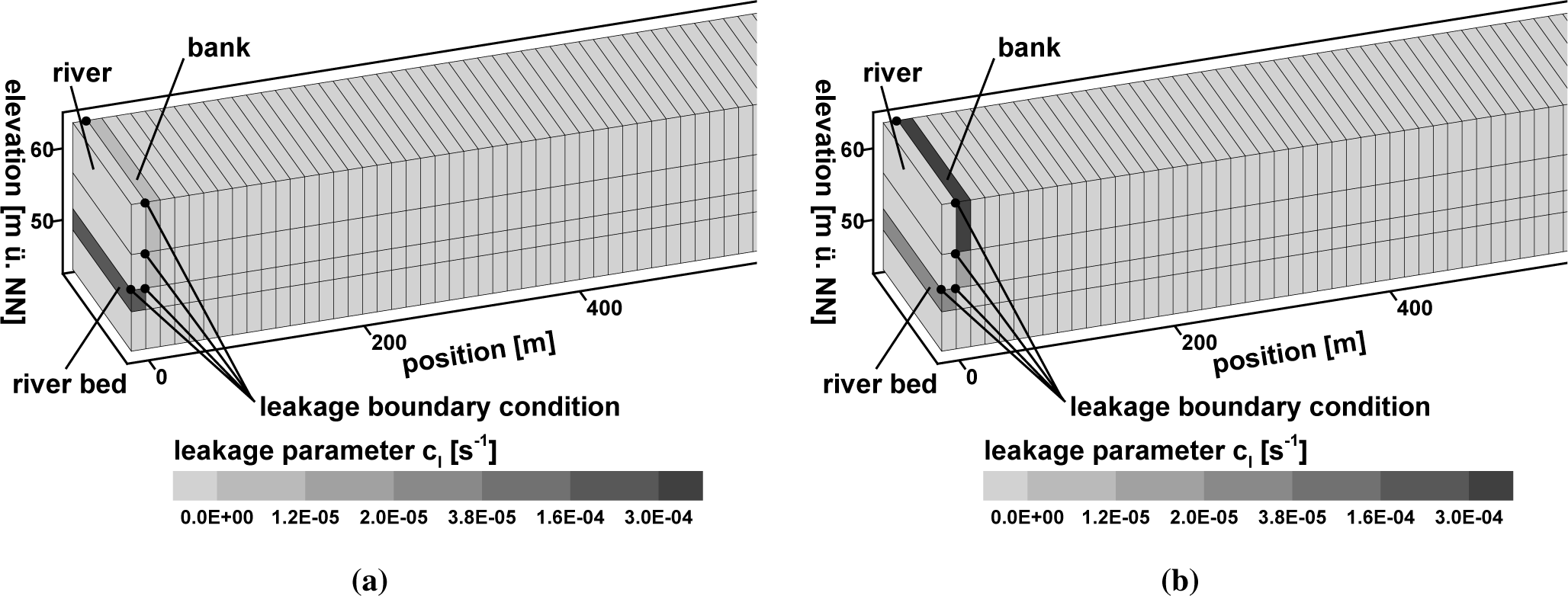
For the current model, the flow equations are solved in three dimensions, but boundary conditions are set in such a way that there is no velocity component perpendicular to the cross-section, so the model is in principle a two-dimensional vertical model. The computational grid and the location of boundary condition nodes are shown in Figures 9 and 10 for the two model variants. The computational grid has been generated automatically, and it consists of one times 247 brick elements in the horizontal plain. Each element has a base area of 13.415 m by 13.415 m, which adds to a length of 3300 m, plus one element length for the river. The vertical dimension is discretized by four element layers. On the left model boundary, two element columns represent the river (the water), the river bed and aquifer material below the river bed and the bank. The element height of the topmost element layer is variable and changes with the free groundwater surface. The movement of the groundwater table is modeled with the BASD method (best adaption to stratigraphic data; see [51]). This method incorporates the free-surface location, which is a priori unknown, as two additional boundary conditions of the three-dimensional formulation of the flow equations.
In the head boundary condition model variant, we set the river stage at the nodes that represent the river itself, while for the leakage boundary condition variant, we applied the boundary condition on those nodes that represent the surface of the interface area. Following Ubell [22], on the right boundary (the Niederterrassenrand), a no flow boundary condition is set, and neither groundwater recharge nor leakage from the aquifer base are considered in the model.
4.3. Calibration Data and Calibration Parameters
A model calibration aims for a good match between simulated values and observed values (the calibration data) by adjusting specific model parameters (the calibration parameters). For the current case, the hydrographs from the seven observation points [12] are used as calibration data. The locations of the observation points are given in Figures 4 and 5, and three hydrographs from the observation points are given in Figure 6. In order to assess the calibration quality, the Nash–Sutcliffe efficiency [52] is calculated for each observation point hydrograph. The hydrographs represent the groundwater level at a point in space over time. Ubell [12] also constructed groundwater tables from the observed data for the whole modeling area, i.e., the cross-sectional profile, for three points in time. These groundwater tables are used as calibration data for visual assessment.
The hydraulic conductivity k and the leakage parameters cl are used as calibration parameters and leakage parameters only in the case of the leakage boundary condition model variant. The finite elements have been divided into eight element zones, as shown in Figure 11. Zones 1, 2 and 3 represent the river bank, and Zones 4 to 8 have been defined based on a preliminary study [53]. Zone 5 and 7 account for the change of the groundwater gradient in Ubell’s groundwater tables (see Figure 12) that indicates discontinuities in the aquifer. Table 3 indicates the usage of calibration parameter zones according to the calibration method and the model variant.
A drainable porosity value of Sy = 17.5 % for elements representing the aquifer has been determined in the preliminary analysis (see [53]). In the vicinity of observation point U05, the storativity value has been set to Sy = 80 % in order to account for a gravel pit. River elements are assigned a value of Sy = 0.
4.4. Calibration Procedure
The model variants have been calibrated manually by carrying out the following steps repeatedly:
comparison of simulated and observed hydrographs, as well as simulated and constructed groundwater tables;
identification of the calibration parameters to be changed and a decision for how to change them;
adjustment of one or multiple calibration parameters according to the decision made in Step (2);
simulation run.
Within the first calibration runs, the modeler gathers experience for how sensitive the model reacts with respect to certain parameter values. For the decisions on how to change a certain calibration parameter (Step (2)), it has been assumed that conductivity values in the river bed are higher than at the bank according to the findings of Giebel and Hommes [40] and Ubell [22]. Decisions were based on the match between observed and simulated hydrographs at the observation points and the match of simulation results to the groundwater tables from Ubell [22].
In order to verify the calibration result, an automatic calibration has been carried out as well. For the automatic calibration, a Feflow module [54] that contains the PEST algorithm [55] has been used. PEST regards the calibration as an optimization problem. With a gradient type optimization algorithm, PEST minimizes the least squares of difference between observed values (the calibration data) and simulated values. Since the optimization algorithm does not necessarily find a global minimum of the objective function, initial parameter values have an impact on the calibration result. According to Ubell [22], we used a homogenous hydraulic conductivity of k = 3.0 · 10−2 m/s as the initial value; for the leakage boundary condition model variant, an initial leakage parameter value of 1.0 1/s has been applied. In order to avoid calibration results that physically make no sense, a confidence interval has been set as a constraint for each calibration parameter:
For the automatic calibration, the parameter zones 4 to 8 were treated as one zone, because for parameter Zones 5 and 7, no corresponding observation hydrograph is available. Test runs showed that the optimization algorithm found results that physically make no sense if there are zones where no calibration data is assigned to.
The Feflow calibration module cannot differentiate between cl,ex and cl,in. Therefore, for the leakage model variant, the automatic calibration has been carried out separately for the infiltration phase and the exfiltration phase of the bank storage event.
4.5. Calibration Results
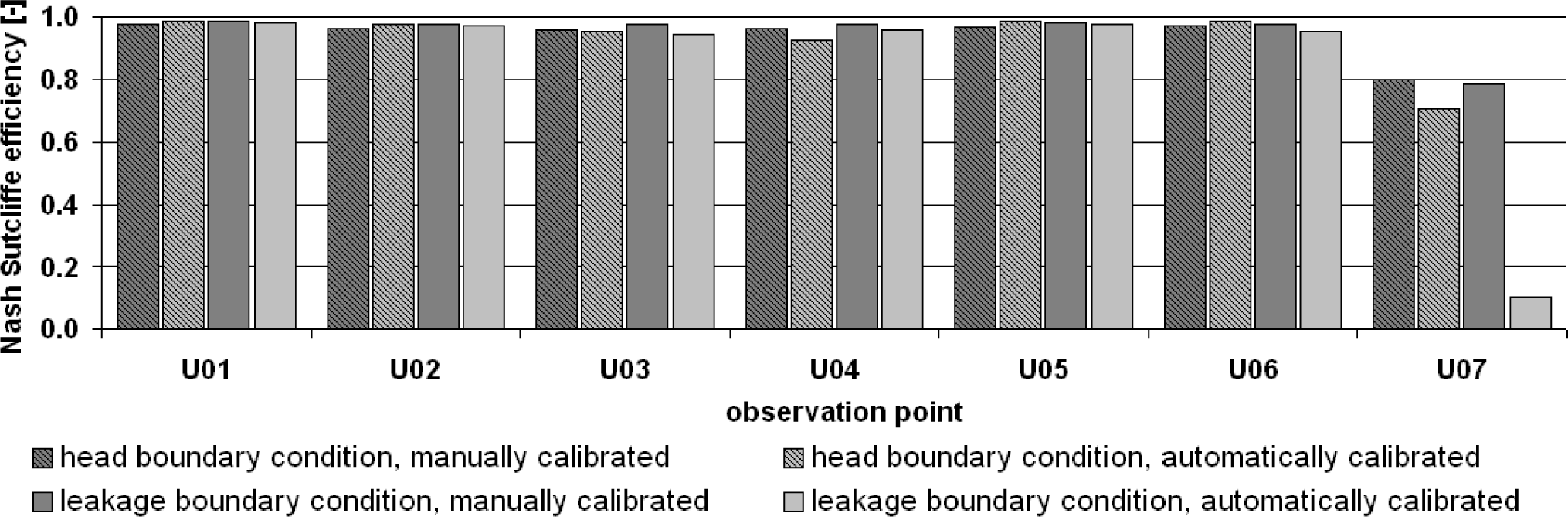
In Table 4, the Nash–Sutcliffe efficiency for the seven observation points for each model variant is given, both for the manual calibration and the automatic calibration. Figure 13 shows a graphical representation. The Nash–Sutcliffe efficiency takes values between −∞ and one, where a Nash–Sutcliffe efficiency of one indicates an exact match between observed and simulated values. In the case of a negative Nash–Sutcliffe efficiency, the observations are better represented by their average value than by simulated values [52].
For observation points U01 to U06, a very good calibration quality for all model variants and both calibration methods has been achieved. The Nash–Sutcliffe efficiencies for observation point U07 indicates a good or acceptable match for the manually calibrated models and the automatically calibrated head boundary condition model as well; however, for the automatically calibrated leakage model, the obtained Nash–Sutcliffe efficiency of 0.103 is not sufficient. Regarding the sum of the Nash–Sutcliffe efficiencies (Table 5), the manual calibration seems to perform better than the automatic calibration; this is not surprising, as in the manual calibration more parameter zones were applied than in the automatic calibration. The manual calibrated leakage model variant gives the best calibration result in terms of Nash–Sutcliffe efficiency.
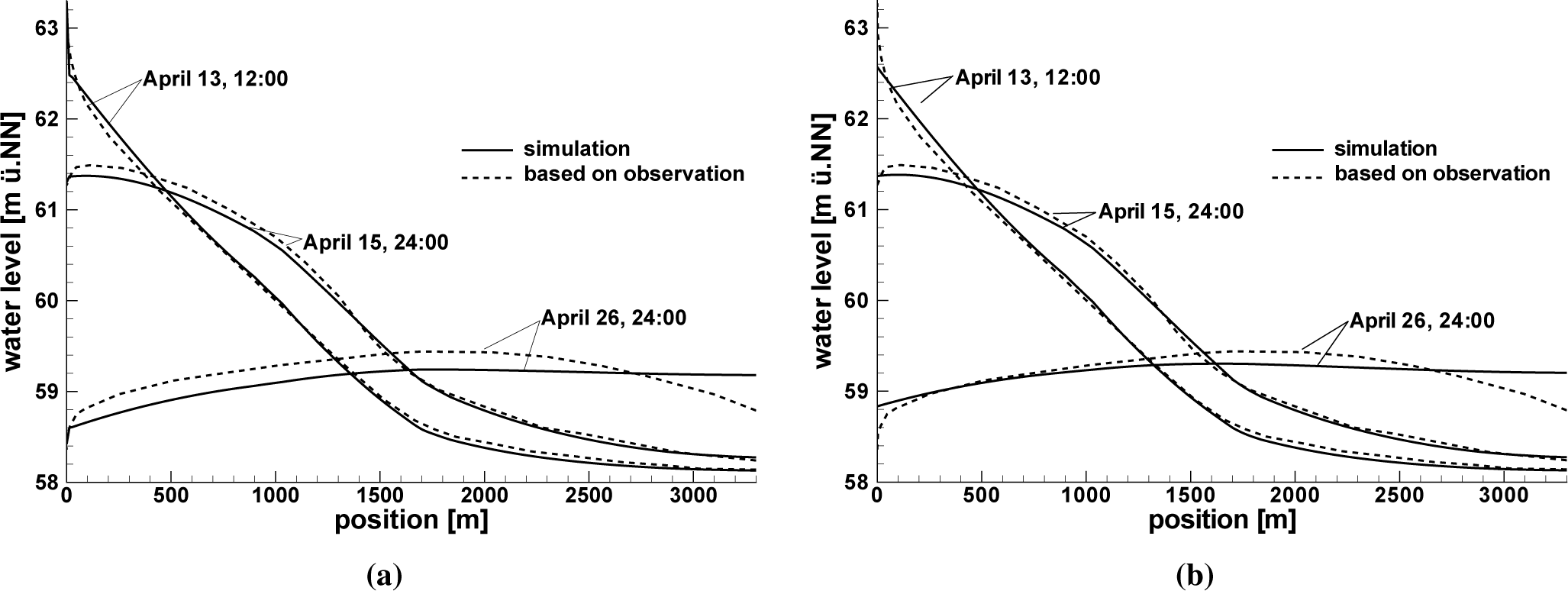
Figure 12 shows a comparison of simulated groundwater tables along the cross-sectional profile from the model with the head boundary condition (Figure 12a) and the leakage boundary condition model variant (Figure 12b) with the groundwater tables Ubell [12] derived from observations. On 13 April, the river stage reaches its maximum. On this day, the groundwater table simulated with the head boundary condition model matches quite well with the groundwater table based on observed values for the whole profile. Two and a half days later, on Day 15, however, the simulated water table lays below the one based on observed values for positions between 0 m and 1400 m. For the point in the simulation time of 26 April, 24:00 h, the match between the simulated groundwater table and the one based on observed data is even worse. Changing the hydraulic conductivity for bank elements would improve the data match for 26 April, but would also affect the water exchange during the infiltration phase. This would worsen the match between simulation results and observations for Days 13 and 15 of April, 1983. Because the leakage approach used here allows one to address the leakage parameters cl for infiltration and exfiltration independently, with the leakage boundary condition model a better match between the simulated groundwater tables and the groundwater tables derived from observed data could be achieved (Figure 12b). As shown in Section 3.3, infiltration and exfiltration follow different flow patterns, so assigning different parameter values for infiltration and exfiltration seems more appropriate for the current case.
The water table in the hinterland of the river bank (positions further than 2600 m from the river in Figure 12) for 26 April is generally not very well represented by simulation results. At this point in time, low flow conditions with groundwater currents parallel to the river occur (see [38]) that are not represented in the models, because the model represents a cross-section perpendicular to the river only. This also might explain the low Nash–Sutcliffe efficiency values obtained for observation point U07.
Figure 9 shows the parameter value distribution of the head boundary condition model variant obtained by manual and automatic calibration. Contour levels of the finite elements indicate the value of hydraulic conductivity in the pictures. The corresponding parameter values are given in Table 3. The parameter distribution differs with the calibration method: while in the manual calibration larger conductivity values are allocated to the river bed, the PEST calibration algorithm has allocated high conductivity values to the upper bank. A similar distribution pattern of calibration parameter values has been obtained with the leakage boundary condition model variant (Figure 10): for the infiltration process, high leakage parameter values are located at the river bed in the manually calibrated model, while in the automatically calibrated model, the high parameter values are located in the bank.
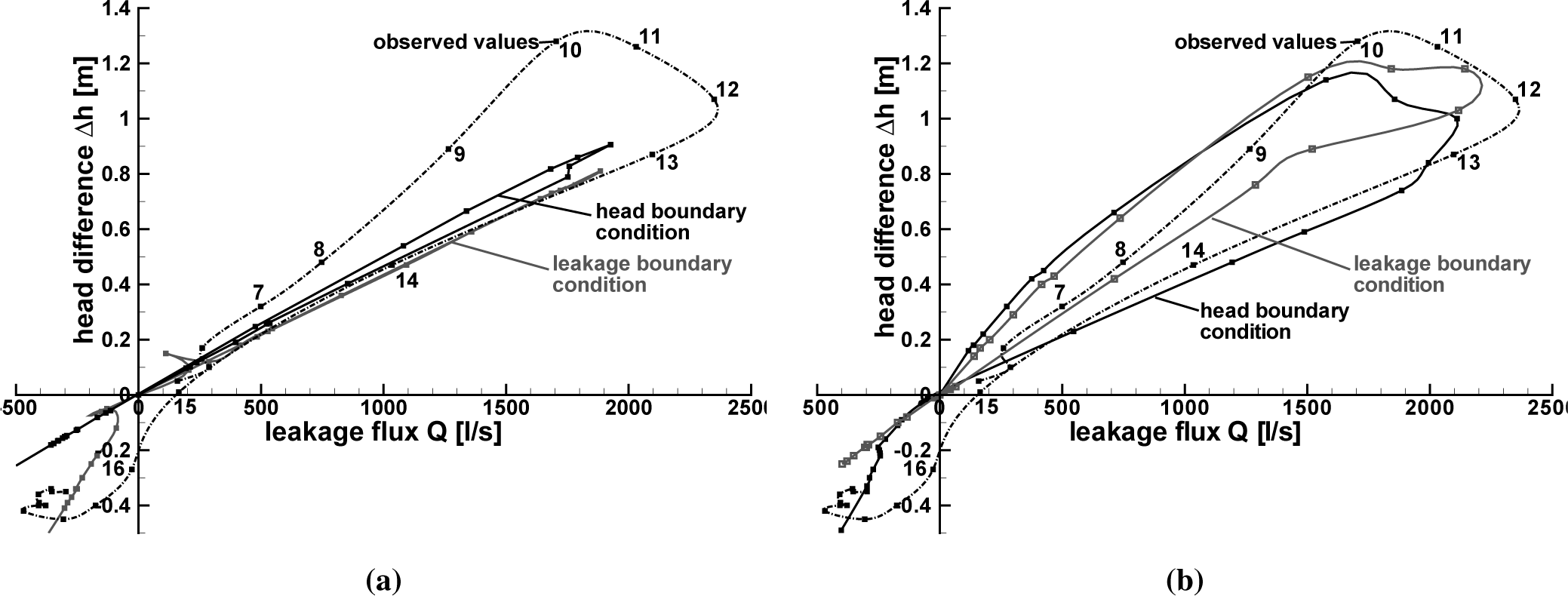
The parameter value distribution has an effect on the simulated Q-∆h-relationship: Figure 14a shows the leakage functions of the manually calibrated models, and Figure 14b shows the two leakage functions obtained with the automatically calibrated models. Only the simulation results of the automatically calibrated models show a distinct hysteretic course. In the beginning and at the end of the flood event, the top element layer contributes only marginally to the total leakage flux. With a rising groundwater level, the calculated interface area A (Equation (12)) increases, but also the top element layer has more impact on the leakage flux calculation (see Figure 3). The optimization algorithm addressed this element layer in order to achieve disproportionally high leakage fluxes during high water, which results in a hysteretic leakage function. In the manual calibration, however, the upper element layers were assigned low values of hydraulic conductivity, according to the findings of Giebel and Hommes [40] and Ubell [22], so the impact of a larger interface area during high groundwater levels is not as great.
Figure 14a also shows that the head boundary condition model variant leads to a uniform slope for negative and positive leakage fluxes, while the leakage function obtained from the manually calibrated leakage boundary condition model gives a different slope for infiltration and exfiltration, respectively. Around the origin, there are outlier values in the curves from models with leakage functions. These outliers arise from the fact that the groundwater level is still unknown when the leakage parameter is chosen according to the flow direction. Feflow does not carry out iterations, even if it turns out that the parameter for the wrong flow direction has been applied.
4.6. Discussion
The Nash–Sutcliffe efficiency and the comparison with constructed groundwater tables indicate that the manually calibrated leakage model variant performs better for the current case than the corresponding model with a head boundary condition. The fact that the leakage boundary condition model variant allows one to address infiltration and exfiltration independently results in a leakage function that matches better with the one derived from observed data, but is also advantageous for the practical calibration work. However, the leakage approach contains the assumption that the conductivity properties of the river bed change with the direction of exchange water flow, which is not necessarily the case, as discussed in Section 3.3.
The manually calibrated models result in a leakage function with a linear and (nearly) non-hysteretic course. The high Nash–Sutcliffe efficiencies obtained with the manually calibrated models indicate that the hysteretic course of the leakage function is not essential to reproduce the measured groundwater levels at the observation points. In the automatically calibrated models, the hysteretic course of the leakage function has been achieved by addressing the elements located at the upper layers, which are only active during high water. The resulting leakage functions match better with the leakage function derived from observed values.
The groundwater model geometry does not represent the real cross-section of the river very well. Doble et al. [56] show that the slope of the river bank itself and the corresponding variation of the interface area have an impact on the exchange of water between river and aquifer. A disproportional high increase of the wetted perimeter p for high river stages, for example when the flow situation changes from bank full discharge towards an inundation of forelands, is not incorporated in the model, because the vertical mesh boundary is required for three-dimensional models in Feflow. High permeability values in the upper parts of the bank (as obtained with the automatic calibration) can compensate for this technical limitation. This allows one also to account for preferential flow paths created by animals or ice crush (see Section 3.3) in the upper part of the bank, which are activated during high water only. However, for the current case, there is no evidence for such a preferential flow path in the literature, and the parameter distribution obtained by automatic calibration does not match qualitatively with the available information on the conductivity properties of the bank and river bed [22,40], whereafter the higher conductivity values are located in the river bed.
A possible change of hydraulic conductivity properties during the flood event due to erosion and sedimentation processes and biogenous stabilization are not taken into account in the groundwater model. A coupled simulation that incorporates river morphology [47] would be necessary to represent this processes. Furthermore, temperature effects have not been considered in the model. We have no information on the relevance of these processes for the current case, but both processes might be responsible for the hysteretic behavior.
Doble et al. [56] show that the capillary fringe above the groundwater table has a damping effect on the rate of flux that infiltrates the bank, because the soil must become saturated before it can convey substantial volumes of water. On the other hand, it takes longer to drain water that is stored in the unsaturated zone than in the case of saturated flow. The groundwater models used in this study assume fully saturated flow. Consequently, the effects of the unsaturated zone on bank storage processes are not taken into account. We have chosen to assume fully saturated flow for two reasons: Firstly, the aquifer characteristics with its comparatively high values of hydraulic conductivity legitimate this assumption. The calibration results show that a saturated flow model is able to reproduce the bank storage event in a good way. Secondly, modeling of variable saturated flow is not feasible for many practical applications, because the extent of the modeling area is too large and variable saturated flow modeling is computationally too expensive or because there is a of lack of data for unsaturated flow properties.
Regrettably, none of the model variants represents the exfiltration process of the analyzed case satisfactorily. Figure 6 shows that the leakage flux still changes after Day 16, while the head difference remains nearly constant. The effects of the bank slope [56] that are not taken into account due to the assumption of a vertical bank may play a role here. There are no model elements that can be activated only for the process of exfiltration in the way that it is possible for the infiltration process under high water levels. However, in the case of exfiltration, only small absolute values of leakage flux occur, so for the current case, the impact of the exfiltration process on the groundwater flow situation is small in comparison to the infiltration process. Thus, the exfiltration process does not affect the calibration quality that much.
Different calibration results lead to a good or acceptable match between observed and simulated values, although the parameter distribution is different. This shows once more the non-uniqueness of the solution of the calibration problem (see [57]). The validation of groundwater models with independent data and the post audit of the modeling concept [58] become important if models are applied for predictive analysis.
5. Summary, Conclusions and Outlook
A subsurface flood is a severe groundwater head rise due to a flood event in a river. Bank storage is one of the important water exchange processes between a river and the contiguous aquifer that governs the subsurface flood propagation. For predictive subsurface flood simulations, it is important to know how to represent the water exchange in a groundwater model. Against this background, we addressed the question of how bank storage can be represented in a numerical groundwater model.
Ubell [12] reports a bank storage event for the Neuwieder Becken in the Middle Rhine area (Germany). The leakage function is hysteretic, and during the infiltration phase, higher leakage fluxes and larger head differences occurred than during the exfiltration phase. Note that we analyzed one bank storage event of a specific site only, so the outcomes of this study are not necessarily transferable to other sites.
For Ubell’s bank storage event, we set up a groundwater model where we applied the river stage as:
head boundary condition; and
leakage boundary condition.
With both approaches, the groundwater model could be calibrated to a good match between observed and computed groundwater levels. This is not surprising, because both approaches are based on a similar conceptual model. For practical applications, however, the leakage boundary condition is recommended, because infiltration and exfiltration can be treated as two different processes. This matches better with the observations and makes the practical calibration work easier. Another advantage is that the interface layer is represented independently of the mesh, which will be relevant especially for models on a larger scale (see, e.g., [30]).
With our model, we obtain a hysteretic characteristic of the leakage function with a vertical variation of leakage parameters or hydraulic conductivity properties, respectively. This approach can represent a variable interface area that changes with the river stage and preferential flow paths that are only active during high water, but not a dynamic change of leakage properties due to erosion, sedimentation and biogenous stabilization. However, the simulations show that a parameter distribution that results in a linear leakage function is sufficient to represent the water interchange between river and aquifer for the analyzed case.
In many conceptual models for the water exchange processes between river and aquifer that are applied in practice (i.e., the program features available in groundwater models), the river is only represented with its water level (see Sections 2.3.2). Consequently, some relevant processes are neglected. These approaches should be further developed in such a way that not only the river stage, but also:
heterogeneous conductivity properties of river bed and river bank;
the relation between river stage and interface area and
a dynamic change of leakage properties (as time series or in dependence of flow properties)
More field observations are desirable to verify existing approaches on bank storage modeling and to extend the conceptual understanding of bank storage processes. The analysis of the bank storage event presented in this paper is based on the volume balance of a two-dimensional vertical cross-section only. As a next step, it is planned to extend the coherent analysis of river stage measurements and groundwater level observations to the horizontal plane. This allows one to take the effects of groundwater flow components parallel to the course of the river into account as well.
Acknowledgments
The authors thank the anonymous reviewers for their comments on the manuscript.
Author Contributions
Bernhard Becker initiated the study and defined the focus of the work. He reviewed the literature (Chapter 2) and did the analysis of Ubell’s Bank Storage event (Chapter 3); Matthias Jansen carried out the modelling study (Chapter 4) under guidance of Bernhard Becker and Benjamin Sinaba; Holger Schüttrumpf reviewed and supervised the work. The study has been carried out at the Institute of Hydraulic Engineering and Water Resources Management at RWTH Aachen University.
Appendix: Ubell’s Volume Balance Method for the Determination of Leakage Flux
A1. Introduction
In order to identify appropriate leakage approaches for a specific site, it is desirable to derive a leakage function based on measured values. While the head difference is easily obtained from gauges and groundwater observation points in the vicinity of a river, it is difficult to determine the amount of water exchanged between the river and the aquifer.
The exchanged amount of water per unit of time can directly be measured with a seepage meter. A drawback of seepage meter observations is that the observed values only represent a point in space and not the whole cross-section. Multiple devices would be necessary. For large rivers, additional practical limitations arise from the fact that the devices must be installed in great water depths. High current velocities during high water conditions make direct seepage measurements a challenging task.
Rushton and Tomlinson [33] derive the leakage flux by base flow separation for normal conditions. However, Mattheß and Ubell [41] point out that usage of base flow separation methods requires a hydraulic gradient from the aquifer towards the river, i.e., effluent conditions, during the observation period. This condition is usually not satisfied during a high water period.
The estimation of the leakage flux by comparison of incoming and outgoing discharge of a river segment has a limited accuracy [26], because in most cases, the leakage flux is small compared to the river discharge, even if the river cuts an aquifer with high values of hydraulic conductivity. Another problem is the exact determination of the river discharge, because in the case of high water, the relation between the river stage and the river discharge is not unique due to transient conditions [59].
A2. The Volume Balance Method
Ubell [12] derives the leakage flux from observation wells that are installed in a line orthogonal to the river (see Figure 15). From the change in groundwater level, he concludes the volume change in the aquifer. Figure 15 shows the initial situation at time t1, where the river stage is h01, and the groundwater level for the observation points is given by h11 to h41. At t2, the increased water level in the river causes water infiltration into the aquifer. The groundwater level rises to h12, h22 and h32, while for observation point 4, the water level does not change. The groundwater storage between t1 and t2 is given by the area A. The change in water volume V′ can be calculated by:
Ubell’s method does not allow one to separate precipitation and the backwater of base flow. Ideal conditions for the application of this method are a groundwater table that is initially horizontal and no precipitation. Another important prerequisite is a groundwater flow pattern that is oriented along the chain of observation points for normal conditions as well as for flood conditions.
References
- Sächsisches Landesamt für Umwelt und Geologie. Einfluss des August Hochwassers 2002 auf das Grundwasser. In Materialien zur Wasserwirtschaft; Sächsisches Landesamt für Umwelt und Geologie: Dresden, Germany, 2003. [Google Scholar]
- Sommer, T.; Ullrich, K. Das unsichtbare Hochwasser—Auswirkungen des August-Hochwasssers 2002 auf das Grundwasser im Stadtgebiet von Dresden. Proceedings of IWASA/Internationales Wasserbau-Symposium Aachen 2004: Hochwasserschutz—eindeichen oder ausweichen, Aachen, Shaker, 6–7 January 2004.
- Becker, B.P.J. Zur Gekoppelten Numerischen Modellierung von unterirdischem Hochwasser. Dissertation; Faculty of Civil Engineering at RWTH Aachen University: Germany, 11 June 2010. Available online: https://publications.rwth-aachen.de/record/63111/files/3288.pdf accessed on 8 February 2015. [Google Scholar]
- Wheather, H.; Peach, D.; Finch, J.; Butler, A. Modeling Groundwater Flooding, Available online: http://www.groundwaterflooding.org accessed on 29 November 2009.
- Cobby, D.; Morris, S.; Parkes, A.; Robinson, V. Groundwater flood risk management: Advances towards meeting the requirements of the EU floods directive. J. Flood Risk Manag. 2009, 2, 111–119. [Google Scholar]
- Huber, G.; Hiller, G.; Braune, A. Konzepte des Hochwasserschutzes für die Bauten des Freistaates Sachsen im Historischen Stadtkern von Dresden. In Tagungsband zum BMBF-Status-Seminar; Druckerei und Verlag Christoph Hille: Dresden, Germany; 8; October; 2003; pp. 57–62. [Google Scholar]
- Kreibich, H.; Thieken, A. Assessment of damage caused by high groundwater inundation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Beyer, K.D. Erhalt der Gebäudestandsicherheit—Sofortmaßnahmen und Dauerlösung/Beispiel des St. Benno-Gymnasiums Dresden. In Tagungsband zum BMBF-Status-Seminar; Druckerei und Verlag Christoph Hille: Dresden, Germany; 8; October; 2003; pp. 63–68. [Google Scholar]
- Becker, B.P.J.; Forberig, S.; Flögel, R.; Schüttrumpf, H.; Köngeter, J. On the Determination of Groundwater Levels for Hazard Maps of Groundwater Head Rise Induced by High Water. Wasserwirtschaft 2011, 12, 10–16, In German. [Google Scholar]
- Pinder, G.; Sauer, S. Numerical Simulation of Flood Wave Modification Due to Bank Storage Effects. Water Resour. Res. 1971, 7, 63–70. [Google Scholar]
- Ubell, K. Surface- and groundwater relationships along the Hungarian reach of the Danube river. In Symposium Surface Waters Hold at the Occasion of General Assembly of Berkeley of I.U.G.G. 19.-31.8.1963; Publication de l’association internationale d’hydrologie scientifique: Berkely, CA, USA, 1964; Volume 63, pp. 502–512. [Google Scholar]
- Ubell, K. Austauschvorgänge zwischen Fluß und Grundwasser—Teil I. Deutsch. Gewässerkundl. Mitt. 1987, 31, 119–125. [Google Scholar]
- Vekerdy, Z.; Meijerink, A.M.J. Statistical and analytical study of the propagation of flood induced groundwater rise in an alluvial aquifer. J. Hydrol. 1998, 205, 112–125. [Google Scholar]
- Affolter, A.; Huggenberger, P.; Scheidler, S.; Epting, J. Adaptives Grundwassermanagement in urbanen Gebieten/Einfluss der Oberflächengewässer-Grundwasser-Interaktion am Beispiel künstlicher Grundwasseranreicherung sowie variabler In-/Exfiltration der Birs (Schweiz). Grundwasser 2010, 15, 147–161. [Google Scholar]
- Spitz, K.; Moreno, J. A Practical Guide to Groundwater and Solute Transport Modeling.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Kinzelbach, W.; Rausch, R. Grundwassermodellierung: Eine Einführung mit Übungen; Gebr. Borntraeger: Berlin, Stuttgart, Germany, 1995. [Google Scholar]
- Forkel, C. Numerische Modelle für die Wasserbaupraxis. Grundlagen, Anwendungen, Qualitätsaspekte; Shaker Verlag GmbH: Aachen, Germany, 2004. [Google Scholar]
- Diersch, H.J.G. FEFLOW® Reference Manual; Wasy GmbH: Berlin, Germany, 2005. [Google Scholar]
- Trefry, M.G.; Muffels, C. Feflow: A finite-element ground water flow and transport modeling tool. Ground Water 2007, 45, 525–528. [Google Scholar]
- Freeze, R.A. Role of Subsurface Flow in Generating Surface Runoff. 1. Base Flow Contributions to Channel Flow. Water Resour. Res. 1972, 8, 609–623. [Google Scholar]
- Cunningham, A.; Sinclair, P. Application and analysis for a coupled surface and groundwater model. J. Hydrol. 1979, 43, 129–148. [Google Scholar]
- Ubell, K. Austauschvorgänge zwischen Fluß und Grundwasser—Teil II. Deutsch. Gewässerkundl. Mitt. 1987, 31, 142–148. [Google Scholar]
- Diersch, H.J.G. Extended formulations of constraints for Cauchy-type (3rd kind) boundary conditions in FEFLOW. In FEFLOW 5.2® White Papers Volume 1; Wasy GmbH: Berlin, Germany, 2005; Chapter 14; pp. 269–273. [Google Scholar]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar]
- Doppler, T.; Hendricks Franssen, H.J.; Kaiser, H.P.; Kuhlmann, U.; Stauffer, F. Field evidence of a dynamic leakage coefficient for modeling river-aquifer interactions. J. Hydrol. 2007, 347, 177–187. [Google Scholar]
- Rushton, K. Representation in regional models of saturated river-aquifer interaction for gaining/losing rivers. J. Hydrol. 2007, 334, 262–281. [Google Scholar]
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar]
- Schälchli, U. The clogging of coarse gravel river beds by fine sediment. Hydrobiologia 1992, 235, 189–197. [Google Scholar]
- Schubert, J. Hydraulic aspects of riverbank filtration—Field studies. J. Hydrol. 2002, 266, 145–161. [Google Scholar]
- Sinaba, B.; Becker, B.; Klauder, W.; Schüttrumpf, H. Specific demands and solutions regarding the FEFLOW large scale groundwater model Erftscholle, Rurscholle and Venloer Scholle. In FEFLOW—Finite Element Subsurface Flow and Transport Simulation System, Proceedings of the 2nd International FEFLOW User Conference, Berlin, Germany, 14–18 September 2009.
- Panday, S.; Huyakorn, P. A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar]
- Krom, T.D.; Graham, D. Accurate simulation methods for braided rivers in numerical groundwater models. Proceedings of the XVI International Conference on Computational Methods in Water Resources, Copenhagen, Denmark, 19–22 June 2006.
- Rushton, K.; Tomlinson, L. Possible mechanisms for leakage between aquifers and rivers. J. Hydrol. 1979, 40, 49–65. [Google Scholar]
- Becker, B.; Nowack, L.; Klauder, W.S.; Köngeter, J.; Schüttrumpf, H. Eine nichtlineare Leakage-Randbedingung für die Modellierung von hochwasserbeeinflusstem Grundwasseranstieg. Wasserwirtschaft 2009, 1–2, 26–31. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, The U.S. Geological SurveyModular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process; Report No. 00-92; U.S. Geological Survey: Reston, VA, USA, 2000. [Google Scholar]
- Becker, B.; Homann, C.; Köngeter, J. Coupling of Large Scale Groundwater Models. Comput. Vis. Sci. 2009, 12, 71–76. [Google Scholar]
- Brockhaus. Enzyklopädie in 30 Bänden; F.A. Brockhaus: Leipzig, Mannheim, 2006; Volume 23. [Google Scholar]
- Giebel, H.; Gölz, E.; Theis, H.J.; Ubell, K. Hydrogeologie und Grundwasserhaushalt im Neuwieder Becken. In Besondere Mitteilungen zum Deutschen Gewässerkundlichen Jahrbuch; Bundesanstalt für Gewässerkunde: Koblenz, Germany, 1990. [Google Scholar]
- Gränitz, F.; Grundmann, L. Das Mittelrheinische Becken; Böhlau Verlag: Köln, Germany, 2003. [Google Scholar]
- Giebel, H.; Hommes, A. Zum Austausch zwischen Fluß- und Grundwasser—Weitergehende Auswertung aus dem Neuwieder Becken. Deutsche Gewässerkundliche Mitteilungen 1988, 32, 18–27. [Google Scholar]
- Mattheß, G.; Ubell, K. Lehrbuch der Hydrogeologie, Bd. 1: Allgemeine Hydrogeologie—Grundwasserhaushalt; Gebr. Borntraeger: Berlin, Stuttgart, Germany, 1983. [Google Scholar]
- Custodio, E.; Llamas, M. Hidrología Subterránea; Ediciones Omega: Barcelona, Spain, 1996; Volume I. [Google Scholar]
- Brunner, P.; Simmons, C.T.; Cook, P.G. Spatial and temporal aspects of the transition from connection to disconnection between rivers, lakes and groundwater. J. Hydrol. 2009, 376, 159–169. [Google Scholar]
- Blaschke, A.P. Auswirkungen der Selbstdichtung auf das Grundwasser in staugeregelten Flüssen. In Wechselwirkungen zwischen Grundwasserleitern und Oberflächengewässern: Beiträge zum Tag der Hydrologie 2002/20. bis 22. März 2002 in Suderburg, Lüneburger Heide; Wittenberg, H., Schöniger, M., Eds.; Fachgemeinschaft Hydrologische Wissenschaften in der ATV-DVWK: München, Germany, 2002. [Google Scholar]
- Schälchli, U. Die Kolmation von Fliessgewässersohlen: Prozesse und Berechnungsgrundlagen; Mitteilungen der Versuchsanstalt für Wasserbau, Hydrologie und Glaziologie/Eidgenössische Technische Hochschule Zürich No. 124; ETH Zürich: Zürich, Switzerland, 1993. [Google Scholar]
- Vázquez-Suñé, E.; Capino, B.; Abarca, E.; Carrera, J. Estimation of Recharge from Floods in Disconnected Stream-Aquifer-Systems. Ground Water 2007, 45, 579–598. [Google Scholar]
- Simpson, S.C.; Meixner, T. Modeling effects of floods on stream bed hydraulic conductivity and groundwater-surface water interactions. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Rushton, K.R. Groundwater Hydrology/Conceptual and Computational Models; John Wiley & Sons Ltd: Chichester, UK, 2003. [Google Scholar]
- Müller, T. Quantifizierung der Uferfiltration bei hohen Flurabständen am Beispiel des Modau-Sandbach-Systems; Hessische Landesanstalt für Umwelt: Wiesbaden, Germany, 1999. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Diersch, H.J.G. Treatment of free surfaces in 2D and 3D groundwater modeling. In FEFLOW 5.2® White Papers Volume 1; Wasy GmbH: Berlin, Germany, 2005; Kapitel 2; pp. 67–100. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptional models. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Jansen, M. Numerische Untersuchungen zum unterirdischen Hochwasser. Diplomarbeit, Institute of Hydraulic Engineering and Water Resources Management, RWTH Aachen University, Aachen, Germany, 22 April 2009.
- Kaiser, J. Kopplung von Feflow mit dem Programm PEST zur Parameterkalibrierung. Kopplung von Feflow mit dem Programm PEST zur Parameterkalibrierung. In Fachtagung Grafik-gestützte Grundwassermodellierung; WASY GmbH: Berlin, Germany, 1998. [Google Scholar]
- Doherty, J.; Brebber, L.; Whyte, P. PEST—Model Independent Parameter Estimation; Watermark Computing: Corinda, Australia, 1994. [Google Scholar]
- Doble, R.; Brunner, P.; McCallum, J.; Cook, P.G. An Analysis of River Bank Slope and Unsaturated Flow Effects on Bank Storage. Ground Water 2012, 50, 77–86. [Google Scholar]
- Konikow, L.F.; Bredehoeft, J.D. Ground-water models cannot be validated. Adv. Water Resour. 1992, 15, 75–83. [Google Scholar]
- Anderson, M.P.; Woessner, W.W. The role of the postaudit in model validation. Adv. Water Resour. 1992, 15, 167–173. [Google Scholar]
- Dyck, S.; Peschke, G. Grundlagen der Hydrologie; Ernst & Sohn: Berlin, Germany, 1983. [Google Scholar]


| Approach | Variable | Value | Unit |
|---|---|---|---|
| Darcy | leakage coefficient cl,in | 1.0 · 10−6 | 1/s |
| interface area A | 1000 | m2 | |
| wetted perimeter (trapezoidal cross-section) | leakage coefficient cl,in | 5.0 · 10−6 | 1/s |
| river bed breadth | 8.0 | m | |
| bank slope | 1:1.55 | ||
| length of river section l | 62.5 | m | |
| Rushton and Tomlinson | leakage parameter C1 | 0.02 | m2/s |
| leakage parameter C2 | 0.8 | 1/m | |
| leakage parameter C3 | 0.04 | m2/s | |
| length of river section l | 1 | m | |
| Observation Point | Distance to the River Bank |
|---|---|
| U01 | – |
| U03 | about 500 m |
| U05 | about 1600 m |
| Model Variant Calibration Variant Parameter Zone | Head Boundary Condition
| Leakage Boundary Condition
| ||||||
|---|---|---|---|---|---|---|---|---|
| Manual | Automatic | Manual
| Automatic
| |||||
| k (m/s) | k (m/s) | k (m/s) | cl,in (1/s) | cl,ex (1/s) | k (m/s) | cl,in (1/s) | cl,ex (1/s) | |
| 1 | 2.0 · 10−4 | 5.2 · 10−3 | 3.0 · 10−2 | 1.2 · 10−5 | 1.2 · 10−5 | 3.6 · 10−2 | 3.0 · 10−4 | 3.6 · 10−5 |
| 2 | 2.0 · 10−4 | 2.8 · 10−4 | 3.0 · 0−2 | 1.2 · 10−5 | 1.2 · 10−5 | 3.6 · 10−2 | 2.0 · 10−5 | 2.2 · 10−5 |
| 3 | 4.0 · 10−4 | 2.3 · 10−5 | 3.0 · 10−2 | 1.6 · 10−4 | 4.9 · 10−5 | 3.6 · 10−2 | 3.8 · 10−5 | 1.0 · 10−4 |
| 4 | 3.0 · 10−2 | 2.9 · 10−2 | 3.0 · 10−2 | 3.6 · 10−2 | ||||
| 5 | 2.5 · 10−2 | 2.9 · 10−2 | 2.5 · 10−2 | 3.6 · 10−2 | ||||
| 6 | 2.0 · 10−2 | 2.9 · 10−2 | 2.0 · 10−2 | n. a. | n. a. | 3.6 · 10−2 | n. a. | n. a. |
| 7 | 2.5 · 10−2 | 2.9 · 10−2 | 2.5 · 10−2 | 3.6 · 10−2 | ||||
| 8 | 3.0 · 10−2 | 2.9 · 10−2 | 3.0 · 10−2 | 3.6 · 10−2 | ||||
| number of parameters | 8 | 4 | 8 | 4 | ||||
| Observation Point
| ||||||||
|---|---|---|---|---|---|---|---|---|
| Calibration Method | Boundary Condition | U01 | U02 | U03 | U04 | U05 | U06 | U07 |
| manual calibration | head | 0.979 | 0.963 | 0.958 | 0.964 | 0.970 | 0.970 | 0.799 |
| leakage | 0.987 | 0.976 | 0.977 | 0.977 | 0.980 | 0.975 | 0.786 | |
| Automatic calibration | head | 0.988 | 0.978 | 0.954 | 0.927 | 0.986 | 0.988 | 0.709 |
| leakage | 0.980 | 0.971 | 0.945 | 0.957 | 0.976 | 0.952 | 0.103 | |
| Calibration Method | Model Variant | Sum of Nash–Sutcliffe Efficiency |
|---|---|---|
| manual calibration | head boundary condition | 6.602 |
| leakage boundary condition | 6.659 | |
| automatic calibration | head boundary condition | 6.528 |
| leakage boundary condition | 5.884 | |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, B.P.J.; Jansen, M.; Sinaba, B.P.; Schüttrumpf, H. On the Modeling of Bank Storage in a Groundwater Model: The April, 1983, Flood Event in the Neuwieder Becken (Middle Rhine). Water 2015, 7, 1173-1201. https://doi.org/10.3390/w7031173
Becker BPJ, Jansen M, Sinaba BP, Schüttrumpf H. On the Modeling of Bank Storage in a Groundwater Model: The April, 1983, Flood Event in the Neuwieder Becken (Middle Rhine). Water. 2015; 7(3):1173-1201. https://doi.org/10.3390/w7031173
Chicago/Turabian StyleBecker, Bernhard P. J., Matthias Jansen, Benjamin P. Sinaba, and Holger Schüttrumpf. 2015. "On the Modeling of Bank Storage in a Groundwater Model: The April, 1983, Flood Event in the Neuwieder Becken (Middle Rhine)" Water 7, no. 3: 1173-1201. https://doi.org/10.3390/w7031173
APA StyleBecker, B. P. J., Jansen, M., Sinaba, B. P., & Schüttrumpf, H. (2015). On the Modeling of Bank Storage in a Groundwater Model: The April, 1983, Flood Event in the Neuwieder Becken (Middle Rhine). Water, 7(3), 1173-1201. https://doi.org/10.3390/w7031173