Abstract
The effectiveness of three simple flood operating rules in reducing the peak flow is compared for four simplified hydrograph shapes. The Minimize Flood Peak rule uses available flood storage capacity to store peak flows from an accurate hydrograph forecast. The less demanding Minimize Flooding Frequency operating rule releases water at or below channel capacity until the flood storage pool is filled and outflows are forced to exceed the channel capacity. The Short Forecast Peak Minimization rule minimizes flood peak over a short foreseeable future with existing flood storage capacity. Four simplified hydrograph shapes (triangular, abrupt wave, flood pulse and broad peak) were used. The Minimize Flood Peak rule reduces peak flows better than alternatives, but is often impractical. The Short Forecast Peak Minimization rule reduces peak flows for a wide range of conditions. The Minimize Flood Frequency rule may be more relevant where damages occur abruptly, as in many leveed systems. All rules reduce peak outflow more efficiently for more steeply rising hydrographs. The approach suggests some general insights for flood operations of reservoirs.
1. Introduction
Reservoir operators commonly manage downstream flooding using a set of operating rules which determine releases during, before and after a storm. During a storm, operators try to store the surge of inflows in available reservoir storage space (flood storage pool) to capture the storm’s peak flow and delay its release until a less damaging time. Reservoir operators are presented with the challenge of knowing when to begin storing water for a flood, how long to retain it, and whether to make releases in anticipation of a storm to make more storage capacity available. Reservoir operation rules help optimize the system and control flooding.
Many reservoir variables can affect downstream flood frequency. Several studies have explored the effects of reservoir storage on regulated flood frequency. Bradley and Porter [1] presented a peak-to-volume approach to calculate the effects of storage volume on downstream peak flood reduction, with reservoir inflows generated by a stochastic method. Ayalew et al. [2] also used a stochastic method of generating flood hydrographs and considered the effects of reservoir stage on outflow due to flood wave dissipation as it travels from the inlet to the outlet. Both studies demonstrated that greater reservoir storage decreases the unit effectiveness in reducing downstream flood peaks. Theoretical analysis and real applications of various flood operation rules have also been implemented for single reservoirs and reservoir systems by Goldman [3] and Ji [4]. This paper provides a general theoretical comparison of three flood operating rules.
Three simple reservoir operating rules were tested to analyze their effectiveness in reducing peak flow: The “Minimize Flood Peak” rule (MFP), the “Minimize Flooding Frequency” (MFF) and the “Short Forecast Peak Minimization” rule (SFPM). The calculated flows in and out of the reservoir using each operation rule are analyzed and compared. The paper ends with conclusions.
2. Methods
In making operating decisions, reservoir operators often rely on river flow forecasts. The intensity and duration of a storm and the hydrology of a watershed determine the size and shape of the hydrograph. Although hydrograph shapes can be complicated, their patterns can be greatly simplified. Four idealized hydrograph shapes are used here to model storm events: triangular, abrupt wave (right-triangle), flood pulse (rectangular), and broad peak (trapezoidal). The hydrograph shape used to model a flood should reflect the shape of likely storms (Figure 1). Simple hydrograph features include peak inflow (Qp,in), peak outflow (Qp,out), peak flow reduction (Δqp), total flow duration (D), maximum inflow duration (d), flood storage volume (V), and ramping rates (r1,r2). The non-shaded region is the reservoir’s outflow over time, which reaches a maximum of Qp,out. Flood volume is the integral of each hydrograph shape. The quantity Δqp is the maximum reduction in peak flow, defined as the maximum inflow minus the maximum outflow. The percent peak reduction is calculated by dividing the maximum reduction in peak flow by the maximum inflow (Δqp/Qp,in). The rising slope r1 and recession slope r2 are the rise and fall of the flow into the reservoir per unit time. The hydrograph’s total flow duration includes all time periods in which the flow exceeds a base (zero for this study).
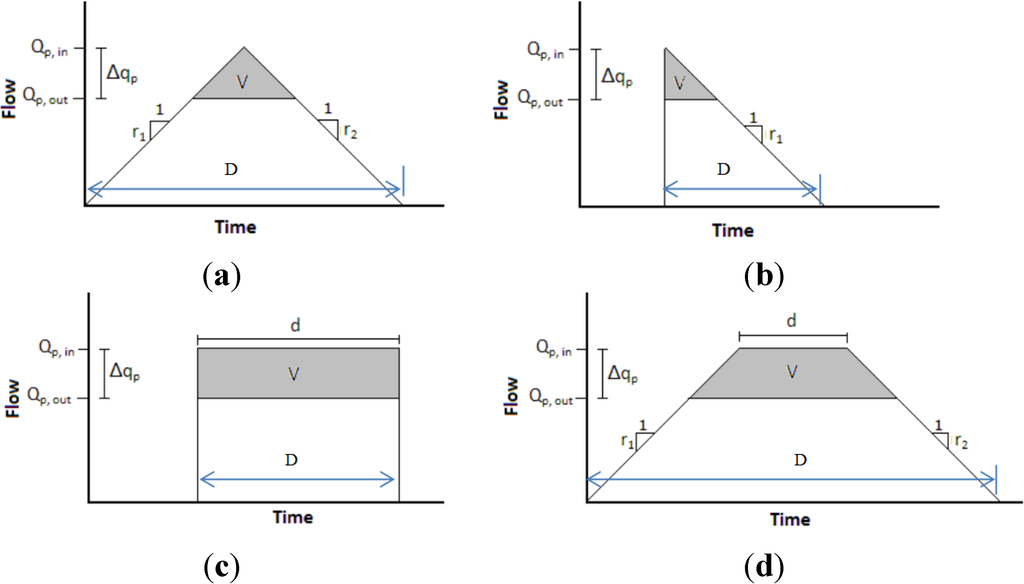
Figure 1.
Four simple hydrographs and optimal peak flow reductions for a fixed flood storage volume [2]. (a) Triangular; (b) Abrupt wave; (c) Flood pulse; (d) Broad peak.
This study focuses on basic reservoir operation rules to reduce the peak downstream flood flow. A simple reservoir model was used with idealized hydrographs of varying shapes and volumes. For simplicity, the triangular hydrograph is isosceles in geometry (r1 = r2). The total flow duration of each hydrograph D (length of the base on the time axis) is set to be 100 time periods for all runs. The broad peak hydrograph maintains a maximum inflow for 60 time periods in all cases. All four hydrograph shapes have the same flood volume for each case. The model’s downstream channel capacity can vary. The reservoir model presented does not consider effects of hydrology or attenuation of the flood wave as it passes through a simulated reservoir. The hydrographs used in analysis are deterministic and idealized rather than based on a probability distribution of precipitation and runoff.
3. Results and Discussion
3.1. Minimize Flood Peak (MFP) with Perfect Forecasting
The MFP operating rule uses available flood storage volume to maximally reduce the reservoir’s peak outflow. The rule relies on a well-forecasted hydrograph to determine the release schedule which minimizes peak outflow. The maximum peak flow reduction (Δqp) can be calculated using the peak inflow and volume for a given flood storage capacity, as in Table 1 for these simple hydrograph shapes.
Ideal peak outflows (Qp,out) are calculated for each hydrograph. As inflow begins to increase, releases increase to match inflow. If storage is not empty, the reservoir would initially release more than the inflow to create additional flood storage. Once inflow reaches the calculated ideal peak outflow, the outflow is capped at this optimal rate and held constant until after the flood peak. Once the peak outflow is reached, the reservoir begins to store water as inflow exceeds reservoir outflow. Inflow increases to a maximum and then begins to decrease, with the reservoir continuing to store water. Eventually, the inflow decreases to less than the ideal peak outflow, and the reservoir begins to drain. When enough water has been released to evacuate the flood storage volume, reservoir outflow is once again synchronized with inflow.

Table 1.
Maximum peak reduction and ideal peak outflow for simple hydrographs given peak inflow (Qp,in), flood duration (D), maximum inflow duration (d) and flood storage volume V Δqp = Qp,in − Qp,out.
| Shape | Triangular | Abrupt wave | Flood pulse | Broad peak |
|---|---|---|---|---|
| Stored volume V = | 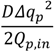 | 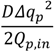 | DΔqp | |
| Peak flow reduction Δqp = | 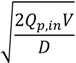 | 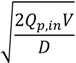 | | |
| Peak flow Qp,out = | 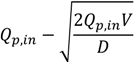 | 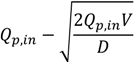 | | |
Figure 2a,b shows how the MFP operation rule affects downstream flow and reservoir storage for an abrupt wave hydrograph and broad peak hydrograph, respectively. The reservoir in this model has a flood storage volume of 3000 units. In this case, the reservoir’s storage captured 30% of the hydrograph’s total volume (10,000 units). Table 2 provides the percent of peak flow reduced for each hydrograph shape the optimal outflow rate.
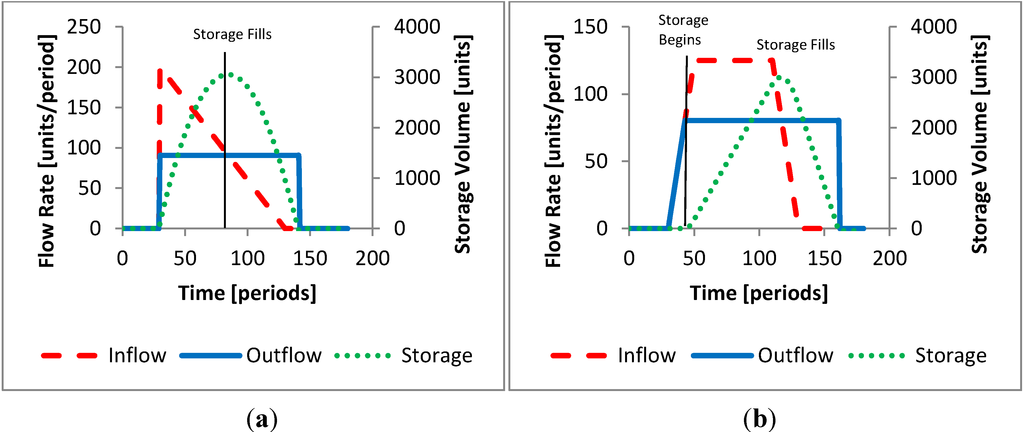
Figure 2.
Minimize flood peak with perfect forecasting for (a) Abrupt wave hydrograph and (b) Broad peak hydrograph.

Table 2.
Modeled results of the minimize flood peak with a perfect forecast operating rule. Storage = 3000 units, Percent of the hydrograph contained = 30%.
| Hydrograph shape | Triangle | Abrupt wave | Pulse | Broad peak |
|---|---|---|---|---|
| % Peak reduction | 55 | 55 | 30 | 36 |
| Optimal outflow | 90.5 | 90.5 | 70 | 80.3 |
As flood volume increases peak flow increases correspondingly and the effectiveness of an additional unit of flood storage in reducing the peak outflow decreases. Graphically, this is because more of the hydrograph’s “shoulder” must be stored to further reduce the peak [5,6].
The hydrograph’s shape affects the maximum peak flow reduction [6]. Figure 3 illustrates the effect of hydrograph shape on the percent peak flow reduction. The graph plots the percent of the hydrograph’s volume stored in the reservoir versus the percent flow reduction with the MFP operating rule for each hydrograph shape.
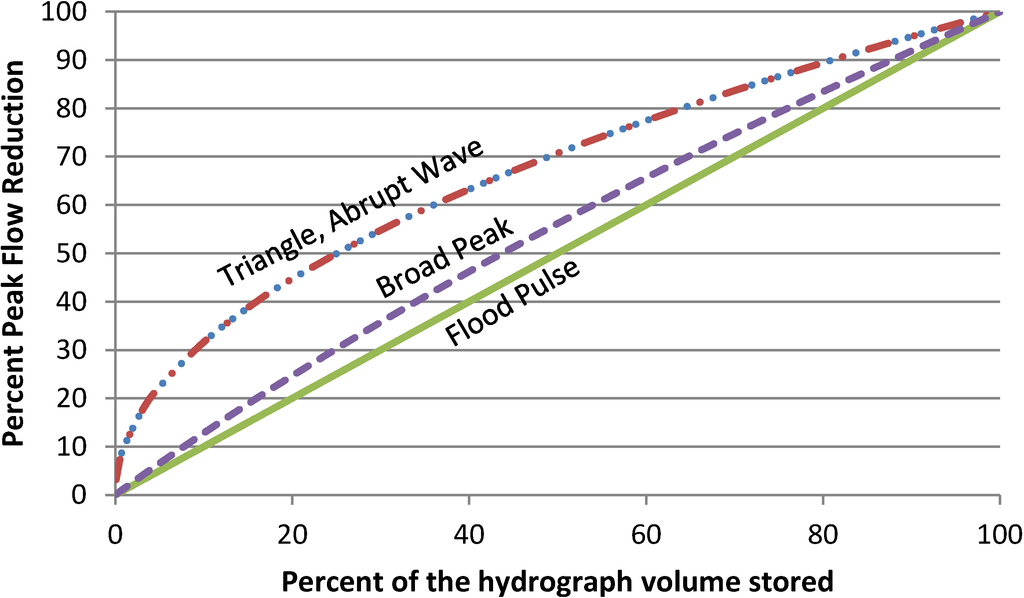
Figure 3.
Effect of hydrograph shape on the Minimize Flood Peak (MFP) rule.
Hydrograph shape affects the peak flow reduction from reservoir storage for most hydrograph volumes [7]. The percent peak flow reduction from the pulse hydrograph is a linear percent of the storm captured in reservoir storage. A triangular hydrograph increases the reservoir’s capability to reduce the peak outflow considerably over the flood pulse and broad peak shapes. This ideal operation rule removes the top portion of the hydrograph only. Since most of a triangle’s area is in the base, removing the top section benefits peak reduction more than rectangular shapes where the volume is uniformly distributed. This can be explained by the derivative of the hydrograph shape area with respect to the reduction, or height h [6]. A broad peak hydrograph can be divided into rectangular and triangular components. The triangular regions of the broad peak hydrograph’s shape increase the reservoir’s ability to reduce peak flow over a flood pulse hydrograph. However, the peak flow of a broad peak hydrograph cannot be reduced as much as a triangular hydrograph of equal volume.
The plots of all four hydrograph shapes converge when the flood volume contained approaches 0% and 100%. When the reservoir receives a water volume much greater than the flood storage capacity, the system is overwhelmed and hydrograph shape has little effect on downstream flood flows. On the other hand, if the flood volume entering the reservoir is less than the volume of flood storage capacity, the flood can be contained completely and hydrograph shape is unimportant.
Greater peak flow reduction occurs with triangular and abrupt wave hydrographs. The skew of the triangle’s shape has no effect on the reservoir’s performance in reducing the peak flow. However, more time is needed to evacuate the flood storage pool with a triangular hydrograph compared to an abrupt wave hydrograph because the peak flows arrive sooner and fill the storage capacity faster.
Implementing the MFP operating rule requires an accurate inflow forecast to determine the reservoir’s optimal release. A forecasted hydrograph which underestimates the actual flood volume would cause the release of too little water. As a result, the flood storage volume will be unable to contain the flood and more than the ideal peak outflow will need to be released part way into the flood. Conversely, the operator would begin by releasing more water than necessary if a forecast hydrograph overestimates the flood, resulting in a loss of water supply storage or unnecessarily large floods downstream.
River forecast errors force reservoir operators to balance the consequences of releasing too much and too little water. Where forecasts are poor, or flood damage rises drastically after flows exceed a downstream channel capacity, other operating rules may be optimal, such as a rule which minimizes the frequency of exceeding an established flood flow.
3.2. Minimize Flooding Frequency (MFF)
A more common reservoir operating rule minimizes the frequency of exceeding a fixed downstream channel flow capacity. If the reservoir releases more than the channel capacity rate, the water will overtop the banks or levees and flood the surrounding area. Whenever possible, reservoir operators avoid releasing more than the channel capacity to prevent flood damages.
The MFF rule is favored when any overtopping causes concave-shaped flood damage (Figure 4). Here, releases less than 50 units per period prevent damage, but any rate greater causes the maximum damage (e.g., overtops a levee). However, the MFP rule would better mitigate flood damages in the convex damage case because reducing flow by any amount reduces damages. A hybrid rule may be optimal where some damages occur before levee overtopping, minimizing peaks over some range for moderate floods before operating strictly within channel capacity.
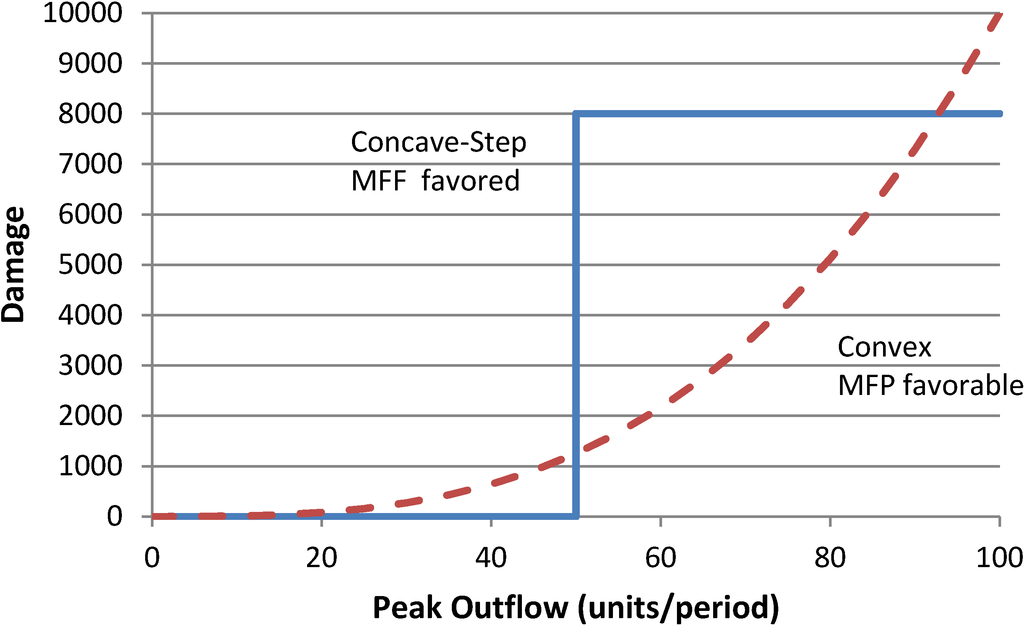
Figure 4.
Damage curve shape affects operating rule performance.
The main objective of the MFF operating rule is to keep reservoir outflow lower than the channel capacity. As inflow increases, outflow is increased at an equal rate until reaching the channel capacity. Outflow is held constant upon reaching the channel capacity and the reservoir stores any excess inflow in the flood storage pool. Ideally, the flood storage pool will contain all excess inflow beyond the channel capacity until inflow subsides below channel capacity and flood storage is emptied. If the flood storage pool fills to capacity, the reservoir must again release water equal to the inflow, providing no further reduction in outflow. Operators often maintain the outflow at the channel capacity until the flood storage pool is empty and then match the outflow to the inflow once again. If the reservoir is not empty and good forecasts exist, then pre-storm releases up to the channel capacity could make more storage available for the coming storm (a case not examined here).
Figure 5 shows the reservoir operation according to the MFF operating rule for a triangular hydrograph and broad peak hydrograph. The reservoir in this model uses the same 3000 unit flood storage pool as before. In the cases presented, the hydrographs have a volume of 6000 units, so the reservoir can capture 50% of total volume. The model has a downstream channel capacity of 50 units per time period, which is not exceeded in these cases. The flood did not require the entire storage pool volume to maintain releases within the channel capacity for any shape. However, the triangular and abrupt wave hydrographs used more flood storage volume than the flood pulse and broad peak shapes to manage this moderate flood.
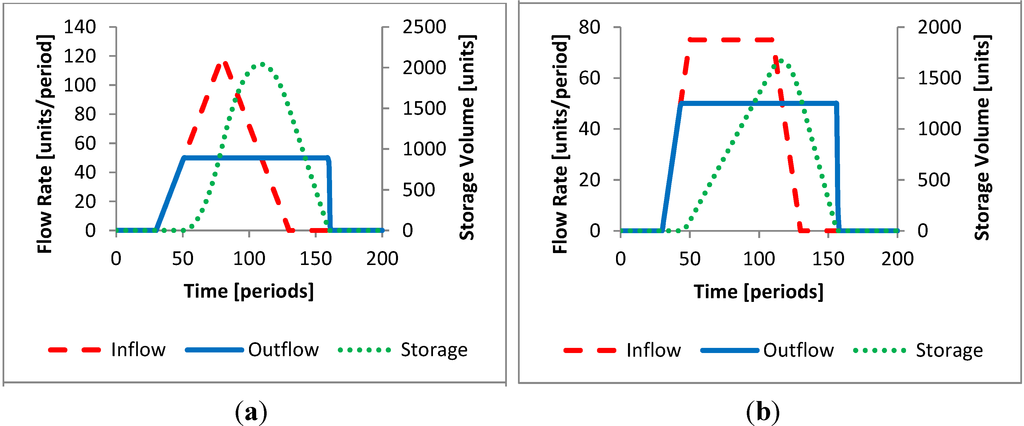
Figure 5.
Minimize flood frequency (flooding prevented) for (a) Triangular hydrograph and (b) Broad peak hydrograph.
Channel capacity and flood storage capacity may be insufficient for large floods. Figure 6 shows inflows to the reservoir that cannot be managed with the MFF rule to avoid flooding. Any point on the plots where the outflow exceeds the channel capacity of 50 units would cause flood damages downstream. For this case, the flood storage could accommodate only 35% of the flood volume.
Although outflow is initially maintained within the channel capacity, ultimately reservoir storage is insufficient to capture all of the water needed to prevent flooding downstream. In large floods, the reservoir may not diminish the downstream flood peak with this rule (Figure 6b), but only delays its onset and reduces its peak duration.
The MFF operating rule does not require river forecasting (except where unregulated inflows enter downstream). The operator tries to manage the release of water within the channel capacity whenever possible. Increasing the channel capacity greatly improves the effectiveness of the operating rule, as this allows a greater volume of flood hydrograph to be accommodated in the channel, particularly for floods with longer duration.
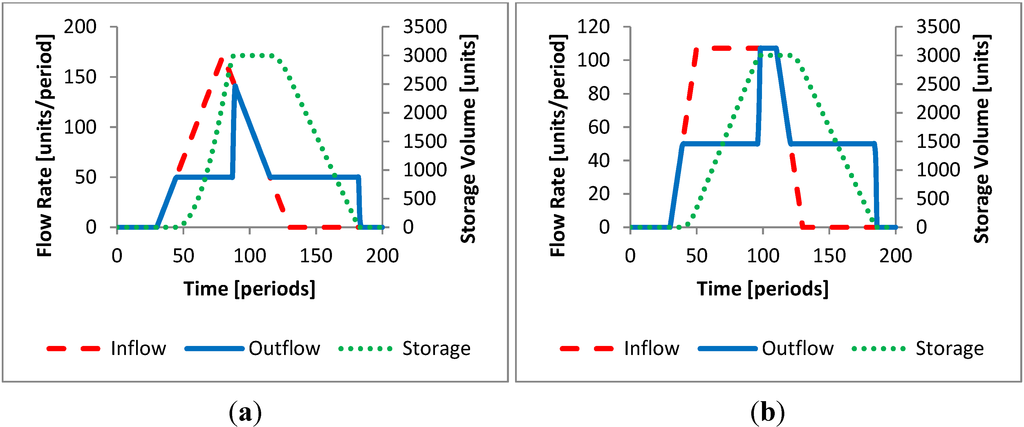
Figure 6.
Minimize flood frequency rule (flooding occurs) for (a) Triangular hydrograph and (b) Broad peak hydrograph.
The MFP operating rule usually reduces the peak outflow more than the MFF rule. The two rules perform equally only when the minimum peak flow from the MFP equals the downstream channel capacity. Figure 7 shows the percent peak reduction using the MFF operating rule as a percentage of the peak flow reduction achieved using the MFP rule for varying channel capacities. The plot was constructed assuming that the flood storage volume of 3000 units captures 30% of the hydrograph volume (the same as Figure 2 and Figure 3 and Table 2). At this maintained flood storage volume, the reservoir’s percent peak reduction was recorded over the range of channel capacities using the MFF rule. The recorded values were normalized by the MFP percent peak reduction presented in Table 2 and plotted on the vertical axis. The two rules are equally effective when the channel capacity equals the optimal outflow of the MFP rule. Figure 7 uses the ideal peak outflow rate determined from the MFP rule to normalize the channel capacity variable.
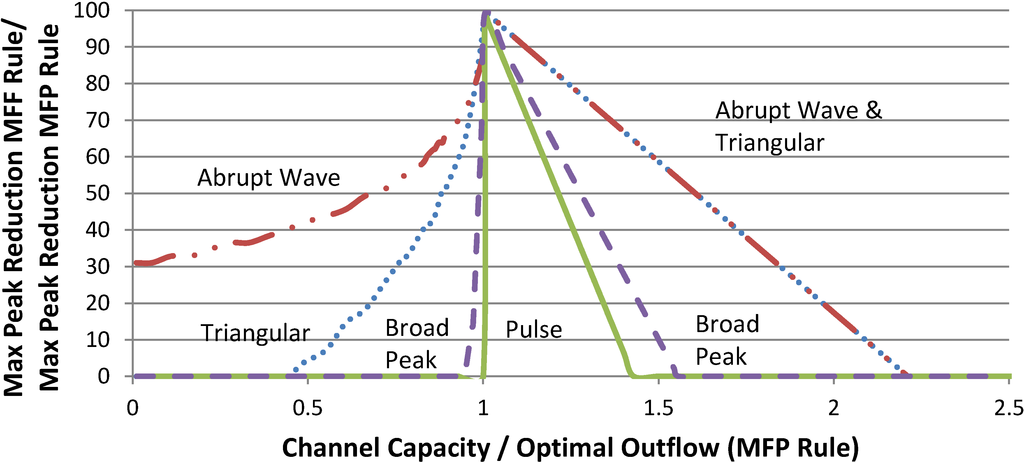
Figure 7.
Efficiency of the MFF rule in reducing peak flow normalized by the peak flow reduction of the MFP rule, for varying channel capacities normalized by the ideal peak outflow of the MFP rule.
Figure 7 shows the relative effectiveness of the MFF and MFP operating rules. The MFF rule is less effective than the MFP rule because flood storage space is used less efficiently for peak flow reduction. The rising portions of the plots represent the non-ideal conditions of Figure 6, where flood storage fills before the inflow subsides below the channel capacity, forcing releases to exceed the channel capacity. When these forced releases are made, little or no peak flow reduction occurs. Similarly, when the flood storage fills before the inflow peak of a triangular hydrograph, no peak reduction occurs. However, the peak flow of the abrupt wave hydrograph can always be reduced with the MFF operating rule because the flood storage pool initially captures the maximum inflow, and never fills before the peak.
The MFF operating rule becomes less effective in reducing peak flood flow as the channel capacity grows larger than the minimal peak outflow optimized with a perfect forecast. However, downstream flooding is prevented during these smaller floods, so maximum peak flow reduction is inconsequential. The descending portions in Figure 7 illustrate the effect of a channel capacity greater than the minimum peak outflow. Figure 5 represents typical flow patterns of a reservoir that releases water at a channel capacity exceeding the minimum regulated peak flow. The decreased peak reduction efficiency in this region arises because the flood storage pool does not fill to capacity. A perfect forecast allows operators to determine the optimal peak-minimizing outflow, using all available storage volume. A channel capacity greater than the minimum peak outflow leaves empty flood storage space after the flood peak has passed.
Although a good forecast can help reduce peak flows with maximum efficiency, the MFF rule is a good operating procedure without flood forecasts (unless unregulated flows enter downstream). Operators often have a partial forecast of upcoming flows and can construct an incomplete hydrograph using upstream flow or precipitation gauges. As gauge readings change over time, the forecasted hydrograph evolves from the additional data, providing a short but incomplete forecast. With some knowledge of what is to come, operators can use a rule to reduce the peak flow from the limited forecast of inflow.
3.3. Short Forecast Peak Minimization (SFPM)
The SFPM rule uses the total storage volume of a reservoir to minimize peak outflow within the forecast period by determining whether or not inflow will exceed the flood storage capacity during the forecast time. If the current outflow can adequately prevent exceeding storage capacity, the release rate is not changed. However, if the current outflow will not prevent overflowing storage within the forecast time, the release rate is increased. The SFPM rule is a simple rule that incorporates inflow forecasts into flood release decisions.
For an unfilled storage capacity at time t (St), the SFPM rule increases the current release rate (Rt-1) in the next time-step (to Rt) so peak release over the forecast period (f) is minimized. The forecast flows from t until the end of the forecast (t + f)(It(τ)) are optimally stored over the forecast period f for a peak-minimizing release:
This SFPM rule continuously adjusts outflow each time step as forecasts and conditions evolve. As inflows subside to less than the channel capacity, the flood storage pool can be evacuated at the channel capacity or the peak outflow rate.
The SFPM rule reduces peak flows effectively for most hydrographs. When the storage and channel capacity are sufficient for the incoming flood, releases with this rule are similar to those for ideal reductions with perfect forecasts. Figure 8 presents the flow patterns where the SFPM rule effectively prevents downstream flooding. In this case, the reservoir’s 3000 units of flood storage capacity capture 50% of the flood volume. The trial used a channel capacity of 50 units per period and a forecast time (τ) of 10 periods. Figure 8 is identical to Figure 5 because releases are maintained within the channel capacity using either rule.
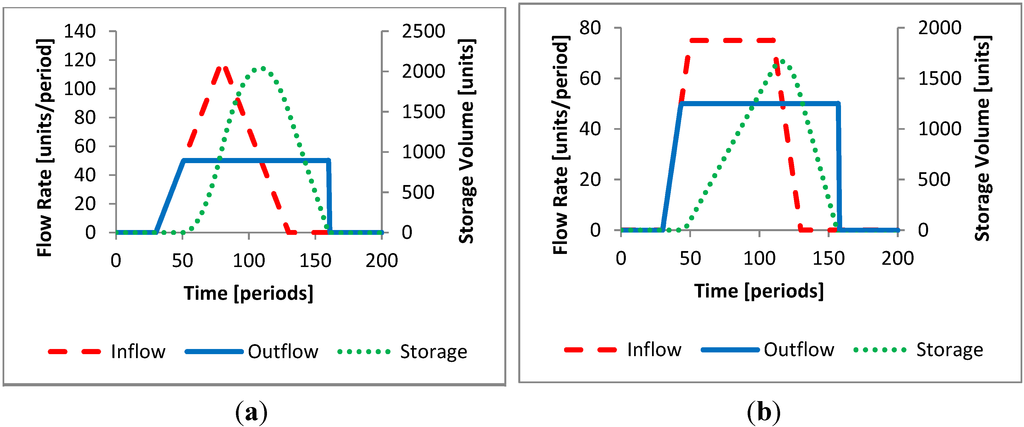
Figure 8.
Short forecast peak minimization operation rule (with flooding prevented) for (a) Triangular hydrograph and (b) Broad peak hydrograph.
Similar to the MFF rule, the SFPM rule becomes less effective for large or long floods which overwhelm the reservoir and channel capacities. However, when the channel capacity is expected to be exceeded, the SFPM rule gradually increases outflow to a maximum rather than abruptly matching the inflow. The gradual increase may prolong the duration that the outflow exceeds channel capacity compared to the MFF rule, but in trade reduces the maximum outflow. Figure 9 presents the operation of two simple hydrographs using the SFPM rule for larger floods. As before, the reservoir is modeled with 3000 units of storage and a channel capacity of 50 units per period. The hydrographs of equal volume has a total duration of 100 periods. The reservoir captures 35% of the hydrographs’ volume (8570 units). The operating rule is programmed to use a forecast time of 10 time periods. For storms shorter than the forecast time, the SFPM rule should perform more like the ideal MFP rule.
Although flooding would have occurred in these cases, the SFPM rule reduced the peak flow. The minimal peak flow reduction for the pulse hydrograph is still more than that would have been accomplished using the MFF rule. The SFPM rule is more versatile and adaptable in reducing peak flow over a wide range of channel capacities. Figure 10 and Figure 11 compare the peak flow reduction with the SFPM rule to the reduction expected using the MFF rule. The reservoir storage is set to be 3000 units and can contain 30% of the hydrograph’s volume, with a 10 time period forecast. The vertical axis of each plot is normalized by the maximum percent peak reduction gained from the MFP rule. The horizontal axis of each plot has been normalized by the optimal channel capacity found from the MFP rule (See Table 2).
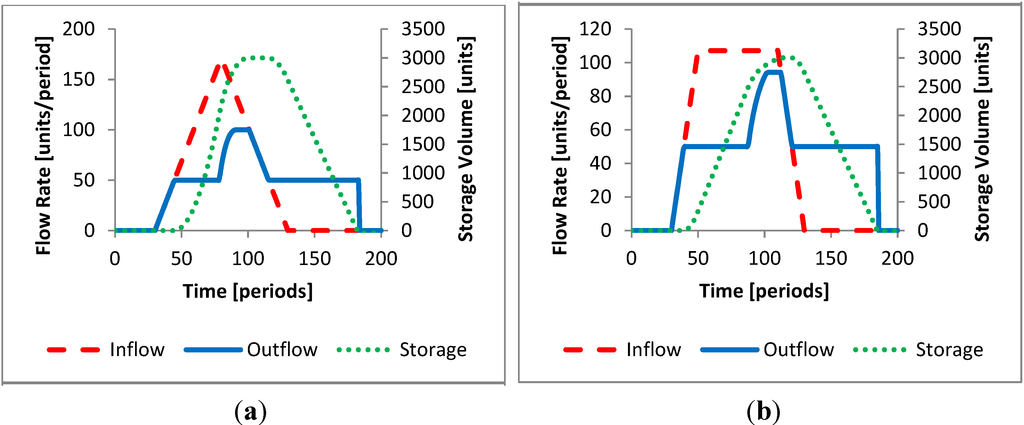
Figure 9.
Short forecast peak minimization (when flooding occurs) for (a) Triangular hydrograph and (b) Broad peak hydrograph.
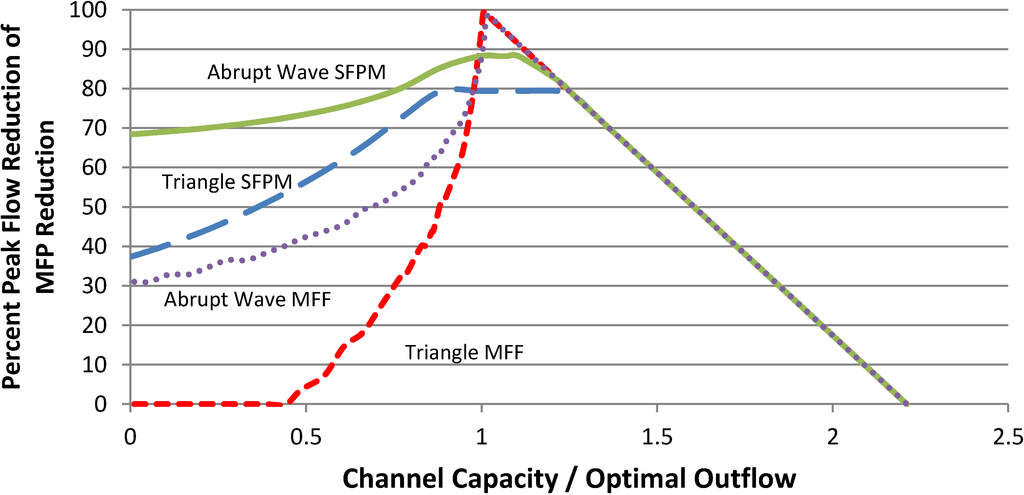
Figure 10.
Comparison of minimize flood frequency (MFF) and short forecast peak minimization (SFPM) rules for triangle and abrupt wave hydrographs.
Figure 10 and Figure 11 show that the SFPM rule reduces peak flows over a wider range of channel capacities and with a greater efficiency than the MFF rule. Both rules prevent flooding at channel capacities exceeding the optimal outflow, but fail to use all reservoir storage space, which would further decrease the percent peak reduction.
An increase in the forecast time increases the efficiency of the SFPM rule as the model can better assess and prepare for the inflows. If the hydrograph’s volume is large and the forecast time is sufficiently long, releases may begin in advance of the flood. These initial releases augment the benefits of the SFPM rule in reducing peak flood flow and effectively expand the flood storage pool in anticipation of a large flood. Figure 12 illustrates the effect of an increasing forecast time on the reservoir‘s ability to reduce peak flows using the SFPM rule. The model uses the same 3000 units of initial flood storage volume to capture 30% of the hydrograph volume, with a channel capacity of 50 per period for all trials.
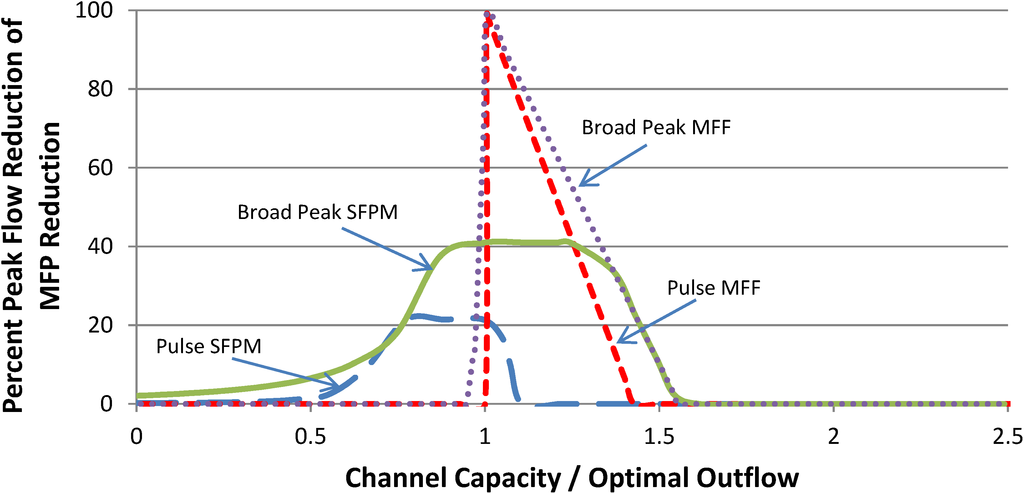
Figure 11.
Comparison of Minimize Flood Frequency (MFF) and Short Forecast Peak Minimization (SFPM) rules for Flood Pulse and Broad Peak Hydrographs.
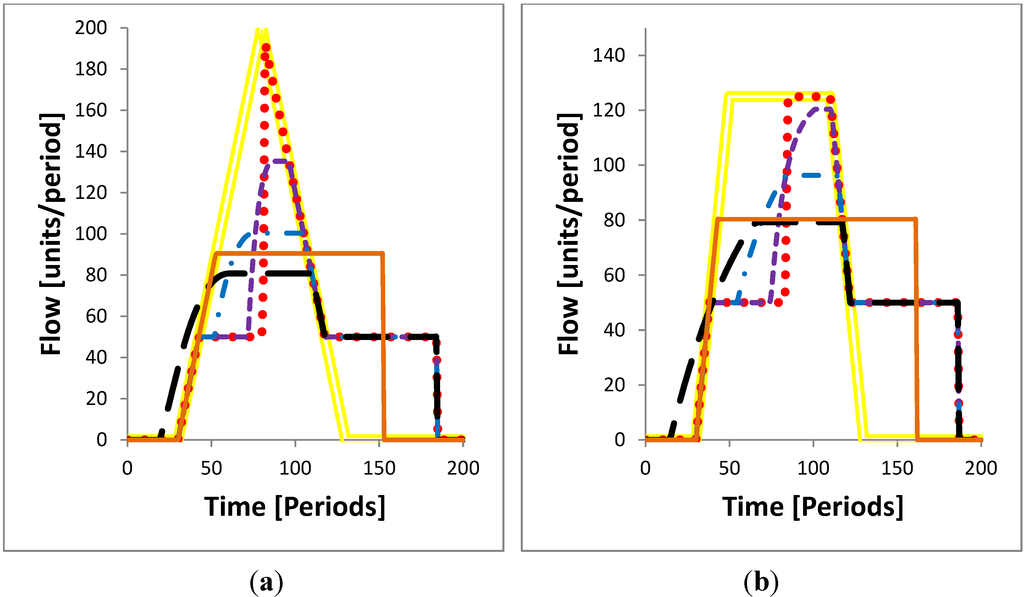
Figure 12.
Effect Forecast Period on Operation using the SFPM Rule for (a) Triangular Hydrograph and (b) Broad Peak Hydrograph.
The peak flow of all four hydrograph shapes can be significantly reduced with longer forecast time. A forecast time of 50 periods with the SFPM rule reduces peak flow better than the MFP rule because releases made before the flood’s arrival creates additional flood storage capacity for the forecast period (our MFP rule does not allow pre-releases to create additional flood storage). For large floods, longer forecast times cause outflows to exceed channel capacity earlier. The longer time over which the outflow exceeds channel capacity significantly reduces the peak flow from the reservoir, as excess inflow volume is more evenly distributed over more time periods. Also, outflow increases less rapidly as forecast time increases, which aids public safety and can help to prevent channel banks sloughing.
3.4. Peak Inflow: Outflow Curves
Figure 13 shows the reservoir’s peak inflow and outflow using the three operating rules. The results expand on work by Ergish [8] (2010) and Goldman [3] (2001). As before, flood duration of 100 periods, storage of 3000 units, and channel capacity of 50 units per period and short forecast of 10 periods are used. As peak inflow increases, flood volume increases, but different rules reduce outflow peaks differently over ranges of peak inflow.
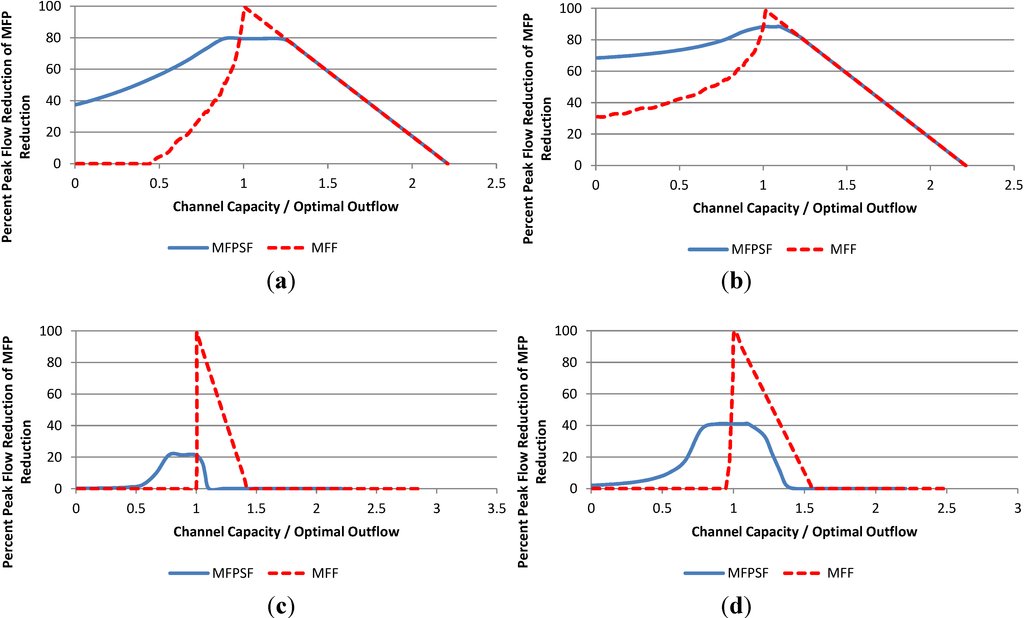
Figure 13.
Peak inflow vs. peak outflow for (a) Triangular hydrograph and (b) Abrupt wave hydrograph (c) Flood pulse hydrograph and (d) Broad peak hydrograph.
The peak outflows of the MFF and SFPM rules lie between outflows from the MFP rule and “No Reservoir” cases. The SFPM rule outperforms the MFF rule for all hydrograph shapes at the channel capacity of 50 units per period. Increasing the channel capacity will improve the efficiency of the MFF and SFPM rules so the MFF and SFPM curves approach the MFP curves. Similarly, as the forecast period increases, the SFPM plot follows the MFP curve more closely, resulting in additional peak reduction. The outflow with an Abrupt Wave hydrograph inflow can be reduced at any inflow with any rule. For the MFF and SFPM rules, all shapes converge with the “No Reservoir” case at large inflows, though at different rates [4,7,8].
4. Conclusions
This study analyzing three simple flood operating rules for reservoirs offers some general insights for reservoir flood operations and the role of flow forecasting and downstream damage functions in optimal flood operations.
Accurate forecasts can help reservoir operators in effective flood operation. With a complete and accurate forecast, operators can achieve a theoretical maximum reduction in the peak flow from a reservoir, or make optimal pre-storm releases to provide additional flood storage capacity available when needed. With no forecast, reservoir operators can only attempt to maintain the channel capacity and hope that inflows subside before the reservoir fills. If peak inflows occur after flood storage capacity fills, flood peak reduction can be minimal. With an incomplete forecast, operators can significantly reduce peak outflow in many cases. Any amount of forecast information can help reduce flooding damage where damages from outflows are convex. However, if damage functions are concave, as with some levee systems, minimizing flooding frequency can be a more desirable objective.
Expanding downstream channel capacity and flood storage volume can increase the flood volume that is allowed to pass through the system without causing harm. Flood storage volume, channel capacities, and inflow forecast length together limit any operating rule in reducing peak flood outflow.
Although the volume of a flood hydrograph can be manipulated in a computer model, in reality the oncoming shape and volume are uncertain. Reservoirs generally reduce flood peaks most effectively for hydrographs with more abrupt shapes. Greater efficiency in peak outflow reduction occurs when peak inflow occurs over a short time. Peak reduction also is aided by having the peak occur abruptly at the beginning of the flood. Reducing the peak flows for pulse hydrographs is a challenge for reservoir operators regardless of the operating rules.
Acknowledgments
Thanks to Nathan Burley for guidance and programming help and Rui Hui and Ben Lord for comments on earlier versions of this work.
Author Contributions
James Connaughton assembled and re-analyzed work originally done by Natalie King, Licheng Dong, Patrick Ji on different aspects of single reservoir operations for floods, as part of their post-graduate research, and placed it into a single coherent paper. Jay Lund served as a general editor.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bradley, A.A.; Potter, K.W. Flood Frequency Analysis of Simulated Flows. Water Resour. Res. 1992, 28, 2375–2385. [Google Scholar] [CrossRef]
- Ayalew, T.; Krajewski, W.; Mantilla, R. Exploring the Effect of Reservoir Storage on Peak Discharge Frequency. J. Hydrol. Eng. ASCE 2013, 18, 1697–1708. [Google Scholar] [CrossRef]
- Goldman, D.M. Quantifying Uncertainty in Estimates of Regulated Flood Frequency Curves. State of the Practice. In Proceedings of the World Water and Environmental Resources Congress, Orlando, FL, USA, 20–24 May 2001; American Society of Civil Engineers: Reston, VA, USA, 2001. [Google Scholar]
- Ji, P. Reservoir Reoperation, Risk and Levee Failure Analysis: Mokulemne River Case. Ph.D. Thesis, Civil and Environmental Engineering Department, University of California, Davis, CA, USA, 2011. [Google Scholar]
- Hydrologic Engineering Center (HEC). Hydrologic Engineering Methods for Water Resources Development; HEC, Corps of Engineers, U.S. Army: Davis, CA, USA, 1976; Volume 7. [Google Scholar]
- Hui, R.; Lund, J. Flood Storage Allocation Rules for Parallel Reservoirs. J. Water Resour. Plan. Manag. 2014. [Google Scholar] [CrossRef]
- Dong, L. Flood Operation Rules for a Single Reservoir. Master’s Thesis, Civil and Environmental Engineering Department, University of California, Davis, CA, USA, 2012. [Google Scholar]
- Ergish, N. Flood Frequency Analysis for Regulated Watersheds. Master’s Thesis, Civil and Environmental Engineering Department, University of California, Davis, CA, USA, 2010. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).