Multilayer Numerical Modeling of Flows through Vegetation Using a Mixing-Length Turbulence Model
Abstract
:1. Introduction
2. Governing Equations
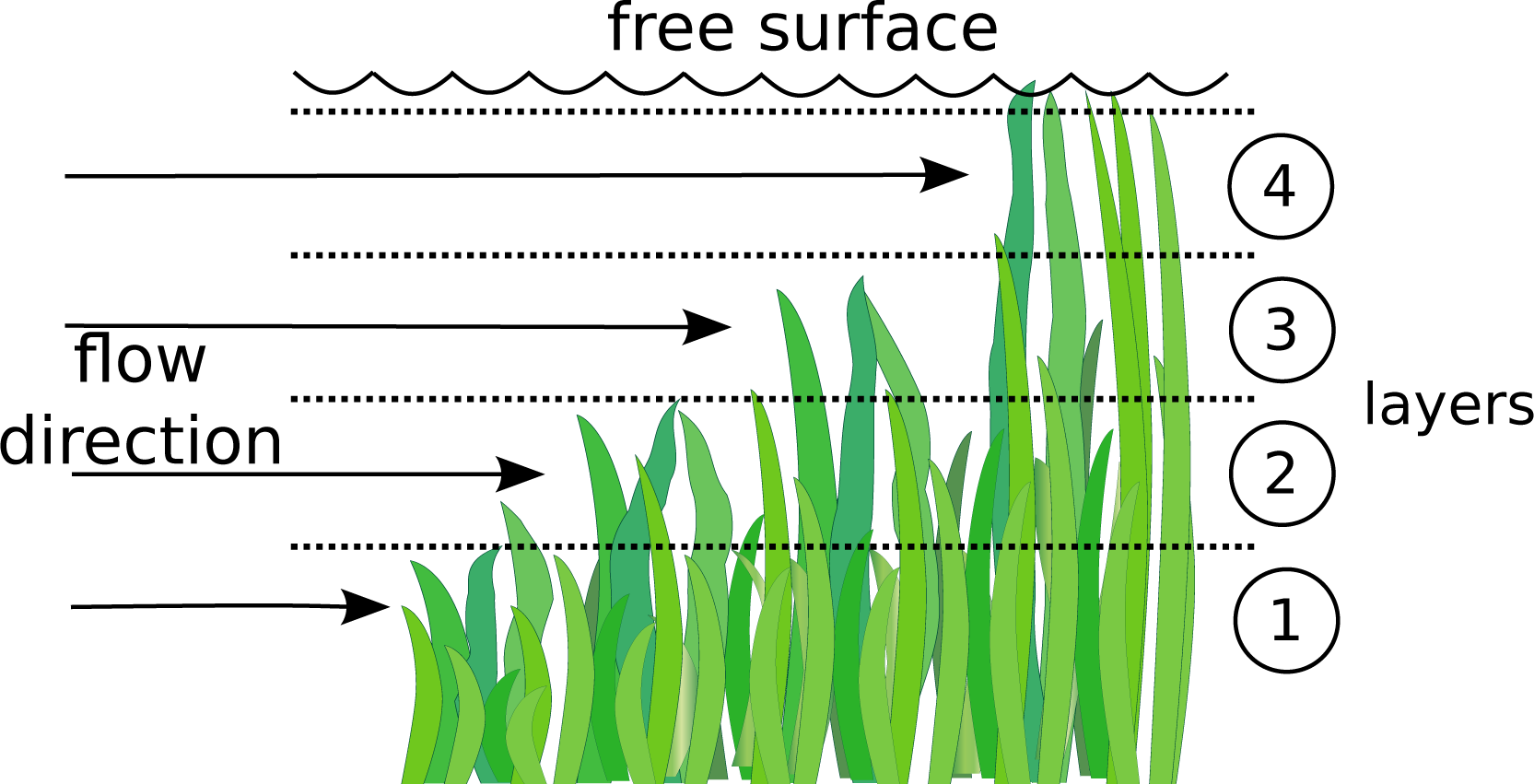
2.1. Turbulence Modeling
2.2. Vegetation and Bottom Shear Stresses
3. Numerical Model
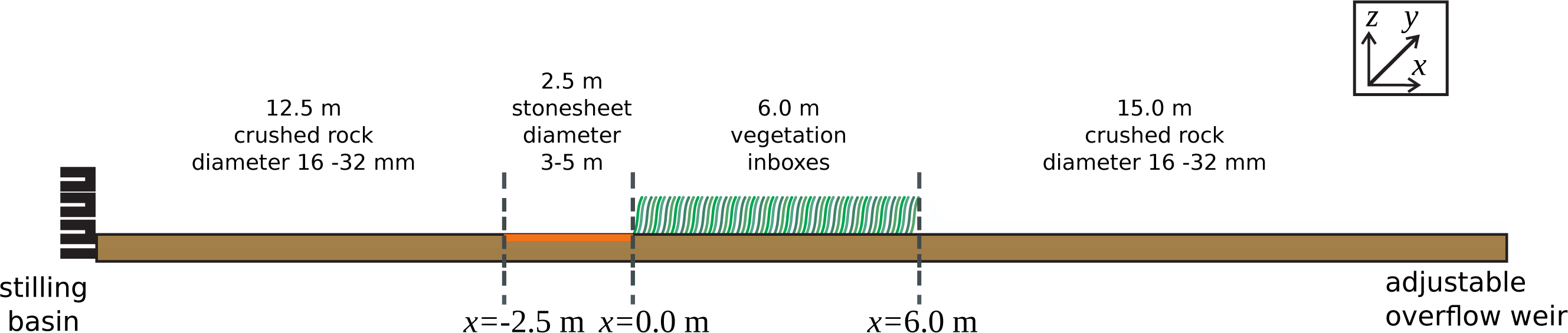
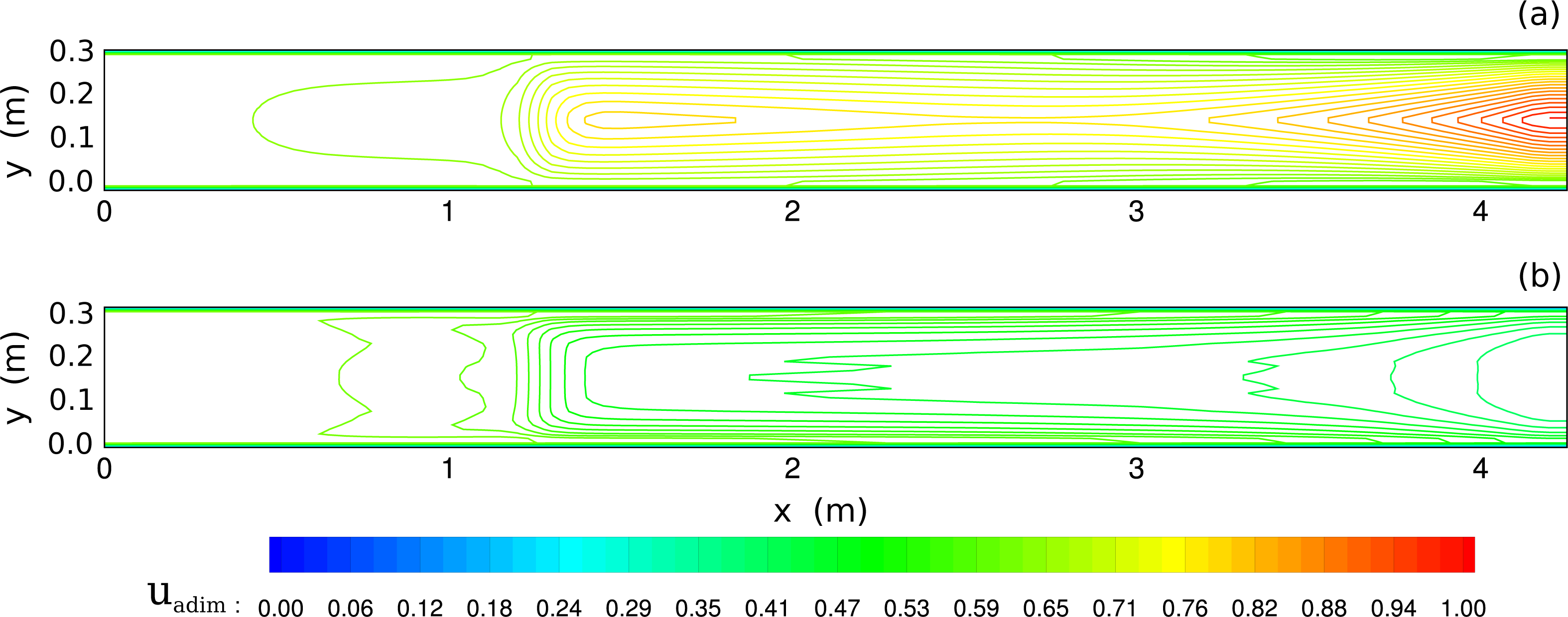
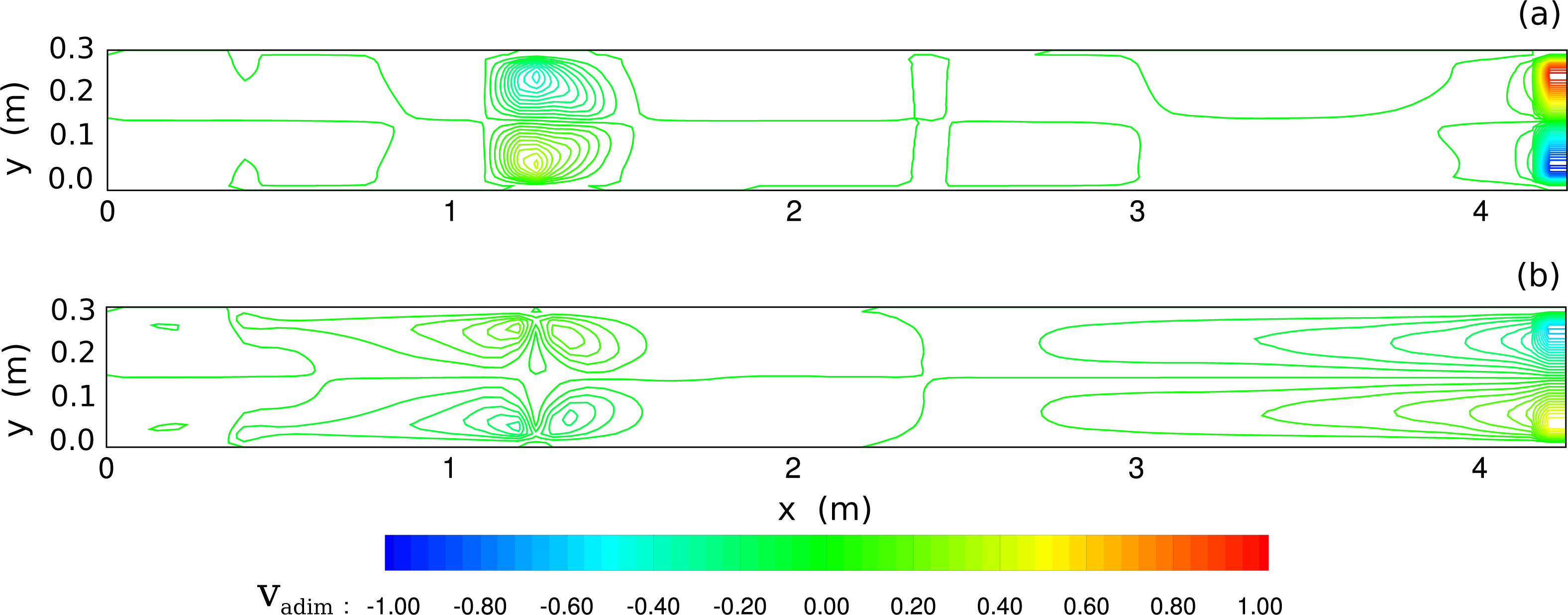
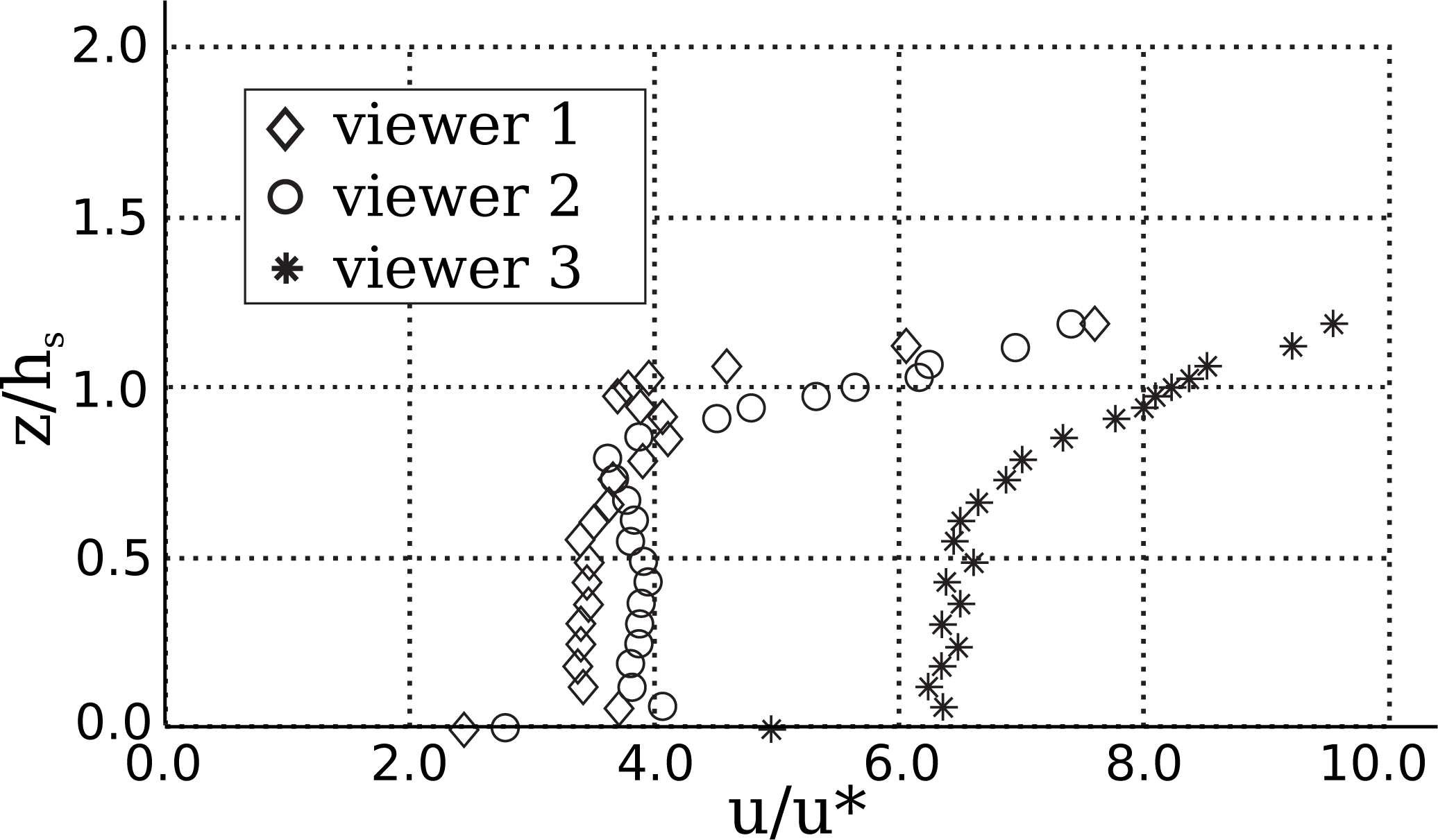
4. Numerical Simulations and Discussion
4.1. Channel with Submerged Vegetation
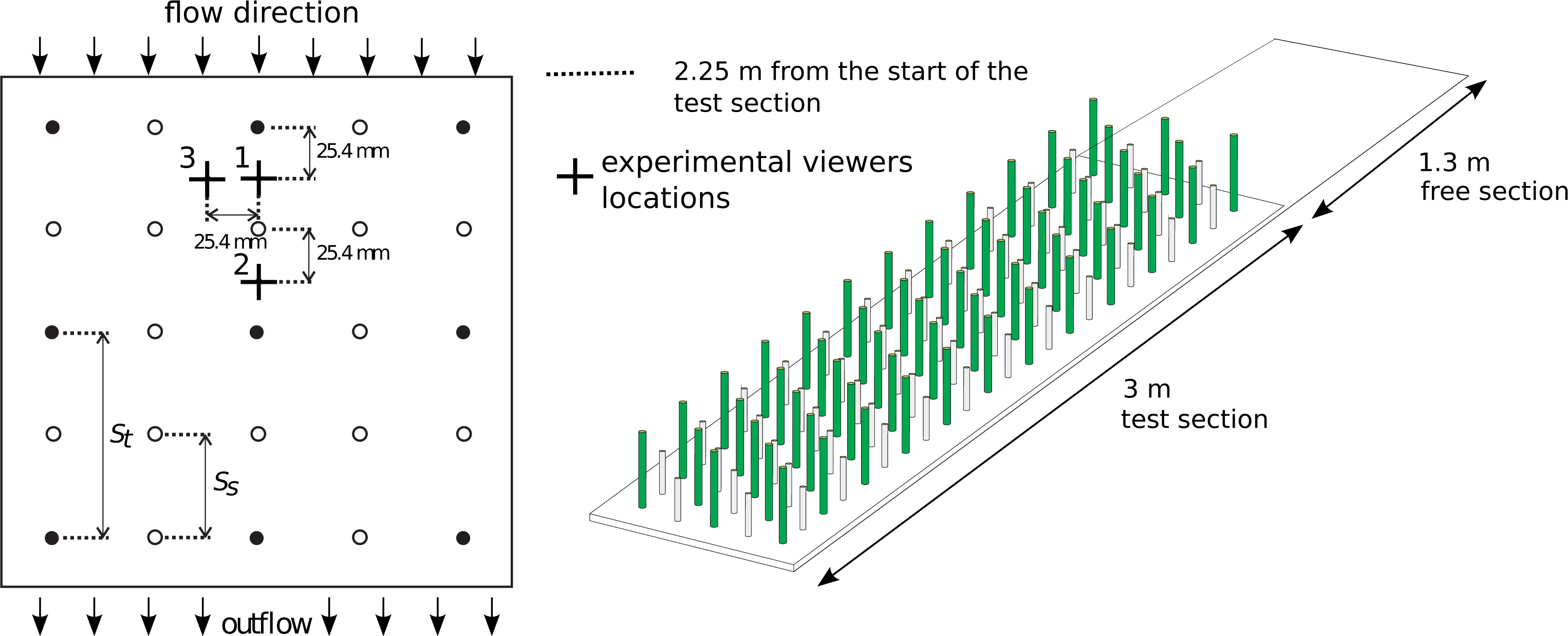
4.2. Channel with Submerged and Emergent Vegetation
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Newson, M.D. River Conservation and Catchment Management, Conservation and Management; Wiley: Chichester, UK, 1992; pp. 385–396. [Google Scholar]
- Ward, J.; Tockner, K.; Uehlinger, U.; Malard, F. Understanding natural patterns and processes in river corridors as the basis for effective river restoration. Regul. Rivers Res. Manag 2001, 17, 311–323. [Google Scholar]
- Nepf, H.; Vivoni, E. Flow structure in depth-limited vegetated flow. J. Geophys. Res 2000, 105, 28547–28557. [Google Scholar]
- Tsujimoto, T. Fluvial processes in streams with vegetation. J. Hydraul. Res 1999, 37, 789–803. [Google Scholar]
- Smart, G.M.; Duncan, M.J.; Walsh, J.M. Relatively rough flow resistance equations. J. Hydraul. Eng 2002, 128, 568–578. [Google Scholar]
- Nikora, V.; Koll, K.; McEwan, I.; McLean, S.; Dittrich, A. Velocity distribution in the roughness layer of rough bed flows. J. Hydraul. Eng 2004, 130, 1036–1042. [Google Scholar]
- Ghisalberti, M. Obstructed shear flows: Similarities across systems and scales. J. Fluid Mech 2009, 641, 51–61. [Google Scholar]
- Cheng, N.S. Representative roughness height of submerged vegetation. Water Resour. Res 2011, 47. [Google Scholar] [CrossRef]
- Nepf, H. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech 2012, 44, 123–142. [Google Scholar]
- Freeman, G.E.; Rahmeyer, W.J.; Copeland, R.R. Determination of Resistance Due to Shrubs and Woody Vegetation; Technical report; U.S. Army Corps of Engineers; Coastal and Hydraulics Laboratory: Washington, DC, USA, 2000. [Google Scholar]
- Järvelä, J. Determination of Flow Resistance of Vegetated Channel Banks and Floodplains. In River Flow; Zech, B., Bousmar, D., Eds.; Swets & Zeitlinger: Helsinki University of Technology, Finland, 2002. [Google Scholar]
- Pechlivanidis, G.I.; Keramaris, E.; Pechlivandis, I.G.; Samaras, G.A. Measuring the turbulent characteristics in an open channel using the PIV method. Glob. NEST J 2012, 14, 378–385. [Google Scholar]
- Stone, B.M.; Shen, H.T. Hydraulic Resistance of Flow in Channels with Cylindrical Roughness. J. Hydraul. Eng 2002, 128, 500–506. [Google Scholar]
- Huthoff, F.; Augustijn, D.C.M.; Hulscher, S.J.M.H. Depth-Averaged Flow in Presence of Submerged Cylindrical Elements. In River Flow; Francis, T., Ed.; Taylor & Francis: London, UK, 2006; pp. 575–582. [Google Scholar]
- Yen, B.C. Open Channel Flow Resistance. J. Hydraul. Eng 2002, 128, 20–39. [Google Scholar]
- Feng, K.; Molz, F.J. A 2-D, diffusion based, wetland flow model. J. Hydrol 1997, 196, 230–250. [Google Scholar]
- Fennema, R.J.; Neidrauer, C.J.; Johnson, R.A.; MacVicor, T.K.; Perkins, W.A.A. Computer Model to Simulate Natural Everglades Hydrology. In Everglades The Ecosystem and Its Restoration; St. Lucie Press: Florida, USA, 1994; pp. 249–289. [Google Scholar]
- Lal-Wasantha, A.M. Performance comparison of overland flow algorithms. J. Hydraul. Division ASCE 1998, 124, 342–349. [Google Scholar]
- Rowinski, P.M.; Kubrak, J. A mixing-length model for predicting vertical velocity distribution in flows through emergent vegetation. Hydrol. Sci. J 2002, 47, 893–904. [Google Scholar]
- Arega, F.; Sanders, B.F. Dispersion Model for Tidal Wetlands. J. Hydraul. Eng 2004, 130, 739–754. [Google Scholar]
- Fischer-Antze, T.; Stoesser, T.; Olsen, N.R.B. 3D numerical modeling of open-channel flow with submerged vegetation. J. Hydraul. Res 2001, 39, 303–310. [Google Scholar]
- Choi, S.U.; Kang, H. Reynolds stress modeling of vegetated open-channel flows. J. Hydraul. Res 2004, 42, 3–11. [Google Scholar]
- Yusuf, B.; Karim, O.A.; Osman, S.A. Numerical solution for open channel flow with submerged flexible vegetation. Int. J. Eng. Tech 2009, 61, 39–50. [Google Scholar]
- Jahra, F.; Yamamoto, H.; Hasegawa, F.; Kawahara, Y. Turbulent Flow Structure in Meandering Vegetated Open Channel; Bundesanstalt für Wasserbau: Higashi-Hiroshima, Japan, 2010; pp. 153–161. [Google Scholar]
- Gao, G.; Falconer, R.A.; Lin, B. Modeling open channel flows with vegetation using a three-dimensional model. J. Water Res. Prot 2011, 3, 114–119. [Google Scholar]
- Shimizu, Y.; Tsujimoto, T. Numerical analysis of turbulent open-channel flow over a vegetation layer using a k-ε turbulence model. J. Hydrosci. Hydraul. Eng 1994, 11, 57–67. [Google Scholar]
- Lopez, F.; Garcia, M.H. Open-Channel Flow Through Simulated Vegetation: Turbulence Modeling and Sediment Transport. Wetlands; Technical Report; Wetlands Research Program technical report, WRP-CP-10; University of Illinois: Urbana IL, USA, 1997. [Google Scholar]
- Neary, V.S. Numerical Solution of Fully Developed Flow with Vegetative Resistance. J. Eng. Mech. ASCE 2003, 129, 558–563. [Google Scholar]
- Naot, D.; Nezu, I.; Nakagawa, H. Hydrodynamic Behavior of Partly Vegetated Open-Channels. J. Hydraul. Eng. ASCE 1996, 122, 625–633. [Google Scholar]
- Alamatian, E.; Jaefarzadeh, M. Evaluation of turbulence models in the simulation of oblique standing shock waves in supercritical channel flows. Int. J. Civ. Eng 2012, 10, 61–71. [Google Scholar]
- Akilli, H.; Akar, A.; Karakus, C. Flow characteristics of circular cylinders arranged side-by-side in shallow water. Flow Meas. Instrum 2004, 15, 187–197. [Google Scholar]
- Fu, H.; Rockwell, D. Shallow flow past a cylinder: Transition phenomena at low Reynolds number. J. Fluid Mech 2005, 540, 75–97. [Google Scholar]
- Fu, H.; Rockwell, D. Shallow flow past a cylinder: Control of the near wake. J. Fluid Mech 2005, 539, 1–24. [Google Scholar]
- Sadeque, M.A.F.; Rajaratnam, N.; Loewen, M.R. Flow around cylinders in open channels. J. Eng. Mech 2008, 134, 60–71. [Google Scholar]
- Sadeque, M.A.F.; Rajaratnam, N.; Loewen, M.R. Effects of bed roughness on flow around bed-mounted cylinders in open channels. J. Eng. Mech 2009, 135, 100–110. [Google Scholar]
- Rodi, W.; Scheuerer, G. Scrutinizing the k-epsilon turbulence model under adverse pressure gradient conditions. J. Fluids Eng. Trans. ASME 1986, 108, 174–179. [Google Scholar]
- Lam, C.K.G.; Bremhorst, K. A modified form of the k-epsilon model for predicting wall turbulence. ASME Trans. J. Fluids Eng 1981, 103, 456–460. [Google Scholar]
- Stansby, P.K. A mixing-length model for shallow turbulent wakes. J. Fluid Mech 2003, 495, 369–384. [Google Scholar]
- Perlin, A.; Moum, J.N.; Klymak, J.M.; Levine, M.D.; Boyd, T.; Kosro, P.M. A modified law-of-the-wall applied to oceanic bottom boundary layers. J. Geophys. Res 2005, 110. [Google Scholar] [CrossRef]
- Kadlec, R.H. Overland flow in wetlands: Vegetation resistance. J. Hydraul. Eng 1990, 116, 691–706. [Google Scholar]
- Casulli, V.; Cheng, R.T. Semi-implicit finite difference methods for three dimentional shallow water flow. Int. J. Numer. Methods Fluids 1992, 15, 629–648. [Google Scholar]
- Ramírez-León, H.; Barrios-Piña, H.; Rodríguez-Cuevas, C.; Couder-Castañeda, C. Baroclinic mathematical modeling of fresh water plumes in the interaction river-sea. Int. J. Numer. Anal. Model 2005, 2, 1–14. [Google Scholar]
- Ramírez-León, H.; Couder-Castañeda, C.; Herrera-Díaz, I.E.; Barrios-Piña, H. Modelación numérica de la descarga térmica de la Central Nucleo-eléctrica de Laguna Verde. Rev. Int. Mét. Num. Cálc. Dis. Ing 2010, 15, 185–211. [Google Scholar]
- Rodríguez, C.; Serre, E.; Rey, C.; Ramírez, H. A numerical model for shallow-water flows: Dynamics of the eddy shedding. Wseas Trans. Environ. Dev 2005, 1, 280–287. [Google Scholar]
- Ramírez-León, H.; Rodríguez-Cuevas, C.; Herrera Díaz, E. Multilayer hydrodinamic model and their application to sediment transport in estuaries. In Special Issue Shangai Conference, Current Trends in High Performance Computing and Its Applications; Springer-Verlag: Berlin, Germany, 2005; pp. 59–70. [Google Scholar]
- Couder, C.; Ramírez, H.; Herrera, E. Numerical Modeling of Coupled Phenomena in Science and Enginering: Practical Use and Examples; Taylor & Francis: London, UK, 2008. [Google Scholar]
- Herrera-Díaz, I.E.; Couder-Castañeda, C.; Ramírez-León, H. A case study of nearshore wave transformation processes along the coast of Mexico near the Laguna verde nuclear power plant using a fast simulation method. Model. Simul. Eng 2010, 1, 8–17. [Google Scholar]
- Järvelä, J. Effect of submerged flexible vegetation on flow structure and resistance. J. Hydrol 2005, 307, 233–241. [Google Scholar]
- Liu, D. Flow through Rigid Vegetation Hydrodynamics, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 12 September 2008.







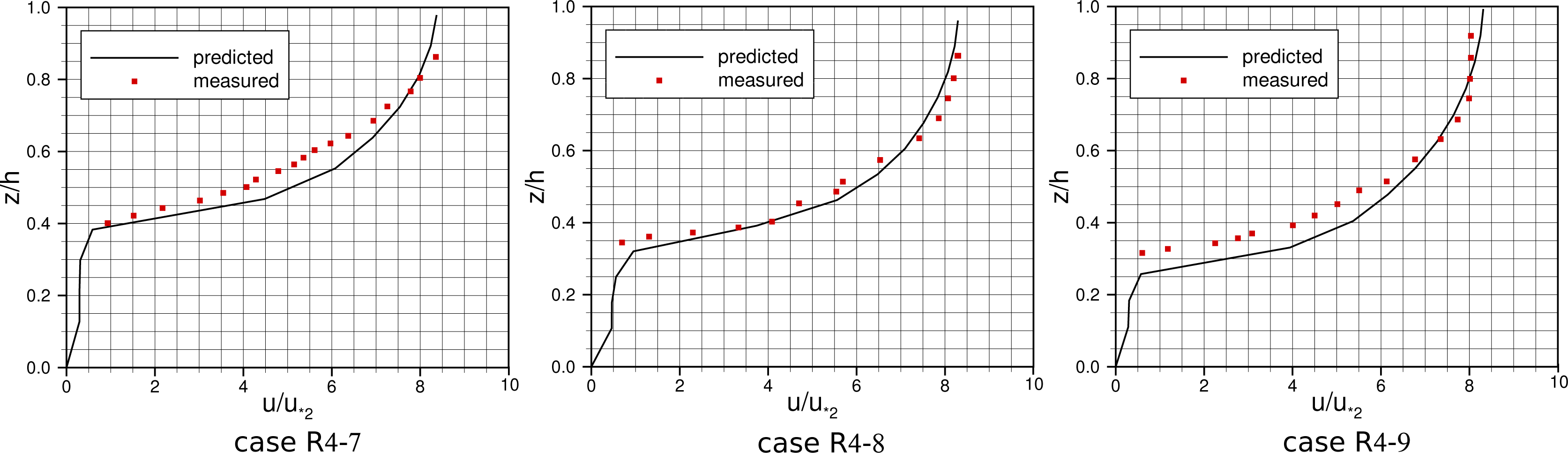


| Case | Q (l/s) | h (m) | U0 (m/s) | Re | Fr | Se | u*2 (m/s) | hp (m) | f |
|---|---|---|---|---|---|---|---|---|---|
| R4-7 | 100 | 0.4950 | 0.1836 | 60,606 | 0.083 | 0.0006 | 0.0416 | 0.220 | 0.68 |
| R4-8 | 100 | 0.7065 | 0.1287 | 60,606 | 0.049 | 0.0002 | 0.027 | 0.260 | 0.50 |
| R4-9 | 143 | 0.7037 | 0.1847 | 86,667 | 0.070 | 0.0003 | 0.0384 | 0.215 | 0.44 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barrios-Piña, H.; Ramírez-León, H.; Rodríguez-Cuevas, C.; Couder-Castañeda, C. Multilayer Numerical Modeling of Flows through Vegetation Using a Mixing-Length Turbulence Model. Water 2014, 6, 2084-2103. https://doi.org/10.3390/w6072084
Barrios-Piña H, Ramírez-León H, Rodríguez-Cuevas C, Couder-Castañeda C. Multilayer Numerical Modeling of Flows through Vegetation Using a Mixing-Length Turbulence Model. Water. 2014; 6(7):2084-2103. https://doi.org/10.3390/w6072084
Chicago/Turabian StyleBarrios-Piña, Hector, Hermilo Ramírez-León, Clemente Rodríguez-Cuevas, and Carlos Couder-Castañeda. 2014. "Multilayer Numerical Modeling of Flows through Vegetation Using a Mixing-Length Turbulence Model" Water 6, no. 7: 2084-2103. https://doi.org/10.3390/w6072084
APA StyleBarrios-Piña, H., Ramírez-León, H., Rodríguez-Cuevas, C., & Couder-Castañeda, C. (2014). Multilayer Numerical Modeling of Flows through Vegetation Using a Mixing-Length Turbulence Model. Water, 6(7), 2084-2103. https://doi.org/10.3390/w6072084




