A Comparative Analysis of In-Situ Wave Measurements and Reanalysis Models for Predicting Coastline Evolution: A Case Study of IJmuiden, The Netherlands
Abstract
1. Introduction
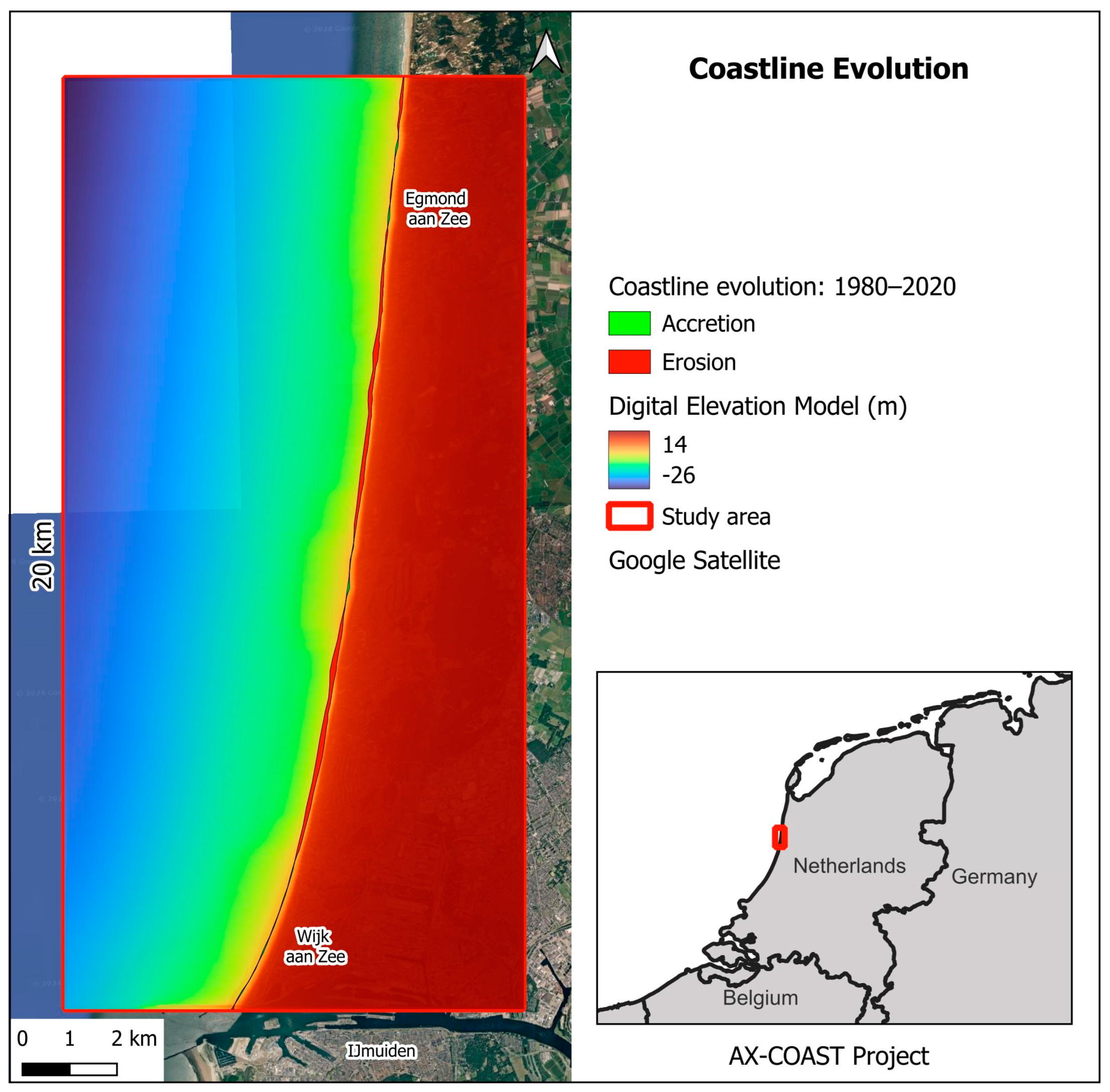
2. IJmuiden (The Netherlands) Study Area
3. Materials and Methods
3.1. Materials
3.1.1. Wave-Climate Data—In Situ and Reanalysis Dataset Characterization
3.1.2. Forcing Agents Scenarios
3.2. Methods
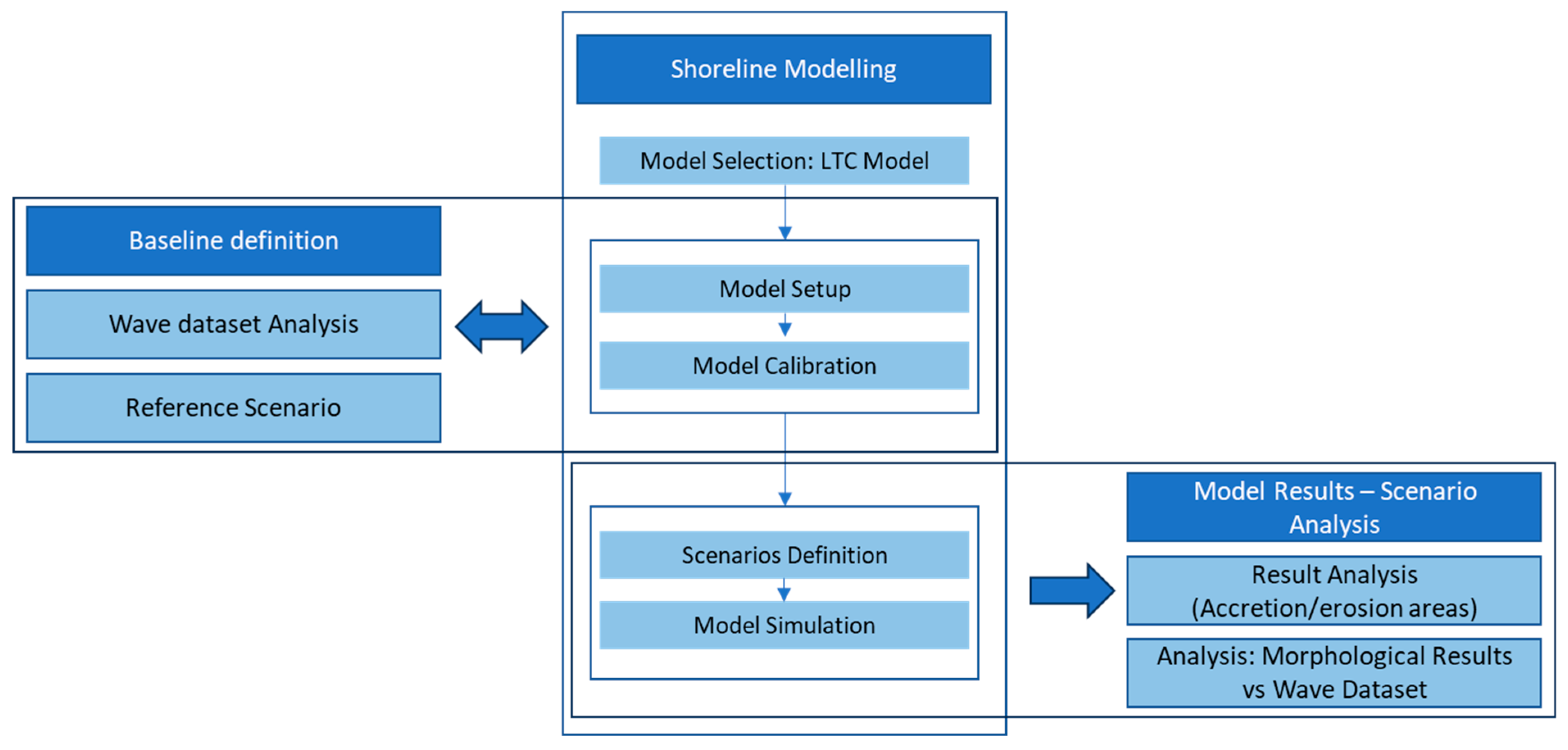
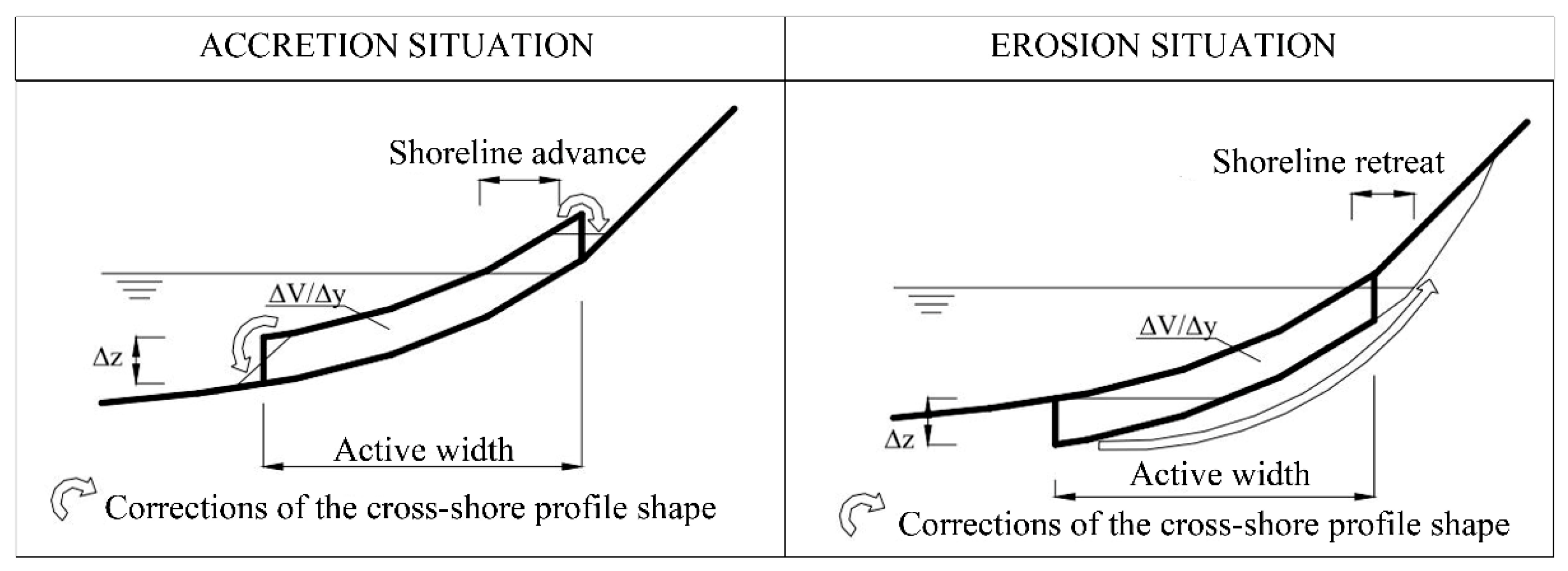
3.2.1. LTC Numerical Model Description
3.2.2. LTC Modelling—Setup
4. Results
Reference Scenario
- (a)
- The 200,000 m3/year Nourishment Scenario
- (b)
- The 250,000 m3/year Nourishment Scenario
- (c)
- Without Artificial Nourishment
- (d)
- Analysis of Mean Retreat Under Different Nourishment Scenarios
- (e)
- Analysis of Relative Error Under Different Nourishment Scenarios
- (f)
- Impact of No Nourishment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Housley, J. Justification for Beach Nourishment. In Coastal Engineering 1996, Proceedings of the 25th International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; ASCE Libary: Orlando, FL, USA, 1996; p. 26. [Google Scholar]
- Coelho, C. Riscos de Exposição de Frentes Urbanas Para Diferentes Intervenções de Defesa Costeira. PhD Thesis, University of Aveiro, Aveiro, Portugal, 2005. [Google Scholar]
- Masselink, G.; Pattiaratchi, C.B. Seasonal Changes in Beach Morphology along the Sheltered Coastline of Perth, Western Australia. Mar. Geol. 2001, 172, 243–263. [Google Scholar] [CrossRef]
- Hanson, H.; Brampton, A.; Capobianco, M.; Dette, H.H.; Hamm, L.; Laustrup, C.; Lechuga, A.; Spanhoff, R. Beach Nourishment Projects, Practices, and Objectives—A European Overview. Coast. Eng. 2002, 47, 81–111. [Google Scholar] [CrossRef]
- Coelho, C.; Silva, R.; Veloso-Gomes, F.; Rodrigues, L. Artificial nourishment and sand by-passing in the aveiro inlet, portugal-numerical studies. Coast. Eng. Proc. 2011, 1, 99. [Google Scholar] [CrossRef]
- Verhagen, H. Method for Artificial Beach Nourishment. In Coastal Engineering, Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4 October 1992; ASCE Libary: Orlando, FL, USA, 1992. [Google Scholar]
- Tondello, M.; Ruol, P.; Sclavo, M.; Capobianco, M. Model Tests for Evaluating Beach Nourishment Performance. In Coastal Engineering, Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22 June 1998; ASCE Libary: Orlando, FL, USA, 1998; Volume 3. [Google Scholar]
- Marinho, B.; Coelho, C.; Larson, M.; Hanson, H. Short-and Long-Term Responses of Nourishments: Barra-Vagueira Coastal Stretch, Portugal. J. Coast. Conserv. 2018, 22, 475–489. [Google Scholar] [CrossRef]
- Ferreira, A.M.; Coelho, C. Artificial Nourishments Effects on Longshore Sediments Transport. J. Mar. Sci. Eng. 2021, 9, 240. [Google Scholar] [CrossRef]
- Davison, T.; Nicholls, R.; Leatherman, S. Beach Nourishment as a Coastal Management Tool: An Annotated Bibliography on Developments Associated with the Artificial Nourishment of Beaches. J. Coast. Res. 1992, 8, 984–1022. [Google Scholar]
- Pais-Barbosa, J.; Ferreira, A.M.; Lima, M.; Filho, L.M.; Roebeling, P.; Coelho, C. Cost-Benefit Analysis of Artificial Nourishments: Discussion of Climate Change Adaptation Pathways at Ovar (Aveiro, Portugal). Ocean. Coast. Manag. 2023, 244, 106826. [Google Scholar] [CrossRef]
- Camus, P.; Losada, I.J.; Izaguirre, C.; Espejo, A.; Menéndez, M.; Pérez, J. Statistical Wave Climate Projections for Coastal Impact Assessments. Earths Future 2017, 5, 918–933. [Google Scholar] [CrossRef]
- Leake, J.; Wolf, J.; Lowe, J.; Stansby, P.; Jacoub, G.; Nicholls, R.; Mokrech, M.; Nicholson-Cole, S.; Walkden, M.; Watkinson, A.; et al. Predicted Wave Climate for the UK: Towards an Integrated Model of Coastal Impacts of Climate Change. In Estuarine and Coastal Modeling, Proceedings of the 10th International Conference on Estuarine and Coastal Modeling, Newport, RI, USA, 5 November 2007; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 393–406. [Google Scholar] [CrossRef]
- Remya, P.G.; Kumar, R.; Basu, S.; Sarkar, A. Wave Hindcast Experiments in the Indian Ocean Using MIKE 21 SW Model. J. Earth Syst. Sci. 2012, 121, 385–392. [Google Scholar] [CrossRef]
- Gómez-Orellana, A.M.; Fernández, J.C.; Dorado-Moreno, M.; Gutiérrez, P.A.; Hervás-Martínez, C. Building Suitable Datasets for Soft Computing and Machine Learning Techniques from Meteorological Data Integration: A Case Study for Predicting Significant Wave Height and Energy Flux. Energies 2021, 14, 468. [Google Scholar] [CrossRef]
- Armenio, E.; De Serio, F.; Mossa, M.; Petrillo, A.F. Coastline Evolution Based on Statistical Analysis and Modeling. Nat. Hazards Earth Syst. Sci. 2019, 19, 1937–1953. [Google Scholar] [CrossRef]
- Jaramillo, C.; Jara, M.S.; González, M.; Medina, R. A Shoreline Evolution Model Considering the Temporal Variability of the Beach Profile Sediment Volume (Sediment Gain/Loss). Coast. Eng. 2020, 156, 103612. [Google Scholar] [CrossRef]
- Baptista, P.; Coelho, C.; Pereira, C.; Bernardes, C.; Veloso-Gomes, F. Beach Morphology and Shoreline Evolution: Monitoring and Modelling Medium-Term Responses (Portuguese NW Coast Study Site). Coast. Eng. 2014, 84, 23–37. [Google Scholar] [CrossRef]
- Jara, M.S.; González, M.; Medina, R. Shoreline Evolution Model from a Dynamic Equilibrium Beach Profile. Coast. Eng. 2015, 99, 1–14. [Google Scholar] [CrossRef]
- Subiyanto; Ahmad, M.F.; Mamat, M.; Husain, M.L. Comparison of Numerical Method for Forward and Backward Time Centered Space for Long-Term Simulation of Shoreline Evolution. Appl. Math. Sci. 2013, 7, 5165–5173. [Google Scholar] [CrossRef]
- Simmons, J.A.; Splinter, K.D.; Harley, M.D.; Turner, I.L. Calibration Data Requirements for Modelling Subaerial Beach Storm Erosion. Coast. Eng. 2019, 152, 103507. [Google Scholar] [CrossRef]
- Kim, T.-K.; Lim, C.; Lee, J.-L. Vulnerability Analysis of Episodic Beach Erosion by Applying Storm Wave Scenarios to a Shoreline Response Model. Front. Mar. Sci. 2021, 8, 759067. [Google Scholar] [CrossRef]
- Li, F.; van Gelder, P.H.A.J.M.; Ranasinghe, R.; Callaghan, D.P.; Jongejan, R.B. Probabilistic Modelling of Extreme Storms along the Dutch Coast. Coast. Eng. 2014, 86, 1–13. [Google Scholar] [CrossRef]
- de Winter, R.C.; Ruessink, B.G. Sensitivity Analysis of Climate Change Impacts on Dune Erosion: Case Study for the Dutch Holland Coast. Clim. Chang. 2017, 141, 685–701. [Google Scholar] [CrossRef]
- Athanasiou, P.; van Dongeren, A.; Giardino, A.; Vousdoukas, M.; Antolinez, J.A.A.; Ranasinghe, R. Estimating Dune Erosion at the Regional Scale Using a Meta-Model Based on Neural Networks. Nat. Hazards Earth Syst. Sci. 2022, 22, 3897–3915. [Google Scholar] [CrossRef]
- Vitousek, S.; Vos, K.; Splinter, K.D.; Erikson, L.; Barnard, P.L. A Model Integrating Satellite-Derived Shoreline Observations for Predicting Fine-Scale Shoreline Response to Waves and Sea-Level Rise Across Large Coastal Regions. J. Geophys. Res. Earth Surf. 2023, 128. [Google Scholar] [CrossRef]
- Athanasiou, P.; van Dongeren, A.; Giardino, A.; Vousdoukas, M.; Antolinez, J.A.A.; Ranasinghe, R. A Clustering Approach for Predicting Dune Morphodynamic Response to Storms Using Typological Coastal Profiles: A Case Study at the Dutch Coast. Front. Mar. Sci. 2021, 8, 747754. [Google Scholar] [CrossRef]
- Sembiring, L.; van Ormondt, M.; van Dongeren, A.; Roelvink, D. A Validation of an Operational Wave and Surge Prediction System for the Dutch Coast. Nat. Hazards Earth Syst. Sci. 2015, 15, 1231–1242. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Ministerie van Verkeer en Waterstaat. Kustnota, Traditie, Trends en Toekomst. Ministerie van Verkeer en Waterstaat; Ministerie van Verkeer en Waterstaat: The Hague, Netherlands, 2000. [Google Scholar]
- Brand, E.; Ramaekers, G.; Lodder, Q. Dutch Experience with Sand Nourishments for Dynamic Coastline Conservation–An Operational Overview. Ocean. Coast. Manag. 2022, 217, 106008. [Google Scholar] [CrossRef]
- Romão, F.; Coelho, C.; Lima, M.; Ásmundsson, H.; Myer, E.M. Cross-Shore Modeling Features: Calibration and Impacts of Wave Climate Uncertainties. J. Mar. Sci. Eng. 2024, 12, 760. [Google Scholar] [CrossRef]
- Luijendijk, A.; De Vroeg, H.; Swinkels, C.; Walstra, D.-J. Coastal response on multiple scales: A pilot study on the ijmuiden port. In Proceedings of the Coastal Sediments, Miami, FL, USA, 2–6 May 2011; World Scientific Publishing Company: Singapore, 2011; pp. 602–615. [Google Scholar] [CrossRef]
- Van Rijn, L. Improvement of Coastline Modelling Software Using Field Data. AX-COAST Report; AX-COAST: Aveiro, Portugal, 2023. [Google Scholar]
- Stronkhorst, J.; Huisman, B.; Giardino, A.; Santinelli, G.; Santos, F.D. Sand Nourishment Strategies to Mitigate Coastal Erosion and Sea Level Rise at the Coasts of Holland (The Netherlands) and Aveiro (Portugal) in the 21st Century. Ocean. Coast. Manag. 2018, 156, 266–276. [Google Scholar] [CrossRef]
- Vermas, T.; Boersen, S.; Wilmink, R.; Lodder, Q. National Analyses of Nourishments; Coastal State Indicators and Driving Forces for Bergen-Egmond, the Netherlands; Rijkswaterstaat and Deltares: Delft, The Netherlands, 2021. [Google Scholar]
- Mummery, J.C. Available Data, Datasets and Derived Information to Support Coastal Hazard Assessment and Adaptation Planning. CoastAdapt Information Manual 3; National Climate Change Adaptation Research Facility: Gold Coast, Australia, 2016. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). ERA 5. 2023. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=overview (accessed on 31 July 2024).
- Copernicus Marine Service Information. Atlantic- European Northwest Shelf- Wave Physics Reanalysis. E.U. Copernicus Marine Service Information (CMEMS). Marine Data Store (MDS). Available online: https://data.marine.copernicus.eu/product/NWSHELF_REANALYSIS_WAV_004_015/description (accessed on 31 July 2024).
- Coelho, C.; Veloso-Gomes, F.; Silva, R. Shoreline Coastal Evolution Model: Two Portuguese Case Studies. In Coastal Engineering, Proceedings of the 30th International Conference, San Diego, CA, USA, 3–8 September 2006; McKee Smith, J., Ed.; World Scientific: San Diego, CA, USA, 2007; pp. 3430–3441. [Google Scholar]
- Coelho, C.; Taveira Pinto, F.; Veloso Gomes, F.; Pais-Barbosa, J. Coastal Evolution and Coastal Works in the Southern Part of Aveiro Lagoon Inlet, Portugal. In Coastal Engineering, Proceedings of the 29th International Conference, National Civil Engineering Laboratory, Lisbon, Portugal, 19–24 September 2004; McKee Smith, J., Ed.; World Scientific: Lisbon, Portugal, 2004; pp. 19–24. [Google Scholar]
- Lima, M.; Coelho, C. Improvement of an Existing Shoreline Evolution Numerical Model. In MARINE VIII: Proceedings of the VIII International Conference on Computational Methods in Marine Engineering, Göteborg, Sweden, 13–15 May 2019; CIMNE: Barcelona, Spain, 2019; pp. 502–513. [Google Scholar]
- Lima, M.; Coelho, C. LTC Shoreline Evolution Model: Assumptions, Evolution, Validation and Application. J. Integr. Coast. Zone Manag. 2017, 17, 5–17. [Google Scholar]
- CERC. Shore Protection Manual; U.S. Coastal Engineering Research Center: Washington, DC, USA, 1984; Volume 1. [Google Scholar]
- Kamphuis, J.W. Alongshore sediment transport rate. J. Waterw. Port. Coast. Ocean. Eng.-ASCE 1991, 117, 624–640. [Google Scholar] [CrossRef]
- Hanson, H.; Kraus, N.C. GENESIS: Generalized Model for Simulating Shoreline Chang—Report 1 Technical Reference, Technical Report CERC; Coastal Engineering Research Center, US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1991. [Google Scholar]
- Silva, R. Avaliação Experimental e Numérica de Parâmetros Associados a Modelos de Evolução Da Linha de Costa. Ph.D. Thesis, Faculdade de Engenharia da Universidade do Porto, Porto, Portugal, 2010. [Google Scholar]
- EMODnet. Available online: https://sextant.ifremer.fr/record/SDN_CPRD_1527_Yearly_Coastal_Survey_2018/ (accessed on 1 February 2024).
- Boak, E.H.; Turner, I.L. Shoreline Definition and Detection: A Review. J. Coast. Res. 2005, 214, 688–703. [Google Scholar] [CrossRef]
- Lima, M.; Coelho, C. COAST: Coastal Optimization Assessment Tool; Lima, M., Coelho, C., Eds.; UA Editora, Universidade de Aveiro: Aveiro, Portugal, 2024. [Google Scholar]
- Coelho, C.; Lima, M.; Ferreira, M. A Cost–Benefit Approach to Discuss Artificial Nourishments to Mitigate Coastal Erosion. J. Mar. Sci. Eng. 2022, 10, 1906. [Google Scholar] [CrossRef]
- Lima, M.; Ferreira, A.M.; Coelho, C. A Cost–Benefit Approach to Assess the Physical and Economic Feasibility of Sand Bypassing Systems. J. Mar. Sci. Eng. 2023, 11, 1829. [Google Scholar] [CrossRef]
- Lima, M.; Coelho, C.; Veloso-Gomes, F.; Roebeling, P. An Integrated Physical and Cost-Benefit Approach to Assess Groins as a Coastal Erosion Mitigation Strategy. Coast. Eng. 2020, 156, 103614. [Google Scholar] [CrossRef]
- Coelho, C.; Narra, P.; Marinho, B.; Lima, M. Coastal Management Software to Support the Decision-Makers to Mitigate Coastal Erosion. J. Mar. Sci. Eng. 2020, 8, 37. [Google Scholar] [CrossRef]
- Larson, M.; Palalane, J.; Fredriksson, C.; Hanson, H. Simulating Cross-Shore Material Exchange at Decadal Scale. Theory and Model Component Validation. Coast. Eng. 2016, 116, 57–66. [Google Scholar] [CrossRef]
- Itzkin, M.; Moore, L.J.; Ruggiero, P.; Hacker, S.D.; Biel, R.G. The Influence of Dune Aspect Ratio, Beach Width and Storm Characteristics on Dune Erosion for Managed and Unmanaged Beaches. Earth Surf. Dyn. 2020, 2020, 1–23. [Google Scholar]
- Passeri, D.L.; Bilskie, M.V.; Hagen, S.C.; Mickey, R.C.; Dalyander, P.S.; Gonzalez, V.M. Assessing the Effectiveness of Nourishment in Decadal Barrier Island Morphological Resilience. Water 2021, 13, 944. [Google Scholar] [CrossRef]
- Veloso-Gomes, F.; Costa, J.; Rodrigues, A.; Taveira-Pinto, F.; Pais-Barbosa, J.; Das Neves, L. Costa Da Caparica Artificial Sand Nourishment and Coastal Dynamics. J. Coast. Res. 2009, 1, 678–682. [Google Scholar]
- de Schipper, M.A.; Ludka, B.C.; Raubenheimer, B.; Luijendijk, A.P.; Schlacher, T.A. Beach Nourishment Has Complex Implications for the Future of Sandy Shores. Nat. Rev. Earth Environ. 2020, 2, 70–84. [Google Scholar] [CrossRef]
- Noordegraaf, I. Economic Valuation of Increased Beach Width at Praia Da Vagueira (central Portugal). Master’s Thesis, Wageningen University Netherlands, Wageningen, The Netherlands, 2020; 80p. [Google Scholar]
- Raybould, M.; Mules, T. A Cost–Benefit Study of Protection of the Northern Beaches of Australia’s Gold Coast. Tour. Econ. 1999, 5, 121–139. [Google Scholar]
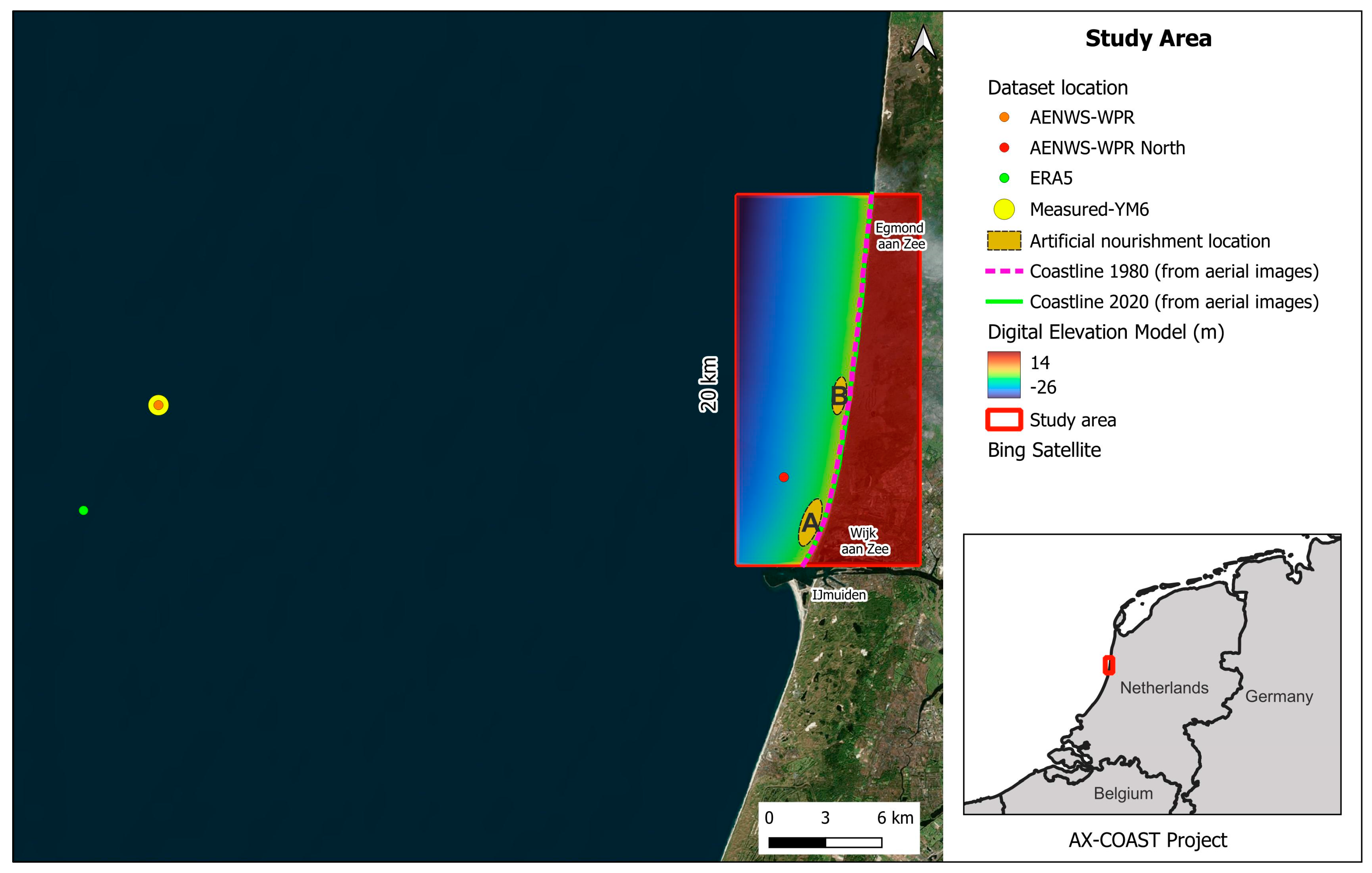




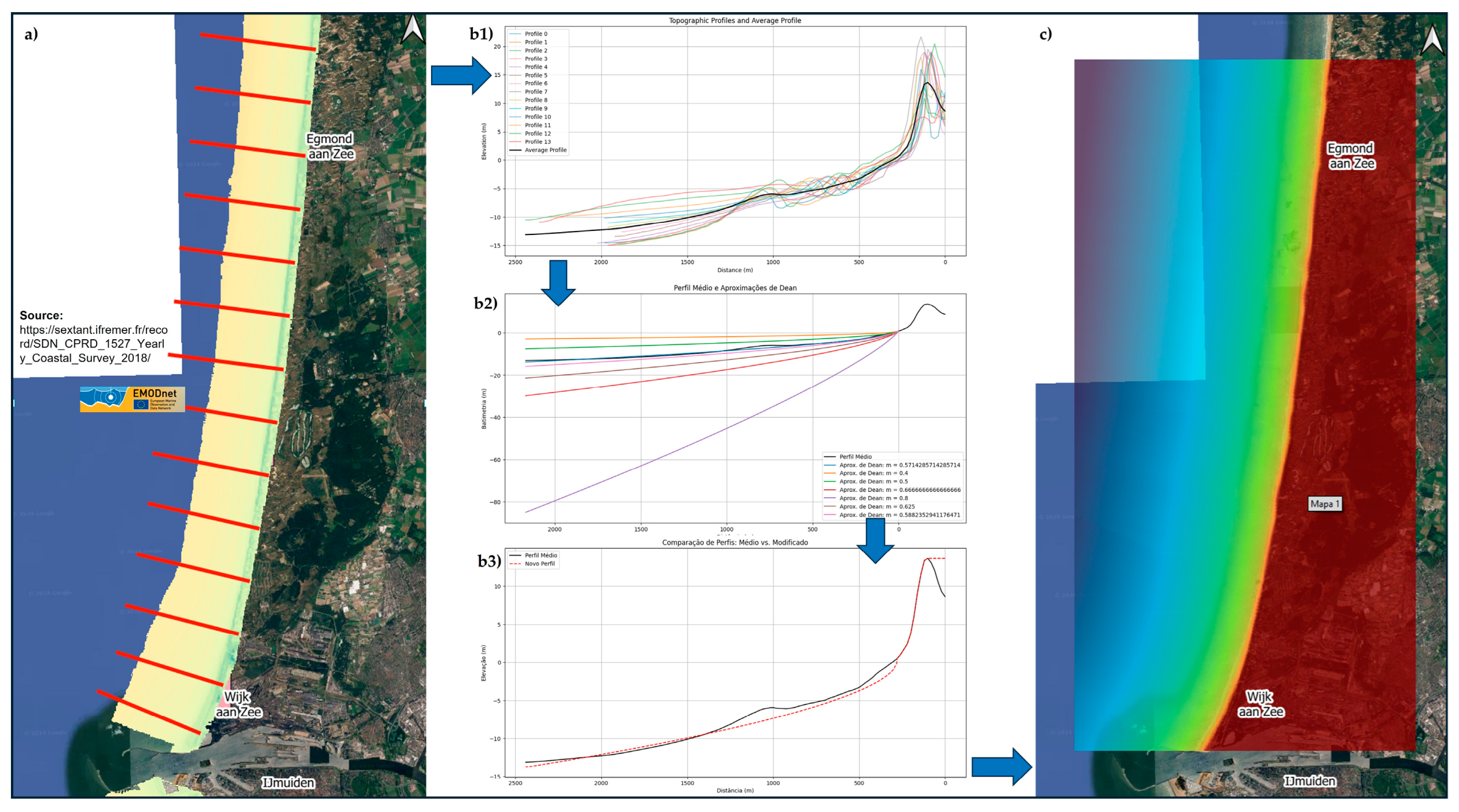


| Parameters | Dataset | Min | Mean | Max/Main D (°) | Std | Percentile * | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 25th | 50th | 75th | 90th | 99th | ||||||
| Hs (m) | Measured-YM6 | 0.09 | 1.27 | 7.17 | 0.83 | 0.66 | 1.07 | 1.66 | 2.40 | 4.06 |
| ERA5 | 0.04 | 1.20 | 7.47 | 0.79 | 0.63 | 1.00 | 1.56 | 2.29 | 3.84 | |
| AENWS-WPR | 0.03 | 1.24 | 6.72 | 0.76 | 0.68 | 1.08 | 1.65 | 2.32 | 3.55 | |
| AENWS-WPR North | 0.02 | 0.94 | 4.56 | 0.64 | 0.44 | 0.78 | 1.28 | 1.84 | 2.89 | |
| Tp (s) | Measured-YM6 | 1.79 | 5.68 | 22.97 | 1.35 | 4.81 | 5.67 | 6.54 | 7.35 | 9.05 |
| ERA5 | 1.83 | 5.97 | 19.35 | 1.85 | 4.73 | 5.79 | 6.90 | 8.18 | 12.00 | |
| AENWS-WPR | 1.65 | 6.33 | 18.85 | 1.97 | 5.05 | 6.18 | 7.42 | 8.75 | 12.42 | |
| AENWS-WPR North | 1.65 | 6.42 | 19.52 | 2.13 | 5.04 | 6.22 | 7.56 | 9.06 | 13.35 | |
| D (°) | Measured-YM6 | - | 235.67 | WSW-SW | 104.57 | - | ||||
| ERA5 | - | 222.97 | SW | 110.14 | ||||||
| AENWS-WPR | - | 230.65 | SW | 112.83 | ||||||
| AENWS-WPR North | - | 275.97 | W | 77.96 | ||||||
| Dataset | Scenarios | Artificial Sand Nourishment | |
|---|---|---|---|
| Volume (×106 m3) Per Year | Total Volume (×106 m3) | ||
| S_Ref (real)—Aerial image coastline | - | - | |
| Measured YM6 (Calibration) | S_YM6_200 | 0.20 | 8 |
| S_YM6_250 | 0.25 | 10 | |
| S_YM6 | - | - | |
| ERA 5 | S_ERA5_200 | 0.20 | 8 |
| S_ERA5_250 | 0.25 | 10 | |
| S_ERA5 | - | - | |
| AENWS-WPR | S_AENWS_200 | 0.20 | 8 |
| S_AENWS_250 | 0.25 | 10 | |
| S_AENWS | - | - | |
| AENWS-WPR North | S_AENWS_N_200 | 0.20 | 8 |
| S_AENWS_N_250 | 0.25 | 10 | |
| S_AENWS_N | - | - | |
| Dataset | Scenarios | Erosion (ha) | Accretion (ha) | Balance (ha) | Relative Error | Mean Retreat/Year (m) | Longshore Transport (m3/year) |
|---|---|---|---|---|---|---|---|
| S_Ref (real) | 87.9 | 6.9 | 81.0 | - | 1.01 | 200,000–300,000 | |
| Measured YM6 (Calibration) | S 200,000 m3 | 90.4 | 14.3 | 76.1 | −6.0% | 0.95 | 231,250 |
| S 250,000 m3 | 90.2 | 18.0 | 72.2 | −10.8% | 0.90 | ||
| S without AN | 95.1 | 7.8 | 87.3 | 7.8% | 1.09 | ||
| ERA 5 | S 200,000 m3 | 89.3 | 15.8 | 73.5 | −9.3% | 0.92 | 180,696 |
| S 250,000 m3 | 89.0 | 19.4 | 69.6 | −14.1% | 0.87 | ||
| S without AN | 94.6 | 9.9 | 84.7 | 4.6% | 1.06 | ||
| AENWS-WPR | S 200,000 m3 | 89.8 | 15.1 | 74.7 | −7.8% | 0.93 | 192,312 |
| S 250,000 m3 | 89.6 | 18.8 | 70.8 | −12.5% | 0.89 | ||
| S without AN | 94.7 | 8.8 | 85.9 | 6.1% | 1.07 | ||
| AENWS-WPR North | S 200,000 m3 | 179.8 | 13.0 | 166.8 | 106.0% | 2.08 | 115,511 |
| S 250,000 m3 | 179.5 | 16.8 | 162.7 | 101.0% | 2.03 | ||
| S without AN | 184.3 | 6.3 | 178.0 | 119.8% | 2.23 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pais-Barbosa, J.; Romão, F.; Lima, M.; Coelho, C. A Comparative Analysis of In-Situ Wave Measurements and Reanalysis Models for Predicting Coastline Evolution: A Case Study of IJmuiden, The Netherlands. Water 2025, 17, 1091. https://doi.org/10.3390/w17071091
Pais-Barbosa J, Romão F, Lima M, Coelho C. A Comparative Analysis of In-Situ Wave Measurements and Reanalysis Models for Predicting Coastline Evolution: A Case Study of IJmuiden, The Netherlands. Water. 2025; 17(7):1091. https://doi.org/10.3390/w17071091
Chicago/Turabian StylePais-Barbosa, Joaquim, Frederico Romão, Márcia Lima, and Carlos Coelho. 2025. "A Comparative Analysis of In-Situ Wave Measurements and Reanalysis Models for Predicting Coastline Evolution: A Case Study of IJmuiden, The Netherlands" Water 17, no. 7: 1091. https://doi.org/10.3390/w17071091
APA StylePais-Barbosa, J., Romão, F., Lima, M., & Coelho, C. (2025). A Comparative Analysis of In-Situ Wave Measurements and Reanalysis Models for Predicting Coastline Evolution: A Case Study of IJmuiden, The Netherlands. Water, 17(7), 1091. https://doi.org/10.3390/w17071091









