Multi-Objective Simulation-Optimization Coupling Model of the Water Transfer Level in the East Route of the South-to-North Water Diversion Project
Abstract
1. Introduction
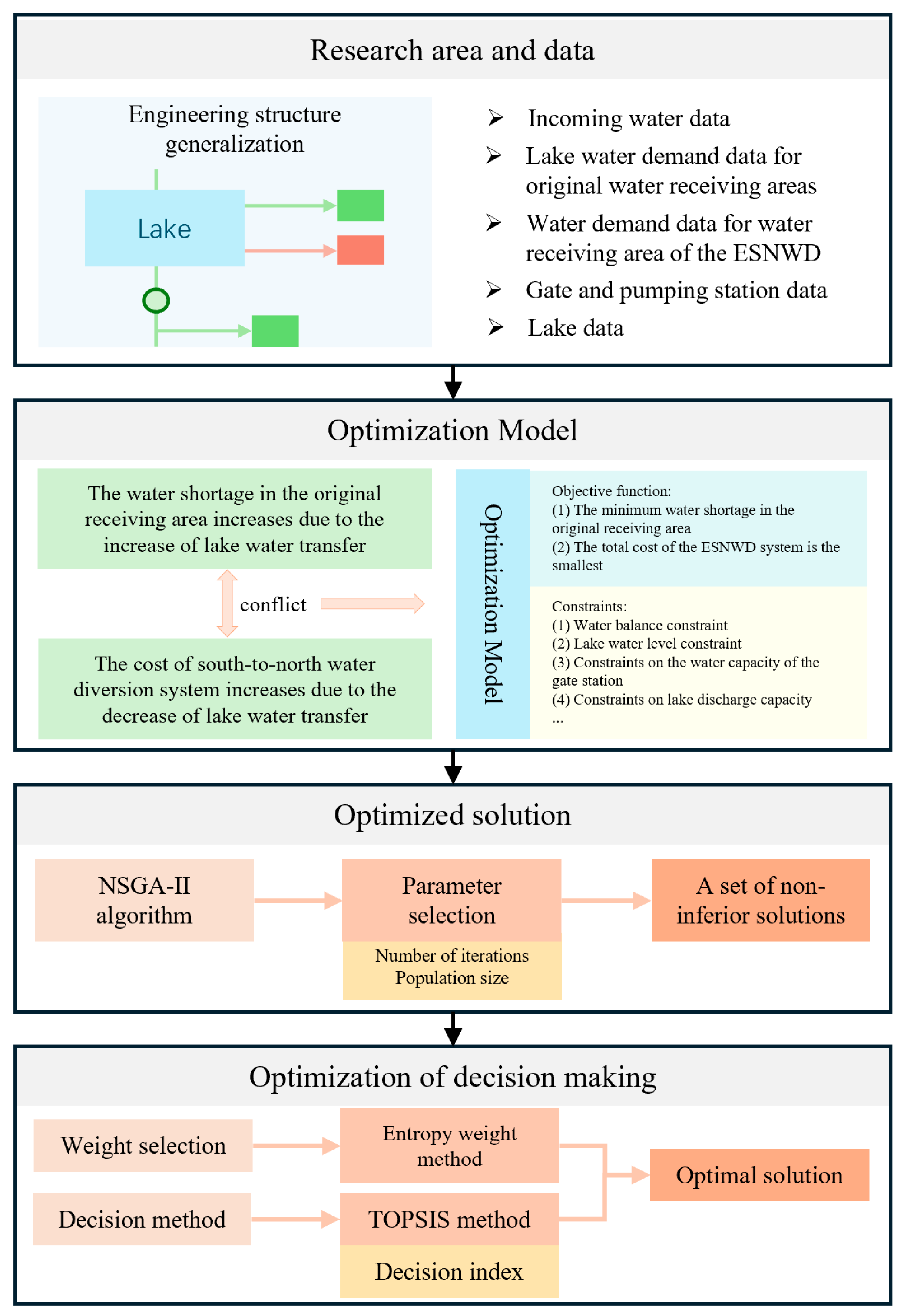
2. Research Area and Data
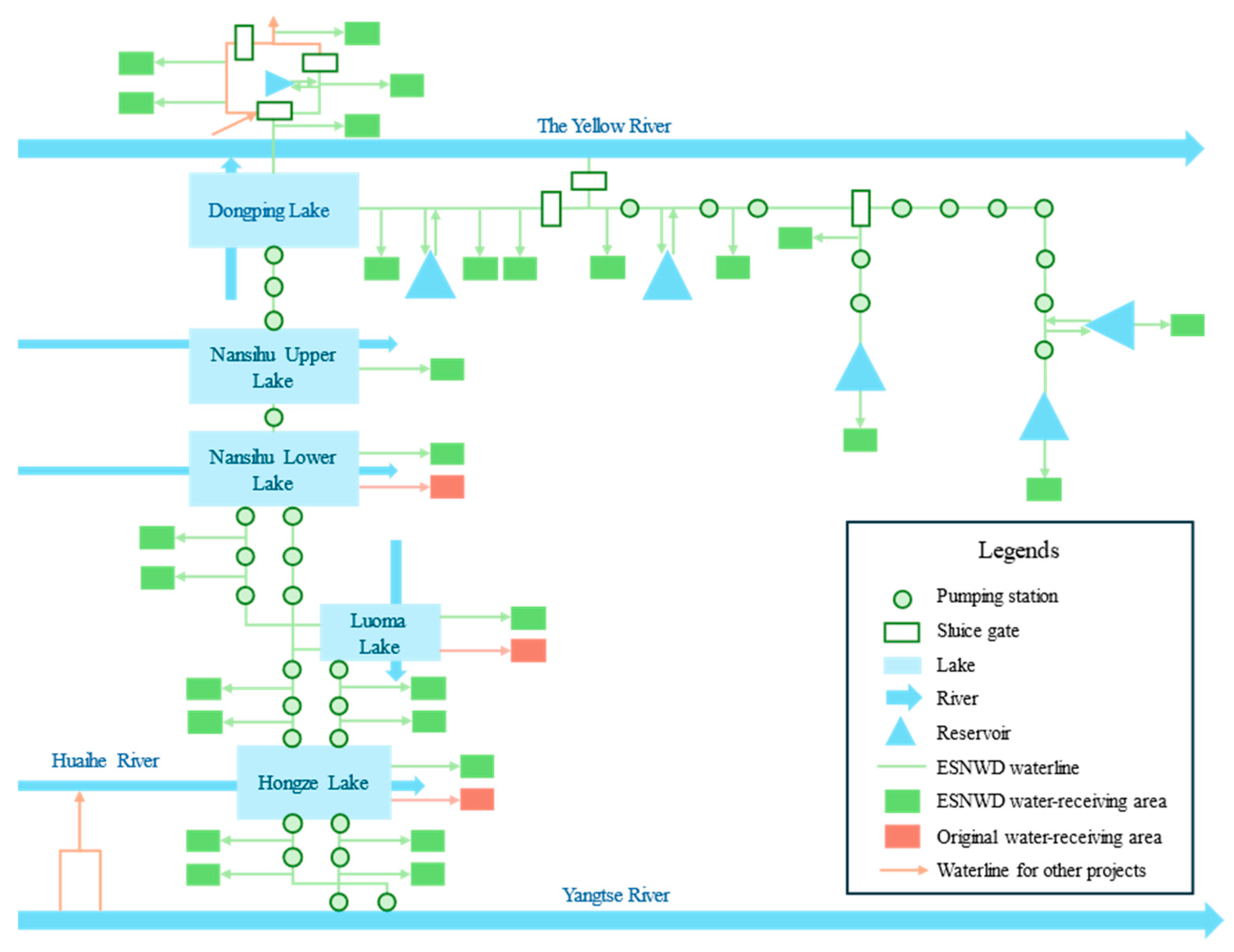
2.1. Overview of the Study Area
2.2. System Generalization
2.3. Scheduling Rule
3. Methods
3.1. Simulation-Optimization Coupling Model
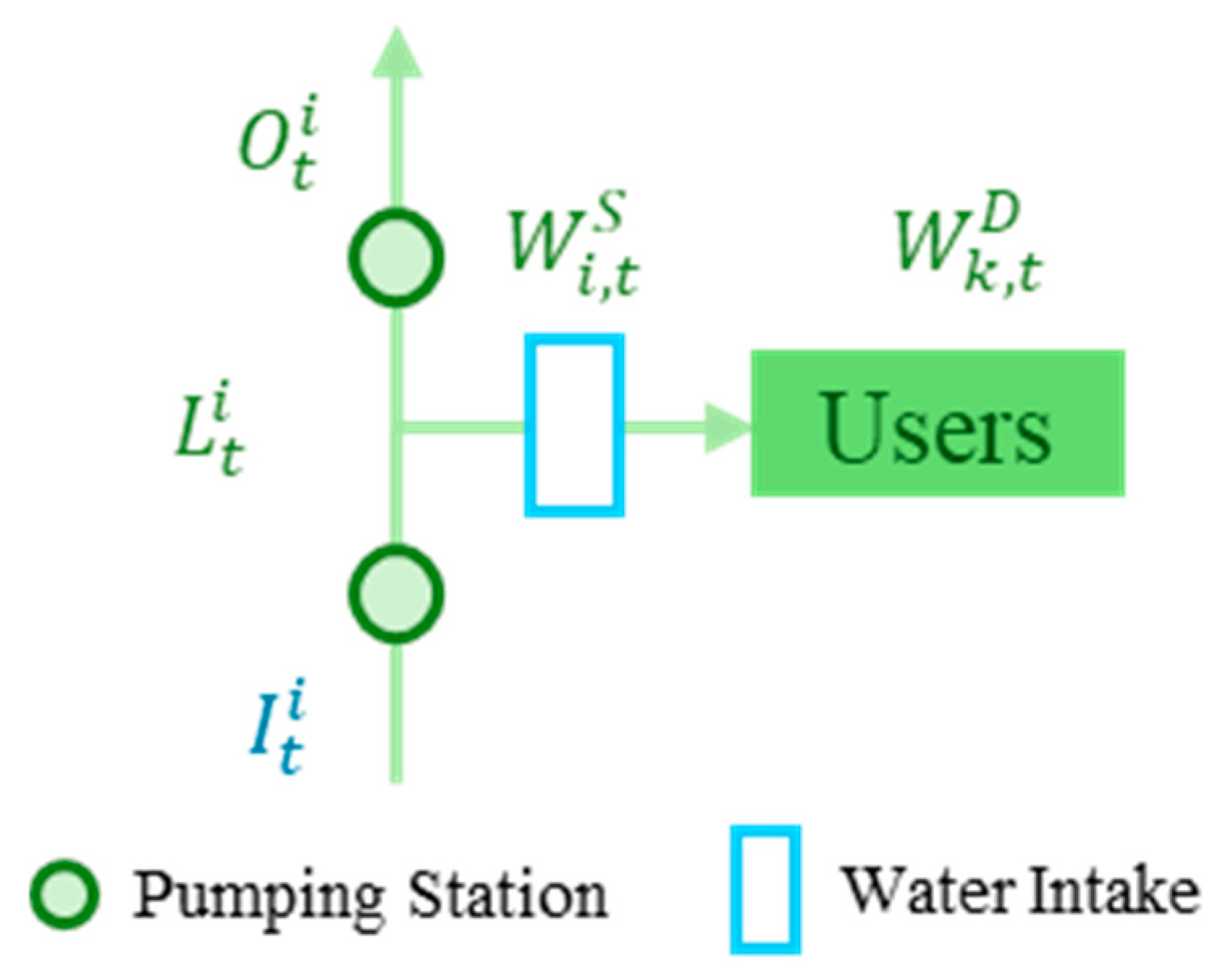
3.1.1. Model Construction
- (1)
- Water source projects: There are 89 water source projects, including generalized water storage projects, generalized water lifting projects, and water diversion projects.
- (2)
- Users: This refers to the receiving areas of water, including 40 along the line and seven original receiving areas of the lakes.
- (3)
- Rivers: They are important water transmission channels with the water conservation facilities contained within them.
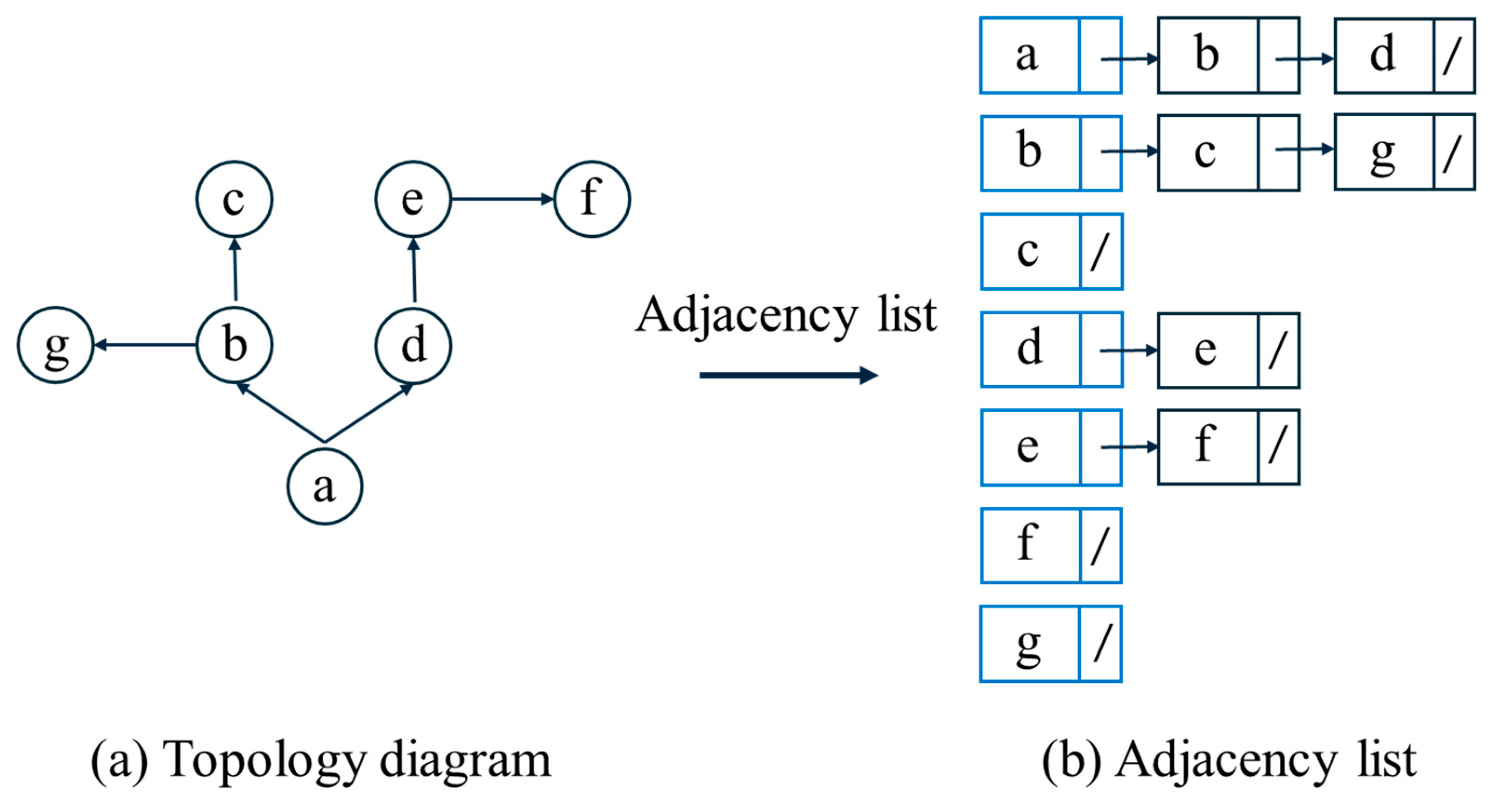
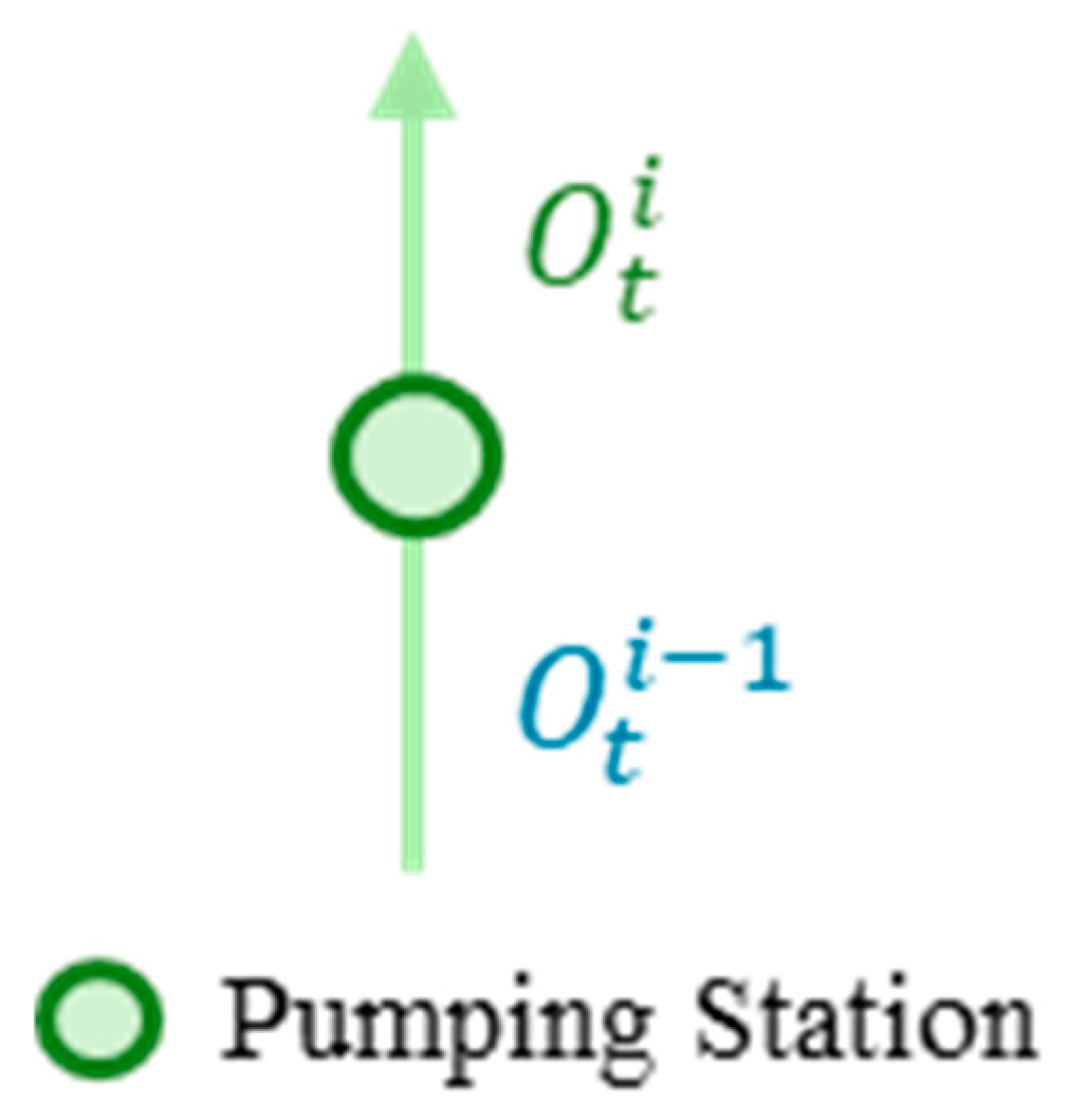
- Source-sink relationship between nodes
- 2.
- Supply-demand relationship between water sources and users
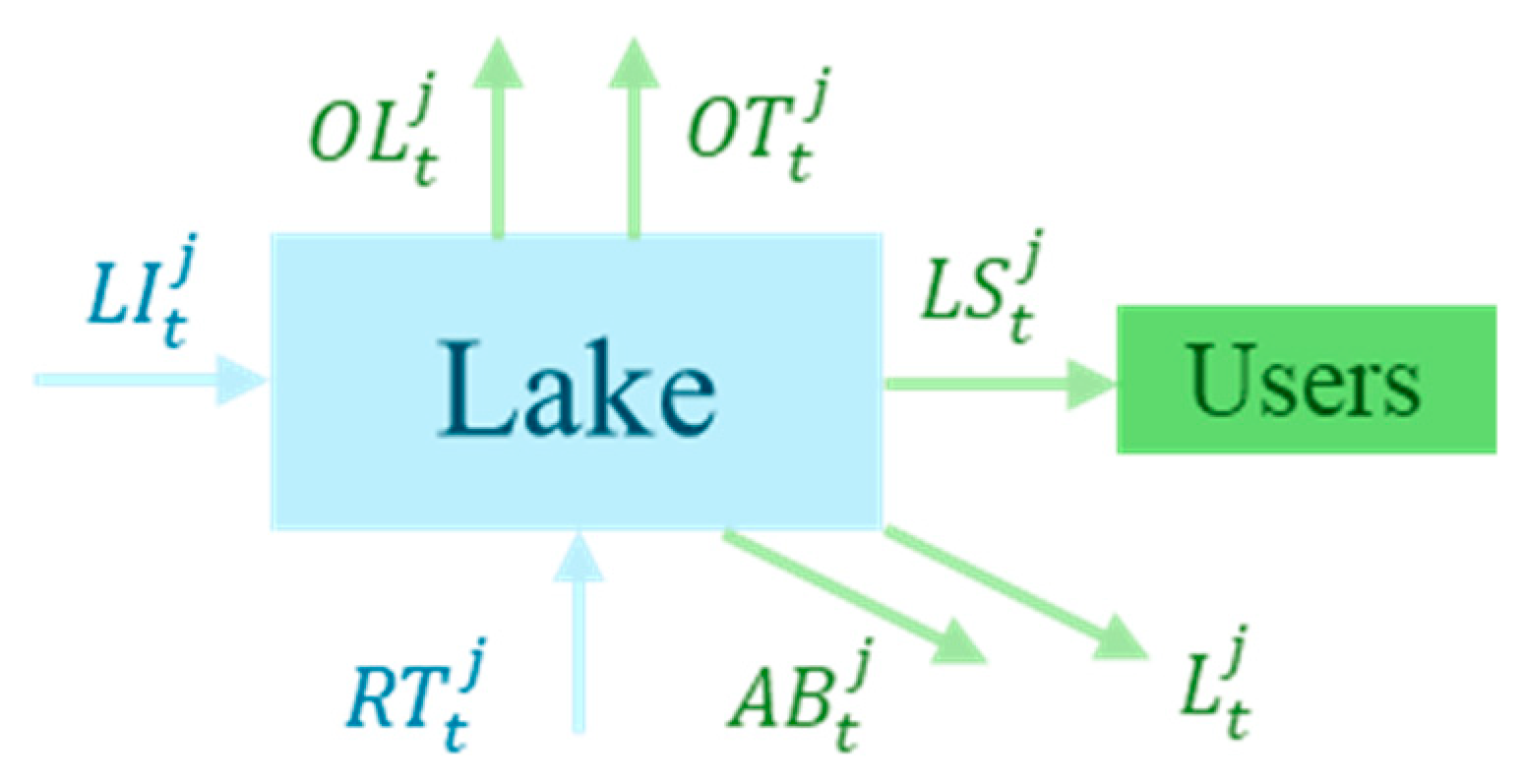
3.1.2. Critical Node Processing
- Water storage project
- 2.
- Water diversion project
- 3.
- Water lifting project
3.1.3. Model Input and Output
- (1)
- Monthly water intake of Hongze Lake, Luoma Lake, Nansihu Lower Lake, Nansihu Upper Lake, and Dongping Lake.
- (2)
- Monthly water transfer process of each receiving unit along the line (including the original receiving area).
- (1)
- Monthly water supply processes, water storage change processes, water level change processes, and monthly and annual water supply statistical values for the lakes along the line.
- (2)
- Monthly water consumption processes of each water-receiving unit along the line (including the original water-receiving area) and monthly and annual water consumption statistics.
- (3)
- Monthly water withdrawal processes of each pumping station along the line, monthly water flow processes of each control node, and statistical values of the monthly and annual water volumes.
- (4)
- Monthly water withdrawal processes at the water intake gate of each section along the line and the monthly and annual water withdrawal statistical values.
3.1.4. Objective Functions
3.1.5. Restrictive Conditions
3.2. NSGA-II Algorithm
3.3. Entropy Weight TOPSIS Method
3.3.1. Homogenization of Indicator Attributes
3.3.2. Construction of Normalized Initial Matrix
3.3.3. Determination of Positive and Negative Ideal Solutions
3.3.4. Determination of Indicator Weights
3.3.5. Proximity Calculation of Each Evaluation Object to the Optimal and Worst Options
3.3.6. Closeness Calculation of Each Evaluation Object to the Optimal Option
4. Results and Discussion
5. Conclusions
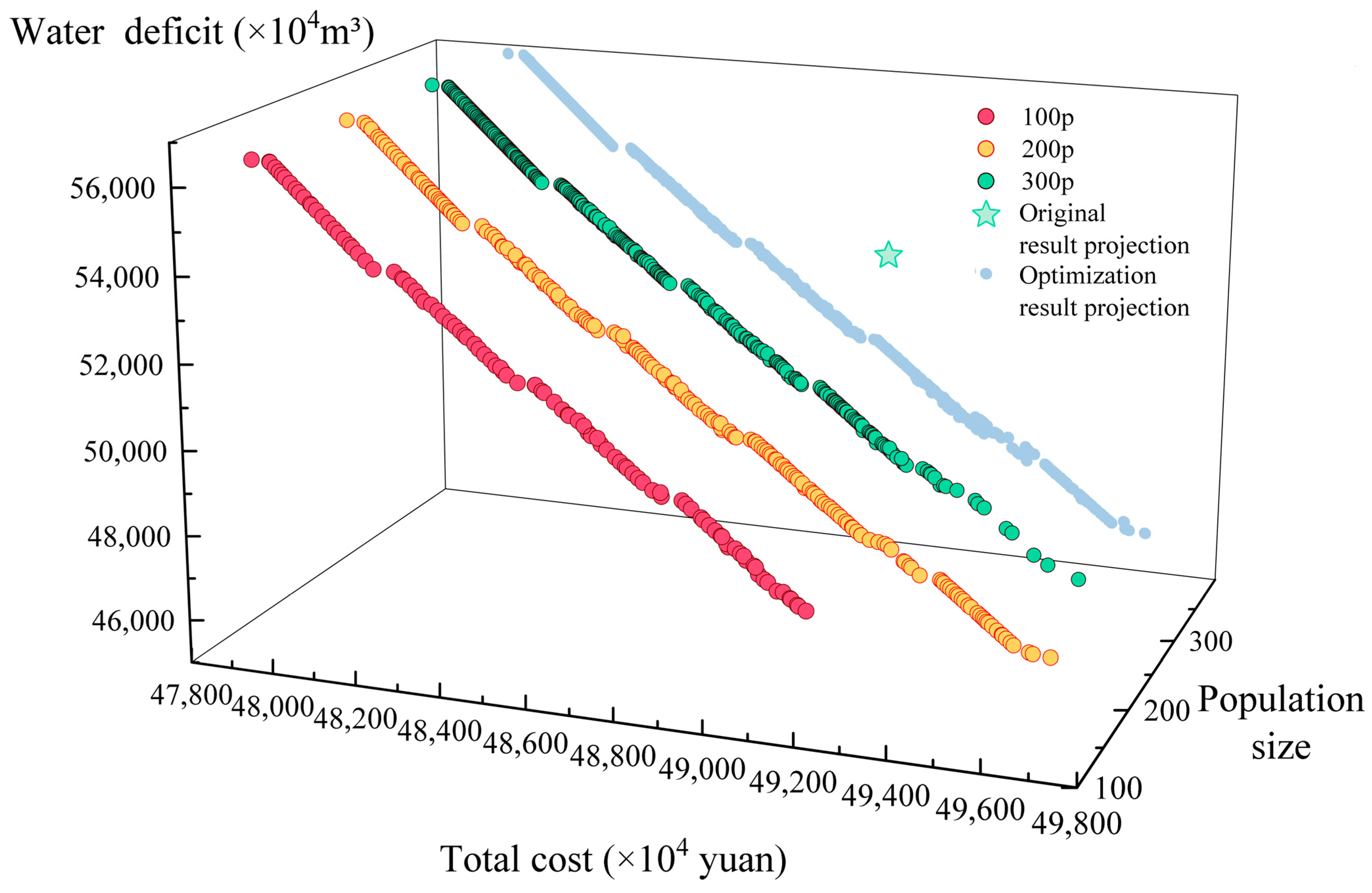
- Different numbers of iterations have less impact on the optimization results, and different population sizes affect the Pareto solution set of the optimization, and ultimately, the decision results. The larger the population size is, the more costs tend to increase, while water shortages in the original water-receiving area are reduced.
- The optimized non-inferior solution set is better than the current northward water transfer level, reduces the cost of the water transfer system, and minimizes the risk of water shortages in the receiving areas. It can also more effectively coordinate the conflicts between water supply and demand, as well as between the original receiving area and the water transfer area.
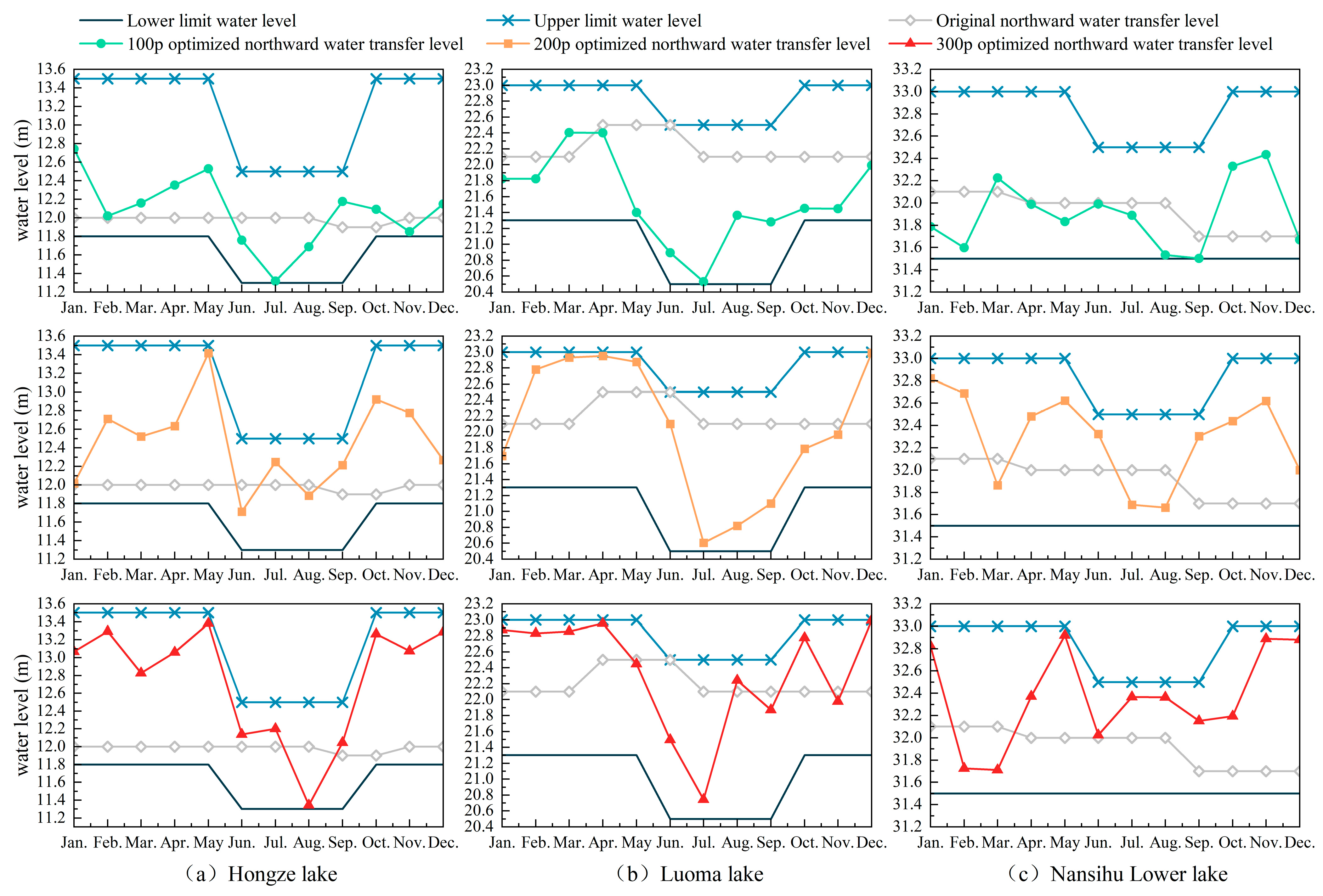
- The optimized northward water transfer level can raise the water level during the non-flood season, reduce the risk of water shortages in the original water-receiving areas, and lower the water level during the flood season to meet flood control needs. However, due to the influence of the algorithm, the optimization results still exhibit the defect of high water-level fluctuation, which should be optimized further.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- China’s 2022 Water Resources Bulletin. Water Resour. Dev. Manag. 2023, 9, 2.
- Zhong, H.; Liao, T.; Fang, G.; Ren, K.; Zhang, S. Exploring optimal joint operating rules for large-scale inter-basin water transfer projects with multiple water sources, diversion routes, and water demand areas. J. Hydrol. Reg. Stud. 2023, 49, 101504. [Google Scholar] [CrossRef]
- Li, M.; Yang, X.; Wang, K.; Di, C.; Xiang, W.; Zhang, J. Exploring China’s water scarcity incorporating surface water quality and multiple existing solutions. Environ. Res. 2024, 246, 118191. [Google Scholar] [CrossRef] [PubMed]
- Chai, Q.; Han, W.; Wan, F.; Ding, Z.; Wu, F. Study on coordinated allocation of conventional and unconventional water resources in typical regions of North China. Front. Earth Sci. 2023, 11, 1–10. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, X.; Liu, X.; Tang, Q. Growing control of climate change on water scarcity alleviation over northern part of China. J. Hydrol. Reg. Stud. 2023, 46, 101332. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, H. South-to-north Water Transfer Schemes for China. Int. J. Water Resour. Dev. 2002, 18, 453–471. [Google Scholar] [CrossRef]
- Sheng, J.; Zhang, R.; Yang, H. Inter-basin water transfers and water rebound effects: The South-North water transfer Project in China. J. Hydrol. 2024, 638, 131516. [Google Scholar] [CrossRef]
- Matrosov, E.S.; Harou, J.J.; Loucks, D.P. A computationally efficient open-source water resource system simulator—Application to London and the Thames Basin. Environ. Modell. Softw. 2011, 26, 1599–1610. [Google Scholar] [CrossRef]
- Felisa, G.; Panini, G.; Pedrazzoli, P.; Di Federico, V. Combined management of groundwater resources and water supply systems at basin scale under climate change. Water Resour. Manag. 2022, 36, 915–930. [Google Scholar] [CrossRef]
- Lennard, A.T.; Macdonald, N.; Clark, S.; Hooke, J.M. The application of a drought reconstruction in water resource management. Hydrol. Res. 2016, 47, 646–659. [Google Scholar] [CrossRef]
- Wurbs, R.A. Modeling river/reservoir system management, water allocation, and supply reliability. J. Hydrol. 2004, 300, 100–113. [Google Scholar] [CrossRef]
- An, S.; Wu, Y.; Liang, W.; Zhang, G.; Chen, J.; Liu, S.; Zhao, F.; Qiu, L.; Yin, X. Enhancing ecohydrological simulation with improved dynamic vegetation growth module in SWAT. J. Hydrol. 2024, 644, 132042. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, J.; Li, Z.; Lai, G.; Du, J.; Xie, S.; Xu, X.; Meng, L.; Li, X.; Zhong, K. Effect of calculation unit division in distributed hydrological models on the analysis of hydrological effects of land use change. Catena 2024, 246, 108445. [Google Scholar] [CrossRef]
- Cetinkaya, C.P.; Fistikoglu, O.; Harmancioglu, N.B.; Fedra, K. Optimization methods applied for sustainable management of water-scarce basins. J. Hydroinf. 2008, 10, 69–95. [Google Scholar] [CrossRef]
- Berhe, F.T.; Melesse, A.M.; Hailu, D.; Sileshi, Y. MODSIM-based water allocation modeling of Awash River Basin, Ethiopia. Catena 2013, 109, 118–128. [Google Scholar] [CrossRef]
- Chhuon, K.; Herrera, E.; Nadaoka, K. Application of integrated hydrologic and river basin management modeling for the optimal development of a multi-purpose reservoir project. Water Resour. Manag. 2016, 30, 3143–3157. [Google Scholar] [CrossRef]
- Suo, M.; Xia, F.; Fan, Y. A fuzzy-interval dynamic optimization model for regional water resources allocation under uncertainty. Sustainability 2022, 14, 1096. [Google Scholar] [CrossRef]
- Ngamsert, R.; Techarungruengsakul, R.; Kaewplang, S.; Hormwichian, R.; Prasanchum, H.; Sivanpheng, O.; Kangrang, A. Optimizing solution in decision supporting system for river basin management consisting of a reservoir system. Water 2023, 15, 2510. [Google Scholar] [CrossRef]
- Rong, Q.; Zhu, S.; Yue, W.; Su, M.; Cai, Y. Predictive simulation and optimal allocation of surface water resources in reservoir basins under climate change. Int. Soil. Water Conserv. Res. 2024, 12, 467–480. [Google Scholar] [CrossRef]
- Spiliotis, M.; Mediero, L.; Garrote, L. Optimization of hedging rules for reservoir operation during droughts based on particle swarm optimization. Water Resour. Manag. 2016, 30, 5759–5778. [Google Scholar] [CrossRef]
- Mirfenderesgi, G.; Mousavi, S.J. Adaptive meta-modeling-based simulation optimization in basin-scale optimum water allocation: A comparative analysis of meta-models. J. Hydroinf. 2016, 18, 446–465. [Google Scholar] [CrossRef]
- Borgomeo, E.; Mortazavi-Naeini, M.; Hall, J.W.; O’Sullivan, M.J.; Watson, T. Trading-off tolerable risk with climate change adaptation costs in water supply systems. Water Resour. Res. 2016, 52, 622–643. [Google Scholar] [CrossRef]
- Fereidoon, M.; Koch, M. SWAT-MODSIM-PSO optimization of multi-crop planning in the Karkheh River Basin, Iran, under the impacts of climate change. Sci. Total Environ. 2018, 630, 502–516. [Google Scholar] [CrossRef] [PubMed]
- Dogan, M.S.; Fefer, M.A.; Herman, J.D.; Hart, Q.J.; Merz, J.R.; Medellín-Azuara, J.; Lund, J.R. An open-source Python implementation of California’s hydroeconomic optimization model. Environ. Modell. Softw. 2018, 108, 8–13. [Google Scholar] [CrossRef]
- Ouyang, S.; Qin, H.; Shao, J.; Lu, J.; Bing, J.; Wang, X.; Zhang, R. Multi-objective optimal water supply scheduling model for an inter-basin water transfer system: The South-to-North Water Diversion Middle Route Project, China. Water Supply 2020, 20, 550–564. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, X.; Liu, J.; Fang, G. Optimal operation of floodwater resources utilization of lakes in South-to-North Water Transfer Eastern Route Project. Sustainability 2021, 13, 4857. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Yazdi, A. Conjunctive Use of Surface and Groundwater with Inter-Basin Transfer Approach: Case Study Piranshahr. Water Resour. Manag. 2014, 28, 1887–1906. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Abyar, M. Development a Novel Integrated Distributed Multi-objective Simulation-optimization Model for Coastal Aquifers Management Using NSGA-II and GMS Models. Water Resour. Manag. 2022, 36, 75–102. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Azadani, M.N.; Kamgar, R. Development of operation multi-objective model of dam reservoir under conditions of temperature variation and loading using NSGA-II and DANN models: A case study of Karaj/Amir Kabir dam. Soft Comput. 2020, 46, 12469–12499. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Safari, R. Development of water re-allocation policy under uncertainty conditions in the inflow to reservoir and demands parameters: A case study of Karaj AmirKabir dam. Soft Comput. 2023, 27, 6521–6547. [Google Scholar] [CrossRef]
- Shi, H.; Cheng, J.; Fang, H.; Lu, X. Optimal allocation of water resources for Jiangsu section of South-to-North Water Transfer East Line Project. Edit. Off. Trans. Chin. Soc. Agric. Eng. 2012, 28, 76–81. [Google Scholar]
- Xi, H.; Xie, Y.; Liu, S.; Mao, Q.; Shen, T.; Zhang, Q. Multi-objective optimal scheduling of generalized water resources based on an inter-basin water transfer project. Water 2023, 15, 3195. [Google Scholar] [CrossRef]
- Huayu, Z.; Tao, L.; Guohua, F.; Shiwei, Z.; Bingyi, Z. Deriving water allocation schemes for interbasin water transfer projects using a novel multiobjective cuckoo search algorithm. J. Water Resour. Plann. Manag. 2024, 150, 6. [Google Scholar]
- Fang, G.; Guo, Y.; Wen, X.; Fu, X.; Lei, X.; Tian, Y.; Wang, T. Multi-objective differential evolution-chaos shuffled frog leaping algorithm for water resources system optimization. Water Resour. Manag. 2018, 32, 3835–3852. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, H.; Wan, W.; Zhao, J. Optimal operation toward energy efficiency of the long-distance water transfer project. J. Hydrol. 2023, 618, 129152. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, X.; Fang, G.; Xu, Y.-P. Many-objective optimization with improved shuffled frog leaping algorithm for inter-basin water transfers. Adv. Water Resour. 2020, 138, 103531. [Google Scholar] [CrossRef]
- Zhuan, X.; Li, W.; Yang, F. Optimal operation scheduling of a pumping station in east route of South-to-north Water Diversion Project. Energy Procedia 2017, 105, 3031–3037. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]


| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hongze Lake | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 11.9 | 11.9 | 12.0 | 12.0 |
| Luoma Lake | 22.1 | 22.1 | 22.1 | 22.5 | 22.5 | 22.5 | 22.1 | 22.1 | 22.1 | 22.1 | 22.1 | 22.1 |
| Nansihu Lower Lake | 32.1 | 32.1 | 32.1 | 32.0 | 32.0 | 32.0 | 32.0 | 32.0 | 31.7 | 31.7 | 31.7 | 31.7 |
| Population Size | Total Cost Index () | Water Deficit Index () | Optimal Distance ( | Worst Distance () | Composite Score Index () | Rank |
|---|---|---|---|---|---|---|
| 100 | 0.1362 | 0.0423 | 0.0926 | 0.1018 | 0.5237 | 1 |
| 0.1388 | 0.0390 | 0.0942 | 0.1029 | 0.5221 | 2 | |
| 0.1411 | 0.0361 | 0.0957 | 0.1040 | 0.5207 | 3 | |
| 0.1429 | 0.0338 | 0.0970 | 0.1049 | 0.5196 | 4 | |
| 0.1438 | 0.0327 | 0.0975 | 0.1053 | 0.5192 | 5 | |
| 0.1456 | 0.0305 | 0.0988 | 0.1062 | 0.5181 | 6 | |
| 0.1474 | 0.0281 | 0.1001 | 0.1072 | 0.5171 | 7 | |
| 0.1487 | 0.0265 | 0.1011 | 0.1079 | 0.5165 | 8 | |
| 0.1755 | 0 | 0.1178 | 0.1254 | 0.5158 | 9 | |
| 0.1505 | 0.0242 | 0.1024 | 0.1090 | 0.5155 | 10 | |
| 200 | 0.0314 | 0.0966 | 0.0644 | 0.0728 | 0.5307 | 1 |
| 0.0314 | 0.0966 | 0.0643 | 0.0728 | 0.5307 | 2 | |
| 0.0321 | 0.0958 | 0.0641 | 0.0723 | 0.5304 | 3 | |
| 0.0328 | 0.0949 | 0.0638 | 0.0719 | 0.5299 | 4 | |
| 0.0329 | 0.0947 | 0.0637 | 0.0718 | 0.5298 | 5 | |
| 0.0336 | 0.0939 | 0.0635 | 0.0714 | 0.5293 | 6 | |
| 0.0299 | 0.0976 | 0.0651 | 0.0732 | 0.5291 | 7 | |
| 0.0340 | 0.0934 | 0.0634 | 0.0712 | 0.5291 | 8 | |
| 0.0549 | 0.0728 | 0.0577 | 0.0648 | 0.5287 | 9 | |
| 0.0348 | 0.0924 | 0.0631 | 0.0707 | 0.5285 | 10 | |
| 300 | 0.0058 | 0.1174 | 0.0534 | 0.0890 | 0.6247 | 1 |
| 0.0040 | 0.1198 | 0.0545 | 0.0907 | 0.6245 | 2 | |
| 0.0087 | 0.1118 | 0.0521 | 0.0848 | 0.6196 | 3 | |
| 0 | 0.1228 | 0.0571 | 0.0930 | 0.6196 | 4 | |
| 0.0095 | 0.1107 | 0.0517 | 0.0840 | 0.6191 | 5 | |
| 0.0182 | 0.1005 | 0.0483 | 0.0770 | 0.6148 | 6 | |
| 0.0182 | 0.1004 | 0.0482 | 0.0770 | 0.6147 | 7 | |
| 0.0177 | 0.1005 | 0.0485 | 0.0770 | 0.6132 | 8 | |
| 0.0124 | 0.1056 | 0.0507 | 0.0803 | 0.6131 | 9 | |
| 0.0174 | 0.1007 | 0.0487 | 0.0771 | 0.6130 | 10 |
| Population Size | Total Cost | Water Deficit |
|---|---|---|
| 100 | 0.5112 | 0.4888 |
| 200 | 0.4836 | 0.5164 |
| 300 | 0.4270 | 0.5730 |
| Northward Water Transfer Level Scheduling Program | Total Cost (×104 yuan) | Rate of Change in Total Costs | Water Deficit (×104 m3) | Rate of Change in Water Deficit |
|---|---|---|---|---|
| Original | 48,978.16 | 52,404.11 | ||
| 100p | 48,268.81 | −1.45% | 54,597.73 | +4.19% |
| 200p | 49,199.21 | +0.45% | 48,286.84 | −7.86% |
| 300p | 49,469.71 | +1.00% | 46,681.14 | −10.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Pei, X.; Guo, X.; Wu, Q.; Hou, Y.; Wang, H.; Song, C.; Xue, Y. Multi-Objective Simulation-Optimization Coupling Model of the Water Transfer Level in the East Route of the South-to-North Water Diversion Project. Water 2025, 17, 839. https://doi.org/10.3390/w17060839
Wan X, Pei X, Guo X, Wu Q, Hou Y, Wang H, Song C, Xue Y. Multi-Objective Simulation-Optimization Coupling Model of the Water Transfer Level in the East Route of the South-to-North Water Diversion Project. Water. 2025; 17(6):839. https://doi.org/10.3390/w17060839
Chicago/Turabian StyleWan, Xinyu, Xinyu Pei, Xuning Guo, Qingyang Wu, Yu Hou, Haomin Wang, Chen Song, and Yuting Xue. 2025. "Multi-Objective Simulation-Optimization Coupling Model of the Water Transfer Level in the East Route of the South-to-North Water Diversion Project" Water 17, no. 6: 839. https://doi.org/10.3390/w17060839
APA StyleWan, X., Pei, X., Guo, X., Wu, Q., Hou, Y., Wang, H., Song, C., & Xue, Y. (2025). Multi-Objective Simulation-Optimization Coupling Model of the Water Transfer Level in the East Route of the South-to-North Water Diversion Project. Water, 17(6), 839. https://doi.org/10.3390/w17060839




