Slope Stability Analysis Considering Degradation of Soil Properties Induced by Intermittent Rainfall
Abstract
1. Introduction
2. Fundamental Theories and Degradation Model
2.1. Theory of Seepage in Unsaturated Soils
2.2. Shear Strength of Unsaturated Soils
2.3. Degradation of Soil Properties for Unsaturated Soils Under Intermittent Rainfall
2.3.1. Simplified Linear Degradation Model
2.3.2. Nonlinear Degradation Model
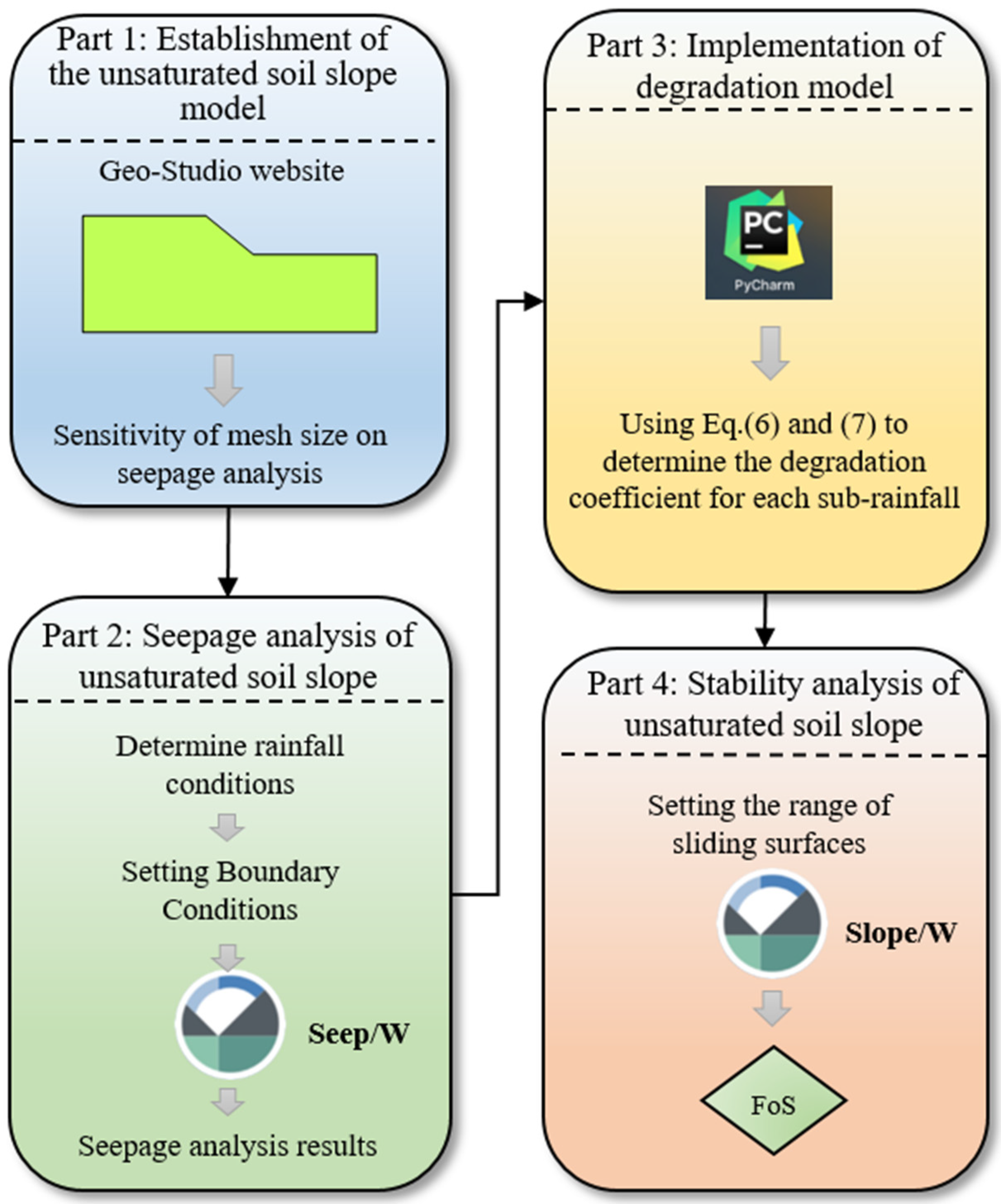
3. The Proposed Methodology
4. Illustrative Examples
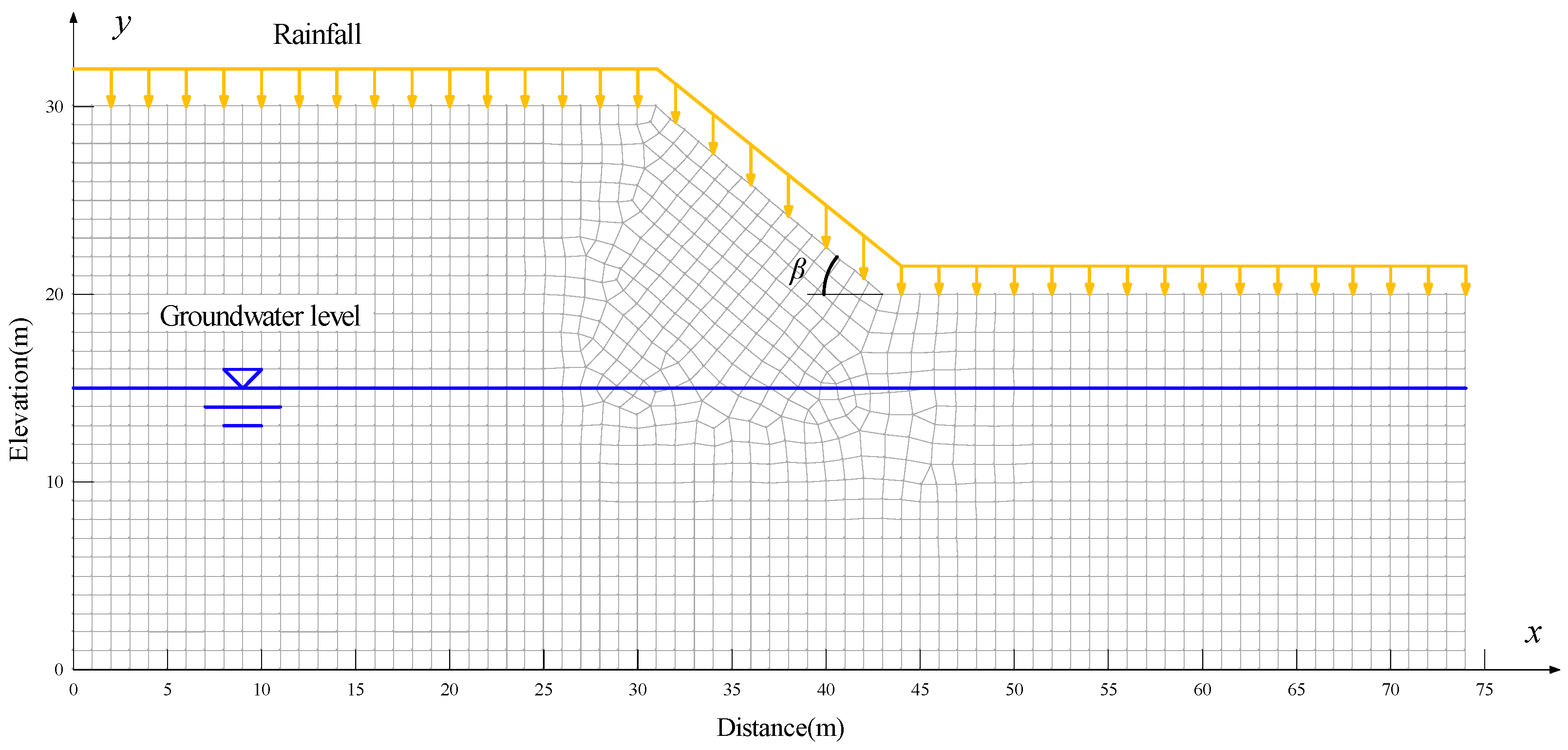
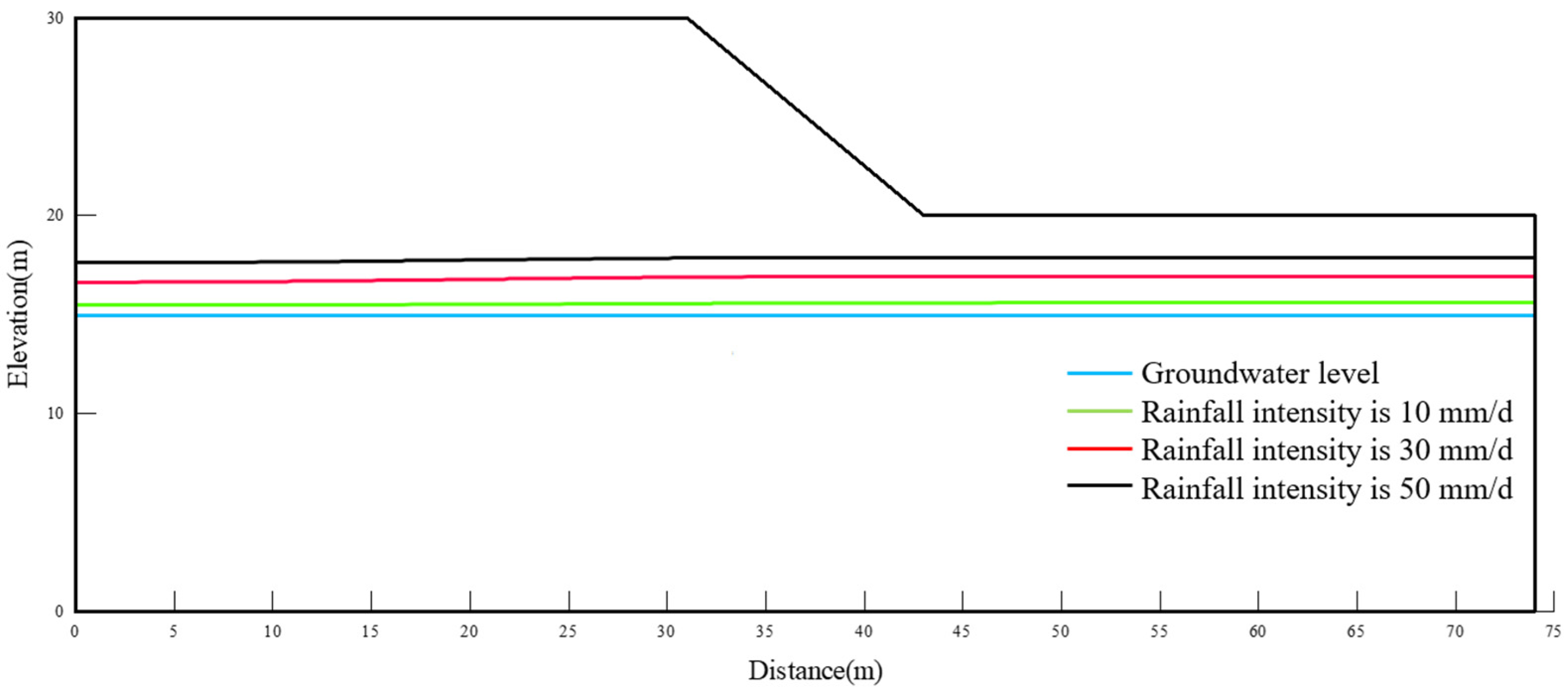
4.1. Establishment of Unsaturated Soil Slope Model
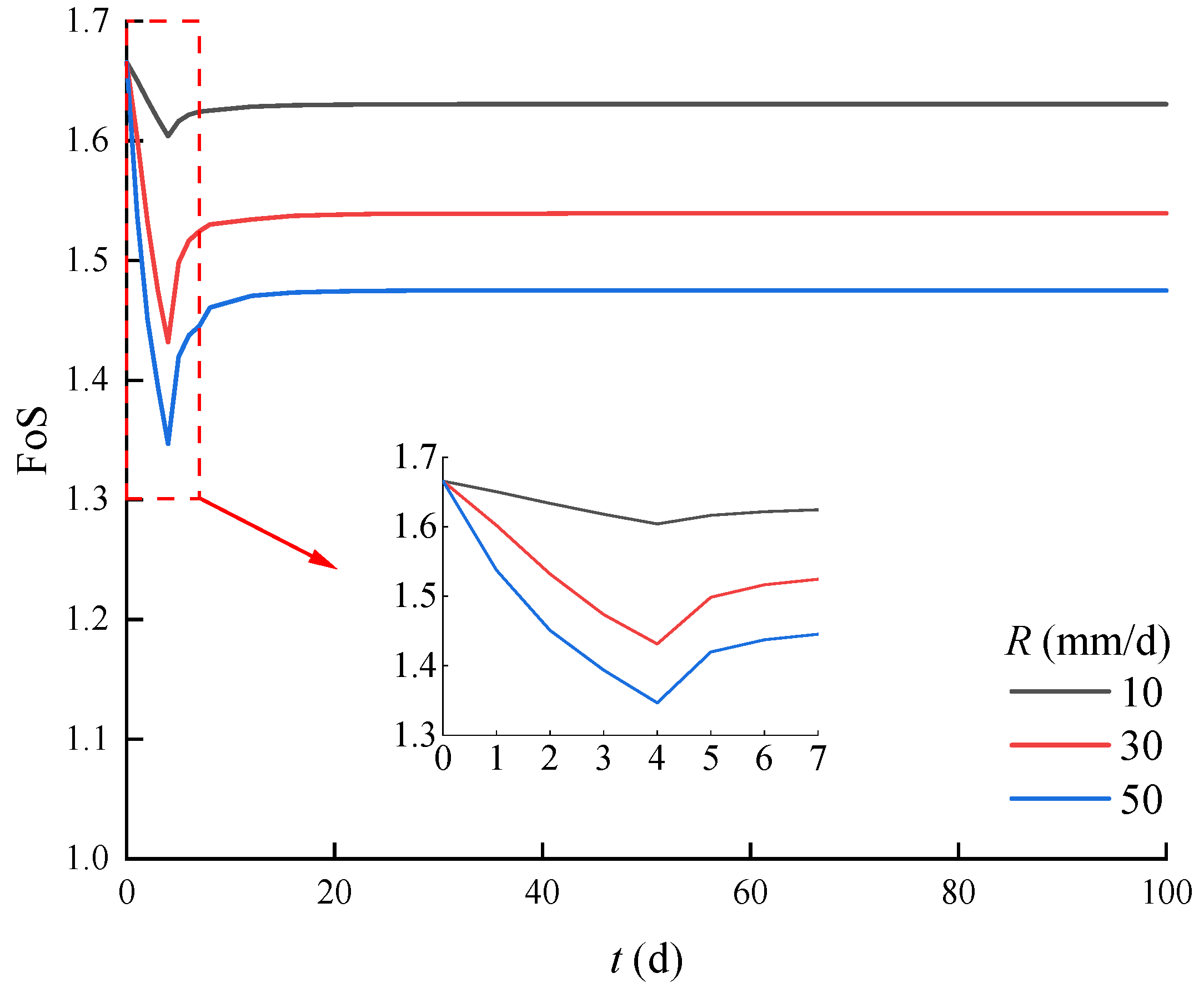
4.2. Seepage and Stability Analysis of Slope with Intermittent Rainfall Without Considering Degradation of Soil Properties
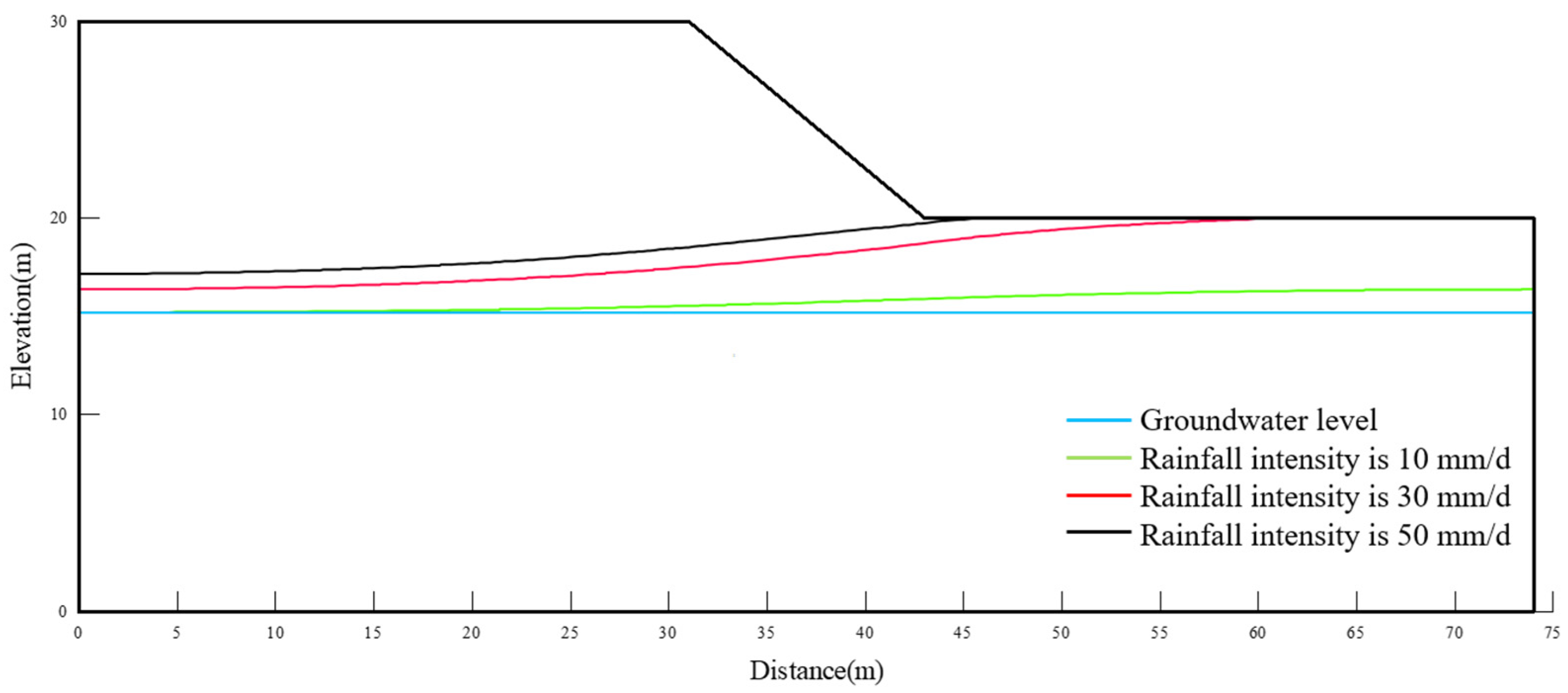
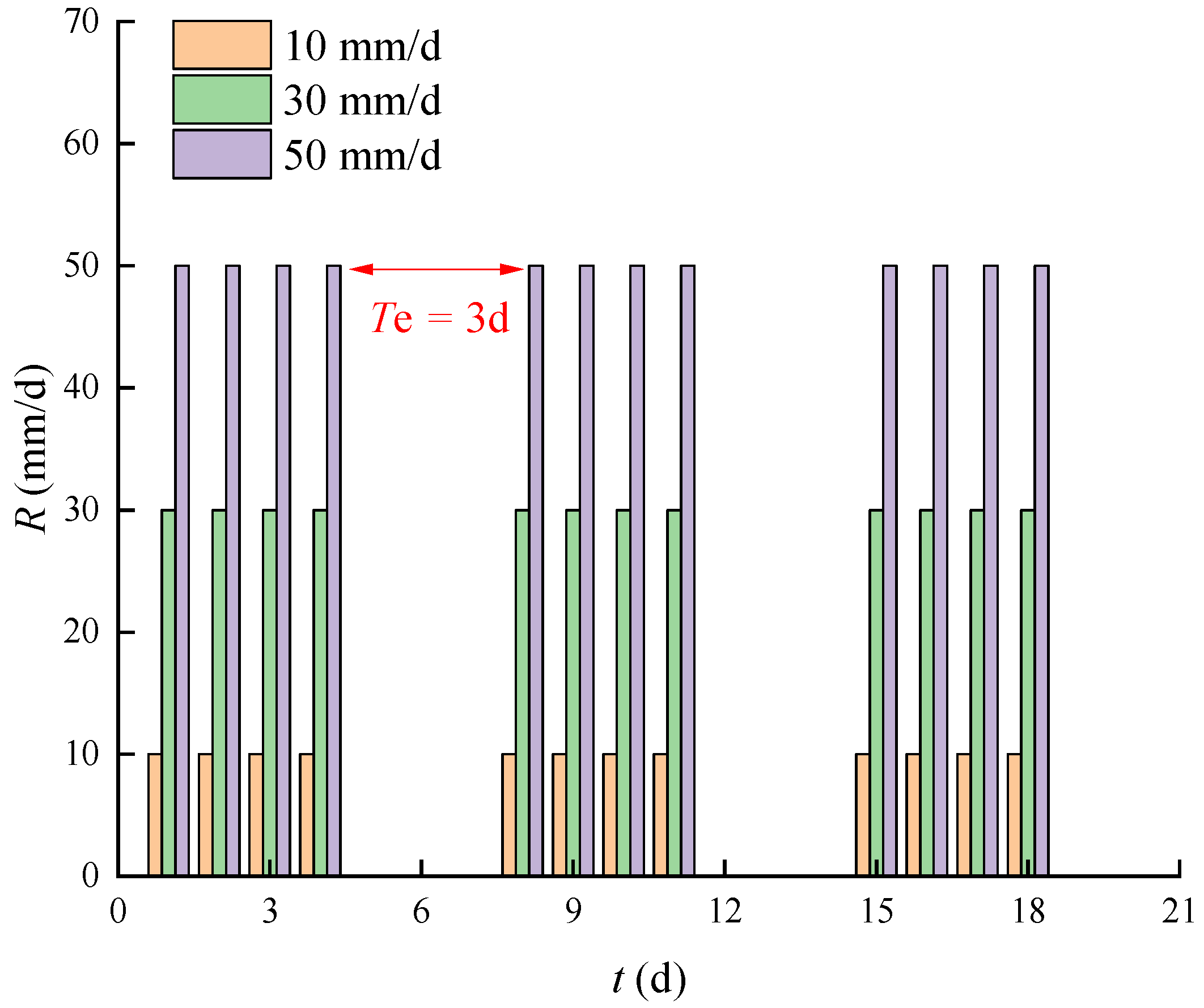
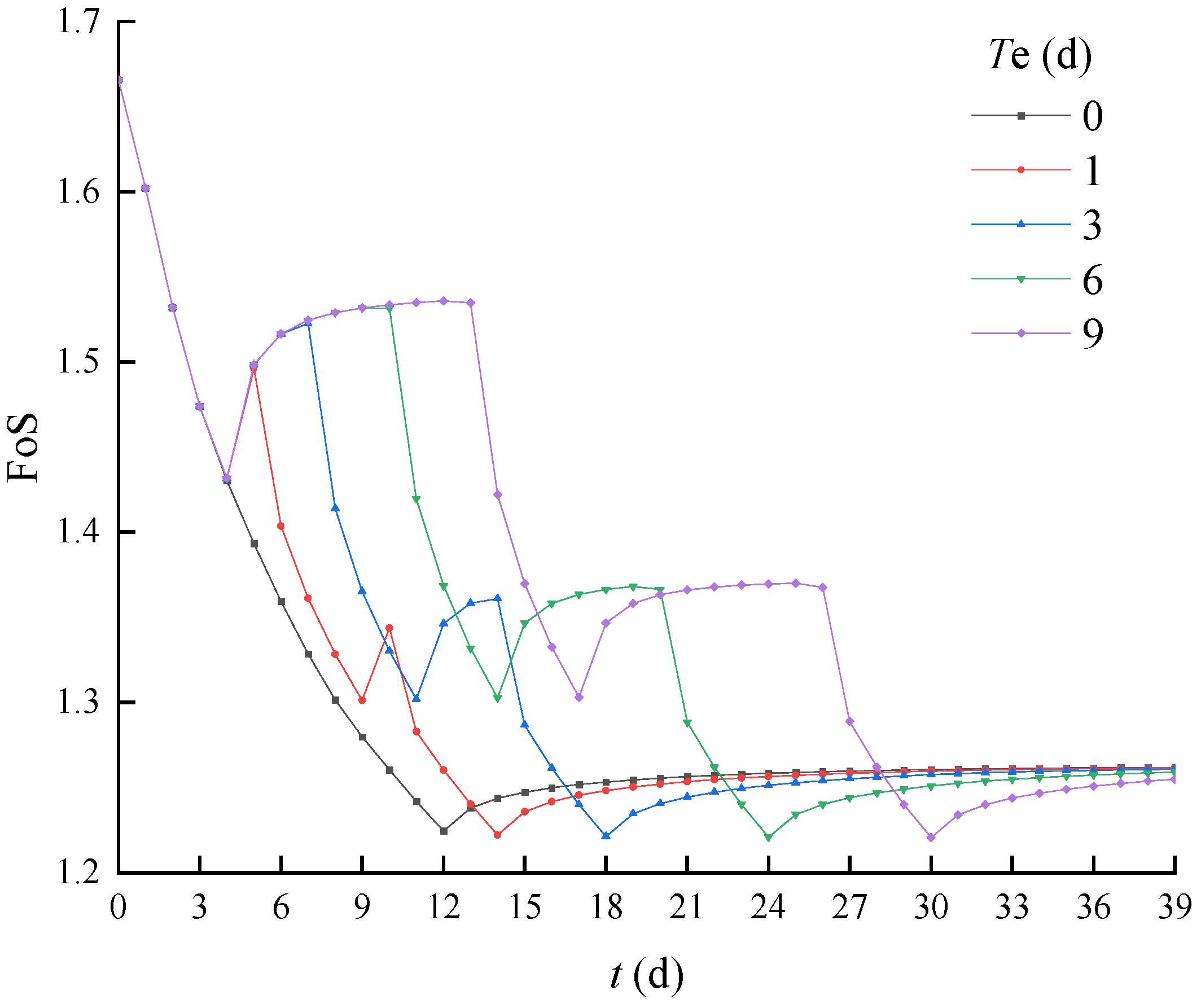
4.2.1. Impact of Rainfall Intensity and Rainfall Duration
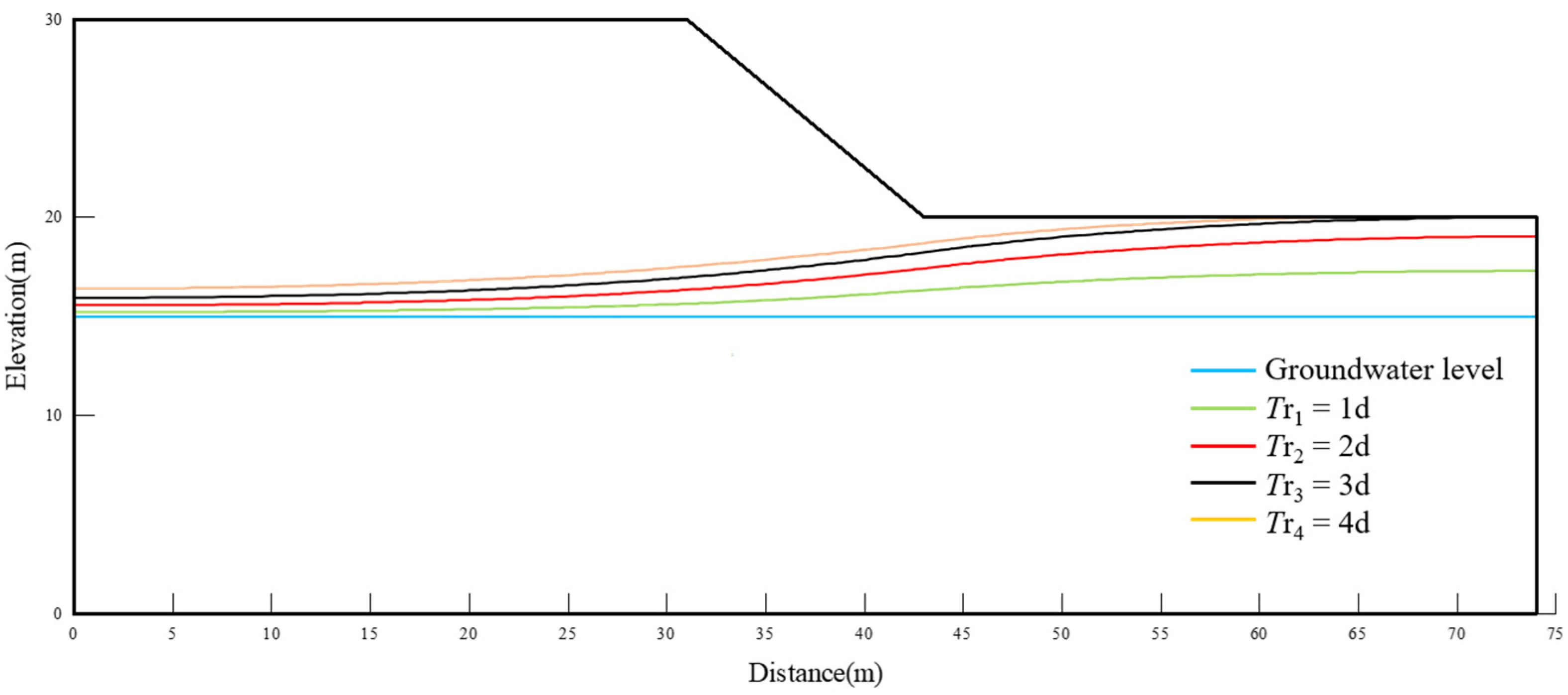
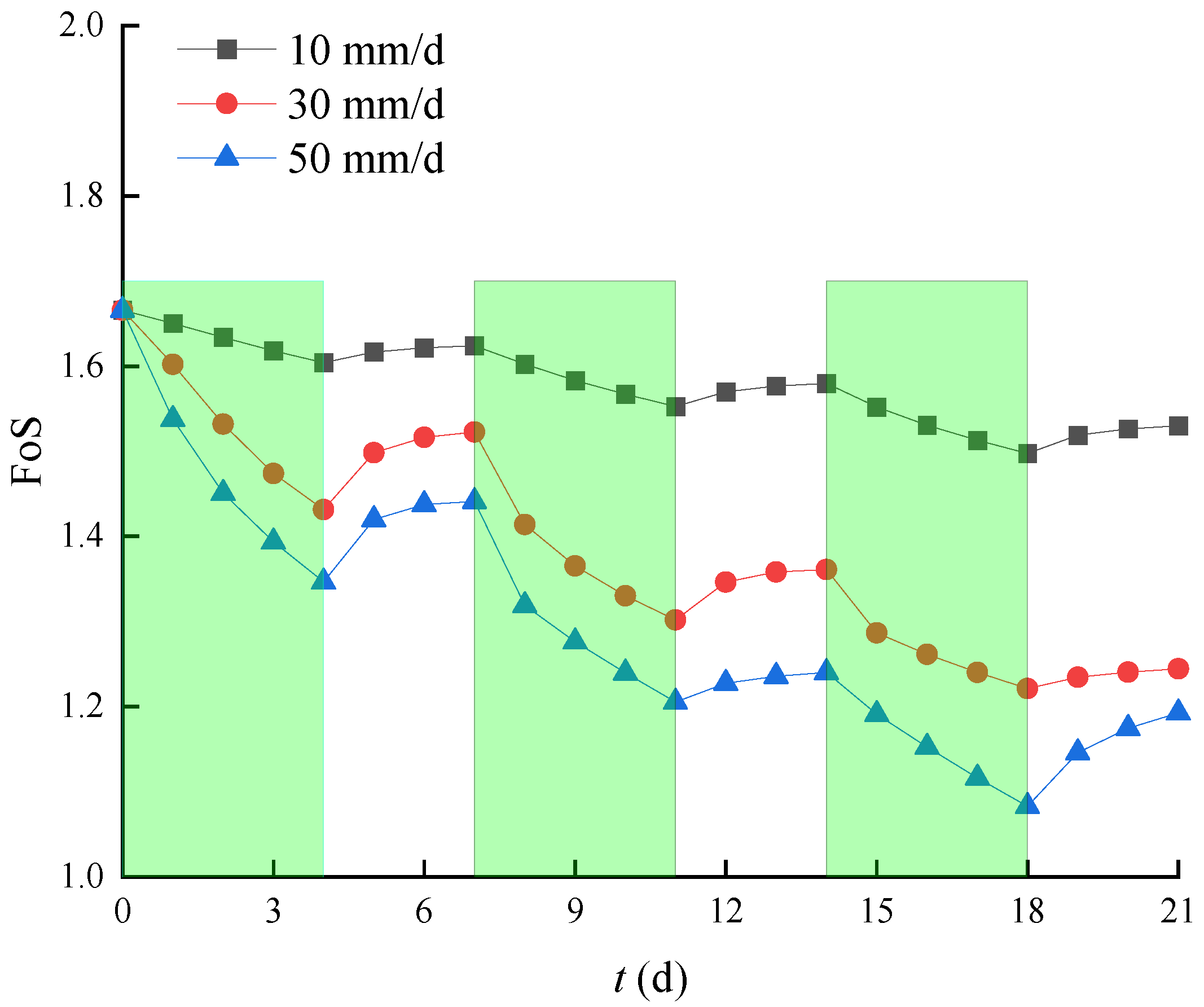
4.2.2. Impact of M and Rainfall Intervals
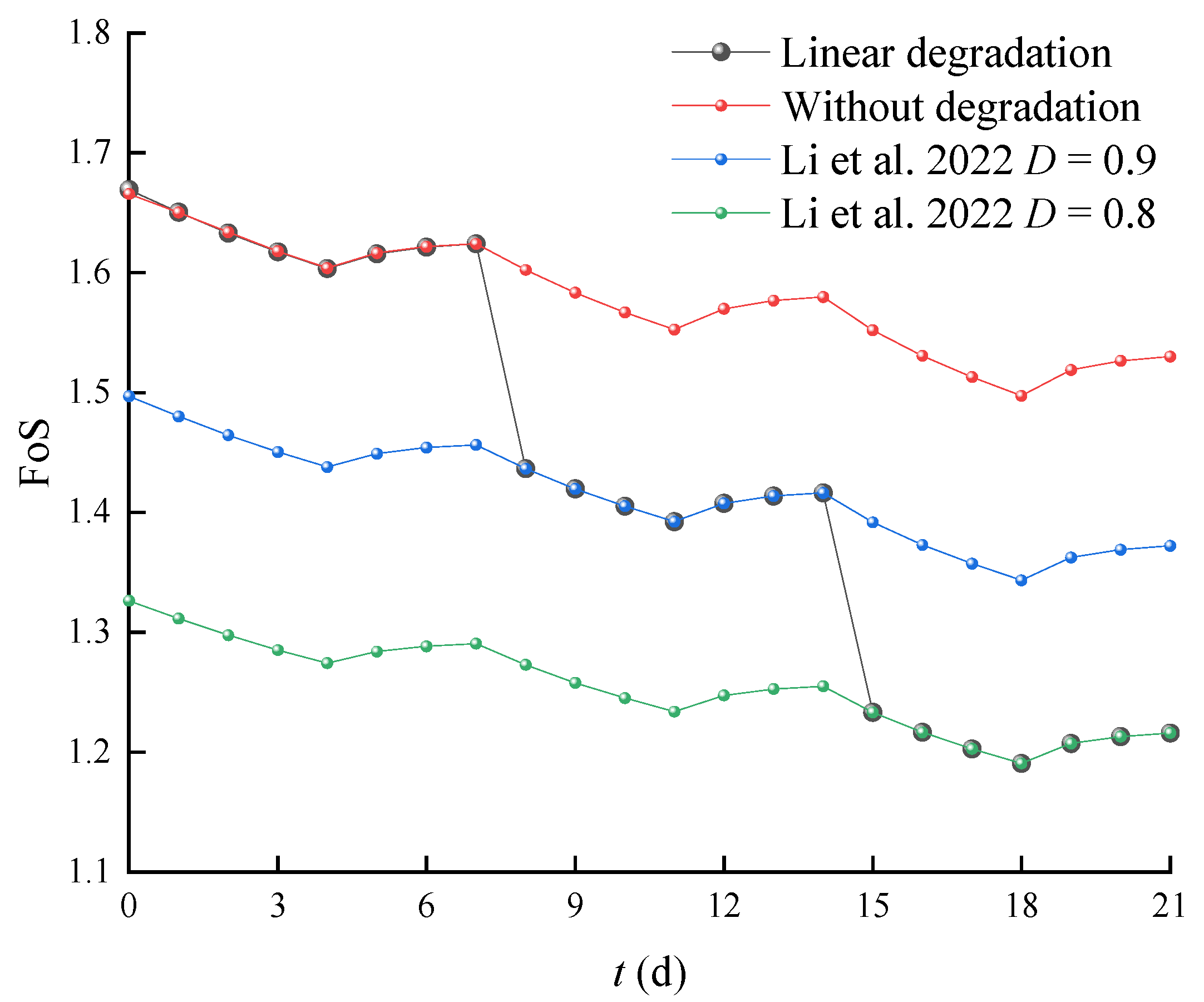
4.3. Slope Stability Analysis with Intermittent Rainfall Considering Linear Degradation of Soil Properties
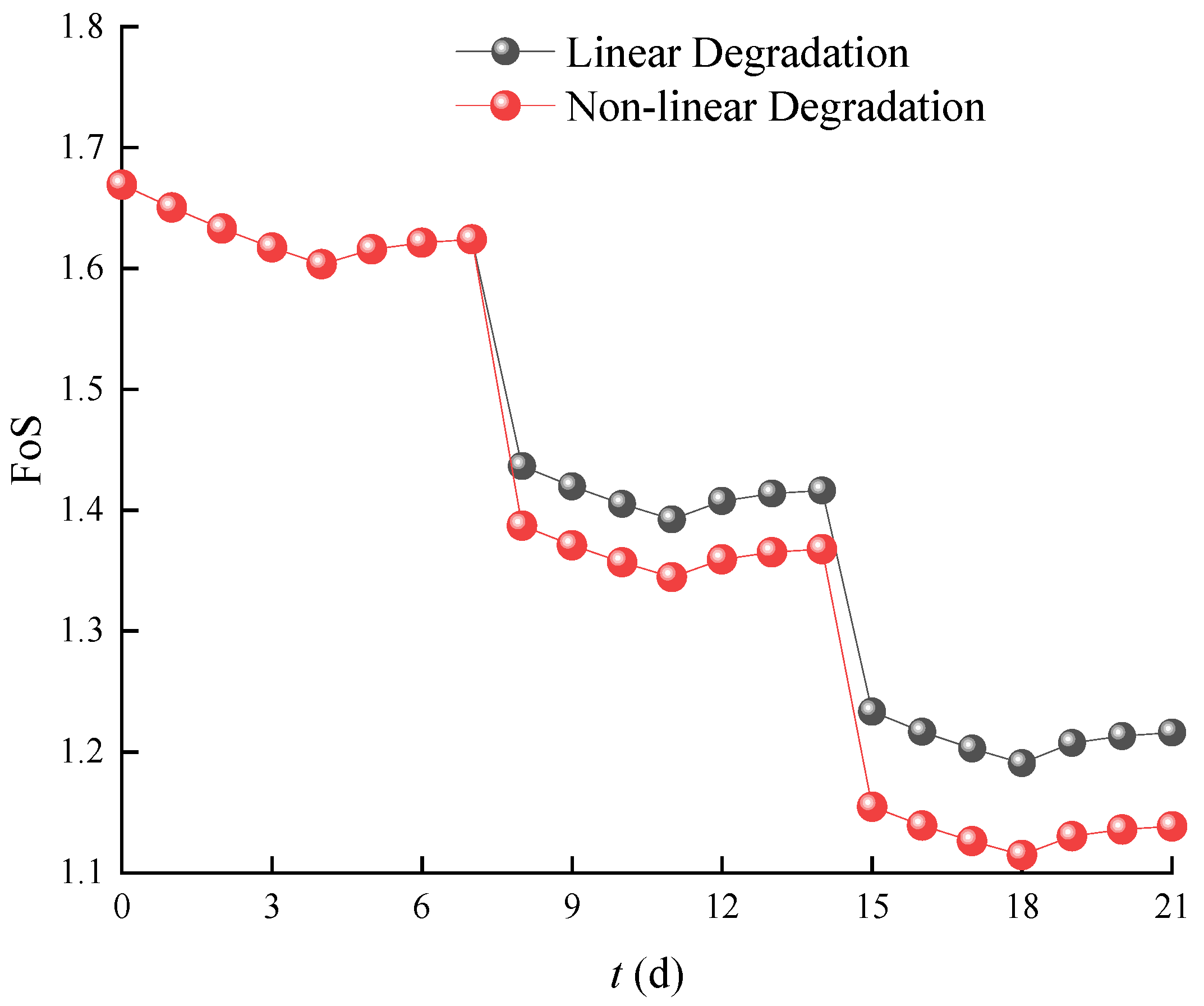
4.4. Slope Stability Analysis with Intermittent Rainfall Considering Non-Linear Degradation of Soil Properties
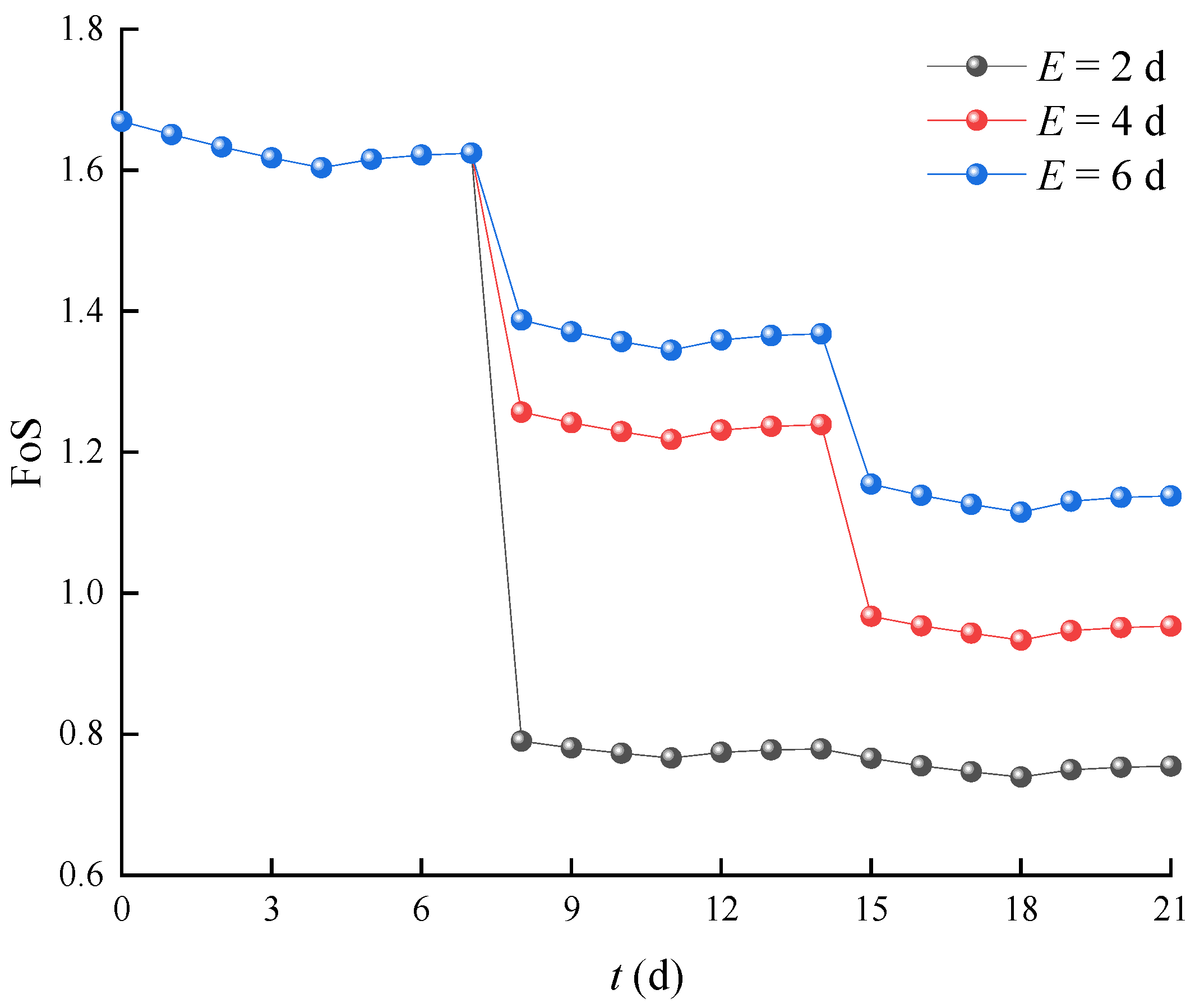
4.5. Sensitivity Analysis of Parameters in Nonlinear Degradation Model
4.5.1. Impact of Parameter E
4.5.2. Impact of Parameter Dmin
5. Discussion
6. Conclusions
- (1)
- The number of sub-rainfalls within one intermittent rainfall exerts a significant influence on the FoS values of unsaturated soil slopes, whereas the influence of rainfall intervals on the minimum FoS at the end of each sub-rainfalls is negligible.
- (2)
- The simplified linear degradation model can simulate the progressive deterioration in the FoS due to the degradation of soil properties induced by rainfall infiltration, whilst the constant and instantaneous degradation model tends to overestimate or underestimate the FoS as compared to the linear degradation model.
- (3)
- Even for moderate rainfall, reinforcement and drainage works should be implemented after considering the degradation of the soil properties induced by intermittent rainfall infiltration, although they are unnecessary when the degradation of the soil properties is omitted.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Tang, G.; Huang, J.; Sheng, D.; Sloan, S.W. Stability analysis of unsaturated soil slopes under random rainfall patterns. Eng. Geol. 2018, 245, 322–332. [Google Scholar] [CrossRef]
- Wang, B.; Vardon, P.; Hicks, M. Rainfall-induced slope collapse with coupled material point method. Eng. Geol. 2018, 239, 1–12. [Google Scholar] [CrossRef]
- Song, X.; Tan, Y. Experimental study on failure of temporary earthen slope triggered by intense rainfall. Eng. Fail. Anal. 2020, 116, 104718. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Leung, A.K. Numerical investigation of rainfall intensity and duration control of rainfall-induced landslide at a specific slope using slope case histories and actual rainfall records. Bull. Eng. Geol. Environ. 2023, 82, 1–20. [Google Scholar] [CrossRef]
- Zong, J.; Zhang, C.; Liu, L.; Liu, L. Modeling Rainfall Impact on Slope Stability: Computational Insights into Displacement and Stress Dynamics. Water 2024, 16, 554. [Google Scholar] [CrossRef]
- Zhuang, Y.; Hu, X.; He, W.; Shen, D.; Zhu, Y. Stability Analysis of a Rocky Slope with a Weak Interbedded Layer under Rainfall Infiltration Conditions. Water 2024, 16, 604. [Google Scholar] [CrossRef]
- Kluger, M.O.; Jorat, M.E.; Moon, V.G.; Kreiter, S.; de Lange, W.P.; Mörz, T.; Robertson, T.; Lowe, D.J. Rainfall threshold for initiating effective stress decrease and failure in weathered tephra slopes. Landslides 2020, 17, 267–281. [Google Scholar] [CrossRef]
- Ng, J.N.; Taib, A.M.; Razali, I.H.; Rahman, N.A.; Mohtar, W.H.M.W.; Karim, O.A.; Desa, S.M.; Awang, S.; Mohd, M.S.F. The Effect of Extreme Rainfall Events on Riverbank Slope Behaviour. Front. Environ. Sci. 2022, 10, 859427. [Google Scholar] [CrossRef]
- Li, L.; Ju, N.; He, C.; Li, C.; Sheng, D. A computationally efficient system for assessing near-real-time instability of regional unsaturated soil slopes under rainfall. Landslides 2019, 17, 893–911. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Lin, H. Models and influencing factors of the delay phenomenon for rainfall on slope stability. Eur. J. Environ. Civ. Eng. 2018, 22, 122–136. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, R.; Zhang, G.; Su, S.; Liu, W. Evaluating and analyzing the stability of loess slope using intermittent rainfall and various rainfall patterns. Arab. J. Geosci. 2022, 15, 218. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, J.; Lv, S.; Liu, L.; Zhang, C. Investigations of the Effect of Artificial Rainfall on the Pore Water Pressure and Slope Surface Displacement of Loess Slopes. Int. J. Géoméch. 2024, 24, 04024064. [Google Scholar] [CrossRef]
- Cai, J.-S.; Yeh, T.-C.J.; Yan, E.-C.; Tang, R.-X.; Hao, Y.-H.; Huang, S.-Y.; Wen, J.-C. Importance of variability in initial soil moisture and rainfalls on slope stability. J. Hydrol. 2019, 571, 265–278. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Tsai, Y.-J. Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability. Water 2018, 10, 479. [Google Scholar] [CrossRef]
- Lee, J.-U.; Cho, Y.-C.; Kim, M.; Jang, S.-J.; Lee, J.; Kim, S. The Effects of Different Geological Conditions on Landslide-Triggering Rainfall Conditions in South Korea. Water 2022, 14, 2051. [Google Scholar] [CrossRef]
- Chen, B.; Shui, W.; Liu, Y.; Deng, R. Analysis of Slope Stability with Different Vegetation Types under the Influence of Rainfall. Forests 2023, 14, 1865. [Google Scholar] [CrossRef]
- Haiou, S.; Fenli, Z.; Leilei, W. Effects of Rainfall Intensity and Slope Gradient on Rill Morphological Characteristics. Trans. Chin. Soc. Agric. Mach. 2015, 7, 162–170. (In Chinese) [Google Scholar]
- Liu, J.; Zeng, L.; Fu, H.Y.; Shi, Z.N.; Zhang, Y.J. Variation law of rainfall infiltration depth and saturation zone of soil slope. J. Cent. South Univ. 2019, 2, 452–459. [Google Scholar]
- Huang, S.P.; Chen, J.Y.; Xiao, H.L.; Tao, G.L. Test on rules of rainfall infiltration and runoff erosion on vegetated slopes with different gradients. Rock Soil Mech. 2023, 12, 3435–3447. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, H.; Tang, B.; Yang, D.; Liu, Y.; Liu, Z.; Ye, B.; Zhou, W.; Zhu, Y. Accelerating Effect of Vegetation on the Instability of Rainfall-Induced Shallow Landslides. Remote Sens. 2022, 14, 5743. [Google Scholar] [CrossRef]
- Xu, G.Z.; Hu, J.B.; Zheng, H.L.; Ji, C.L.; Li, X.; Zhang, N. Stability analysis of unsaturated and non-homogeneous two-dimensional slope under seepage. Build. Struct. 2022, S2, 2624–2630. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Conte, E. Rainfall Threshold for Shallow Landslide Triggering Due to Rising Water Table. Water 2022, 14, 2966. [Google Scholar] [CrossRef]
- Sengani, F.; Mulenga, F. Influence of Rainfall Intensity on the Stability of Unsaturated Soil Slope: Case Study of R523 Road in Thulamela Municipality, Limpopo Province, South Africa. Appl. Sci. 2020, 10, 8824. [Google Scholar] [CrossRef]
- Luo, X.Q.; Kong, L.W.; Yan, J.B.; Gao, Z.A.; Tian, S.K. In-situ borehole shear test and shear strength response characteristics of expansive soil under different saturations. Rock Soil Mech. 2024, 1, 153–163. (In Chinese) [Google Scholar] [CrossRef]
- Jing, J.; Hou, J.; Sun, W.; Chen, G.; Ma, Y.; Ji, G. Study on Influencing Factors of Unsaturated Loess Slope Stability under Dry-Wet Cycle Conditions. J. Hydrol. 2022, 612, 128187. [Google Scholar] [CrossRef]
- Sun, Z.H.; Wang, S.H.; Yang, T.J. Infiltration Mechanism and Stability Analysis of Multilayer Soil Slope Under Rainfall Conditions. J. Northeast. Univ. 2020, 8, 1201–1208. [Google Scholar] [CrossRef]
- Wang, C.L.; Tang, D.; Li, Y.F.; Jiang, Z.M.; Wang, Y.X. Slope stability analysis based on considering the effect of water content on soil shear strength parameters. Technol. Innov. Appl. 2024, 6, 61–64. (In Chinese) [Google Scholar] [CrossRef]
- Li, D.; Li, L.; Cheng, Y.; Hu, J.; Lu, S.; Li, C.; Meng, K. Reservoir slope reliability analysis under water level drawdown considering spatial variability and degradation of soil properties. Comput. Geotech. 2022, 151, 104947. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Xu, Y.; Su, C.; Huang, Z.; Yang, C.; Yang, Y. Research on the protection of expansive soil slopes under heavy rainfall by anchor-reinforced vegetation systems. Geotext. Geomembr. 2022, 50, 1147–1158. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Lin, H.; Zhong, W.; Wang, H.; Xu, W. Effect of Soil–Water Characteristic Parameters on Saturation Line and Stability of Slope. Geotech. Geol. Eng. 2017, 35, 2715–2726. [Google Scholar] [CrossRef]
- Lin, H.; Zhong, W. Influence of Rainfall Intensity and Its Pattern on the Stability of Unsaturated Soil Slope. Geotech. Geol. Eng. 2019, 37, 615–623. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, L.; Wan, Y.; Chen, H. Reliability analysis of three-dimensional reinforced slope considering the spatial variability in soil parameters. Stoch. Environ. Res. Risk Assess. 2024, 38, 1583–1596. [Google Scholar] [CrossRef]
- Tang, G.-P.; Zhao, L.-H.; Li, L.; Chen, J.-Y. Combined influence of nonlinearity and dilation on slope stability evaluated by upper-bound limit analysis. J. Cent. South Univ. 2017, 24, 1602–1611. [Google Scholar] [CrossRef]
- Gu, D.; Liu, H.; Gao, X.; Huang, D.; Zhang, W. Influence of Cyclic Wetting–Drying on the Shear Strength of Limestone with a Soft Interlayer. Rock Mech. Rock Eng. 2021, 54, 4369–4378. [Google Scholar] [CrossRef]
- Liao, K.; Wu, Y.; Miao, F.; Li, L.; Xue, Y. Time-varying reliability analysis of Majiagou landslide based on weakening of hydro-fluctuation belt under wetting-drying cycles. Landslides 2021, 18, 267–280. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Li, L.; Tang, H.; Xiong, F. Weakening laws of slip zone soils during wetting–drying cycles based on fractal theory: A case study in the Three Gorges Reservoir (China). Acta Geotech. 2020, 15, 1909–1923. [Google Scholar] [CrossRef]
- Niu, G.; Sun, D.; Kong, L.; Shao, L.; Wang, H.; Wang, Z. Investigation into the shear strength of a weakly expansive soil over a wide suction range. Acta Geotech. 2024, 19, 3059–3073. [Google Scholar] [CrossRef]
- GB 50330-2013; Technical Code for Building Slope Engineering. National Standard of the People’s Republic of China: Beijing, China, 2013.
- Yang, Y.-S.; Yeh, H.-F.; Ke, C.-C.; Wei, L.-W.; Chen, N.-C. The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory. Geosciences 2024, 14, 274. [Google Scholar] [CrossRef]
- Gu, X.; Song, L.; Xia, X.; Yu, C. Finite Element Method-Peridynamics Coupled Analysis of Slope Stability Affected by Rainfall Erosion. Water 2024, 16, 2210. [Google Scholar] [CrossRef]

| Analysis | Properties | Values |
|---|---|---|
| Stability | c0 | 2 kPa |
| φ0 | 26° | |
| γ | 20 kN/m3 | |
| Seepage | θs | 0.45 |
| θr | 0.05 | |
| a | 0.01 kPa−1 | |
| n | 1.5 | |
| Ks | 1 × 10−6 m/s |
| Ri/mm/d | Tri/d | Tei/d | M |
|---|---|---|---|
| 10 | 1 | 3 | 1 |
| 30 | 2 | 6 | 3 |
| 50 | 3 | 9 | |
| 4 |
| R | 10 mm/d | 10 mm/d | 10 mm/d |
|---|---|---|---|
| E | 2 d | 4 d | 6 d |
| Dmin | 0.5 | 0.5 | 0.5 |
| R | 10 mm/d | 20 mm/d | 30 mm/d |
|---|---|---|---|
| E | 6 d | 6 d | 6 d |
| Dmin | 0.5 | 0.45 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Li, L. Slope Stability Analysis Considering Degradation of Soil Properties Induced by Intermittent Rainfall. Water 2025, 17, 814. https://doi.org/10.3390/w17060814
Wang M, Li L. Slope Stability Analysis Considering Degradation of Soil Properties Induced by Intermittent Rainfall. Water. 2025; 17(6):814. https://doi.org/10.3390/w17060814
Chicago/Turabian StyleWang, Minghao, and Liang Li. 2025. "Slope Stability Analysis Considering Degradation of Soil Properties Induced by Intermittent Rainfall" Water 17, no. 6: 814. https://doi.org/10.3390/w17060814
APA StyleWang, M., & Li, L. (2025). Slope Stability Analysis Considering Degradation of Soil Properties Induced by Intermittent Rainfall. Water, 17(6), 814. https://doi.org/10.3390/w17060814





