The Effect of Entrainment Model on Debris-Flow Simulation—Comparison of Two Simple 1D Models
Abstract
1. Introduction
2. Materials and Methods
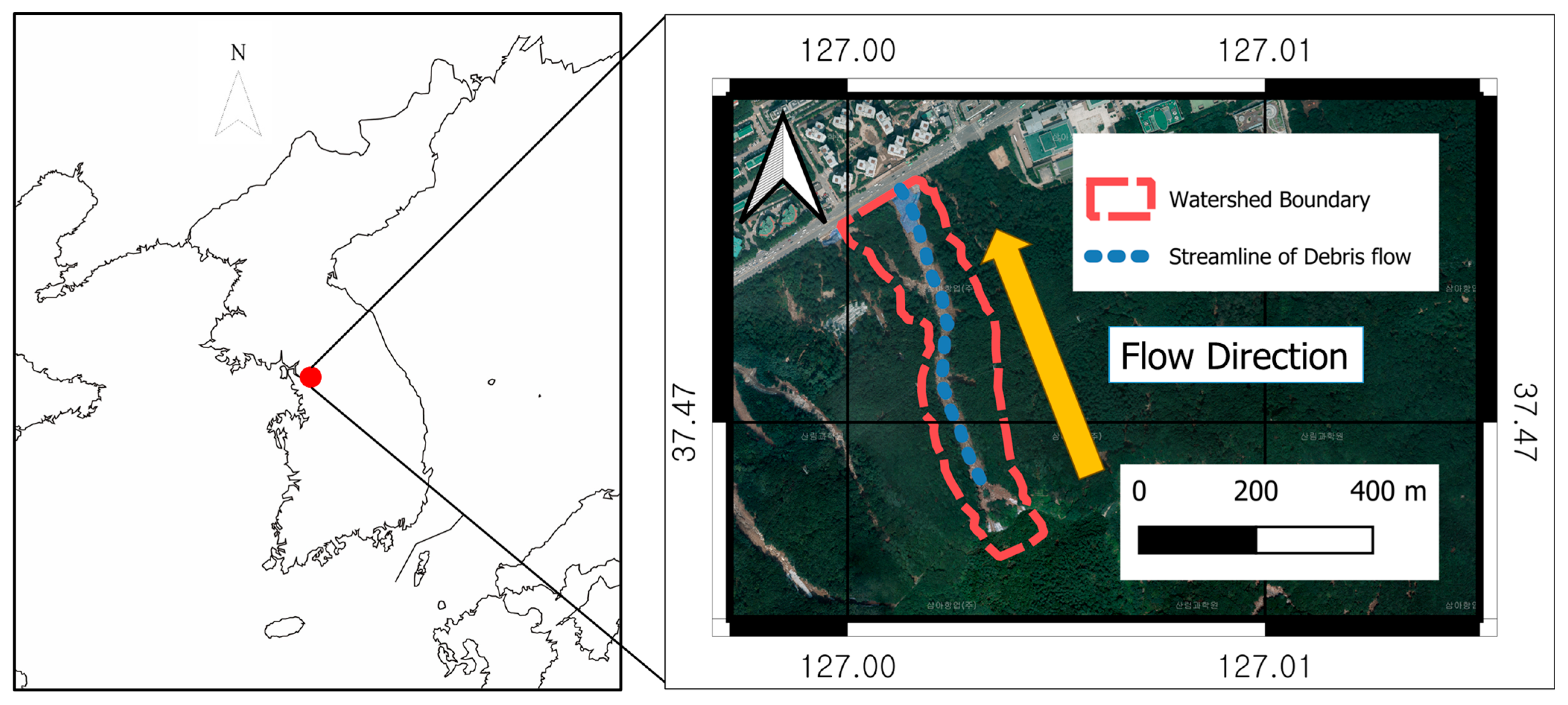
2.1. Study Site
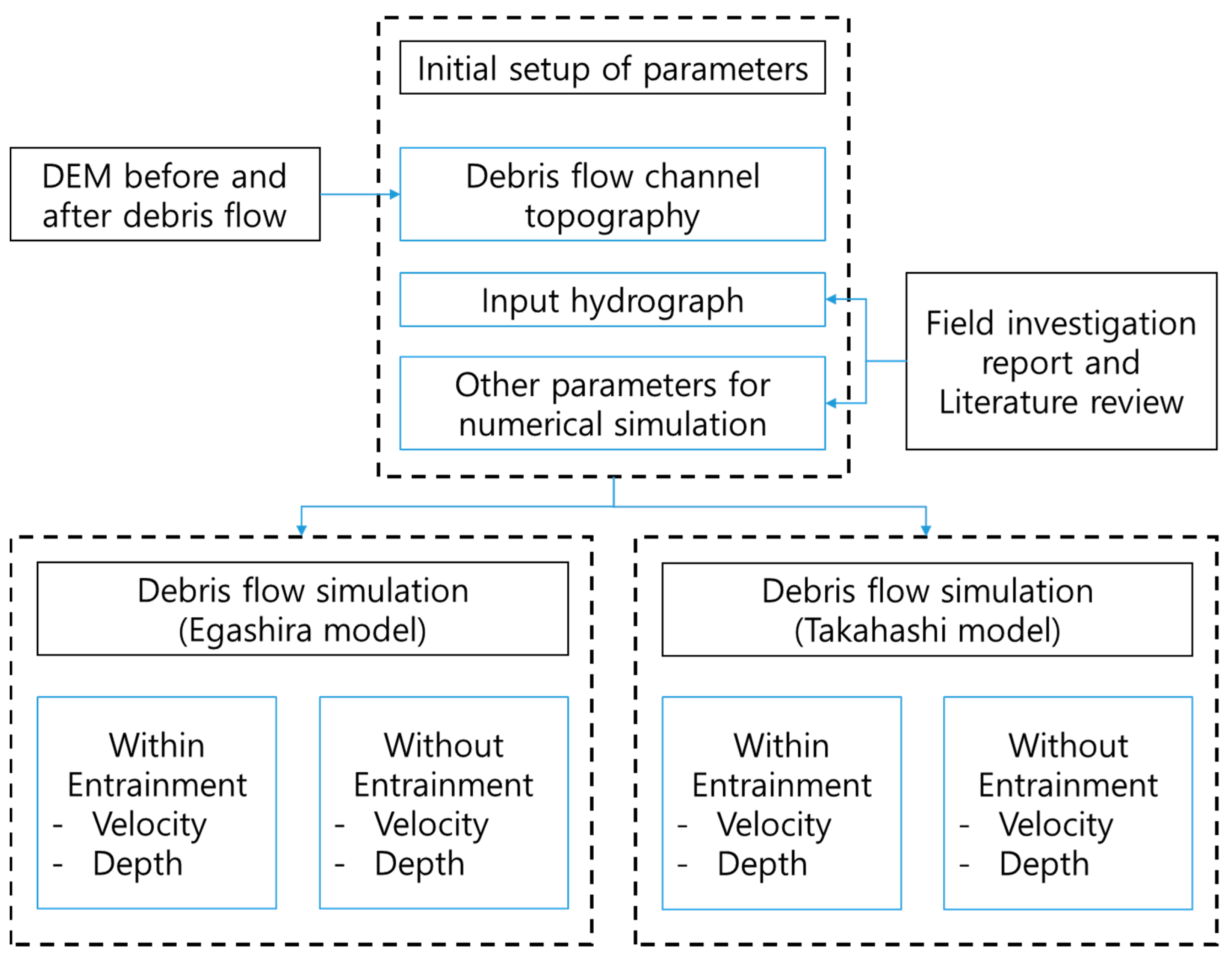
2.2. Debris-Flow Simulation
2.2.1. Governing Equation
2.2.2. Parameters Settings
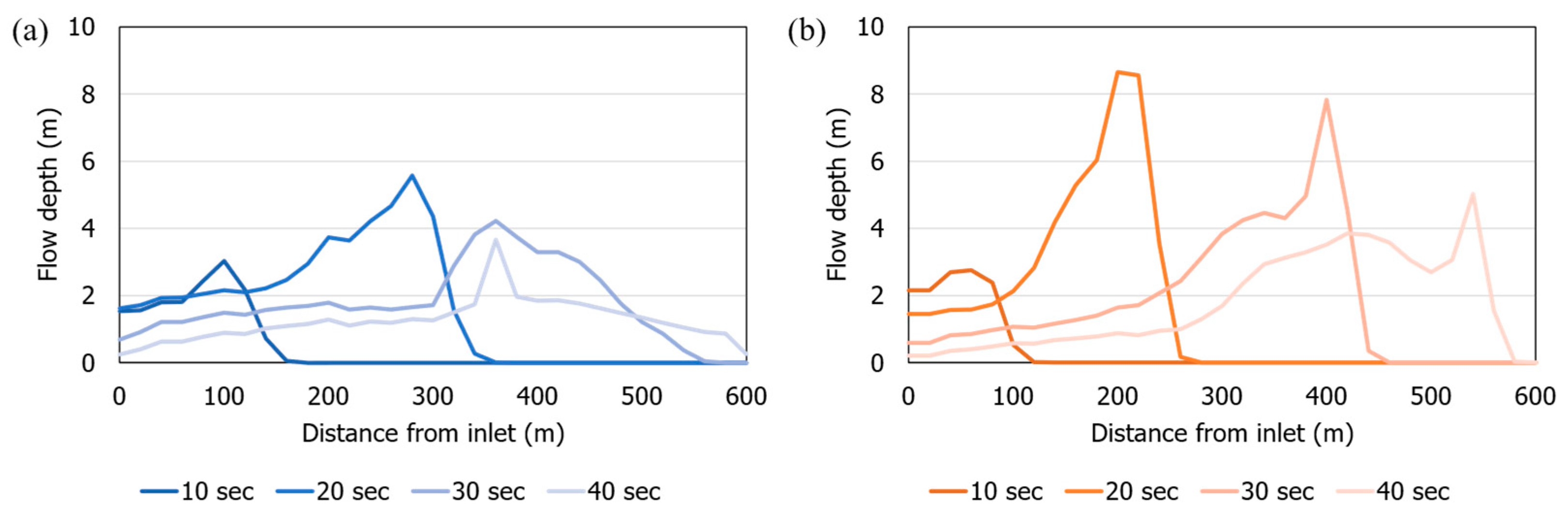
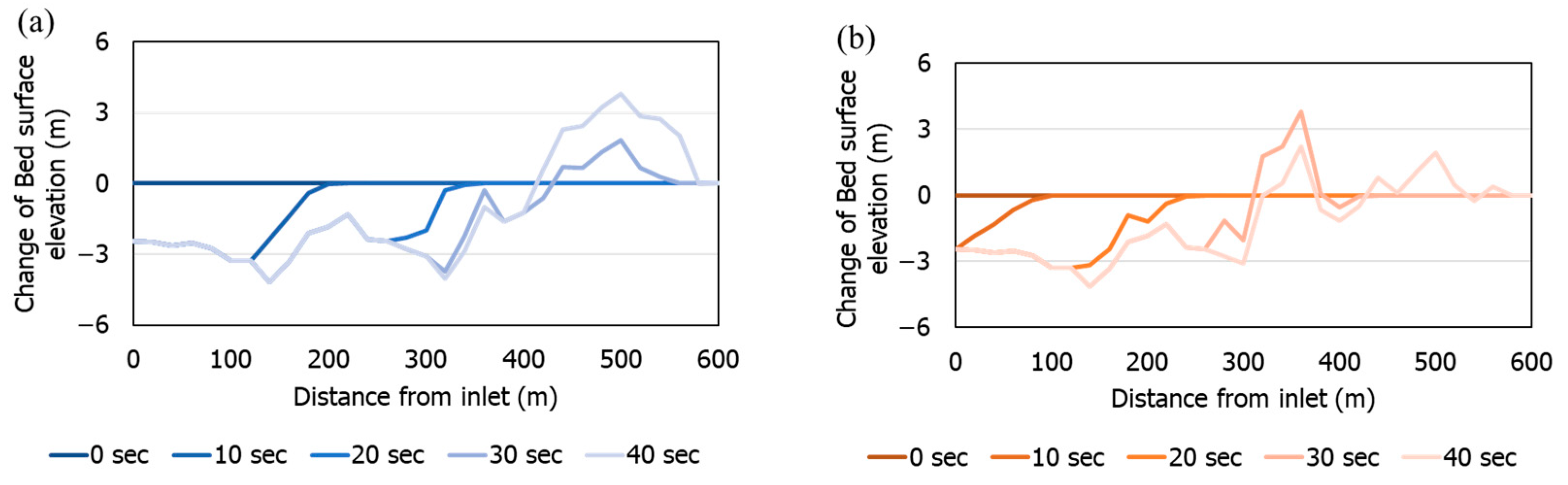
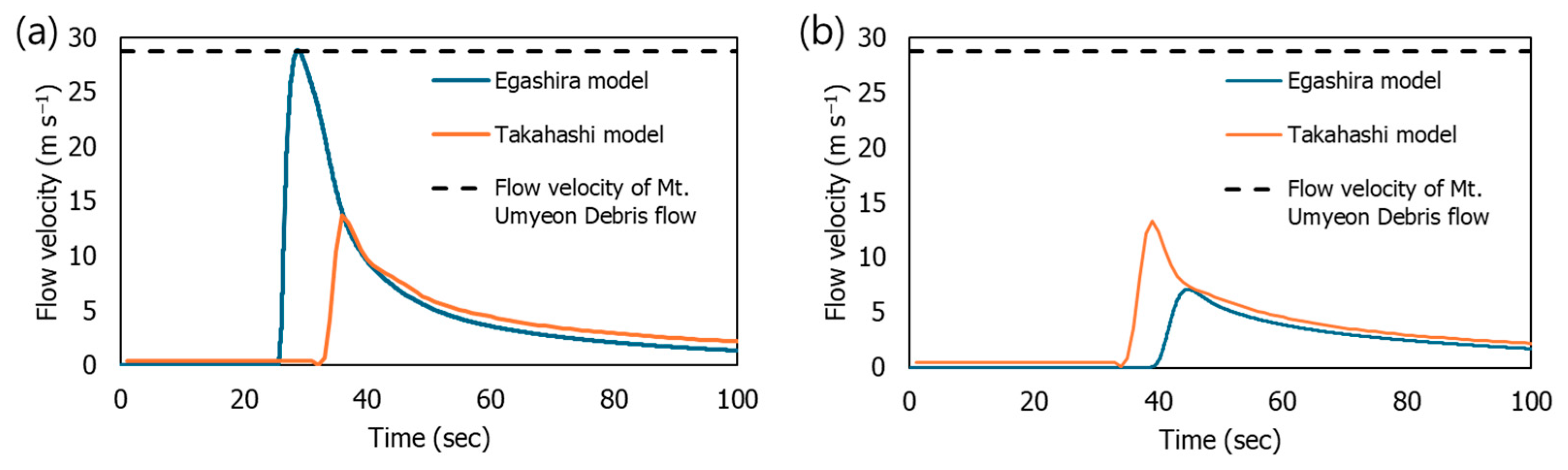
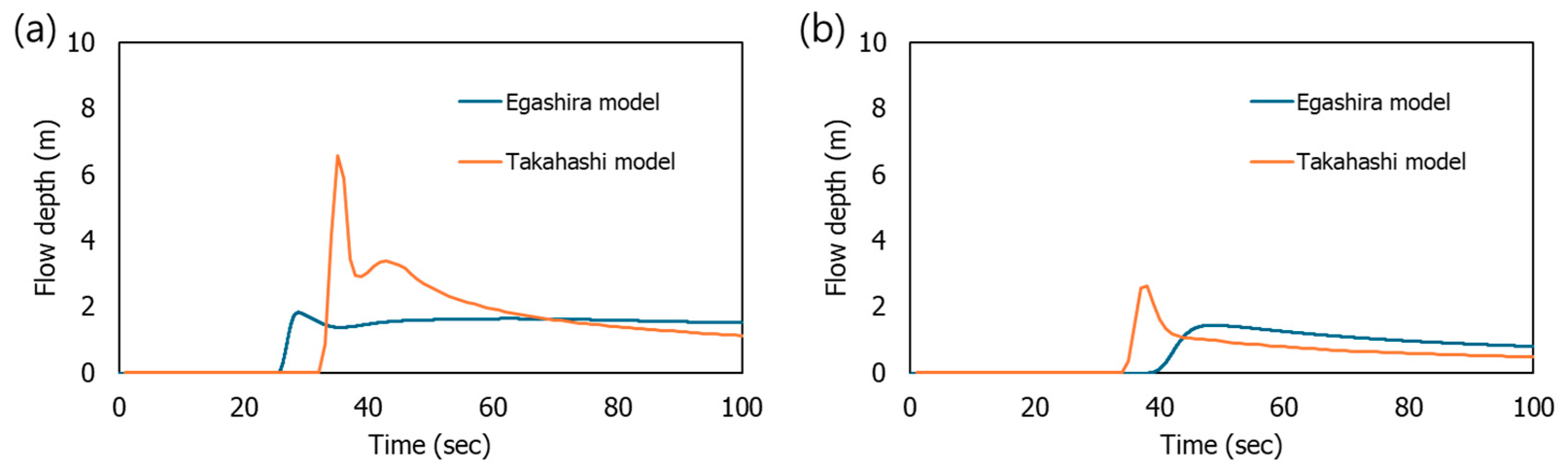
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hungr, O.; Evans, S.; Bovis, M.; Hutchinson, J. A review of the classification of landslides of the flow type. Environ. Eng. Geosci. 2001, 7, 221–238. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flow: Mechanics, Prediction and Countermeasures, 2nd ed.; CRC Press/Balkema: Leiden, The Netherlands, 2014. [Google Scholar]
- Dowling, C.A.; Santi, P.M. Debris flows and their toll on human life: A global analysis of debris-flow fatalities from 1950 to 2011. Nat. Hazards 2014, 71, 203–227. [Google Scholar] [CrossRef]
- Hu, K.; Wei, F.; Li, Y. Real-time measurement and preliminary analysis of debris-flow impact force at Jiangjia Ravine, China. Earth Surf. Process. Landf. 2011, 36, 1268–1278. [Google Scholar] [CrossRef]
- Jakob, M. Debris-flow hazard analysis. In Debris-flow Hazards and Related Phenomena; Jacob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 411–443. [Google Scholar]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth-Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Hübl, J.; Suda, J.; Proske, D.; Kaitna, R.; Scheidl, C. Debris flow impact estimation. In Proceedings of the 11th International Symposium on Water Management and Hydraulic Engineering, Ohrid, Macedonia, 1–5 September 2009; pp. 1–5. [Google Scholar]
- Scheidl, C.; Chiari, M.; Kaitna, R.; Mullegger, M.; Krawtschuk, A.; Zimmermann, T.; Proske, D. Analysing Debris-Flow Impact Models, Based on a Small Scale Modeling Approach. Surv. Geophys. 2013, 34, 121–140. [Google Scholar] [CrossRef]
- Korea Forest Service. Landslide Information System. Available online: https://sansatai.forest.go.kr/ (accessed on 17 November 2024).
- Armanini, A. On the dynamic impact of debris flows. In Recent Developments on Debris Flows; Armanini, A., Michiue, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 64, pp. 208–226. [Google Scholar]
- Canelli, L.; Ferrero, A.M.; Migliazza, M.; Segalini, A. Debris flow risk mitigation by the means of rigid and flexible barriers—Experimental tests and impact analysis. Nat. Hazards Earth Syst. Sci. 2012, 12, 1693–1699. [Google Scholar] [CrossRef]
- Hungr, O.; Morgan, G.; Kellerhals, R. Quantitative analysis of debris torrent hazards for design of remedial measures. Can. Geotech. J. 1984, 21, 663–677. [Google Scholar] [CrossRef]
- Lo, D.O.K. Review of Natural Terrain Landslide Debris-Resisting Barrier Design; Geotechnical Engineering Office, Civil Engineering Department: Hong Kong, China, 2000.
- National Institute for Land and Infrastructure Management. Manual of Technical Standard for Designing Sabo Facilities Against Debris Flow and Driftwood; National Institute for Land and Infrastructure Management: Tsukuba, Japan, 2016.
- Christen, M.; Kowalski, J.; Bartelt, P. RAMMS: Numerical simulation of dense snow avalanches in three-dimensional terrain. Cold Reg. Sci. Technol. 2010, 63, 1–14. [Google Scholar] [CrossRef]
- George, D.L.; Iverson, R.M. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. II. Numerical predictions and experimental tests. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130820. [Google Scholar] [CrossRef]
- Lee, D.-H.; Lee, S.R.; Park, J.-Y. Numerical Simulation of Debris Flow Behavior at Mt. Umyeon using the DAN3D Model. J. Korean Soc. Hazard Mitig. 2019, 19, 195–202. [Google Scholar] [CrossRef]
- Lee, S.; An, H.; Kim, M.; Lee, G.; Shin, H. Evaluation of different erosion–entrainment models in debris-flow simulation. Landslides 2022, 19, 2075–2090. [Google Scholar] [CrossRef]
- Nakatani, K.; Wada, T.; Satofuka, Y.; Mizuyama, T. Development of “Kanako 2D (Ver. 2.00),” a user-friendly one-and two-dimensional debris flow simulator equipped with a graphical user interface. Int. J. Eros. Control Eng. 2008, 1, 62–72. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Fischer, J.-T. A mechanical erosion model for two-phase mass flows. Int. J. Multiph. Flow 2020, 132, 103416. [Google Scholar] [CrossRef]
- Reid, M.E.; Iverson, R.M.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Entrainment of bed sediment by debris flows: Results from large-scale experiments. In Proceedings of the Fifth International Conference on Debris-Flow Hazards Mitigation, Mechanics, Prediction and Assessment, Editrice Universita La Sapienza, Rome, Italy, 14–17 June 2011; pp. 367–374. [Google Scholar]
- Egashira, S.; Honda, N.; Itoh, T. Experimental study on the entrainment of bed material into debris flow. Phys. Chem. Earth Part C Sol. Terr. Planet. Sci. 2001, 26, 645–650. [Google Scholar] [CrossRef]
- Frank, F.; McArdell, B.W.; Huggel, C.; Vieli, A. The importance of entrainment and bulking on debris flow runout modeling: Examples from the Swiss Alps. Nat. Hazards Earth Syst. Sci. 2015, 15, 2569–2583. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; Tang, C.; Xu, L.; He, Y.; Huang, X.; Wang, W. Numerical simulation of debris-flow behavior incorporating a dynamic method for estimating the entrainment. Eng. Geol. 2015, 190, 52–64. [Google Scholar] [CrossRef]
- Iverson, R.M.; Ouyang, C. Entrainment of bed material by Earth-surface mass flows: Review and reformulation of depth-integrated theory. Rev. Geophys. 2015, 53, 27–58. [Google Scholar] [CrossRef]
- McDougall, S.; Hungr, O. Dynamic modeling of entrainment in rapid landslides. Can. Geotech. J. 2005, 42, 1437–1448. [Google Scholar] [CrossRef]
- Takahashi, T.; Nakagawa, H. Prediction of Stony Debris Flow Induced by Severe Rainfall. J. Jpn. Soc. Eros. Control Eng. 1991, 44, 12–19. [Google Scholar]
- Denlinger, R.P.; Iverson, R.M. Flow of variably fluidized granular masses across three-dimensional terrain: 2. Numerical predictions and experimental tests. J. Geophys. Res. Solid Earth 2001, 106, 553–566. [Google Scholar] [CrossRef]
- Shen, P.; Zhang, L.; Wong, H.F.; Peng, D.; Zhou, S.; Zhang, S.; Chen, C. Debris flow enlargement from entrainment: A case study for comparison of three entrainment models. Eng. Geol. 2020, 270, 105581. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, Y.; Lee, J.K.; Kim, J. The 27 July 2011 debris flows at Umyeonsan, Seoul, Korea. Landslides 2015, 12, 799–813. [Google Scholar] [CrossRef]
- Seoul Metropolitan Goverment. Supplimentary Investigation of Cause of Mt. Umyeon Landslide; Seoul Metropolitan Goverment: Seoul, Republic of Korea, 2014.
- Schiavo, M.; Gregoretti, C.; Boreggio, M.; Barbini, M.; Bernard, M. Probabilistic identification of debris-flow pathways in mountain fans within a stochastic framework. J. Geophys. Res. Earth Surf. 2024, 129, e2024JF007946. [Google Scholar] [CrossRef]
- Eu, S. Long-Term Stability Analysis of Erosion Control Dam Considering Debris-Flow Entrainment Impact Force Simulation. Doctoral Dissertation, Seoul National University, Seoul, Republic of Korea, 2020. [Google Scholar]
- Cueto-Felgueroso, L.; Santillán, D.; García-Palacios, J.H.; Garrote, L. Comparison between 2D shallow-water simulations and energy-momentum computations for transcritical flow past channel contractions. Water 2019, 11, 1476. [Google Scholar] [CrossRef]
- Egashira, S. Stoppage and Deposition Mechanism of Debris Flow (2). J. Jpn. Soc. Eros. Control Eng. 1993, 46, 51–56. [Google Scholar]
- Barnhart, K.R.; Jones, R.P.; George, D.L.; McArdell, B.W.; Rengers, F.K.; Staley, D.M.; Kean, J.W. Multi-model comparison of computed debris flow runout for the 9 January 2018 Montecito, California post-wildfire event. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006245. [Google Scholar] [CrossRef]
- Seoul Metropolitan Goverment. Mt. Umyeon Lansdlide Recovery Plan. Lot No.1: Raemian, Imgwang and Jeonwon Area; Seoul Metropolitan Government: Seoul, Republic of Korea, 2012.
- Nishiguchi, Y.; Uchida, T. Long-runout-landslide-induced debris flow: The role of fine sediment deposition processes in debris flow propagation. J. Geophys. Res. F Earth Surf. 2022, 127, e2021JF006452. [Google Scholar] [CrossRef]
- Uchida, T.; Nishiguchi, Y.; Nakatani, K.; Satofuka, Y.; Yamakoshi, T.; Okamoto, A.; Mizuyama, T. New numerical simulation procedure for large-scale debris flows (Kanako-LS). Int. J. Eros. Control Eng. 2013, 6, 58–67. [Google Scholar] [CrossRef]
- Jang, S. Sediment-Related Disaster Risk Assessment by the Use of Physically-Based Models Considering the Effect of Tree Roots on Soil Reinforcement in a Forested Catchment. Doctoral Dissertation, Kangwon National University, Chuncheon, Republic of Korea, 2019. [Google Scholar]
- Lim, Y.-H. A Study on the Application of Numerical Simulation to Erosion Control Facility using KANAKO 2D. Doctoral Dissertation, Kangwon National University, Chuncheon, Republic of Korea, 2017. [Google Scholar]
- Liu, J.; Nakatani, K.; Mizuyama, T. Effect assessment of debris flow mitigation works based on numerical simulation by using Kanako 2D. Landslides 2013, 10, 161–173. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Seo, J.; Woo, C.; Lee, C.; Kim, D. Characteristics of Sediment Discharge Based on GIS Spatial Analysis of Area Damaged by Debris Flow. J. Korean Soc. Hazard Mitig. 2018, 18, 89–96. [Google Scholar] [CrossRef]
- Godt, J.W.; Coe, J.A. Alpine debris flows triggered by a 28 July 1999 thunderstorm in the central Front Range, Colorado. Geomorphology 2007, 84, 80–97. [Google Scholar] [CrossRef]
- Rickenmann, D. Runout prediction methods. In Debris-Flow Hazards and Related Phenomena; Jacob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 305–324. [Google Scholar]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]

| Parameter [Unit] | Symbol | Value | Reference |
|---|---|---|---|
| Internal friction angle (°) | Φ | 0.50 | [32] |
| Particle density (kg m−3) | Σ | 2600 | [32] |
| Restitution coefficient | e | 0.8 | [23] |
| Momentum correction coefficient | β | 1.25 | [23] |
| Erosion rate coefficient | δe | 0.0007 | [20] |
| Deposition rate coefficient | δd | 0.05 | [20] |
| Mean diameter of sediments [m] | d | 0.2 | [32] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eu, S.; Im, S. The Effect of Entrainment Model on Debris-Flow Simulation—Comparison of Two Simple 1D Models. Water 2025, 17, 761. https://doi.org/10.3390/w17050761
Eu S, Im S. The Effect of Entrainment Model on Debris-Flow Simulation—Comparison of Two Simple 1D Models. Water. 2025; 17(5):761. https://doi.org/10.3390/w17050761
Chicago/Turabian StyleEu, Song, and Sangjun Im. 2025. "The Effect of Entrainment Model on Debris-Flow Simulation—Comparison of Two Simple 1D Models" Water 17, no. 5: 761. https://doi.org/10.3390/w17050761
APA StyleEu, S., & Im, S. (2025). The Effect of Entrainment Model on Debris-Flow Simulation—Comparison of Two Simple 1D Models. Water, 17(5), 761. https://doi.org/10.3390/w17050761








