Multi-Scale Analysis Based on Wavelet Transform of Reservoir and River Total Phosphorus Correlation and Determination of Monitoring Time Scales
Abstract
1. Introduction
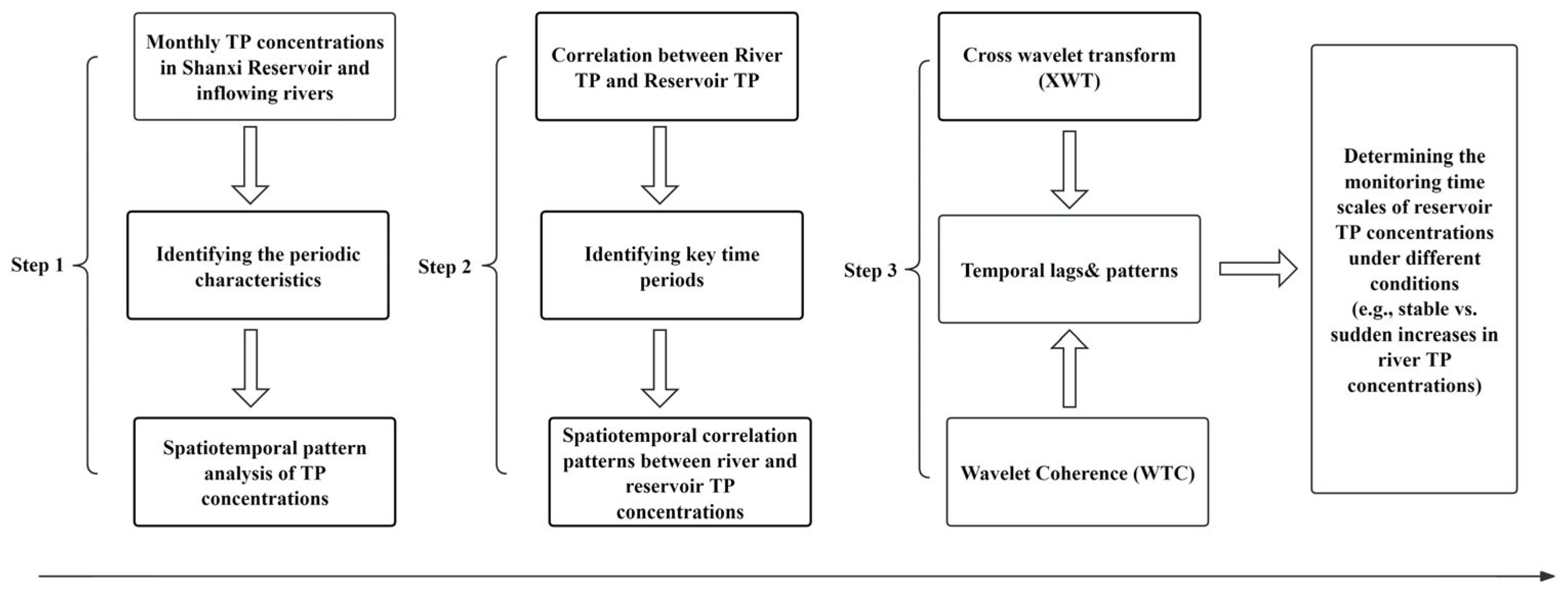
2. Materials and Methods
2.1. Study Site and Data
2.2. Indicator Selection and Data Source
2.3. Nonlinear Time Series Analysis Methods
2.3.1. Wavelet Transform
2.3.2. Cross Wavelet Transform and Wavelet Coherence
2.3.3. Statistical Analysis
3. Results
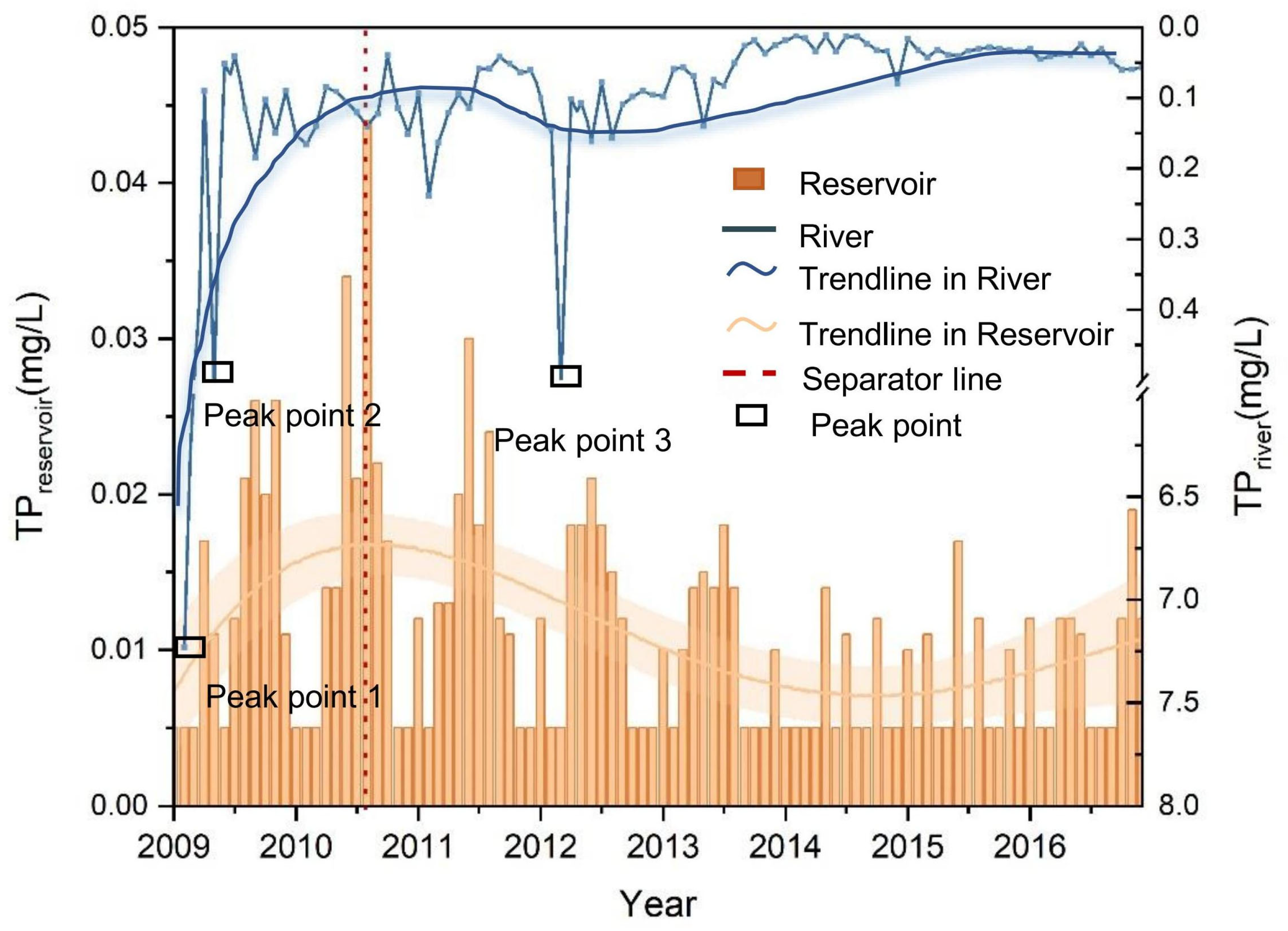
3.1. Total Phosphorus Characteristics
3.2. Exploration of Wavelet Basis and Temporal Scale Rationality
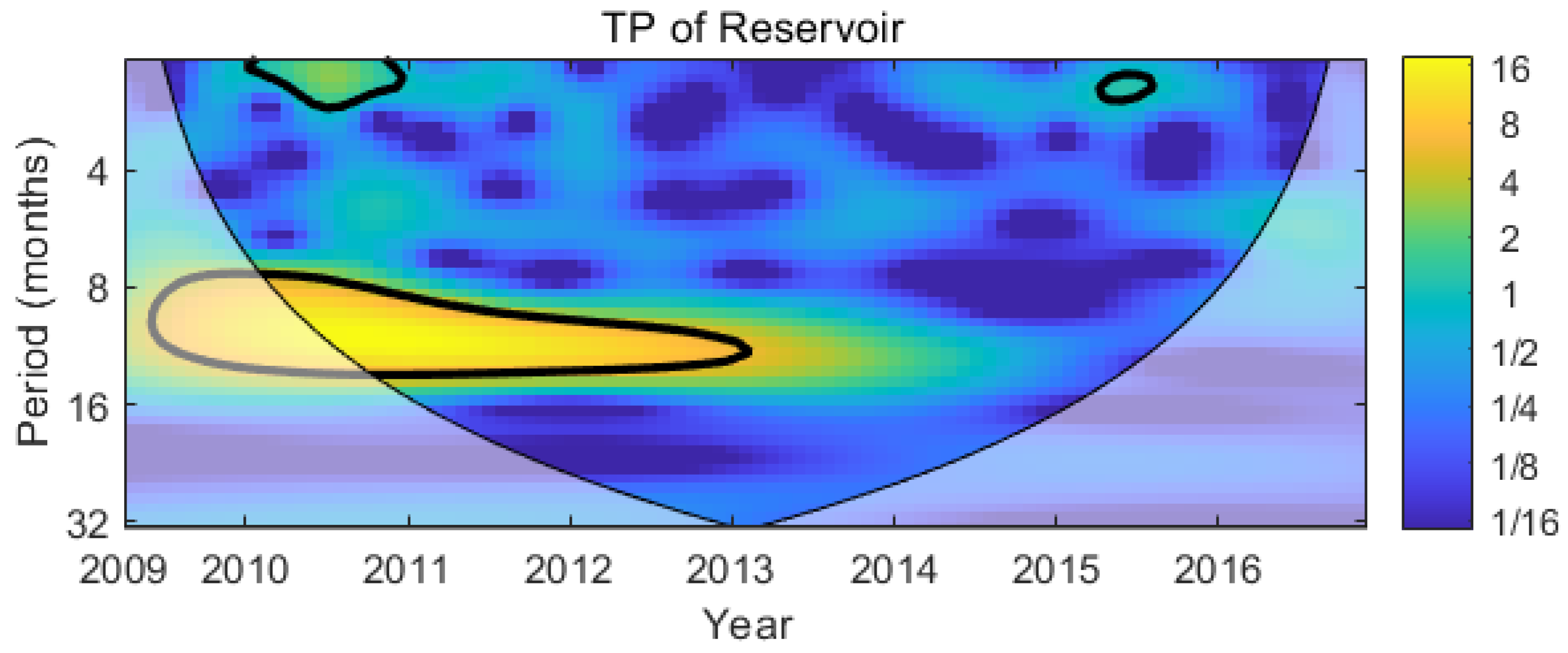
3.3. Temporal Characteristics of the Wavelet Spectrum of Total Phosphorus
3.4. Frequency Domain Characteristics of the Wavelet Spectrum of Total Phosphorus
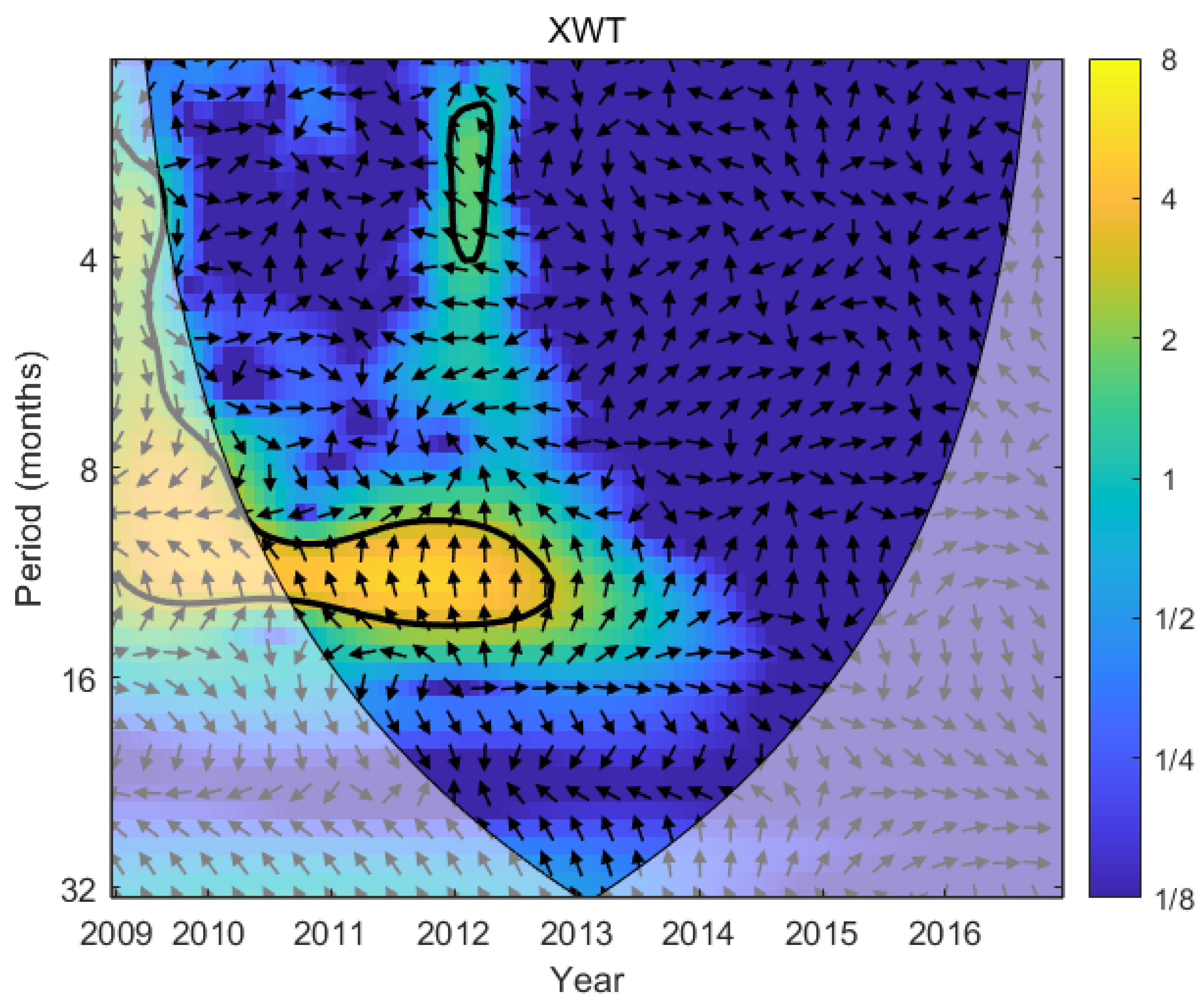
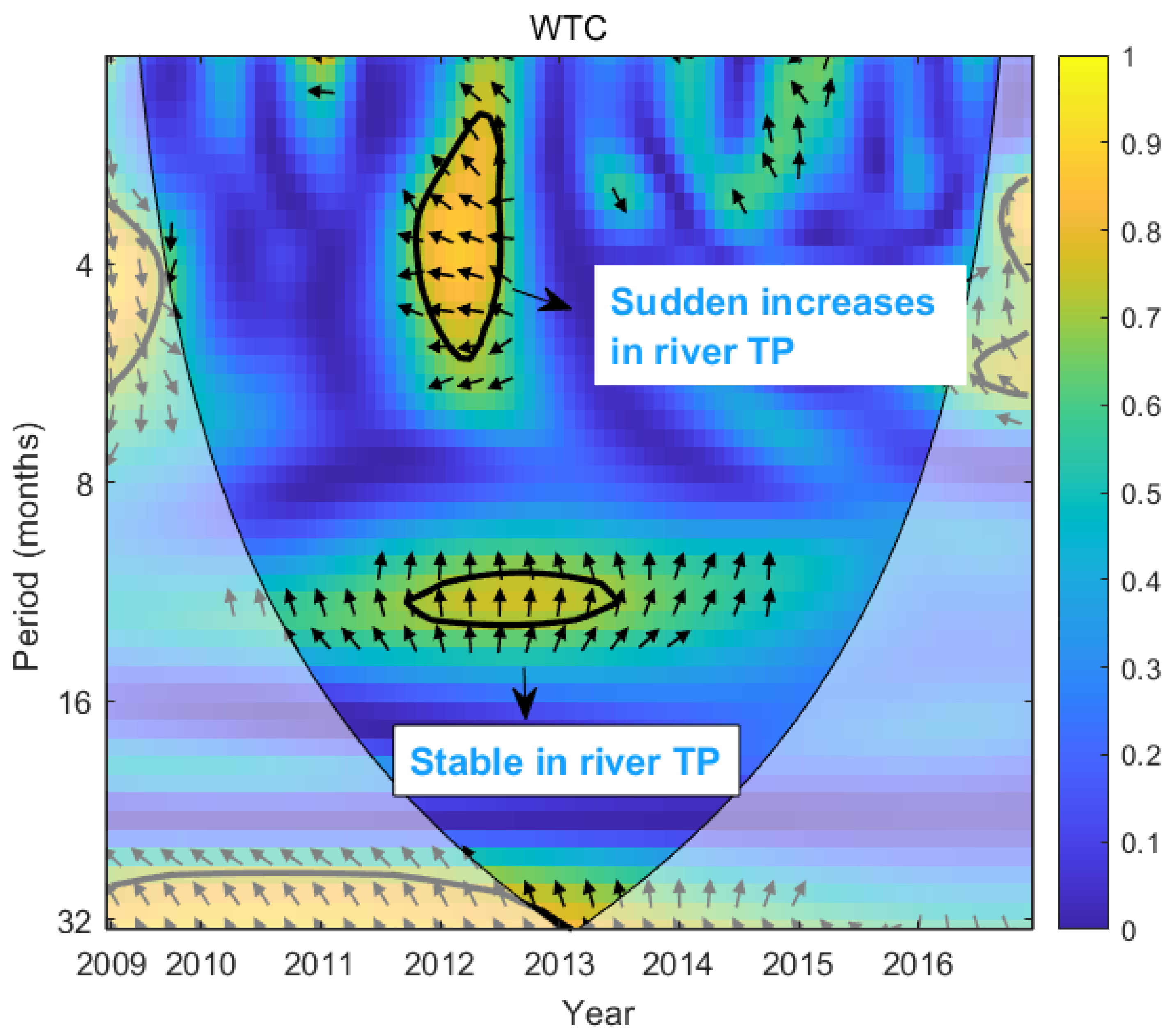
3.5. Cross Wavelet Transform and Wavelet Coherence Analysis
3.5.1. Common Periodic Fluctuations at Different Time Scales
3.5.2. Phase Relationship
4. Discussion
4.1. Differences in TP Fluctuation Cycles Between Reservoir and Inflowing Rivers
4.2. Sensitive Time Scales of Reservoir TP Response to River TP Under Varying Conditions
4.3. Determination of Monitoring Time Scales
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TP | Total phosphorus |
| CWT | Wavelet transform |
| XWT | Cross wavelet transform |
| WTC | Wavelet coherence |
References
- Di Baldassarre, G.; Wanders, N.; AghaKouchak, A.; Kuil, L.; Rangecroft, S.; Veldkamp, T.I.E.; Garcia, M.; Van Oel, P.R.; Breinl, K.; Van Loon, A.F. Water shortages worsened by reservoir effects. Nat. Sustain. 2018, 1, 617–622. [Google Scholar] [CrossRef]
- Kong, X.; Ghaffar, S.; Determann, M.; Friese, K.; Jomaa, S.; Mi, C.; Shatwell, T.; Rinke, K.; Rode, M. Reservoir water quality deterioration due to deforestation emphasizes the indirect effects of global change. Water Res. 2022, 221, 118721. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Shen, S.-L.; Zhou, A. Indices and models of surface water quality assessment: Review and perspectives. Environ. Pollut. 2022, 308, 119611. [Google Scholar] [CrossRef]
- Mullungal, M.N.; Thalayappil, S.; Peediyakkathodi, S.; Salas, P.M.; Sujatha, C.H.; Kumar, C.S.R. Vertical Distribution of Phosphorous Fractions and Bioavailability of the Nutrient in the Southern Indian Ocean. Int. J. Environ. Res. 2022, 16, 77. [Google Scholar] [CrossRef]
- Varol, M. Spatio-temporal changes in surface water quality and sediment phosphorus content of a large reservoir in Turkey. Environ. Pollut. 2020, 259, 113860. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Y.; Wang, T.; Wang, Z.; Hu, S.; Gao, S. Dynamic spatiotemporal change of net anthropogenic phosphorus inputs and its response of water quality in the Liao river basin. Chemosphere 2023, 331, 138757. [Google Scholar] [CrossRef]
- Bao, Y.; Zhang, D.; Wang, Y.; Yang, Z.; Hu, P.; Chen, H.; Nie, B.; Liu, X.; Huang, W.; Li, J.; et al. Analysis of nitrogen migration and transformation in the typical deep and large reservoir of the Lancang River—Evidence from nitrogen and oxygen isotopes. J. Hydrol. 2024, 640, 131701. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, C.; Wang, L.; Li, Y.; Zhang, W.; Niu, L.; Zhang, H.; Wang, L. Nitrogen cycling processes and the role of multi-trophic microbiota in dam-induced river-reservoir systems. Water Res. 2021, 206, 117730. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Xu, C.; Yang, S.; Li, B. Investigating the effects of inflow river water quality on lake nutrient-concentration variations: A case study in Gehu Lake, China. Mar. Freshw. Res. 2023, 74, 865–876. [Google Scholar] [CrossRef]
- Tang, X.; Li, R.; Wang, D.; Jing, Z.; Zhang, W. Reservoir flood regulation affects nutrient transport through altering water and sediment conditions. Water Res. 2023, 233, 119728. [Google Scholar] [CrossRef]
- Ibáñez, C.; Caiola, N.; Barquín, J.; Belmar, O.; Benito-Granell, X.; Casals, F.; Fennessy, S.; Hughes, J.; Palmer, M.; Peñuelas, J.; et al. Ecosystem-level effects of re-oligotrophication and N:P imbalances in rivers and estuaries on a global scale. Glob. Change Biol. 2023, 29, 1248–1266. [Google Scholar] [CrossRef]
- Whitney, C.T.; Wollheim, W.M.; Gold, A.J.; Buonpane, J.M. Small Reservoirs as Nitrogen Transformers: Accounting for Seasonal Variability in Inorganic and Organic Nitrogen Processing. J. Geophys. Res. Biogeosci. 2023, 128, e2023JG007635. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, Y.; Huang, X.; Liu, Y.; Guan, M.; Tian, Y. Hydrological conditions can change the effects of major nutrients and dissolved organic matter on phytoplankton community dynamics in a eutrophic river. J. Hydrol. 2024, 628, 130503. [Google Scholar] [CrossRef]
- Montefiore, L.R.; Kaplan, D.; Phlips, E.J.; Milbrandt, E.C.; Arias, M.E.; Morrison, E.; Nelson, N.G. Downstream Nutrient Concentrations Depend on Watershed Inputs More Than Reservoir Releases in a Highly Engineered Watershed. Water Resour. Res. 2024, 60, e2023WR035590. [Google Scholar] [CrossRef]
- Zhi, X.; Xu, Y.; Chen, L.; Chen, S.; Zhang, Z.; Meng, X.; Shen, Z. The synergistic response between temperature, flow field and nutrients in the tributary disturbed by the Three Gorges reservoir. J. Hydrol. 2024, 639, 131636. [Google Scholar] [CrossRef]
- Kim, D.; Lim, J.-H.; Chun, Y.; Nayna, O.K.; Begum, M.S.; Park, J.-H. Phytoplankton nutrient use and CO2 dynamics responding to long-term changes in riverine N and P availability. Water Res. 2021, 203, 117510. [Google Scholar] [CrossRef]
- Yang, H.F.; Zhu, Q.Y.; Liu, J.A.; Zhang, Z.L.; Yang, S.L.; Shi, B.W.; Zhang, W.X.; Wang, Y.P. Historic changes in nutrient fluxes from the Yangtze River to the sea: Recent response to catchment regulation and potential linkage to maritime red tides. J. Hydrol. 2023, 617, 129024. [Google Scholar] [CrossRef]
- Marcé, R.; Moreno-Ostos, E.; Armengol, J. The role of river inputs on the hypolimnetic chemistry of a productive reservoir: Implications for management of anoxia and total phosphorus internal loading. Lake Reserv. Manag. 2008, 24, 87–98. [Google Scholar] [CrossRef]
- Sunardi, S.; Ariyani, M.; Agustian, M.; Withaningsih, S.; Parikesit, P.; Juahir, H.; Ismail, A.; Abdoellah, O.S. Water corrosivity of polluted reservoir and hydropower sustainability. Sci. Rep. 2020, 10, 11110. [Google Scholar] [CrossRef]
- Tefs, A.A.G.; Stadnyk, T.A.; Koenig, K.A.; Déry, S.J.; MacDonald, M.K.; Slota, P.; Crawford, J.; Hamilton, M. Simulating river regulation and reservoir performance in a continental-scale hydrologic model. Environ. Model. Softw. 2021, 141, 105025. [Google Scholar] [CrossRef]
- Araújo, F.G.; Costa De Azevedo, M.C.; Lima Ferreira, M.D.N. Seasonal changes and spatial variation in the water quality of a eutrophic tropical reservoir determined by the inflowing river. Lake Reserv. Manag. 2011, 27, 343–354. [Google Scholar] [CrossRef]
- Carey, C.C.; Hanson, P.C.; Lathrop, R.C.; St. Amand, A.L. Using wavelet analyses to examine variability in phytoplankton seasonal succession and annual periodicity. J. Plankton Res. 2016, 38, 27–40. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B. Using discrete wavelet transforms to analyze trends in streamflow and precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Q.; Recknagel, F.; Li, R. Wavelet analysis of time-lags in the response of cyanobacteria growth to water quality conditions in Lake Taihu, China. Ecol. Inform. 2014, 22, 52–57. [Google Scholar] [CrossRef]
- Li, W.; Qin, B.; Zhang, Y. Multi-temporal scale characteristics of algae biomass and selected environmental parameters based on wavelet analysis in Lake Taihu, China. Hydrobiologia 2015, 747, 189–199. [Google Scholar] [CrossRef]
- Yin, J.; Xia, J.; Xia, Z.; Cai, W.; Liu, Z.; Xu, K.; Wang, Y.; Zhang, R.; Dong, X. Temporal Variation and Spatial Distribution in the Water Environment Helps Explain Seasonal Dynamics of Zooplankton in River-Type Reservoir. Sustainability 2022, 14, 13719. [Google Scholar] [CrossRef]
- Zhu, S.; Dong, Z.; Yang, B.; Zeng, G.; Liu, Y.; Zhou, Y.; Meng, J.; Wu, S.; Shao, Y.; Yang, J.; et al. Spatial Distribution, Source Identification, and Potential Ecological Risk Assessment of Heavy Metal in Surface Sediments from River-Reservoir System in the Feiyun River Basin, China. Int. J. Environ. Res. Public Health 2022, 19, 14944. [Google Scholar] [CrossRef]
- Yates, F. The Analysis of Multiple Classifications with Unequal Numbers in the Different Classes. J. Am. Stat. Assoc. 1934, 29, 51–66. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, Q.; Kuczyńska-Kippen, N.; Gao, X. An Ensemble Kalman Filter approach to assess the effects of hydrological variability, water diversion, and meteorological forcing on the total phosphorus concentration in a shallow reservoir. Sci. Total Environ. 2020, 724, 138215. [Google Scholar] [CrossRef]
- Weigand, S.; Bol, R.; Reichert, B.; Graf, A.; Wiekenkamp, I.; Stockinger, M.; Luecke, A.; Tappe, W.; Bogena, H.; Puetz, T.; et al. Spatiotemporal Analysis of Dissolved Organic Carbon and Nitrate in Waters of a Forested Catchment Using Wavelet Analysis. Vadose Zone J. 2017, 16, 1–2. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, Q.; Song, S.; Lu, Y.; Yang, S.; Fang, Z.; Shi, Z. A climate-water quality assessment framework for quantifying the contributions of climate change and human activities to water quality variations. J. Environ. Manag. 2023, 333, 117441. [Google Scholar] [CrossRef]
- Guo, W.; He, N.; Ban, X.; Wang, H. Multi-scale variability of hydrothermal regime based on wavelet analysis—The middle reaches of the Yangtze River, China. Sci. Total Environ. 2022, 841, 156598. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wen, Y.; Lai, H.; Zhao, Q. Drought response analysis based on cross wavelet transform and mutual entropy. Alex. Eng. J. 2020, 59, 1223–1231. [Google Scholar] [CrossRef]
- Yerdelen, C.; Abdelkader, M.; Eris, E. Assessment of drought in SPI series using continuous wavelet analysis for Gediz Basin, Turkey. Atmos. Res. 2021, 260, 105687. [Google Scholar] [CrossRef]
- Dong, H.; Yu, G.; Lin, T.; Li, Y. An energy-concentrated wavelet transform for time-frequency analysis of transient signal. Signal Process. 2023, 206, 108934. [Google Scholar] [CrossRef]
- Robinson, K.-L.; Bogena, H.R.; Wang, Q.; Cammeraat, E.; Bol, R. Effects of deforestation on dissolved organic carbon and nitrate in catchment stream water revealed by wavelet analysis. Front. Water 2022, 4, 1003693. [Google Scholar] [CrossRef]
- Wang, Q.; Qu, Y.; Robinson, K.-L.; Bogena, H.; Graf, A.; Vereecken, H.; Tietema, A.; Bol, R. Deforestation alters dissolved organic carbon and sulfate dynamics in a mountainous headwater catchment—A wavelet analysis. Front. For. Glob. Chang. 2022, 5, 1044447. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- A Practical Guide to Wavelet Analysis in: Bulletin of the American Meteorological Society Volume 79 Issue 1. 1998. Available online: https://journals.ametsoc.org/view/journals/bams/79/1/1520-0477_1998_079_0061_apgtwa_2_0_co_2.xml (accessed on 17 February 2025).
- Damos, P.; Caballero, P. Detecting seasonal transient correlations between populations of the West Nile Virus vector Culex sp. and temperatures with wavelet coherence analysis. Ecol. Inform. 2021, 61, 101216. [Google Scholar] [CrossRef]
- Broday, D.M. Studying the Time Scale Dependence of Environmental Variables Predictability Using Fractal Analysis. Environ. Sci. Technol. 2010, 44, 4629–4634. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Zha, W.; Huo, S.; Niu, L.; Zhang, X. Spatiotemporal variation of phosphorus in the Three Gorges Reservoir: Impact of upstream cascade reservoirs. Environ. Sci. Pollut. Res. 2022, 29, 56739–56749. [Google Scholar] [CrossRef] [PubMed]
- Howarth, R.W.; Chan, F.; Swaney, D.P.; Marino, R.M.; Hayn, M. Role of external inputs of nutrients to aquatic ecosystems in determining prevalence of nitrogen vs. phosphorus limitation of net primary productivity. Biogeochemistry 2021, 154, 293–306. [Google Scholar] [CrossRef]
- Haynes, R.J.; Naidu, R. Phosphorus—An essential input for agriculture yet a key pollutant of surface waters. In Inorganic Contaminants and Radionuclides; Elsevier: Amsterdam, The Netherlands, 2024; pp. 405–426. ISBN 978-0-323-90400-1. [Google Scholar]
- Zhang, P.; Peng, C.; Zhang, J.; Zhang, J.; Chen, J.; Zhao, H. Long-Term Harmful Algal Blooms and Nutrients Patterns Affected by Climate Change and Anthropogenic Pressures in the Zhanjiang Bay, China. Front. Mar. Sci. 2022, 9, 849819. [Google Scholar] [CrossRef]
- Hejzlar, J.; Šámalová, K.; Boers, P.; Kronvang, B. Modelling Phosphorus Retention in Lakes and Reservoirs. Water Air Soil Pollut. Focus 2006, 6, 487–494. [Google Scholar] [CrossRef]
- Li, C.; Zhang, P.; Zhu, G.; Chen, C.; Wang, Y.; Zhu, M.; Xu, H.; Jiang, C.; Zou, W.; Shi, P.; et al. Dynamics of nitrogen and phosphorus profile and its driving forces in a subtropical deep reservoir. Environ. Sci. Pollut. Res. 2022, 29, 27738–27748. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, M.C.H.; Bowden, W.B.; Shanley, J.B.; Vermilyea, A.; Wemple, B.; Schroth, A.W. Using in situ UV-Visible spectrophotometer sensors to quantify riverine phosphorus partitioning and concentration at a high frequency. Limnol. Ocean. Methods 2018, 16, 840–855. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Shi, K.; Zhu, G.; Zhou, Y.; Zhang, Y.; Guo, Y. Monitoring spatiotemporal variations in nutrients in a large drinking water reservoir and their relationships with hydrological and meteorological conditions based on Landsat 8 imagery. Sci. Total Environ. 2017, 599–600, 1705–1717. [Google Scholar] [CrossRef]
- Jiang, J.; Zheng, Y.; Pang, T.; Wang, B.; Chachan, R.; Tian, Y. A comprehensive study on spectral analysis and anomaly detection of river water quality dynamics with high time resolution measurements. J. Hydrol. 2020, 589, 125175. [Google Scholar] [CrossRef]
- Hughes, S.E.; Marion, J.W. Cyanobacteria Growth in Nitrogen- & Phosphorus-Spiked Water from a Hypereutrophic Reservoir in Kentucky, USA. J. Environ. Prot. 2021, 12, 75–89. [Google Scholar] [CrossRef]
- Garcia, M.; Ridolfi, E.; Di Baldassarre, G. The interplay between reservoir storage and operating rules under evolving conditions. J. Hydrol. 2020, 590, 125270. [Google Scholar] [CrossRef]
- Dai, H.; Mao, J.; Jiang, D.; Wang, L. Longitudinal Hydrodynamic Characteristics in Reservoir Tributary Embayments and Effects on Algal Blooms. PLoS ONE 2013, 8, e68186. [Google Scholar] [CrossRef] [PubMed]
- Song, Y. Hydrodynamic impacts on algal blooms in reservoirs and bloom mitigation using reservoir operation strategies: A review. J. Hydrol. 2023, 620, 129375. [Google Scholar] [CrossRef]
- Lu, T.; Chen, N.; Duan, S.; Chen, Z.; Huang, B. Hydrological controls on cascade reservoirs regulating phosphorus retention and downriver fluxes. Environ. Sci. Pollut. Res. 2016, 23, 24166–24177. [Google Scholar] [CrossRef]
- Withers, P.J.A.; Jarvie, H.P. Delivery and cycling of phosphorus in rivers: A review. Sci. Total Environ. 2008, 400, 379–395. [Google Scholar] [CrossRef] [PubMed]
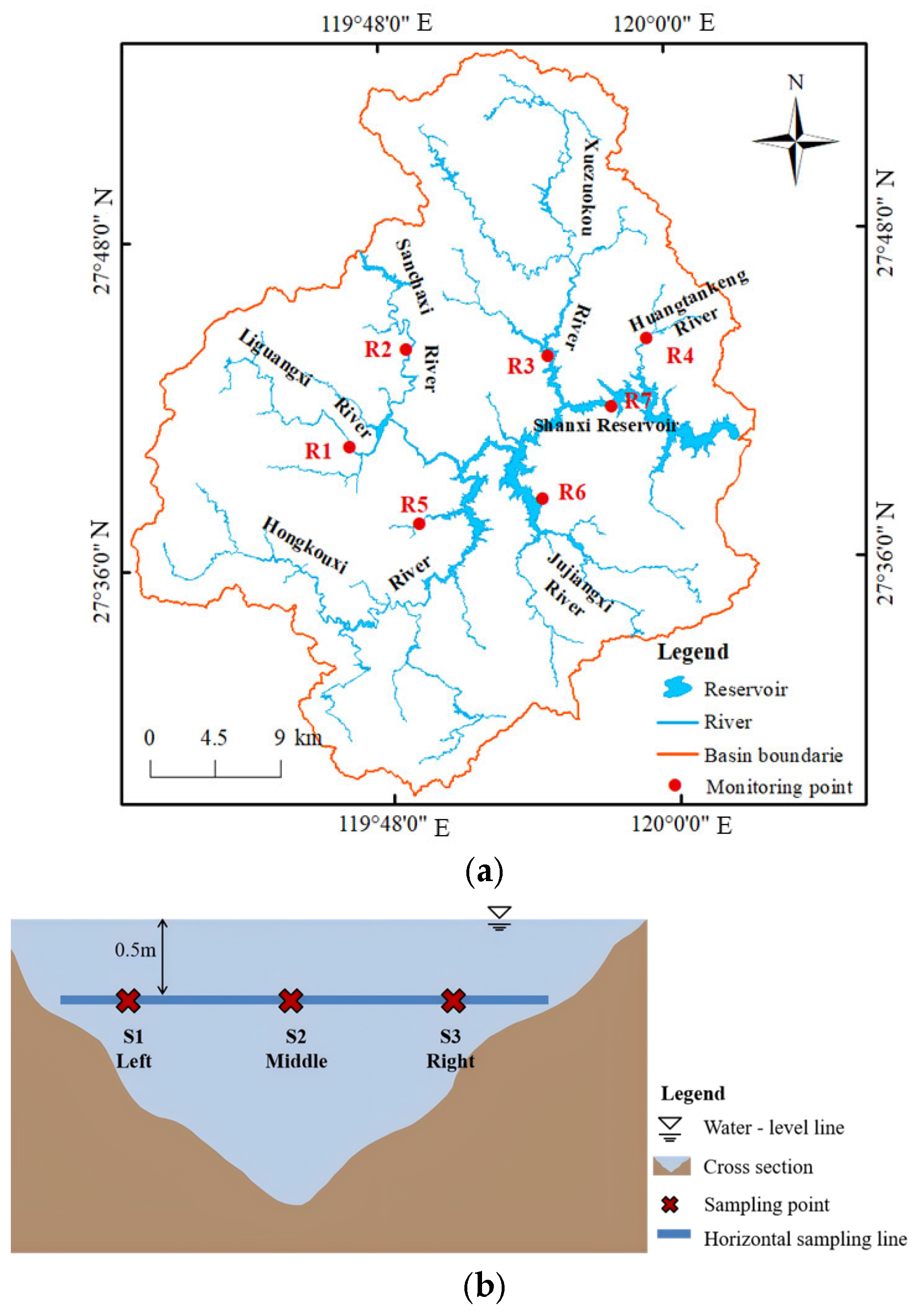

| Site Number | Name of River | Annual Runoff Volume (m3/s) | Weight Coefficient |
|---|---|---|---|
| R1 | Liguangxi River | 1.77 | 0.12 |
| R2 | Sanchaxi River | 3.13 | 0.21 |
| R3 | Xuezuokou River | 3.37 | 0.22 |
| R4 | Huangtankeng River | 0.63 | 0.04 |
| R5 | Hongkouxi River | 4.18 | 0.28 |
| R6 | Jujiangxi River | 2.04 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xia, J.; Li, M.; Bol, R.; Wang, Q.; Wang, Y.; Zu, J.; Wang, Q.; Ji, S.; Zhan, H. Multi-Scale Analysis Based on Wavelet Transform of Reservoir and River Total Phosphorus Correlation and Determination of Monitoring Time Scales. Water 2025, 17, 712. https://doi.org/10.3390/w17050712
Liu Z, Xia J, Li M, Bol R, Wang Q, Wang Y, Zu J, Wang Q, Ji S, Zhan H. Multi-Scale Analysis Based on Wavelet Transform of Reservoir and River Total Phosphorus Correlation and Determination of Monitoring Time Scales. Water. 2025; 17(5):712. https://doi.org/10.3390/w17050712
Chicago/Turabian StyleLiu, Zewen, Jihong Xia, Mengshi Li, Roland Bol, Qiqi Wang, Yue Wang, Jiayi Zu, Qihua Wang, Shuyi Ji, and Hongli Zhan. 2025. "Multi-Scale Analysis Based on Wavelet Transform of Reservoir and River Total Phosphorus Correlation and Determination of Monitoring Time Scales" Water 17, no. 5: 712. https://doi.org/10.3390/w17050712
APA StyleLiu, Z., Xia, J., Li, M., Bol, R., Wang, Q., Wang, Y., Zu, J., Wang, Q., Ji, S., & Zhan, H. (2025). Multi-Scale Analysis Based on Wavelet Transform of Reservoir and River Total Phosphorus Correlation and Determination of Monitoring Time Scales. Water, 17(5), 712. https://doi.org/10.3390/w17050712






