Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data
Abstract
1. Introduction
2. Methodology
2.1. DBSCAN Algorithm
2.1.1. Calculating the Sensitivity of Parameter Settings
2.1.2. Limitations of 3D Data Anomaly Detection
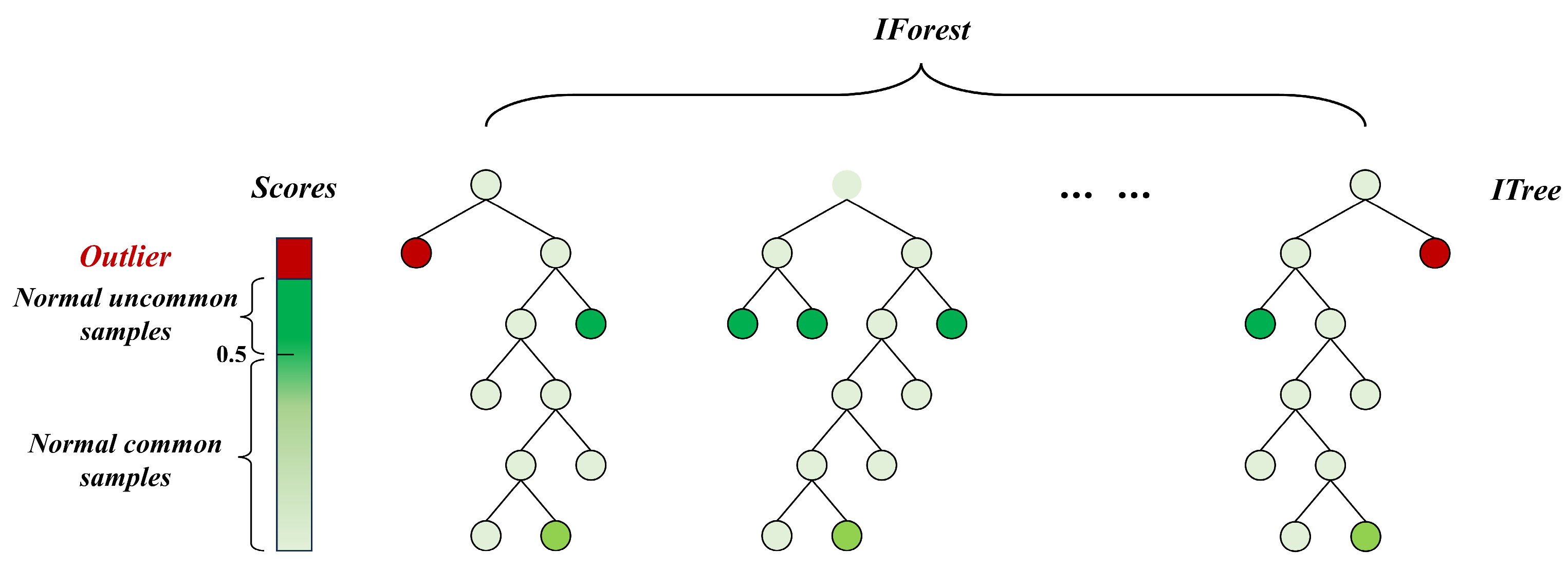
2.2. Isolated Forest Algorithm
- where is the path length of node x in the isolated tree from the root to the leaf node. When the sample size of the dataset is n, the expected value of the average path length of the points in the isolated tree is [23]
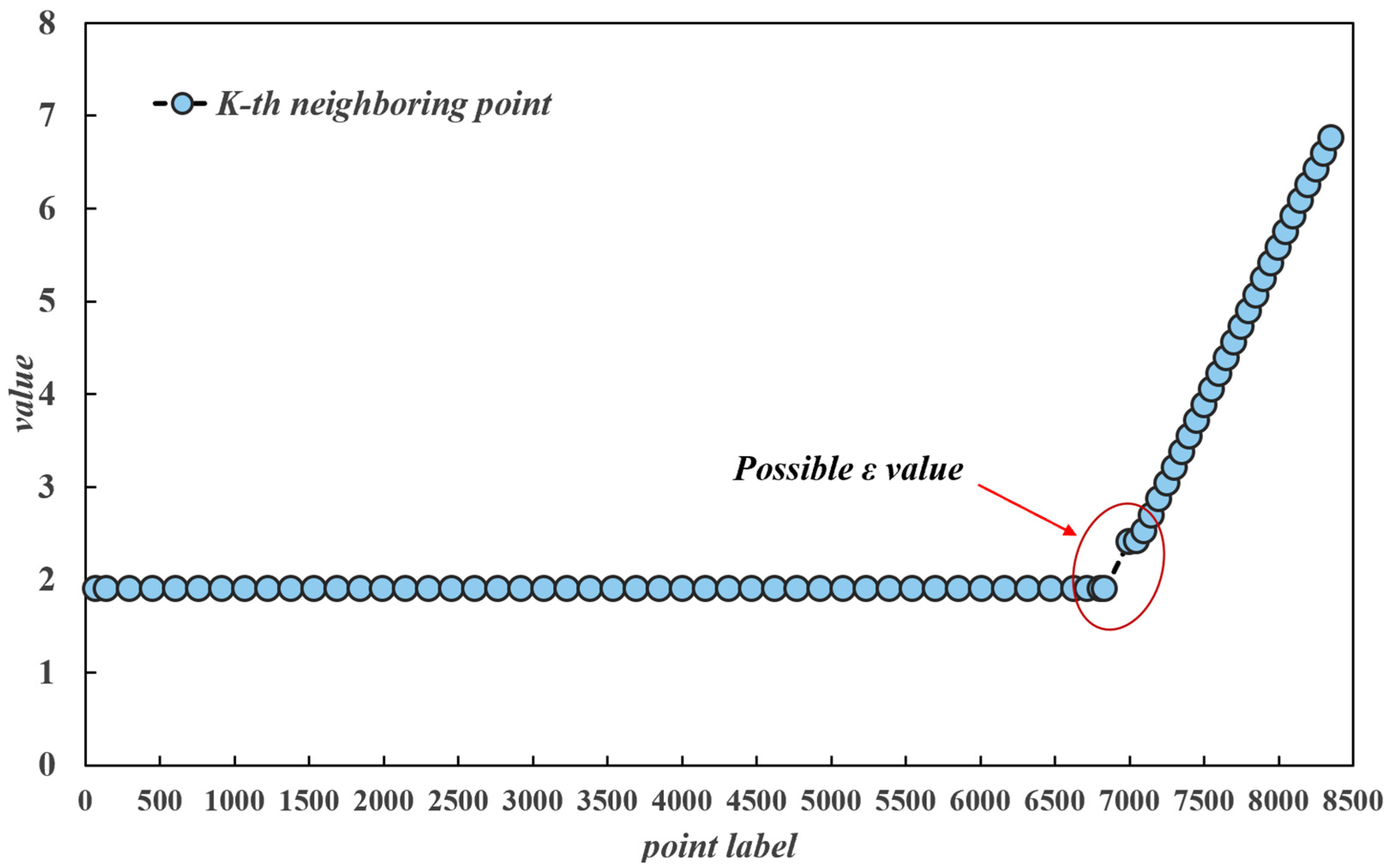
2.3. K-Distance Chart
2.4. Kd-Tree
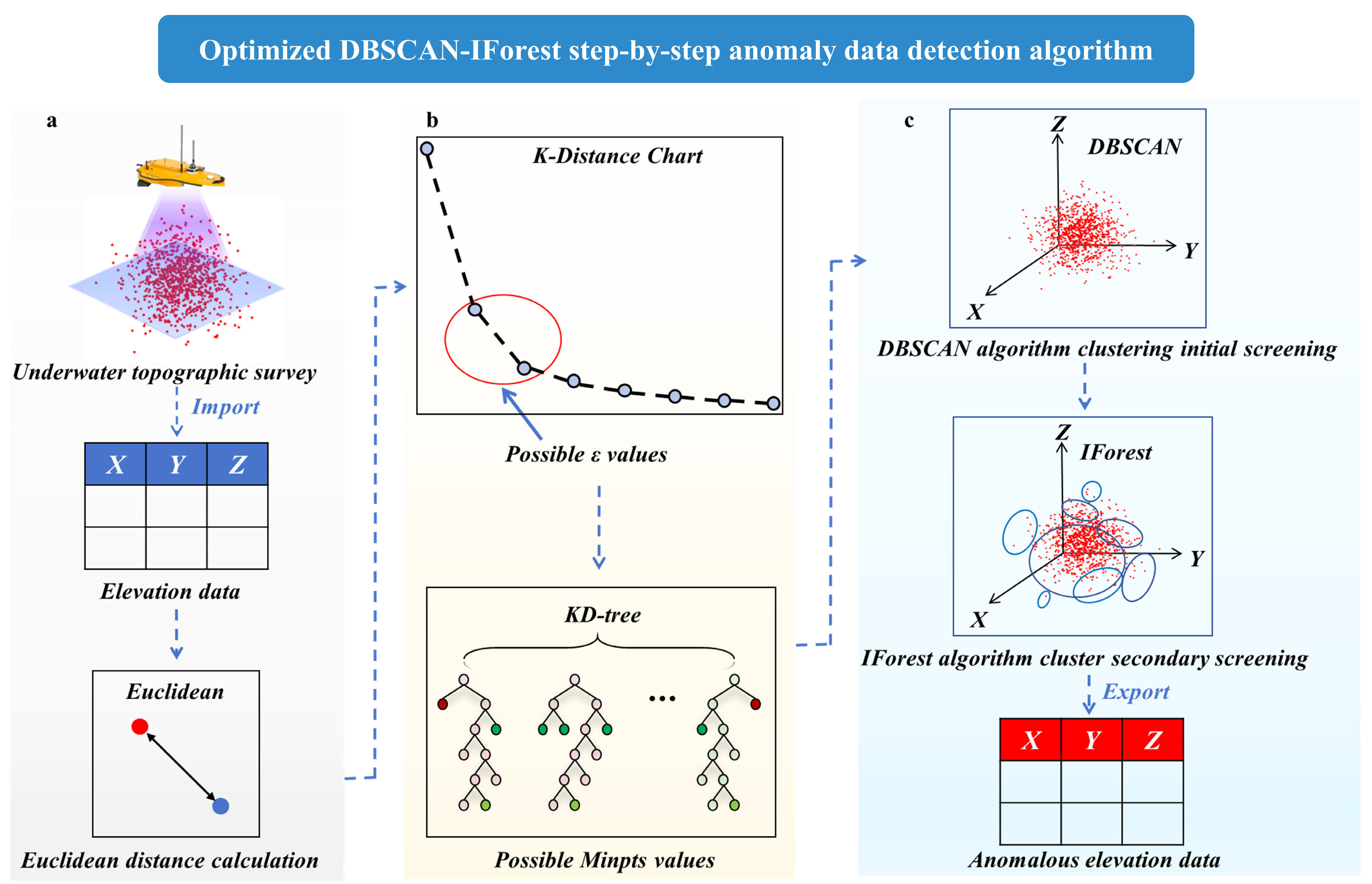
2.5. Constructing the Model for the Anomaly Detection Algorithm for Underwater Terrain Data
- (1)
- ε parameter determination. For a given dataset, the distance from each data point to its kth nearest neighbour is calculated, and each point in the dataset is traversed, after which the kth-nearest-neighbour distances of all the data points are sorted in ascending order to obtain an ordered distance sequence. The sorted distance sequence is used as the vertical axis of the K-distance graph, and the index of the data points is used as the horizontal axis. Considering that the underwater terrain data are three-dimensional and exist in three-dimensional space, the Euclidean distance is taken as the distance metric, which is calculated by the following formula [25]:
- (2)
- Minpts parameter determination. After the value of ε is calculated, the Kd-tree is used to find the optimal Minpts value. Considering the interference of artificially given search thresholds, range search is used for the Kd-tree. First, the Kd-tree is constructed as the spatial index of the data, and each point is queried to obtain the set of its neighbouring points within the radius ε, i.e., the set of points that satisfy ε; the number of neighbouring points is . Then, the statistical analysis method uses the value of Minpts with the largest frequency value N.
- (3)
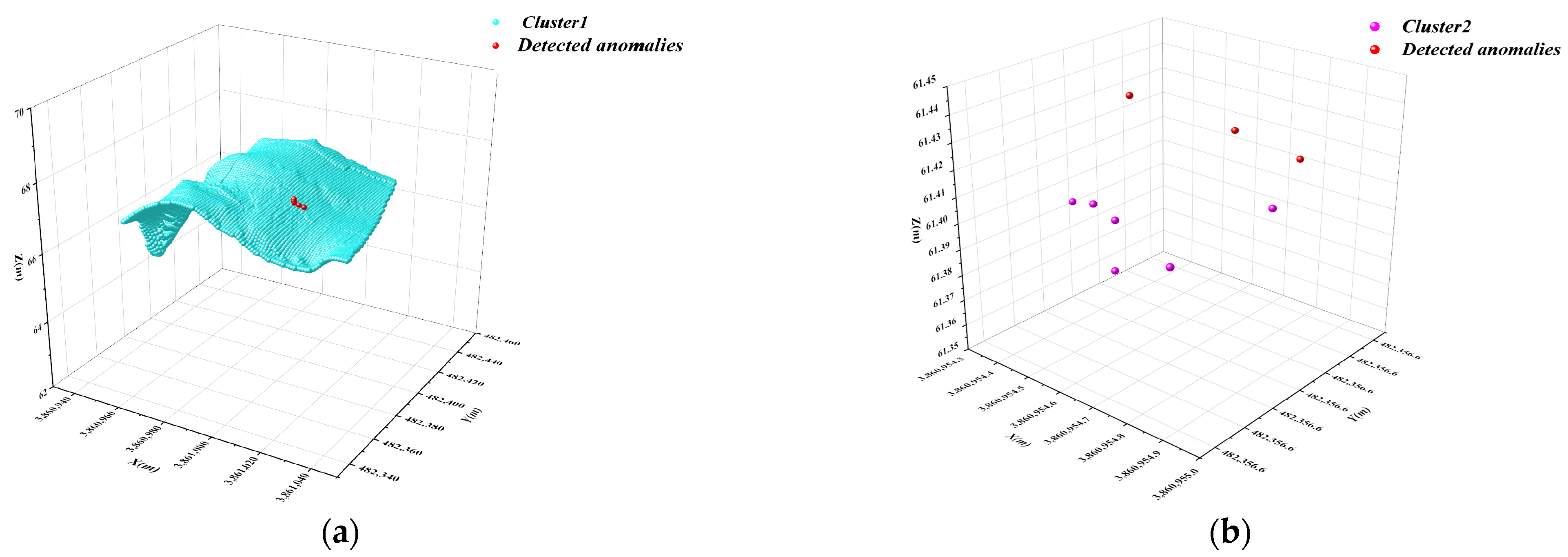
- First-round screening by the DBSCAN algorithm. In the screening by this algorithm, the dataset is divided into numerous subclusters, and the values in each cluster that do not satisfy the screening conditions of the DBSCAN algorithm are marked as anomalies. After this calculation, the original dataset is divided into numerous subclusters, and local outliers in each cluster, which have fewer than Minpts neighbours within the radius, are identified.
- (4)
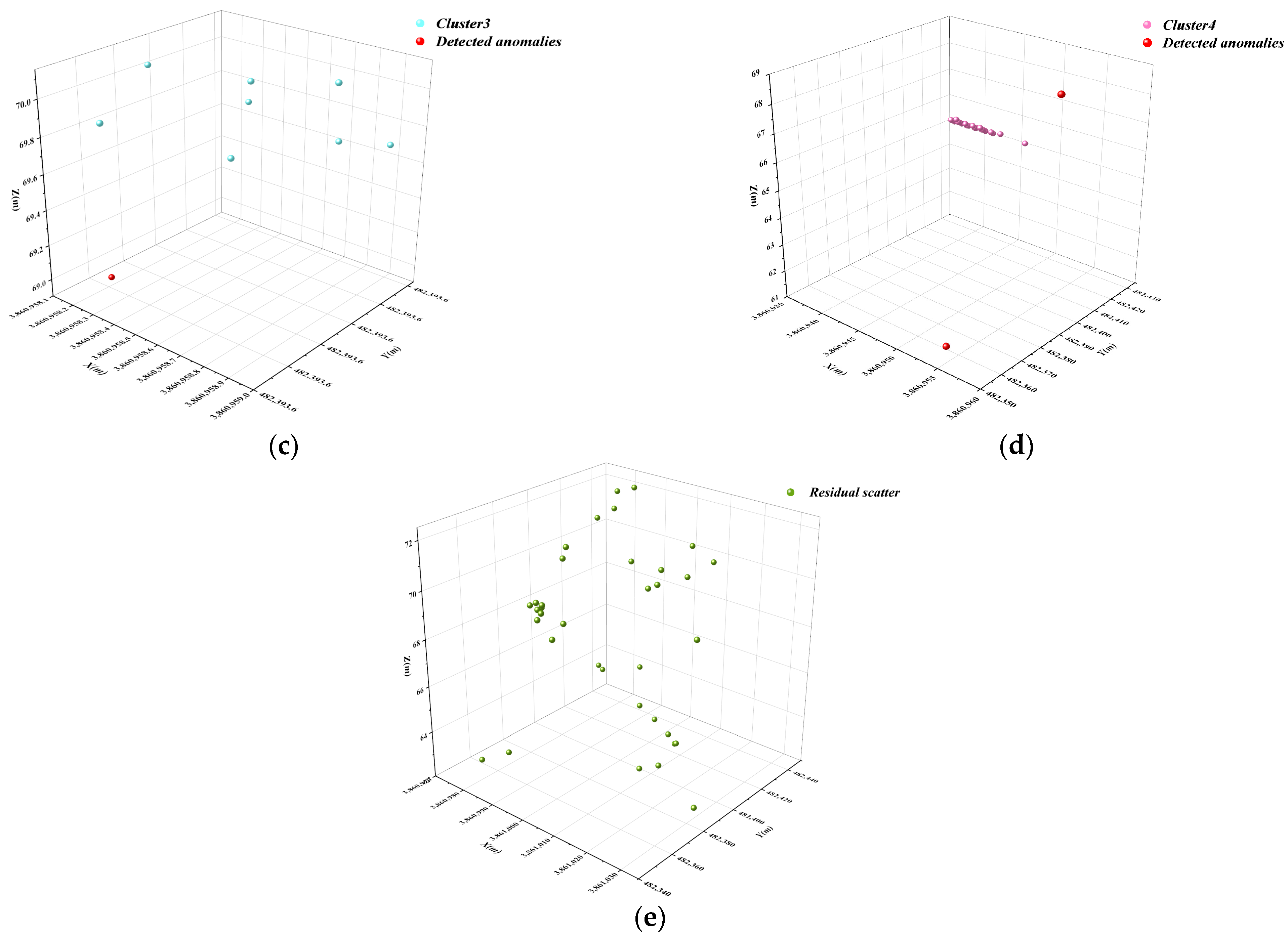
- Secondary detection by the IForest algorithm. Because the DBSCAN algorithm is unable to identify regional outliers with more than Minpts neighbours, the isolated forest algorithm is subsequently applied to the model to carry out secondary screening of the subclusters; this completes the step-by-step anomaly detection process, and the outliers obtained from these two steps of detection are combined to obtain the final results of anomaly detection.
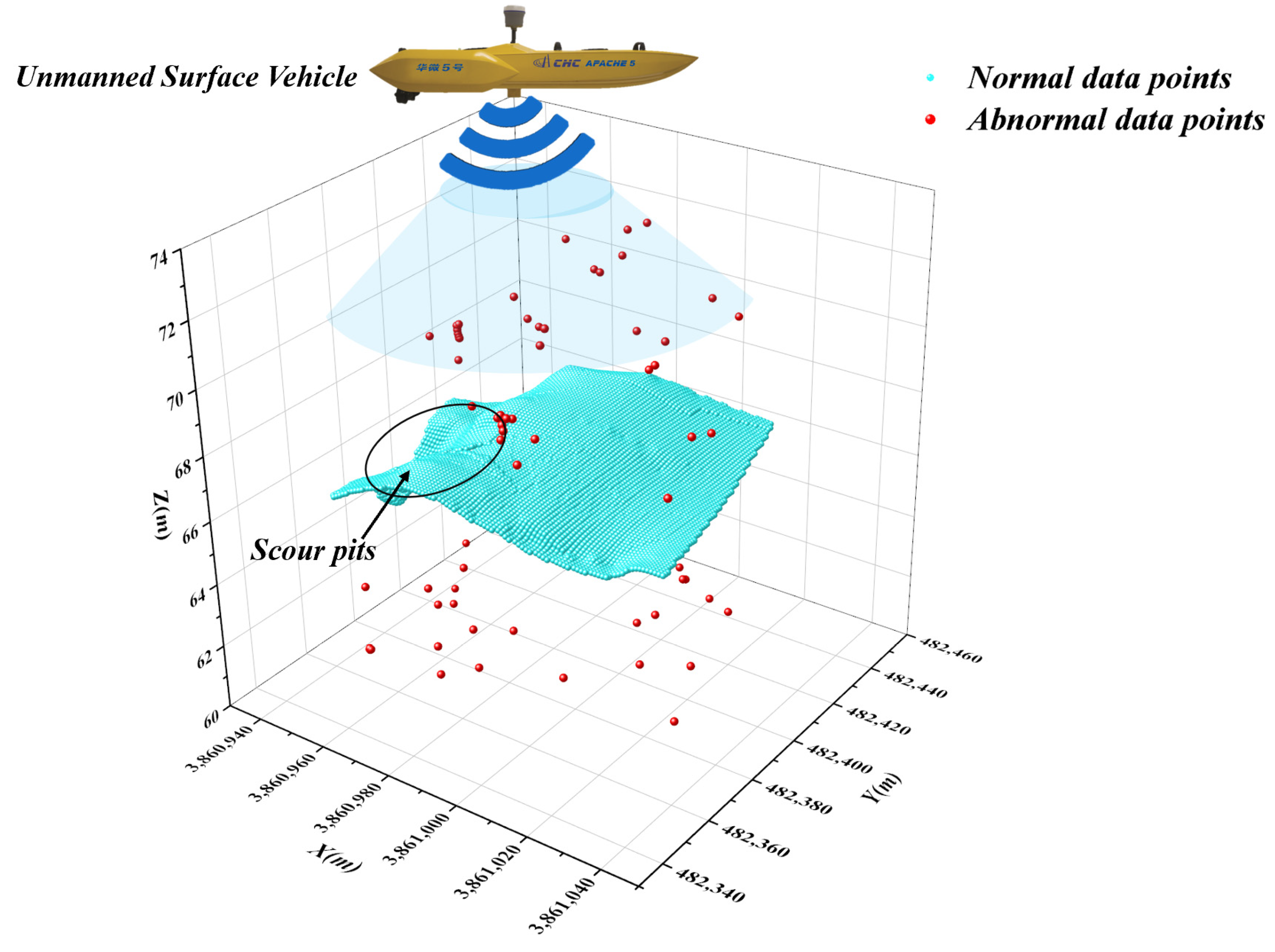
2.6. Data Acquisition
3. Results and Analyses
3.1. Optimisation of the DBSCAN Algorithm Parameters
3.2. Underwater Terrain Data Clustering and Primary Screening with DBSCAN
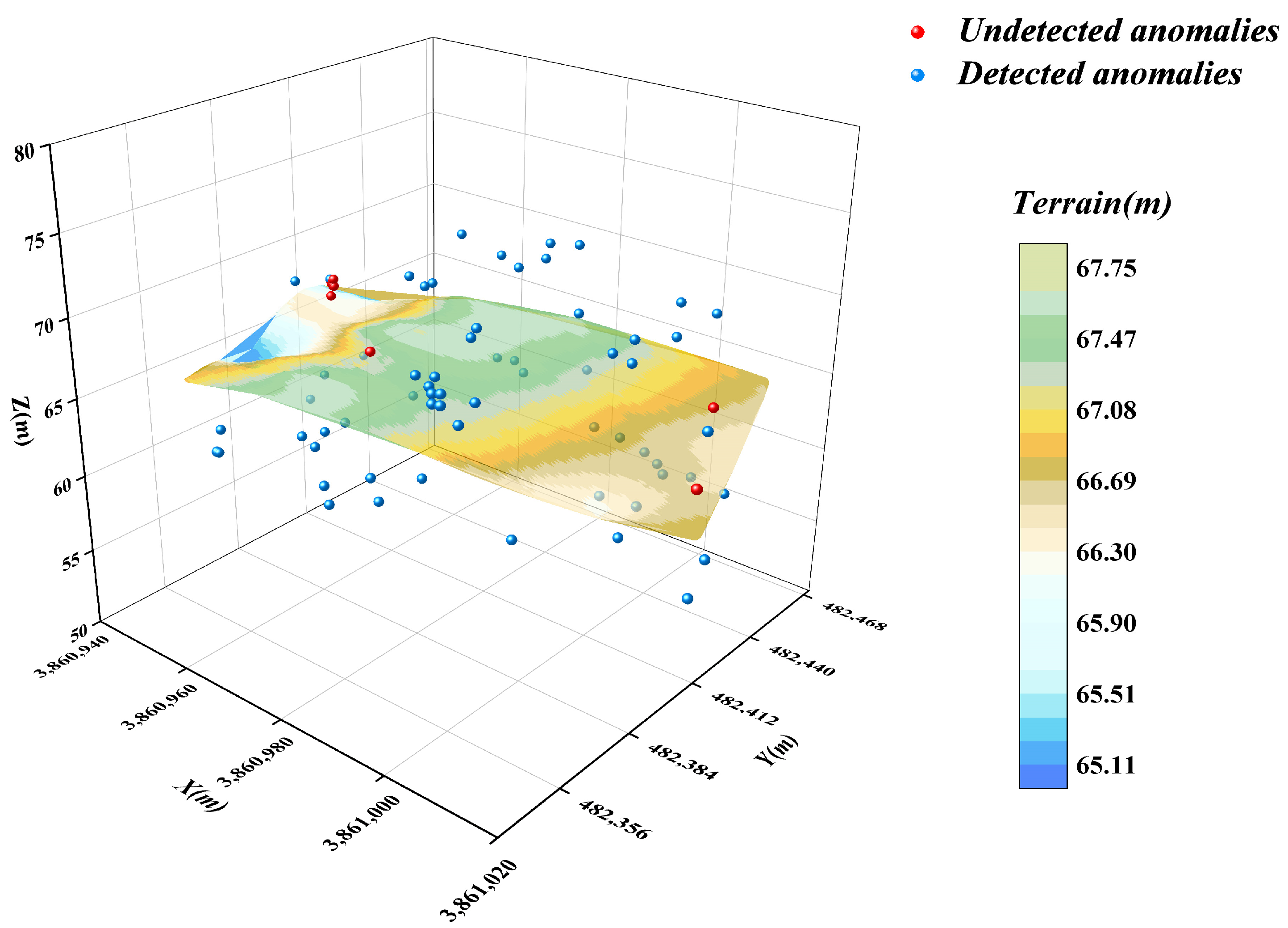
3.3. Isolated Forest Algorithm for Secondary Anomaly Screening of Subcluster Data
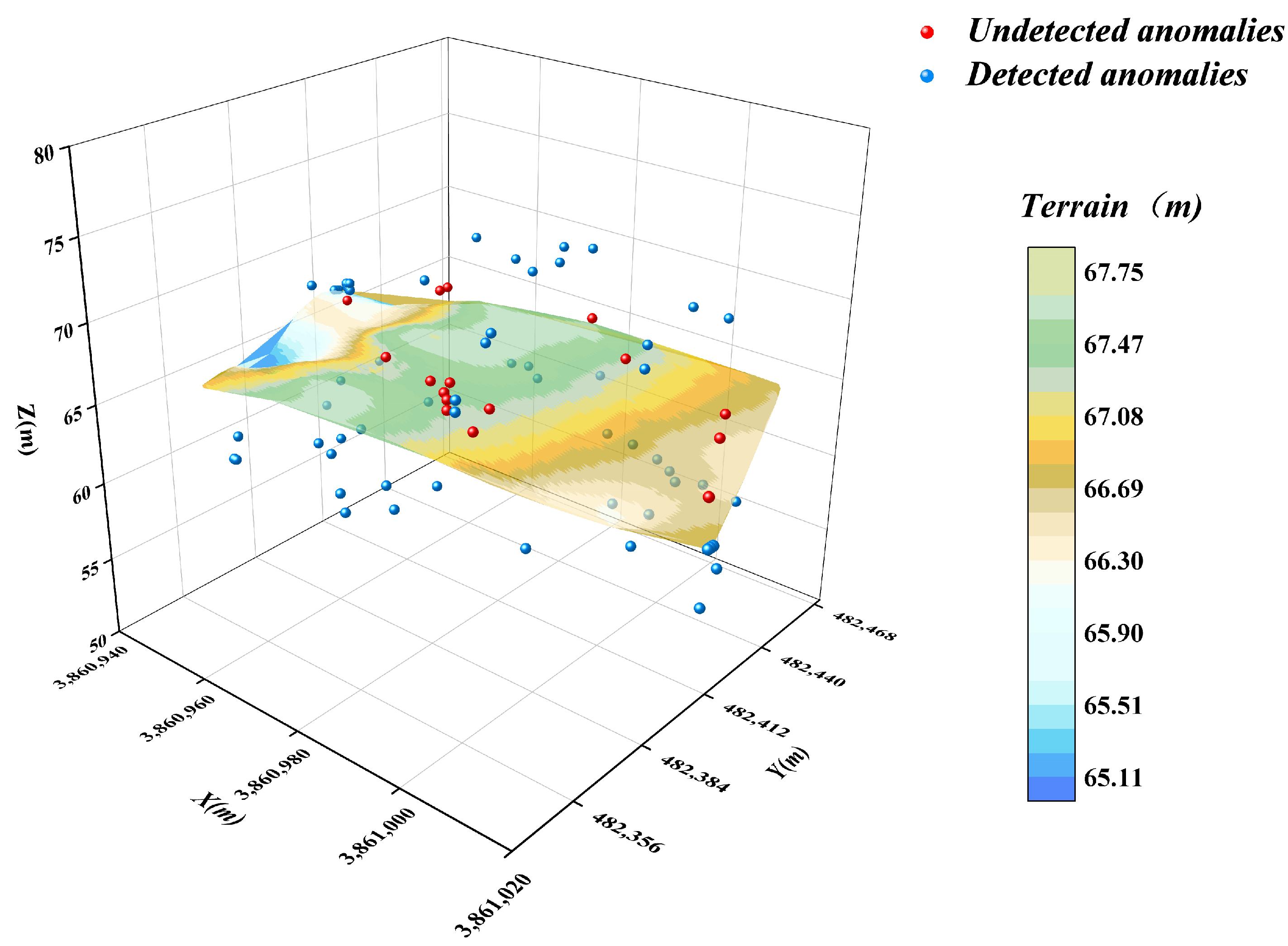
4. Detection Effectiveness of Relevant Anomaly Detection Methods
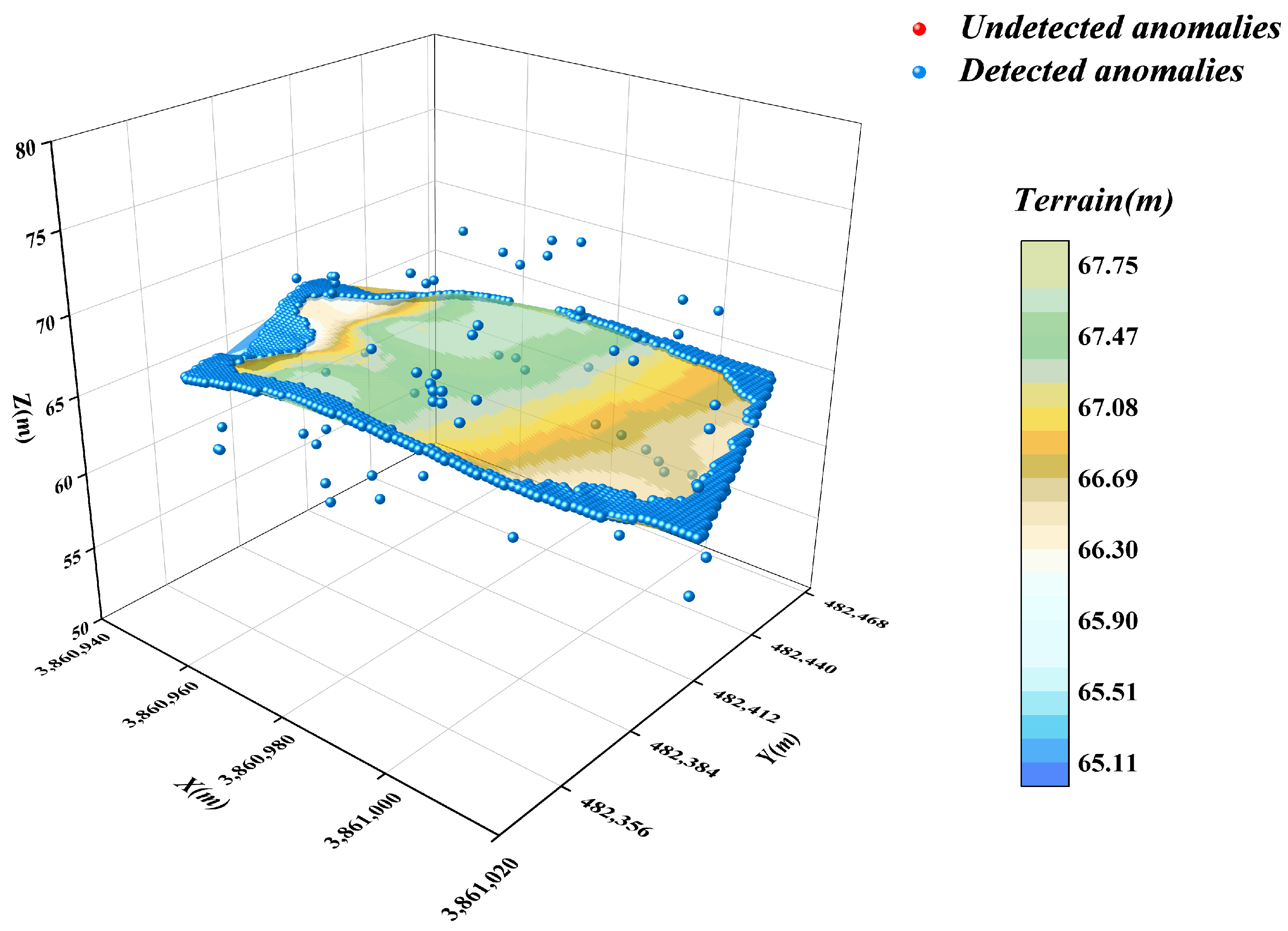
4.1. DBSCAN Algorithm
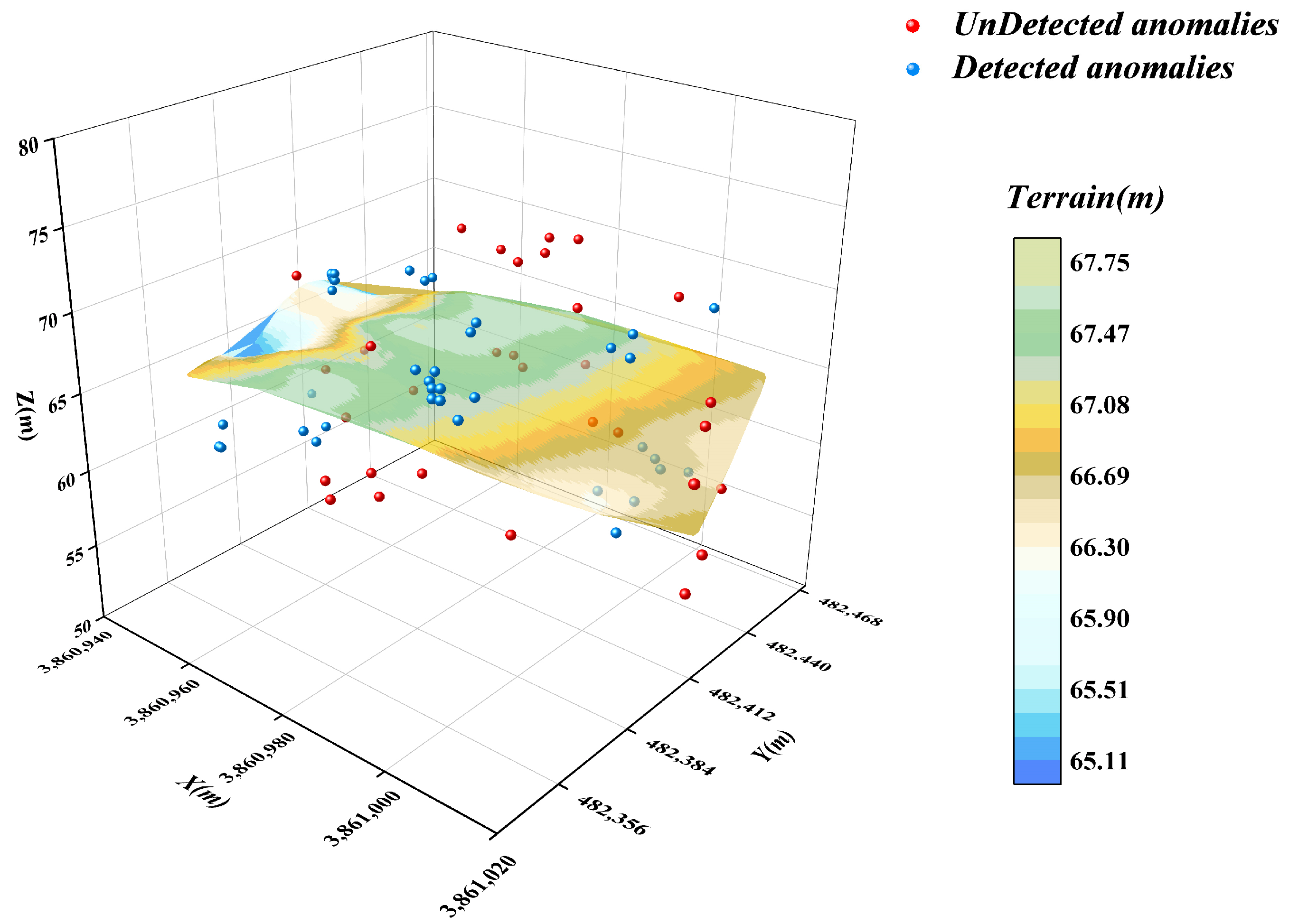
4.2. Isolated Forest Algorithm
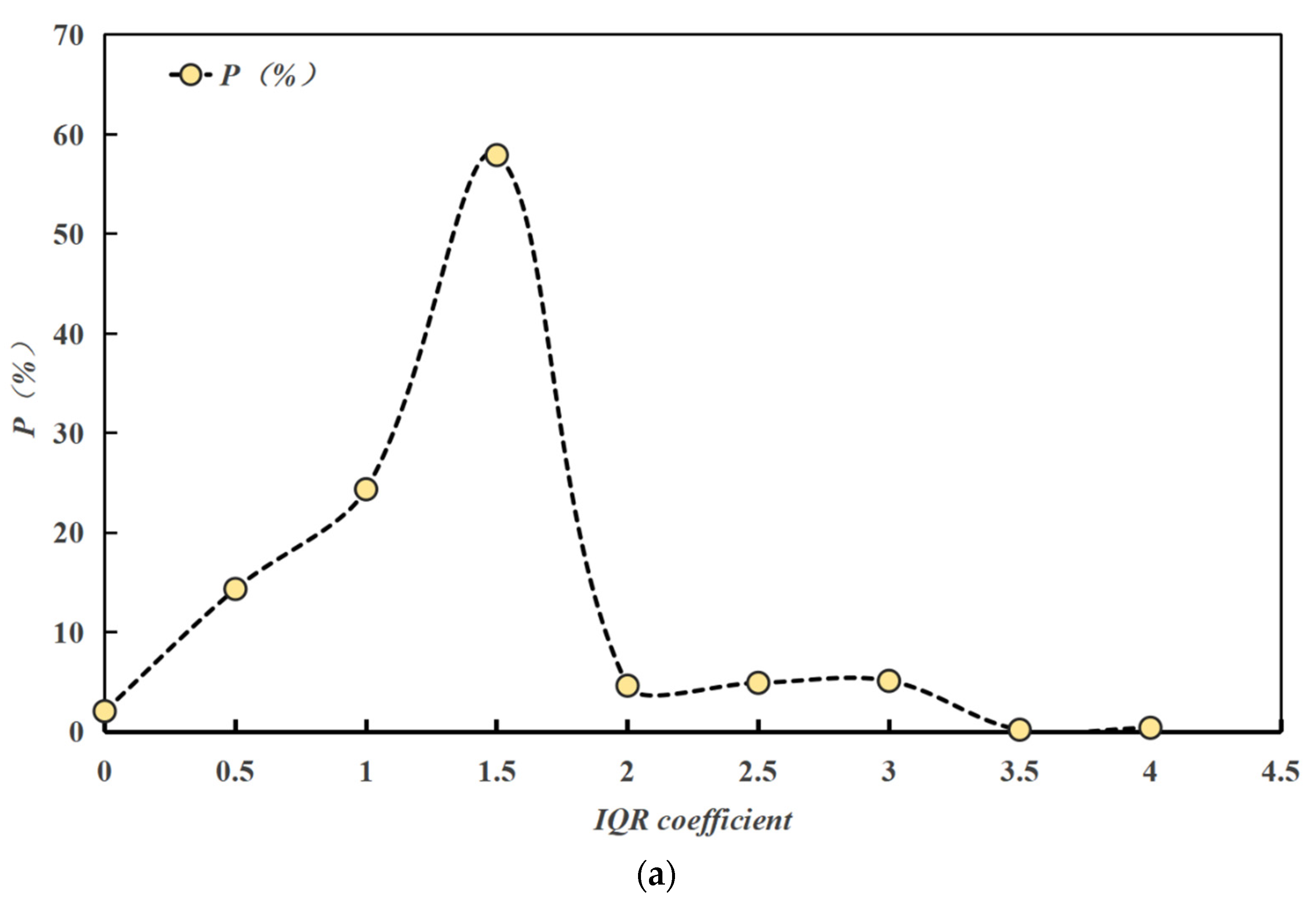
4.3. Box Plot Method
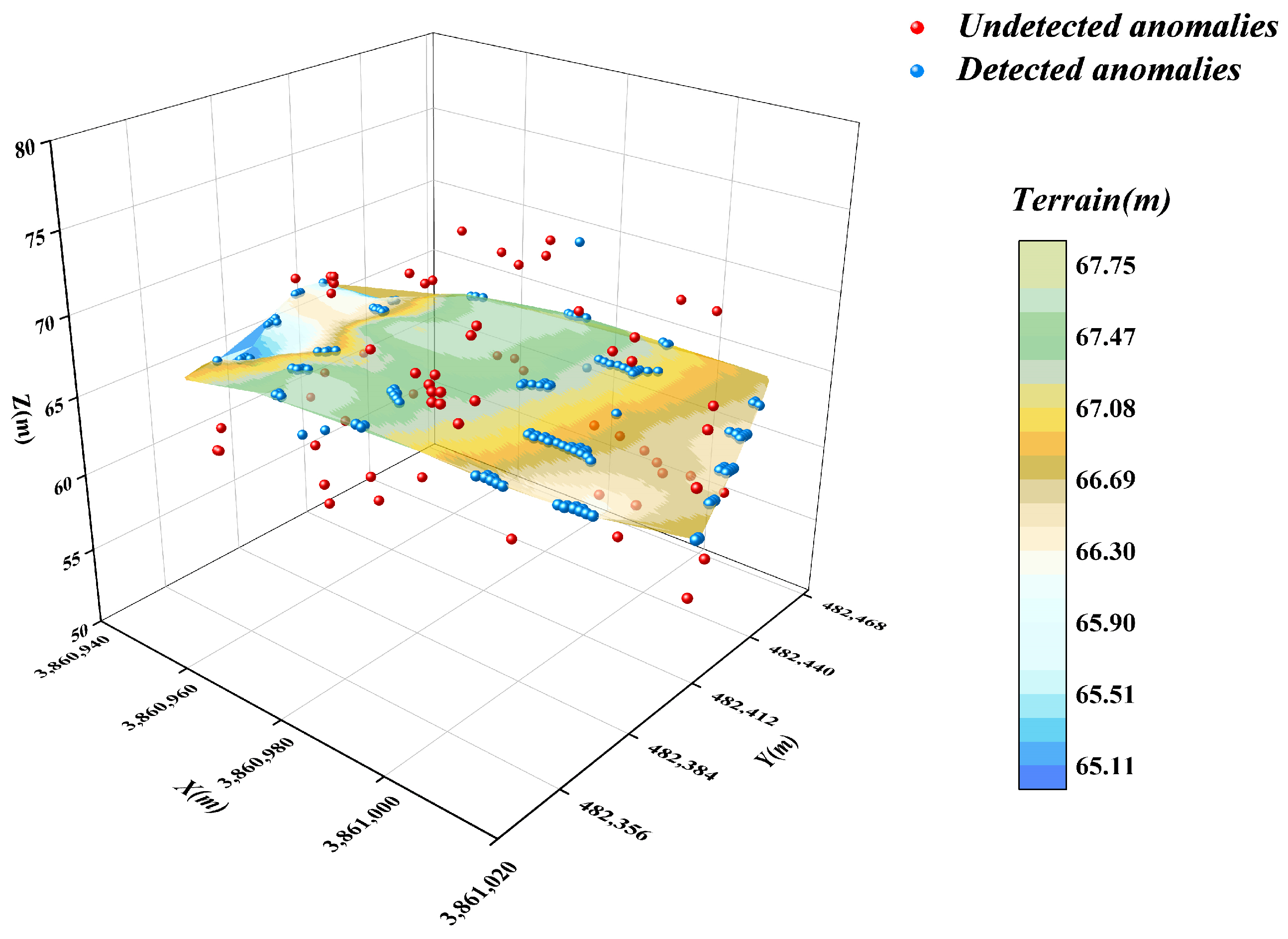
4.4. LOF Algorithm
4.5. K-Means Algorithm
4.6. Spatial Autocorrelation Algorithm
4.7. Autoencoder Algorithm
5. Conclusions
- (1)
- In this paper, an optimised DBSCAN-IForest stepwise anomaly detection algorithm is proposed, which integrates the K-distance map and Kd-tree techniques to accurately determine the ε and Minpts parameters in the DBSCAN algorithm; the algorithm follows step-by-step processing, in which the DBSCAN algorithm is used to initially screen the underwater terrain data in clusters. The isolated forest algorithm is subsequently introduced to perform more detailed outlier detection on the preliminary subclusters. The results show that the detection rate of the algorithm reaches 93.75%, higher than those of the other detection methods, which demonstrates the significant superiority of the algorithm.
- (2)
- The effectiveness of commonly used anomalous data detection methods is verified by examples. Among these methods, the DBSCAN algorithm is based on the principle of density reachability, and its anomaly detection results are sensitive to the setting of the neighbourhood radius ε and the minimum number of points Minpts, this may affect the stability of the results. The isolated forest algorithm identifies anomalies by measuring the degree of isolation of the data points in the feature space; it is effective in identifying the outliers at a single point but performs poorly in addressing regional anomalies. The box-and-line diagram method is based on the characteristics of the data distribution. It is easy to perform, but the accuracy is easily affected by the IQR coefficients. The LOF algorithm identifies anomalies by comparing local densities, but its results are significantly dependent on the selection of the value k of the number of initial neighbourhood points. K-means is prone to misjudging the data in the boundary region. In addition, the spatial autocorrelation algorithm has a limited ability to detect local anomalies. The autoencoder identifies anomalies by learning the feature representation of the data, but its detection effect is average in the case of complex and diverse underwater terrain data.
- (3)
- The optimised DBSCAN-IForest algorithm proposed in this study has good applicability in underwater subsurface data detection, and the research results not only provide valuable reference data for anomalous data detection in other fields but also help improve hydrological measurement technology to reach a higher level of scientific and automated development. However, this study has certain limitations. Firstly, the sample size of the dataset used for analysis is limited, which may affect the generalizability of the results to broader or more diverse underwater environments. Secondly, variations in data collection conditions, such as changes in underwater topography, equipment performance, and environmental factors, could introduce uncertainties into the detection process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H. Research on the Theory and Method of Processing Anomalies in Bathymetry of Multibeam System. Ph.D. Thesis, PLA Information Engineering University, Zhengzhou, China, 2012. (In Chinese). [Google Scholar]
- Cheng, X. Research on Key Technology of Multibeam Measurement Data Processing. Master’s Thesis, Shandong University of Architecture, Jinan, China, 2014. (In Chinese). [Google Scholar]
- Huang, S.Q.; You, H.; Wang, Y.T. Environmental monitoring ofnatural disasters using synthetic aperture radar image multi-directional characteristics. Int. J. Remote Sens. 2015, 36, 3160–3183. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Ding, J. Combining LiDAR, SAR, and DEM Data for Estimating Understory Terrain Using Machine Learning-Based Methods. Forests 2024, 15, 1992. [Google Scholar] [CrossRef]
- Cao, D.; Wang, C.; Du, M.; Xi, X. A Multiscale Filtering Method for Airborne LiDAR Data Using Modified 3D Alpha Shape. Remote Sens. 2024, 16, 1443. [Google Scholar] [CrossRef]
- Blaszczak-Bak, W.; Birylo, M. Study of the Impact of Landforms on the Groundwater Level Based on the Integration of Airborne Laser Scanning and Hydrological Data. Remote Sens. 2024, 16, 3102. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Cui, X.; Chang, B.; Zhang, S.; He, J.; Zhi, Z.; Zhang, W. Anomaly Detection in Multibeam Bathymetric Point Clouds Integrating Prior Constraints with Geostatistical Prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 17903–17916. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, J.; Wang, S. A Dual Robust Strategy for Removing Outliers in Multi-Beam Sounding to Improve Seabed Terrain Quality Estimation. Sensors 2024, 24, 1476. [Google Scholar] [CrossRef] [PubMed]
- Yoshimura, N.; Kuzuno, H.; Shiraishi, Y.; Morii, M. DOC-IDS: A Deep Learning-Based Method for Feature Extraction and Anomaly Detection in Network Traffic. Sensors 2022, 22, 4405. [Google Scholar] [CrossRef] [PubMed]
- Nicholaus, I.T.; Park, J.R.; Jung, K.; Lee, J.S.; Kang, D.-K. Anomaly Detection of Water Level Using Deep Autoencoder. Sensors 2021, 21, 6679. [Google Scholar] [CrossRef]
- Hu, G.; Zhou, X. Detection of Bathymetric Data Outliers in Ocean Surveying and Mapping. In Compilation of Papers on Ocean Development and Sustainable Development in the 14th Session of the 2004 Academic Annual Meeting of the Chinese Association for Science and Technology; Chinese Society of Surveying and Mapping: Beijing, China, 2004; p. 6. (In Chinese) [Google Scholar]
- Zhang, R.; Bian, S.; Liu, Y.; Li, H. Conditional Variation Self-Coding Algorithm for Large-Area Bathymetric Anomaly Detection. J. Surv. Mapp. 2019, 48, 1182–1189. (In Chinese) [Google Scholar]
- Long, J.; Zhang, H.; Zhao, J. A Comprehensive Deep Learning-Based Outlier Removal Method for Multibeam Bathymetric Point Cloud. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–22. [Google Scholar] [CrossRef]
- Huang, X.; Huang, C.; Zhai, G.; Lu, X.; Xiao, G.; Sui, L.; Deng, K. Data Processing Method of Multibeam Bathymetry Based on Sparse Weighted LS-SVM Machine Algorithm. IEEE J. Ocean. Eng. 2020, 45, 1538–1551. [Google Scholar] [CrossRef]
- Li, H.; Ye, W.; Liu, J.; Tan, W.; Pirasteh, S.; Fatholahi, S.N.; Li, J. High-Resolution Terrain Modeling Using Airborne LiDAR Data with Transfer Learning. Remote Sens. 2021, 13, 3448. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. ACM Sigmod. Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Abdelazeem, M.; Abazeed, A.; Kamal, H.A.; Mohamed, M.O.A. Towards an Accurate Real-Time Digital Elevation Model Using Various GNSS Techniques. Sensors 2024, 24, 8147. [Google Scholar] [CrossRef]
- Bozzano, M.; Varni, F.; De Martino, M.; Quarati, A.; Tambroni, N.; Federici, B. An Integrated Approach to Riverbed Morphodynamic Modeling Using Remote Sensing Data. J. Mar. Sci. Eng. 2024, 12, 2055. [Google Scholar] [CrossRef]
- Chen, P.; Li, Z.; Liu, G.; Wang, Z.; Chen, J.; Shi, S.; Shen, J.; Li, L. Underwater Terrain Matching Method Based on Pulse-Coupled Neural Network for Unmanned Underwater Vehicles. J. Mar. Sci. Eng. 2024, 12, 458. [Google Scholar] [CrossRef]
- Hu, X.; Gao, Y.; Liu, K.; Xiang, L.; Luo, B.; Li, L. Surface Electromyographic Responses During Rest on Mattresses with Different Firmness Levels in Adults with Normal BMI. Sensors 2024, 25, 14. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Zhou, A.; Cao, J. DBSCAN Algorithm Based on Data Partitioning. Comput. Res. Dev. 2000, 37, 1153–1159. (In Chinese) [Google Scholar]
- Xiong, Z.; Zhu, D.; Liu, D.; He, S.; Zhao, L. Anomaly Detection of Metallurgical Energy Data Based on iForest-AE. Appl. Sci. 2022, 12, 9977. [Google Scholar] [CrossRef]
- Li, X.; Gao, X.; Yan, B.; Chen, C.; Chen, B.; Li, J.; Xu, J. An Approach of Data Anomaly Detection in Power Dispatching Streaming Data Based on Isolation Forest Algorithm. Power Syst. Technol. 2019, 43, 1447–1456. (In Chinese) [Google Scholar]
- Liu, W.; Mu, X.; Huang, Y. Anomaly Detection Method Based on Multi-Resolution Grid. Comput. Eng. Appl. 2020, 56, 78–85. (In Chinese) [Google Scholar]
- Qi, C.; He, W.; Jiao, Y.; Ma, Y.; Cai, W.; Ren, S. Survey on Anomaly Detection Algorithms for Unmanned Aerial Vehicle Flight Data. J. Comput. Appl. 2023, 43, 1833–1841. (In Chinese) [Google Scholar]
- Whitehurst, D.; Joshi, K.; Kochersberger, K.; Weeks, J. Post-Flood Analysis for Damage and Restoration Assessment Using Drone Imagery. Remote Sens. 2022, 14, 4952. [Google Scholar] [CrossRef]
- Chen, P.; Seo, D.; Maity, B.; Dutt, N. KDTree-SOM: Self-Organizing Map Based Anomaly Detection for Lightweight Autonomous Embedded Systems. In Proceedings of the Great Lakes Symposium on VLSI 2024, Clearwater, FL, USA, 12–14 June 2024. [Google Scholar]
- Zhao, J.; Yang, L. The Improvement and Implementation of DBSCAN Clustering Algorithm. Microelectron. Comput. 2009, 26, 189–192. (In Chinese) [Google Scholar]
- Zhu, C.; Huang, P.; Li, L. Generalized Isolation Forest Anomaly Detection Algorithm Based on Expert Feedback. Appl. Res. Comput. 2024, 41, 88–93. (In Chinese) [Google Scholar]
- Qiao, T.; Tong, D.; Wang, J.; Guan, T.; Wu, B. Outlier Detection and Correction for Rolling Speed Based on Kmeans-EMD and IWOA-Elman. J. Water Resour. Water Eng. 2022, 33, 124–131. (In Chinese) [Google Scholar]
- Wang, X.; Bai, Y. The Global Minmax k-Means Algorithm. SpringerPlus 2016, 5, 1665. [Google Scholar] [CrossRef] [PubMed]
- Deng, T.; Huang, Y.; Gu, J. Diagnosis of Spatial Autocorrelation in Spatial Analysis. Chin. J. Health Stat. 2013, 30, 343–346. (In Chinese) [Google Scholar]
- Lai, J.; Wang, X.; Xiang, Q.; Song, Y.; Quan, W. Review on Autoencoder and Its Application. J. Commun. 2021, 42, 1–15. (In Chinese) [Google Scholar]







| Entry | Description/Information |
|---|---|
| Date | 9 September 2024 |
| Location | Zhengzhou city |
| Discharge | 867 m3/s |
| Sensor | Single-beam sounder |
| Sediment concentration | 2 kg/m3 |
| Flow rate | 1.2 m/s |
| temperature of the body of water | 12 °C |
| ε Value | Minpts Value | Total Detected | Detection Rate P |
|---|---|---|---|
| 0.5 | [2, 11] | [6956, 6973] | [1.14%, 1.15%] |
| 1 | [2, 9] | [1962, 6973] | [1.14%, 4.07%] |
| 1.5 | [2, 9] | [61, 63] | [76.25%, 78.75%] |
| 2 | [2, 9] | [56, 60] | [70.00%, 75.00%] |
| 3 | [2, 25] | [38, 70] | [47.50%, 87.5%] |
| 4 | [2, 45] | [16, 44] | [20.00%, 55.00%] |
| K Value | Total Anomalies Detected | Number of Detected Anomalies | Detection Rate P |
|---|---|---|---|
| 1 | 53 | 53 | 66.25% |
| 2 | 71 | 71 | 88.75% |
| 3 | 71 | 68 | 81.40% |
| 4 | 142 | 68 | 40.70% |
| 5 | 70 | 67 | 80.16% |
| 6 | 71 | 65 | 74.38% |
| 7 | 130 | 64 | 39.38% |
| 8 | 183 | 63 | 27.11% |
| 9 | 70 | 69 | 85.01% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Su, M.; Zhang, B.; Yue, Y.; Wang, J.; Deng, Y. Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data. Water 2025, 17, 626. https://doi.org/10.3390/w17050626
Li M, Su M, Zhang B, Yue Y, Wang J, Deng Y. Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data. Water. 2025; 17(5):626. https://doi.org/10.3390/w17050626
Chicago/Turabian StyleLi, Mingyang, Maolin Su, Baosen Zhang, Yusu Yue, Jingwen Wang, and Yu Deng. 2025. "Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data" Water 17, no. 5: 626. https://doi.org/10.3390/w17050626
APA StyleLi, M., Su, M., Zhang, B., Yue, Y., Wang, J., & Deng, Y. (2025). Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data. Water, 17(5), 626. https://doi.org/10.3390/w17050626






