Machine Learning-Based Reconstruction and Prediction of Groundwater Time Series in the Allertal, Germany
Abstract
1. Introduction
2. Site Description and Explorative Data Analysis (EDA)
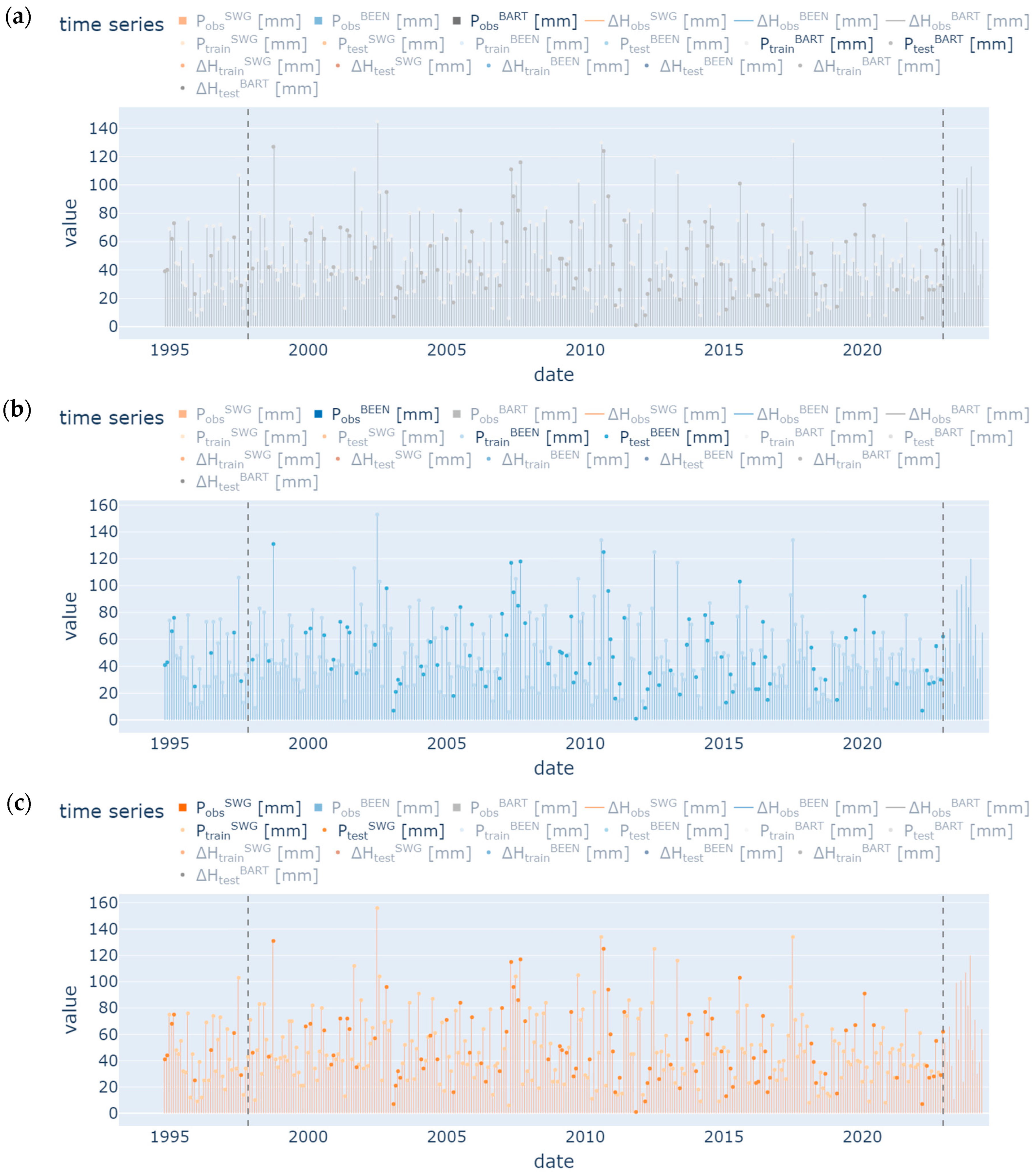
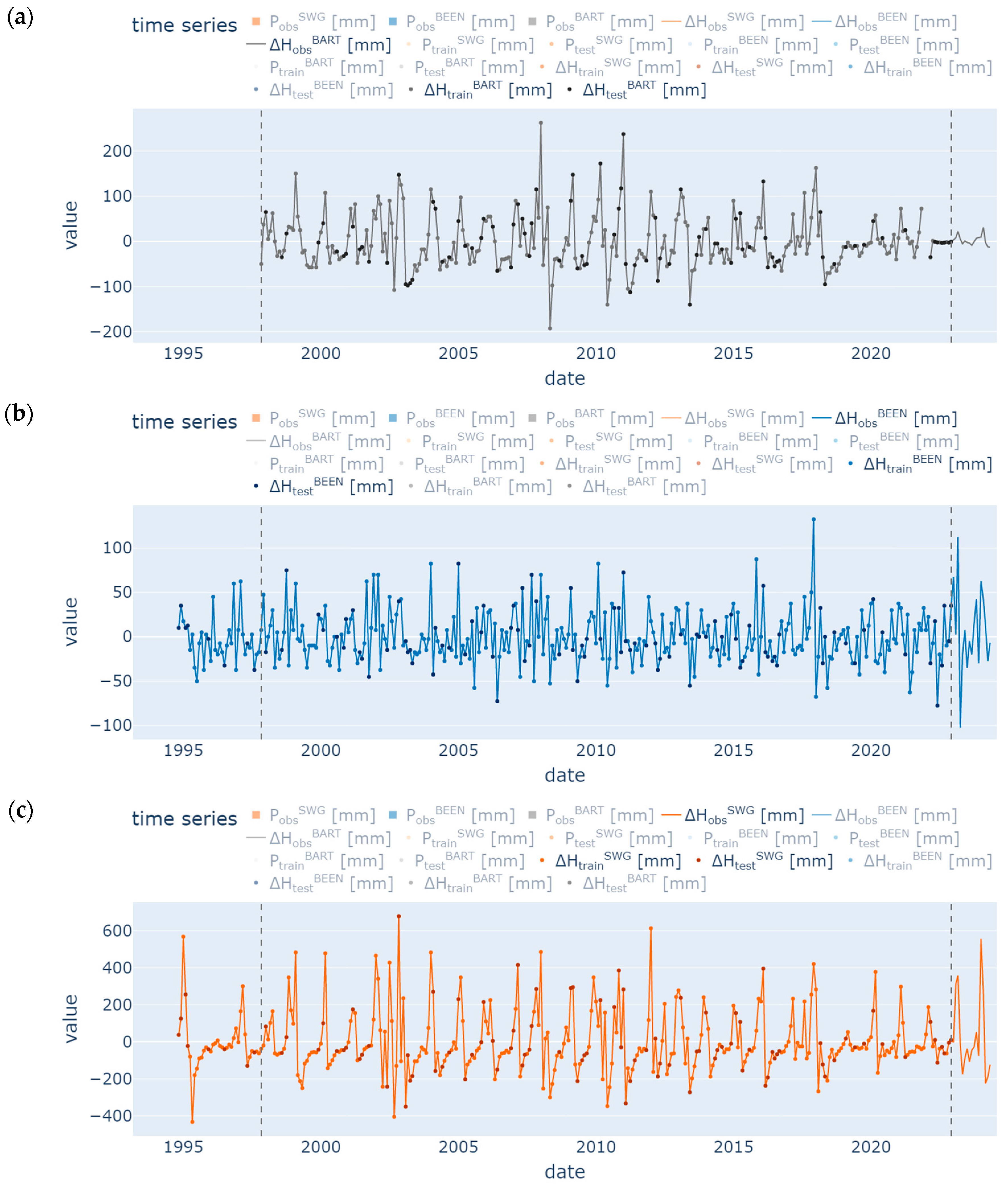
2.1. Study Area and Data Preprocessing
2.2. Explorative Data Analysis (EDA)
3. Machine Learning (ML) Methods and Workflow
3.1. Deep Learning Frameworks—Artificial Neural Network
3.1.1. TensorFlow
3.1.2. PyTorch
3.2. Classical Machine Learning Algorithms
3.2.1. Random Forest Regression
3.2.2. XGBoost (eXtreme Gradient Boosting)
3.2.3. Multiple Linear Regression (MLR)
3.3. Performance Metrics
3.4. Workflow
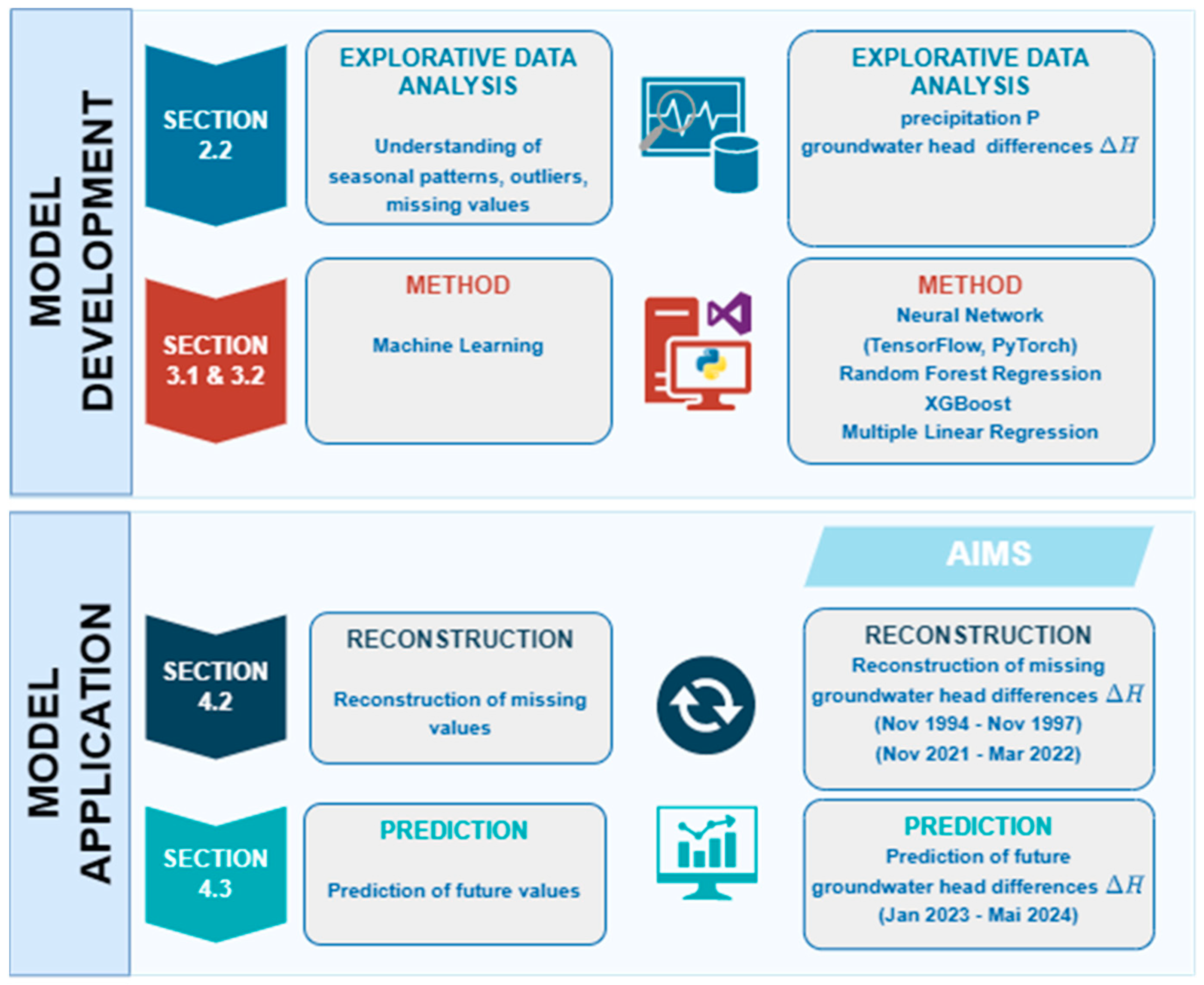
4. Results
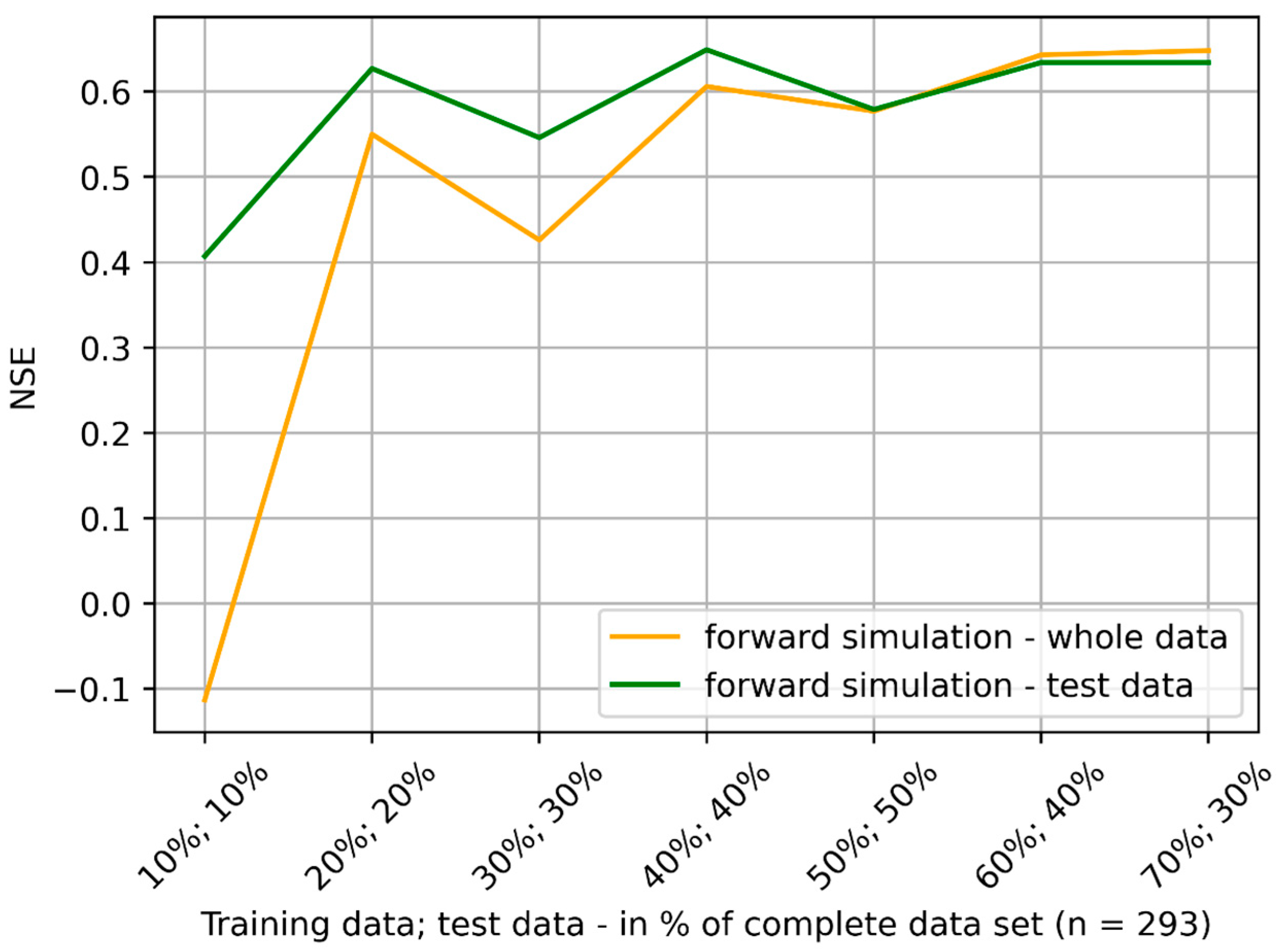
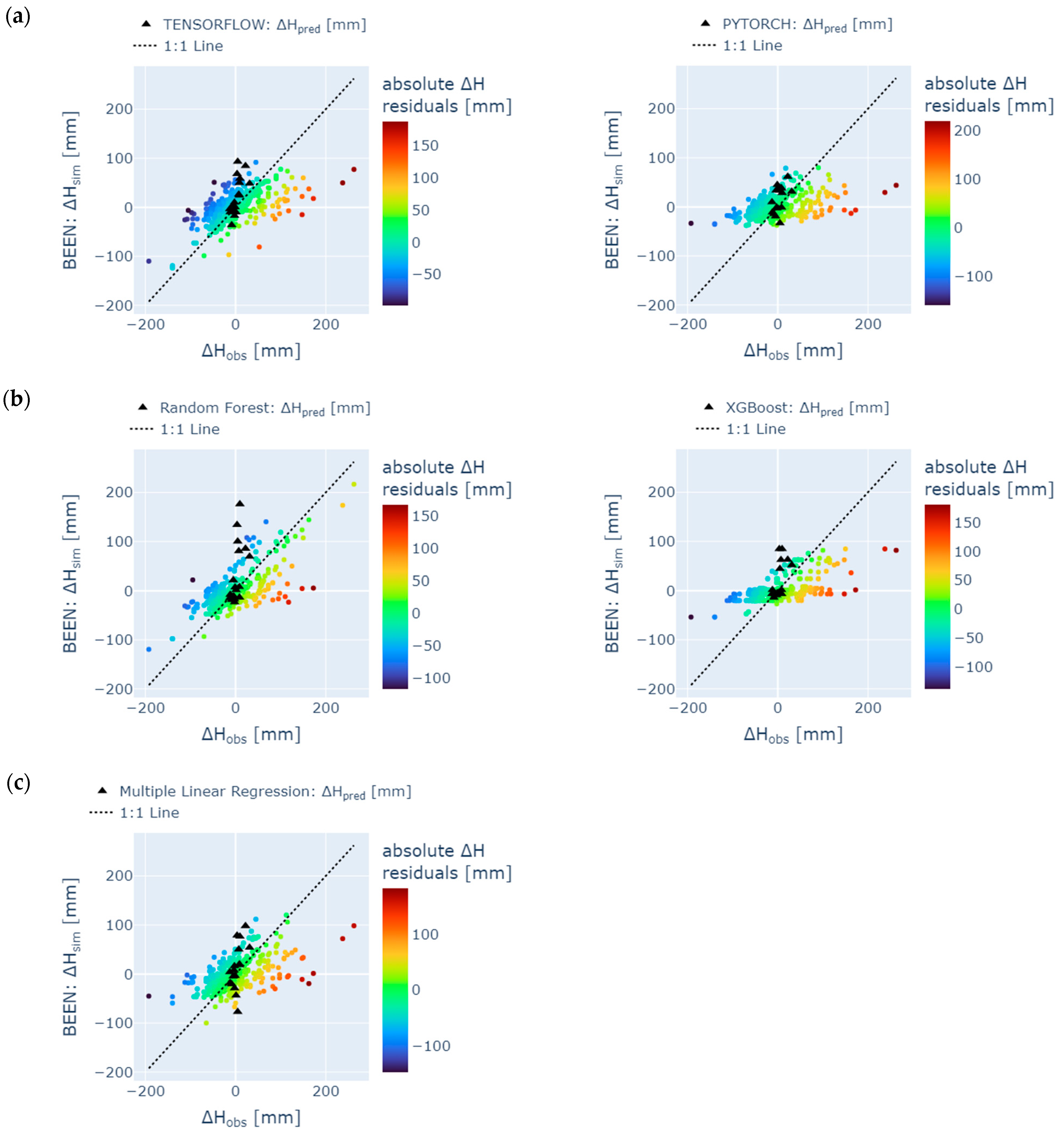
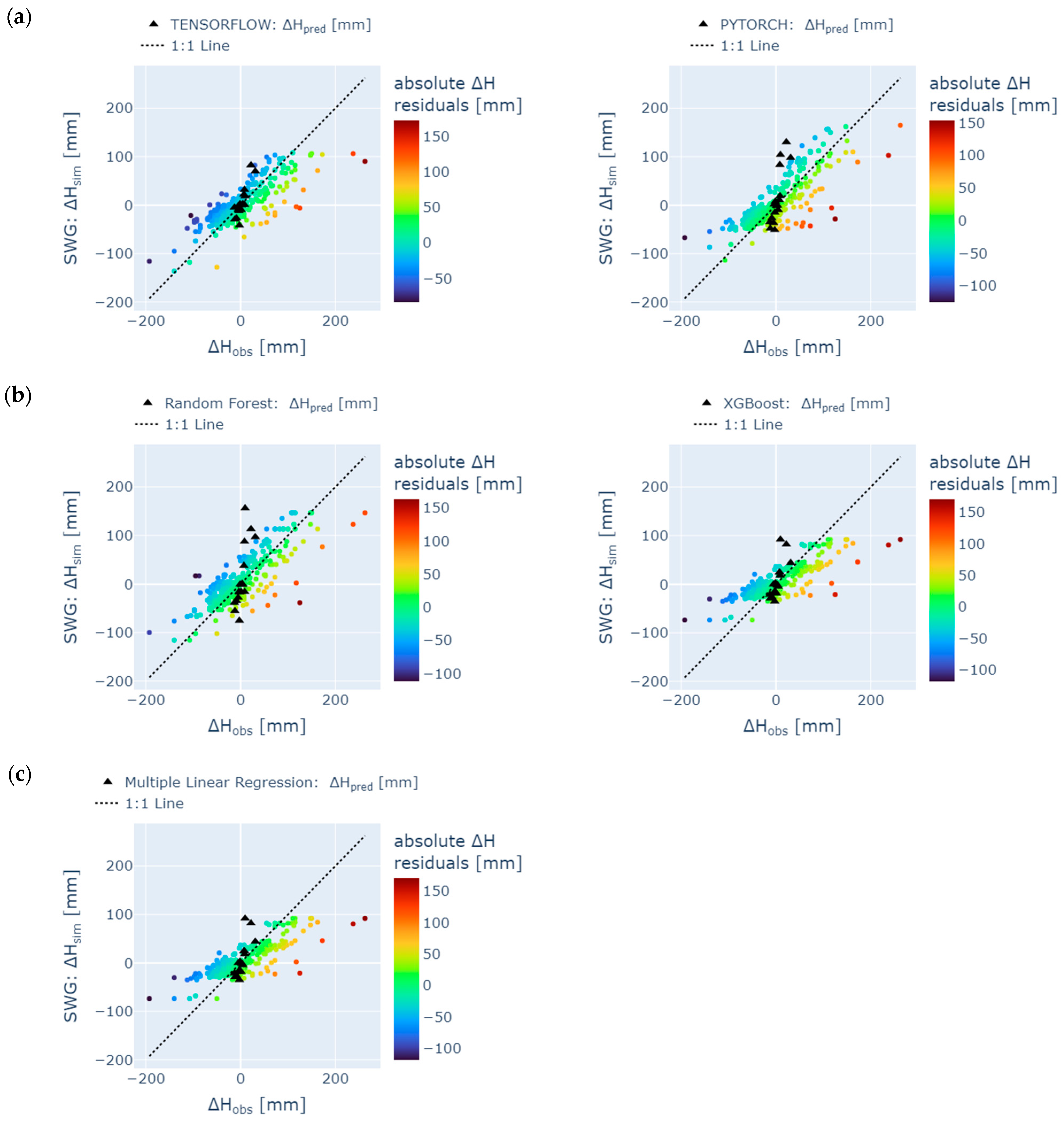
4.1. Training and Testing
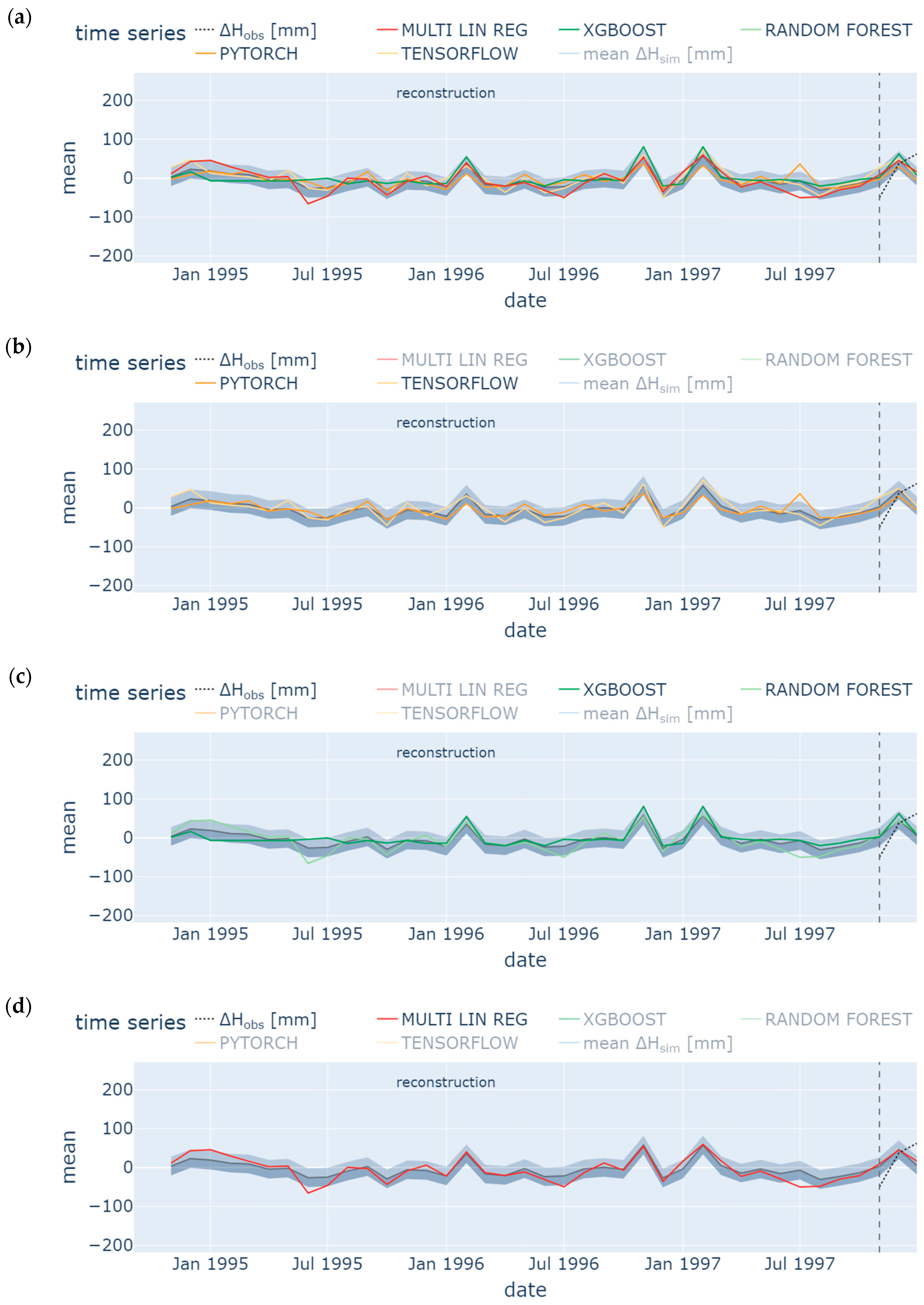
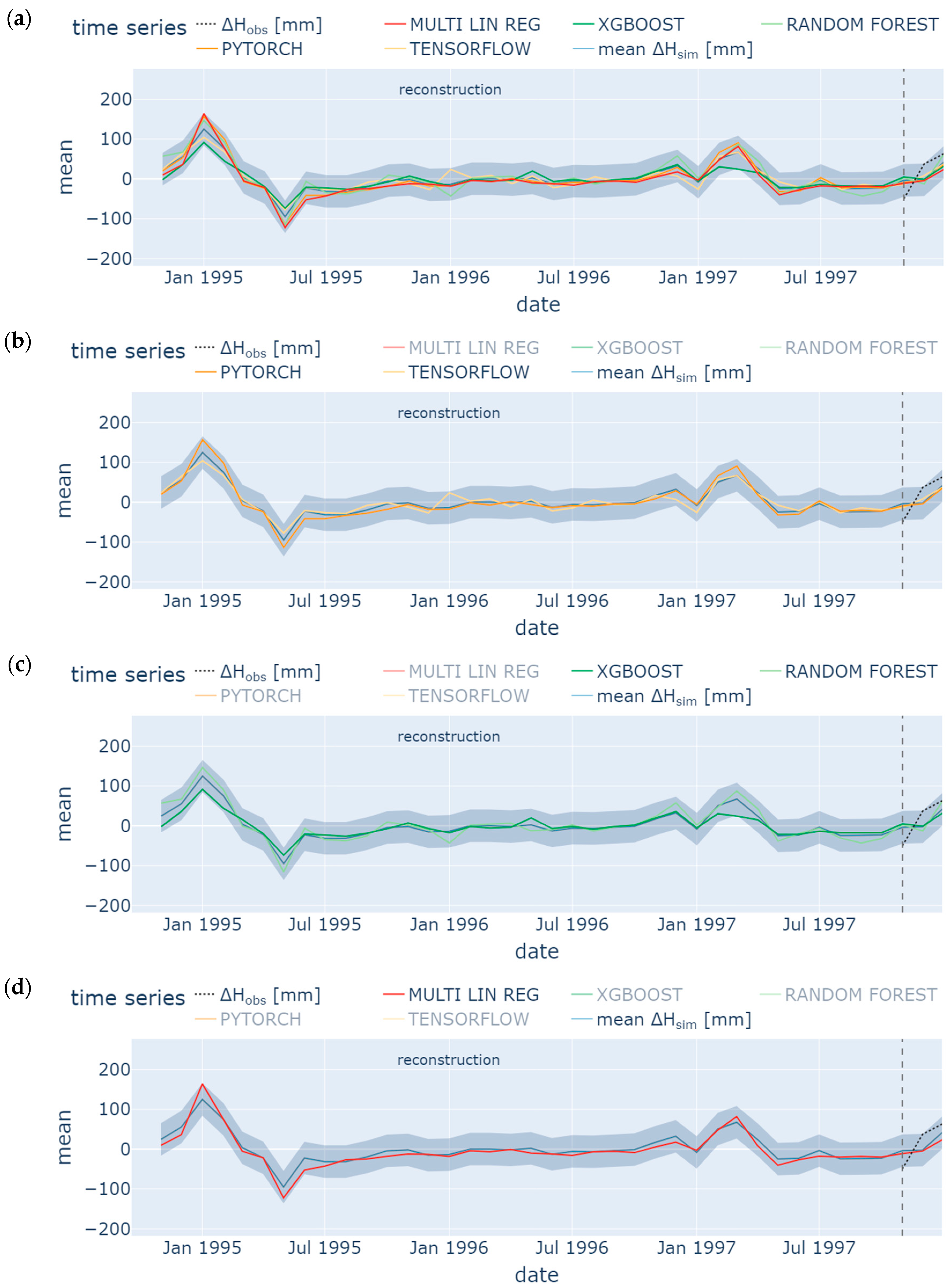
4.2. Reconstruction
4.3. Prediction
5. Discussion
5.1. Significance of Simplified Machine Learning Models and Input Data
5.2. Uncertainty Reduction in Gap-Based Time Series
5.3. Drawbacks and Limitations of the Present Study
6. Summary and Conclusions
- (1)
- Missing groundwater heads were successfully reconstructed (1995 to 1997) and predicted (January 2023 to May 2024) by using few input data. However, only the model ensemble based on data from the neighboring station SWG gave adequate results. It was shown in the prior-to-model-development explorative data analysis that data from SWG and BART correlate (groundwater head differences from both stations show NSE = 0.75), which leads to an accurate model in the present study (NSE = 0.65 (test) to 0.71 (training) for one exemplary ML model). In contrast, BART and BEEN show a low grade of data correlation (for groundwater head differences NSE = 0.49). The model ensemble predicts groundwater head differences with an insufficient accuracy (NSE = 0.3 (test) to 0.46 (training) for an exemplary ML model). Hence, if data are sufficiently correlated, ML methods are applicable also for a time series data consisting of few data. The considered monitoring stations have to be located in the same study area. Overfitting can be challenging such that a suitable model should have similar training and prediction NSEs to avoid this behavior.
- (2)
- TensorFlow, PyTorch, Random Forest, XGBoost, and Multiple Linear Regression show similar results, especially during hydrological summer months when low variation occurred; hence, for time series analysis, each ML methods is applicable in order to detect seasonal trend analysis. Specifically, the Random Forest model and the ANN using the TensorFlow package performed best with a train/test NSE of 0.7/0.53 and 0.71/0.65, respectively. However, results from the latter were less prone to overfitting. These results confirm some findings from the literature [104]. However, other studies have shown that the support vector machine method (which was not considered in the present study) outperformed the ANN [105], while XGBoost outperformed the ANN [70]. The most appropriate ML method may vary from location to location. It depends on various factors such as the specific characteristics of the dataset, the location with its specific conditions, and the experience of the operator training, testing, and analyzing the model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Phase | Explanation | Machine Learning Method |
|---|---|---|
| Learning Rate | Controls how much to adjust the weights of the model during training. Crucial for convergence. Typical values range from 10−6 to 10−1. | TensorFlow, PyTorch, XGBoost, MLR |
| Number of Epochs | Total number of times the entire dataset is processed through the model during training. Can range from 10 to several hundred. | TensorFlow, PyTorch |
| Optimizer | Algorithm used to minimize the loss function, such as SGD, Adam, or RMSprop. | TensorFlow, PyTorch |
| Dropout Rate | Proportion of neurons randomly dropped during training to reduce overfitting. Typically set between 0.1 and 0.5. | PyTorch |
| Activation Functions | Functions applied to the output of neurons in hidden layers, such as ReLU, sigmoid, or tanh. | PyTorch |
| Number of Layers and Units per Layer | Defines the depth and width of the neural network. | PyTorch |
| Loss Function | The choice of loss function is critical in regression tasks. Common choices include Mean Squared Error (MSE) and Mean Absolute Error (MAE). | PyTorch |
| Number of Trees (n_estimators) | The number of decision trees in the forest. Common choices range from 100 to 1000. | Random Forest, XGBoost |
| Maximum Depth (max_depth) | The maximum depth of each tree. Limiting the depth prevents the trees from becoming too complex and overfitting. | Random Forest, XGBoost |
| Minimum Samples per Leaf (min_samples_leaf) | The minimum number of samples required to be at a leaf node. Usually set to small numbers like 1, 2, 4. | Random Forest |
| Minimum Samples to Split (min_samples_split) | The minimum number of samples required to split an internal node. Commonly set to 2. | Random Forest |
| Criterion (criterion) | The function to measure the quality of a split. In regression, common options include MSE (Mean Squared Error) and MAE (Mean Absolute Error). | Random Forest |
Appendix B
- n is the number of groundwater head observations;
- is the actual value for the ith groundwater head observation;
- is the calculated value for the ith groundwater head observation.
- is the mean of the observed values.
References
- Hayley, K. The present state and future application of cloud computing for numerical groundwater modeling. Groundwater 2017, 55, 678–682. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Adams, K.H.; Reager, J.T.; Rosen, P.; Wiese, D.N.; Farr, T.G.; Rao, S.; Haines, B.J.; Argus, D.F.; Liu, Z.; Smith, R.; et al. Remote sensing of groundwater: Current capabilities and future directions. Water Resour. Res. 2022, 58, e2022WR032219. [Google Scholar] [CrossRef]
- Brunner, P.; Hendricks Franssen, H.-J.; Kgotlhang, L.; Bauer-Gottwein, P.; Kinzelbach, W. How can remote sensing contribute in groundwater modeling? Hydrogeol. J. 2007, 15, 5–18. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Zamora, P.B.; Siringan, F.P.; Lapus, M.R.; Rodolfo, R.S.; Jacinto, G.S.; San Diego-McGlone, M.L.; Villanoy, C.L.; Cabrera, O.; Senal, M.I. Linking regional sources and pathways for submarine groundwater discharge at a reef by electrical resistivity tomography, 222Rn, and salinity measurements. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Tran, T.V.; Buckel, J.; Maurischat, P.; Tang, H.; Yu, Z.; Hördt, A.; Guggenberger, G.; Zhang, F.; Schwalb, A.; Graf, T. Delineation of a Quaternary aquifer using integrated hydrogeological and geophysical estimation of hydraulic conductivity on the Tibetan Plateau, China. Water 2021, 13, 1412. [Google Scholar] [CrossRef]
- Barchard, K.A.; Pace, L.A. Preventing human error: The impact of data entry methods on data accuracy and statistical results. Comput. Hum. Behav. 2011, 27, 1834–1839. [Google Scholar] [CrossRef]
- Osborne, J.W. Dealing with Missing or Incomplete Data: Debunking the Myth of Emptiness. In Best Practices in Data Cleaning: A Complete Guide to Everything You Need to Do Before and After Collecting Your Data; SAGE Publications, Inc.: Newbury Park, CA, USA, 2013; pp. 105–138. [Google Scholar]
- Kang, H. The prevention and handling of the missing data. Korean J. Anesthesiol. 2013, 64, 402–406. [Google Scholar] [CrossRef] [PubMed]
- Hunt, R.J.; Fienen, M.N.; White, J.T. Revisiting “an exercise in groundwater model calibration and prediction” after 30 years: Insights and new directions. Groundwater 2020, 58, 168–182. [Google Scholar] [CrossRef]
- Freyberg, D.L. An exercise in ground-water model calibration and prediction. Groundwater 1988, 26, 350–360. [Google Scholar] [CrossRef]
- Hodgson, F.D. The use of multiple linear regression in simulating ground-water level responses. Groundwater 1978, 16, 249–253. [Google Scholar] [CrossRef]
- Jobson, J.D. Multiple Linear Regression, in Applied Multivariate Data Analysis: Regression and Experimental Design; Springer: New York, NY, USA, 1991; pp. 219–398. [Google Scholar]
- Huang, S.; Krysanova, V.; Österle, H.; Hattermann, F.F. Simulation of spatiotemporal dynamics of water fluxes in Germany under climate change. Hydrol. Process. 2010, 24, 3289–3306. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Koch, J.; Berger, H.; Henriksen, H.J.; Sonnenborg, T.O. Modelling of the shallow water table at high spatial resolution using random forests. Hydrol. Earth Syst. Sci. 2019, 23, 4603–4619. [Google Scholar] [CrossRef]
- Fathian, F. Introduction of multiple/multivariate linear and nonlinear time series models in forecasting streamflow process. In Advances in Streamflow Forecasting; Elsevier: Amsterdam, The Netherlands, 2021; pp. 87–113. [Google Scholar]
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater level forecasting with artificial neural networks: A comparison of long short-term memory (LSTM), convolutional neural networks (CNNs), and non-linear autoregressive networks with exogenous input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687. [Google Scholar] [CrossRef]
- Dastjerdi, S.Z.; Sharifi, E.; Rahbar, R.; Saghafian, B. Downscaling WGHM-Based Groundwater Storage Using Random Forest Method: A Regional Study over Qazvin Plain, Iran. Hydrology 2022, 9, 179. [Google Scholar] [CrossRef]
- Kratzert, F.; Gauch, M.; Nearing, G.; Klotz, D. NeuralHydrology—A Python library for Deep Learning research in hydrology. J. Open Source Softw. 2022, 7, 4050. [Google Scholar] [CrossRef]
- Ehteram, M.; Banadkooki, F.B. A Developed Multiple Linear Regression (MLR) Model for Monthly Groundwater Level Prediction. Water 2023, 15, 3940. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Sharma, K.V.; Mehta, D.J.; Caloiero, T. Advanced Machine Learning Techniques to Improve Hydrological Prediction: A Comparative Analysis of Streamflow Prediction Models. Water 2023, 15, 2572. [Google Scholar] [CrossRef]
- Latif, S.D.; Ahmed, A.N. A review of deep learning and machine learning techniques for hydrological inflow forecasting. Environ. Dev. Sustain. 2023, 25, 12189–12216. [Google Scholar] [CrossRef]
- Seidu, J.; Ewusi, A.; Kuma, J.S.Y.; Ziggah, Y.Y.; Voigt, H.-J. Impact of data partitioning in groundwater level prediction using artificial neural network for multiple wells. Int. J. River Basin Manag. 2023, 21, 639–650. [Google Scholar] [CrossRef]
- Logashenko, D.; Litvinenko, A.; Tempone, R.; Wittum, G. Estimation of uncertainties in the density driven flow in fractured porous media using MLMC. arXiv 2024, arXiv:2404.18003. [Google Scholar] [CrossRef]
- Bakker, M.; Schaars, F. Solving groundwater flow problems with time series analysis: You may not even need another model. Groundwater 2019, 57, 826–833. [Google Scholar] [CrossRef] [PubMed]
- LHW. Geodatenportal. 07.11.2024 07.01.2024. Available online: https://gld.lhw-sachsen-anhalt.de/ (accessed on 25 June 2024).
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S. Jupyter Notebooks–a publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas; IOS Press: Amsterdam, The Netherlands, 2016; pp. 87–90. [Google Scholar]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- DWD. Climate Data Center. 07.11.2024 05.01.2024. Available online: https://www.dwd.de/DE/leistungen/cdc/climate-data-center.html?nn=17626 (accessed on 29 June 2024).
- QGIS. QGIS Geographic Information System. 2024. Available online: http://www.qgis.org (accessed on 25 May 2024).
- Sherman, G. The PyQGIS Programmer’s Guide; Locate Press: London, UK, 2014. [Google Scholar]
- Pang, J.; Zhang, H.; Xu, Q.; Wang, Y.; Wang, Y.; Zhang, O.; Hao, J. Hydrological evaluation of open-access precipitation data using SWAT at multiple temporal and spatial scales. Hydrol. Earth Syst. Sci. 2020, 24, 3603–3626. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Deep learning shows declining groundwater levels in Germany until 2100 due to climate change. Nat. Commun. 2022, 13, 1221. [Google Scholar] [CrossRef] [PubMed]
- Sahour, H.; Gholami, V.; Vazifedan, M. A comparative analysis of statistical and machine learning techniques for mapping the spatial distribution of groundwater salinity in a coastal aquifer. J. Hydrol. 2020, 591, 125321. [Google Scholar] [CrossRef]
- TensorFlow Developers. TensorFlow, v2.12.0; Zenodo: Geneva, Switzerland, 2024. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. PyTorch; v.2.3.1. An Imperative Style, High-Performance Deep Learning Library. Advances in Neural Information Processing Systems 32; Zenodo: Geneva, Switzerland, 2019. [Google Scholar]
- Joy, T.T.; Rana, S.; Gupta, S.; Venkatesh, S. Hyperparameter tuning for big data using Bayesian optimisation. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016. [Google Scholar]
- Kim, J.-Y.; Cho, S.-B. Evolutionary optimization of hyperparameters in deep learning models. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019. [Google Scholar]
- Nematzadeh, S.; Kiani, F.; Torkamanian-Afshar, M.; Aydin, N. Tuning hyperparameters of machine learning algorithms and deep neural networks using metaheuristics: A bioinformatics study on biomedical and biological cases. Comput. Biol. Chem. 2022, 97, 107619. [Google Scholar] [CrossRef] [PubMed]
- Wunsch, A.; Liesch, T.; Goldscheider, N. Towards understanding the influence of seasons on low-groundwater periods based on explainable machine learning. Hydrol. Earth Syst. Sci. 2024, 28, 2167–2178. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX symposium on operating systems design and implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Qin, J.; Liang, J.; Chen, T.; Lei, X.; Kang, A. Simulating and Predicting of Hydrological Time Series Based on TensorFlow Deep Learning. Pol. J. Environ. Stud. 2019, 28, 795–802. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Simon and Schuster: New York, NY, USA, 2021. [Google Scholar]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting groundwater table in a flood prone coastal city with long short-term memory and recurrent neural networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef]
- Solgi, R.; Loaiciga, H.A.; Kram, M. Long short-term memory neural network (LSTM-NN) for aquifer level time series forecasting using in-situ piezometric observations. J. Hydrol. 2021, 601, 126800. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.; Boithias, L.; Pachepsky, Y.; Kim, K.; Chun, J.A.; Cho, K.H. AI4Water v1.0, an open-source python package for modeling hydrological time series using data-driven methods. Geosci. Model Dev. 2022, 15, 3021–3039. [Google Scholar] [CrossRef]
- Novac, O.-C.; Chirodea, M.C.; Novac, C.M.; Bizon, N.; Oproescu, M.; Stan, O.P.; Gordan, C.E. Analysis of the Application Efficiency of TensorFlow and PyTorch in Convolutional Neural Network. Sensors 2022, 22, 8872. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Shuai, P.; Sun, A.; Mudunuru, M.K.; Chen, X. Knowledge-informed deep learning for hydrological model calibration: An application to Coal Creek Watershed in Colorado. Hydrol. Earth Syst. Sci. 2023, 27, 2621–2644. [Google Scholar] [CrossRef]
- Shin, M.-J.; Kim, J.-W.; Moon, D.-C.; Lee, J.-H.; Kang, K.G. Comparative analysis of activation functions of artificial neural network for prediction of optimal groundwater level in the middle mountainous area of Pyoseon watershed in Jeju Island. J. Korea Water Resour. Assoc. 2021, 54, 1143–1154. [Google Scholar]
- Rodriguez-Galiano, V.; Mendes, M.P.; Garcia-Soldado, M.J.; Chica-Olmo, M.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using Random Forest and multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (Southern Spain). Sci. Total Environ. 2014, 476, 189–206. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M. Random Forests with R; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Louppe, G. Understanding random forests: From theory to practice. arXiv 2014, arXiv:1407.7502. [Google Scholar]
- Fratello, M.; Tagliaferri, R. Decision trees and random forests. In Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics; Elsvier: Amsterdam, The Netherlands, 2018; Volume 1. [Google Scholar]
- Amro, A.; Al-Akhras, M.; Hindi, K.E.; Habib, M.; Shawar, B.A. Instance Reduction for Avoiding Overfitting in Decision Trees. J. Intell. Syst. 2021, 30, 438–459. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Pham, L.T.; Luo, L.; Finley, A. Evaluation of random forests for short-term daily streamflow forecasting in rainfall-and snowmelt-driven watersheds. Hydrol. Earth Syst. Sci. 2021, 25, 2997–3015. [Google Scholar] [CrossRef]
- Madani, A.; Niyazi, B. Groundwater Potential Mapping Using Remote Sensing and Random Forest Machine Learning Model: A Case Study from Lower Part of Wadi Yalamlam, Western Saudi Arabia. Sustainability 2023, 15, 2772. [Google Scholar] [CrossRef]
- Moghaddam, D.D.; Rahmati, O.; Panahi, M.; Tiefenbacher, J.; Darabi, H.; Haghizadeh, A.; Haghighi, A.T.; Nalivan, O.A.; Bui, D.T. The effect of sample size on different machine learning models for groundwater potential mapping in mountain bedrock aquifers. Catena 2020, 187, 104421. [Google Scholar] [CrossRef]
- Afrifa, S.; Zhang, T.; Appiahene, P.; Varadarajan, V. Mathematical and machine learning models for groundwater level changes: A systematic review and bibliographic analysis. Future Internet 2022, 14, 259. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Arshad, A.; Mirchi, A.; Vilcaez, J.; Akbar, M.U.; Madani, K. Reconstructing high-resolution groundwater level data using a hybrid random forest model to quantify distributed groundwater changes in the Indus Basin. J. Hydrol. 2024, 628, 130535. [Google Scholar] [CrossRef]
- Brenner, C.; Frame, J.; Nearing, G.; Schulz, K. Schätzung der Verdunstung mithilfe von Machine- und Deep Learning-Methoden. Osterr. Wasser-Und Abfallwirtsch. 2021, 73, 295–307. [Google Scholar] [CrossRef]
- Feigl, M.; Lebiedzinski, K.; Herrnegger, M.; Schulz, K. Vorhersage der Fließgewässertemperaturen in österreichischen Einzugsgebieten mittels Machine Learning-Verfahren. Osterr. Wasser-Und Abfallwirtsch. 2021, 73, 308–328. [Google Scholar] [CrossRef]
- Yang, Y.; Chui, T.F.M. Modeling and interpreting hydrological responses of sustainable urban drainage systems with explainable machine learning methods. Hydrol. Earth Syst. Sci. 2021, 25, 5839–5858. [Google Scholar] [CrossRef]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in water resources engineering: A systematic literature review (December 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Gzar, D.A.; Mahmood, A.M.; Abbas, M.K. A Comparative Study of Regression Machine Learning Algorithms: Tradeoff Between Accuracy and Computational Complexity. Math. Model. Eng. Probl. 2022, 9, 1217. [Google Scholar] [CrossRef]
- Seelbach, P.W.; Hinz, L.C.; Wiley, M.J.; Cooper, A.R. Use of multiple linear regression to estimate flow regimes for all rivers across Illinois, Michigan, and Wisconsin. Fish. Res. Rep 2011, 2095, 1–35. [Google Scholar]
- Bedi, S.; Samal, A.; Ray, C.; Snow, D. Comparative evaluation of machine learning models for groundwater quality assessment. Environ. Monit. Assess. 2020, 192, 1–23. [Google Scholar] [CrossRef]
- Singha, S.; Pasupuleti, S.; Singha, S.S.; Singh, R.; Kumar, S. Prediction of groundwater quality using efficient machine learning technique. Chemosphere 2021, 276, 130265. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Thomas, B.F.; Behrangi, A.; Famiglietti, J.S. Precipitation intensity effects on groundwater recharge in the southwestern United States. Water 2016, 8, 90. [Google Scholar] [CrossRef]
- Ali, Y.A.; Awwad, E.M.; Al-Razgan, M.; Maarouf, A. Hyperparameter search for machine learning algorithms for optimizing the computational complexity. Processes 2023, 11, 349. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Frei, C.; Schöll, R.; Fukutome, S.; Schmidli, J.; Vidale, P.L. Future change of precipitation extremes in Europe: Intercomparison of scenarios from regional climate models. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Hancock, J.; Khoshgoftaar, T.M. Impact of hyperparameter tuning in classifying highly imbalanced big data. In Proceedings of the 2021 IEEE 22nd International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 10–12 August 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- A Ilemobayo, J.; Durodola, O.; Alade, O.; J Awotunde, O.; T Olanrewaju, A.; Falana, O.; Ogungbire, A.; Osinuga, A.; Ogunbiyi, D.; Ifeanyi, A. Hyperparameter Tuning in Machine Learning: A Comprehensive Review. J. Eng. Res. Rep. 2024, 26, 388–395. [Google Scholar] [CrossRef]
- Maliva, R. Modeling of Climate Change and Aquifer Recharge and Water Levels. In Climate Change and Groundwater: Planning and Adaptations for a Changing and Uncertain Future: WSP Methods in Water Resources Evaluation Series No. 6; Springer: Berlin/Heidelberg, Germany, 2021; pp. 89–111. [Google Scholar]
- Faridatul, M.I. A comparative study on precipitation and groundwater level interaction in the highly urbanized area and its periphery. Curr. Urban Stud. 2018, 6, 209. [Google Scholar] [CrossRef]
- Wang, D.; Li, P.; He, X.; He, S. Exploring the response of shallow groundwater to precipitation in the northern piedmont of the Qinling Mountains, China. Urban Clim 2022, 47, 101379. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Luijendijk, E.; Moeck, C.; van der Velde, Y.; Allen, S.T. Global recharge data set indicates strengthened groundwater connection to surface fluxes. Geophys. Res. Lett. 2022, 49, e2022GL099010. [Google Scholar] [CrossRef]
- Post, V.E.; Asmuth, J.R. Hydraulic head measurements-new technologies, classic pitfalls. Hydrogeol. J. 2013, 21, 737–750. [Google Scholar] [CrossRef]
- Rau, G.C.; Post, V.E.; Shanafield, M.; Krekeler, T.; Banks, E.W.; Blum, P. Error in hydraulic head and gradient time-series measurements: A quantitative appraisal. Hydrol. Earth Syst. Sci. 2019, 23, 3603–3629. [Google Scholar] [CrossRef]
- Huff, F. Sampling errors in measurement of mean precipitation. J. Appl. Meteorol. 1970, 9, 35–44. [Google Scholar] [CrossRef]
- Harrison, D.; Driscoll, S.; Kitchen, M. Improving precipitation estimates from weather radar using quality control and correction techniques. Meteorol. Appl. 2000, 7, 135–144. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Chen, N.-C.; Wen, H.-Y.; Li, F.-M.; Hsu, S.-M.; Ke, C.-C.; Lin, Y.-T.; Huang, C.-C. Investigation and Estimation of Groundwater Level Fluctuation Potential: A Case Study in the Pei-Kang River Basin and Chou-Shui River Basin of the Taiwan Mountainous Region. Appl. Sci. 2022, 12, 7060. [Google Scholar] [CrossRef]
- Giuntoli, I.; Vidal, J.-P.; Prudhomme, C.; Hannah, D.M. Future hydrological extremes: The uncertainty from multiple global climate and global hydrological models. Earth Syst. Dyn. 2015, 6, 267–285. [Google Scholar] [CrossRef]
- Corinna, C.; Mehryar, M.; Michael, R.; Afshin, R. Sample selection bias correction theory. In International Conference on Algorithmic Learning Theory; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Tsuchihara, T.; Yoshimoto, S.; Shirahata, K.; Nakazato, H.; Ishida, S. Analysis of groundwater-level fluctuation and linear regression modeling for prediction of initial groundwater level during irrigation of rice paddies in the Nasunogahara alluvial fan, central Japan. Environ. Earth Sci. 2023, 82, 473. [Google Scholar] [CrossRef]
- Boeing, F.; Wagener, T.; Marx, A.; Rakovec, O.; Kumar, R.; Samaniego, L.; Attinger, S. Increasing influence of evapotranspiration on prolonged water storage recovery in Germany. Environ. Res. Lett. 2024, 19, 024047. [Google Scholar] [CrossRef]
- Chen, Z.; Grasby, S.E.; Osadetz, K.G. Predicting average annual groundwater levels from climatic variables: An empirical model. J. Hydrol. 2002, 260, 102–117. [Google Scholar] [CrossRef]
- Heo, J.; Kim, T.; Park, H.; Ha, T.; Kang, H.; Yang, M. A study of a correlation between groundwater level and precipitation using statistical time series analysis by land cover types in urban areas. Korean J. Remote Sens. 2021, 37, 1819–1827. [Google Scholar]
- Neukum, C.; Azzam, R. Impact of climate change on groundwater recharge in a small catchment in the Black Forest, Germany. Hydrogeol. J. 2012, 20, 547–560. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Sadegh, M. Groundwater level modeling with machine learning: A systematic review and meta-analysis. Water 2022, 14, 949. [Google Scholar] [CrossRef]
- Mirarabi, A.; Nassery, H.R.; Nakhaei, M.; Adamowski, J.; Akbarzadeh, A.H.; Alijani, F. Evaluation of data-driven models (SVR and ANN) for groundwater-level prediction in confined and unconfined systems. Environ. Earth Sci. 2019, 78, 489. [Google Scholar] [CrossRef]
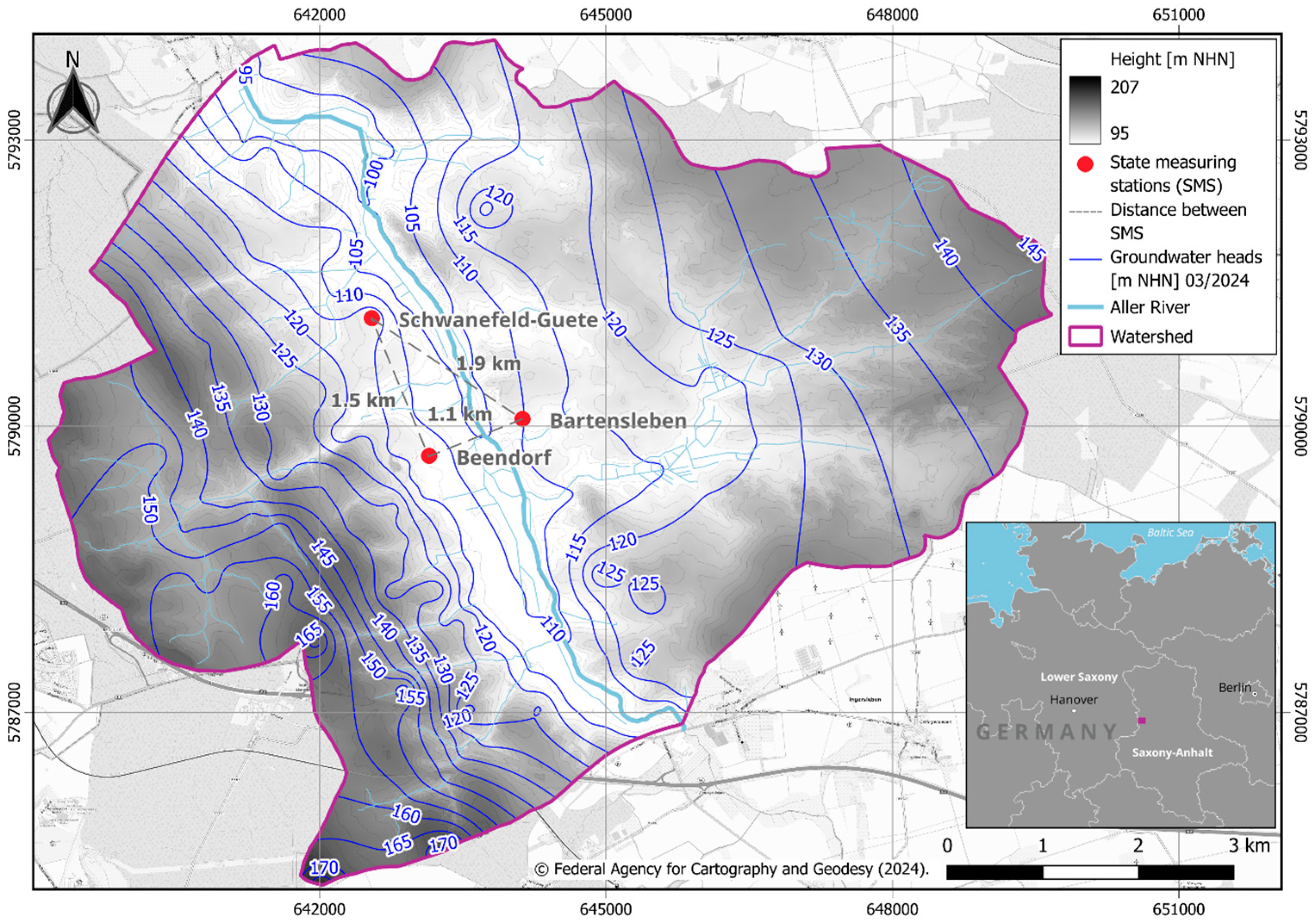

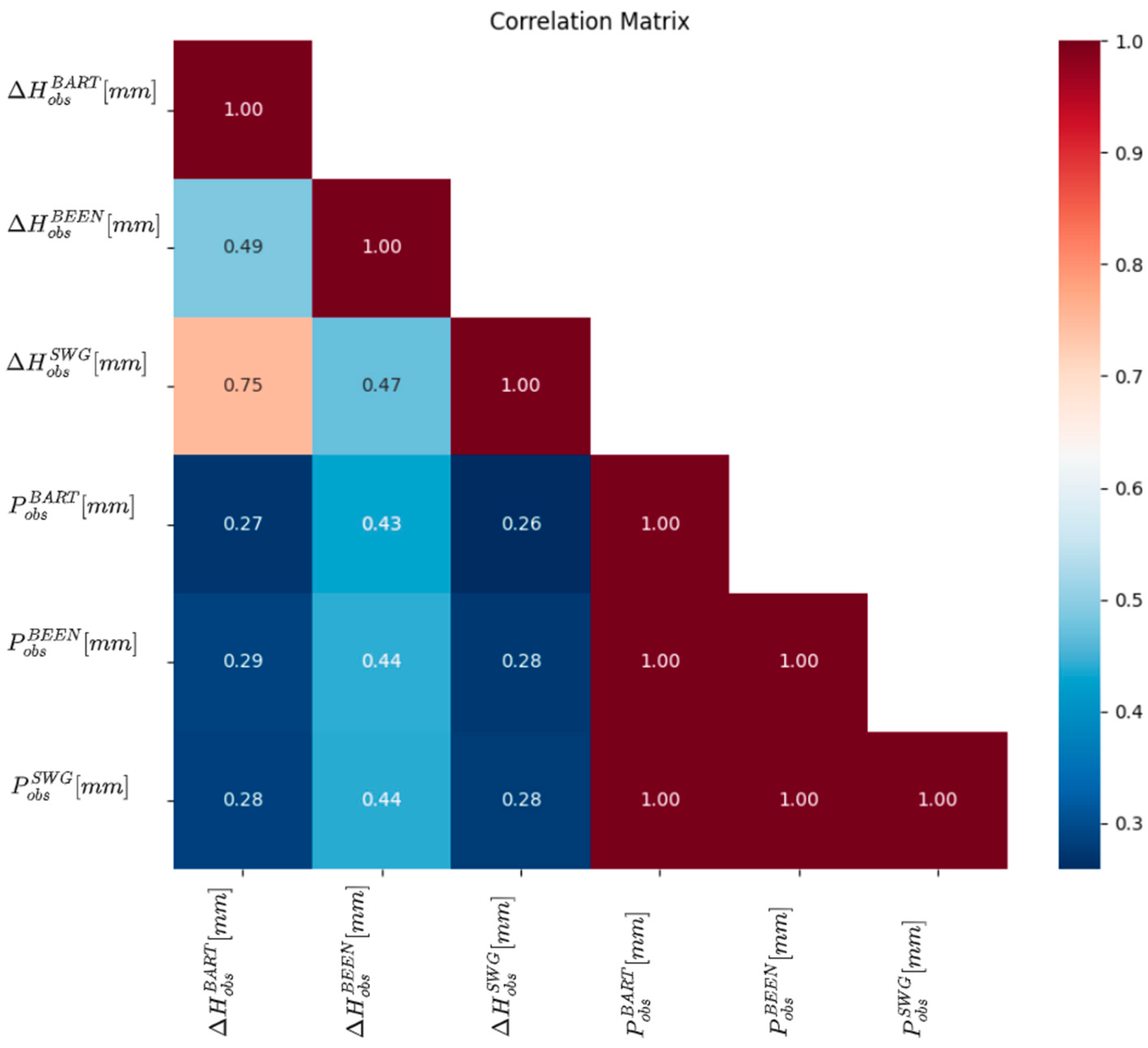
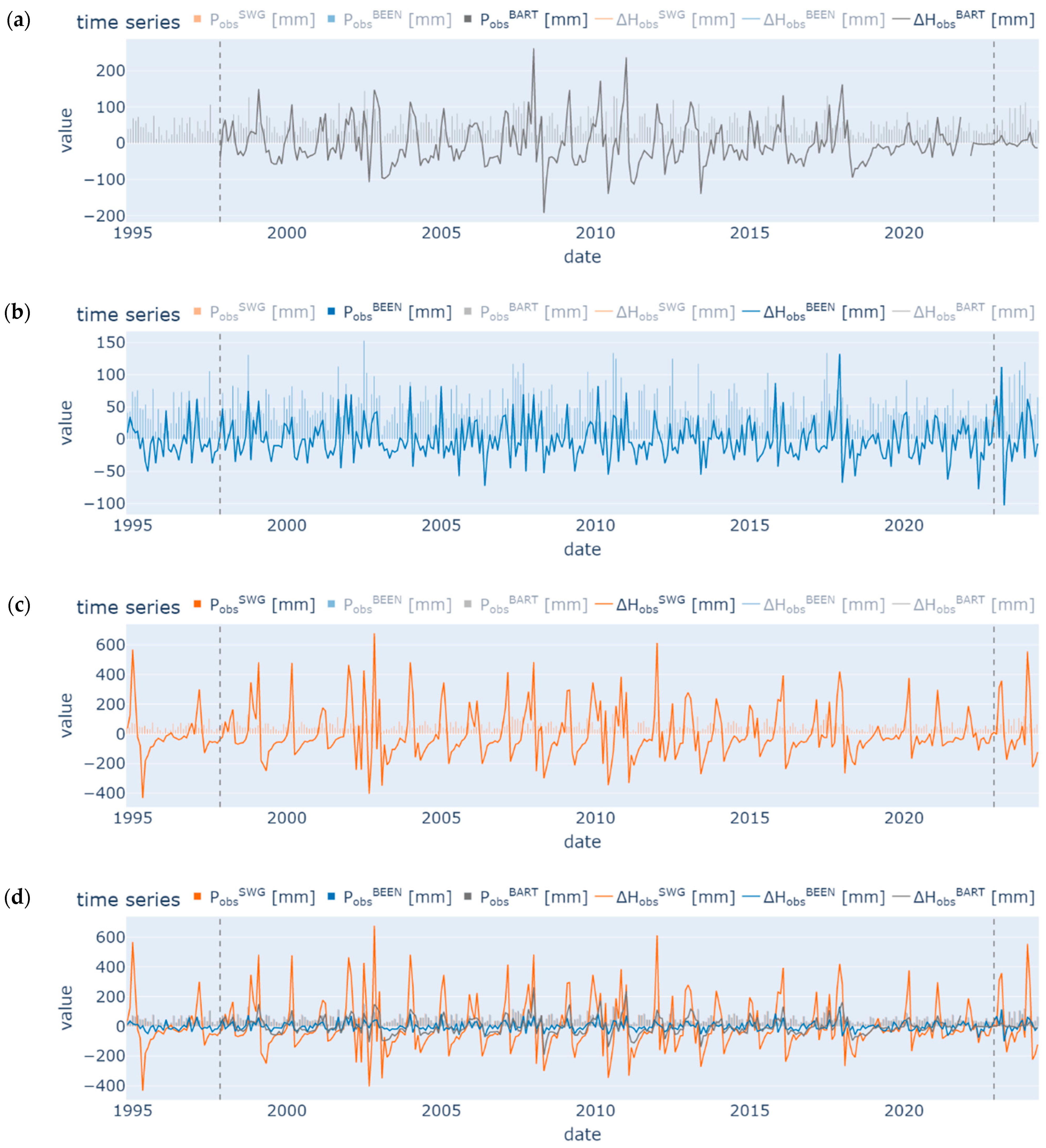
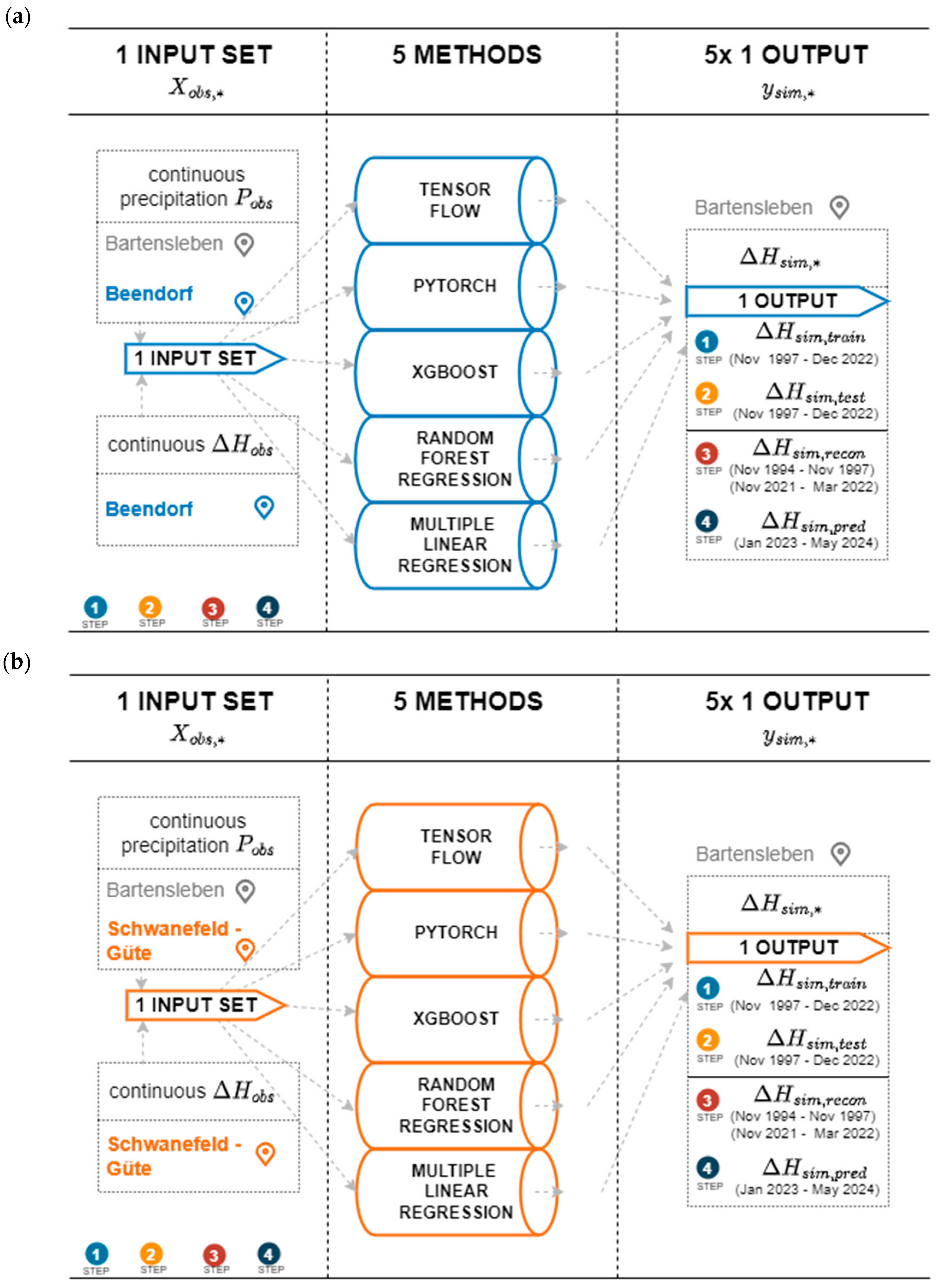


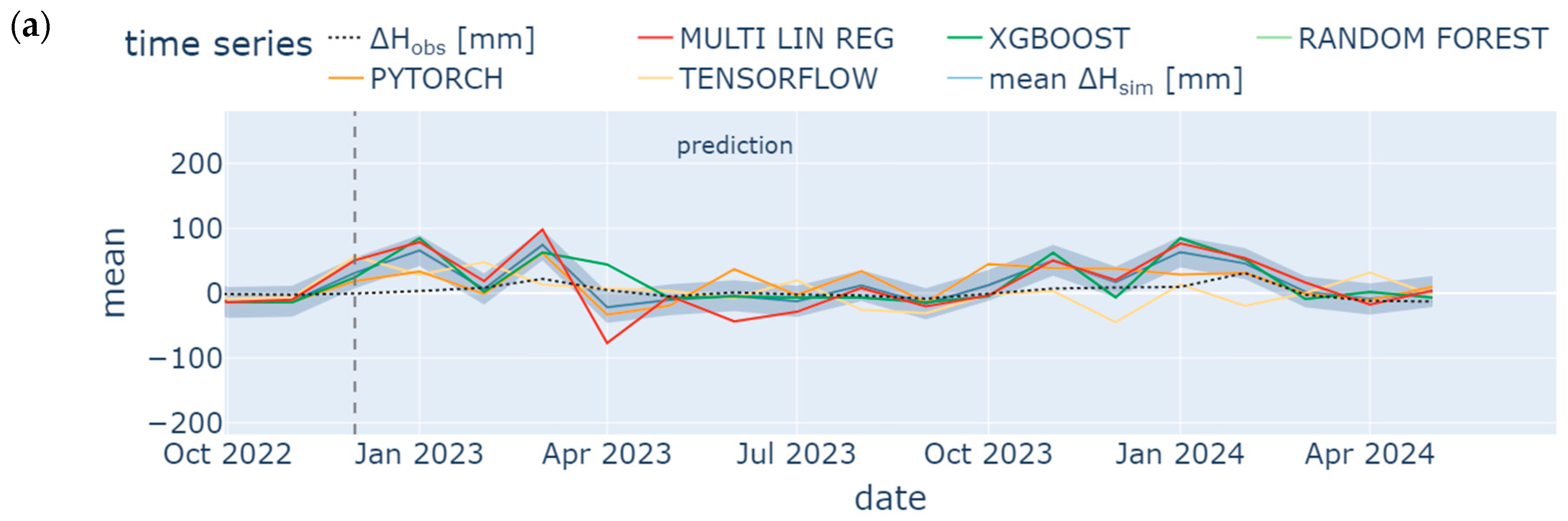
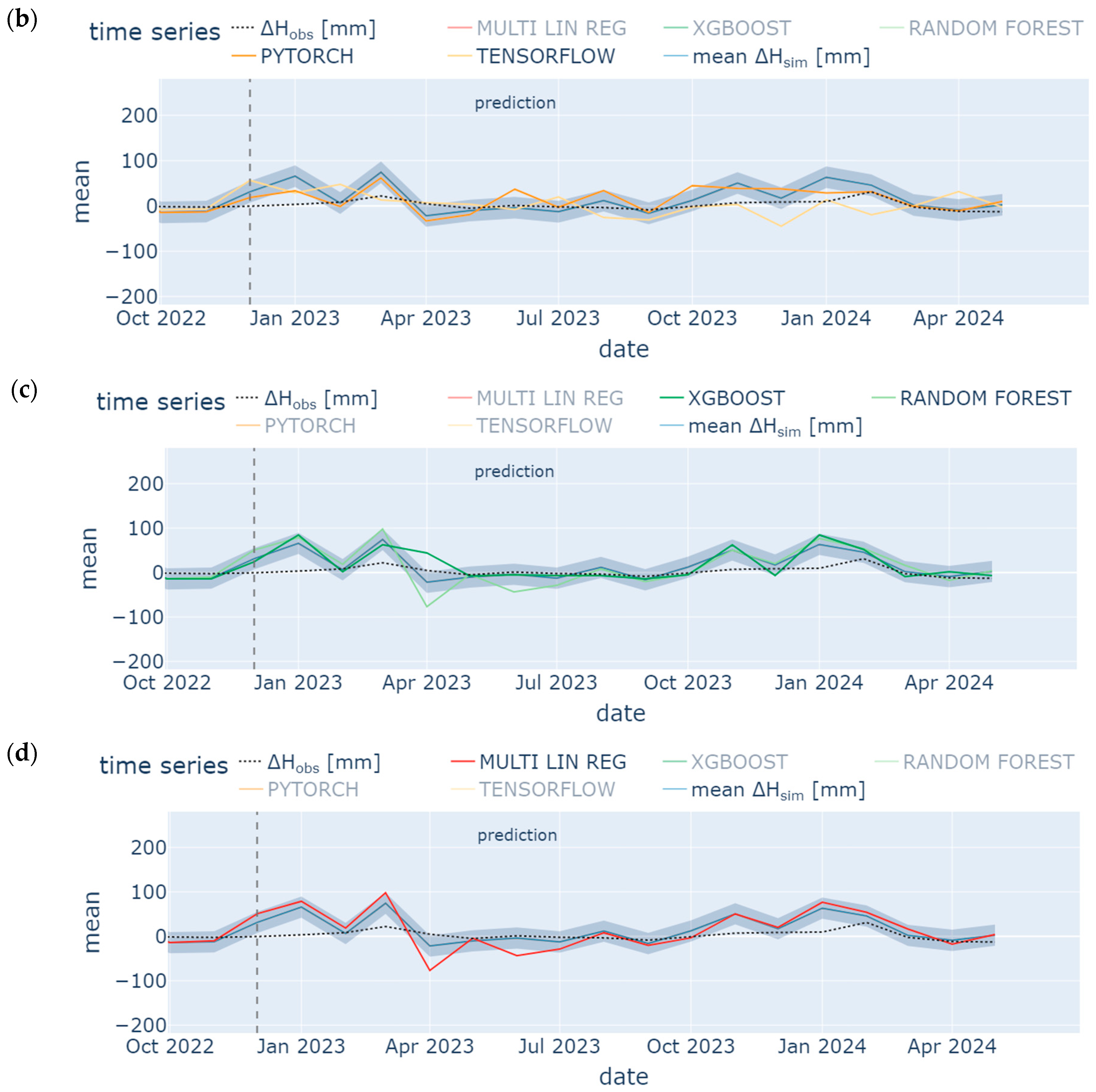
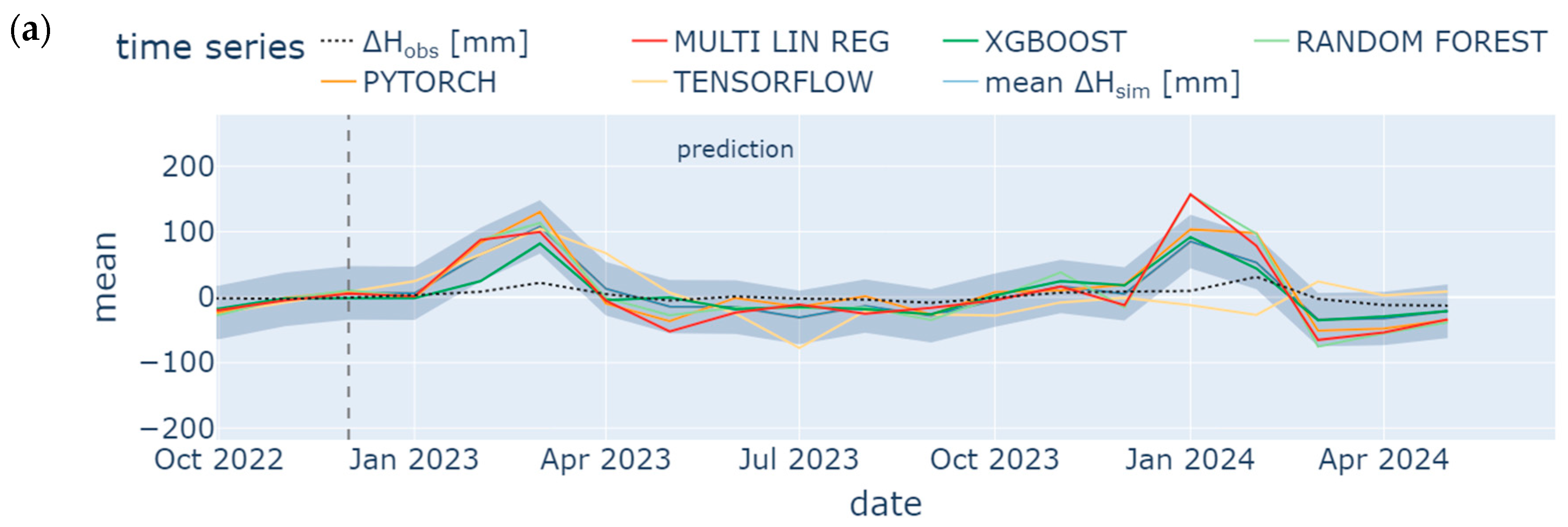
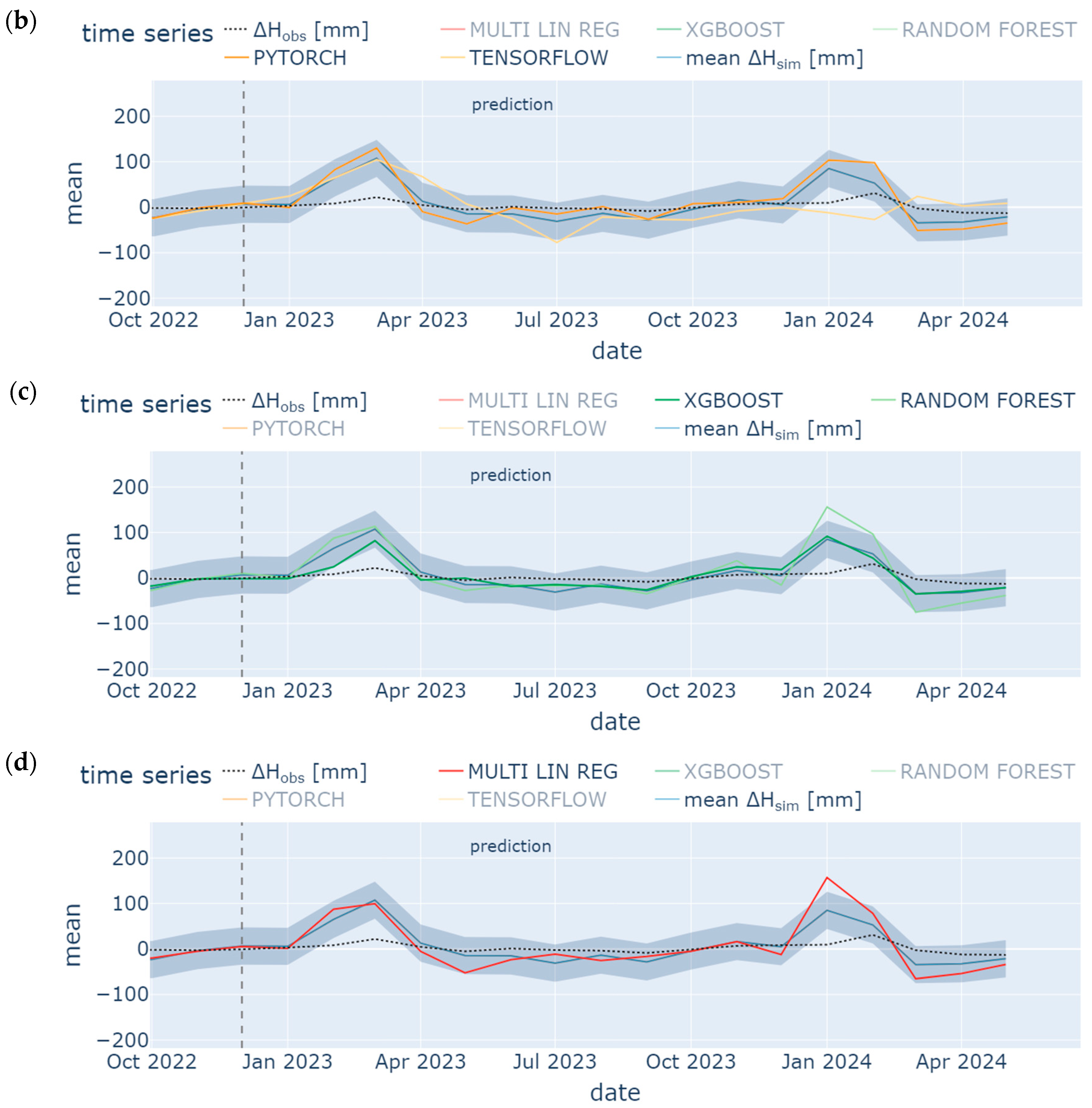
| Monitoring Name | BART | BEEN | SWG |
|---|---|---|---|
| Time Period—Start | November 1997 | November 1994 | November 1994 |
| Time Period—End | May 2024 | May 2024 | May 2024 |
| Monitoring Type | GW-monitoring tube | GW-monitoring tube | GW-monitoring tube |
| Easting | 644125 | 643147 | 642547 |
| Northing | 5790076 | 5789689 | 5791133 |
| Monitoring Interval | Daily | Weekly | Weekly |
| Unit | m | M | m |
| Base [m] | 9 | 5 | 31 |
| Measuring Point [m] | 122.05 | 115.84 | 122.54 |
| Groundwater Body | Upper Aller Mesozoic bedrock on the right | Upper Aller Mesozoic bedrock on the left | Upper Aller Mesozoic bedrock on the left |
| Monitoring Name | BART | BEEN | SWG |
|---|---|---|---|
| Time Period—Start | January 1881 | January 1881 | January 1881 |
| Time Period—End | May 2024 | May 2024 | May 2024 |
| Interpolation Type | Inverse-distance, raster type | Inverse-distance, raster type | Inverse-distance, raster type |
| Unit | mm | Mm | mm |
| Data Statistics | [mm] | (b) Precipitation [mm] | ||||
|---|---|---|---|---|---|---|
| Monitoring Name | BART | BEEN | SWG | BART | BEEN | SWG |
| Count | 316 | 355 | 355 | 355 | 355 | 355 |
| Mean | −0.22 | −0.29 | 0.2 | 47 | 49 | 49 |
| Std. | 57 | 31 | 168 | 26 | 27 | 27 |
| Min | −193 | −103 | −433 | 1 | 1 | 1 |
| 10% | −58 | −33 | −175 | 19 | 19 | 19 |
| 25% | −35 | −20 | −83 | 29 | 30 | 30 |
| 50% | −10 | −5 | −38 | 42 | 45 | 44 |
| 75% | 26 | 15 | 54 | 63 | 65 | 66 |
| 90% | 73 | 38 | 237 | 80 | 83 | 83 |
| Max | 263 | 133 | 678 | 145 | 153 | 156 |
| Hyperparameter | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression |
|---|---|---|---|---|---|
| Learning Rate | 0.01 | 0.001 | 0.1 | ||
| Number of Epochs | 1000 | 10 | |||
| Optimizer | Adamax | Adam | |||
| Activation Functions | ReLu | ReLu | |||
| Number of Layers and Units per Layer | 2 | 2 | |||
| Neurons | 3:250:1950:1 | 3:1050:256:1 | |||
| Loss Function | MSE | MSE | |||
| Dropout Rate | 0.4 | ||||
| Number of Trees (n_estimators) | 10 | 8 | |||
| Maximum Depth (max_depth) | 5 | 3 | |||
| Minimum Samples per Leaf (min_samples_leaf) | 1 | ||||
| Minimum Samples to Split (min_samples_split) | 2 | ||||
| Criterion (criterion) | Squared error | Squared error | |||
| −10.174 | |||||
| [mm] | 12.234 | ||||
| [mm] | −12.512 | ||||
| [mm] | 0.797 |
| Hyperparameter | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression |
|---|---|---|---|---|---|
| Learning Rate | 0.01 | 0.001 | 0.1 | ||
| Number of Epochs | 1000 | 1000 | |||
| Optimizer | Adamax | Adam | |||
| Activation Functions | ReLu | ReLu | |||
| Number of Layers and Units per Layer | 2 | 2 | |||
| Neurons | 3:750:1850:1 | 3:256:8:1 | |||
| Loss Function | MSE | MSE | |||
| Dropout Rate | 0.4 | ||||
| Number of Trees (n_estimators) | 4 | 100 | |||
| Maximum Depth (max_depth) | 10 | 6 | |||
| Minimum Samples per Leaf (min_samples_leaf) | 2 | ||||
| Minimum Samples to Split (min_samples_split) | 10 | ||||
| Criterion (criterion) | Squared error | Squared error | |||
| −5.218 | |||||
| [mm] | 1.128 | ||||
| [mm] | −1.071 | ||||
| [mm] | 0.280 |
| May–October BEEN | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression | Observed |
|---|---|---|---|---|---|---|
| count | 175 | 175 | 175 | 175 | 175 | 157 |
| mean | −10 | 0 | −12 | −6 | −14 | −27 |
| std | 29 | 24 | 28 | 16 | 28 | 36 |
| min | −124 | −38 | −120 | −54 | −100 | −193 |
| 25% | −23 | −18 | −23 | −7 | −31 | −48 |
| 50% | −8 | −5 | −15 | −7 | −15 | −25 |
| 75% | 5 | 12 | −3 | −4 | −1 | −5 |
| max | 53 | 80 | 108 | 60 | 87 | 108 |
| May–October SWG | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression | Observed |
|---|---|---|---|---|---|---|
| count | 175 | 175 | 175 | 175 | 175 | 157 |
| mean | −16 | −18 | −18 | −12 | −21 | −27 |
| std | 24 | 24 | 28 | 17 | 28 | 36 |
| min | −136 | −114 | −116 | −74 | −123 | −193 |
| 25% | −25 | −30 | −34 | −21 | −29 | −48 |
| 50% | −14 | −20 | −18 | −16 | −18 | −25 |
| 75% | −4 | −9 | −1 | −2 | −12 | −5 |
| max | 68 | 82 | 113 | 60 | 135 | 108 |
| Phase | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression |
|---|---|---|---|---|---|
| TRAIN | |||||
| MSE | 732.43 | 1064.59 | 689.06 | 1116.30 | 1312.28 |
| MAE | 18.69 | 23.86 | 19.16 | 24.00 | 26.44 |
| NSE | 0.71 | 0.70 | 0.81 | 0.69 | 0.64 |
| TEST | |||||
| MSE | 1412.91 | 1452.25 | 1389.62 | 1489.22 | 1523.56 |
| MAE | 28.18 | 27.23 | 27.03 | 27.26 | 27.16 |
| NSE | 0.65 | 0.53 | 0.55 | 0.51 | 0.50 |
| PREDICT | |||||
| MSE | 1338.06 | 1234.11 | 1015.11 | 1206.24 | 2739.21 |
| MAE | 30.07 | 25.31 | 22.53 | 24.72 | 37.33 |
| NSE | 0.66 | 0.62 | 0.69 | 0.63 | −32.78 |
| Phase | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression |
|---|---|---|---|---|---|
| TRAIN | |||||
| MSE | 1353.69 | 2895.67 | 1339.18 | 2162.52 | 2469.69 |
| MAE | 26.85 | 40.99 | 28.83 | 36.06 | 37.65 |
| NSE | 0.46 | 0.20 | 0.63 | 0.40 | 0.31 |
| TEST | |||||
| MSE | 2846.9 | 2432.60 | 2429.47 | 2256.11 | 1988.08 |
| MAE | 39.98 | 37.72 | 37.93 | 36.04 | 33.38 |
| NSE | 0.3 | 0.21 | 0.21 | 0.26 | 0.35 |
| PREDICT | |||||
| MSE | 2652.13 | 2688.76 | 2553.15 | 2361.79 | 1704.11 |
| MAE | 42.18 | 40.23 | 38.47 | 36.48 | 31.05 |
| NSE | 0.33 | 0.18 | 0.22 | 0.28 | −13.02 |
| May–October BEEN | TensorFlow | PyTorch | Random Forest Regression | XGBoost | Multiple Linear Regression | Observed |
|---|---|---|---|---|---|---|
| count | 120 | 120 | 120 | 120 | 120 | 106 |
| mean | 21 | 28.58 | 32 | 18 | 20 | 34 |
| std | 49 | 60.08 | 60 | 38 | 60 | 65 |
| min | −128 | −81 | −102 | −74 | −103 | −113 |
| 25% | −18 | −26 | −4 | −10 | −22 | −6 |
| 50% | 19 | 20 | 40 | 23 | 15 | 29 |
| 75% | 58 | 80 | 73 | 38 | 63 | 71 |
| max | 108 | 165 | 156 | 92 | 176 | 263 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, T.V.; Peche, A.; Kringel, R.; Brömme, K.; Altfelder, S. Machine Learning-Based Reconstruction and Prediction of Groundwater Time Series in the Allertal, Germany. Water 2025, 17, 433. https://doi.org/10.3390/w17030433
Tran TV, Peche A, Kringel R, Brömme K, Altfelder S. Machine Learning-Based Reconstruction and Prediction of Groundwater Time Series in the Allertal, Germany. Water. 2025; 17(3):433. https://doi.org/10.3390/w17030433
Chicago/Turabian StyleTran, Tuong Vi, Aaron Peche, Robert Kringel, Katrin Brömme, and Sven Altfelder. 2025. "Machine Learning-Based Reconstruction and Prediction of Groundwater Time Series in the Allertal, Germany" Water 17, no. 3: 433. https://doi.org/10.3390/w17030433
APA StyleTran, T. V., Peche, A., Kringel, R., Brömme, K., & Altfelder, S. (2025). Machine Learning-Based Reconstruction and Prediction of Groundwater Time Series in the Allertal, Germany. Water, 17(3), 433. https://doi.org/10.3390/w17030433






