Determination of Equilibrium Loading by Empirical Models for the Modeling of Breakthrough Curves in a Fixed-Bed Column: From Experience to Practice
Abstract
1. Introduction
2. Methods
3. Results and Discussion
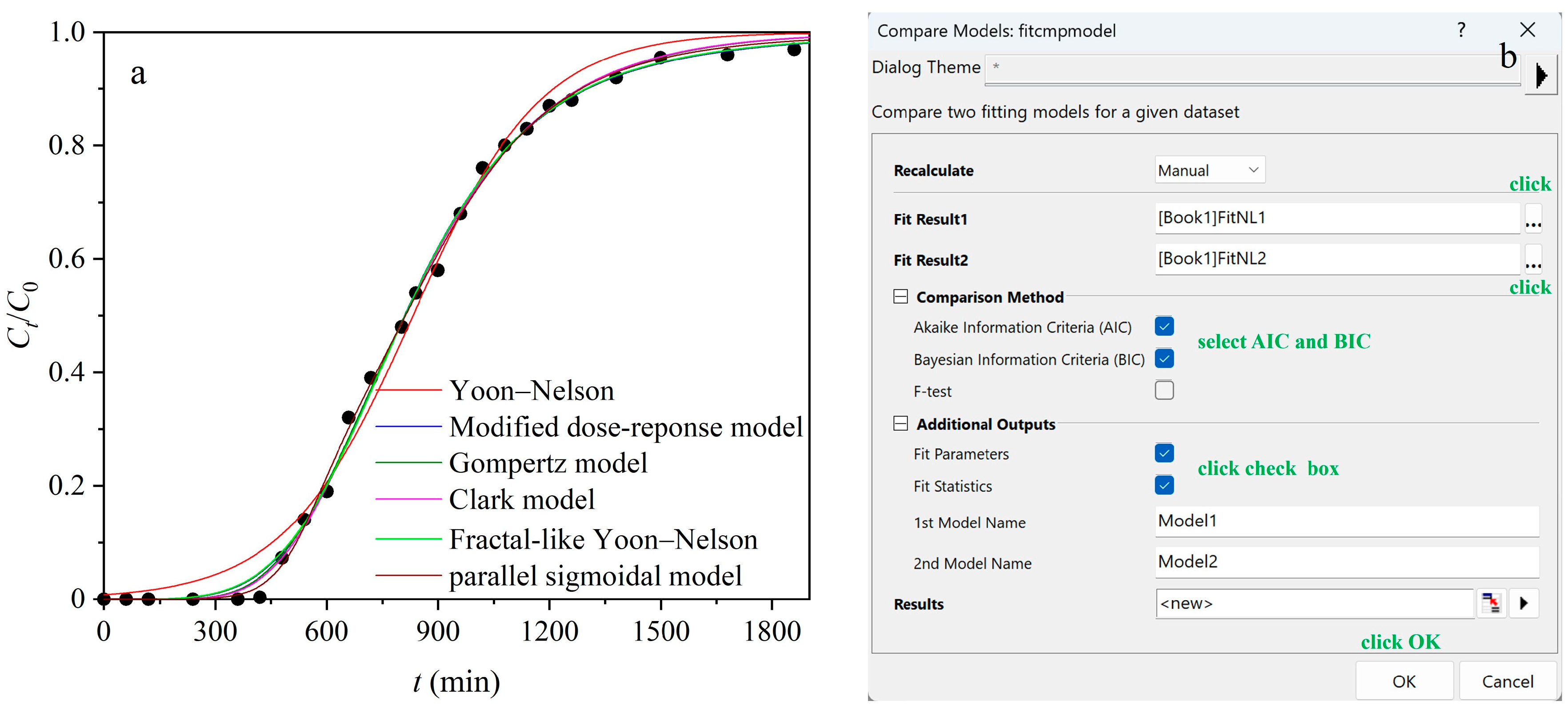
3.1. Empirical Breakthrough Models
3.1.1. Yoon–Nelson Model
3.1.2. Modified Dose–Response Model
3.1.3. Gompertz Model
3.1.4. Clark Model
3.1.5. Fractal-like Yoon–Nelson Model
3.1.6. Parallel Sigmoidal Model
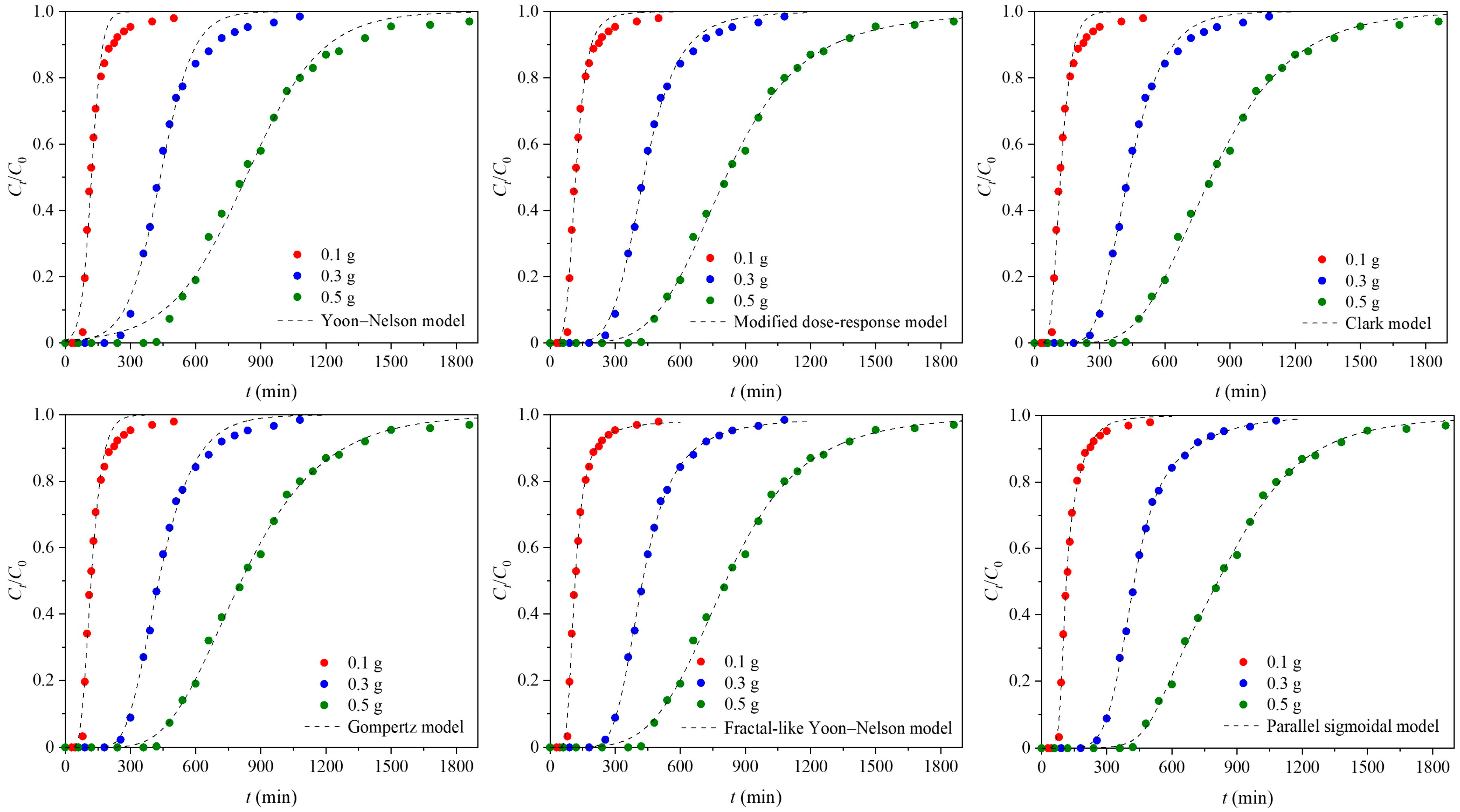
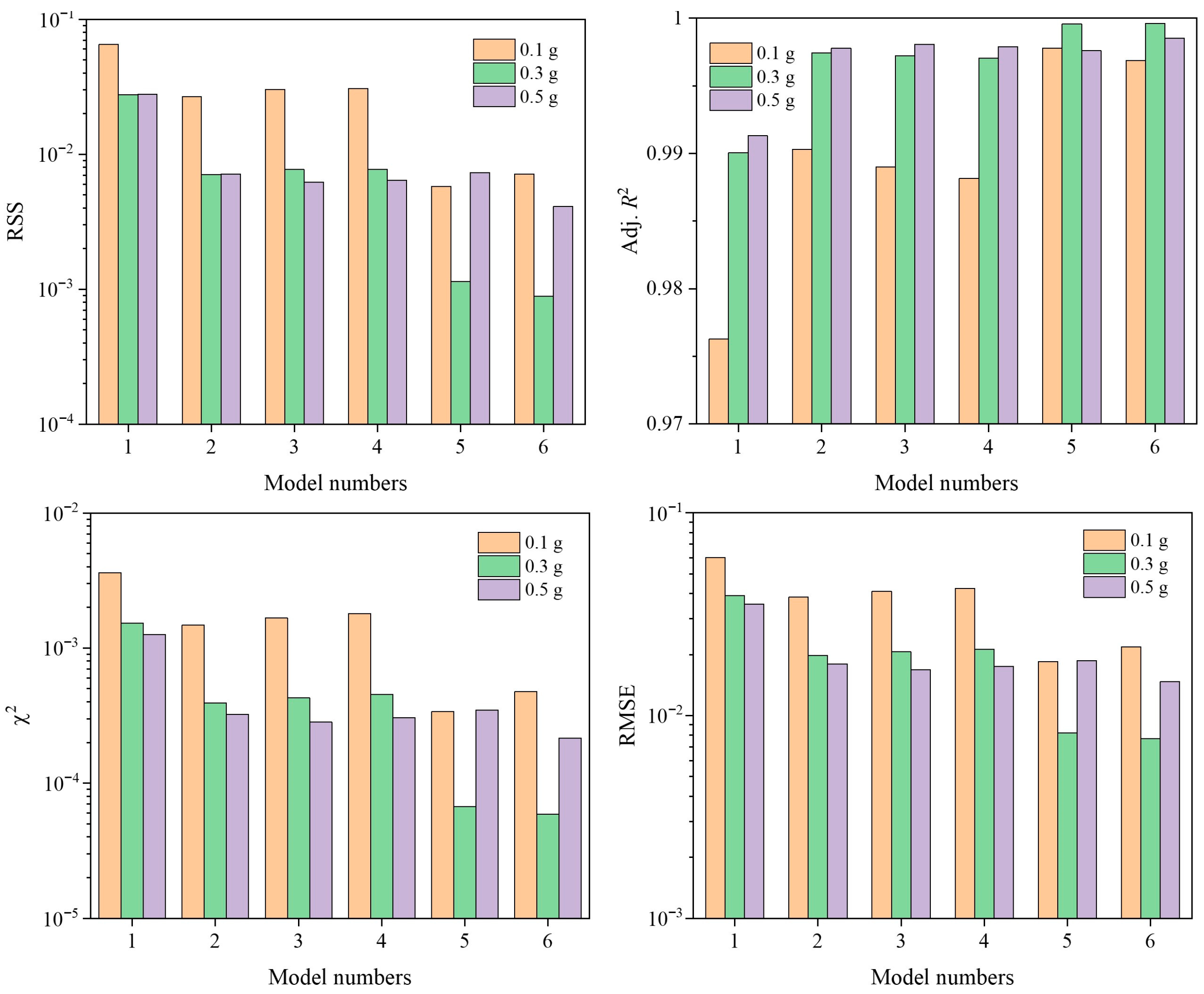
3.2. Fitting Quality
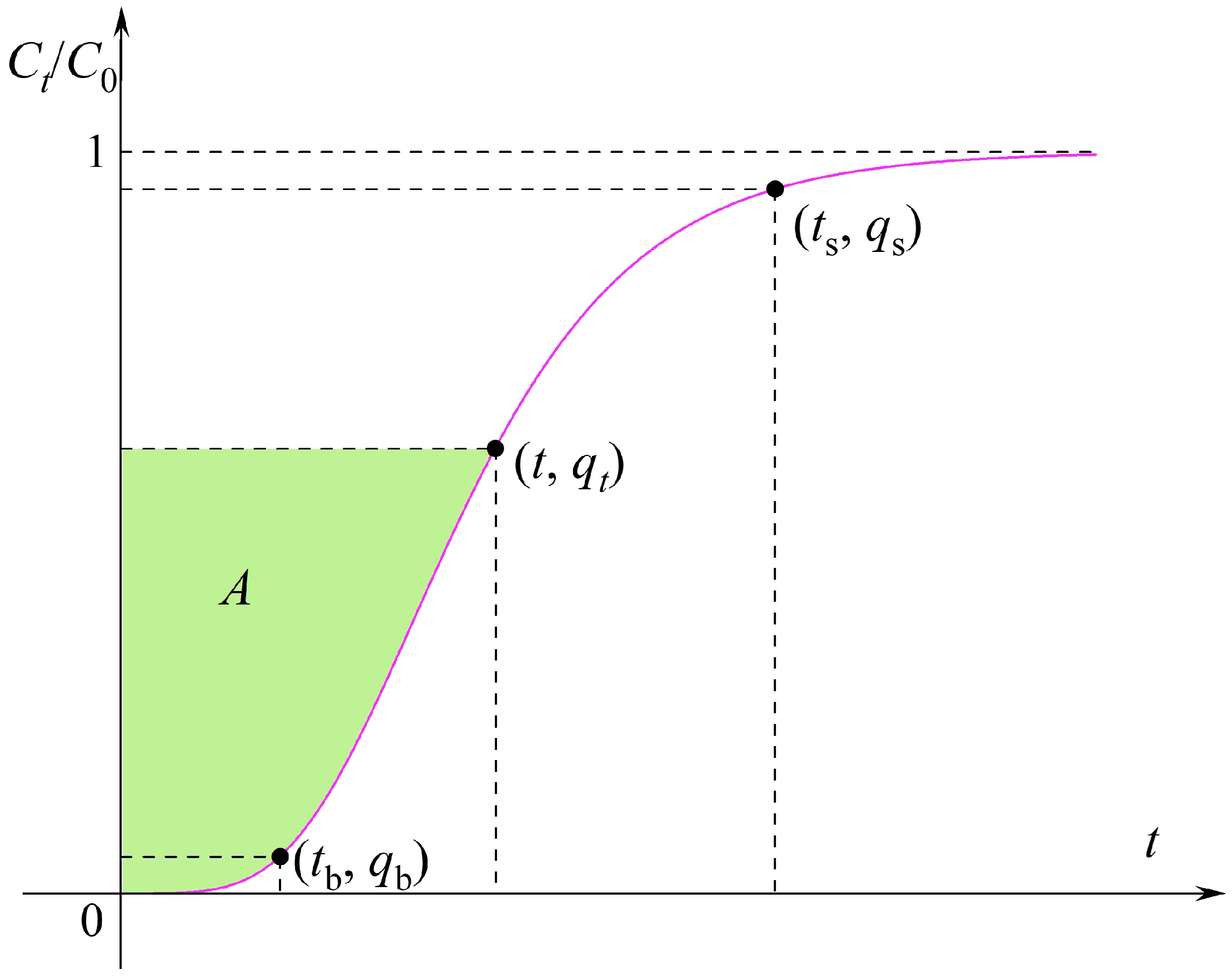
3.3. Equilibrium Loading
3.4. Model Comparison
4. Research Significance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | empirical parameter in the modified dose–response model (a > 1) |
| A | Clark constant |
| b | empirical parameter in the modified dose–response model (mL) |
| influent concentration (mg L−1) | |
| effluent concentration at time t (mg L−1) | |
| h | fractal-like exponent |
| Yoon–Nelson rate constant | |
| fractal-like Yoon–Nelson rate constant (min−(1−h)) | |
| empirical parameter in the parallel sigmoidal model | |
| empirical parameter in the parallel sigmoidal model | |
| n | number of data points or Freundlich constant |
| m | mass of the adsorbent packed in the column (g) |
| p | proportion of each part in two-stage adsorption mechanism or number of the model parameters |
| breakthrough capacity (mg g−1) | |
| saturation capacity (mg g−1) | |
| equilibrium loading (mg g−1) | |
| r | Clark constant (min−1) |
| t | operating time (min) |
| breakthrough time (min) | |
| saturation time (min) | |
| total operating time (min) | |
| v | volumetric flow rate (mL min−1) |
| observed values (y = Ct/C0) | |
| ýi | predicted values |
| χ2 | reduced chi-square |
| τ | operating time required to reach 50% breakthrough (min) |
| empirical parameter in the parallel sigmoidal model (min) | |
| empirical parameter in the parallel sigmoidal model (min) | |
| RSS | residual sum of squares |
| Adj. R2 | adjusted coefficient of determination |
| RMSE | root of mean squared error |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
Appendix A
References
- Hu, Q.; Yang, X.; Huang, L.; Li, Y.; Hao, L.; Pei, Q.; Pei, X. A critical review of breakthrough models with analytical solutions in a fixed-bed column. J. Water Process Eng. 2024, 59, 105065. [Google Scholar] [CrossRef]
- Juela, D.; Vera, M.; Cruzat, C.; Astudillo, A.; Vanegas, E. A new approach for scaling up fixed-bed adsorption columns for aqueous systems: A case of antibiotic removal on natural adsorbent. Process Saf. Environ. Prot. 2022, 159, 953–963. [Google Scholar] [CrossRef]
- Taka, A.L.; Klink, M.J.; Mbianda, X.Y.; Naidoo, E.B. Chitosan nanocomposites for water treatment by fixed-bed continuous flow column adsorption: A review. Carbohydr. Polym. 2021, 255, 117398. [Google Scholar] [CrossRef]
- Worch, E. Adsorption Technology in Water Treatment: Fundamentals, Processes, and Modeling; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2012. [Google Scholar]
- Suzaki, P.Y.R.; Munaro, M.T.; Triques, C.C.; Kleinübing, S.J.; Klen, M.R.F.; Bergamasco, R.; de Matos Jorge, L.M. Phenomenological mathematical modeling of heavy metal biosorption in fixed-bed columns. Chem. Eng. J. 2017, 326, 389–400. [Google Scholar] [CrossRef]
- Suzaki, P.Y.R.; Triques, C.C.; Munaro, M.T.; Steffen, V.; Kleinübing, S.J.; Klen, M.R.F.; Bergamasco, R.; de Matos Jorge, L.M. Phenomenological modeling and simulation of competitive biosorption of ternary heavy metal systems in a fixed bed column. Chem. Eng. Res. Des. 2023, 196, 701–710. [Google Scholar] [CrossRef]
- Hamdaoui, O. Removal of copper(II) from aqueous phase by Purolite C100-MB cation exchange resin in fixed bed columns: Modeling. J. Hazard. Mater. 2009, 161, 737–746. [Google Scholar] [CrossRef]
- Bohart, G.S.; Adams, E.Q. Some aspects of the behavior of charcoal with respect to chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef]
- Thomas, H.C. Chromatography: A problem in kinetics. Ann. N. Y. Acad. Sci. 1948, 49, 161–182. [Google Scholar] [CrossRef]
- Hu, Q.; Xie, Y.; Feng, C.; Zhang, Z. Fractal-like kinetics of adsorption on heterogeneous surfaces in the fixed-bed column. Chem. Eng. J. 2019, 358, 1471–1478. [Google Scholar] [CrossRef]
- Rojas-Mayorga, C.K.; Bonilla-Petriciolet, A.; Sánchez-Ruiz, F.J.; Moreno-Pérez, J.; Reynel-Ávila, H.E.; Aguayo-Villarreal, I.A.; Mendoza-Castillo, D.I. Breakthrough curve modeling of liquid-phase adsorption of fluoride ions on aluminum-doped bone char using micro-columns: Effectiveness of data fitting approaches. J. Mol. Liq. 2015, 208, 114–121. [Google Scholar] [CrossRef]
- Clark, R.M. Evaluating the cost and performance of field-scale granular activated carbon systems. Environ. Sci. Technol. 1987, 21, 573–580. [Google Scholar] [CrossRef]
- Yan, G.; Viraraghavan, T.; Chen, M. A new model for heavy metal removal in a biosorption column. Adsorpt. Sci. Technol. 2001, 19, 25–43. [Google Scholar] [CrossRef]
- Hu, Q.; He, Z.; Zhang, Y.; Ma, S.; Huang, L. One-pot solvothermal synthesis of Ca-Fe-La composite for advanced removal of phosphate from aqueous solutions in a fixed-bed column: Modeling and resource utilization. Environ. Technol. Innov. 2024, 36, 103888. [Google Scholar] [CrossRef]
- Yoon, Y.H.; Nelson, J.H. Application of gas adsorption kinetics I. A theoretical model for respirator cartridge service life. Am. Ind. Hyg. Assoc. J. 1984, 45, 509–516. [Google Scholar] [CrossRef]
- Tejedor, J.; Álvarez-Briceño, R.; Guerrero, V.H.; Villamar-Ayala, C.A. Removal of caffeine using agro-industrial residues in fixed-bed columns: Improving the adsorption capacity and efficiency by selecting adequate physical and operational parameters. J. Water Process. Eng. 2023, 53, 103778. [Google Scholar] [CrossRef]
- Hu, Q.; Xie, Y.; Feng, C.; Zhang, Z. Prediction of breakthrough behaviors using logistic, hyperbolic tangent and double exponential models in the fixed-bed column. Sep. Purif. Technol. 2019, 212, 572–579. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Huang, X.; Zhang, Q.; Wang, T.; Guo, X. Guideline for modeling solid-liquid adsorption: Kinetics, isotherm, fixed bed, and thermodynamics. Chemosphere 2024, 349, 140736. [Google Scholar] [CrossRef]
- Kopelman, R. Fractal reaction kinetics. Science 1988, 241, 1620–1626. [Google Scholar] [CrossRef]
- de Oliveira, J.T.; Costa, L.R.D.C.; Agnol, G.D.; Féris, L.A. Experimental design and data prediction by Bayesian statistics for adsorption of tetracycline in a GAC fixed-bed column. Sep. Purif. Technol. 2023, 319, 124097. [Google Scholar] [CrossRef]
- Jiang, S.; Lyu, Y.; Zhang, J.; Zhang, X.; Yuan, M.; Zhang, Z.; Jin, G.; He, B.; Xiong, W.; Yi, H. Continuous adsorption removal of organic pollutants from wastewater in a UiO-66 fixed bed column. J. Environ. Chem. Eng. 2024, 12, 111951. [Google Scholar] [CrossRef]
- Montagnaro, F.; Balsamo, M. Modelling CO2 adsorption dynamics onto amine-functionalised sorbents: A fractal-like kinetic perspective. Chem. Eng. Sci. 2018, 192, 603–612. [Google Scholar] [CrossRef]
- Haerifar, M.; Azizian, S. Fractal-like kinetics for adsorption on heterogeneous solid surfaces. J. Phys. Chem. C 2014, 118, 1129–1134. [Google Scholar] [CrossRef]
- Balsamo, M.; Montagnaro, F. Liquid–solid adsorption processes interpreted by fractal-like kinetic models. Environ. Chem. Lett. 2019, 17, 1067–1075. [Google Scholar] [CrossRef]
- Blagojev, N.; Kukić, D.; Vasić, V.; Šćiban, M.; Prodanović, J.; Bera, O. A new approach for modelling and optimization of Cu(II) biosorption from aqueous solutions using sugar beet shreds in a fixed-bed column. J. Hazard. Mater. 2019, 363, 366–375. [Google Scholar] [CrossRef]
- Mendes, P.A.P.; Rodrigues, A.E.; Horcajada, P.; Serre, C.; Silva, J.A.C. Single and multicomponent adsorption of hexane isomers in the microporous ZIF-8. Microporous Mesoporous Mater. 2014, 194, 146–156. [Google Scholar] [CrossRef]
- Nordin, A.H.; Ngadi, N.; Nordin, M.L.; Noralidin, N.A.; Nabgan, W.; Osman, A.Y.; Shaari, R. Spent tea waste extract as a green modifying agent of chitosan for aspirin adsorption: Fixed-bed column, modeling and toxicity studies. Int. J. Biol. Macromol. 2023, 253, 126501. [Google Scholar] [CrossRef]
- Najafi, H.; Maklavani, N.A.; Asasian-Kolur, N.; Sharifian, S.; Harasek, M. Copper oxide-incorporated pillared clay granular nanocomposite for efficient single and binary, batch and fixed bed column adsorption of levofloxacin and crystal violet. Chem. Eng. Sci. 2024, 295, 120184. [Google Scholar] [CrossRef]

| m (g) | Yoon–Nelson model | qb (mg g−1) | tb (min) | qs (mg g−1) | ts (min) | q0 (mg g−1) | |||||
| kYN (min−1) | τ (min) | ||||||||||
| 0.1 | 4.12 × 10−2 | 120.7 | 36.59 | 49.9 | 89.73 | 191.6 | 90.66 | ||||
| 0.3 | 1.32 × 10−2 | 437.4 | 52.46 | 213.5 | 108.44 | 661.3 | 109.41 | ||||
| 0.5 | 5.80 × 10−3 | 832.1 | 47.55 | 324.4 | 123.70 | 1339.8 | 124.96 | ||||
| m (g) | Modified dose–response model | qb (mg g−1) | tb (min) | qs (mg g−1) | ts (min) | q0 (mg g−1) | |||||
| a | b (mL) | ||||||||||
| 0.1 | 4.620 | 296.7 | 46.64 | 62.8 | 93.88 | 224.5 | 96.14 | ||||
| 0.3 | 5.527 | 1078.7 | 62.83 | 253.3 | 111.82 | 735.1 | 113.54 | ||||
| 0.5 | 4.619 | 2023.5 | 63.60 | 427.9 | 128.03 | 1531.0 | 129.66 | ||||
| m (g) | Gompertz model | qb (mg g−1) | tb (min) | qs (mg g−1) | ts (min) | q0 (mg g−1) | |||||
| k (min−1) | τ (min) | ||||||||||
| 0.1 | 2.81 × 10−2 | 105.8 | 49.65 | 66.7 | 93.40 | 211.6 | 94.75 | ||||
| 0.3 | 8.99 × 10−3 | 389.9 | 66.60 | 267.9 | 112.12 | 720.3 | 113.48 | ||||
| 0.5 | 3.96 × 10−3 | 717.1 | 65.50 | 440.00 | 127.50 | 1467.1 | 129.01 | ||||
| m (g) | Clark model | qb (mg g−1) | tb (min) | qs (mg g−1) | ts (min) | q0 (mg g−1) | |||||
| A | r (min−1) | n | |||||||||
| 0.1 | 1.64 × 10−2 | 2.87 × 10−2 | 1.0008 | 50.99 | 68.4 | 93.83 | 210.3 | 95.15 | |||
| 0.3 | 1.30 × 10−2 | 8.99 × 10−3 | 1.0004 | 66.71 | 268.3 | 112.24 | 720.8 | 113.59 | |||
| 0.5 | 1.09 × 10−2 | 4.01 × 10−3 | 1.0006 | 66.72 | 448.1 | 127.98 | 1462.6 | 129.48 | |||
| m (g) | Fractal-like Yoon–Nelson model | qb (mg g−1) | tb (min) | qs (mg g−1) | ts (min) | q0 (mg g−1) | |||||
| kYN,0 (min−(1−h)) | τ (min) | h | |||||||||
| 0.1 | 895.3 | 115.8 | 2.092 | 54.78 | 73.4 | 99.24 | 298.6 | 104.43 | |||
| 0.3 | 930.1 | 426.8 | 1.839 | 69.52 | 279.5 | 114.74 | 827.5 | 116.88 | |||
| 0.5 | 3.505 | 810.3 | 0.959 | 63.10 | 424.7 | 127.84 | 1520.5 | 129.48 | |||
| m (g) | Parallel sigmoidal model | qb (mg g−1) | tb (min) | qs (mg g−1) | ts (min) | q0 (mg g−1) | |||||
| k1 (min) | τ1 (min) | k2 (min−1) | τ2 (min) | p | |||||||
| 0.1 | 8.916 | 101.8 | 4.097 | 158.8 | 0.559 | 55.21 | 74.1 | 98.20 | 262.5 | 101.11 | |
| 0.3 | 6.909 | 411.1 | 5.257 | 736.2 | 0.873 | 67.94 | 273.5 | 114.86 | 834.3 | 116.69 | |
| 0.5 | 9.606 | 572.5 | 5.378 | 900.4 | 0.226 | 69.61 | 467.0 | 127.85 | 1480.2 | 129.50 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Zhang, Y.; Pei, Q.; Li, S. Determination of Equilibrium Loading by Empirical Models for the Modeling of Breakthrough Curves in a Fixed-Bed Column: From Experience to Practice. Water 2025, 17, 329. https://doi.org/10.3390/w17030329
Hu Q, Zhang Y, Pei Q, Li S. Determination of Equilibrium Loading by Empirical Models for the Modeling of Breakthrough Curves in a Fixed-Bed Column: From Experience to Practice. Water. 2025; 17(3):329. https://doi.org/10.3390/w17030329
Chicago/Turabian StyleHu, Qili, Yunhui Zhang, Qiuming Pei, and Shule Li. 2025. "Determination of Equilibrium Loading by Empirical Models for the Modeling of Breakthrough Curves in a Fixed-Bed Column: From Experience to Practice" Water 17, no. 3: 329. https://doi.org/10.3390/w17030329
APA StyleHu, Q., Zhang, Y., Pei, Q., & Li, S. (2025). Determination of Equilibrium Loading by Empirical Models for the Modeling of Breakthrough Curves in a Fixed-Bed Column: From Experience to Practice. Water, 17(3), 329. https://doi.org/10.3390/w17030329








