Impacts of the Degree of Heterogeneity on Design Flood Estimates: Region of Influence vs. Fixed Region Approaches
Abstract
1. Introduction
2. Data and Methodology
2.1. Selection of Study Area
2.2. Formation of Regions
2.3. Evaluation of Homogeneity of the Selected Regions
- H < 1: a proposed region is regarded as acceptably homogeneous;
- 1 ≤ H < 2: a proposed region is possibly heterogeneous;
- H ≥ 2: a proposed region is regarded as definitely heterogeneous.
2.4. Regional Estimation Model Development
2.5. Evaluation Criteria
3. Results
3.1. Exploratory Analysis
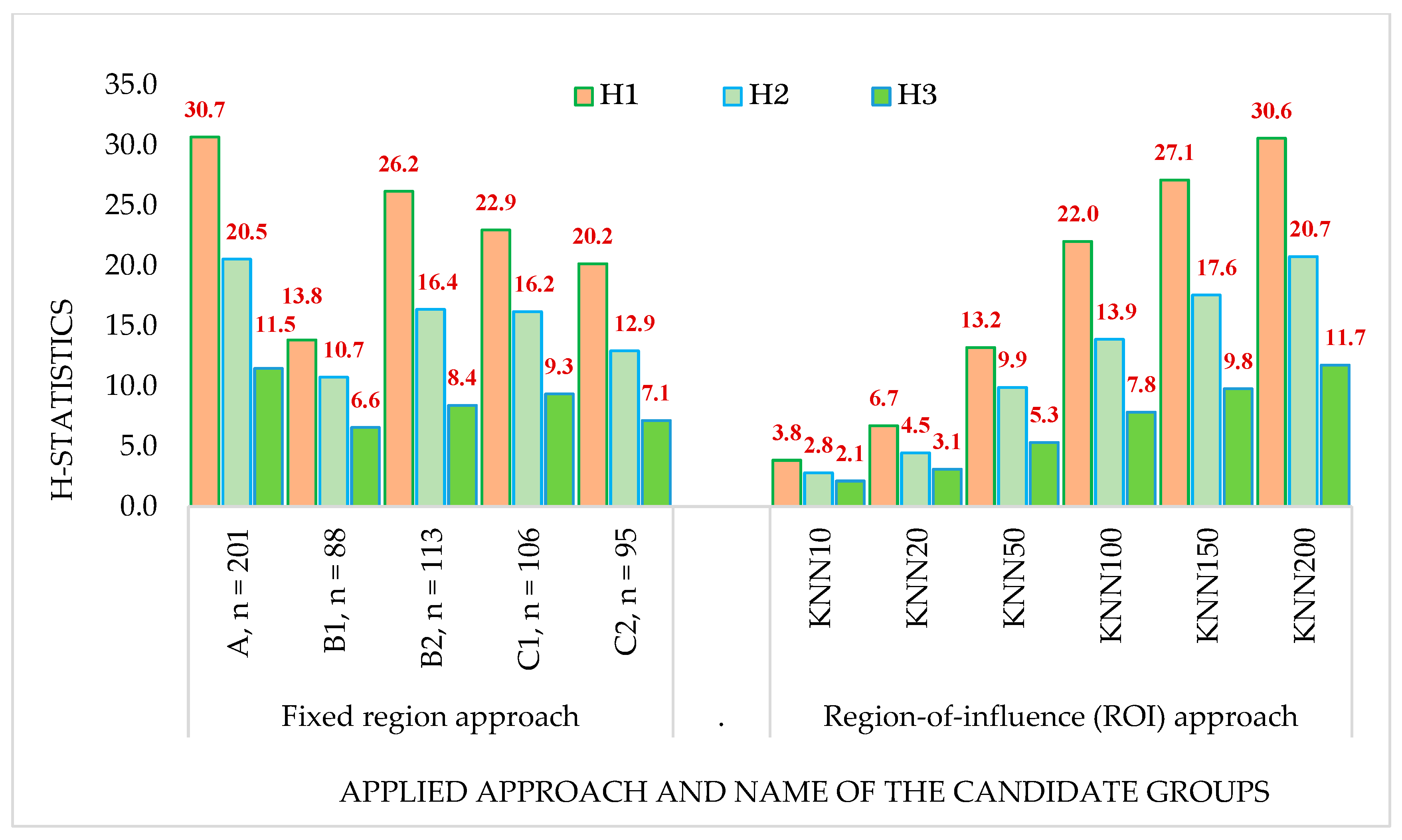
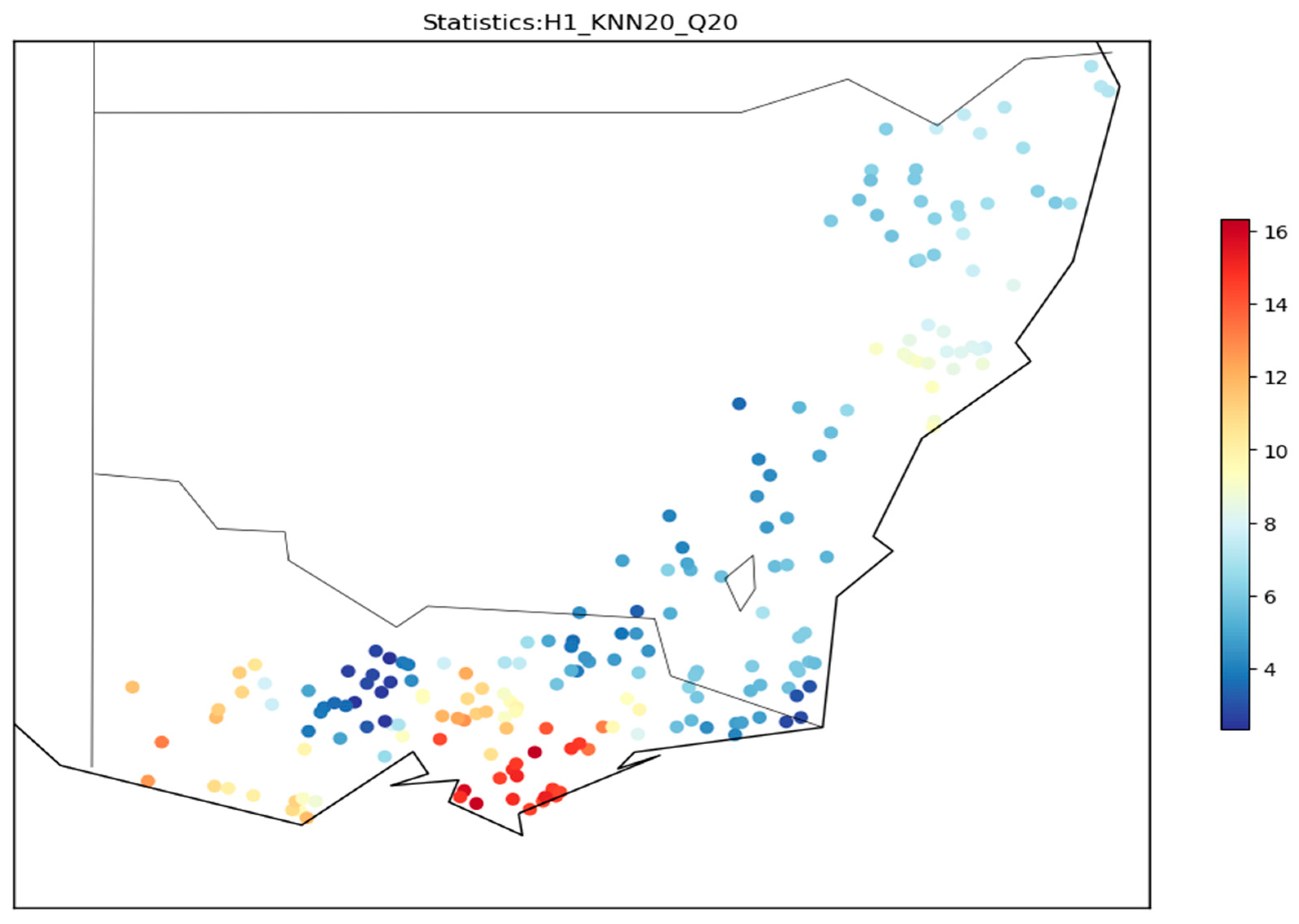
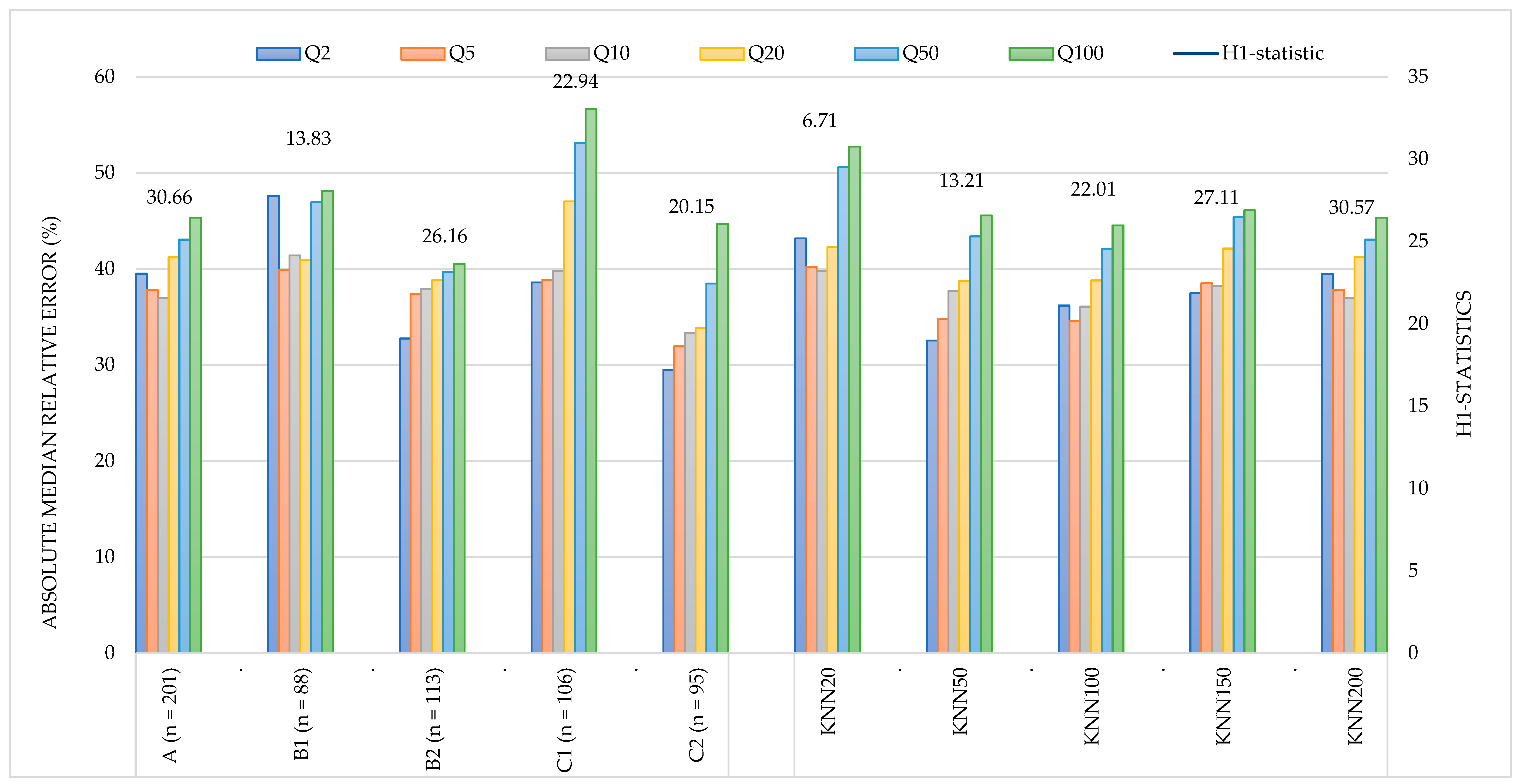
3.2. Discordancy, Heterogeneity, and Z-Statistics of the Assumed Regions
3.3. Discordancy and Comparison of Fixed Region and ROI Approaches in Identification of Homogeneous Regions
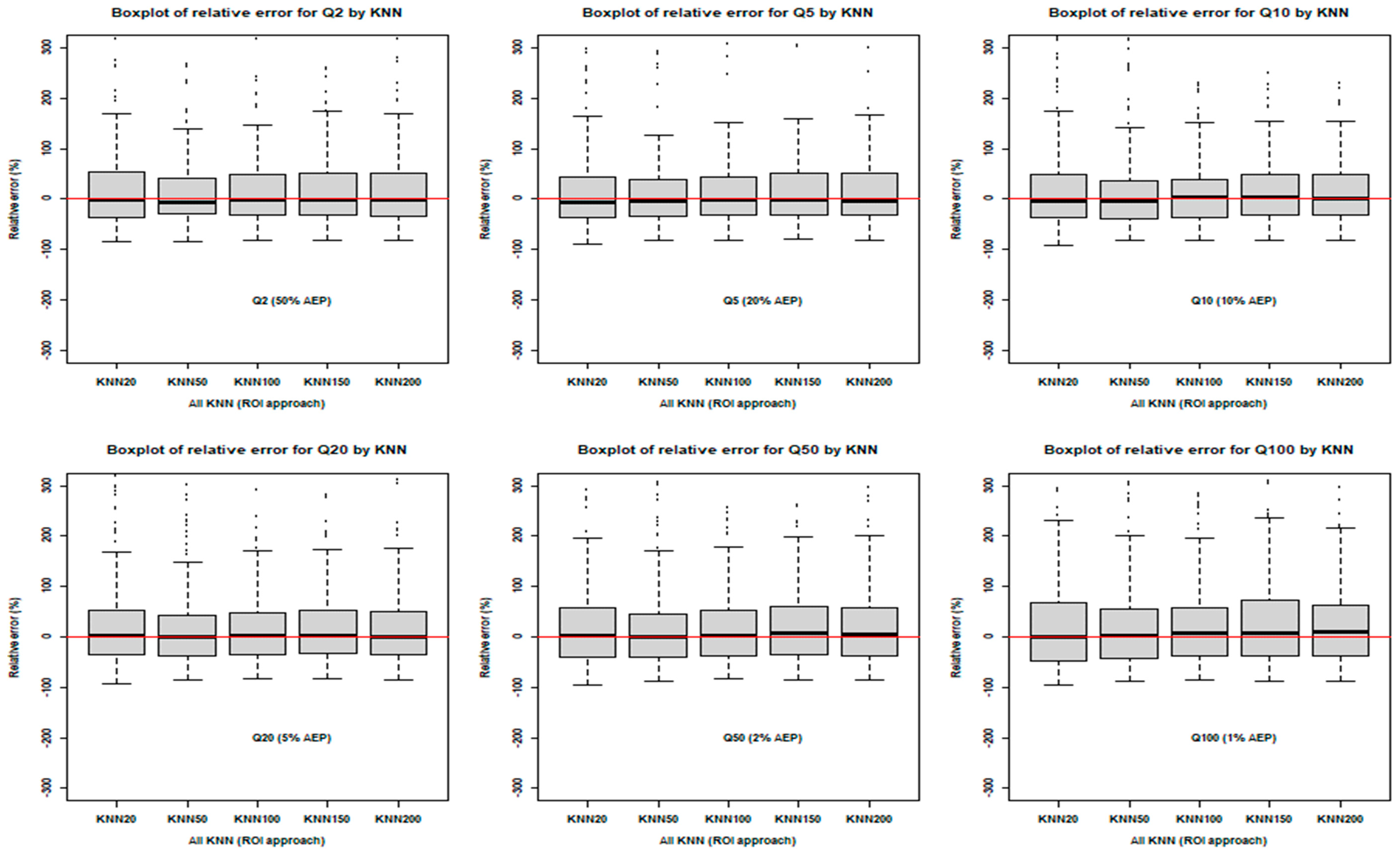
3.4. Comparison of Fixed-Region and ROI Approaches
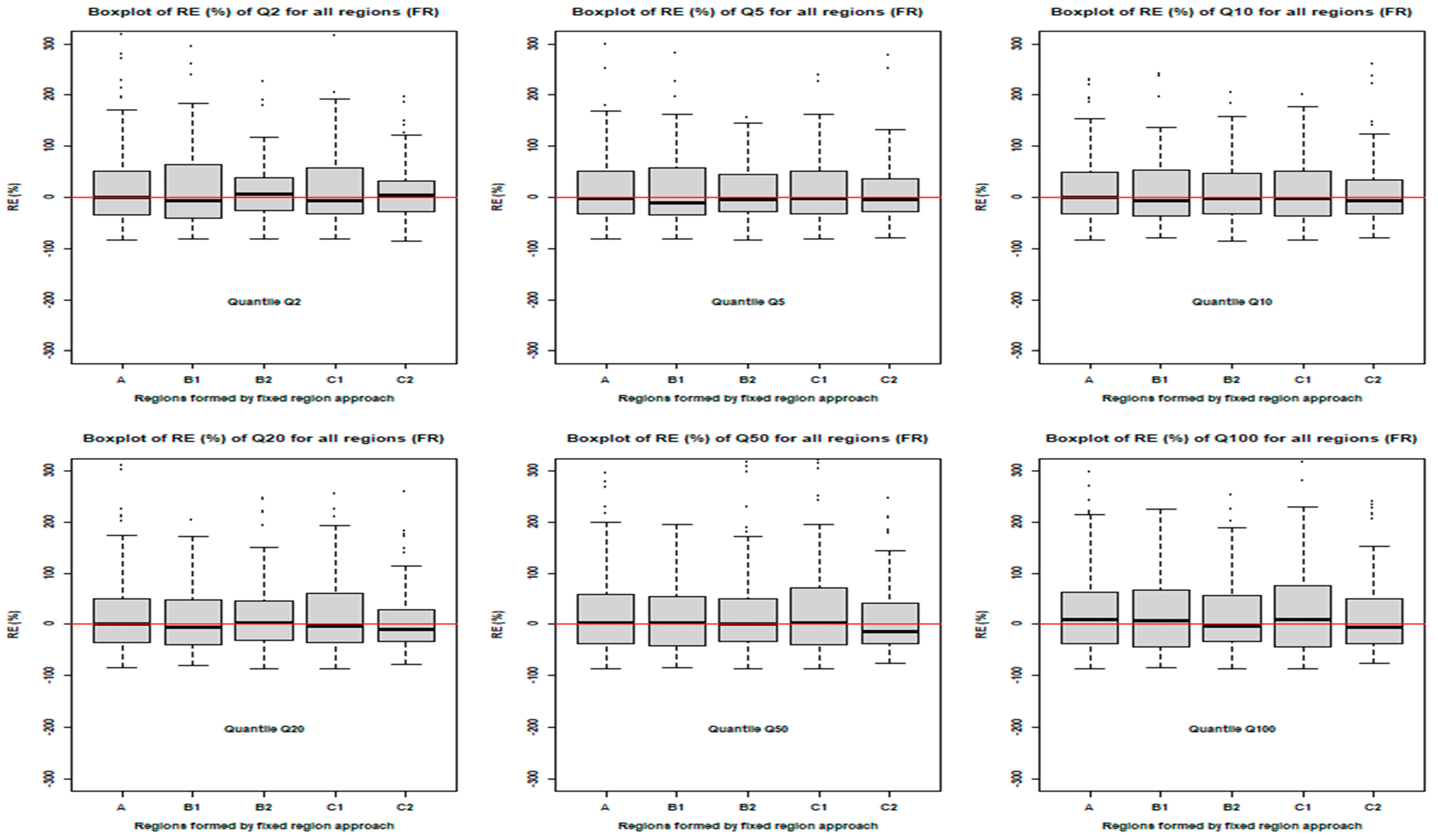
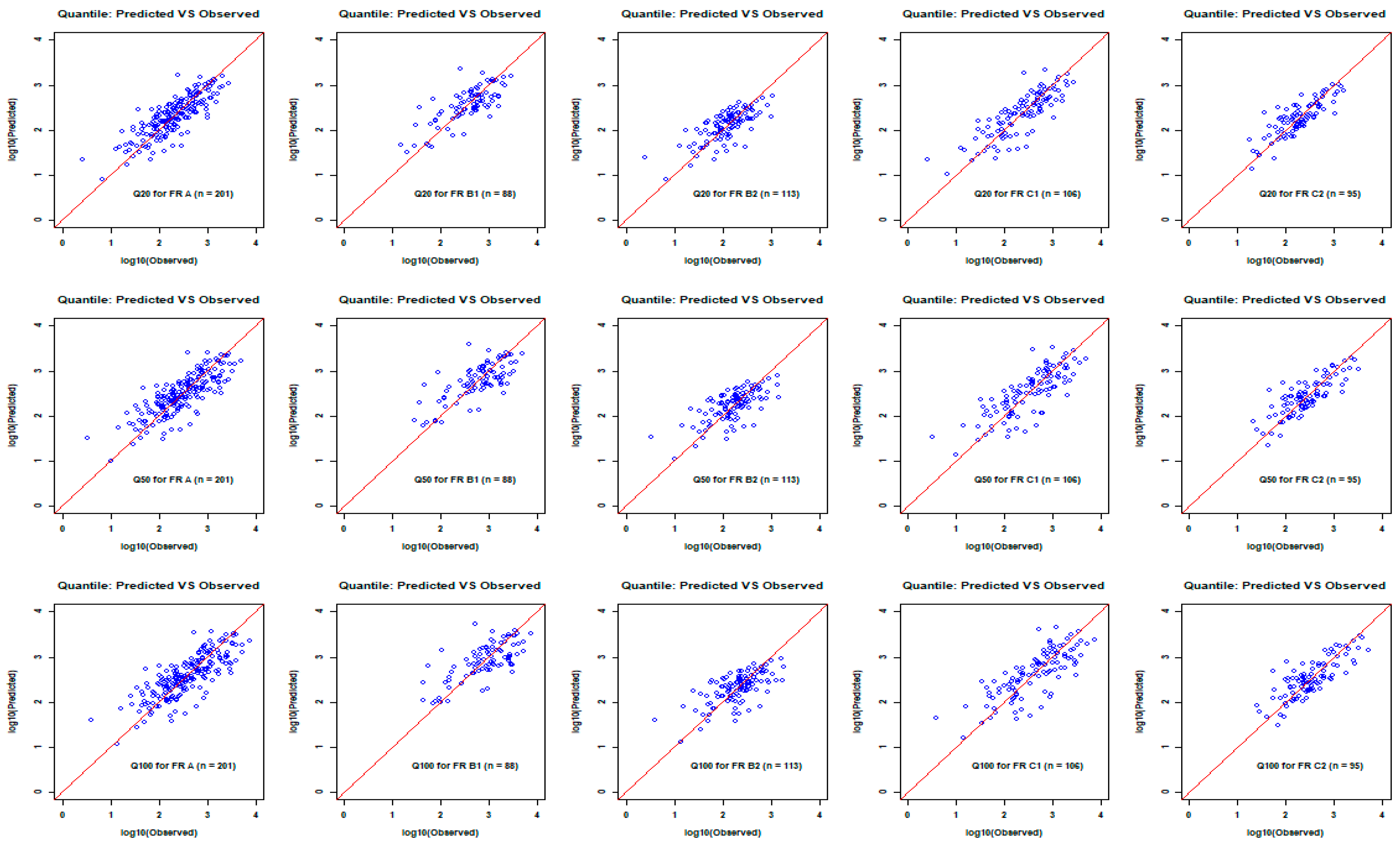
3.4.1. Prediction Equation Development and Performance
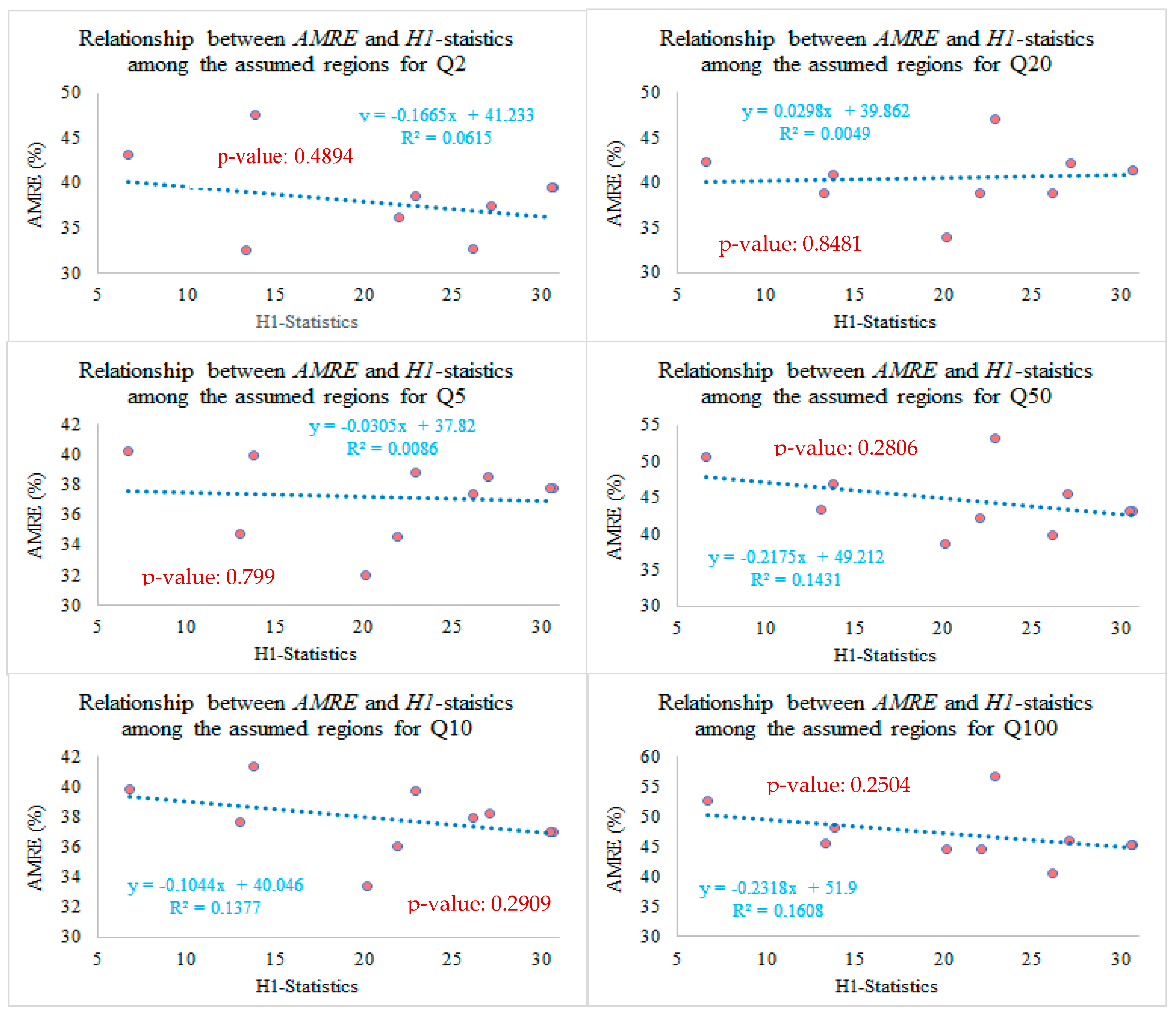
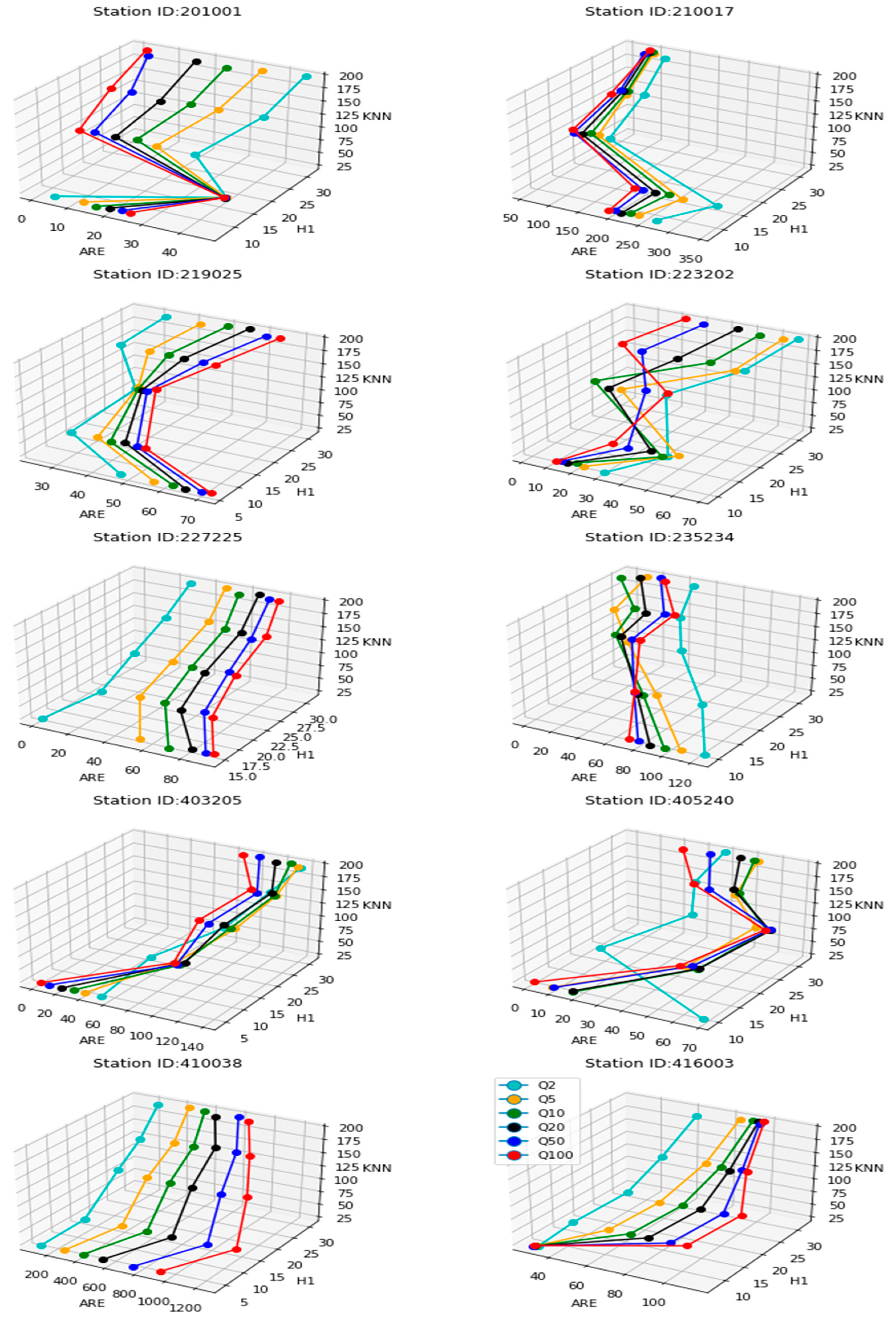
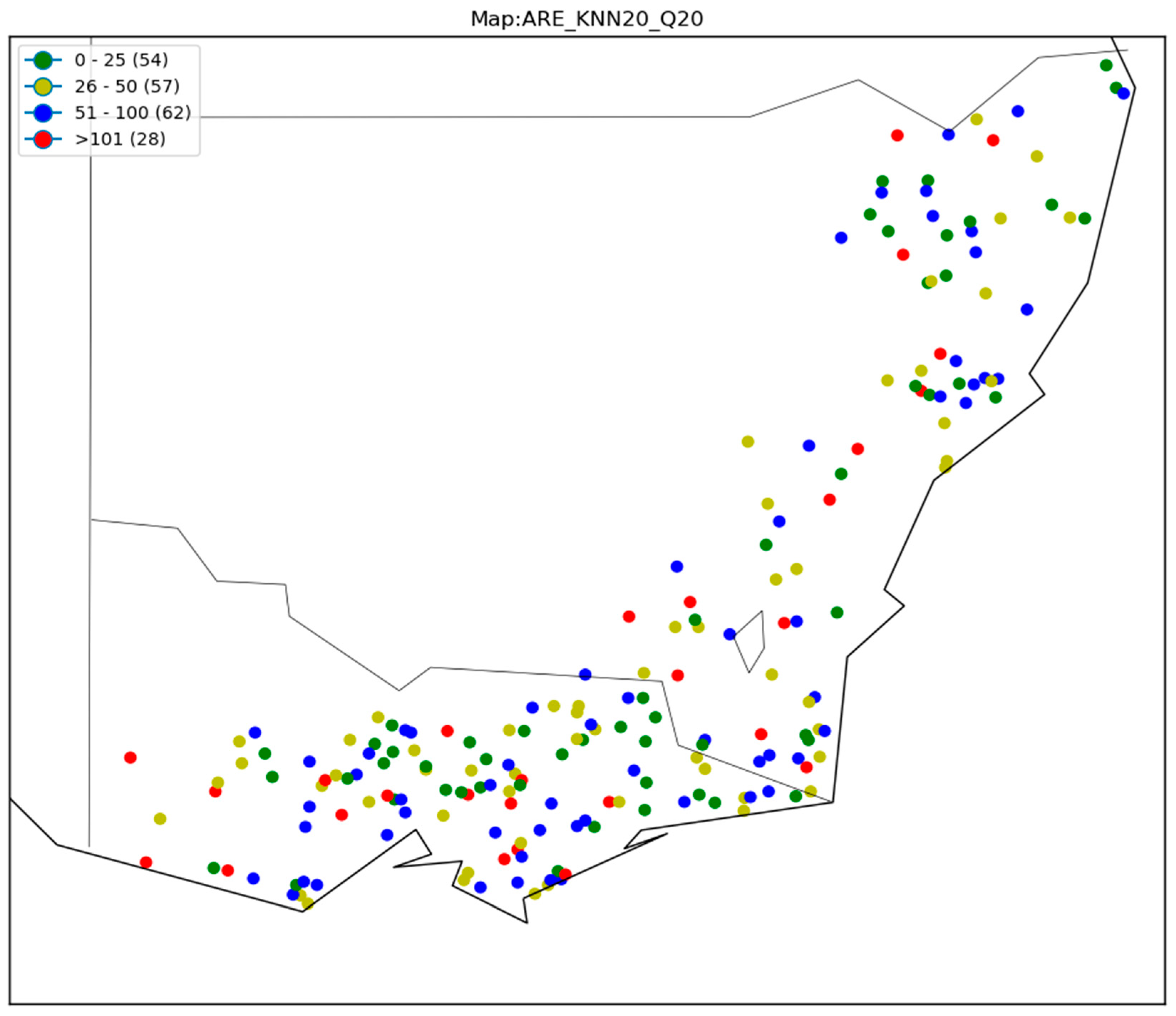
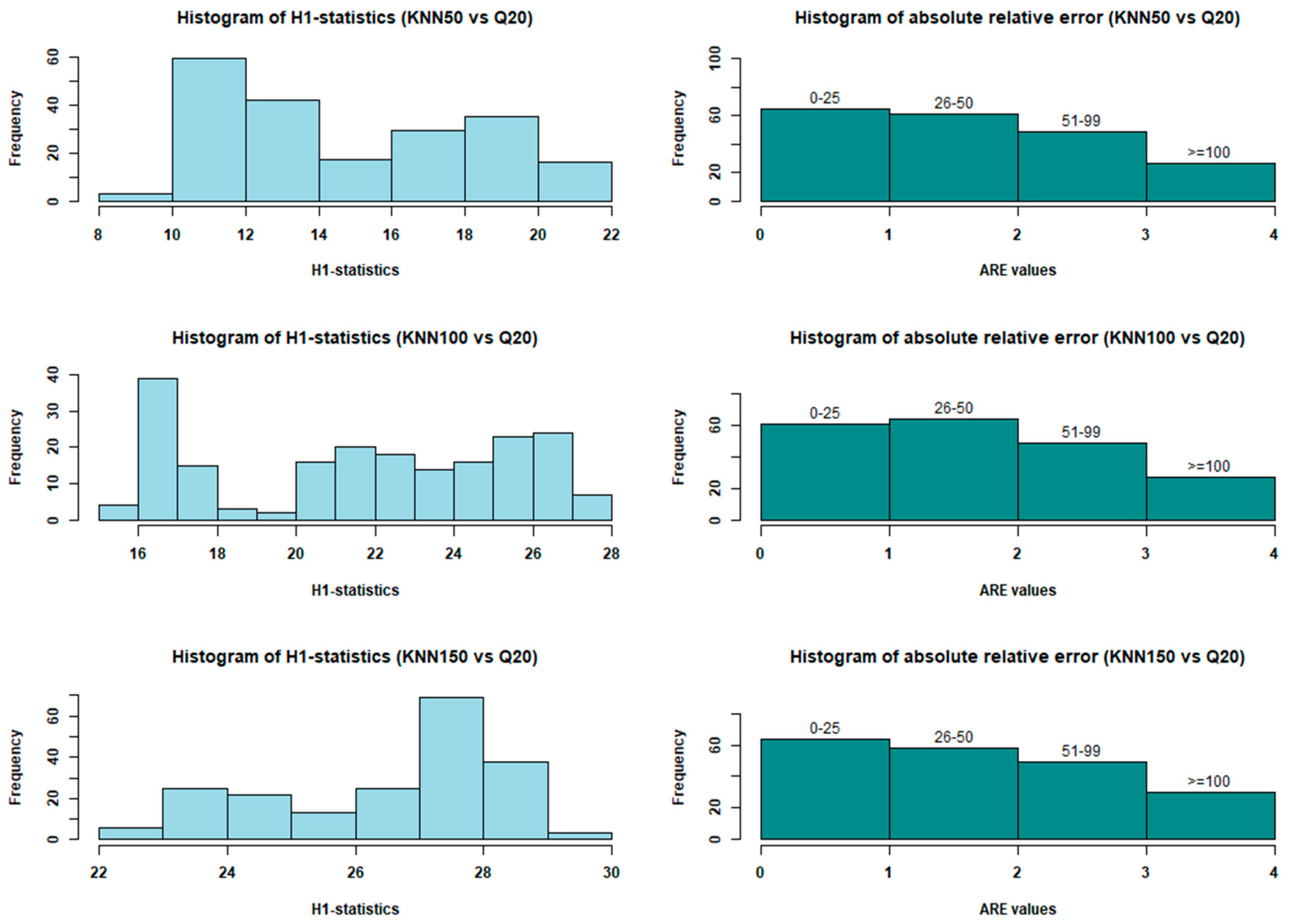
3.4.2. Assessment of the Impact of Homogeneity on Prediction Accuracy
4. Discussion
5. Conclusions
- (i)
- The Pearson Type III (PE3) and Generalized Pareto (GPA) distributions are identified as the most suitable probability distributions for RFFA in southeast Australia.
- (ii)
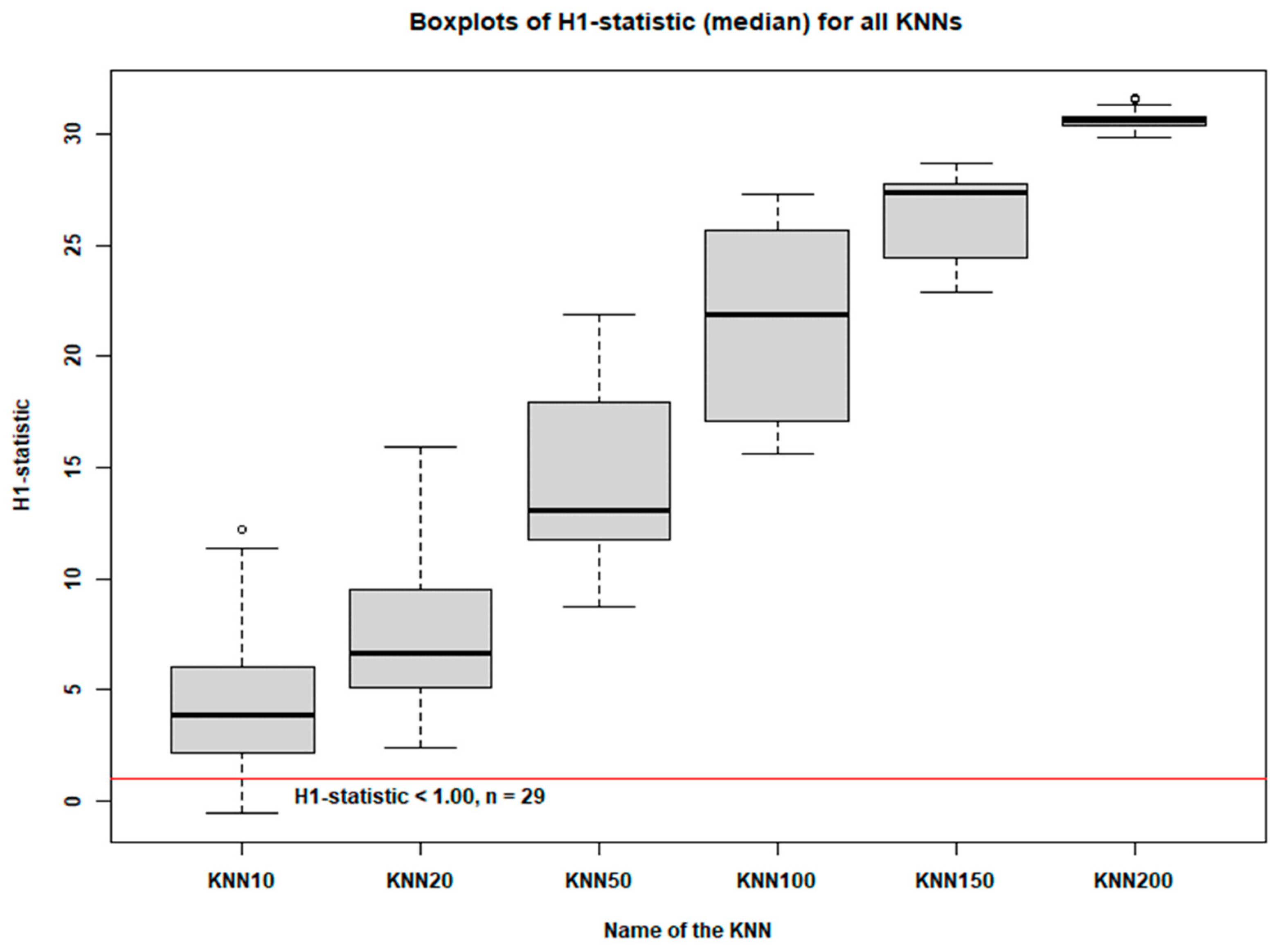
- The majority of the proposed regions exhibit high levels of heterogeneity. Although the KNN10 approach identifies 29 regions with acceptable homogeneity (H1 < 1.00), these regions include fewer than 20 sites each and are therefore considered too small to be statistically robust.
- (iii)
- The absolute median relative error (AMRE) values associated with the developed regression equations range from 29.50% for the 2-year return period (Q2) to 56.66% for the 100-year return period (Q100), with an overall median AMRE of 39.79%.
- (iv)
- The level of regional heterogeneity appears to have minimal influence on the accuracy of flood quantile predictions using regression-based methods in this region.
- (v)
- The ROI approach consistently outperforms the fixed-region approach in terms of predictive accuracy, particularly for the 20-year return period (Q20).
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dalrymple, T. Flood-Frequency Analyses (No. 1543); Manual of Hydrology: Part 3; United States Government Printing Office: Washington, DC, USA, 1960.
- Shu, C.; Ouarda, T.B. Flood frequency analysis at ungauged sites using artificial neural networks in canonical correlation analysis physiographic space. Water Resour. Res. 2007, 43, 7. [Google Scholar] [CrossRef]
- Burn, D.H. An appraisal of the “region of influence” approach to flood frequency analysis. Hydrol. Sci. J. 1990, 35, 149–165. [Google Scholar] [CrossRef]
- Cunnane, C. Review of statistical models for flood frequency estimation. In Hydrologic Frequency Modelling; Springer: Dordrecht, The Netherlands, 1987; pp. 49–95. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Tasker, G.D. Regional hydrologic analysis: 1. Ordinary, weighted, and generalized least squares compared. Water Resour. Res. 1985, 21, 1421–1432. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework—Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2012, 430–431, 142–161. [Google Scholar] [CrossRef]
- Mediero, L.; Kjeldsen, T.; Macdonald, N.; Kohnova, S.; Merz, B.; Vorogushyn, S.; Wilson, D.; Alburquerque, T.; Blöschl, G.; Bogdanowicz, E. Identification of coherent flood regions across Europe by using the longest streamflow records. J. Hydrol. 2015, 528, 341–360. [Google Scholar] [CrossRef]
- Pinos, J.; Quesada-Román, A. Flood Risk-Related Research Trends in Latin America and the Caribbean. Water 2021, 14, 10. [Google Scholar] [CrossRef]
- Singh, A.K.; Chavan, S.R. An approach to regional flood frequency analysis for general peak discharge distribution datasets. J. Hydrol. 2025, 650, 132493. [Google Scholar] [CrossRef]
- Wiltshire, S.E. Grouping basins for regional flood frequency analysis. Hydrol. Sci. J. 1985, 30, 151–159. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Gao, S.; Chen, M.; Gourley, J.J.; Hong, Y. Spatiotemporal characteristics of US floods: Current status and forecast under a future warmer climate. Earth’s Future 2022, 10, e2022EF002700. [Google Scholar] [CrossRef]
- Zrinji, Z.; Burn, D.H. Regional flood frequency with hierarchical region of influence. J. Water Resour. Plan. Manag. 1996, 122, 245–252. [Google Scholar] [CrossRef]
- Basu, B.; Srinivas, V.V. Regional flood frequency analysis using kernel-based fuzzy clustering approach. Water Resour. Res. 2014, 50, 3295–3316. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Bâ, K.M.; Diaz-Delgado, C.; Cârsteanu, A.; Chokmani, K.; Gingras, H.; Quentin, E.; Trujillo, E.; Bobée, B. Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. J. Hydrol. 2008, 348, 40–58. [Google Scholar] [CrossRef]
- Durocher, M.; Burn, D.H.; Mostofi Zadeh, S. A nationwide regional flood frequency analysis at ungauged sites using ROI/GLS with copulas and super regions. J. Hydrol. 2018, 567, 191–202. [Google Scholar] [CrossRef]
- Burn, D.H. Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, 3. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Flood frequency regionalisation—Spatial proximity vs. catchment attributes. J. Hydrol. 2005, 302, 283–306. [Google Scholar] [CrossRef]
- Eng, K.; Milly, P.; Tasker, G.D. Flood regionalization: A hybrid geographic and predictor-variable region-of-influence regression method. J. Hydrol. Eng. 2007, 12, 585–591. [Google Scholar] [CrossRef]
- Tasker, G.D.; Hodge, S.A.; Barks, C.S. Region of Influence Regression for Estimating the 50-Year Flood At Ungaged Sites 1. JAWRA J. Am. Water Resour. Assoc. 1996, 32, 163–170. [Google Scholar] [CrossRef]
- Zhang, Z.; Stadnyk, T.A. Investigation of Attributes for Identifying Homogeneous Flood Regions for Regional Flood Frequency Analysis in Canada. Water 2020, 12, 2503. [Google Scholar] [CrossRef]
- Thomas, D.; Benson, M.A. Generalization of Streamflow Characteristics from Drainage-Basin Characteristics; US Government Printing Office: Washington, DC, USA, 1970.
- Kuczera, G.; Franks, S. At-site flood frequency analysis. In Australian rainfall & runoff; Ball, J., Babister, M., Nathan, R., Weeks, B., Weinmann, E., Retallick, M., Testoni, I., Coombers, P., Roso, S., Ward, M., et al., Eds.; Commonwealth of Australia: Symonston, Australia, 2019; Chapter 2, Book 3. [Google Scholar]
- Durocher, M.; Chebana, F.; Ouarda, T.B. On the prediction of extreme flood quantiles at ungauged locations with spatial copula. J. Hydrol. 2016, 533, 523–532. [Google Scholar] [CrossRef]
- Chebana, F.; Charron, C.; Ouarda, T.B.; Martel, B. Regional frequency analysis at ungauged sites with the generalized additive model. J. Hydrometeorol. 2014, 15, 2418–2428. [Google Scholar] [CrossRef]
- Wazneh, H.; Chebana, F.; Ouarda, T.B. Optimal depth-based regional frequency analysis. Hydrol. Earth Syst. Sci. 2013, 17, 2281–2296. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A. Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia. Water 2020, 12, 781. [Google Scholar] [CrossRef]
- Rahman, A.S.; Khan, Z.; Rahman, A. Application of independent component analysis in regional flood frequency analysis: Comparison between quantile regression and parameter regression techniques. J. Hydrol. 2020, 581, 124372. [Google Scholar] [CrossRef]
- Rosbjerg, D.; Bloschl, G.; Burn, D.; Castellarin, A.; Croke, B.; Di Baldassarre, G.; Iacobellis, V.; Kjeldsen, T.R.; Kuczera, G.; Merz, R. Prediction of floods in ungauged basins. In Runoff Prediction in Ungauged Basins: Synthesis Across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013; pp. 189–225. [Google Scholar]
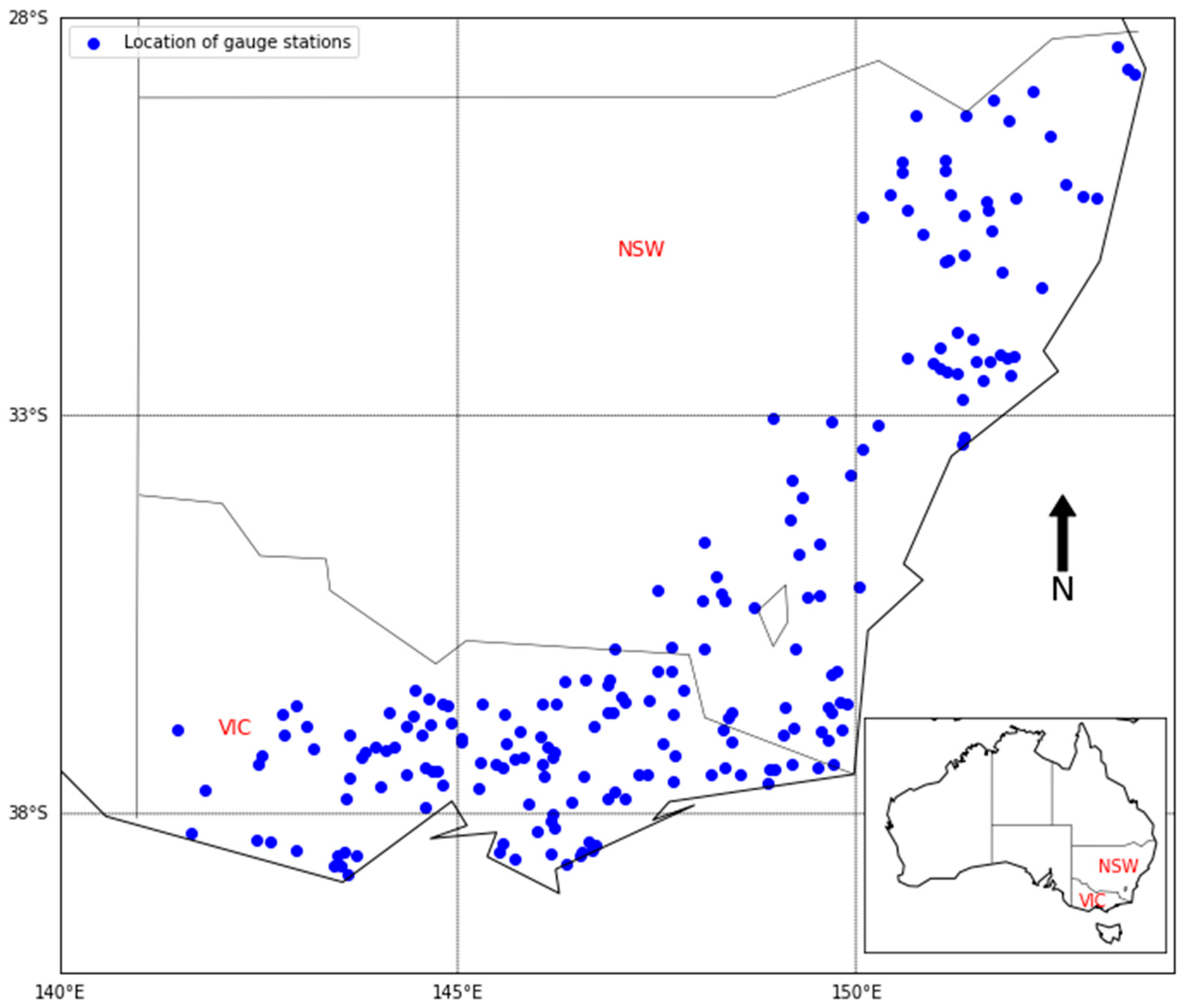
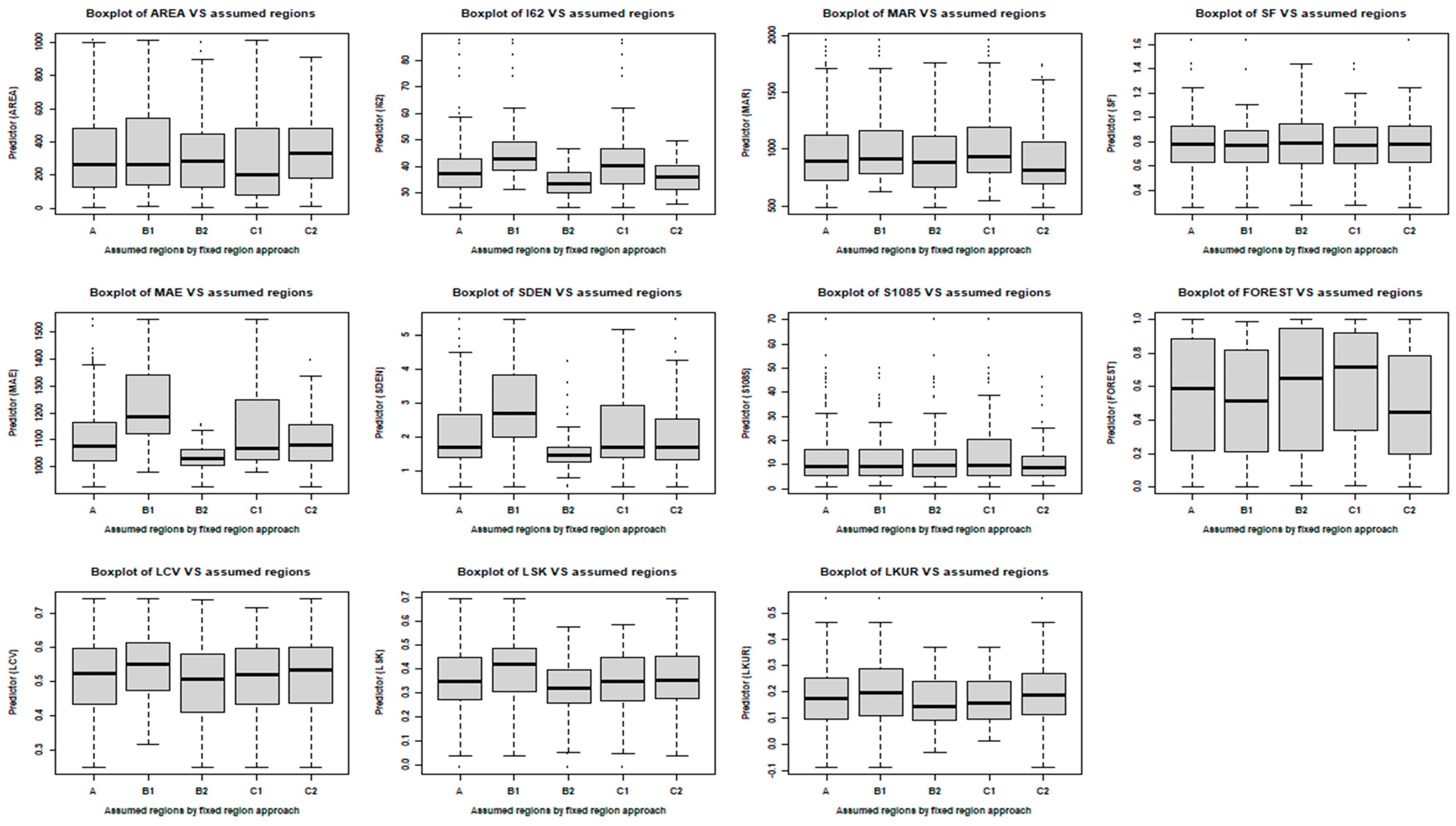


| Station Characteristics | Minimum | Maximum | Median | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Catchment area (AREA, km2) | 3.00 | 1010.00 | 261.00 | 333.99 | 262.40 |
| Rainfall intensity (I62) (mm/h) | 24.60 | 87.30 | 37.30 | 39.16 | 10.07 |
| Mean annual rainfall (MAR) (mm) | 484.39 | 1953.23 | 891.64 | 962.26 | 314.47 |
| Shape factor (SF) | 0.26 | 1.63 | 0.78 | 0.78 | 0.21 |
| Mean annual evapotranspiration (MAE) (mm) | 925.90 | 1543.30 | 1076.70 | 1117.96 | 129.31 |
| Stream density (SDEN) (/km) | 0.52 | 5.47 | 1.69 | 2.10 | 1.06 |
| Mainstream slope (S1085) (m/km) | 0.80 | 69.90 | 9.50 | 13.19 | 11.67 |
| Forest (FOREST) (fraction) | 0.00 | 1.00 | 0.59 | 0.55 | 0.34 |
| Regionalization Approach | Region Notation | Number of Stations (n) | Di-Values (≥3.00) | Z-Statistics | |||||
|---|---|---|---|---|---|---|---|---|---|
| Lowest | Highest | GLO | GEV | GNO | PE3 | GPA | |||
| Fixed-region approach | A | 201 | 3.26 | 6.43 | 16.55 | 12.49 | 7.27 | −1.77 | −0.04 |
| B1 | 88 | 3.05 | 5.43 | 9.82 | 7.73 | 4.06 | −2.28 | 0.65 | |
| B2 | 113 | 3.09 | 5.04 | 14.15 | 10.38 | 6.65 | 0.16 | −0.49 | |
| C1 | 106 | 3.34 | 5.36 | 14.41 | 11.12 | 7.11 | 0.15 | 1.12 | |
| C2 | 95 | 3.05 | 7.18 | 9.69 | 7.08 | 3.53 | −2.61 | −1.09 | |
| Region-of-influence (ROI) approach | KNN10 | 10 | - | - | 3.93 | 3.00 | 1.79 | −0.34 | 0.07 |
| KNN20 | 20 | - | - | 5.27 | 4.19 | 2.33 | −0.75 | 0.18 | |
| KNN50 | 50 | 3.07 | 5.53 | 8.29 | 6.38 | 3.64 | −1.03 | 0.35 | |
| KNN100 | 100 | 3.14 | 5.40 | 11.55 | 8.73 | 4.90 | −1.52 | −0.76 | |
| KNN150 | 150 | 3.62 | 7.70 | 14.37 | 10.72 | 6.27 | −1.46 | −0.47 | |
| KNN200 | 200 | 3.26 | 6.43 | 16.82 | 12.70 | 7.42 | −1.74 | 0.01 | |
| Region (No. of Sites) | Regression Coefficients | Adj-R2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β0 | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 | ||
| Cons | AREA (km2) | I62 (mm/h) | MAR (mm) | SF | MAE (mm) | SDEN (/km) | S1085 (m/km) | FOREST (Fraction) | ||
| A (201) | −4.05 | 0.70 | 2.90 | −0.91 | −0.28 | 0.94 | 0.36 | −0.01 | −0.01 | 0.68 |
| B1 (88) | −1.24 | 0.73 | 3.10 | −0.91 | −0.55 | −0.13 | 0.40 | 0.07 | −0.03 | 0.62 |
| B2 (113) | −1.67 | 0.63 | 2.32 | −0.69 | 0.08 | 0.35 | 0.08 | −0.09 | 0.06 | 0.57 |
| C1 (106) | −5.00 | 0.73 | 3.30 | −0.87 | −0.40 | 1.00 | 0.08 | 0.07 | 0.00 | 0.70 |
| C2 (95) | −6.39 | 0.78 | 1.07 | −0.51 | −0.16 | 2.15 | 0.57 | 0.02 | −0.07 | 0.71 |
| KNN20 (20) | −4.19 | 0.81 | 2.07 | −0.88 | −0.43 | 1.65 | 0.19 | 0.10 | −0.12 | 0.81 |
| KNN50 (50) | −5.99 | 0.77 | 1.89 | −0.83 | −0.10 | 1.76 | 0.25 | 0.01 | −0.05 | 0.66 |
| KNN100 (100) | −2.36 | 0.62 | 3.33 | −1.18 | 0.16 | 0.39 | 0.50 | −0.10 | 0.01 | 0.60 |
| KNN150 (150) | −4.94 | 0.66 | 3.33 | −0.94 | −0.18 | 1.12 | 0.40 | −0.10 | 0.01 | 0.60 |
| KNN200 (200) | −4.05 | 0.70 | 2.90 | −0.91 | −0.28 | 0.94 | 0.36 | −0.01 | −0.01 | 0.68 |
| Evaluation Criteria | Quantiles | Fixed Region | Region-of-Influence (ROI) Approach | Overall Statistics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B1 | B2 | C1 | C2 | KNN20 | KNN50 | KNN100 | KNN150 | KNN200 | Statistics | FR | ROI | ||
| R2 | Q2 | 0.72 | 0.73 | 0.71 | 0.80 | 0.69 | 0.84 | 0.74 | 0.69 | 0.70 | 0.72 | MIN | 0.53 | 0.58 |
| Q5 | 0.73 | 0.73 | 0.68 | 0.79 | 0.73 | 0.84 | 0.71 | 0.66 | 0.68 | 0.73 | MAX | 0.80 | 0.84 | |
| Q10 | 0.72 | 0.70 | 0.64 | 0.77 | 0.73 | 0.83 | 0.69 | 0.63 | 0.66 | 0.72 | Mean | 0.69 | 0.70 | |
| Q20 | 0.70 | 0.67 | 0.61 | 0.74 | 0.72 | 0.82 | 0.68 | 0.62 | 0.63 | 0.70 | Median | 0.70 | 0.69 | |
| Q50 | 0.68 | 0.62 | 0.57 | 0.70 | 0.71 | 0.81 | 0.66 | 0.60 | 0.60 | 0.68 | SD | 0.06 | 0.08 | |
| Q100 | 0.66 | 0.59 | 0.53 | 0.67 | 0.70 | 0.79 | 0.64 | 0.59 | 0.58 | 0.66 | Range | 0.27 | 0.26 | |
| AMRE | Q2 | 39.49 | 47.62 | 32.74 | 38.58 | 29.50 | 43.17 | 32.53 | 36.18 | 37.47 | 39.49 | MIN | 29.50 | 32.53 |
| Q5 | 37.80 | 39.90 | 37.38 | 38.84 | 31.93 | 40.21 | 34.77 | 34.58 | 38.50 | 37.80 | MAX | 56.66 | 52.73 | |
| Q10 | 36.98 | 41.39 | 37.94 | 39.78 | 33.34 | 39.79 | 37.69 | 36.07 | 38.23 | 36.98 | Mean | 40.72 | 40.85 | |
| Q20 | 41.25 | 40.93 | 38.80 | 47.00 | 33.81 | 42.30 | 38.72 | 38.79 | 42.12 | 41.25 | Median | 39.72 | 40.00 | |
| Q50 | 43.04 | 46.93 | 39.66 | 53.13 | 38.48 | 50.60 | 43.38 | 42.10 | 45.41 | 43.04 | SD | 6.06 | 4.63 | |
| Q100 | 45.34 | 48.12 | 40.51 | 56.66 | 44.69 | 52.73 | 45.54 | 44.51 | 46.08 | 45.34 | Range | 27.16 | 20.20 | |
| MSE | Q2 | 2515 | 4833 | 613 | 3189 | 1012 | 4926 | 2633 | 2679 | 2476 | 2515 | MIN | 613 | 2476 |
| Q5 | 13,167 | 27,029 | 3836 | 18,573 | 4695 | 34,690 | 17,671 | 16,733 | 13,240 | 13,167 | MAX | 1,576,140 | 3,201,044 | |
| Q10 | 36,475 | 78,942 | 9546 | 55,357 | 12,713 | 113,209 | 55,254 | 49,666 | 37,089 | 36,475 | Mean | 208,866 | 353,981 | |
| Q20 | 94,459 | 209,806 | 19,797 | 147,944 | 35,210 | 333,229 | 150,509 | 130,180 | 95,555 | 94,459 | Median | 40,902 | 95,007 | |
| Q50 | 309,517 | 686,275 | 45,329 | 480,016 | 136,189 | 1,247,541 | 490,891 | 410,848 | 306,193 | 309,517 | SD | 367,830 | 641,000 | |
| Q100 | 722,328 | 1,576,140 | 80,856 | 1,087,259 | 362,360 | 3,201,044 | 1,109,517 | 915,078 | 700,116 | 722,328 | Range | 1,575,528 | 3,198,568 | |
| BIAS | Q2 | −9.53 | −12.34 | −3.79 | −9.45 | −5.21 | 1.68 | −6.33 | −7.99 | −8.34 | −9.53 | MIN | −233.05 | −169.16 |
| Q5 | −20.05 | −24.10 | −10.20 | −18.50 | −11.36 | 4.82 | −10.69 | −13.63 | −14.22 | −20.05 | MAX | −3.79 | 93.24 | |
| Q10 | −33.25 | −40.63 | −17.61 | −31.20 | −20.14 | 9.93 | −15.48 | −20.44 | −21.66 | −33.25 | Mean | −58.19 | −29.25 | |
| Q20 | −54.95 | −69.81 | −27.61 | −53.63 | −35.31 | 20.36 | −23.68 | −31.83 | −34.90 | −54.95 | Median | −34.28 | −20.25 | |
| Q50 | −105.43 | −140.90 | −46.05 | −108.35 | −71.63 | 49.83 | −44.67 | −59.46 | −68.51 | −105.43 | SD | 58.94 | 50.09 | |
| Q100 | −169.16 | −233.05 | −65.26 | −179.05 | −118.10 | 93.24 | −73.51 | −95.85 | −113.74 | −169.16 | Range | 229.26 | 262.40 | |
| RBIAS | Q2 | 22.24 | 29.41 | 16.83 | 21.77 | 16.49 | 31.10 | 24.71 | 24.54 | 27.98 | 22.24 | MIN | 14.63 | 21.41 |
| Q5 | 21.41 | 27.60 | 19.67 | 23.44 | 14.63 | 30.88 | 26.42 | 25.33 | 26.55 | 21.41 | MAX | 56.20 | 68.05 | |
| Q10 | 23.55 | 31.18 | 23.21 | 27.71 | 16.78 | 35.11 | 30.00 | 28.19 | 28.37 | 23.55 | Mean | 29.08 | 33.75 | |
| Q20 | 26.91 | 36.90 | 27.06 | 33.28 | 20.07 | 41.96 | 34.41 | 31.87 | 31.34 | 26.91 | Median | 27.33 | 31.22 | |
| Q50 | 32.76 | 46.93 | 32.59 | 42.18 | 25.65 | 54.96 | 41.15 | 37.58 | 36.48 | 32.76 | SD | 10.24 | 10.18 | |
| Q100 | 38.13 | 56.20 | 37.15 | 50.01 | 30.66 | 68.05 | 46.87 | 42.45 | 41.16 | 38.13 | Range | 41.57 | 46.64 | |
| RRMSE | Q2 | 0.15 | 0.13 | 0.10 | 0.12 | 0.11 | 0.03 | 0.10 | 0.13 | 0.13 | 0.15 | MIN | 0.10 | 0.03 |
| Q5 | 0.13 | 0.10 | 0.11 | 0.10 | 0.10 | 0.03 | 0.07 | 0.09 | 0.09 | 0.13 | MAX | 0.21 | 0.21 | |
| Q10 | 0.13 | 0.10 | 0.13 | 0.10 | 0.10 | 0.04 | 0.06 | 0.08 | 0.09 | 0.13 | Mean | 0.14 | 0.10 | |
| Q20 | 0.15 | 0.12 | 0.15 | 0.12 | 0.12 | 0.05 | 0.06 | 0.09 | 0.09 | 0.15 | Median | 0.13 | 0.09 | |
| Q50 | 0.18 | 0.14 | 0.17 | 0.15 | 0.15 | 0.08 | 0.08 | 0.10 | 0.12 | 0.18 | SD | 0.03 | 0.04 | |
| Q100 | 0.21 | 0.16 | 0.20 | 0.19 | 0.18 | 0.12 | 0.09 | 0.12 | 0.14 | 0.21 | Range | 0.11 | 0.18 | |
| RMSNE | Q2 | 0.93 | 1.10 | 0.84 | 0.89 | 0.72 | 1.34 | 1.17 | 1.05 | 1.11 | 0.93 | MIN | 0.70 | 0.93 |
| Q5 | 0.95 | 1.15 | 0.98 | 1.00 | 0.70 | 1.40 | 1.31 | 1.16 | 1.07 | 0.95 | MAX | 2.25 | 2.85 | |
| Q10 | 1.03 | 1.30 | 1.08 | 1.13 | 0.81 | 1.52 | 1.46 | 1.29 | 1.13 | 1.03 | Mean | 1.20 | 1.43 | |
| Q20 | 1.13 | 1.51 | 1.18 | 1.29 | 0.94 | 1.75 | 1.63 | 1.42 | 1.22 | 1.13 | Median | 1.14 | 1.35 | |
| Q50 | 1.29 | 1.89 | 1.32 | 1.52 | 1.14 | 2.26 | 1.87 | 1.61 | 1.36 | 1.29 | SD | 0.34 | 0.42 | |
| Q100 | 1.42 | 2.25 | 1.43 | 1.72 | 1.31 | 2.85 | 2.07 | 1.76 | 1.47 | 1.42 | Range | 1.55 | 1.92 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Morshed, M.A.; Mim, S.T.; Rafi, R.S.M.H.; Khan, Z.; Maity, R.; Rahman, A. Impacts of the Degree of Heterogeneity on Design Flood Estimates: Region of Influence vs. Fixed Region Approaches. Water 2025, 17, 2765. https://doi.org/10.3390/w17182765
Ahmed A, Morshed MA, Mim ST, Rafi RSMH, Khan Z, Maity R, Rahman A. Impacts of the Degree of Heterogeneity on Design Flood Estimates: Region of Influence vs. Fixed Region Approaches. Water. 2025; 17(18):2765. https://doi.org/10.3390/w17182765
Chicago/Turabian StyleAhmed, Ali, Mohammad A. Morshed, Sadia T. Mim, Ridwan S. M. H. Rafi, Zaved Khan, Rajib Maity, and Ataur Rahman. 2025. "Impacts of the Degree of Heterogeneity on Design Flood Estimates: Region of Influence vs. Fixed Region Approaches" Water 17, no. 18: 2765. https://doi.org/10.3390/w17182765
APA StyleAhmed, A., Morshed, M. A., Mim, S. T., Rafi, R. S. M. H., Khan, Z., Maity, R., & Rahman, A. (2025). Impacts of the Degree of Heterogeneity on Design Flood Estimates: Region of Influence vs. Fixed Region Approaches. Water, 17(18), 2765. https://doi.org/10.3390/w17182765









