Developing a Composite Hydrological Drought Index Using the VIC Model: Case Study in Northern Thailand
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Model and Data
2.2.1. Climate Data
2.2.2. Spatial Data
2.3. Methodology
2.3.1. VIC Model Simulation and Parameter Extraction
2.3.2. Development of the Composite Hydrological Drought Index (CHDI)
- CHDI represents the Composite Hydrological Drought Index, which reflects the water level values at the gauge.
- β0 is the intercept, representing the expected water level when PC1 equal to 0.
- β1 is the slope coefficient of PC1.
2.3.3. Assessing the Performance of the CHDI
2.3.4. Computational Requirements
3. Results
3.1. Correlation Between Observed and VIC-Simulated Hydrological Variables
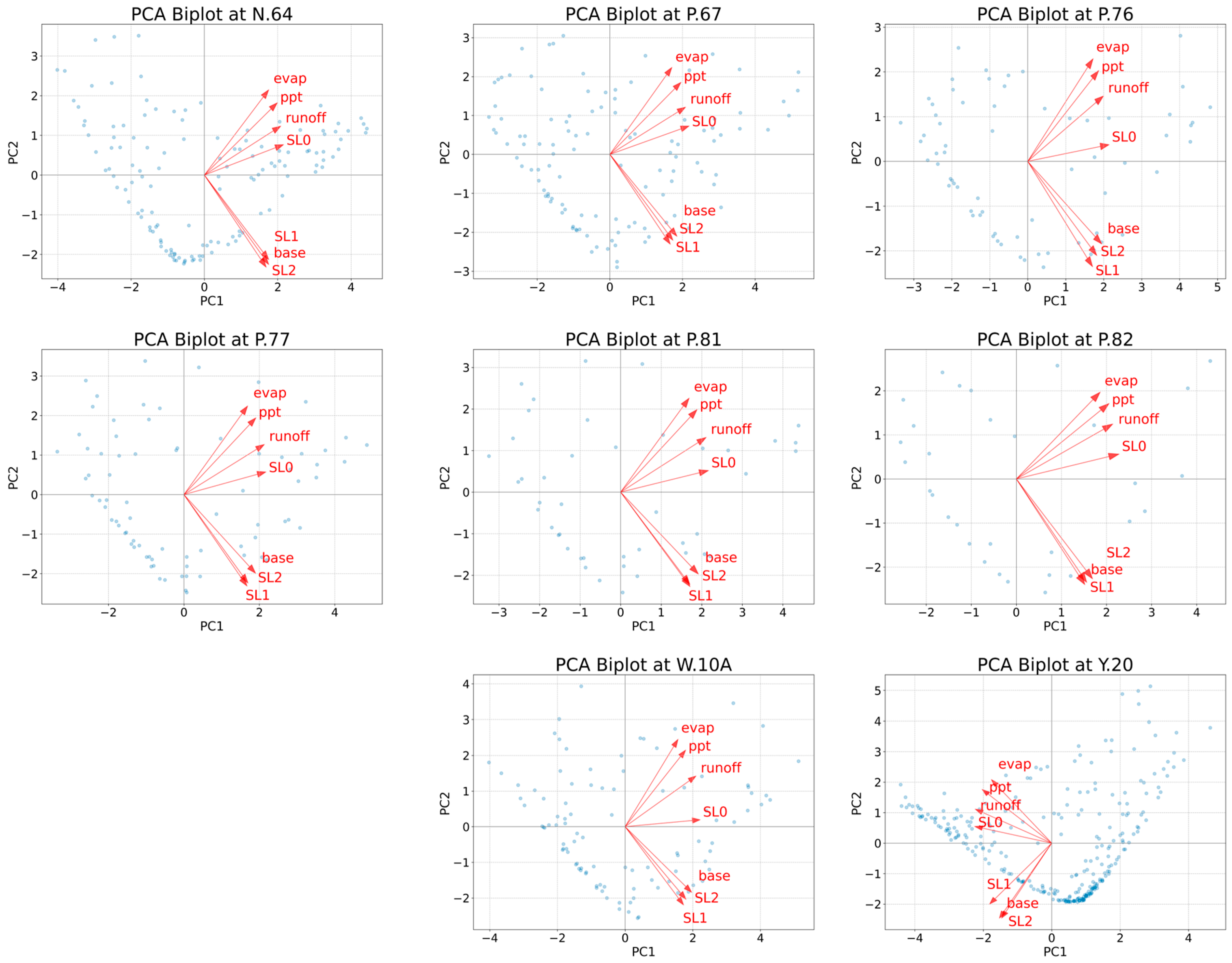
3.2. Development of the Composite Hydrological Drought Index
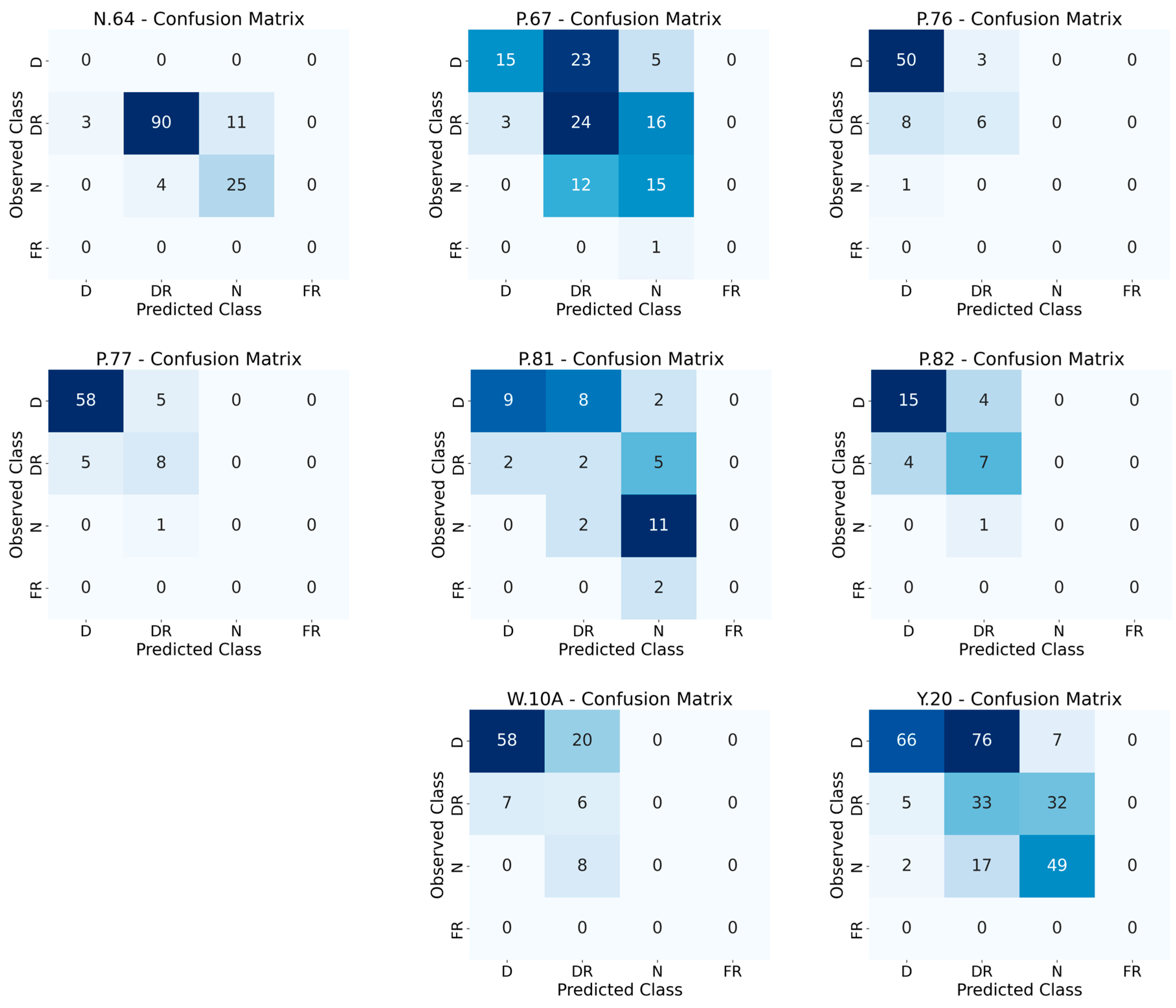
3.3. Performance of the Composite Hydrological Drought Index
3.4. Drought Analysis in the Baseline Period
4. Discussion
Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trenberth, K.; Dai, A.; van der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Change 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Beule, L.; Lanhenke Buareal, K.; Buajan, S.; Preechamart, S.; Muangsong, C.; Pumijumnong, N. A 177 years extended of teak chronology revealing to the climate variability in phrae province, northern of thailand. Appl. Environ. Res. 2020, 42, 85–100. [Google Scholar] [CrossRef]
- Kume, T.; Takizawa, H.; Yoshifuji, N.; Tanaka, N.; Tanaka, K.; Tantasirin, C.; Suzuki, M. Severe drought resulting from seasonal and interannual variability in rainfall and its impact on transpiration in a hill evergreen forest in northern thailand. In Forest Environments in the Mekong River Basin; Springer: Tokyo, Japan, 2007; pp. 45–55. [Google Scholar] [CrossRef]
- Beule, L.; Lanhenke, J.-F.; Tantanee, S. Trends in precipitation in Thailand from 1964 to 2012. Asia-Pac. J. Sci. Technol. 2017, 21, 1–5. [Google Scholar] [CrossRef]
- Gosling, S.N.; Arnell, N.W. A global assessment of the impact of climate change on water scarcity. Clim. Change 2013, 134, 371–385. [Google Scholar] [CrossRef]
- Jitanugoon, S. Water resources development in thailand. In Proceedings of the 4th International Conference on Research in Social Sciences, Brussels, Belgium, 29–31 October 2021. [Google Scholar] [CrossRef]
- Bangkok Post. Assessing Drought Impact. 18 March 2020. Available online: https://www.bangkokpost.com/business/general/1881185/assessing-drought-impact (accessed on 3 November 2024).
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Gusyev, M.A.; Magome, J.; Hasegawa, A.; Takeuchi, K.; Fukushima, Y. Drought risk assessment with the use of ensemble hydrological predictions. J. Hydrol. 2015, 526, 502–516. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, S.; Zhang, H.; Bai, Y.; Zhang, J. Monitoring drought using composite drought indices based on remote sensing. Sci. Total Environ. 2020, 711, 134585. [Google Scholar] [CrossRef] [PubMed]
- Faiz, M.A.; Zhang, Y.; Zhang, X.; Ma, N.; Aryal, S.K.; Ha, T.T.V.; Baig, F.; Naz, F. A composite drought index developed for detecting large-scale drought characteristics. J. Hydrol. 2022, 605, 127308. [Google Scholar] [CrossRef]
- Bravo, R.Z.B.; Cunha, A.P.M.D.A.; Leiras, A.; Cyrino Oliveira, F.L. A new approach for a drought composite index. Nat. Hazards 2021, 108, 755–773. [Google Scholar] [CrossRef]
- Abdourahamane, Z.S.; Garba, I.; Boukary, A.G.; Mirzabaev, A. Spatiotemporal characterization of agricultural drought in the Sahel region using a composite drought index. J. Arid. Environ. 2022, 204, 104789. [Google Scholar] [CrossRef]
- Pandya, P.; Gontia, N.K.; Parmar, H.V. Development of PCA-based composite drought index for agricultural drought assessment using remote-sensing. J. Agrometeorol. 2022, 24, 384–392. [Google Scholar] [CrossRef]
- Sharafi, S.; Ghaleni, M.M. Enhancing drought monitoring and prediction in diverse climates by using composite drought indices. Stoch. Environ. Res. Risk Assess. 2023, 38, 1–21. [Google Scholar] [CrossRef]
- Başakın, E.E.; Stoy, P.C.; Demirel, M.C.; Ozdogan, M.; Otkin, J.A. Combined drought index using high-resolution hydrological models and explainable artificial intelligence techniques in Türkiye. Remote Sens. 2024, 16, 3799. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Zhang, Q.; Yang, T.; Pan, Y.; Sun, P. A remote sensing and artificial neural network-based integrated agricultural drought index: Index development and applications. Catena 2020, 186, 104394. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, D.; Tian, W.; Zhao, H.; Geng, S.; Lu, H.; Ma, G.; Huang, J.; Choy Lim Kam Sian, K.T. Construction of an integrated drought monitoring model based on deep learning algorithms. Remote Sens. 2023, 15, 667. [Google Scholar] [CrossRef]
- Hanadé Houmma, I.; Gadal, S.; El Mansouri, L.; Garba, M.; Gbetkom, P.G.; Mamane Barkawi, M.B.; Hadria, R. A new multivariate agricultural drought composite index based on random forest algorithm and remote sensing data developed for Sahelian agrosystems. Geomat. Nat. Hazards Risk 2023, 14, 2223384. [Google Scholar] [CrossRef]
- Hamman, J.; Nijssen, B.; Bohn, T.J.; Gergel, D.R.; Mao, Y. The variable infiltration capacity model version 5 (vic-5): Infrastructure improvements for new applications and reproducibility. Geosci. Model Dev. 2018, 11, 3481–3496. [Google Scholar] [CrossRef]
- Luong, N.D.; Hiep, N.H.; Bui, T.H. Investigating the spatio-temporal variation of soil moisture and agricultural drought towards supporting water resources management in the red river basin of vietnam. Sustainability 2021, 13, 4926. [Google Scholar] [CrossRef]
- Apurv, T.; Cai, X. Impact of droughts on water supply in u.s. watersheds: The role of renewable surface and groundwater resources. Earth’s Future 2020, 8, e2020EF001648. [Google Scholar] [CrossRef]
- Zhu, B.; Xie, X.; Wang, Y.; Zhao, X. The benefits of continental-scale high-resolution hydrological modeling in the detection of extreme hydrological events in china. Remote Sens. 2023, 15, 2402. [Google Scholar] [CrossRef]
- Thanapakpawin, P.; Boonya-aroonnet, S.; Chankarn, A.; Chitradon, R.; Snidvongs, A. Chapter 7 thailand drought risk management: Macro and micro strategies. In Droughts in Asian Monsoon Region; Community, Environment and Disaster Risk Management; Emerald Group Publishing Limited: Braffo, UK, 2011; pp. 121–140. [Google Scholar] [CrossRef]
- Goodwin, D.; Holman, I.; Sutcliffe, C.; Salmoral, G.; Pardthaisong, L.; Visessri, S.; Ekkawatpanit, C.; Rey, D. The contribution of a catchment-scale advice network to successful agricultural drought adaptation in northern thailand. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20210293. [Google Scholar] [CrossRef]
- Gopalan, S.P.; Hanasaki, N.; Champathong, A.; Tebakari, T. Impact assessment of reservoir operation in the context of climate change adaptation in the Chao Phraya River basin. Hydrol. Process. 2020, 35, e14005. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple hydrologically Based Model of Land Surface Water and Energy Fluxes for GSMs. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Abrams, M.; Yamaguchi, Y.; Crippen, R. ASTER GLOBAL DEM (GDEM) VERSION 3. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLIII-B4-2022, 593–598. [Google Scholar] [CrossRef]
- FAO; IIASA; ISRIC; ISSCAS; JRC. Harmonized World Soil Database (Version 1.2). 2012. Available online: https://www.fao.org/soils-portal/data-hub/soil-maps-and-databases/harmonized-world-soil-database-v12/en/ (accessed on 10 August 2023).
- Friedl, M.; Sulla-Menashe, D. MCD12C1 MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 0.05Deg CMG V006 [Data Set]; NASA Land Processes Distributed Active Archive Center: Sioux Falls, SD, USA, 2015. [Google Scholar] [CrossRef]
- Pratoomchai, W.; Ekkawatpanit, C.; Yoobanpot, N.; Lee, K.T.A. Dilemma between Flood and Drought Management: Case Study of the Upper Chao Phraya Flood-Prone Area in Thailand. Water 2022, 14, 4056. [Google Scholar] [CrossRef]
- Kongmuang, C.; Tantanee, S.; Seejata, K. Urban flood hazard map using gis of muang sukhothai district, thailand. Geogr. Tech. 2020, 15, 143–152. [Google Scholar] [CrossRef]
- Srisuk, K.; Chusanatus, S.; Munyou, S.; Archwichai, L.; Pholkern, K.; Boonsongka, P. Ranking the suitability of sub-watersheds for ponding-based methods of managed aquifer recharge in lower yom river basin, thailand. J. Geol. Resour. Eng. 2014, 2, 158–166. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.; Jiao, W.; Zhang, H.; Huang, C.; Tong, Q. Studying drought phenomena in the continental united states in 2011 and 2012 using various drought indices. Remote Sens. Environ. 2017, 190, 96–106. [Google Scholar] [CrossRef]
- Heim, R.R.; Bathke, D.J.; Bonsal, B.; Cooper, E.W.T.; Hadwen, T.; Kodama, K.; McEvoy, D.; Muth, M.; Nielsen-Gammon, J.W.; Weight, E. A review of user perceptions of drought indices and indicators used in the diverse climates of north america. Atmosphere 2023, 14, 1794. [Google Scholar] [CrossRef]
- Otkin, J.A.; Zhong, Y.; Ford, T.W.; Anderson, M.C.; Hain, C.; Hoell, A.; Svoboda, M.; Wang, H. Multivariate evaluation of flash drought across the united states. Water Resour. Res. 2024, 60, e2024WR037333. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate drought index: An information theory based approach for integrated drought assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
- Strohmeier, S.; López, P.L.; Haddad, M.; Nangia, V.; Karrou, M.; Montanaro, G.; Boudhar, A.; Linés, C.; Veldkamp, T.; Sterk, G. Surface runoff and drought assessment using global water resources datasets—From oum er rbia basin to the moroccan country scale. Water Resour. Manag. 2019, 34, 2117–2133. [Google Scholar] [CrossRef]
- Jarihani, B.; Sidle, R.C.; Bartley, R.; Roth, C.; Wilkinson, S. Characterisation of hydrological response to rainfall at multi spatio-temporal scales in savannas of semi-arid australia. Water 2017, 9, 540. [Google Scholar] [CrossRef]
- Vichta, T.; Deutscher, J.; Hemr, O.; Tomášová, G.; Žižlavská, N.; Brychtová, M.; Bajer, A.; Shukla, M.K. Combined effects of rainfall-runoff events and antecedent soil moisture on runoff generation processes in an upland forested headwater area. Hydrol. Process. 2024, 38, e15216. [Google Scholar] [CrossRef]
- Cui, A.; Li, J.; Zhou, Q.; Zhu, H.; Liu, H.; Yang, C.; Wu, G.; Li, Q. Propagation dynamics from meteorological drought to grace-based hydrological drought and its influencing factors. Remote Sens. 2024, 16, 976. [Google Scholar] [CrossRef]
- Brunner, M.I.; Stahl, K. Temporal hydrological drought clustering varies with climate and land-surface processes. Environ. Res. Lett. 2023, 18, 034011. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. A nonparametric multivariate multi-index drought monitoring framework. J. Hydrometeorol. 2014, 15, 89–101. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Gosling, S.N.; Kummu, M.; Flörke, M.; Pfister, S.; Hanasaki, N.; Wada, Y.; Zhang, X.; Oki, T. Water scarcity assessments in the past, present, and future. Earth’s Future 2017, 5, 545–559. [Google Scholar] [CrossRef]
- Kong, X.; Li, Z.; Liu, Z. Flood prediction in ungauged basins by physical-based topkapi model. Adv. Meteorol. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Muhebwa, A.; Gleason, C.J.; Feng, D.; Taneja, J. Improving discharge predictions in ungauged basins: Harnessing the power of disaggregated data modeling and machine learning. Water Resour. Res. 2024, 60, e2024WR037122. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, Q.; Ye, M.; Hao, W.; Chen, Y.; Zheng, Y.; Zhong, Z.; Yan, J.; Sun, X.; Li, F. The ancient lithospheric parameters of impact basins on the far side of the moon based on the mantle and mare basalt load model. J. Geophys. Res. Planets 2024, 129, e2023JE008006. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W. Pca−arma-based control charts for performance monitoring of multivariable feedback control. Ind. Eng. Chem. Res. 2010, 49, 2228–2241. [Google Scholar] [CrossRef]
- Maneechot, L.; Chang, J.H.-W.; He, K.; Hu, M.; Wan-Mohtar, W.A.A.Q.I.; Ilham, Z.; García Castro, C.; Wong, Y.J. Adaptive Neuro-Fuzzy Optimization of Reservoir Operations Under Climate Variability in the Chao Phraya River Basin. Water 2025, 17, 1740. [Google Scholar] [CrossRef]
- Chagas, V.B.P.; Chaffe, P.L.B.; Blöschl, G. Drought-rich periods are more likely than flood-rich periods in brazil. Water Resour. Res. 2024, 60, e2023WR035851. [Google Scholar] [CrossRef]
- Lun, D.; Fischer, S.; Viglione, A.; Blöschl, G. Detecting flood-rich and flood-poor periods in annual peak discharges across europe. Water Resour. Res. 2020, 56, e2019WR026575. [Google Scholar] [CrossRef]
- Ndayiragije, J.M.; Li, F. Effectiveness of drought indices in the assessment of different types of droughts, managing and mitigating their effects. Climate 2022, 10, 125. [Google Scholar] [CrossRef]
- Kim, S.; Parhi, P.; Jun, H.; Lee, J. Evaluation of drought severity with a bayesian network analysis of multiple drought indices. J. Water Resour. Plan. Manag. 2018, 144, 05017016. [Google Scholar] [CrossRef]
- Damkjaer, S.; Taylor, R.G. The measurement of water scarcity: Defining a meaningful indicator. Ambio 2017, 46, 513–531. [Google Scholar] [CrossRef]
- Lee, T.; Kong, Y.; Singh, V.P.; Lee, J. Autoencoder-based composite drought indices. Environ. Res. Lett. 2024, 19, 074007. [Google Scholar] [CrossRef]
- Leelaruban, N.; Padmanabhan, G.; Oduor, P.G. Examining the relationship between drought indices and groundwater levels. Water 2017, 9, 82. [Google Scholar] [CrossRef]
- Briones, J.V.; Sutanudjaja, E.H.; Jong, S.d.; Wanders, N. Modelling groundwater hydrological drought and its recovery given natural and anthropogenic scenarios in south america. Hydrol. Process. 2024, 38, e15340. [Google Scholar] [CrossRef]
- Sutanto, S.J.; Lanen, H.V. Hydrological drought characteristics based on groundwater and runoff across europe. Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 281–290. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P.; McKenzie, A. Changes in groundwater drought associated with anthropogenic warming. Hydrol. Earth Syst. Sci. 2019, 23, 1393–1408. [Google Scholar] [CrossRef]
- Birk, S.; Griebler, C.; Haas, J.C.; Retter, A.; Kokimova, A.; Englisch, C.; Gaviria, S.; Grath, J.; Brielmann, H.; Stumpp, C. Impact of Extreme Hydrological Events on the Quantity and Quality of Groundwater in Alpine Regions—Multiple-Index Application for an Integrative Hydrogeo-Ecological Assessment. 2023. Available online: https://epub.oeaw.ac.at/?arp=0x003e7b83 (accessed on 20 May 2025).
- Ochoa-Tocachi, B.F.; Buytaert, W.; Bièvre, B.D. Regionalization of land-use impacts on streamflow using a network of paired catchments. Water Resour. Res. 2016, 52, 6710–6729. [Google Scholar] [CrossRef]
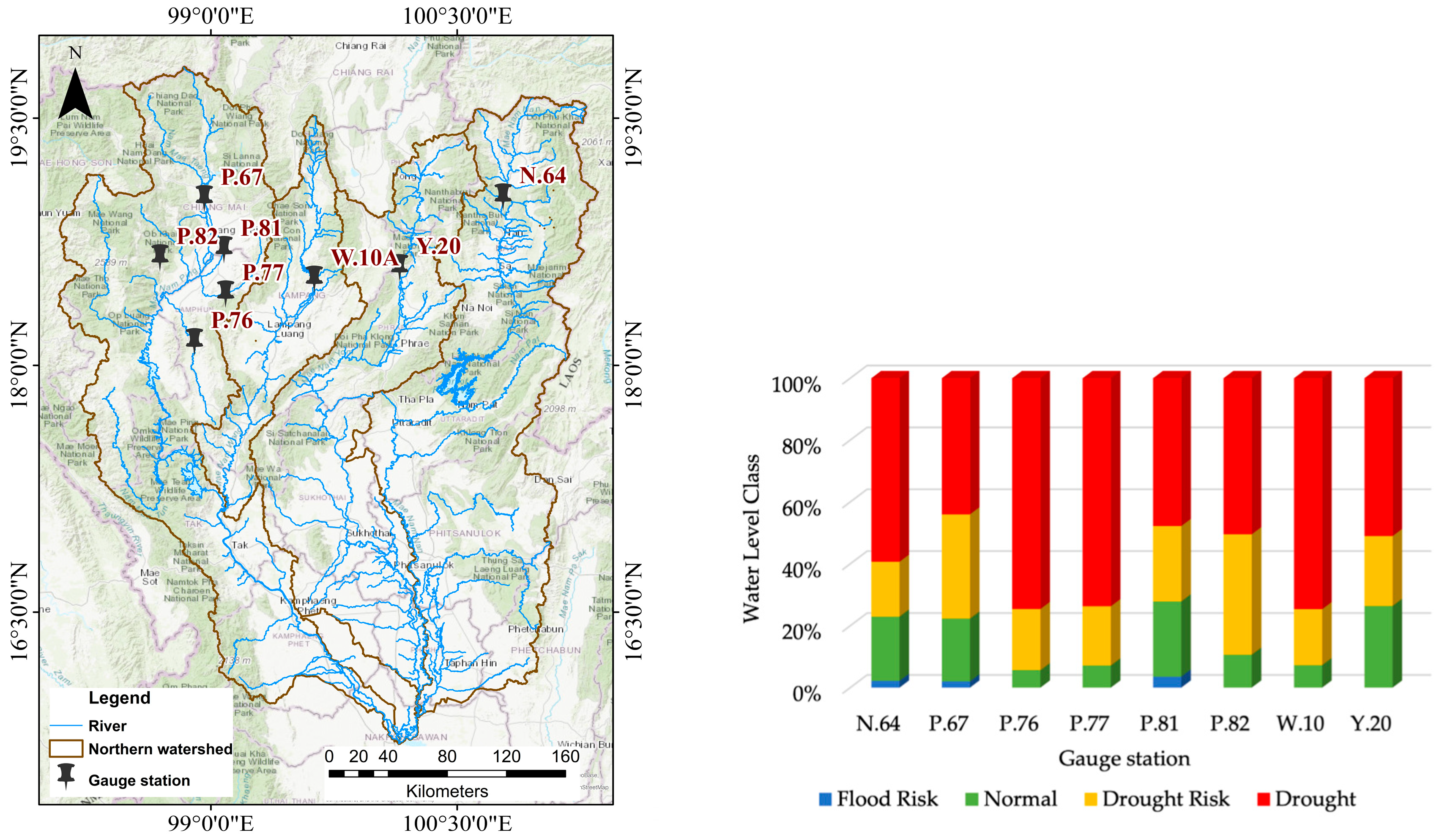



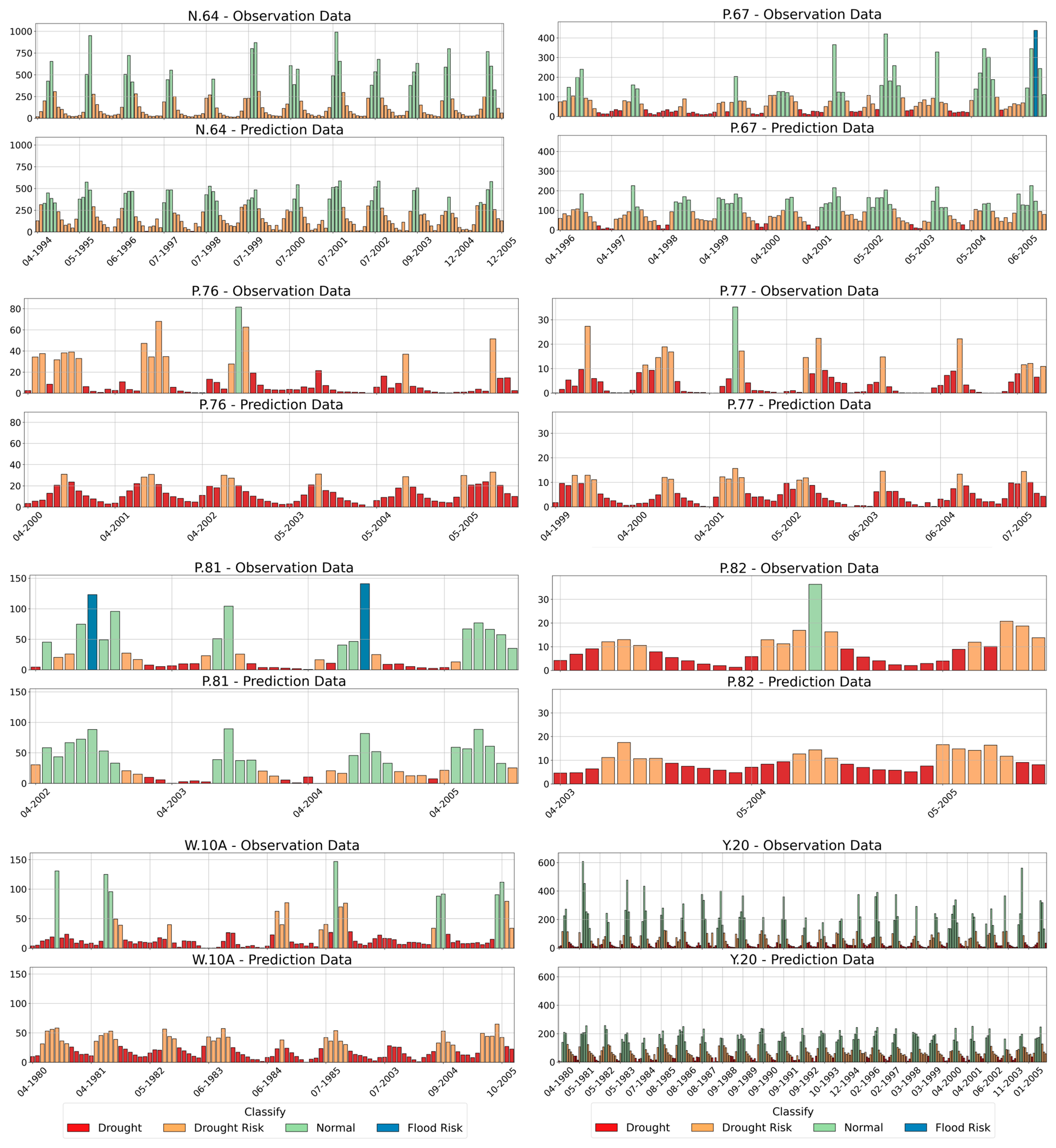
| Categories | Water Level |
|---|---|
| Drought | Less than 10% |
| Drought risk | 10–30% |
| Normal | 30–70% |
| Flood risk | More than 70% |
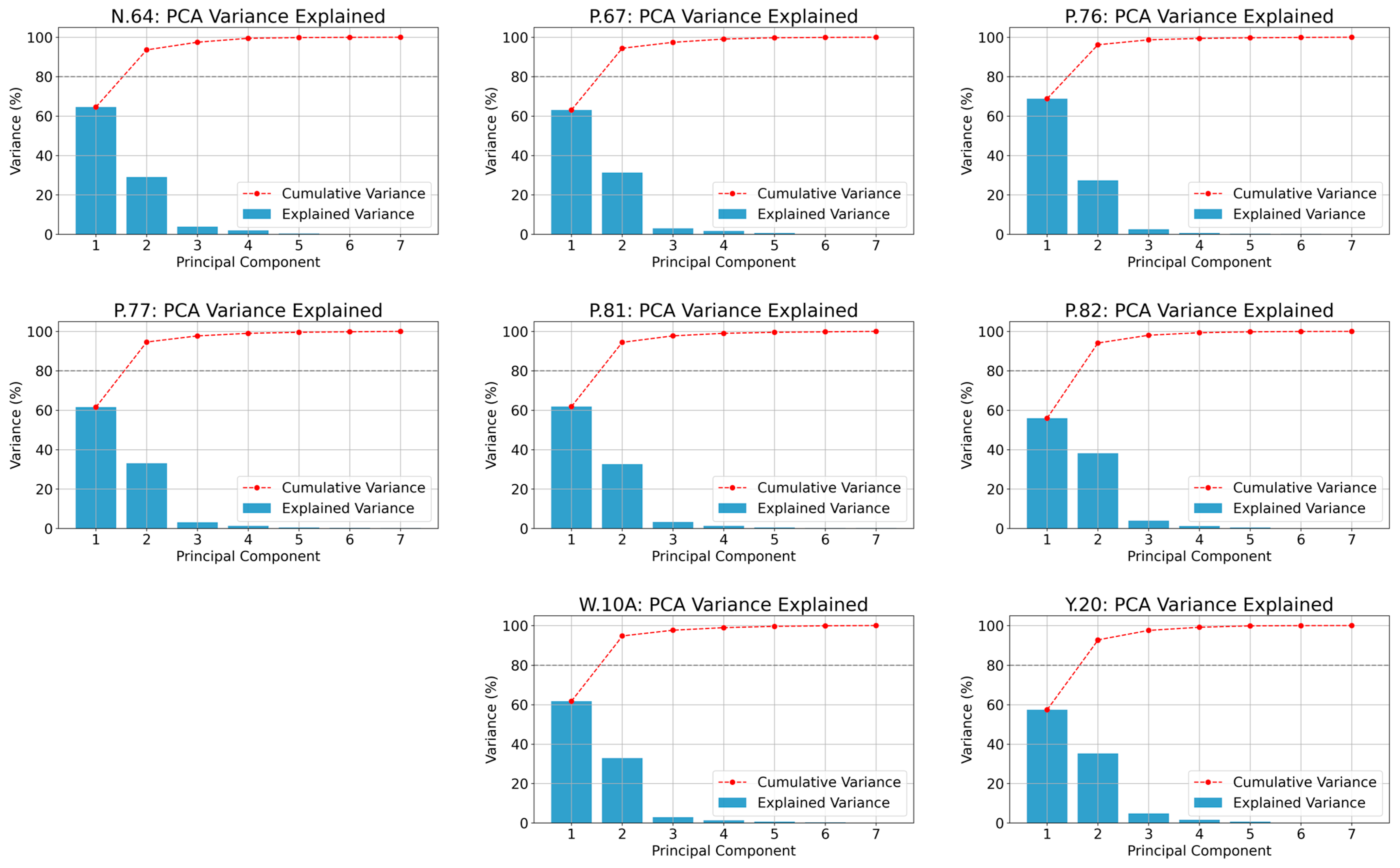
| Variable | Eigen Vector (PC1) | |||||||
|---|---|---|---|---|---|---|---|---|
| N.64 | P.67 | P.76 | P.77 | P.81 | P.82 | W.10A | Y.20 | |
| Baseflow | 0.35 | 0.37 | 0.39 | 0.38 | 0.38 | 0.34 | 0.39 | −0.31 |
| Evaporation | 0.35 | 0.34 | 0.34 | 0.34 | 0.34 | 0.37 | 0.31 | −0.35 |
| Precipitation | 0.40 | 0.39 | 0.37 | 0.38 | 0.38 | 0.41 | 0.36 | −0.41 |
| Runoff | 0.41 | 0.42 | 0.40 | 0.43 | 0.42 | 0.43 | 0.42 | −0.45 |
| Surface layer soil moisture | 0.43 | 0.44 | 0.43 | 0.43 | 0.43 | 0.45 | 0.44 | −0.45 |
| First-layer soil moisture | 0.35 | 0.33 | 0.34 | 0.33 | 0.34 | 0.30 | 0.35 | −0.36 |
| Second-layer soil moisture | 0.34 | 0.35 | 0.36 | 0.34 | 0.34 | 0.31 | 0.36 | −0.29 |
| PC1 Variance Explained | 64.6% | 63.1% | 68.8% | 61.5% | 61.8% | 55.9% | 61.8% | 57.4% |
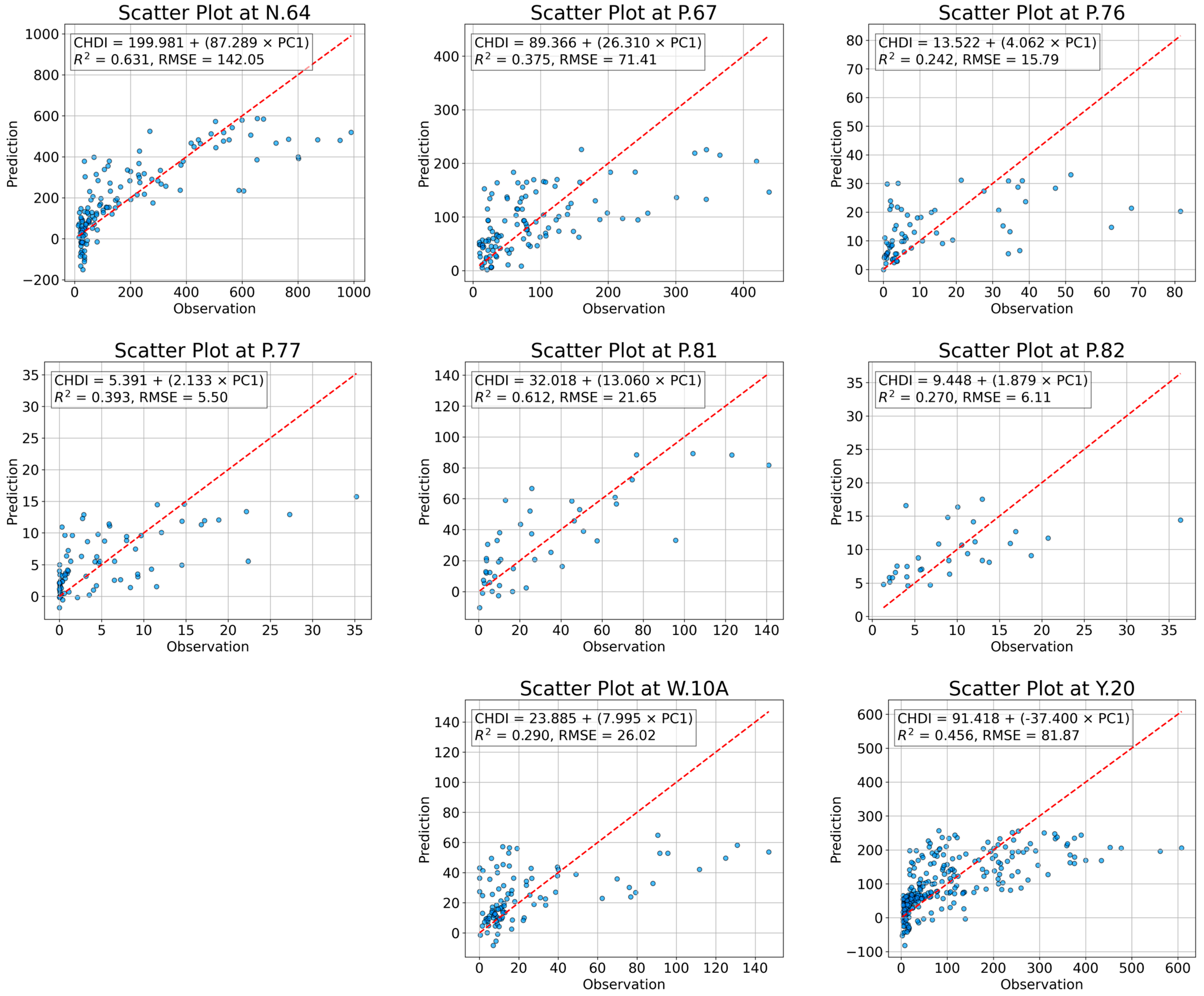
| Station | Equation |
|---|---|
| N.64 | Predicted water level = 199.981 + (87.289 × PC1) |
| P.67 | Predicted water level = 89.366 + (26.310 × PC1) |
| P.76 | Predicted water level = 13.522 + (4.062 × PC1) |
| P.77 | Predicted water level = 5.391 + (2.133 × PC1) |
| P.81 | Predicted water level = 32.018 + (13.060 × PC1) |
| P.82 | Predicted water level = 9.448 + (1.879 × PC1) |
| W.10A | Predicted water level = 23.885 + (7.995 × PC1) |
| Y.20 | Predicted water level = 91.418 + (−37.400 × PC1) |
| STATION | R | p-Value | NSE | S.D. Obs | S.D. Pred | RMSE | MAE | IOA | R2 |
|---|---|---|---|---|---|---|---|---|---|
| N.64 | 0.79 | 4.12 × 10−30 | 0.63 | 234 | 186 | 142 | 97 | 0.88 | 0.63 |
| P.67 | 0.61 | 4.56 × 10−13 | 0.37 | 90 | 55 | 71 | 51 | 0.73 | 0.37 |
| P.76 | 0.49 | 2.07 × 10−5 | 0.24 | 18 | 9 | 16 | 10 | 0.61 | 0.24 |
| P.77 | 0.63 | 1.03 × 10−9 | 0.39 | 7 | 4 | 5 | 4 | 0.75 | 0.39 |
| P.81 | 0.78 | 5.90 × 10−10 | 0.61 | 35 | 27 | 22 | 16 | 0.87 | 0.61 |
| P.82 | 0.52 | 2.72 × 10−3 | 0.27 | 7 | 4 | 6 | 4 | 0.63 | 0.27 |
| W.10A | 0.54 | 8.96 × 10−9 | 0.29 | 31 | 17 | 26 | 18 | 0.66 | 0.29 |
| Y.20 | 0.68 | 1.42 × 10−39 | 0.46 | 111 | 75 | 82 | 58 | 0.78 | 0.46 |
| Gauge | Statistical | Drought | Drought Risk | Normal | Flood Risk | Accuracy |
|---|---|---|---|---|---|---|
| N.64 | precision | 0.00 | 0.96 | 0.69 | 0.00 | 0.865 |
| recall | 0.00 | 0.87 | 0.86 | 0.00 | ||
| f1-score | 0.00 | 0.91 | 0.77 | 0.00 | ||
| P.67 | precision | 0.83 | 0.41 | 0.00 | 0.41 | 0.474 |
| recall | 0.35 | 0.56 | 0.00 | 0.56 | ||
| f1-score | 0.49 | 0.47 | 0.00 | 0.47 | ||
| P.76 | precision | 0.85 | 0.67 | 0.00 | 0.00 | 0.824 |
| recall | 0.94 | 0.43 | 0.00 | 0.00 | ||
| f1-score | 0.89 | 0.52 | 0.00 | 0.00 | ||
| P.77 | precision | 0.92 | 0.57 | 0.00 | 0.00 | 0.857 |
| recall | 0.92 | 0.62 | 0.00 | 0.00 | ||
| f1-score | 0.92 | 0.59 | 0.00 | 0.00 | ||
| P.81 | precision | 0.82 | 0.17 | 0.00 | 0.55 | 0.512 |
| recall | 0.47 | 0.22 | 0.00 | 0.85 | ||
| f1-score | 0.60 | 0.19 | 0.00 | 0.67 | ||
| P.82 | precision | 0.79 | 0.58 | 0.00 | 0.00 | 0.710 |
| recall | 0.79 | 0.64 | 0.00 | 0.00 | ||
| f1-score | 0.79 | 0.61 | 0.00 | 0.00 | ||
| W.10A | precision | 0.89 | 0.18 | 0.00 | 0.00 | 0.646 |
| recall | 0.74 | 0.46 | 0.00 | 0.00 | ||
| f1-score | 0.81 | 0.26 | 0.00 | 0.00 | ||
| Y.20 | precision | 0.90 | 0.26 | 0.56 | 0.00 | 0.516 |
| recall | 0.44 | 0.47 | 0.72 | 0.00 | ||
| f1-score | 0.59 | 0.34 | 0.63 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapyai, D.; Chotamonsak, C.; Chantara, S.; Limsakul, A. Developing a Composite Hydrological Drought Index Using the VIC Model: Case Study in Northern Thailand. Water 2025, 17, 2732. https://doi.org/10.3390/w17182732
Lapyai D, Chotamonsak C, Chantara S, Limsakul A. Developing a Composite Hydrological Drought Index Using the VIC Model: Case Study in Northern Thailand. Water. 2025; 17(18):2732. https://doi.org/10.3390/w17182732
Chicago/Turabian StyleLapyai, Duangnapha, Chakrit Chotamonsak, Somporn Chantara, and Atsamon Limsakul. 2025. "Developing a Composite Hydrological Drought Index Using the VIC Model: Case Study in Northern Thailand" Water 17, no. 18: 2732. https://doi.org/10.3390/w17182732
APA StyleLapyai, D., Chotamonsak, C., Chantara, S., & Limsakul, A. (2025). Developing a Composite Hydrological Drought Index Using the VIC Model: Case Study in Northern Thailand. Water, 17(18), 2732. https://doi.org/10.3390/w17182732








