Hybrid ITSP-LSTM Approach for Stochastic Citrus Water Allocation Addressing Trade-Offs Between Hydrological-Economic Factors and Spatial Heterogeneity
Abstract
1. Introduction
2. Materials and Methods
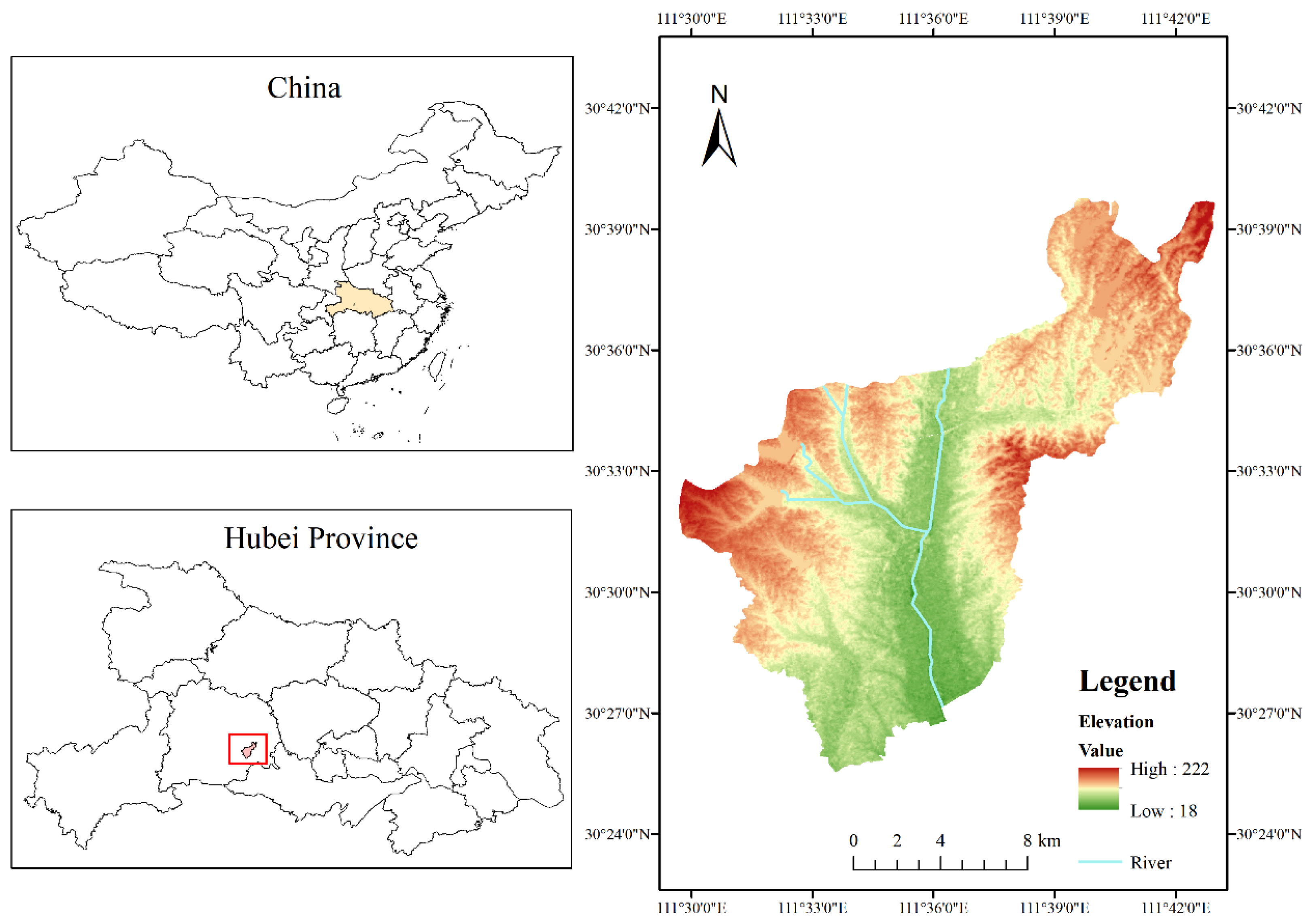
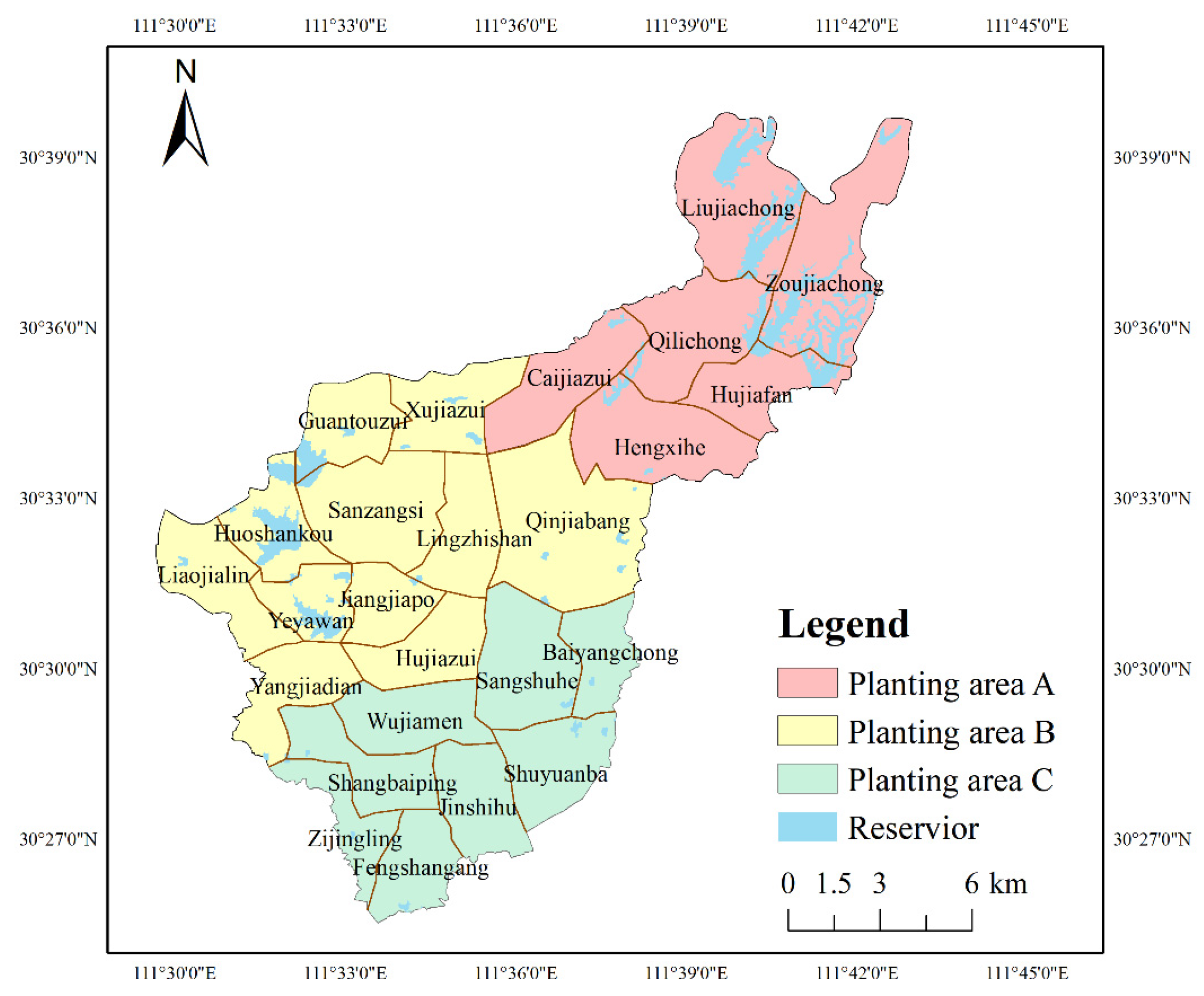
2.1. Study Area
2.2. Research Framework
2.3. Available Water Supply Calculation
2.4. Citrus Irrigation Water Requirement Calculation
2.5. Water Supply and Demand Prediction Based on the Long Short-Term Memory Method
2.6. Establishment of Interval Two-Stage Stochastic Programming Model
- (1)
- Available water supply constraint for water sources:where represents the maximum available water supply from water source i, m3;
- (2)
- Crop water requirement constraint:where represents the minimum water requirement for the normal growth of citrus in the j planting area, m3; represents the maximum water requirement for the normal growth of citrus in the j planting area.
- (3)
- Non-negativity constraint:
2.7. Solution of the Interval Two-Stage Stochastic Programming Model
2.8. Profit Coefficient
3. Results
3.1. Water Resource Zoning Strategies and Supply–Demand Balance for Citrus Irrigation
3.2. Prediction of Water Supply and Demand for Citrus Irrigation in Planning Year
3.3. Target Value of Citrus Water Distribution in Advance
3.4. System Net Benefit and Penalty Rates per Unit Transferred Water
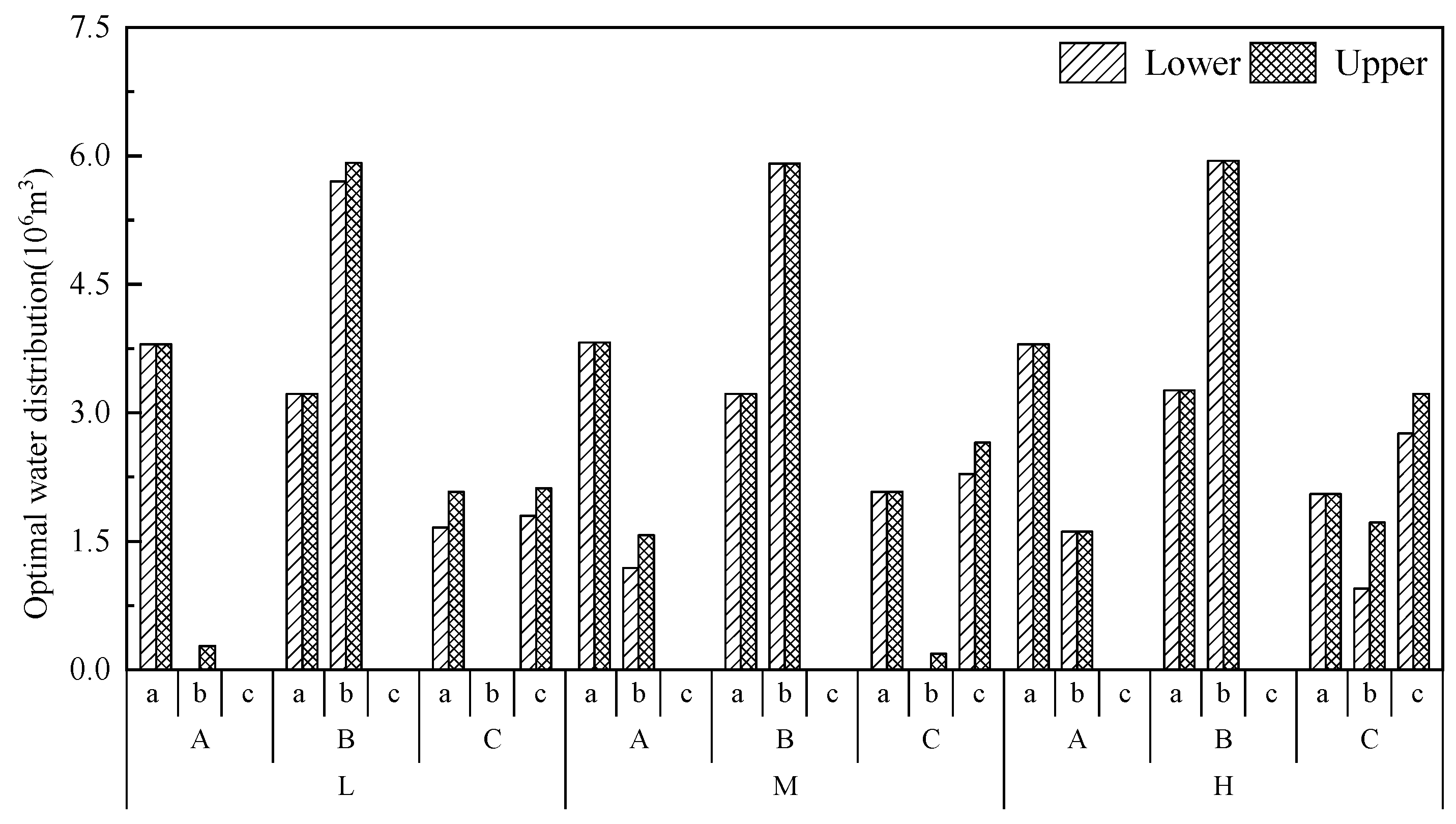
3.5. Optimal Water Allocation Schemes for Citrus Irrigation
4. Discussions
4.1. Stochastic Citrus Water Allocation Integrating Hydrological and Economic Factors
4.2. Spatial Heterogeneity and Trade-Offs in Citrus Water Allocation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehta, P.; Siebert, S.; Kummu, M.; Deng, Q.; Ali, T.; Marston, L.; Xie, W.; Davis, K.F. Half of Twenty-First Century Global Irrigation Expansion Has Been in Water-Stressed Regions. Nat. Water 2024, 2, 254–261. [Google Scholar] [CrossRef]
- Cao, X.; Wu, M.; Guo, X.; Zheng, Y.; Gong, Y.; Wu, N.; Wang, W. Assessing Water Scarcity in Agricultural Production System Based on the Generalized Water Resources and Water Footprint Framework. Sci. Total Environ. 2017, 609, 587–597. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, T.; Wu, P.; Wang, Y.; Zhao, X.; Yin, Y. Impacts of Future Climate and Agricultural Land-use Changes on Regional Agricultural Water Use in a Large Irrigation District of Northwest China. Land Degrad. Dev. 2019, 30, 1158–1171. [Google Scholar] [CrossRef]
- Saccon, P. Water for Agriculture, Irrigation Management. Appl. Soil Ecol. 2018, 123, 793–796. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, W. Spatio-Temporal Patterns and Drivers of Irrigation Water Requirement in Mainland China. Agric. Water Manag. 2025, 308, 109283. [Google Scholar] [CrossRef]
- Zhu, H.; Huang, G.H.; Guo, P.; Qin, X.S. A Fuzzy Robust Nonlinear Programming Model for Stream Water Quality Management. Water Resour. Manag. 2009, 23, 2913–2940. [Google Scholar] [CrossRef]
- Ren, C.F.; Guo, P.; Li, M.; Gu, J.J. Optimization of Industrial Structure Considering the Uncertainty of Water Resources. Water Resour. Manag. 2013, 27, 3885–3898. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Ren, C. Water Resources Management Models Based on Two-Level Linear Fractional Programming Method under Uncertainty. J. Water Resour. Plan. Manag. 2015, 141, 05015001. [Google Scholar] [CrossRef]
- Tang, X.; He, Y.; Qi, P.; Chang, Z.; Jiang, M.; Dai, Z. A New Multi-Objective Optimization Model of Water Resources Considering Fairness and Water Shortage Risk. Water 2021, 13, 2648. [Google Scholar] [CrossRef]
- Liu, B.; Liu, R.; Yan, Z.; Ren, S.; Zhao, X.; Liu, G. Optimal Allocation of Soil and Water Resources in Agriculture under the Total Regional Evapotranspiration Indicator: A Case Study in Guangping, China. Ecol. Indic. 2024, 160, 111855. [Google Scholar] [CrossRef]
- Li, M.; Sun, H.; Liu, D.; Singh, V.P.; Fu, Q. Multi-Scale Modeling for Irrigation Water and Cropland Resources Allocation Considering Uncertainties in Water Supply and Demand. Agric. Water Manag. 2021, 246, 106687. [Google Scholar] [CrossRef]
- Jain, S.; Ramesh, D.; Trivedi, M.C.; Edla, D.R. Evaluation of Metaheuristic Optimization Algorithms for Optimal Allocation of Surface Water and Groundwater Resources for Crop Production. Agric. Water Manag. 2023, 279, 108181. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.H. A Multi-Level Taguchi-Factorial Two-Stage Stochastic Programming Approach for Characterization of Parameter Uncertainties and Their Interactions: An Application to Water Resources Management. Eur. J. Oper. Res. 2015, 240, 572–581. [Google Scholar] [CrossRef]
- Tarebari, H.; Javid, A.H.; Mirbagheri, S.A.; Fahmi, H. Optimal Water Allocation by Equilibrating between Agricultural and Environmental Sectors in River Basins. Appl. Ecol. Environ. Res. 2018, 16, 7467–7483. [Google Scholar] [CrossRef]
- Aljanabi, A.A.; Mays, L.W.; Fox, P. Optimization Model for Agricultural Reclaimed Water Allocation Using Mixed-Integer Nonlinear Programming. Water 2018, 10, 1291. [Google Scholar] [CrossRef]
- Garajová, E.; Hladík, M.; Rada, M. Interval Linear Programming under Transformations: Optimal Solutions and Optimal Value Range. Cent. Eur. J. Oper. Res. 2019, 27, 601–614. [Google Scholar] [CrossRef]
- Suo, M.; Xia, F.; Fan, Y. A Fuzzy-Interval Dynamic Optimization Model for Regional Water Resources Allocation under Uncertainty. Sustainability 2022, 14, 1096. [Google Scholar] [CrossRef]
- Parsinejad, M.; Yazdi, A.B.; Araghinejad, S.; Nejadhashemi, A.P.; Tabrizi, M.S. Optimal Water Allocation in Irrigation Networks Based on Real Time Climatic Data. Agric. Water Manag. 2013, 117, 1–8. [Google Scholar] [CrossRef]
- Lu, W.T.; Dai, C.; Fu, Z.H.; Liang, Z.Y.; Guo, H.C. An Interval-Fuzzy Possibilistic Programming Model to Optimize China Energy Management System with CO2 Emission Constraint. Energy 2018, 142, 1023–1039. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, X.; Chen, C.; Li, Y.; Huang, G.; Li, Y. Analysis of Industry-Air Quality Control in Ecologically Fragile Coal-Dependent Cities by an Uncertain Gaussian Diffusion-Hurwicz Criterion Model. Energy Policy 2019, 132, 1191–1205. [Google Scholar] [CrossRef]
- Lv, Y. Planning Regional Water Resources System Using an Interval Fuzzy Bi-Level Programming Method. J. Environ. Inform. 2010, 16, 43–56. [Google Scholar] [CrossRef]
- Nematian, J. An Extended Two-Stage Stochastic Programming Approach for Water Resources Management under Uncertainty. J. Environ. Inform. 2015, 27, 72–84. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; Guo, P.; Huo, Z. An Improved Interval-Based Fuzzy Credibility-Constrained Programming Approach for Supporting Optimal Irrigation Water Management under Uncertainty. Agric. Water Manag. 2020, 238, 106185. [Google Scholar] [CrossRef]
- Bekri, E.; Disse, M.; Yannopoulos, P. Optimizing Water Allocation under Uncertain System Conditions for Water and Agriculture Future Scenarios in Alfeios River Basin (Greece)—Part B: Fuzzy-Boundary Intervals Combined with Multi-Stage Stochastic Programming Model. Water 2015, 7, 6427–6466. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, P.; Huo, Z. Irrigation Water Resources Management under Uncertainty: An Interval Nonlinear Double-Sided Fuzzy Chance-Constrained Programming Approach. Agric. Water Manag. 2021, 245, 106658. [Google Scholar] [CrossRef]
- Guo, P.; Huang, G.H.; Zhu, H.; Wang, X.L. A Two-Stage Programming Approach for Water Resources Management under Randomness and Fuzziness. Environ. Model. Softw. 2010, 25, 1573–1581. [Google Scholar] [CrossRef]
- Xie, Y.L.; Huang, G.H.; Li, W.; Li, J.B.; Li, Y.F. An Inexact Two-Stage Stochastic Programming Model for Water Resources Management in Nansihu Lake Basin, China. J. Environ. Manag. 2013, 127, 188–205. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.H.; Loucks, D.P. An Inexact Two-Stage Stochastic Programming Model for Water Resources Management under Uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 95–118. [Google Scholar] [CrossRef]
- Nifa, K.; Boudhar, A.; Ouatiki, H.; Elyoussfi, H.; Bargam, B.; Chehbouni, A. Deep Learning Approach with LSTM for Daily Streamflow Prediction in a Semi-Arid Area: A Case Study of Oum Er-Rbia River Basin, Morocco. Water 2023, 15, 262. [Google Scholar] [CrossRef]
- Wu, M.; Liu, P.; Liu, L.; Zou, K.; Luo, X.; Wang, J.; Xia, Q.; Wang, H. Improving a Hydrological Model by Coupling It with an LSTM Water Use Forecasting Model. J. Hydrol. 2024, 636, 131215. [Google Scholar] [CrossRef]
- Hashemi, S.; Samadianfard, S.; Nazemi, A.H. Sequence-to-Sequence and Meta LSTM Techniques Enhanced by Remote Sensing for Advanced Evapotranspiration Estimation. Earth Sci. Inform. 2025, 18, 386. [Google Scholar] [CrossRef]
- Luo, Y.; Meng, X.; Zhai, Y.; Zhang, D.; Ma, K. Prediction of Water Quality in Agricultural Watersheds Based on VMD-GA-LSTM Model. Mathematics 2025, 13, 1951. [Google Scholar] [CrossRef]
- Koohikeradeh, E.; Jose Gumiere, S.; Bonakdari, H. NDMI-Derived Field-Scale Soil Moisture Prediction Using ERA5 and LSTM for Precision Agriculture. Sustainability 2025, 17, 2399. [Google Scholar] [CrossRef]
- Berríos, P.; Temnani, A.; Zapata, S.; Forcén-Muñoz, M.; Franco, J.A.; Pérez-Pastor, A. Sensitivity to Water Deficit of the Second Stage of Fruit Growth in Late Mandarin Trees. Irrig. Sci. 2023, 41, 35–47. [Google Scholar] [CrossRef]
- Yu, A.; Cai, E.; Yang, M.; Li, Z. An Analysis of Water Use Efficiency of Staple Grain Productions in China: Based on the Crop Water Footprints at Provincial Level. Sustainability 2022, 14, 6682. [Google Scholar] [CrossRef]
- Liu, X.; Ma, S.; Fang, Y.; Wang, S.; Guo, P. A Novel Approach to Identify Crop Irrigation Priority. Agric. Water Manag. 2023, 275, 108008. [Google Scholar] [CrossRef]
- Navarro, J.M.; Botía, P.; Pérez-Pérez, J.G. Influence of Deficit Irrigation Timing on the Fruit Quality of Grapefruit (Citrus Paradisi Mac.). Food Chem. 2015, 175, 329–336. [Google Scholar] [CrossRef]
- Fung, K.F.; Chew, K.S.; Huang, Y.F.; Ahmed, A.N.; Teo, F.Y.; Ng, J.L.; Elshafie, A. Evaluation of Spatial Interpolation Methods and Spatiotemporal Modeling of Rainfall Distribution in Peninsular Malaysia. Ain Shams Eng. J. 2022, 13, 101571. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, Z.; Duan, C.; Lin, Z.; Hao, K.; Li, H.; Zhong, Y. Multispectral Inversion of Citrus Multi-Slope Evapotranspiration by UAV Based on Modified RSEB Model. Water 2024, 16, 1520. [Google Scholar] [CrossRef]
- Fontanier, C.H.; Aitkenhead-Peterson, J.A.; Wherley, B.G.; White, R.H.; Thomas, J.C. Effective Rainfall Estimates for St. Augustinegrass Lawns under Varying Irrigation Programs. Agron. J. 2021, 113, 3720–3729. [Google Scholar] [CrossRef]
- Muratoglu, A.; Bilgen, G.K.; Angin, I.; Kodal, S. Performance Analyses of Effective Rainfall Estimation Methods for Accurate Quantification of Agricultural Water Footprint. Water Res. 2023, 238, 120011. [Google Scholar] [CrossRef]
- Laib, O.; Khadir, M.T.; Mihaylova, L. Toward Efficient Energy Systems Based on Natural Gas Consumption Prediction with LSTM Recurrent Neural Networks. Energy 2019, 177, 530–542. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Douglas, E.M.; Fekete, B.M.; Schumann, A.H.; Vörösmarty, C.J. The Significance of Local Water Resources Captured in Small Reservoirs for Crop Production—A Global-Scale Analysis. J. Hydrol. 2010, 384, 264–275. [Google Scholar] [CrossRef]
- Manassaldi, J.I.; Mussati, M.C.; Incer-Valverde, J.; Morosuk, T.; Mussati, S.F. Renewable Energy-Water Nexus: Optimal Design of an Integrated System Including a Single Flash Geothermal Plant, Kalina Cycle, and Seawater Desalination Units. Renew. Energy 2024, 236, 121395. [Google Scholar] [CrossRef]
- Zhen, J.L.; Wu, C.B.; Liu, X.R.; Huang, G.H.; Liu, Z.P. Energy-Water Nexus Planning of Regional Electric Power System within an Inexact Optimization Model in Tangshan City, China. J. Clean. Prod. 2020, 266, 121997. [Google Scholar] [CrossRef]
- Cao, M.; Liu, W.; Xu, B.; Wang, L.; Zhang, Y.; Zhang, Y. Multi-Scenario Optimization Model for Operation of Inter-Basin Water Transfer-Supply Systems Considering Cost–Benefit Relationships. J. Water Clim. Change 2023, 14, 2872–2884. [Google Scholar] [CrossRef]


| Developmental Phase | Time Interval | Lower Limit Temperature t1 (°C) | Preference-Temperature t0 (°C) | Ceiling Temperature t2 (°C) | Crop Coefficient Kc |
|---|---|---|---|---|---|
| Germination stage | 15 February–15 April | 8.1 | 14.0 | 26.0 | 0.48 |
| Blooming stage | 16 April–15 May | 11.8 | 20.0 | 30.0 | 0.65 |
| Physiological fruit drop stage | 16 May–20 June | 13.0 | 21.0 | 30.0 | 0.76 |
| Development stage | 21 June–5 October | 13.0 | 22.0 | 34.0 | 0.95 |
| Maturation stage | 6 October–20 November | 13.0 | 21.0 | 27.0 | 0.70 |
| Flower bud differentiation stage | 21 November–15 February | −5.0 | 12.5 | 23.0 | 0.39 |
| Citrus Planting Zones | Water Supply Zones | Cultivated Area (hm2) | Water Supply (106 m3) | Citrus Planting Water Demand (106 m3) | Water Shortage (106 m3) | ||
|---|---|---|---|---|---|---|---|
| Reservoirs Water Supply (106 m3) | Weirs Water Supply (106 m3) | Total (106 m3) | |||||
| A | a | 2077.67 | 10.13 | 0.29 | 10.42 | 7.01 | 0 |
| B | b | 3520.67 | 5.94 | 0.44 | 6.38 | 11.88 | 5.50 |
| C | c | 2265.33 | 1.40 | 0.75 | 2.15 | 7.65 | 5.49 |
| Water Supply Zones | Reservoirs Water Supply (106 m3) | Weirs Water Supply (106 m3) | Total (106 m3) | ||
|---|---|---|---|---|---|
| Upper Limit | Lower Limit | Upper Limit | Lower Limit | ||
| a | 11.43 | 10.67 | 0.37 | 0.33 | [11.01, 11.80] |
| b | 7.03 | 6.51 | 0.78 | 0.67 | [7.18, 7.81] |
| c | 1.90 | 1.57 | 0.81 | 0.74 | [2.31, 2.71] |
| Water Inflow Level | Probability | Water Supply for Zone a (106 m3) | Water Supply for Zone b (106 m3) | Water Supply for Zone c (106 m3) |
|---|---|---|---|---|
| Low(L) | 0.2 | [8.81, 9.44] | [5.75, 6.24] | [1.85, 2.17] |
| Medium(M) | 0.6 | [11.01, 11.80] | [7.18, 7.80] | [2.31, 2.71] |
| High(H) | 0.2 | [13.21, 14.16] | [8.62, 9.37] | [2.77, 3.25] |
| Citrus Planting Zones | Planting Area (hm2) | Irrigation Module (m3/hm2) | Pre-Water Distribution Target (106 m3) | ||
|---|---|---|---|---|---|
| Water Supply for Zone A | Water Supply for Zone B | Water Supply for Zone C | |||
| A | 2077.67 | [3122.25, 3706.95] | [3.24, 3.85] | [1.62, 1.93] | [1.62, 1.93] |
| B | 3520.67 | [2.75, 3.26] | [5.50, 6.53] | [2.75, 3.26] | |
| C | 2265.33 | [1.77, 2.10] | [1.77, 2.10] | [3.54, 4.20] | |
| Economic Coefficient | A | B | C | |||
|---|---|---|---|---|---|---|
| (CNY/m3) | Coefficient | Penalty Coefficient | Coefficient | Penalty Coefficient | Coefficient | Penalty Coefficient |
| A | [9.68, 10.19] | [12.58, 13.25] | [8.71, 9.17] | [13.33, 11.92] | [8.23, 8.66] | [10.70, 11.26] |
| B | [8.94, 9.41] | [11.62, 12.24] | [9.93, 10.46] | [12.91, 13.60] | [8.44, 8.96] | [10.98, 11.56] |
| C | [8.58, 9.03] | [11.15, 11.74] | [8.10, 8.53] | [10.53, 11.09] | [9.53, 10.04] | [12.39, 13.05] |
| Water Inflow Level | Citrus Planting Zones | Water Supply Zones | Optimal Water Distribution Target (106 m3) | Water Deficit (106 m3) | Optimal Water Allocation (106 m3) | zij,opt |
|---|---|---|---|---|---|---|
| L | A | a | 3.85 | 0 | 3.85 | 1 |
| b | 3.26 | 0 | 3.26 | 1 | ||
| c | 2.10 | [0, 0.41] | [1.69, 2.10] | 1 | ||
| B | a | 3.26 | 0 | 3.26 | 1 | |
| b | 5.98 | [0, 0.23] | [5.75, 5.98] | 0.466 | ||
| c | 2.75 | 2.75 | 0 | 0 | ||
| C | a | 2.10 | [0, 0.41] | [1.69, 2.10] | 0 | |
| b | 1.77 | 1.76 | 0 | 0 | ||
| c | 3.54 | [1.37, 1.69] | [1.85, 2.17] | 0 | ||
| M | A | a | 3.85 | 0 | 3.85 | 1 |
| b | 1.62 | [0, 0.41] | [1.21, 1.62] | 0 | ||
| c | 1.62 | 1.62 | 0 | 0 | ||
| B | a | 3.26 | 0 | 3.26 | 1 | |
| b | 5.98 | 0 | 5.98 | 0.466 | ||
| c | 2.75 | 2.75 | 0 | 0 | ||
| C | a | 2.10 | 0 | 2.10 | 1 | |
| b | 1.77 | [1.56, 1.77] | [0, 0.21] | 0 | ||
| c | 3.54 | [0.83, 1.23] | [2.31, 2.71] | 0 | ||
| H | A | a | 3.85 | 0 | 3.85 | 1 |
| b | 1.62 | 0 | 1.62 | 0 | ||
| c | 1.62 | 1.62 | 0 | 0 | ||
| B | a | 3.26 | 0 | 3.26 | 1 | |
| b | 5.98 | 0 | 5.98 | 0.466 | ||
| c | 2.75 | 2.75 | 0 | 0 | ||
| C | a | 2.10 | 0 | 2.10 | 1 | |
| b | 1.77 | [0, 0.75] | [1.02, 1.77] | 0 | ||
| c | 3.54 | [0.29, 0.77] | [2.77, 3.25] | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Hu, R.; Zheng, Y.; Yu, Y.; Cai, Y.; Zhu, S. Hybrid ITSP-LSTM Approach for Stochastic Citrus Water Allocation Addressing Trade-Offs Between Hydrological-Economic Factors and Spatial Heterogeneity. Water 2025, 17, 2665. https://doi.org/10.3390/w17182665
Xu W, Hu R, Zheng Y, Yu Y, Cai Y, Zhu S. Hybrid ITSP-LSTM Approach for Stochastic Citrus Water Allocation Addressing Trade-Offs Between Hydrological-Economic Factors and Spatial Heterogeneity. Water. 2025; 17(18):2665. https://doi.org/10.3390/w17182665
Chicago/Turabian StyleXu, Wen, Rui Hu, Yifei Zheng, Ying Yu, Yanpeng Cai, and Shijiang Zhu. 2025. "Hybrid ITSP-LSTM Approach for Stochastic Citrus Water Allocation Addressing Trade-Offs Between Hydrological-Economic Factors and Spatial Heterogeneity" Water 17, no. 18: 2665. https://doi.org/10.3390/w17182665
APA StyleXu, W., Hu, R., Zheng, Y., Yu, Y., Cai, Y., & Zhu, S. (2025). Hybrid ITSP-LSTM Approach for Stochastic Citrus Water Allocation Addressing Trade-Offs Between Hydrological-Economic Factors and Spatial Heterogeneity. Water, 17(18), 2665. https://doi.org/10.3390/w17182665






