Investigating Basin-Scale Water Dynamics During a Flood in the Upper Tenryu River Basin
Abstract
1. Introduction
2. Target Basin and Flood Event
3. Materials and Methods
3.1. Observed Data
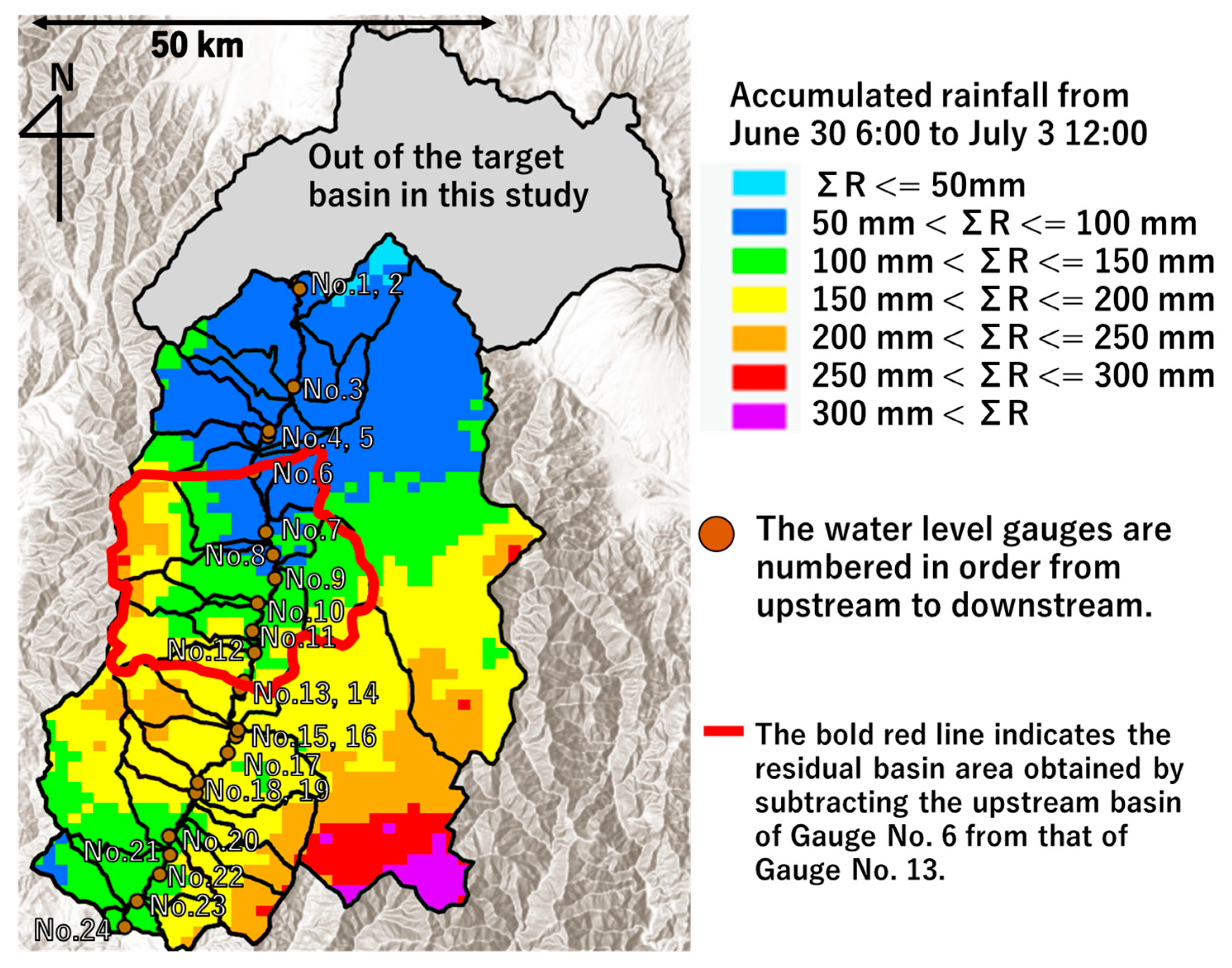
3.1.1. Rainfall Data
3.1.2. Discharge Data
3.1.3. Water Level Data
3.2. Rainfall–Runoff Simulation Model
3.3. Two-Dimensional Unsteady Flow Model
4. Results
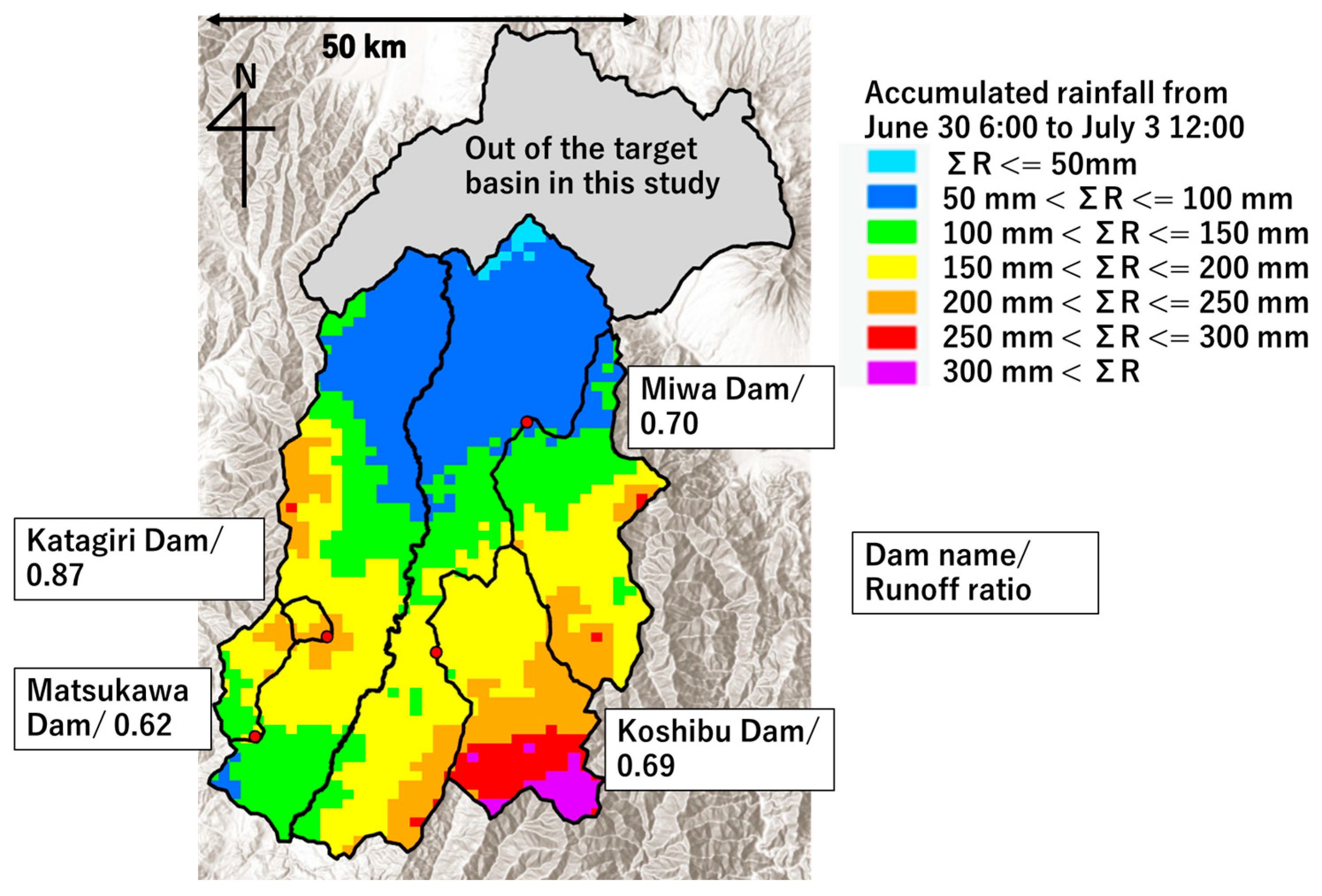
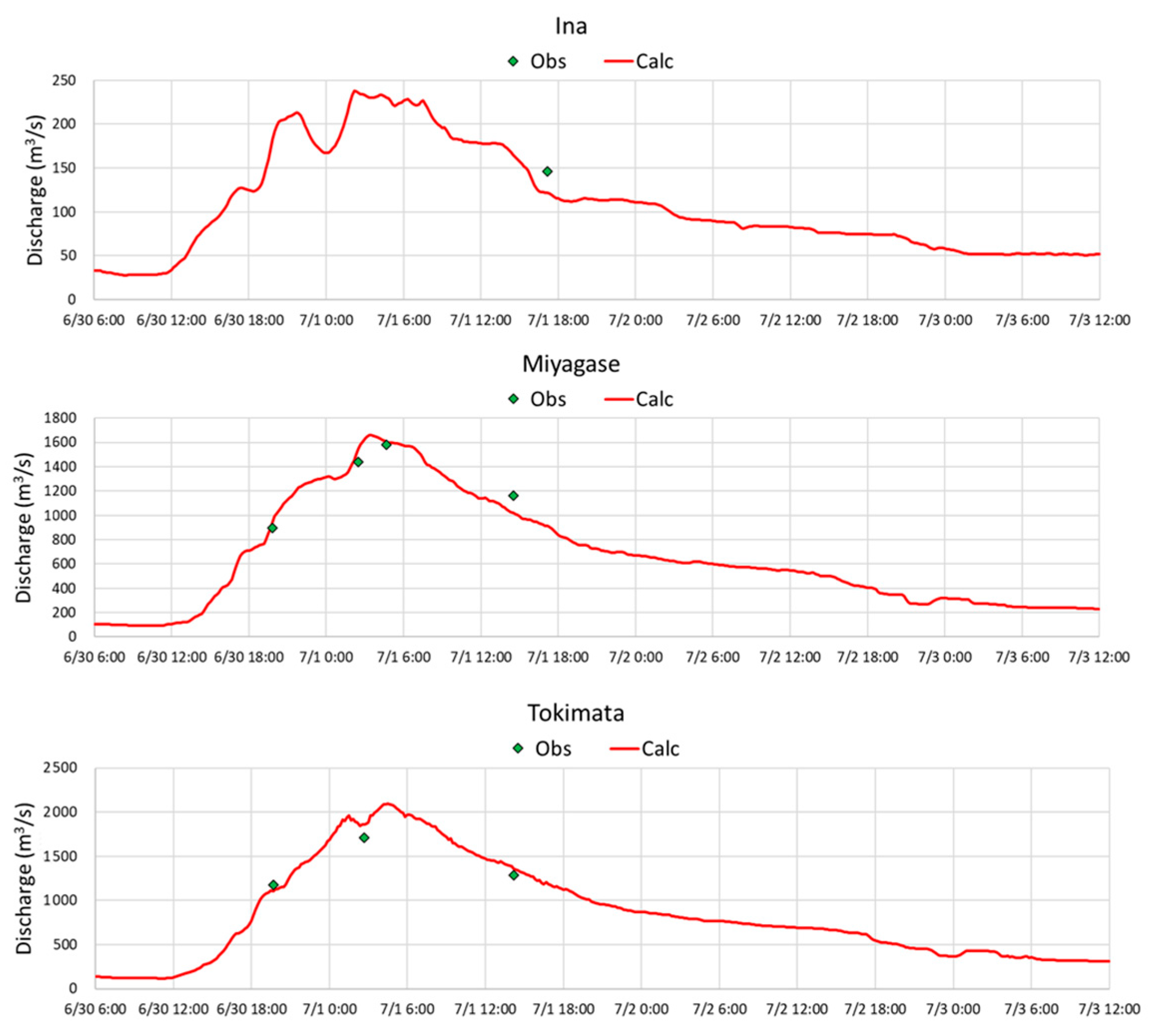
4.1. Rainfall–Runoff Relationships in Dam Basins
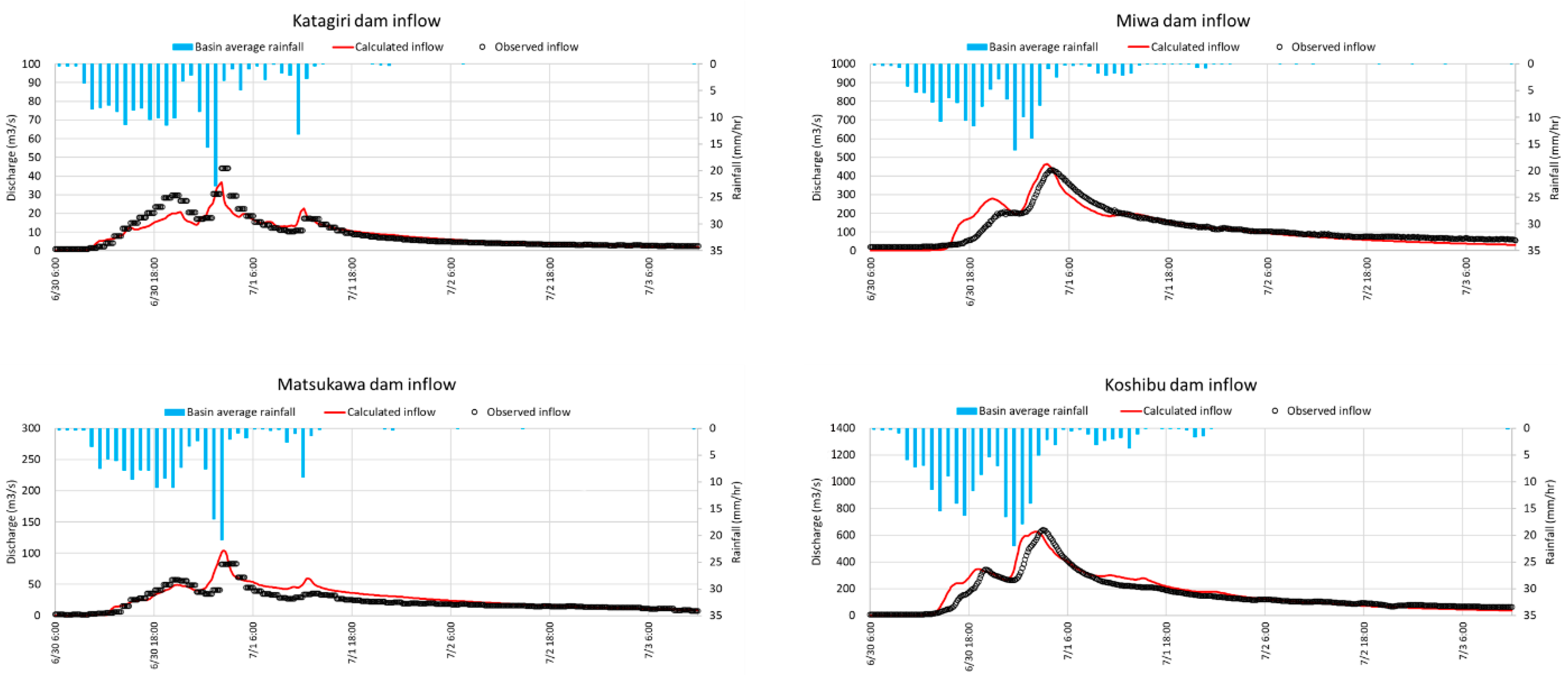
4.2. Validation of the Rainfall–Runoff Simulation
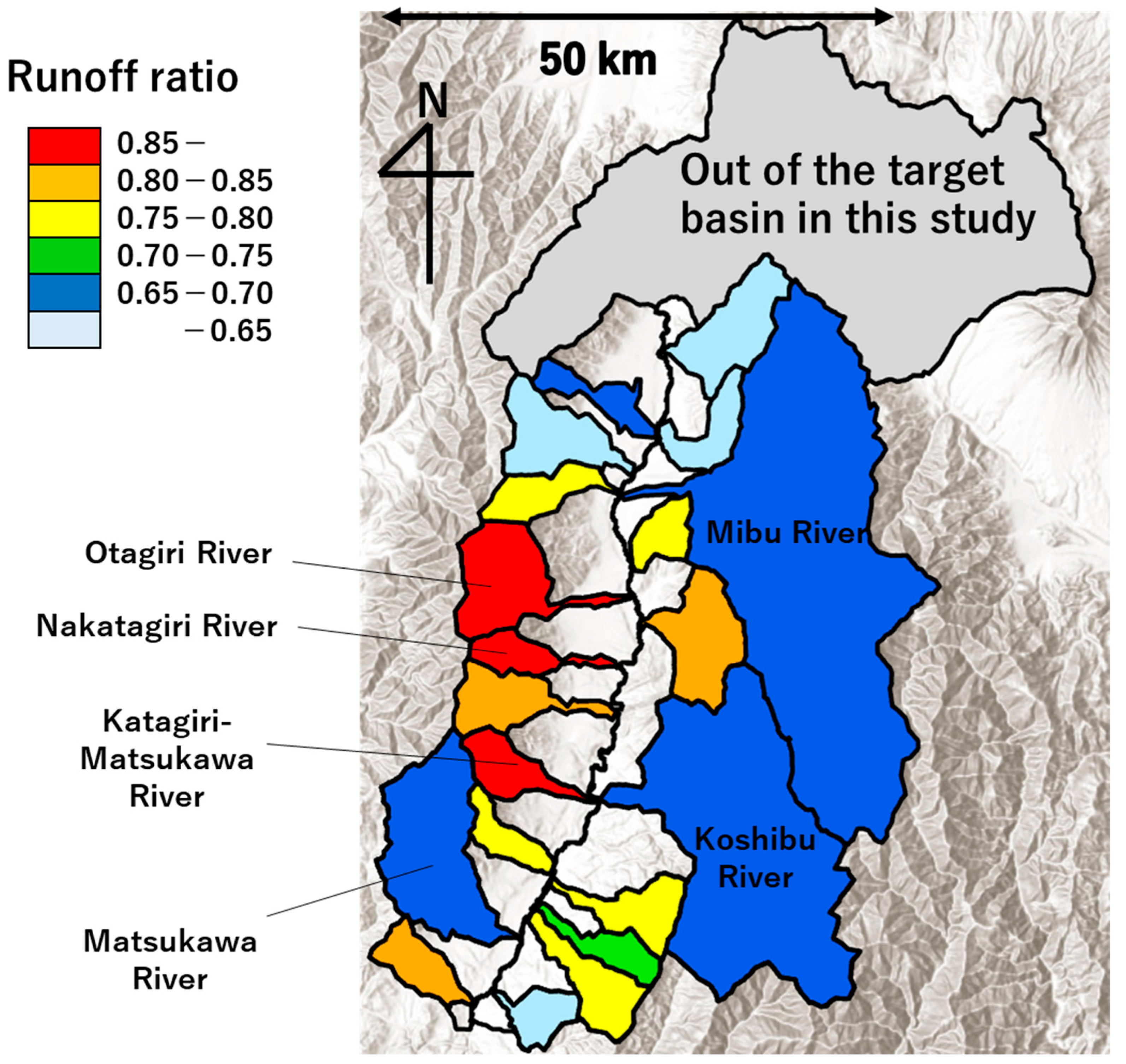
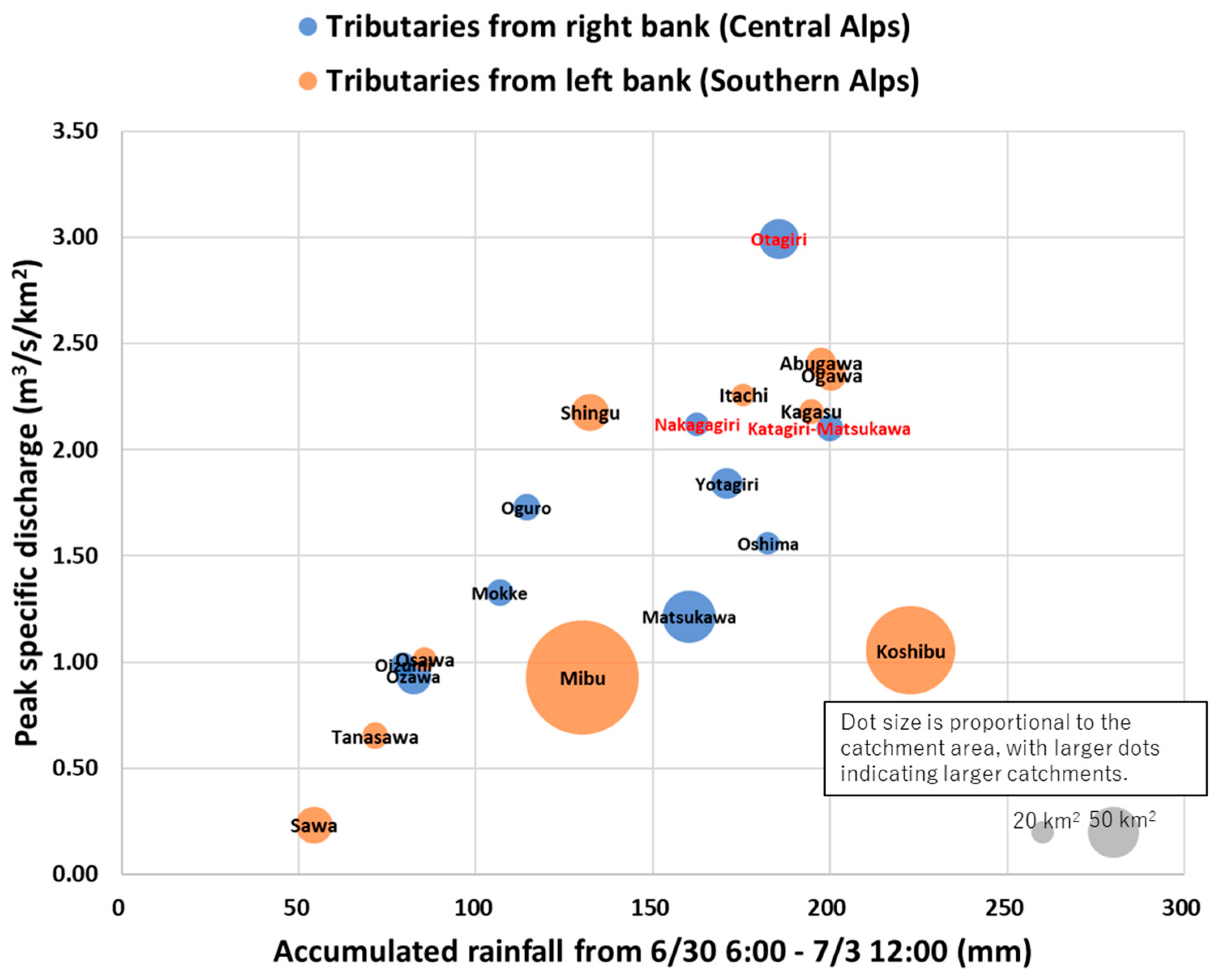
4.3. Runoff Characteristics of the Tributary Basins
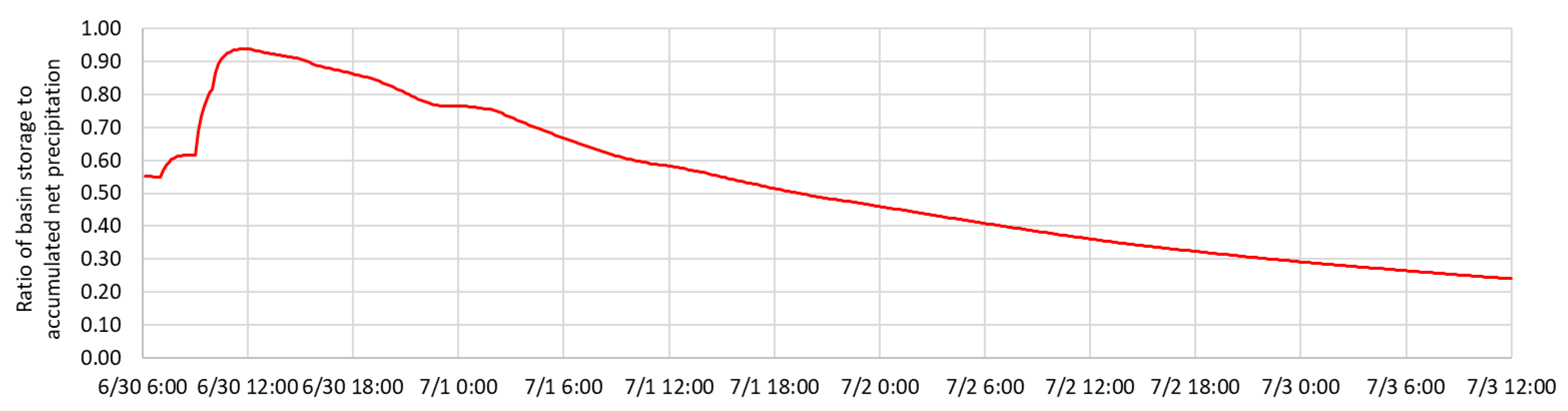
4.4. Investigation of the Basin Storage
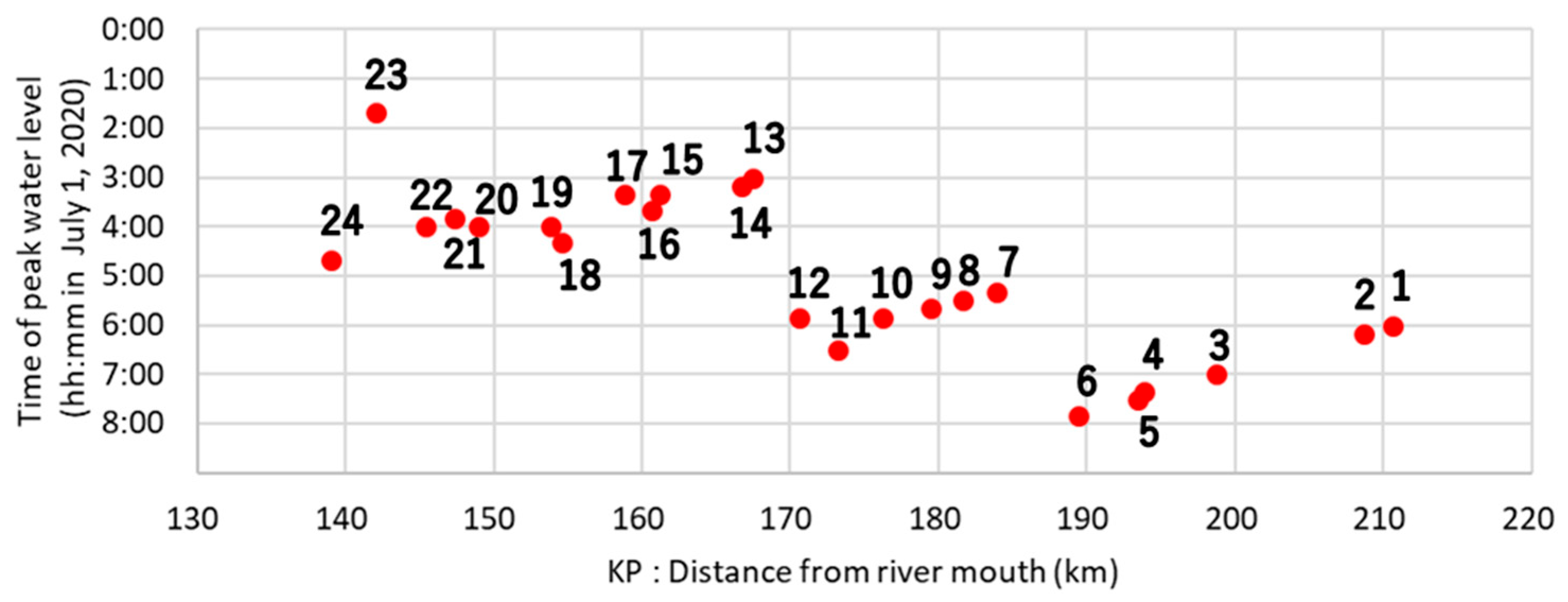
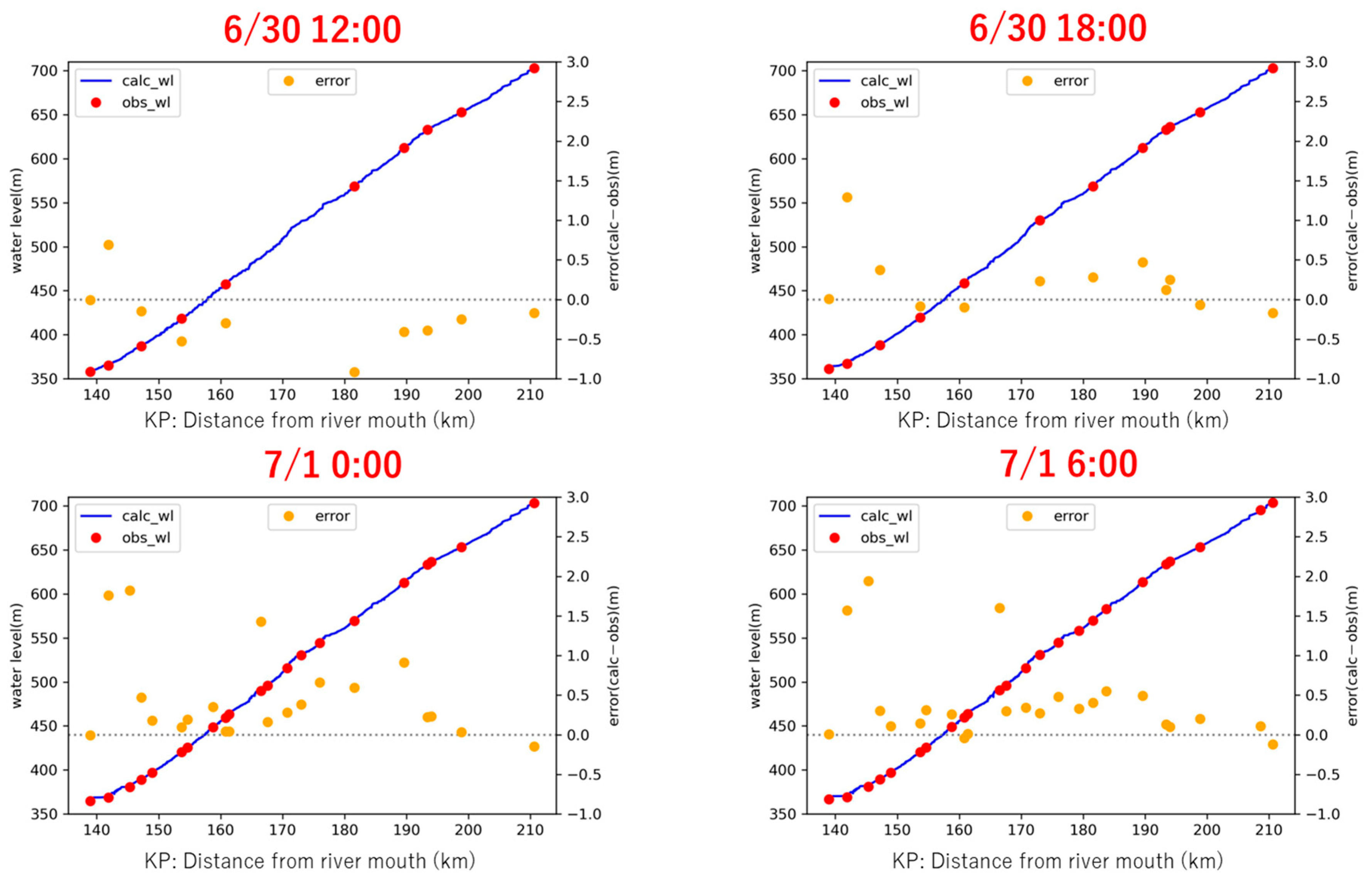
4.5. Flood Propagation Based on Water Level Data
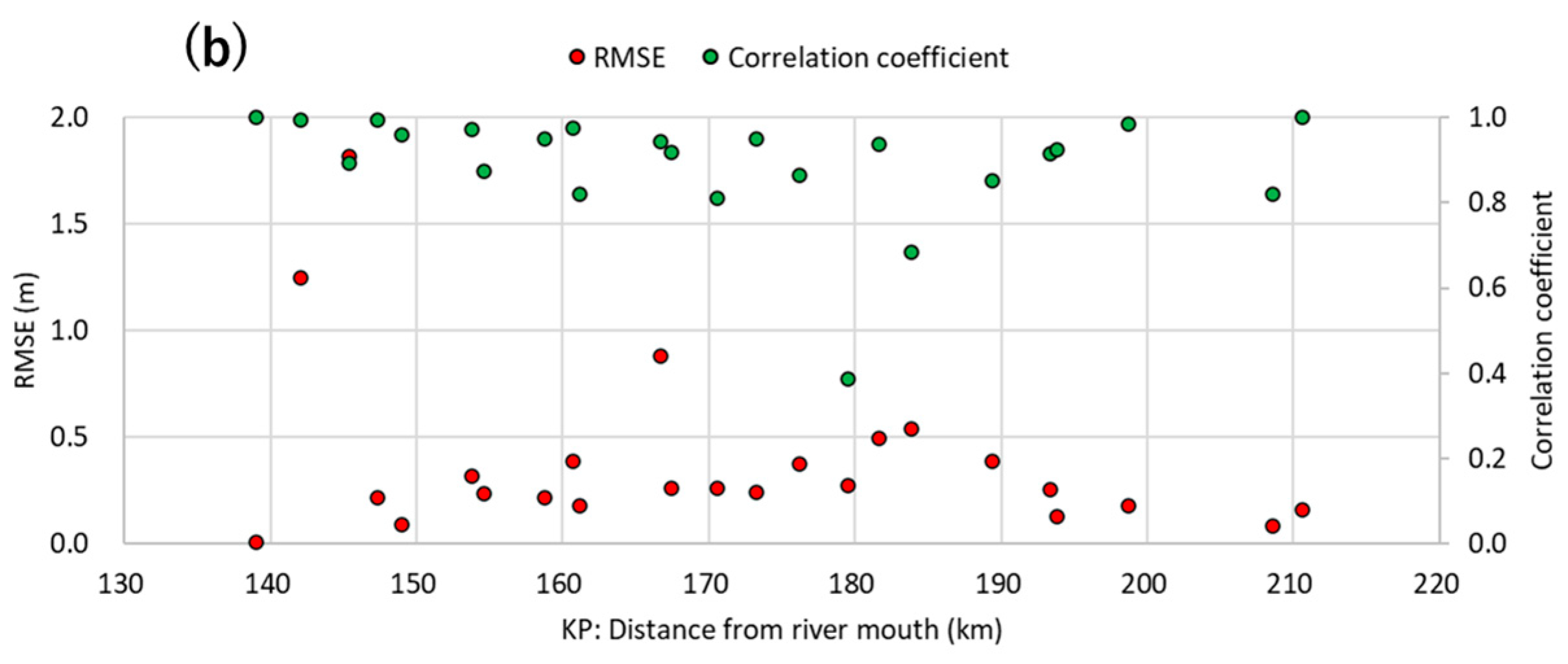
4.6. Validation of Two-Dimensional Unsteady Flow Simulation
4.7. Flood Propagation Based on the Simulation Results
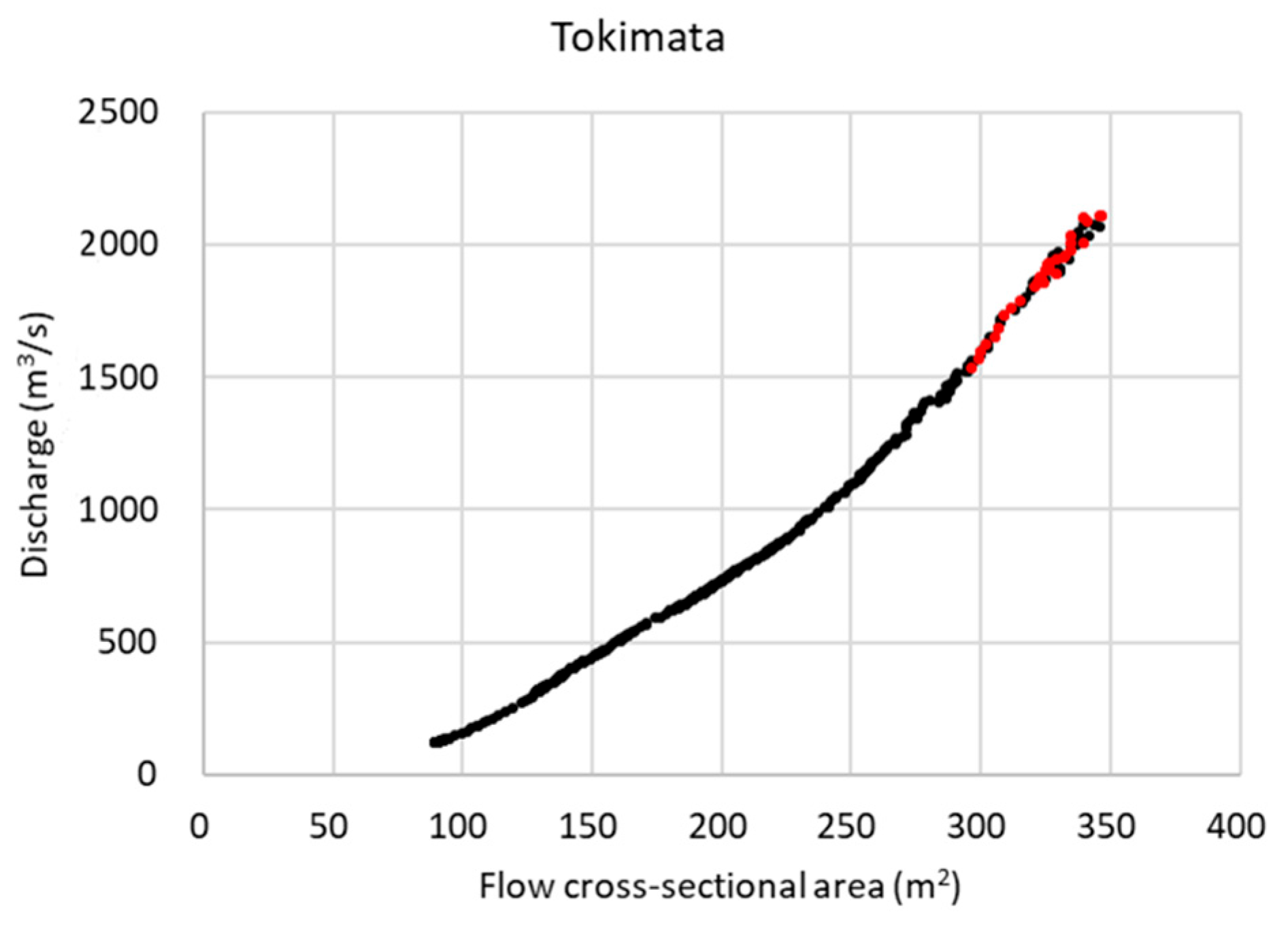
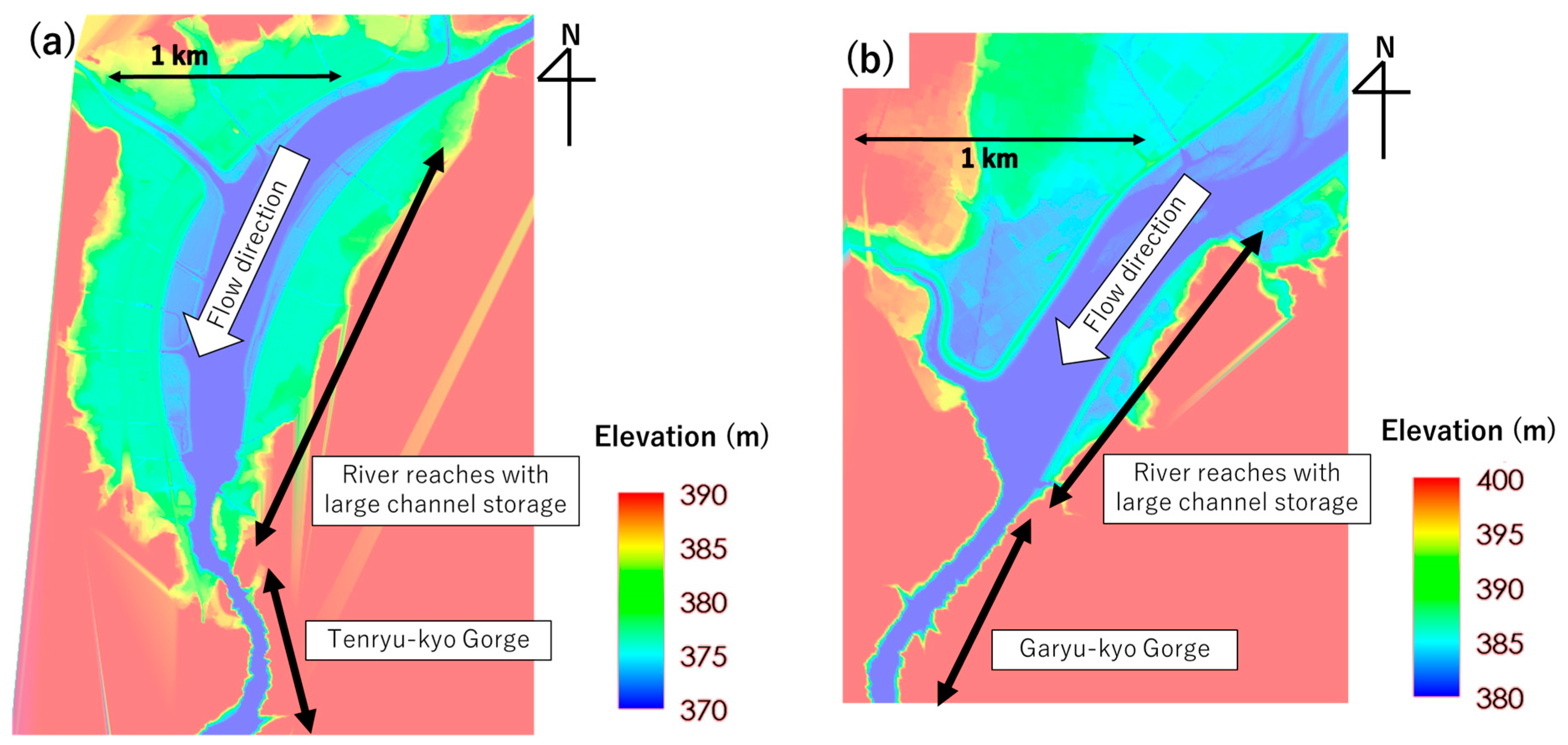
4.8. Investigation of River Channel Storage
5. Discussion
5.1. Interpretation of Rainfall–Runoff Characteristics
5.2. Comprehensive Understanding of Flood Propagation
5.3. Quantitative Discussion of Basin Storage and River Channel Storage
5.4. Discussion Regarding Simulation Errors and Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- River Basin Disaster Resilience and Sustainability by All. Available online: https://www.mlit.go.jp/river/kokusai/pdf/pdf21.pdf (accessed on 8 June 2025).
- Black, P.E. Watershed functions. J. Am. Water Resour. Assoc. 1997, 33, 1–11. [Google Scholar] [CrossRef]
- Sayama, T.; McDonnell, J.J.; Dhakal, A.; Sullivan, K. How much water can a watershed store? Hydrol. Process. 2011, 25, 3899–3908. [Google Scholar] [CrossRef]
- Reager, J.T.; Famiglietti, J.S. Characteristic mega-basin water storage behavior using GRACE. Water Resour. Res. 2013, 49, 3314–3329. [Google Scholar] [CrossRef] [PubMed]
- Tabata, K.; Fukuoka, S.; Deguchi, K. Analysis of Discharge Capacity and Flood Storage Rate during 2015 Large Flood in the Kinu River. In Proceedings of the 12th International Conference on Hydroscience & Engineering, Tainan, Taiwan, 6–10 November 2016. [Google Scholar]
- Hoshino, T.; Koseki, H.; Okabe, Y.; Yasuda, H. Study on the hydraulic interaction in the channel network on low-lying area of Shinano River basin. Adv. River Eng. 2013, 19, 289–294. [Google Scholar]
- Coss, S.; Durand, M.T.; Shum, C.K.; Yi, Y.; Yang, X.; Pavelsky, T.; Getirana, A.; Yamazaki, D. Channel water storage anomaly: A new remotely sensed quantity for global river analysis. Geophys. Res. Lett. 2023, 50, e2022GL100185. [Google Scholar] [CrossRef]
- Spencer, S.A.; Silins, U.; Anderson, A.E. Precipitation–runoff and storage dynamics in watersheds underlain by till and permeable bedrock in Alberta’s Rocky Mountains. Water Resour. Res. 2019, 55, 10690–10706. [Google Scholar] [CrossRef]
- Takemura, Y.; Fukuoka, S. Effects of channel shape on propagation characteristics of flood flows through a valley. J. Flood Risk Manag. 2014, 7, 152–158. [Google Scholar] [CrossRef]
- 3L Water Level Gauge. Available online: https://www.mlit.go.jp/river/kokusai/pdf/pdf03.pdf (accessed on 8 June 2025).
- Shige-eda, M.; Akiyama, J.; Okubo, K.; Nakashima, H. Numerical simulations of rainfall-runoff and flood inundation flows based on radar rainfall in the Kagetsu River Basin on Kyushu-Hokubu heavy rain in 2017. Adv. River Eng. 2018, 24, 451–456. [Google Scholar]
- Mitsui, N.; Omi, Y.; Kashiwada, J.; Kubota, R.; Ito, T.; Tanaka, M.; Nihei, Y. Development and application of a coupled model (RRI-RF2D) of rainfall-runoff analysis and planar two-dimensional analysis for river and flood flows. J. Jpn. Soc. Civ. Eng. 2025, 81, 24–16020. [Google Scholar] [CrossRef]
- Fukuoka, S.; Ishii, Y. Temporal and spatial distributions of flood water storage volume of the main river and tributaries in the Ishikari River basin. Proc. IAHS 2024, 386, 47–53. [Google Scholar] [CrossRef]
- Iwashita, H.; Onda, Y.; Ichiyanagi, K. Storm-runoff characteristics of the three small steep watersheds, upstream of the Tenryu River. Bull. Nagoya Univ. For. 1994, 13, 85–108. [Google Scholar]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall–runoff–inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Sayama, T.; Tatebe, Y.; Tanaka, S. An emergency response-type rainfall–runoff–inundation simulation for 2011 Thailand floods. J. Flood Risk Manag. 2015, 10, 65–78. [Google Scholar] [CrossRef]
- Sayama, T.; Tatebe, Y.; Iwami, Y.; Tanaka, S. Hydrologic sensitivity of flood runoff and inundation: 2011 Thailand floods in the Chao Phraya River basin. Nat. Hazards Earth Syst. Sci. 2015, 15, 1617–1630. [Google Scholar] [CrossRef]
- Yamazaki, D.; Togashi, S.; Takeshima, A.; Sayama, T. High-resolution flow direction map of Japan. J. JSCE 2018, 8, 234–240. [Google Scholar] [CrossRef]
- Kondo, J.; Nakazono, M.; Watanabe, T. Hydrological climate in Japan (2). J. Jpn. Soc. Hydrol. Water Resour. 1992, 5, 29–36. [Google Scholar] [CrossRef]
- Japan Meteorological Agency. Available online: https://www.data.jma.go.jp/cpd/longfcst/kaisetsu/tenkinissuu/tenkinissuu.html (accessed on 2 July 2025).
- Nagata, N. General-coordinate-based river flow computation. In Hydraulics Formulae: Hydraulics Worked Examples with CD-ROM; Japan Society of Civil Engineers, Ed.; Maruzen: Tokyo, Japan, 2002. [Google Scholar]
- iRIC Sofrware. Available online: https://i-ric.org/en/about/ (accessed on 8 June 2025).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hayashi, T. Mathematical theory and experiment of flood waves. Trans. Jpn. Soc. Civ. Eng. 1953, 1953, 13–26. [Google Scholar] [CrossRef][Green Version]
- Hewlett, J.D.; Hibbert, A.R. Factors affecting the response of small watersheds to precipitation in humid areas. In Proceedings of the International Symposium on Forest Hydrology, University Park, PA, USA, 29 August–10 September 1965. [Google Scholar]
- Lehman, P.; Hinz, C.; McGrath, G.; Tromp-van Meerveld, H.J.; McDonnell, J.J. Rainfall threshold for hillslope outflow: An emergent property of flow pathway connectivity. Hydrol. Earth Syst. Sci. 2007, 11, 1047–1063. [Google Scholar] [CrossRef]
- Hromadka, T.V., II; Whitley, R.J. The rational method for peak flow rate estimation. J. Am. Water Resour. Assoc. 1994, 30, 1001–1009. [Google Scholar] [CrossRef]
- Kang, M.S.; Goo, J.H.; Song, I.; Chun, J.A.; Her, Y.G.; Hwang, S.W.; Park, S.W. Estimating design floods based on the critical storm duration for small watersheds. J. Hydro-Environ. Res. 2013, 7, 209–218. [Google Scholar] [CrossRef]
- Lapides, D.A.; Sytsma, A.; Crompton, O.; Thompson, S. Rational method time of concentration can underestimate peak discharge for hillslopes. J. Hydraul. Eng. 2021, 147, 06021014. [Google Scholar] [CrossRef]
- Jain, S.C. Open Channel Flow; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001; p. 241. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Takemura, Y.; Fukuoka, S. Effects of river morphology on propagation and transformation of discharge and water level hydrographs of flood flows through river valley. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, 35–54. [Google Scholar] [CrossRef]
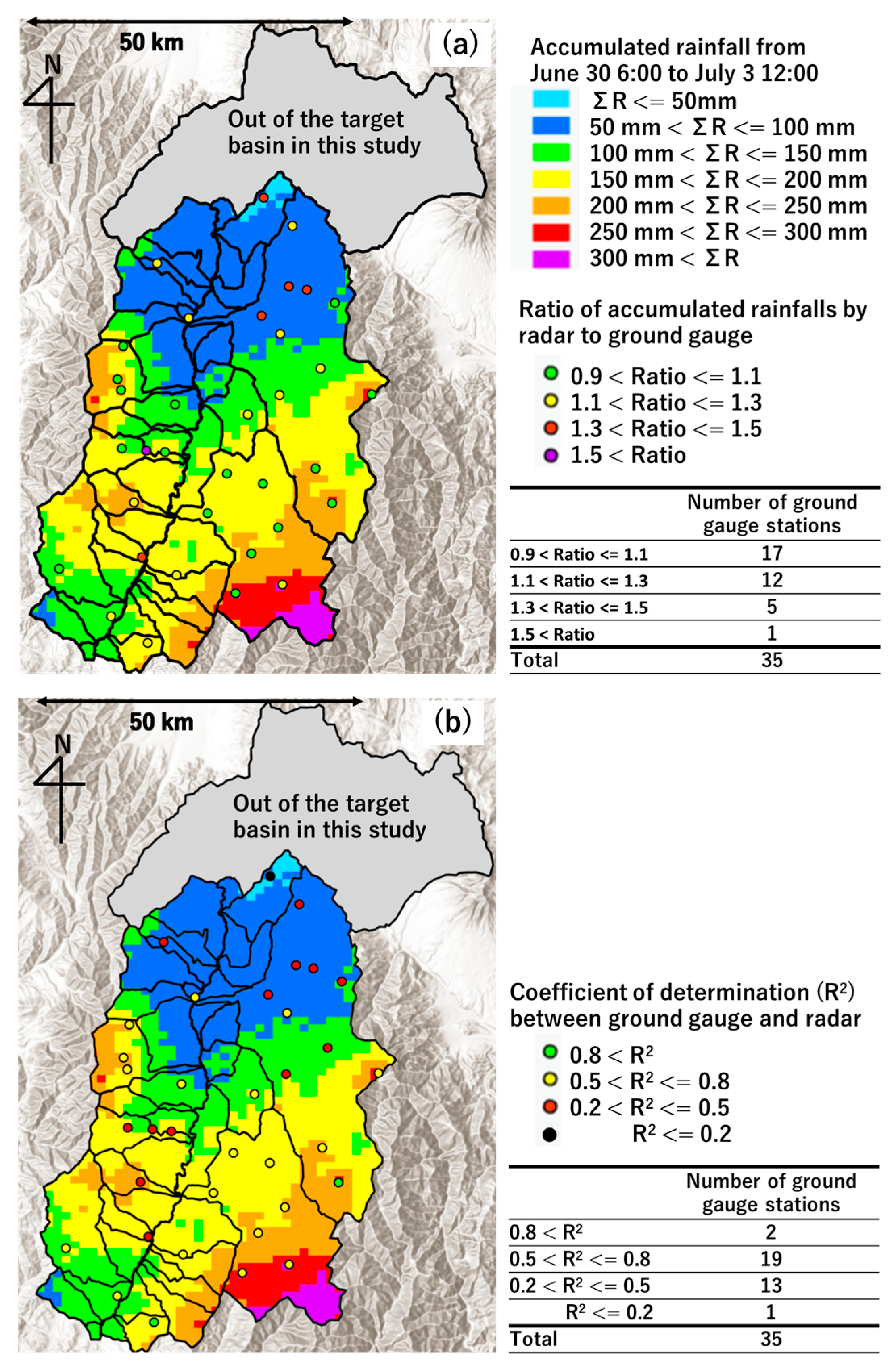











| Data | Observation Method | Number of Stations (Spatial Resolution) | Temporal Resolution |
|---|---|---|---|
| Rainfall | Radar | (1 km) | 1 h |
| Ground gauge | 35 stations (55 km2/station) | 10 min | |
| Discharge | Dam inflow/outflow | 4 dams | 10 min |
| Observation station along river channel | 4 stations (18 km/station) | 10 min * | |
| Water level | Observation station along river channel | 24 stations (3 km/station) | 10 min |
| Parameter | Unconsolidated Sediment | Consolidated and Partially Consolidated Sediments | Igneous Rock | Metamorphic and Mylonitic Rocks |
|---|---|---|---|---|
| ka (m/s) | 0.1500 | 0.12500 | 0.02500 | 0.10000 |
| km (m/s) | 0.0375 | 0.03125 | 0.00625 | 0.02500 |
| da (m) | 1.50 | 1.50 | 1.50 | 1.50 |
| dm (m) | 0.15 | 0.90 | 0.45 | 0.15 |
| Nash–Sutcliffe Coefficient | Runoff Ratio | ||
|---|---|---|---|
| Obs * | Calc * | ||
| Katagiri dam | 0.83 | 0.87 | 0.82 |
| Matsukawa dam | 0.68 | 0.62 | 0.73 |
| Miwa dam | 0.82 | 0.70 | 0.69 |
| Koshibu dam | 0.87 | 0.69 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudo, S.; Yorozuya, A.; Yamada, K. Investigating Basin-Scale Water Dynamics During a Flood in the Upper Tenryu River Basin. Water 2025, 17, 2086. https://doi.org/10.3390/w17142086
Kudo S, Yorozuya A, Yamada K. Investigating Basin-Scale Water Dynamics During a Flood in the Upper Tenryu River Basin. Water. 2025; 17(14):2086. https://doi.org/10.3390/w17142086
Chicago/Turabian StyleKudo, Shun, Atsuhiro Yorozuya, and Koji Yamada. 2025. "Investigating Basin-Scale Water Dynamics During a Flood in the Upper Tenryu River Basin" Water 17, no. 14: 2086. https://doi.org/10.3390/w17142086
APA StyleKudo, S., Yorozuya, A., & Yamada, K. (2025). Investigating Basin-Scale Water Dynamics During a Flood in the Upper Tenryu River Basin. Water, 17(14), 2086. https://doi.org/10.3390/w17142086






