Incorporation of Horizontal Aquifer Flow into a Vertical Vadose Zone Model to Simulate Natural Groundwater Table Fluctuations
Abstract
1. Introduction
- Eliminating uncertainties associated with field measurements and aquifer heterogeneity, the performance of HYDRUS-1D models with quadratic and linear drainage boundary conditions is evaluated using reference 2D HGS simulations.
- HYDRUS-1D’s extended quadratic and linear drainage equations are applied and tested to compare them methodically with reference 2D solutions.
- To fully assess model performance under various hydrological conditions, several scenarios that alter soil type, groundwater table depth, and profile position within the catchment are run.
- i.
- To assess the degree to which GWT fluctuations can be accurately reproduced by 1D models with system-dependent drainage boundary conditions as compared to a 2D reference model.
- ii.
- To compare the simulation results of groundwater movement and unsaturated flow between the HGS and modified HYDRUS-1D models.
- iii.
2. Materials and Methods
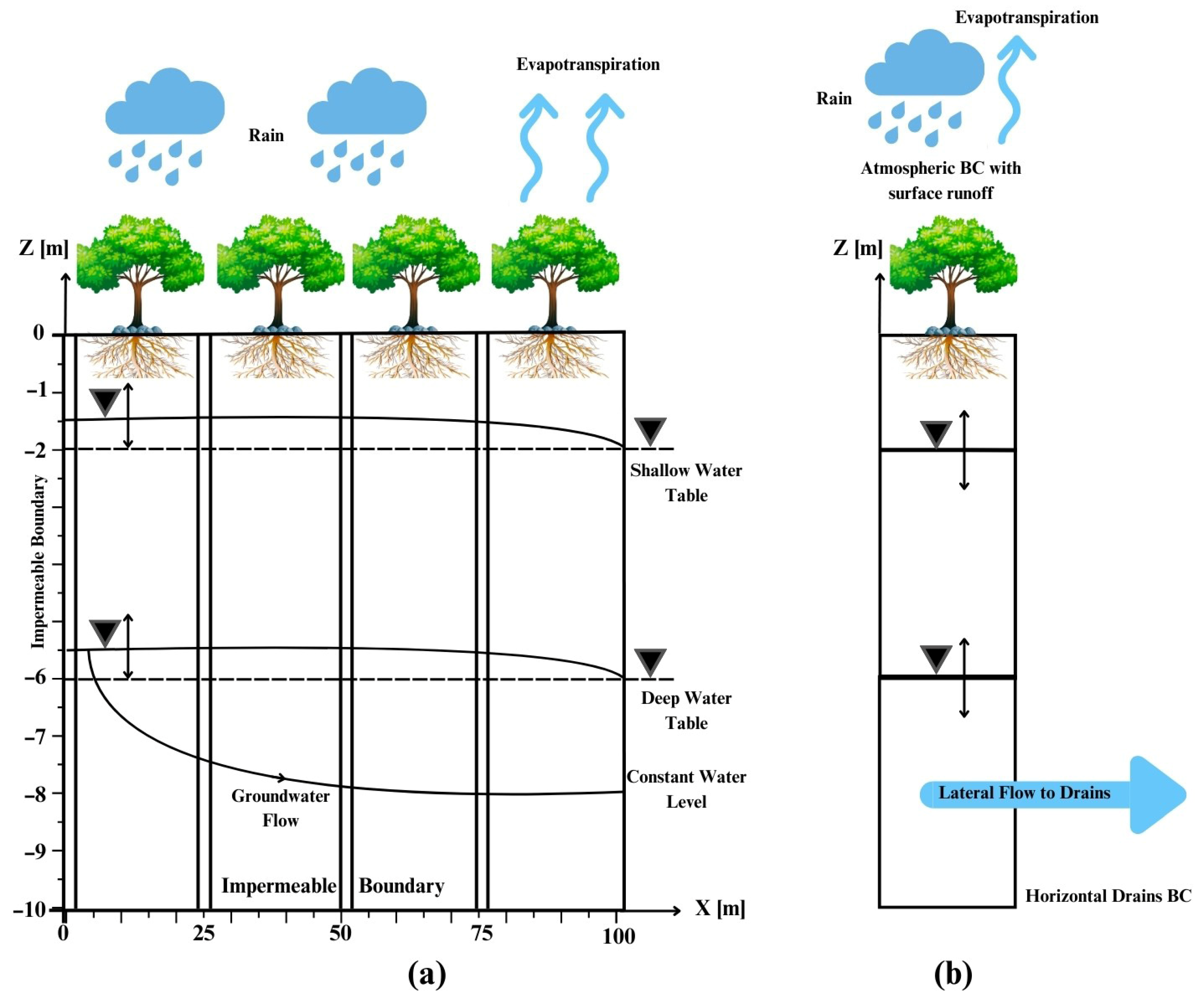
2.1. General Simulation Setup
2.2. HGS Simulations
2.3. HYDRUS-1D Simulations
2.4. Convergence Analysis
2.5. Sensitivity Analysis
3. Results and Discussion
3.1. Steady State Simulation SA_6m
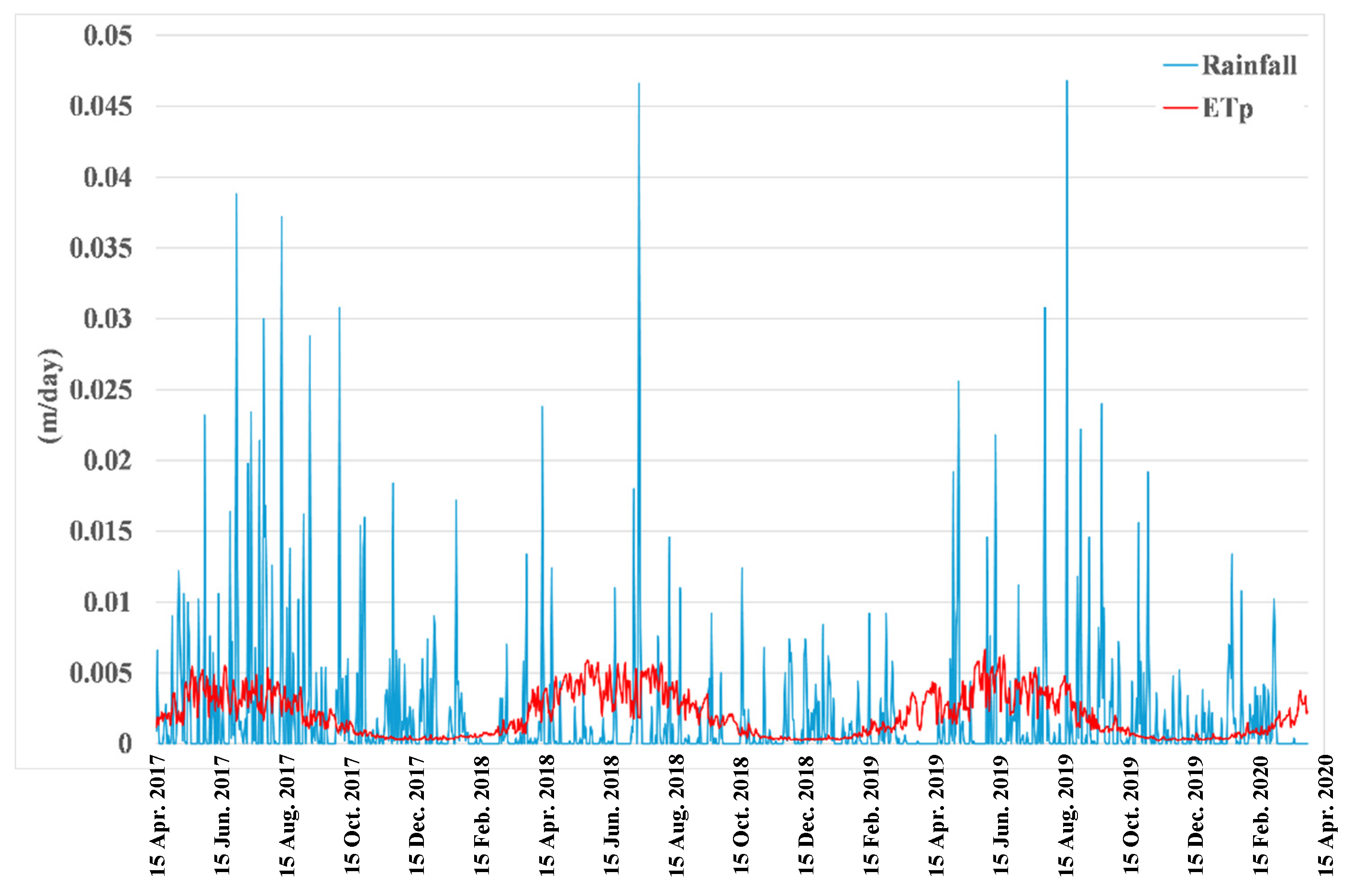
3.2. Simulations SA_6m for the Scenario with Actual Weather Conditions
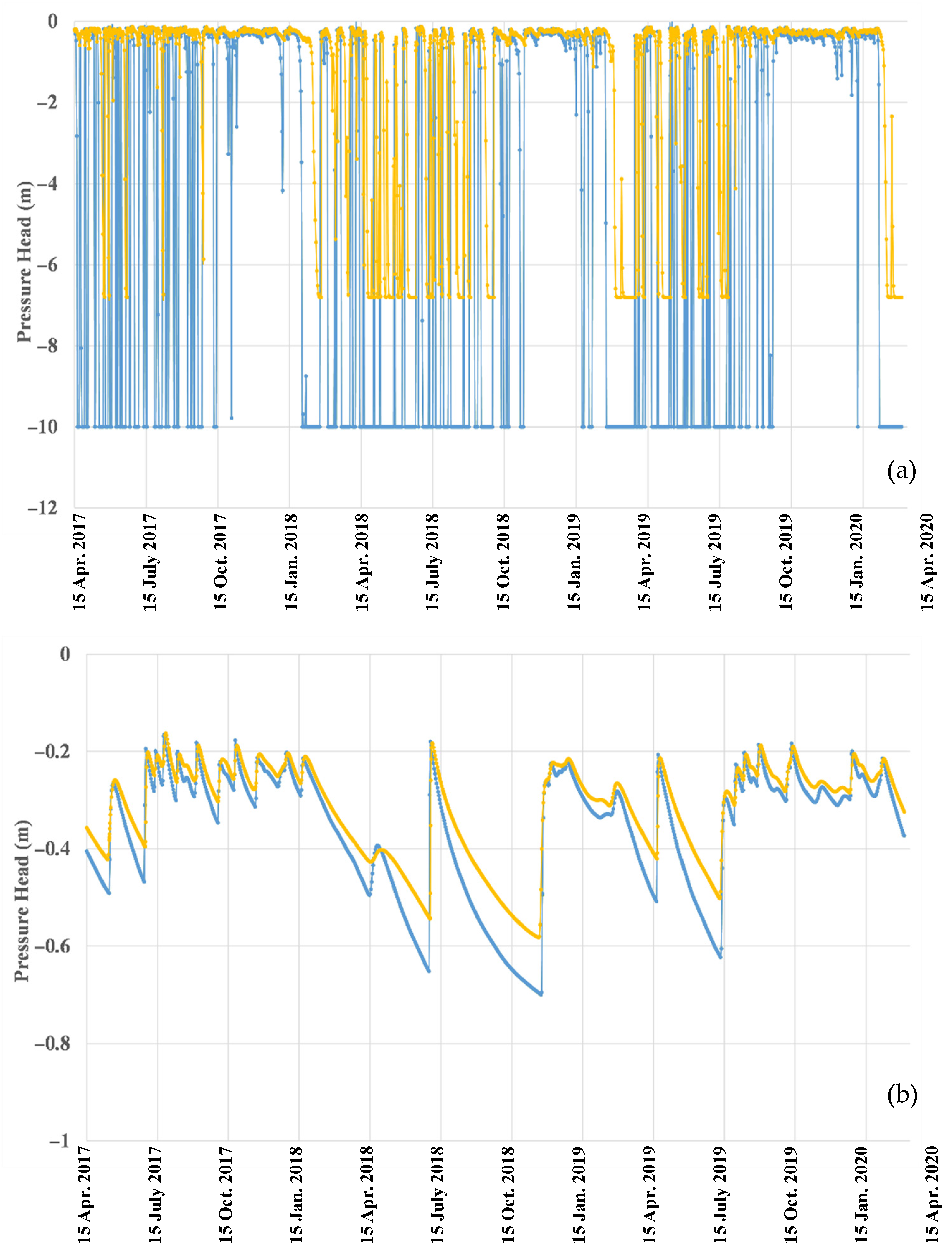
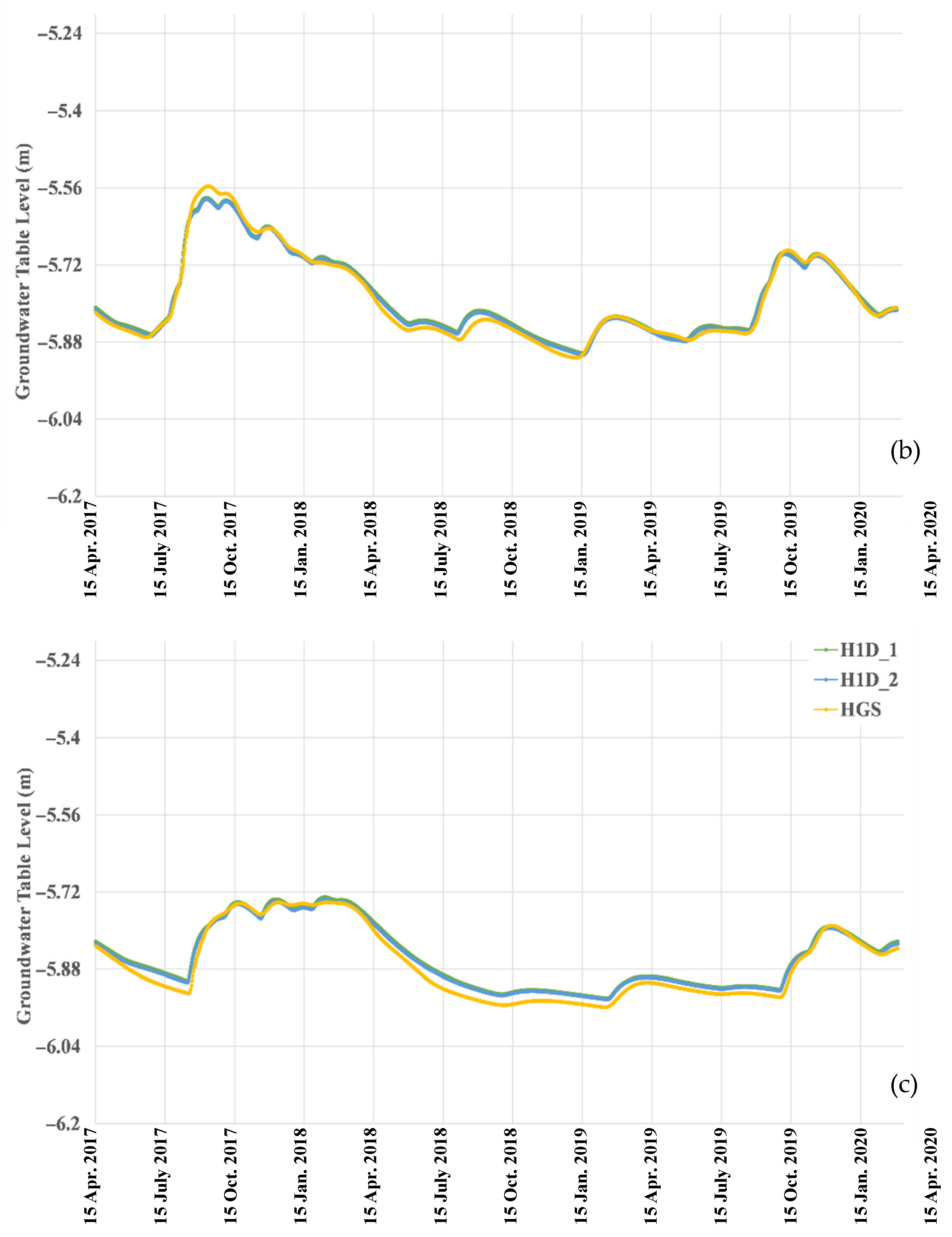
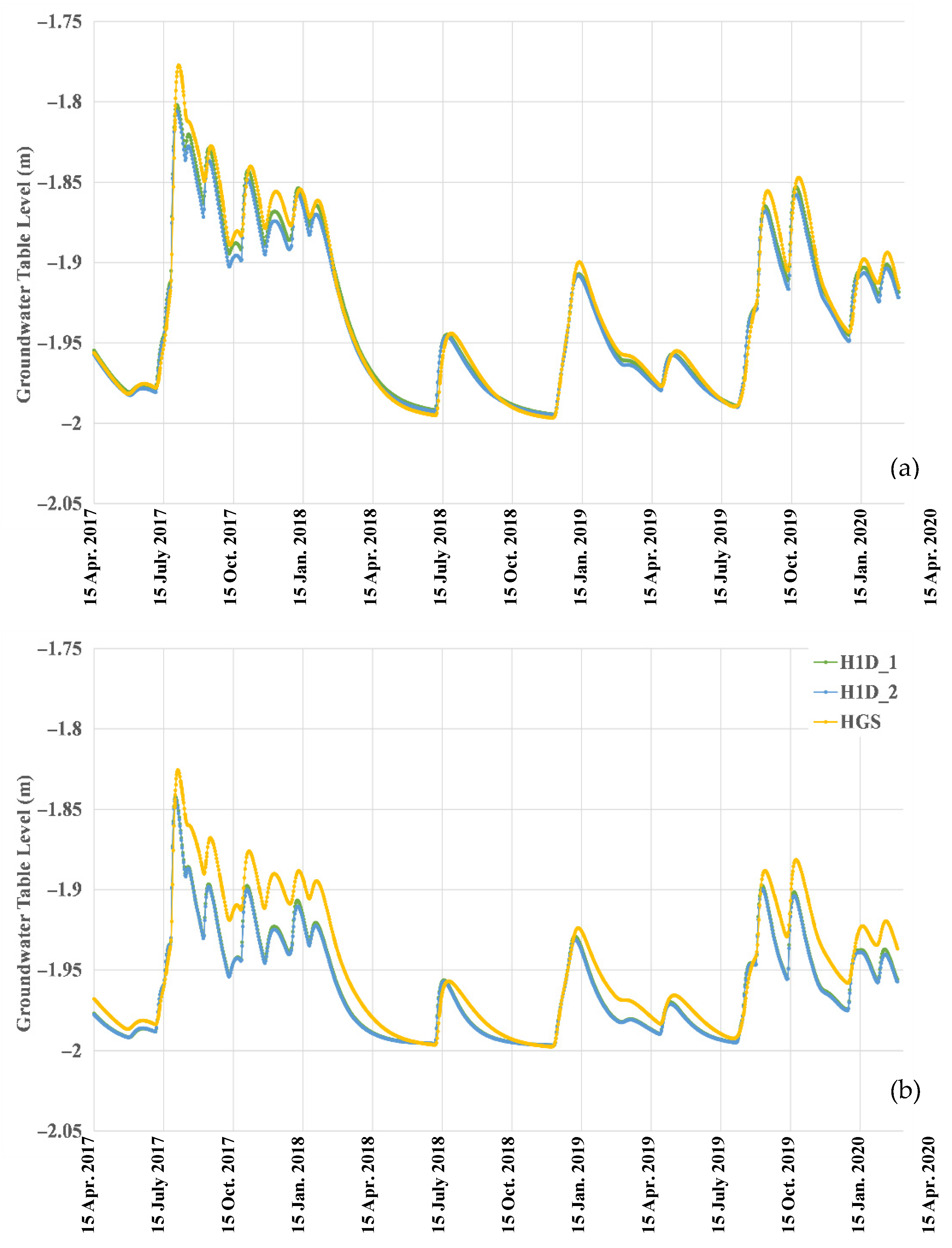
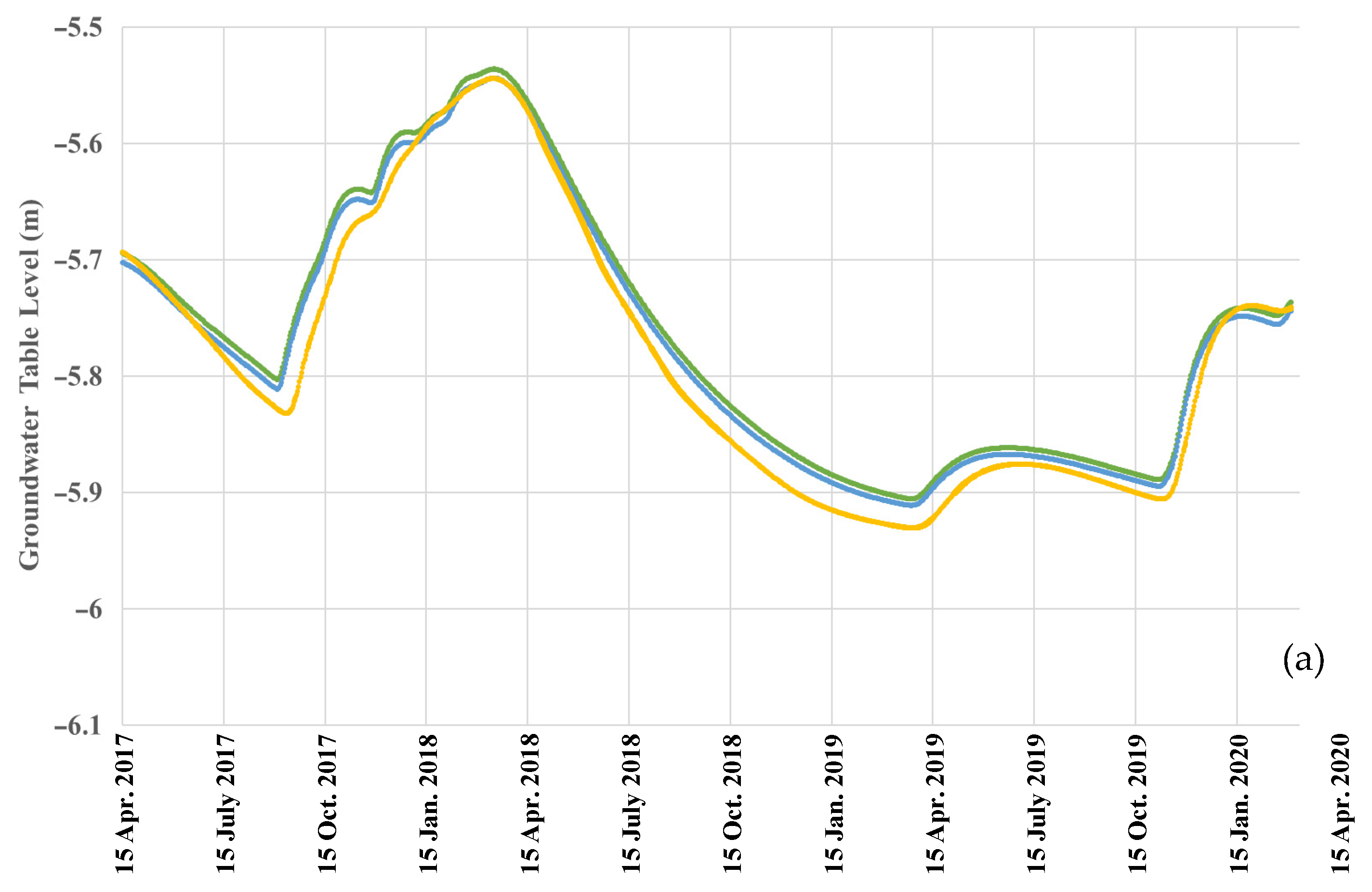
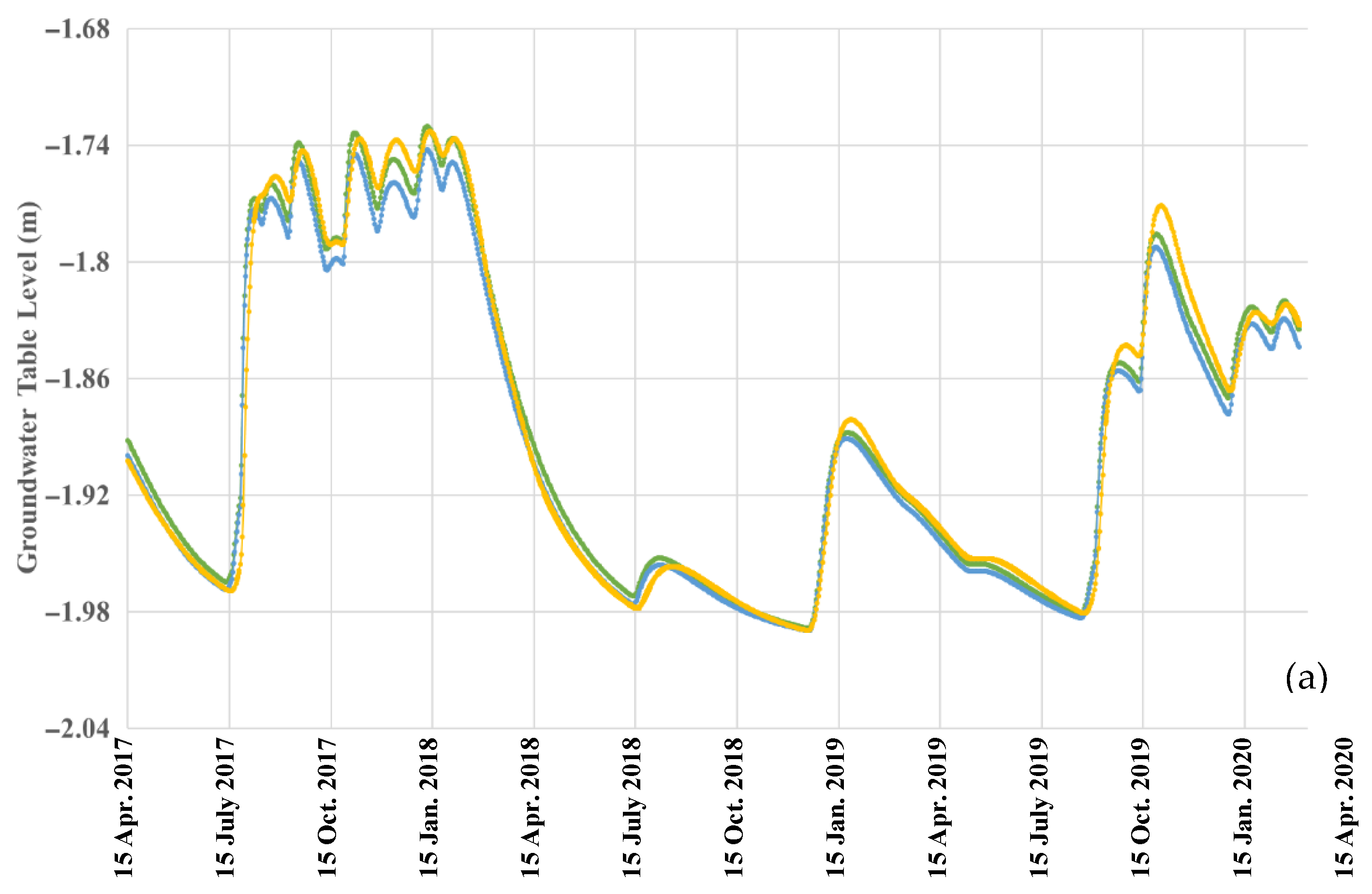
3.2.1. Pressure Heads and Water Table Fluctuations at x = 0 m
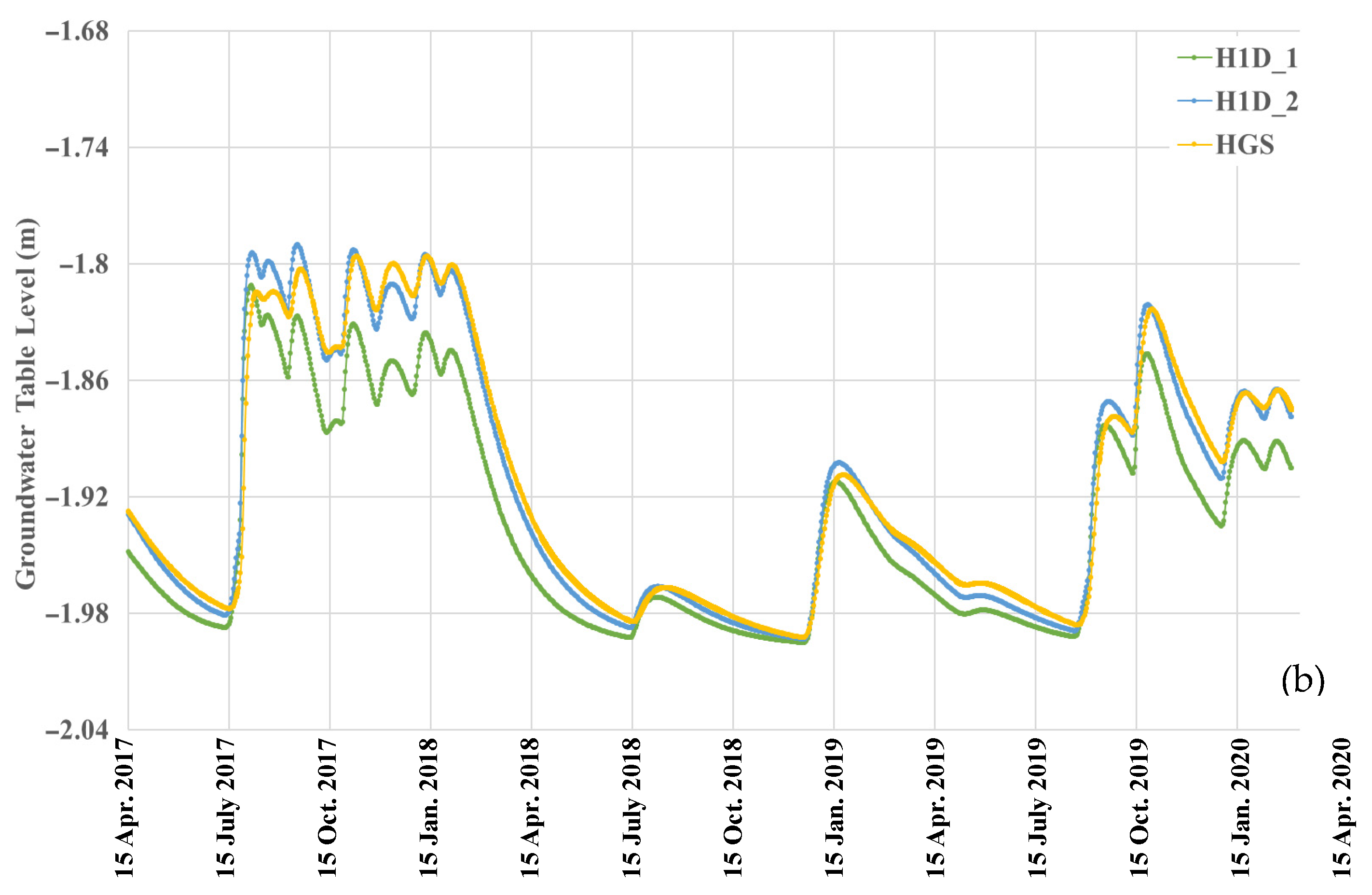
3.2.2. Pressure Heads and Water Table Fluctuations at x = 50 m
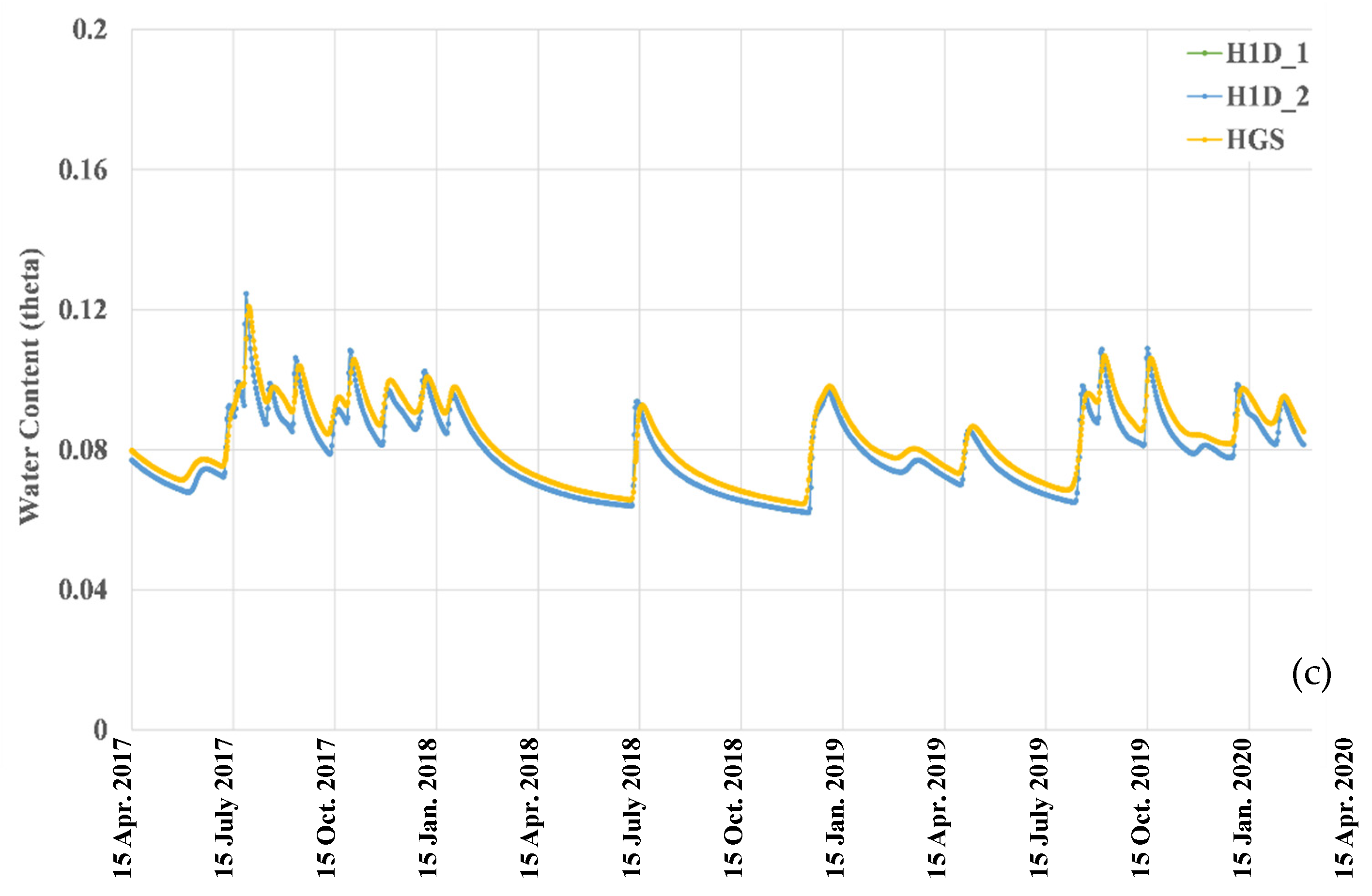
3.2.3. Soil Water Contents
3.3. Simulations SA_6m for Scenarios with and Without Evaporation and Transpiration
3.4. Simulations SA_2m
3.5. Simulations LS_6m
3.6. Simulations LS_2m
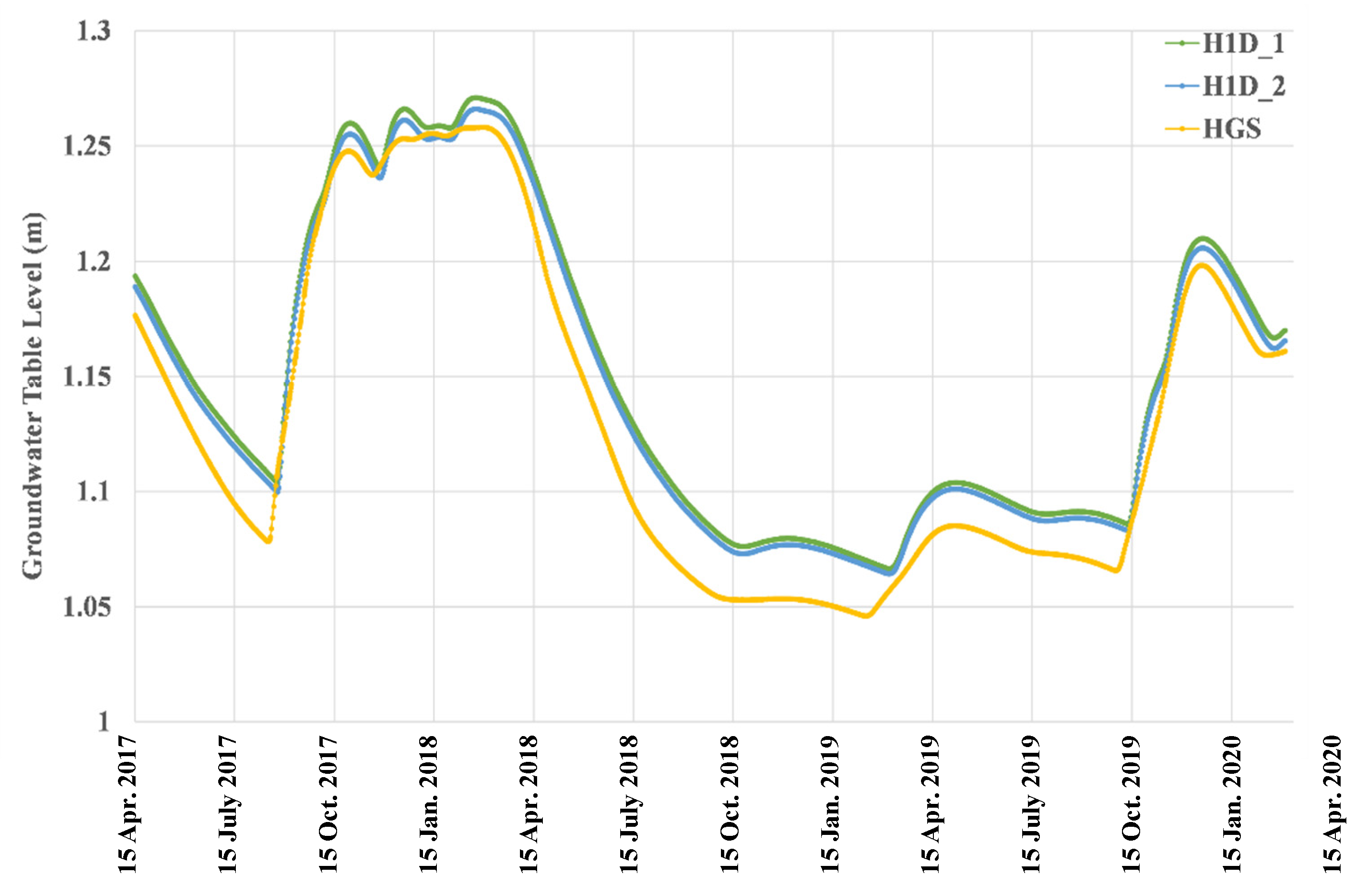
3.7. Simulations with Low Permeability Lens in the Vadose Zone
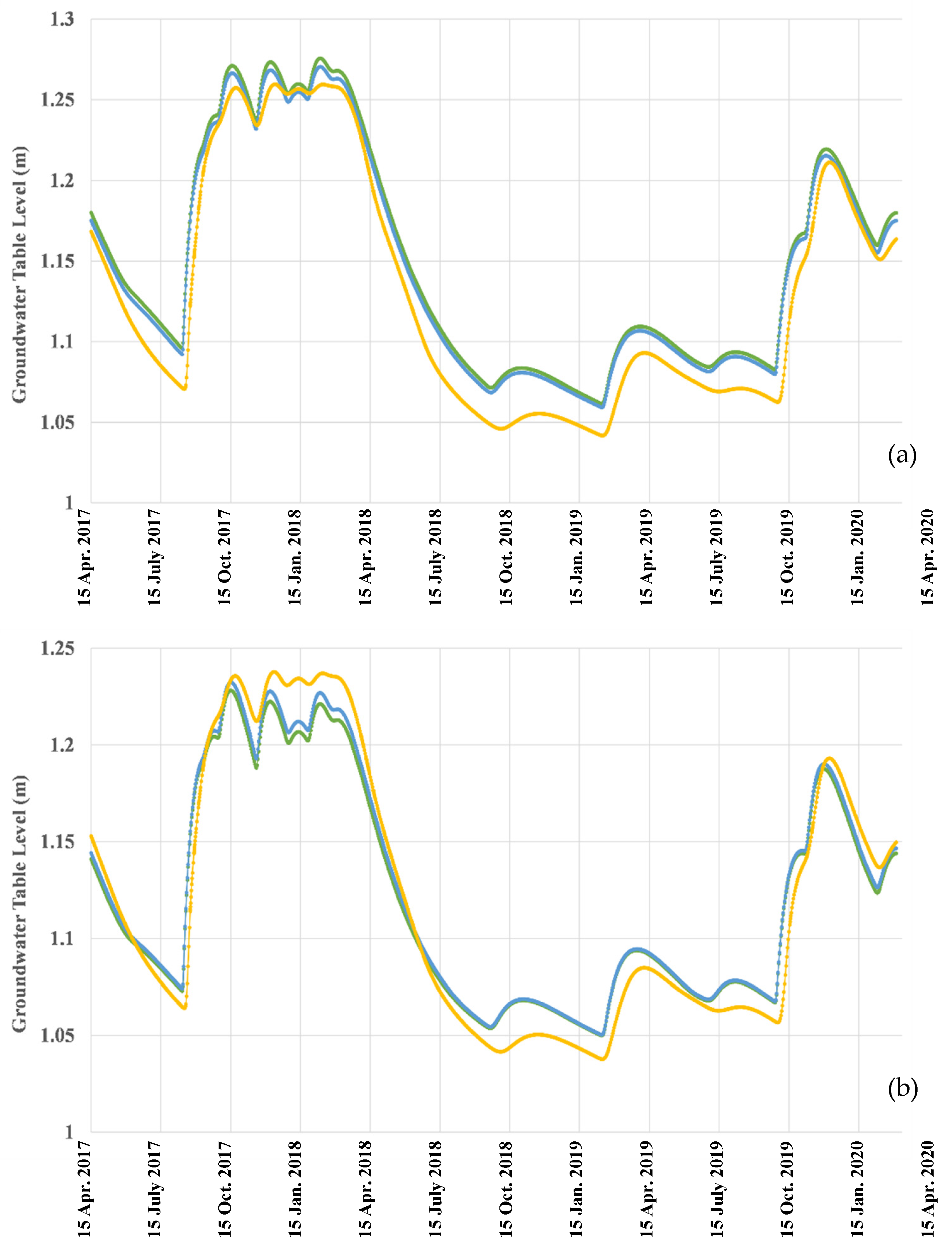
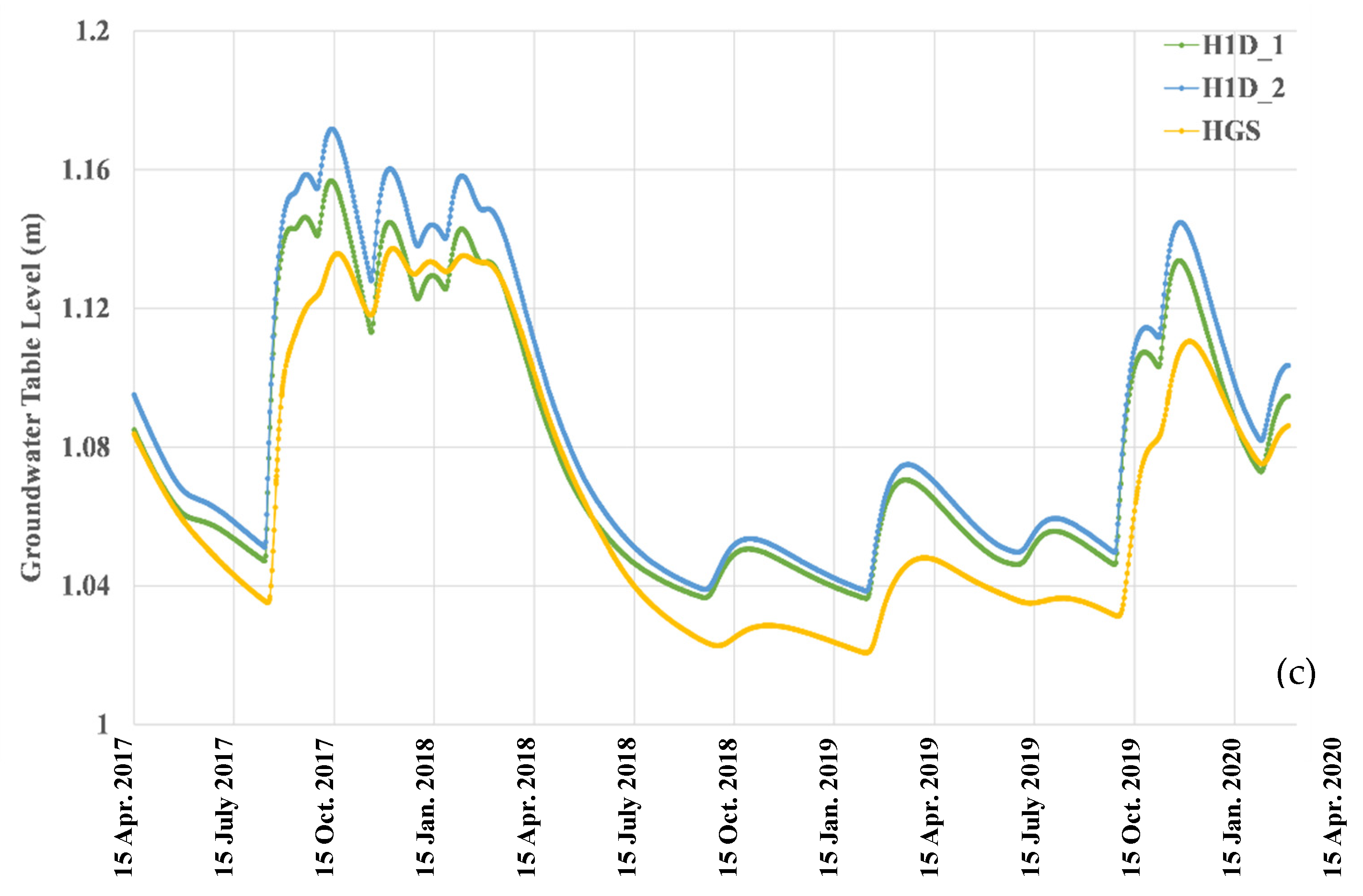
3.8. Simulations with Varying Permeability in Horizontal Direction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D | One-Dimensional |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| BC | Boundary Condition |
| CD | Conductance (Parameter in Drainage Equations) |
| ET | Evapotranspiration |
| ETP | Potential Evapotranspiration |
| GHB | General Head Boundary |
| GTW | Groundwater Table |
| H1D_1 | HYDRUS-1D model with Quadratic Drainage Boundary Condition |
| H1D_2 | HYDRUS-1D model with Linear Drainage Boundary Condition |
| LAI | Leaf Area Index |
| RE | Richards Equation |
| RDF | Root Distribution Function |
| RWU | Root Water Uptake |
| SA_6m | Sandy soil with water at 6 m depth |
| SA_2m | Sandy soil with water at 2 m depth |
| LS_6m | Loamy sand soil with water at 6 m depth |
| LS_2m | Loamy sand soil with water at 2 m depth |
| RMSE | Root mean square error |
Appendix A
| HydroGeoSphere | HYDRUS-1D | |||
|---|---|---|---|---|
| Parameters of the Transpiration Function [-] | Sand | Loamy Sand | Feddes Model Parameters (m) | |
| Wilting point (θwp) | 0.105 | 0.139 | Anaerobiosis point pressure head (h1) | −0.25 |
| Field capacity (θfc) | 0.107 | 0.151 | Upper pressure head limit of maximum root uptake (h2) | −2 |
| Oxic limit (θo) | 0.205 | 0.329 | Lower pressure head limit of root uptake increase (h3) | −8 |
| Anoxic limit (θan) | 0.498 | 0.634 | Wilting point pressure head (h4) | −80 |
| Residual saturation (Swr) | 0.1046 | 0.1390 | ||
| Mesh/Scenario | Model | Min (m) | Max (m) | Range (m) | Mean (m) | Std Dev (m) | RMSE vs. Finest (m) |
|---|---|---|---|---|---|---|---|
| SA_6m with 101 nodes | H1D_1 | −6 | −5.761 | 0.239 | −5.927 | 0.0674 | 0.0347 |
| H1D_2 | −6 | −5.765 | 0.235 | −5.929 | 0.0659 | 0.0345 | |
| HGS | −6.027 | −5.767 | 0.26 | −5.942 | 0.073 | 0.0924 | |
| SA_6m with 202 nodes | H1D_1 | −5.985 | −5.742 | 0.243 | −5.909 | 0.0695 | 0.0165 |
| H1D_2 | −5.985 | −5.747 | 0.238 | −5.911 | 0.068 | 0.0163 | |
| HGS | −6.035 | −5.775 | 0.26 | −5.949 | 0.0743 | 0.0945 | |
| SA_6m with 404 nodes | H1D_1 | −5.978 | −5.731 | 0.247 | −5.894 | 0.0725 | 0 |
| H1D_2 | −5.978 | −5.736 | 0.242 | −5.897 | 0.0709 | 0 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| SA_6m with 606 nodes | H1D_1 | −5.992 | −5.744 | 0.248 | −5.911 | 0.0722 | 0.0178 |
| H1D_2 | −5.992 | −5.749 | 0.243 | −5.914 | 0.0707 | 0.0177 | |
| HGS | −6.025 | −5.764 | 0.261 | −5.939 | 0.0727 | 0.0914 | |
| SA_6m with 808 nodes | H1D_1 | −5.999 | −5.75 | 0.249 | −5.918 | 0.0728 | 0.0238 |
| H1D_2 | −5.999 | −5.755 | 0.244 | −5.92 | 0.0712 | 0.0238 | |
| HGS | −6.024 | −5.763 | 0.261 | −5.938 | 0.0723 | 0.0901 |
| Parameter/Scenario | Model | Min (m) | Max (m) | Range (m) | Mean (m) | Std Dev (m) | RMSE vs. Baseline (m) |
|---|---|---|---|---|---|---|---|
| SA_6m with −10 Ks | H1D_1 | −5.978 | −5.731 | 0.247 | −5.896 | 0.0723 | 0.0031 |
| H1D_2 | −5.978 | −5.736 | 0.242 | −5.898 | 0.0705 | 0.0032 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| SA_6m with −20 Ks | H1D_1 | −5.978 | −5.732 | 0.246 | −5.897 | 0.0724 | 0.0064 |
| H1D_2 | −5.978 | −5.736 | 0.242 | −5.9 | 0.0706 | 0.0064 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| SA_6m with baseline Ks | H1D_1 | −5.978 | −5.731 | 0.247 | −5.894 | 0.0725 | 0 |
| H1D_2 | −5.978 | −5.736 | 0.242 | −5.897 | 0.0709 | 0 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| SA_6m with +10 Ks | H1D_1 | −5.978 | −5.73 | 0.248 | −5.893 | 0.0726 | 0.0028 |
| H1D_2 | −5.978 | −5.735 | 0.243 | −5.896 | 0.0703 | 0.0028 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| SA_6m with +20 Ks | H1D_1 | −5.978 | −5.73 | 0.248 | −5.893 | 0.0719 | 0.0052 |
| H1D_2 | −5.978 | −5.735 | 0.243 | −5.896 | 0.0703 | 0.0051 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 |
Appendix B
| Scenario | Model | Min (m) | Max (m) | Range (m) | Mean (m) | Std Dev (m) | RMSE vs. HGS (m) |
|---|---|---|---|---|---|---|---|
| SA_6m x at 0 | H1D_1 | −5.978 | −5.731 | 0.247 | −5.894 | 0.0725 | 0.086 |
| H1D_2 | −5.978 | −5.736 | 0.242 | −5.897 | 0.0709 | 0.085 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| SA_6m x at 50 | H1D_1 | −5.978 | −5.823 | 0.155 | −5.929 | 0.0441 | 0.061 |
| H1D_2 | −5.978 | −5.831 | 0.147 | −5.933 | 0.0416 | 0.06 | |
| HGS | −6 | −5.803 | 0.197 | −5.935 | 0.0564 | 0 | |
| SA_2m x at 0 | H1D_1 | −1.998 | −1.802 | 0.196 | −1.947 | 0.0459 | 0.066 |
| H1D_2 | −1.998 | −1.806 | 0.192 | −1.95 | 0.0443 | 0.065 | |
| HGS | −2 | −1.777 | 0.223 | −1.951 | 0.0493 | 0 | |
| SA_2m x at 50 | H1D_1 | −1.998 | −1.842 | 0.155 | −1.969 | 0.0295 | 0.048 |
| H1D_2 | −1.998 | −1.844 | 0.154 | −1.97 | 0.0289 | 0.048 | |
| HGS | −2 | −1.826 | 0.174 | −1.963 | 0.0373 | 0 | |
| LS_6m x at 0 | H1D_1 | −5.978 | −5.536 | 0.441 | −5.848 | 0.1279 | 0.199 |
| H1D_2 | −5.978 | −5.544 | 0.434 | −5.852 | 0.1249 | 0.193 | |
| HGS | −6 | −5.544 | 0.456 | −5.887 | 0.1343 | 0 | |
| LS_6m x at 50 | H1D_1 | −5.978 | −5.705 | 0.272 | −5.901 | 0.079 | 0.126 |
| H1D_2 | −5.978 | −5.704 | 0.274 | −5.902 | 0.0792 | 0.126 | |
| HGS | −6 | −5.653 | 0.347 | −5.916 | 0.0996 | 0 | |
| LS_2m x at 0 | H1D_1 | −1.999 | −1.73 | 0.268 | −1.912 | 0.0761 | 0.117 |
| H1D_2 | −1.999 | −1.742 | 0.256 | −1.916 | 0.0731 | 0.111 | |
| HGS | −2 | −1.733 | 0.268 | −1.96 | 0.0301 | 0 | |
| LS_2m x at 50 | H1D_1 | −1.999 | −1.811 | 0.187 | −1.948 | 0.0497 | 0.072 |
| H1D_2 | −1.999 | −1.79 | 0.208 | −1.934 | 0.0602 | 0.089 | |
| HGS | −2 | −1.796 | 0.204 | −1.971 | 0.0227 | 0 | |
| SA_6m without EP and TP | H1D_1 | −5.978 | −5.312 | 0.666 | −5.718 | 0.1351 | 0.172 |
| H1D_2 | −5.978 | −5.307 | 0.671 | −5.721 | 0.1369 | 0.173 | |
| HGS | −6 | −5.316 | 0.684 | −5.742 | 0.144 | 0 | |
| SA_6m with EP and without TP | H1D_1 | −5.978 | −5.58 | 0.397 | −5.837 | 0.0975 | 0.111 |
| H1D_2 | −5.978 | −5.584 | 0.394 | −5.841 | 0.0965 | 0.111 | |
| HGS | −6 | −5.557 | 0.443 | −5.843 | 0.1051 | 0 | |
| SA_6m with EP and TP | H1D_1 | −5.978 | −5.731 | 0.247 | −5.894 | 0.0725 | 0.086 |
| H1D_2 | −5.978 | −5.736 | 0.242 | −5.897 | 0.0709 | 0.085 | |
| HGS | −6 | −5.741 | 0.259 | −5.913 | 0.0746 | 0 | |
| low permeability lens | H1D_1 | 1.022 | 1.271 | 0.249 | 1.103 | 0.0772 | 0.089 |
| H1D_2 | 1.022 | 1.266 | 0.244 | 1.101 | 0.0755 | 0.088 | |
| HGS | 1 | 1.258 | 0.258 | 1.083 | 0.0754 | 0 | |
| K1 | H1D_1 | 1.022 | 1.276 | 0.253 | 1.11 | 0.0745 | 0.089 |
| H1D_2 | 1.022 | 1.27 | 0.248 | 1.107 | 0.073 | 0.088 | |
| HGS | 1 | 1.26 | 0.26 | 1.087 | 0.0751 | 0 | |
| K2 | H1D_1 | 1.022 | 1.228 | 0.206 | 1.09 | 0.0594 | 0.077 |
| H1D_2 | 1.022 | 1.232 | 0.21 | 1.092 | 0.0608 | 0.078 | |
| HGS | 1 | 1.238 | 0.238 | 1.079 | 0.0686 | 0 | |
| K3 | H1D_1 | 1.022 | 1.157 | 0.135 | 1.062 | 0.0368 | 0.05 |
| H1D_2 | 1.022 | 1.172 | 0.149 | 1.068 | 0.0412 | 0.054 | |
| HGS | 1 | 1.137 | 0.137 | 1.045 | 0.039 | 0 |
References
- Hunt, R.J.; Prudic, D.E.; Walker, J.F.; Anderson, M.P. Importance of Unsaturated Zone Flow for Simulating Recharge in a Humid Climate. Groundwater 2008, 46, 551–560. [Google Scholar] [CrossRef]
- Panday, S.; Huyakorn, P.S. A Fully Coupled Physically-Based Spatially-Distributed Model for Evaluating Surface/Subsurface Flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar] [CrossRef]
- Rossman, N.R.; Zlotnik, V.A.; Rowe, C.M.; Szilagyi, J. Vadose Zone Lag Time and Potential 21st Century Climate Change Effects on Spatially Distributed Groundwater Recharge in the Semi-Arid Nebraska Sand Hills. J. Hydrol. 2014, 519, 656–669. [Google Scholar] [CrossRef]
- Huang, Y.; Chang, Q.; Li, Z. Land Use Change Impacts on the Amount and Quality of Recharge Water in the Loess Tablelands of China. Sci. Total Environ. 2018, 628–629, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Musuuza, J.L.; Van Loon, A.F.; Teuling, A.J.; Barthel, R.; Ten Broek, J.; Mai, J.; Samaniego, L.; Attinger, S. Multiscale Evaluation of the Standardized Precipitation Index as a Groundwater Drought Indicator. Hydrol. Earth Syst. Sci. 2016, 20, 1117–1131. [Google Scholar] [CrossRef]
- Xue, D.; Dai, H.; Liu, Y.; Liu, Y.; Zhang, L.; Lv, W. Interaction Simulation of Vadose Zone Water and Groundwater in Cele Oasis: Assessment of the Impact of Agricultural Intensification, Northwestern China. Agriculture 2022, 12, 641. [Google Scholar] [CrossRef]
- Mechal, A.; Karuppannan, S.; Bayisa, A. Groundwater Recharge Estimation in the Ziway Lake Watershed, Ethiopian Rift: An Approach Using SWAT and CMB Techniques. Sustain. Water Resour. Manag. 2024, 10, 130. [Google Scholar] [CrossRef]
- Manzoni, A.; Porta, G.M.; Guadagnini, L.; Guadagnini, A.; Riva, M. A Comprehensive Framework for Stochastic Calibration and Sensitivity Analysis of Large-Scale Groundwater Models. Hydrol. Earth Syst. Sci. 2024, 28, 2661–2682. [Google Scholar] [CrossRef]
- Yun, S.-M.; Jeon, H.-T.; Cheong, J.-Y.; Kim, J.; Hamm, S.-Y. Combined Analysis of Net Groundwater Recharge Using Water Budget and Climate Change Scenarios. Water 2023, 15, 571. [Google Scholar] [CrossRef]
- González-Ortigoza, S.; Hernández-Espriú, A.; Arciniega-Esparza, S. Regional Modeling of Groundwater Recharge in the Basin of Mexico: New Insights from Satellite Observations and Global Data Sources. Hydrogeol. J. 2023, 31, 1971–1990. [Google Scholar] [CrossRef]
- Sasidharan, S.; Bradford, S.A.; Šimůnek, J.; Kraemer, S.R. Virus Transport from Drywells under Constant Head Conditions: A Modeling Study. Water Res. 2021, 197, 117040. [Google Scholar] [CrossRef] [PubMed]
- Sasidharan, R.; Hartman, S.; Liu, Z.; Martopawiro, S.; Sajeev, N.; van Veen, H.; Yeung, E.; Voesenek, L.A.C.J. Signal Dynamics and Interactions during Flooding Stress. Plant Physiol. 2018, 176, 1106–1117. [Google Scholar] [CrossRef]
- Marwaha, N.; Kourakos, G.; Levintal, E.; Dahlke, H.E. Identifying Agricultural Managed Aquifer Recharge Locations to Benefit Drinking Water Supply in Rural Communities. Water Resour. Res. 2021, 57, e2020WR028811. [Google Scholar] [CrossRef]
- Niswonger, R.G.; Morway, E.D.; Triana, E.; Huntington, J.L. Managed Aquifer Recharge through Off-season Irrigation in Agricultural Regions. Water Resour. Res. 2017, 53, 6970–6992. [Google Scholar] [CrossRef]
- Kourakos, G.; Dahlke, H.E.; Harter, T. Increasing Groundwater Availability and Seasonal Base Flow Through Agricultural Managed Aquifer Recharge in an Irrigated Basin. Water Resour. Res. 2019, 55, 7464–7492. [Google Scholar] [CrossRef]
- Aquanty. HydroGeoSphere–User Manual; Aquanty Inc.: Waterloo, ON, Canada, 2013. [Google Scholar]
- Therrien, R.; McLaren, R.G.; Sudicky, E.A.; Panday, S.M. HydroGeoSphere: A Three-Dimensional Numerical Model Describing Fully-Integrated Subsurface and Surface Flow and Solute Transport; Groundwater Simulations Group, University of Waterloo: Waterloo, ON, Canada, 2010; p. 838. [Google Scholar]
- Camporese, M.; Paniconi, C.; Putti, M.; Orlandini, S. Surface-subsurface Flow Modeling with Path-based Runoff Routing, Boundary Condition-based Coupling, and Assimilation of Multisource Observation Data. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Kollet, S.J.; Smith, S.G.; Woodward, C.S.; Falgout, R.D.; Ferguson, I.M.; Baldwin, C.; Bosl, W.J.; Hornung, R.; Ashby, S. ParFlow User’s Manual; International Ground Water Modeling Center Report GWMI; International Ground Water Modeling Center: Golden, CO, USA, 2009. [Google Scholar]
- Simunek, J.; Van Genuchten, M.T.; Sejna, M. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; University of California-Riverside Research Reports; University of California Riverside: Riverside, CA, USA, 2005; Volume 3, pp. 1–240. [Google Scholar]
- Refshaard, J.; Storm, B. MIKE SHE; Water Resources Publications: Lone Tree, CO, USA, 1995. [Google Scholar]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System —Systeme Hydrologique Europeen, “SHE”, 1: History and Philosophy of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Szymkiewicz, A.; Gorczewska-Langner, W.; Pruszkowska-Caceres, M.; Angulo-Jaramillo, R.; Šimůnek, J. Estimation of Groundwater Recharge in a Shallow Sandy Aquifer Using Unsaturated Zone Modeling and Water Table Fluctuation Method. J. Hydrol. 2022, 605, 127283. [Google Scholar] [CrossRef]
- Leterme, B.; Gedeon, M.; Jacques, D. Groundwater Recharge Modeling of the Nete Catchment (Belgium) Using the HYDRUS 1D—MODFLOW Package. In Proceedings of the 4th International Conference “HYDRUS Software Applications to Subsurface Flow and Contaminant Transport Problems”, Prague, Czech Republic, 21–22 March 2013; Department of Soil Science and Geology, Czech University of Life Sciences, Šimůnek, J., van Genuchten, M.T., Kodešová, R., Eds.; PC-PROGRESS: Prague, Czech Republic, 2013; pp. 235–244. [Google Scholar]
- Xu, Y. Book Review: Estimating Groundwater Recharge, by Richard W Healy (Cambridge University Press, 2010). Hydrogeol. J. 2011, 19, 1451–1452. [Google Scholar] [CrossRef]
- Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Jefimow, M. Climate Change Impact on Groundwater Resources in Sandbar Aquifers in Southern Baltic Coast. Sci. Rep. 2024, 14, 11828. [Google Scholar] [CrossRef]
- Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Szymkiewicz, A.; Gorczewska-Langner, W.; Angulo-Jaramillo, R.; Šimůnek, J. Impact of Climate Change on Groundwater Recharge in Shallow Young Glacial Aquifers in Northern Poland. Sci. Total Environ. 2023, 877, 162904. [Google Scholar] [CrossRef] [PubMed]
- Oad, V.K.; Szymkiewicz, A.; Khan, N.A.; Ashraf, S.; Nawaz, R.; Elnashar, A.; Saad, S.; Qureshi, A.H. Time Series Analysis and Impact Assessment of the Temperature Changes on the Vegetation and the Water Availability: A Case Study of Bakun-Murum Catchment Region in Malaysia. Remote Sens. Appl. 2023, 29, 100915. [Google Scholar] [CrossRef]
- Koelmans, A. Integrated Modelling of Eutrophication and Organic Contaminant Fate & Effects in Aquatic Ecosystems. A Review. Water Res. 2001, 35, 3517–3536. [Google Scholar] [CrossRef]
- McKone, T.E. Alternative Modeling Approaches for Contaminant Fate in Soils: Uncertainty, Variability, and Reliability. Reliab. Eng. Syst. Saf. 1996, 54, 165–181. [Google Scholar] [CrossRef]
- Sarma, R.; Singh, S.K. Simulating Contaminant Transport in Unsaturated and Saturated Groundwater Zones. Water Environ. Res. 2021, 93, 1496–1509. [Google Scholar] [CrossRef] [PubMed]
- Go, J.; Lampert, D.J.; Stegemann, J.A.; Reible, D.D. Predicting Contaminant Fate and Transport in Sediment Caps: Mathematical Modelling Approaches. Appl. Geochem. 2009, 24, 1347–1353. [Google Scholar] [CrossRef]
- Tong, X.; Mohapatra, S.; Zhang, J.; Tran, N.H.; You, L.; He, Y.; Gin, K.Y.-H. Source, Fate, Transport and Modelling of Selected Emerging Contaminants in the Aquatic Environment: Current Status and Future Perspectives. Water Res. 2022, 217, 118418. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Version 4.0, HYDRUS Software Series 1; University of California Riverside: Riverside, CA, USA, 2008. [Google Scholar]
- van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; van Walsum, P.E.V.; Groenendijk, P.; van Diepen, C.A. Theory of SWAP Version 2.0; DLO Winand Staring Centre for Integrated Land, Soil and Water Research: Wageningen, The Netherlands; Wageningen Agricultural University: Wageningen, The Netherlands, 1997. [Google Scholar]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Šimůnek, J.; Leterme, B.; Beegum, S.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W.; Angulo-Jaramillo, R.; Jacques, D. Simulations of Freshwater Lens Recharge and Salt/Freshwater Interfaces Using the HYDRUS and SWI2 Packages for MODFLOW. J. Hydrol. Hydromech. 2018, 66, 246–256. [Google Scholar] [CrossRef]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Implementation of Solute Transport in the Vadose Zone into the “HYDRUS Package for MODFLOW”. Groundwater 2019, 57, 392–408. [Google Scholar] [CrossRef]
- Seo, H.S.; Simunek, J.; Poeter, E.P. Documentation of the Hydrus Package for Modflow-2000, the Us Geological Survey Modular Ground-Water Model; IGWMC-International Ground Water Modeling Center: Golden, CO, USA, 2007. [Google Scholar]
- Pawlowicz, M.; Balis, B.; Szymkiewicz, A.; Šimůnek, J.; Gumuła-Kawęcka, A.; Jaworska-Szulc, B. HMSE: A Tool for Coupling MODFLOW and HYDRUS-1D Computer Programs. SoftwareX 2024, 26, 101680. [Google Scholar] [CrossRef]
- Tong, X.; You, L.; Zhang, J.; Chen, H.; Nguyen, V.T.; He, Y.; Gin, K.Y.-H. A comprehensive modelling approach to understanding the fate, transport and potential risks of emerging contaminants in a tropical reservoir. Water Res. 2021, 200, 117298. [Google Scholar] [CrossRef] [PubMed]
- Locatelli, L.; Binning, P.J.; Sanchez-Vila, X.; Søndergaard, G.L.; Rosenberg, L.; Bjerg, P.L. A Simple Contaminant Fate and Transport Modelling Tool for Management and Risk Assessment of Groundwater Pollution from Contaminated Sites. J. Contam. Hydrol. 2019, 221, 35–49. [Google Scholar] [CrossRef] [PubMed]
- Meyer, P.D.; Rockhold, M.L.; Gee, G.W. Uncertainty Analyses of Infiltration and Subsurface Flow and Transport for SDMP Sites (No. NUREG/CR-6565; PNNL-11705); US Nuclear Regulatory Commission (NRC): Washington, DC, USA; Div. of Regulatory Applications, Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 1997. [Google Scholar]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing Appropriate Techniques for Quantifying Groundwater Recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Healy, R.W. Estimating Groundwater Recharge; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Jie, Z.; van Heyden, J.; Bendel, D.; Barthel, R. Combination of Soil-Water Balance Models and Water-Table Fluctuation Methods for Evaluation and Improvement of Groundwater Recharge Calculations. Hydrogeol. J. 2011, 19, 1487–1502. [Google Scholar] [CrossRef]
- Bear, J.; Cheng, A.H.-D. Modeling Groundwater Flow and Contaminant Transport; Springer: Dordrecht, The Netherlands, 2010; ISBN 978-1-4020-6681-8. [Google Scholar]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Updating the Coupling Algorithm between HYDRUS and MODFLOW in the HYDRUS Package for MODFLOW. Vadose Zone J. 2018, 17, 1–8. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Version 4.17; University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Kroes, J.G.; van Dam, J.C.; Bartholomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Mulder, H.M.; Supit, I.; van Walsum, P.E.V. SWAP Version 4. Theory Description and User Manual; Wageningen University & Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Vonk, M. Performance of Nonlinear Time Series Models to Simulate Synthetic Groundwater Table Time Series from an Unsaturated Zone Model. Master’s Thesis, Delft University of Technology, The Hague, The Netherlands, 2021. [Google Scholar]
- Hopmans, J.W.; Stricker, J.N.M. Stochastic Analysis of Soil Water Regime in a Watershed. J. Hydrol. 1989, 105, 57–84. [Google Scholar] [CrossRef]
- Neto, D.C.; Chang, H.K.; van Genuchten, M.T. A Mathematical View of Water Table Fluctuations in a Shallow Aquifer in Brazil. Groundwater 2016, 54, 82–91. [Google Scholar] [CrossRef]
- Corona, C.R.; Gurdak, J.J.; Dickinson, J.E.; Ferré, T.P.A.; Maurer, E.P. Climate Variability and Vadose Zone Controls on Damping of Transient Recharge. J. Hydrol. 2018, 561, 1094–1104. [Google Scholar] [CrossRef]
- Corona, C.R.; Ge, S.; Anderson, S.P. Water-Table Response to Extreme Precipitation Events. J. Hydrol. 2023, 618, 129140. [Google Scholar] [CrossRef]
- Brunner, P.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Groundwater 2012, 50, 170–176. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil. Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley Sons: New York, NY, USA, 1978. [Google Scholar]
- Wesseling, J.G.; Elbers, J.A.; Kabat, P.; Van den Broek, B.J. SWATRE: Instructions for Input; Internal Note; Winand Staring Centre: Wageningen, The Netherlands, 1991; Volume 700. [Google Scholar]
- Ritzema, H.P. Drainage Principles and Applications. ILRI Publication 16; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1994; Volume 181. [Google Scholar]
- Kabala, Z.J.; Milly, P.C.D. Sensitivity Analysis of Infiltration, Exfiltration, and Drainage in Unsaturated Miller-Similar Porous Media. Water Resour. Res. 1991, 27, 2655–2666. [Google Scholar] [CrossRef]
- Kabala, Z.J.; Milly, P.C.D. Sensitivity Analysis of Partial Differential Equations: A Case for Functional Sensitivity. Numer. Methods Partial. Differ. Equ. 1991, 7, 101–112. [Google Scholar] [CrossRef]
- Kabala, Z.J. Sensitivity Analysis of a Pumping Test on a Well with Wellbore Storage and Skin. Adv. Water Resour. 2001, 24, 483–504. [Google Scholar] [CrossRef]





| Soil Material | θr [-] | θs [-] | α [1/m] | n [-] | m [-] | Ks [m/d] | τ [-] |
|---|---|---|---|---|---|---|---|
| Sand | 0.045 | 0.43 | 14.5 | 2.68 | 0.627 | 7.128 | 0.5 |
| Loamy Sand | 0.057 | 0.41 | 12.4 | 2.28 | 0.570 | 3.502 | 0.5 |
| Models | Observation Point No (Depth Below the Ground Level) | Pressure Head [m] | Water Content [-] |
|---|---|---|---|
| HYDRUS-1D | 1 (0 m) | −0.17 | 0.12 |
| 2 (2 m) | 0.85 | 0.43 | |
| 3 (7 m) | 5.86 | 0.43 | |
| HydroGeoSphere | 1 (0 m) | −0.16 | 0.12 |
| 2 (2 m) | 0.82 | 0.43 | |
| 3 (7 m) | 5.82 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oad, V.K.; Szymkiewicz, A.; Berezowski, T.; Gumuła-Kawęcka, A.; Šimůnek, J.; Jaworska-Szulc, B.; Therrien, R. Incorporation of Horizontal Aquifer Flow into a Vertical Vadose Zone Model to Simulate Natural Groundwater Table Fluctuations. Water 2025, 17, 2046. https://doi.org/10.3390/w17142046
Oad VK, Szymkiewicz A, Berezowski T, Gumuła-Kawęcka A, Šimůnek J, Jaworska-Szulc B, Therrien R. Incorporation of Horizontal Aquifer Flow into a Vertical Vadose Zone Model to Simulate Natural Groundwater Table Fluctuations. Water. 2025; 17(14):2046. https://doi.org/10.3390/w17142046
Chicago/Turabian StyleOad, Vipin Kumar, Adam Szymkiewicz, Tomasz Berezowski, Anna Gumuła-Kawęcka, Jirka Šimůnek, Beata Jaworska-Szulc, and René Therrien. 2025. "Incorporation of Horizontal Aquifer Flow into a Vertical Vadose Zone Model to Simulate Natural Groundwater Table Fluctuations" Water 17, no. 14: 2046. https://doi.org/10.3390/w17142046
APA StyleOad, V. K., Szymkiewicz, A., Berezowski, T., Gumuła-Kawęcka, A., Šimůnek, J., Jaworska-Szulc, B., & Therrien, R. (2025). Incorporation of Horizontal Aquifer Flow into a Vertical Vadose Zone Model to Simulate Natural Groundwater Table Fluctuations. Water, 17(14), 2046. https://doi.org/10.3390/w17142046








