Abstract
The construction and operation of high dam projects at high altitudes have led to concerns about the effectiveness of flood discharge security predictions resulting from the greater flood discharge atomized rain caused by ambient pressure reduction. In this study, self-similar characteristics and variation in atomized raindrop size distributions are analyzed to understand the phenomenon of increased atomized rain intensity under low ambient pressure from a mesoscopic scale. The monographic experiments are characterized by a low ambient pressure range (0.66P0–1.02P0) and a high waterjet velocity range (13.89–15.74 m/s). When the ambient pressure decreases by 0.10P0 (P0 = 101.325 kPa) from the reference atmospheric pressure condition as the other conditions remain fixed, the total number concentration in a two-dimensional atomized raindrop spectrum (number/(54 cm2)) and the peak value of the individual three-dimensional number concentration (number/(m3·mm) increase, which can lead to the required industry standard protective level of atomized zones increasing by one level in some cases. In addition, the spectrum trend and typical particle size ranges of the atomized raindrop size distributions present self-similarity as the ambient pressure decreases. The above studies further confirm the effects of low-ambient pressure enhancement on flood discharge atomized rain intensity, which can provide a theoretical basis for the development of random splash simulation models characterized by low pressure for high-altitude hydropower stations.
1. Introduction
Rain hazards derived from extreme rain events (i.e., urban flooding [1], flash floods [2], soil erosion [3], building erosion [4], streambank erosion [5], and hydroelectric accidents [6,7]) have attracted interest as public safety problems at home and abroad. The direct disasters induced by heavy precipitation include confluence, erosion, infiltration, and other physical behaviors. Moreover, the absence of effective predictions and protective measures for these direct disasters often leads to a cascade of secondary disasters that inflict socioeconomic damage. In addition to natural rain, heavy precipitation at hydropower stations stems from another source: flood discharge atomization. This phenomenon has garnered considerable attention due to its undeniable threats not only to the hydropower station itself but also to the surrounding downstream environment [8,9,10,11,12]. As shown in Figure 1, the movement path of atomized rain mainly extends from splash zones downstream along the flow direction, which is unlike that of natural rain moving from cloud systems to the ground along the height direction [13]. Therefore, atomized rain is always concentrated in the downstream zone and varies in a dynamic changing process with obvious divisions. It is influenced by various factors, including hydraulic release conditions, design of release structures, regional topography, unique geological formations, and prevailing climatic characteristics [14]. In previous studies on atomized events, the influence of hydraulic factors has gradually been recognized, but the coupling analysis of environmental factors still remains a challenge because of a lack of thematic research. In particular, at high-altitude hydropower stations, low ambient pressure is a typical meteorological characteristic that affects the formation and diffusion of atomized rain. Therefore, it is important to mechanistically explore the influence of low ambient pressure on flood discharge atomization to adapt to the new demand for the development of hydropower projects.

Figure 1.
Atomized rain fields induced by different flood discharge atomized sources at the Jinping-1 hydropower station. (a,b) Atomized source of a dam orifice discharge. (c) Atomized source of a spillway tunnel discharge [13].
Atomized areas can be classified as atomized rainstorm zones that require protection when their atomized rain intensity exceeds 10 mm/h. With the update of the engineering problem library induced by flood discharge atomized rain, the risk cognitions and protective technologies have improved. However, challenges persist in atomized prediction across various processes, locations, and scales. The risk perception of atomized rain-induced landslides has strengthened since one million cubic meters of landslides occurred at the Longyangxia hydropower station in 1988 and 1989 [12]. The relationship between discharge patterns and atomization intensities indicates that the problem of atomized rain induced by bottom-flow dissipation is weaker than that caused by ski-jump energy dissipation. Specifically, the prototypical atomized ranges of the Ertan hydropower station reached 0 + 2000 m along the flow direction and 1215 m in the elevation direction, which are greater than their corresponding design values of 1000 m and 75 m for ski-jump energy dissipation in its collision design [10,11]; however, those of the Xiangjiaba hydropower station are concentrated in the energy dissipation area and have almost no effect on the humidity of its downstream county [15]. The atomized predictions of ski-jump energy dissipation were subsequently introduced and developed into large-scale energy dissipation projects, such as the design projects of Wudongde, Baihetan, Lianghekou, Rumei, and the operation projects of Ertan, Laxiwa, Nazixia, Shuibuya, etc. [14]. Among the abovementioned hydropower stations, the maximum crest elevations of the Laxiwa, Longyangxia, and Nazixia hydropower stations are 2460.00 m, 2610.00 m, and 3204.60 m, corresponding to dam heights of 250 m, 178.0 m, and 121.5 m, respectively. Additionally, the maximum crest elevations of the Lianghekou and Rumei hydropower stations are 2875.00 m and 2902.00 m, corresponding to dam heights of 295.0 m and 315.0 m, respectively. The number of high-head hydropower stations at high altitudes is increasing. However, the impact of low ambient pressure is currently not taken into account in the atomized analysis of these projects. This oversight is likely to lead to an underestimation of the effects of atomized rain at high-altitude hydropower stations, due to the enhancement effect that low ambient pressure has on the downstream atomized rain field.
To mitigate and avoid atomized rain hazards, atomized scopes are evaluated in different regions with individual levels of engineering and nonengineering protective measures. In addition to prototypical and scale models, nonscale models, named “random splash experiments”, are established with a major focus on atomized rain indices and factors during waterjet splashing processes [14,16]. The precipitation intensity and droplet spectrum are the principal macroscopic and microscopic characteristics of atomized rain fields, such as natural rain. In studies of atomized rain intensity, early random splash experiments controlled hydraulic conditions produced by the hydraulic impact of a single falling waterjet into a water cushion and the midair collision of two water jets under atmospheric ambient pressure [17,18,19,20]; however, a depressurized random splash experiment recently indicated that ambient pressure conditions are also important because lower ambient pressure can increase the area of an atomized storm [21]. The atomized raindrop size distributions can be statistically analyzed through a graph or digital signal acquisition. The relationships between rain intensity and raindrops information can be used for both the calculation of atomized light rain intensity according to the raindrop correlation parameters determined in advance and the exploration of atomized rain intensity laws characterized by dominant rainfall intensity and frequency under atmospheric pressure [22,23]. With statistical models of spectrum characteristics, atomized rain intensity distributions can be experimentally demonstrated or calculated by ignoring ambient pressure effects, among which experimental results of atomized raindrop size distributions are still limited [9,24]. Although atomized raindrop size distributions have been described and applied in random splash numerical models, the effects of low ambient pressure are still poorly understood [14]. To explore the enhancement mechanism of low ambient pressure on atomized rain, it is essential to gain insight into atomized raindrop size distributions in depressurized random splash experiments to further promote the development of atomization prediction methods that consider high-altitude flood discharge.
Depressurized experiments are widely applied and highly important in numerous fields, such as astrobiology models to predict the habitability of Mars [25], flame-geometry descriptors of fire jets and the diffusion characteristics of water mists to ensure fire safety in plateau areas [26,27], the splash form of liquid droplets to inhibit splashing action [28], the cracking properties of concrete to explore its plateau application [29], and the impact and splash characteristics of falling waterjets to guide flood discharge safety [21,30]. Analogously, these experiments require artificial low-pressure environments. Unlike other depressurized experiments, the ambient pressure stability of random splash experiments is an important challenge. This is primarily due to the involvement of two-stage multiphase coupling processes, which involve aerated waterjet movement based on a continuous phase and the diffusion of numerous droplets based on a discrete phase [31,32]. In general, the relationship between the splash and impact processes is characterized by negative compensation interactions without considering the influence of ambient pressure. However, the enhancement effects of the low ambient pressure not only appeared in the atomized rain field downstream of the water-collision locations but also in the impact pressure field near the water-collision locations. These phenomena were observed in depressurized experiments of model waterjets released from a pressure orifice with initial velocities of approximately 10 m/s and a surface orifice with initial velocities of approximately 5 m/s [21,30]. When these effects are applied synchronously to prototype engineering applications, the protection standards need to be improved in the flood discharge process. Precisely obtaining multiple factors, i.e., the water-entry velocity, water-entry angle, water-entry position, atomized source moisture, bucket nappe wind, and so on, is still limited, both experimentally and computationally [18,19,33,34]. Consequently, we have not explored the influence of independent factors but have focused on the terminal effect of the atomized field.
Although a clear relationship between atomized raindrops and ambient pressure is not available at present, other studies related to altitude have suggested that depressurized effects should be considered. In view of the droplet splash process, Xu et al. [35] and Latka et al. [36] reported that the ejected droplets splashed by a liquid drop and a solid surface can be impacted by ambient pressure and wall roughness. Xu et al. [35] reported that as the ambient pressure decreases, less liquid is ejected in the process of corona splashing on the smooth wall. Latka et al. [36] further reported that the ambient pressure needs to be considered during thin-sheet formation and prompt splashing. In view of the droplet diffusion process, the influence of ambient pressure on the natural raindrop spectrum is objective. Under climate conditions in the same area with different elevations, Song et al. [37] noted that a decrease in altitude can decrease the contribution rate of small raindrop particles to precipitation intensity. Li et al. [38] reported that the locations of raindrop diameter attenuation are in the order of mountain-side, mountain-bottom, and mountain-top, irrespective of rain type, and that the raindrop size distributions for convective precipitation are more sensitive to altitude than those for stratiform precipitation by comparing stratiform and convective precipitation raindrop size distribution datasets at Huangshan (vertical evolution at 1860 m, 1351 m, and 464 m). The raindrop size distribution (RSD) is the change in individual three-dimensional number concentration (number/(m3·mm)) with raindrop particle size. Under climate conditions in different areas with different elevations, Sumesh et al. [39] reported that surface drop concentrations at a mid-altitude of 400 m show bimodal RSDs, whereas those at high altitudes of 1820 m represent monomodal RSDs regardless of rain class by characterizing the RSDS parameters of stratiform precipitation in the western Ghats Mountains. Wu et al. [40] detected large variability in RSDs in the Tibetan Plateau and southern China. This variability can be described by standardized gamma, whose parameters vary with changes in rain rate and precipitation type. Based on the above discussion, low ambient pressure should play an important role in the microdynamic mechanism (evaporation, collision, coalescence, breakup, etc.) of raindrops or raindrop groups. Thus, the ambient pressure is likely to affect the descriptive characteristics of raindrop size distributions with different ambient pressures.
Therefore, the study of raindrop size distributions under a low ambient pressure environment is not only the content of flood discharge atomization theory but also a practical necessity for numerical calculation of atomization at high-altitude hydropower stations [14]. To fill the above gaps, this study is a follow-up of the enhancement effect of low ambient pressure on downstream atomized rain intensity induced by depressurized random splash experiments. In this study, the atomized rain was generated by the collision process of a high-speed rectangular waterjet and a narrow water cushion under various low ambient pressure conditions. The observation device is an OTT Parsivel2 (Beijing Sichuang Minda Measurement and Control Technology Co., LTD, Beijing, China) suspended in a horizontal guide rail with six measuring points along the overflow center line. In the following sections, the structure design and measurement method of the two-phase experimental platform will be introduced; the atomized quantitative precipitation estimation will be considered to access the protection level variation in atomized areas; the statistical characteristics of atomized raindrop size distribution will be analyzed and discussed; and the main conclusions and prospects will be summarized in the end to pave the way for a follow-up study.
2. Experimental Setup and Measurements
2.1. Design and Regulation of the Experimental Platform
A novel test control system chartered by high-speed waterjets and low ambient pressures was used to carry out the depressurized random splash experiments at the State Key Laboratory of Hydraulic Engineering Simulation and Safety (current name: State Key Laboratory of Hydraulic Engineering Intelligent Construction and Operation) of Tianjin University. The hydraulic depressurized chamber is intended for hydrodynamic simulations of high-altitude hydropower stations, not for traditional cavitation studies, so the vacuum degree is designed with reference to the absolute air pressure in the high-altitude area. The raindrop size distribution measurement methods are generally based on the principles of laser signals and image identification. It is reasonable to adopt various chemical test papers combined with postprocessing of graphics in the instantaneous atomized raindrop size distribution collection of random splash experiments under atmospheric pressure. However, this method is not suitable for the measurement of depressurized random splash experiments because measurement times are difficult to control, measurement conditions are difficult to switch, and instantaneous atomized raindrop size databases are not conducive to the statistical analysis of time–history characteristics. Therefore, an OTT Parsivel2 with a 54 mm2 rectangular area is introduced to collect the atomized raindrop size in real time, which can be moved horizontally along the flow direction via a remotely controlled horizontal slide rail. The experimental area is in the depressurized chamber that is connected with water-regulating and air-regulating systems, in which the atomized rain is splashed by a high-speed rectangular waterjet from a constricted nozzle that impacts a rectangular water cushion with an initial depth of 56 cm. The experimental coupling conditions between water flow and ambient pressure are adjusted with reasonable shunt designs and effective monitoring devices. In detail, the layout of the depressurized chamber is shown in Figure 2a,b, the layout of the measurement instrument and points is shown in Figure 2c, the air-regulating system is shown in Figure 3a, and the water-regulating system is shown in Figure 3b.
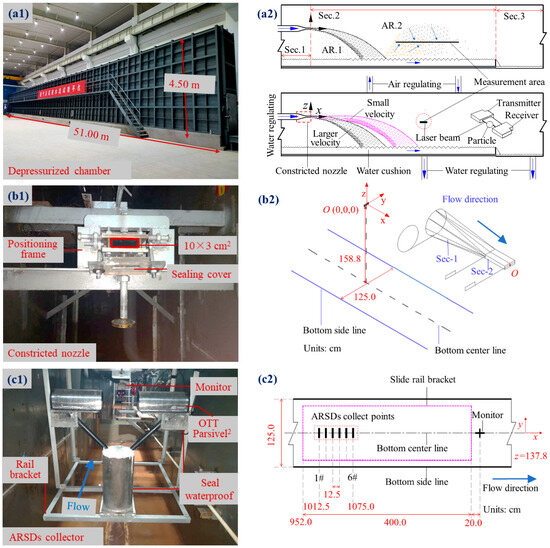
Figure 2.
Physical diagram and partial design of the depressurized random splash experiments. (a1) Physical image of the depressurized chamber; (a2) Schematic diagram in the depressurized chamber; (b1) Physical image of the internal nozzle in the depressurized chamber; (b2) Schematic diagram of the internal nozzle in the depressurized chamber; (c1) Physical image of the measurement instrument and point layout (ARSDS is short for atomized raindrop distributions); (c2) Relative coordinates of measurement instrument and point layout (ARSDS is short for atomized raindrop distributions).
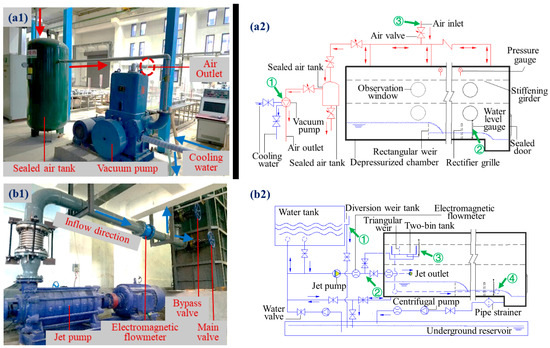
Figure 3.
Physical and schematic diagram of the water- and air-regulating systems in the depressurized random splash experiments. (a1) Physical picture of air-regulating system layout; (a2) Schematic diagram of air-regulating system layout; (b1) Physical picture of water-regulating system layout; (b2) Schematic diagram of water-regulating system layout.
As shown in Figure 2a, the depressurized chamber has a sealable steel structure that is 51.00 m long, 4.50 m high, and 1.25 m wide in internal volume, in which three sections are divided along the flow direction, corresponding to the inflow Sec. I, the working Sec. II, and the outflow Sec. III, respectively. As rectangular waterjets are typically shaped as discharge waterjets, rectangular waterjets can also be considered component units of specially shaped waterjets in theoretical and numerical studies of flood discharge atomization. The main gathering parameters include the atomized raindrop distributions of six measurement points, the inflow discharge of the waterjet, and the ambient pressure in the depressurized chamber; two types of affiliated measurement indicators include the water level in the drainage area and the visual monitoring device in the measurement and drainage areas. The acquisition terminals of the above instruments are arranged on a measurement platform that is placed outside the depressurized chamber.
As shown in Figure 2b, to achieve stable high-speed rectangular waterjet discharge conditions, a constricted nozzle made of stainless steel was designed. This nozzle features a transition section measuring 55.0 cm in length and a rectifying section that is 20 cm long, with connection surfaces transitioning from an upstream circular cross-section (D = 209 cm) to a downstream rectangular cross-section (10.00 cm wide × 3.00 cm high), ultimately leading to the same rectangular surface at the exit. In the experiment, the streamlined nozzle effectively prevented water from detaching from the pipe wall, thereby mitigating the risk of local negative pressure and cavitation issues. Furthermore, no abnormal sounds or vibrations were detected at the nozzle during testing, and there were no indications of pitting or hollow erosion marks following the test. Consequently, we conclude that there are no cavitation-related problems at the nozzle that could potentially impact the test results, thus fulfilling all testing requirements. Furthermore, the center point (O) of the nozzle outlet surface is positioned 1.588 m above the bottom surface of the depressurized chamber, simulating an atomized rain field characterized by limited transverse diffusion while allowing for sufficient diffusion in both the flow and height directions. When the waterjet impacts the water cushion below, it generates a substantial number of atomized raindrops that are dispersed throughout space-time domains—particularly downstream from where collisions occur within the water body—which has been designated as the measurement area for atomized raindrop size distributions.
As shown in Figure 2c, to alleviate the diffusion interference caused by atomized rain, the instrument is secured firmly on a tray located beneath a straight slide rail. The four connecting rods are strategically positioned downstream of the instrument. To safeguard against water ingress, an appropriately designed partition protection mechanism has been implemented for the exterior of the instrument. To clearly define the spatial positions of the measurement points, we first establish the location of the center point within the designated measurement area as the coordinate reference for our measurement points. We subsequently designate point O—the geometric center of the nozzle outlet surface—as the origin of the coordinate system. We define the axes as follows: the x-axis represents the flow direction, the y-axis denotes the transverse direction, and the z-axis corresponds to the vertical direction. In analogous random splash experiments involving high-speed water jets with velocities of approximately 10 m/s, it has been demonstrated that there is a negligible transverse gradient in the two-dimensional distributions of downstream atomized rain (with rain intensities ≥ 2 mm/h). Consequently, six measurement points (labelled points #1 through 6) were arranged along the overflow centerline at a z-coordinate of 20 cm. To minimize errors arising from overlapping particles during heavy precipitation events, point #1 was positioned at a distance of 1012.5 cm from the coordinate origin, with an interval of 12.50 cm between adjacent measurement points.
As illustrated in Figure 3a, the air circulation within the depressurized chamber comprises two distinct pathways. The first pathway involves reducing the ambient pressure of the chamber through a vacuum pump connected to a sealed air tank. The second pathway facilitates the influx of external air into the depressurized chamber, driven by the existing differential pressure. Consequently, five suction air pipes located at the top of the depressurized chamber are individually linked to both exhaust and replenishment pipes, allowing for precise adjustment of the required airflow path by corresponding valves. During this adjustment process, real-time monitoring of ambient pressure within the depressurized chamber is conducted using an absolute pressure sensor installed at the top center front of the chamber. This sensor boasts an accuracy of 0.1% FS and operates within a range of 0 to 10 m. Additionally, water depth is measured utilizing a self-balancing manometer positioned downstream from the drainage area alongside a meter ruler. It is imperative that under enclosed conditions with atmospheric pressure, downstream water levels do not rise; conversely, these levels must not fall below the specified minimum design ambient pressures in similar enclosed environments. In addition, the testing was conducted in January, during which the recorded average temperature was 12 °C.
As illustrated in Figure 3b, high-speed waterjets derive energy from pumps, which increase velocity through a constricted nozzle and regulate waterjet inflow discharge via two branch pipes. The system is designed to recycle water through an underground reservoir and includes a centrifugal pump, an elevated water tank with a diversion weir tank, a jet pump, a #1 electromagnetic flowmeter, and two upstream branch pipes, along with another centrifugal pump downstream. Meanwhile, the rated head of 210 m for the jet pump provides a reliable assurance of water pressure within the supply system, ensuring the stability of the high-speed waterjet. In the inflow section of the depressurized chamber, one branch pipe connects to a #2 electromagnetic flowmeter and horizontally leads to a constricted nozzle for supplying the waterjet discharge. Another branch pipe connects to the inflow orifice of a dual-bin tank (with dimensions of 2.50 m long × 0.85 cm wide × 0.63 cm high for both the inflow and outflow sections) separated by a right-angled triangular weir (with right-angled lengths measuring 4 inches) to regulate the inflow discharge of the waterjet. During the measurement periods, the inflow discharge of the experimental events is recorded by the #2 electromagnetic flowmeter while being monitored synchronously through the discharge difference between the #1 electromagnetic flowmeter and the triangular weir. During non-measurement periods, it is possible to seal the branch pipe for waterjet discharge using a removable sealing cover to maintain air isolation within the piping system. In addition, the water tanks used for the experiment were thoroughly cleaned prior to testing, and the water utilized was sourced from tap water. Given that the quality of tap water is generally stable and no adverse factors affected its quality during the testing process, it is considered appropriate to regard the water quality as a constant variable.
Moreover, for both the waterproof design of testing instruments (specifically, an OTT Parsivel2) within the depressurized chamber and the sealing design of instrument lines (utilizing a threading device) that pass through this chamber, achieving a perfect seal under differential pressure is crucial. In the sealing process, the use of TL990-KP800 cable refractory sealing material is feasible for anti-pressure packing due to its noncorrosive properties and its ease of removal.
2.2. Design and Optimization of the Test Conditions
In the depressurized random splash experiments, a total of 25 atomized events were conducted, corresponding to five inflow discharge rates Vm (m3/h) and five ambient pressures Pn at six measurement points (#1–6) along the overflow centerline. Each event consisted of three sets lasting 10 min (total duration: 30 min), as detailed in Table 1. The average exit velocity is subsequently calculated by dividing the inflow discharge by the outlet area of the constricted nozzle (30.00 cm2). The generation of a distinctly observable splash effect necessitates specific conditions regarding the Weber number of the spattering body. When the Weber number of the splashing droplets reaches 500, pronounced splashing is observed [41]. Furthermore, when the Weber number on the surface of the water jet utilized in an atomized physical model exceeds 500, it ensures that the water jet is fully dispersed and fragmented. The outcomes derived from this can be applied to mechanism research and related extensions [42]. However, it is important to note that the formula for calculating the Weber number at the surface of a water jet involves taking the square root of the traditional droplet’s Weber number, with the radius of curvature along its longitudinal flow trajectory serving as a characteristic length. This value is smaller at the outlet of the waterjet but increases significantly as diffusion occurs within the waterjet. Consequently, achieving exit velocities for rectangular water jets pumped to approximately 15 m/s satisfies requirements for studying the atomization phenomena associated with these jets. Thus, such tests can be regarded as a generalized monomer test analysis at a 1:1 scale ratio. Additionally, conversions may be made based on similarities in scale modeling.

Table 1.
Test parameters of the depressurized random splash experiments.
The initial step in data analysis involves calculating the atomized rainfall intensity RID (mm/h) (Formulas (1 and 2), see [43,44]) at the measurement point under normal ambient pressure. This corresponds to the actual atmospheric pressure within the laboratory setting (P1 = 1.02P0)) for further analysis. As illustrated in Figure 4, the atomized rain intensity directed downstream toward test surfaces 1# to 6# under various inflow conditions, with an ambient pressure of P1 (1.02P0), demonstrates that the atomized rain intensity increases as the inflow rate of the waterjet on the same test surface rises. Conversely, when the inflow rate of the waterjet remains constant, it exhibits a decreasing trend along the flow direction, which aligns with existing research findings [9]. Boundary values of 2, 10, 40, 200, and 600 mm/h have been selected for characteristic lines of rainfall intensity in accordance with industry standards outlined in the design specifications for concrete arch dams (SL282-2018) and spillways (SL253-2018). As illustrated in Figure 4, test surface #6 (flow direction coordinate of 10.750 m) under working condition D(1–3)1 and test surface #5 (flow direction coordinate of 10.625 m) under working condition D(3–5)1 belong to the above different protected zones. Therefore, these conditions can be considered baseline conditions for analysis. It can collaboratively reflect the impact of the inflow discharge from the waterjet and the measurement location on the test surface.
Here, is the per-unit sampling period, 60 s; is the precipitation measured during this sampling interval, mm; is the graded particle number, which refers to the quantity of particles per unit sampling period corresponding to a specific subchannel within a 30 × 32 coordinate matrix without two small particle size channels (Table A1); and is the effective sampling area estimated related to graded diameter sizes (Di, mm), a flow length (W, m) of 0.03 m, and a transverse width (L, m) of 0.18 m (Equation (1)).
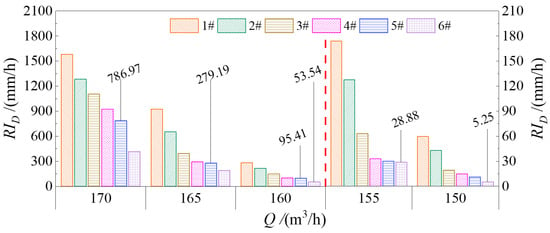
Figure 4.
Atomized rain intensity distribution under experimental conditions of D(1–5)1. (P (D(1–5)1) = 1.02 P0; Q(D11)–Q(D51) = (150–170) m3/h; ΔQ = 5 m3/h).
3. Experimental Results and Discussion
3.1. Effects of Low Ambient Pressure on the Two-Dimensional Atomized Raindrop Spectrum
The two-dimensional atomized raindrop spectra of the above baseline conditions are compared under a normal ambient pressure environment (P1 = 1.02P0) and a low ambient pressure environment (P5 = 0.66P0), as shown in Figure 5. In total, 32 equidistant intervals are established along both the vertical and horizontal coordinates, with corresponding measurements of the particle equivalent diameter Di (mm) and falling velocity Vzj (m/s) indicated. The one-minute average particle counts nij in each subchannel during the sampling period were categorized into nine distinct color levels. Nst represents the number concentration (number/(54 cm2)) across all subchannels within a one-minute timeframe.
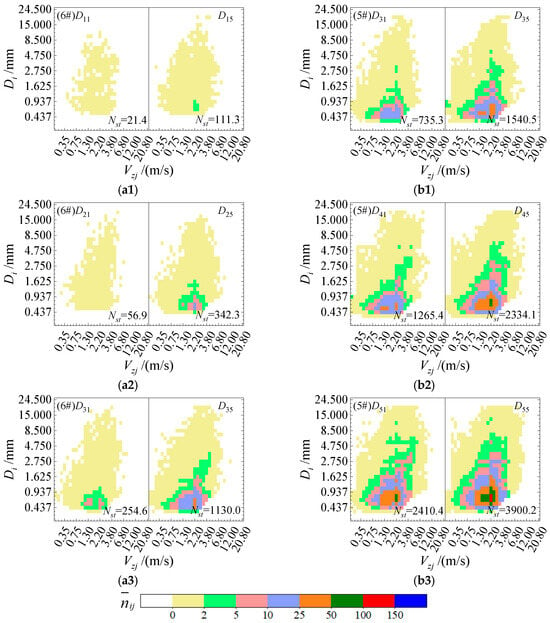
Figure 5.
Two-dimensional atomized raindrop spectrum of typical atomizing rain intensity conditions under different ambient pressures (P(D(1–3)1 and D(3–5)1) = 1.02 P0, P(D(1–3)5 and D(3–5)5) = 0.66 P0; the flow direction coordinate of the test surface #5 and 6 is 10.625 m and 10.750 m, respectively). (a1) RID(D11) = 5.25 mm/h, Q(D1p) = 150 m3/h; (a2) RID(D21) = 28.88 mm/h, Q(D2p) = 155 m3/h; (a3) RID(D31) = 53.54 mm/h, Q(D3p) = 160 m3/h; (b1) RID(D31) = 95.41 mm/h, Q(D3p) = 160 m3/h; (b2) RID(D41) = 279.19 mm/h, Q(D4p) = 165 m3/h; (b3) RID(D51) = 786.97 mm/h, Q(D5p) = 170 m3/h.
Figure 5 shows that the atomized raindrop size two-dimensional sequence diagrams exhibit a continuous spectrum in both velocity and scale from the perspective of distribution and morphology. The distribution domain demonstrates geometric similarity, characterized by a “skewed pear shape” that lacks large droplet regions at low velocities and small droplet regions at high velocities. The total number of particles across all subchannels within a one-minute timeframe, Nst and the one-minute average particle counts in each subchannel nij are influenced not only by the inflow rate of the waterjet and the position of the measuring point but also by the environmental ambient pressure.
With increasing atomized rain intensity under baseline conditions, the influence rate of Nst on low ambient pressure initially increases, then decreases, and ultimately stabilizes. When the environmental ambient pressure decreases by 0.10 P0 relative to the baseline conditions, the increase rate of Nst is 0.51 times greater when the atomized rainfall intensity approaches or exceeds 100 mm/h. In contrast, when the atomized rainfall intensity is less than 100 mm/h, the influence rate of Nst increases by a factor of 1.45. Moreover, the variation in color gradients representing nij in each subchannel indicates that when other conditions are held constant, a decrease in ambient pressure results in a significant increase in nij during the sampling period within the small particle size range. In contrast, the changes observed within the larger particle size range are relatively minor.
Furthermore, by utilizing a particle diameter of 5 mm (the 20th particle size category in Table A1 of Appendix A) as the boundary, the number-dominated isovolumetric diameter of the rain intensity (RID)nd and the mass-dominated isovolumetric diameter of the rain intensity (RID)md can be calculated, as shown in Table 2. These metrics reflect the contribution of raindrop intensities from two distinct particle size segments. With increasing atomized rain intensity under baseline conditions, the growth rate of the atomized rain intensity initially decreases before fluctuating. When the environmental ambient pressure decreases by 0.10P0 relative to the baseline conditions, the fluctuation range of the RID increase rate is 0.38 to 0.87, corresponding to a rainfall intensity range of 28.88 mm/h to 1066.91 mm/h. The fluctuation range of the RID increase rate is 1.69 when the atomized rain intensity is 5.25 mm/h. In addition, when the atomized rain intensity under baseline conditions approaches or exceeds 20 mm/h, the impact of low ambient pressure on the ratios of (RID)nd and (RID)md becomes negligible. Consequently, their ratios remain relatively stable, with average values of 0.87 and 0.13, respectively.

Table 2.
Variation characteristics of atomized rain intensity induced by low ambient pressure.
The significant increase in the number of particles within the small droplet size range during atomization clearly serves as a driving characteristic for the increase in atomized rainfall intensity under low ambient pressure. Additionally, an increase in the number of particles within the larger droplet size range can also contribute to the intensification of atomized rainfall under low ambient pressure conditions; however, this nonconstant increase may lead to greater randomness in the atomized rain intensity.
3.2. Effects of Low Ambient Pressure on Three-Dimensional Atomized Raindrop Spectra
The three-dimensional atomized raindrop spectra under the aforementioned baseline conditions are presented in single logarithmic coordinates. These spectra are compared in two different environments: normal ambient pressure (P1 = 1.02P0) and low ambient pressure (P5 = 0.66P0), as illustrated in Figure 6. The ordinate of Figure 6 represents the individual three-dimensional number concentration of atomized raindrops, denoted as N(Di) (particle counts/(m3·mm)), corresponding to 32 distinct raindrop diameter sizes with unequal spacing. N(Di) is calculated via Formulas (3) and (4), see [45]. (mm) is the channel width of each particle size class. The falling velocity of the particles at each velocity level Vj (m/s) is calculated as the average falling velocity Vzj (Di) (m/s) measured at each particle size level. The fitted spectral pattern adheres to a gamma distribution, employing the M246 moment estimation method.
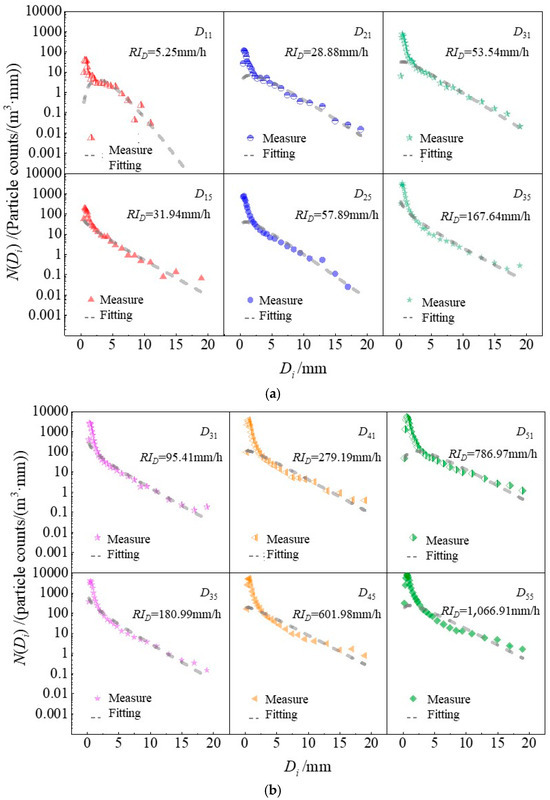
Figure 6.
Three-dimensional atomized raindrop spectra of typical atomizing rain events intensity conditions under different ambient pressures: (a): Mearing points of #6 (Flow Direction coordinates are 10.750 m); (b): Mearing points #5 (the flow direction coordinates are 10.625 m) (P(Dq1) = 1.02P0, P(Dq5) = 0.66P0; Q(D1p)–Q(D5p) = (150–170) m3/h, ΔQ = 5 m3/h).
As shown in Figure 6, the primary spectral type of these three-dimensional atomized raindrop spectra is unimodal. As the size of the atomized raindrop particles increases, their concentration initially rises before subsequently declining. The main peak is predominantly located within the small particle size range of less than 1 mm, while minor fluctuations are primarily observed in the tail end of the larger particle size segment. The peak value of the number concentration of atomized raindrops N(Di) is influenced not only by the inflow rate of the waterjet and the position of the measuring point but also by environmental ambient pressure.
With increasing atomized rain intensity under baseline conditions, the influence of the N(Di) peak value on low ambient pressure initially increases, then decreases, and ultimately stabilizes. When the environmental ambient pressure decreases by 0.10P0 relative to the baseline conditions, the rate of increase in the N(Di) peak value is 0.41 times greater when the atomized rainfall intensity approaches or exceeds 100 mm/h. In contrast, when the atomized rainfall intensity is less than 100 mm/h, the rate of increase in the N(Di) peak value increases by a factor of 1.48. Moreover, the three-dimensional atomized raindrop spectrum is self-similar and can be approximated using a gamma distribution curve. The fitted particle size in the mid-range aligns with the measured values; however, discrepancies are observed at both ends of the size spectrum, along with peak-shaving characteristics. This phenomenon is attributed to the broad spectral width of atomized raindrop distributions and the high concentration of small droplets, which results in significant increases and decreases in rates on either side of the main peak.
Figure 6 also shows that the ranges for the modal particle size, maximum particle size, and minimum particle size are relatively stable, measuring 0.437–0.687 mm, 0.312–0.562 mm, and 11.000–19.000 mm, respectively. When the atomized rain intensity is 5.25 mm/h, the corresponding maximum diameter is 11.000 mm, which is similar to the maximum particle size (10 mm) of atomized rain measured using the prototype at Wantangshui Power Station [22]. The range of the maximum diameter of atomized raindrops under different conditions is between 17.000 mm and 19.000 mm, with a concentration of raindrops at approximately 19 mm. This finding is consistent with the maximum size range of raindrops observed in the splash area as measured by Qiu Haijuan et al. during their model tests [46]. When the atomized rain intensity exceeds 10 mm/h, the resulting atomized raindrops can be compared with the mixed-phase precipitation raindrop spectrum characteristic of “heavy rainfall combined with hail or snowflakes” on a particle size scale [47,48,49,50].
It is evident that the impact of ambient pressure reduction on the three-dimensional atomized raindrop spectra is primarily observed in the spectral peak values, whereas it does not significantly affect the spectral type or range. The spectral types exhibit self-similarity, making it scientifically valid to fit them using a gamma approximation.
3.3. Effects of Low Ambient Pressure on the Statistical Characteristics of the Atomized Raindrop Spectrum
The reduction in ambient pressure, the migration upstream of measurement points, and the increase in inflow discharge are key factors that contribute to the heightened intensity of atomization rain. Based on the preceding analysis, it is imperative to conduct a more in-depth investigation into the influence of ambient pressure on key statistical particle size parameters of atomized raindrops under consistent rain intensities during atomization. Under the same atomized rain intensity, the arithmetic mean diameter of atomized raindrops (Dave) and the relationship between the mass-weighted mean diameter of atomized raindrops ((Dm)ave) in different ambient pressure environments are illustrated in Figure 7.
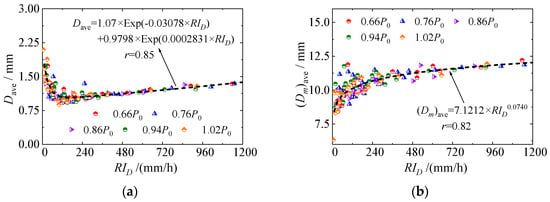
Figure 7.
Statistical Characteristics of the Atomized Raindrop Spectrum. (a) Correlation analysis of RID–Dave; (b) (Dm)ave–RID under a series of test conditions.
As depicted in Figure 7, the Dave and (Dm)ave of atomized raindrops fluctuate around the fitted curve under varying pressure conditions, while maintaining consistent atomized rain intensity. The observed trends are not distinctly pronounced when influenced by ambient pressure. As the atomized rain intensity increases, the Dave of the atomized raindrops initially decreases rapidly before gradually increasing. The minimum value of Dave corresponding to this atomized rain intensity is 153.78 mm/h, with a range of 0.88–1.88 mm. In contrast, (Dm)ave shows an exponential growth trend that eventually stabilizes, with an interval ranging from 6.32 to 12.03 mm. In addition, the (Dm)ave of atomized raindrops, along with the generalized intercept parameter , can represent the synthesis of both the overall diameter and the number concentration within the three-dimensional spectrum of an atomized raindrop. A correlation analysis was performed between the logarithm of and (Dm)ave, , and RID. The findings are presented in Figure 8.
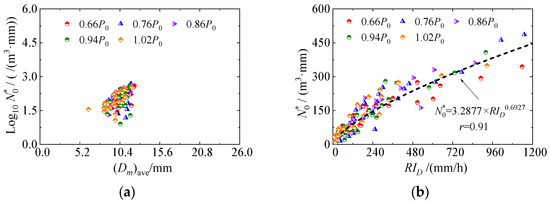
Figure 8.
Statistical Characteristics of the Atomized Raindrop Spectrum. (a) Correlation analysis of log10()–(Dm)ave; (b) –RID under a series of test conditions.
As also depicted in Figure 8, the of the atomized raindrop fitting spectrum corresponding to the same (Dm)ave and of the atomized raindrop fitting spectrum related to identical RID are a multivalued discrete distribution and have no obvious correlation with the ambient pressure. The of the fitting spectrum of atomized raindrops tends to increase with increasing (Dm)ave. The of the fitting spectrum of atomized raindrops is positively correlated with the RID. In the description of the natural raindrop spectrum, when tends to be stable with increasing (Dm)ave, the collision and fragmentation of natural raindrops tends to be balanced with increasing rain intensity [51,52]. Similarly, the atomized raindrops within the test area undergo dynamic evolution through processes of collision and fragmentation, with their activity increasing in correlation with the intensity of atomized rainfall.
4. Numerical Model Application Optimization
For existing flood discharge facilities, variations in reservoir depth can lead to corresponding changes in the upstream water level. Additionally, the dynamics of the associated waterjets are influenced by alterations in their inflow flow rate. This study presents a generalized model that is not derived from any specific project. While the high-speed water jet is supplied by a jet pump designed to regulate the inflow flow rate, the magnitude of this flow rate can qualitatively indicate the water level within the reservoir. In relation to prototype projects, it is important to note that ejection conditions are diverse. Consequently, employing a constant physical model presents challenges and makes it difficult to efficiently analyze the influence range of fogging rain within these projects. Therefore, a semi-empirical and semi-theoretical numerical prediction model for random splashing during jet atomization is considered valuable.
Random splash simulation models involving semiempirical and semitheoretical methods, which are developed based on the principles of Lagrangian mechanics, constitute a significant theory for the numerical prediction of flood discharge atomization. The Runge–Kutta method is employed to track the trajectories of both the water jet and the droplets, whereas the Monte Carlo method is utilized to assess the cumulative impact of the droplets on the terrain boundaries. Here, the application of experimental findings is examined to enhance the theoretical framework of stochastic numerical models.
In theory, a fundamental assumption is that the atomized water droplets are spherical and independent of the effective splashing volume on the outer surface of the waterjet dV. The quantity of atomized water droplets nD is calculated using Formula (5), whereas the distribution of their diameters f(D) is determined via Formula (6) [33]. The proportions of different atomized raindrop size counts are relatively stable in the numerical calculations.
The probability density of the number concentration corresponding to the median value of each group of atomized raindrops with varying diameters is illustrated in Figure 9. Its predominant spectral type is unimodal, and its skewness trend increases rapidly and then decreases gradually as the particle size of the atomized raindrops increases, ultimately resulting in a left-skewed distribution. The positions of the main peaks are predominantly concentrated within the small particle size range, specifically for particles less than 1 mm in diameter. Furthermore, the impact of variations in the testing conditions on the probability density of the number concentration of spray droplets appears to be minimal, with a range between 1.13 and 1.93.
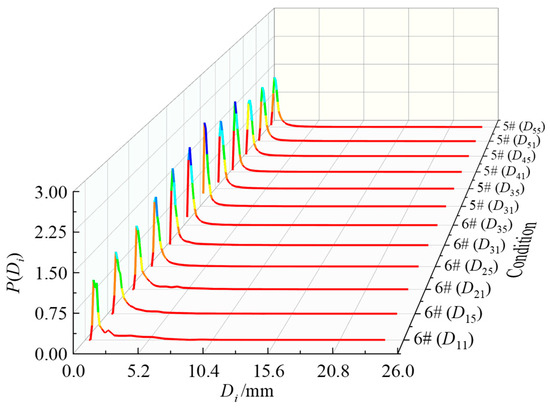
Figure 9.
The probability density of the number concentration corresponding to the median value of each group of atomized raindrops with varying diameters (P(Dq1) = 1.02P0,P(Dq5) = 0.66P0; Q(D1p) –Q(D5p) = (150–170) m3/h, ΔQ = 5 m3/h).
Therefore, when evaluating the impact of low ambient pressure on the atomization source, as the measurement area for the spectrum of atomized raindrops is located within a rainstorm zone, it can be classified as a downstream source of atomization. The distribution ratio of atomized raindrops across various particle sizes remains relatively stable.
In previous experiments, atomized rain was collected by an inclined plate positioned downstream of the water tongue impact area. The measured atomized rainfall can be considered the atomized source for the downstream region. When the ambient pressure is reduced by 0.10P0, the average rate of atomization on the inclined test surface ranges from 115 to 127.68 m3/h. Correspondingly, there is a linear increase between 0.28 L/h and 2.83 L/h, with a relative growth rate ranging from 20.48% to 11.56% [21].
In this work, the atomized rain calculation is based on the raindrop spectrum at specific measurement points. The enhancement characteristics of rain intensity at various atomization planes under low pressure are illustrated in Figure 10a,b. The color code represents the atomized rain areas corresponding to specific rainfall intensity thresholds of 10 mm/h, 40 mm/h, 200 mm/h, and 600 mm/h. These categories are designated class ①, class ②, class ③, class ④, and class ⑤, respectively. Additionally, rainfall intensities of 1000 mm/h and above are classified as class ⑤+. Based on the test conditions of normal ambient pressure (P1 = 1.02P0), the average growth rate Δη of the rain intensity ΔRID on the spray surface of the discharge flow was calculated when the ambient pressure was decreased by 0.1P0, as depicted in Figure 10c.
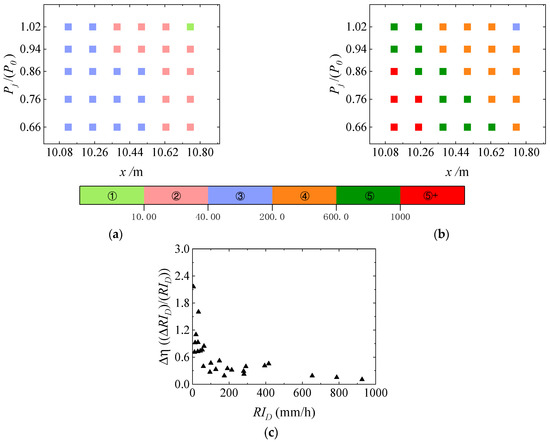
Figure 10.
The enhancement characteristics of rain intensity at various atomization planes under low pressure. (a) Test conditions are D1(1–5) with an inflow discharge of 150 m3/h; (b) Test conditions are D4(1–5) with an inflow discharge of 165 m3/h; (c) Relative growth law of atomized rain intensity under low ambient pressure.
According to the analysis presented in Figure 10, as the environmental air pressure decreases (1.02P0, 0.94 P0, 0.86 P0, 0.76 P0, 0.66 P0), the measurement area under working condition D1(1–5) (Q1 = 150 m3/h, V1 = 13.89 m/s) shifts in atomized classification from levels ① to ③ to ② to ③; conversely, for working condition D4(1–5) (Q4 = 165 m3/h, V3 = 15.28 m/s), the corresponding atomized classification changes from levels ③ to ⑤ to levels ④ to ⑤+.
Therefore, when evaluating the impact of low ambient pressure on the protection of the atomization field, the atomized classification of the testing surface is influenced by low air pressure environments. This may result in a one-level enhancement of the atomization protection level in certain areas, without the occurrence of multi-level increases, as all other conditions remain constant. This effect arises because as the reference rainfall intensity on the atomization surface increases, the average growth rate of the rainfall intensity affected by low air pressure initially declines sharply before gradually stabilizing.
5. Conclusions
With the aim of decreasing the degree of aggravated risk of atomized rain at high-altitude hydropower stations, this study provides insights into the atomized raindrop size distributions of random splash experiments characterized by high-speed velocities and low-pressure environments. Random splash experiments were conducted under coupling conditions with high inflow discharge rates and low ambient pressures. The effects of low pressure on the atomized raindrop size distributions at six measuring points downstream along the overflow centerline collected by OTT Parsivel2 can be summarized as follows:
- (1)
- The two-dimensional atomized raindrop spectra reveal that the intensity of atomized rain increases with the increasing total number concentration of two-dimensional raindrop spectra at low ambient pressure. Notably, the diameter of the small particles within the subchannels significantly increases. In terms of the rain intensity components, the proportion of the number-dominated isovolumetric diameter of the rain intensity and the mass-dominated isovolumetric diameter of rain intensity remains relatively stable and is not influenced by variations in ambient pressure;
- (2)
- According to the three-dimensional raindrop spectra, the increase in atomized rain intensity under low pressure is reflected in both the quantity and concentration of atomized rain, with the most pronounced effects occurring at peak levels. The maximum particle size and range are influenced by the intensity of atomized rain; however, the impact of low pressure appears to be less significant. The relationship between the atomized raindrop number concentration and characteristic particle size exhibits a unimodal distribution that skews toward smaller particles, which can be effectively modelled using the gamma distribution;
- (3)
- Under the same atomized rain intensity, the atomized raindrops undergo a dynamic evolution characterized by collision and fragmentation, with their quantity increasing in response to heightened atomized rain intensity. Notably, there is no significant correlation between the statistical characteristics of three-dimensional raindrop spectra and low ambient pressure, although the relationships among the arithmetic mean diameter of atomized raindrops, the mass-weighted mean diameter of atomized raindrops, and the generalized intercept parameter concerning the atomized rain intensity exhibit a clear trend;
- (4)
- Combined with the experimental results, this study provides a substantial reference for establishing random splash simulation models characterized by low pressure. It is advisable to appropriately increase the amount of the atomization source to accurately reflect the impact of low pressure on the atomized rain intensity within existing empirical formulas for the distribution of atomized raindrop diameters. When atomized protection is categorized into zones, enhancing the area adjacent to the characteristic rain intensity line is crucial, as its protection level may need to be elevated by one grade in accordance with current industry standards.
The statistical characteristics of atomized raindrop size distribution datasets under depressurized experimental conditions clearly demonstrated self-enhancing redistribution features. When investigating the enhancement effect of low ambient pressure on atomized rain intensity, it can be generalized that a proportional rise in the total number of particles generated by splashed atomized raindrops, without considering minor variations in particle size distribution, can establish a sufficient condition for advancements in numerical random splash models concerning low ambient pressure effects. To predicting rain protection scopes at a high-altitude hydropower station, future research should focus on how low ambient pressure affects the boundary conditions of atomization sources under identical discharge conditions, including trajectory distance of aerated waterjets; future research also should focus on the investigation of thematic mechanism experiments in conjunction with engineering challenges and explore the characteristics of atomized fields and sources from multiple perspectives, including water quality, water volume, and water temperature, so as to facilitate the development of advanced meteorological models for atomized protection in high-altitude areas by integrating both physical and numerical methods.
Author Contributions
Conceptualization, J.L.; methodology, J.L. and D.L. (Dan Liu); formal analysis, F.L. and D.L. (Dan Liu); data curation, D.L. (Dan Liu); writing—original draft preparation, D.L. (Dan Liu) and J.S.; writing—review and editing, D.L. (Dongming Liu), B.M., L.Y., Y.Z., C.X. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by State Key Laboratory of Hydraulic Engineering Intelligent Construction and Operation, Tianjin University, grant number HESS-2216, National Natural Science Foundation of China, grant number U1765202, China Postdoctoral Science Foundation, grant number 2023M732603, the Joint Funds of the Zhejiang Provincial Natural Science Foundation of China, grant number LZJWY22E090003, University-Level Key Course of Zhejiang University of Water Resources and Electric Power, grant number ZDKC202319, Scientific research foundation of Zhejiang University of Water Resources and Electric Power, grant number xky2022002 and Nanxun scholars program of ZJWEU, grant number RC2025011034, and Science and Technology Projects of Xizang Autonomous Region, China, grant number XZ202501ZY0109. All workers from the State Key Laboratory of Hydraulic Engineering, Intelligent Construction, and Operation of Tianjin University are acknowledged. The authors are also grateful for the assistance of the anonymous reviewers.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to express their sincere gratitude to all those who have offered selfless help during the course of this research.
Conflicts of Interest
Jizhong Shi was employed by the company Zhejiang East China Engineering Consulting Co., Ltd. of PowerChina Huadong Engineering Corporation Limited. Yongsheng Zheng was employed by the company Yalong River Hydropower Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A

Table A1.
Graded diameter size and fall velocity of atomized raindrop size distributions databases collected by the OTT Parsivel2.
Table A1.
Graded diameter size and fall velocity of atomized raindrop size distributions databases collected by the OTT Parsivel2.
| Classes Number | Raindrop Diameter Sizes | Raindrop Fall Velocities | ||
|---|---|---|---|---|
| Mid-Value of Class (mm) | Class Width (mm) | Mid-Value of Class (m/s) | Class Width (m/s) | |
| 1 | 0.062 * | 0.125 | 0.050 | 0.100 |
| 2 | 0.187 * | 0.125 | 0.150 | 0.100 |
| 3 | 0.312 | 0.125 | 0.250 | 0.100 |
| 4 | 0.437 | 0.125 | 0.350 | 0.100 |
| 5 | 0.562 | 0.125 | 0.450 | 0.100 |
| 6 | 0.687 | 0.125 | 0.550 | 0.100 |
| 7 | 0.812 | 0.125 | 0.650 | 0.100 |
| 8 | 0.937 | 0.125 | 0.750 | 0.100 |
| 9 | 1.062 | 0.125 | 0.850 | 0.100 |
| 10 | 1.187 | 0.125 | 0.950 | 0.100 |
| 11 | 1.375 | 0.250 | 1.100 | 0.200 |
| 12 | 1.625 | 0.250 | 1.300 | 0.200 |
| 13 | 1.875 | 0.250 | 1.500 | 0.200 |
| 14 | 2.215 | 0.250 | 1.700 | 0.200 |
| 15 | 2.375 | 0.250 | 1.900 | 0.200 |
| 16 | 2.750 | 0.500 | 2.200 | 0.400 |
| 17 | 3.250 | 0.500 | 2.600 | 0.400 |
| 18 | 3.750 | 0.500 | 3.000 | 0.400 |
| 19 | 4.250 | 0.500 | 3.400 | 0.400 |
| 20 | 4.750 | 0.500 | 3.800 | 0.400 |
| 21 | 5.500 | 1.000 | 4.400 | 0.800 |
| 22 | 6.500 | 1.000 | 5.200 | 0.800 |
| 23 | 7.500 | 1.000 | 6.000 | 0.800 |
| 24 | 8.500 | 1.000 | 6.800 | 0.800 |
| 25 | 9.500 | 1.000 | 7.600 | 0.800 |
| 26 | 11.000 | 2.000 | 8.800 | 1.600 |
| 27 | 13.000 | 2.000 | 10.400 | 1.600 |
| 28 | 15.000 | 2.000 | 12.000 | 1.600 |
| 29 | 17.000 | 2.000 | 13.600 | 1.600 |
| 30 | 19.000 | 2.000 | 15.200 | 1.600 |
| 31 | 21.500 | 3.000 | 17.600 | 3.200 |
| 32 | 24.500 | 3.000 | 20.800 | 3.200 |
Notes: The first and second particle sizes represented by * are discarded in the database analysis due to the low signal-to-noise ratios of the instrument. The median of the subsequent class is determined by adding the class width at the level of the current median to the existing median, whether in terms of raindrop diameter sizes or raindrop fall velocities.
References
- Ward, P.J.; Jongman, B.; Aerts, J.C.J.H.; Bates, P.D.; Botzen, W.J.W.; Diaz Loaiza, A.; Hallegatte, S.; Kind, J.M.; Kwadijk, J.; Scussolini, P.; et al. A global framework for future costs and benefits of river-flood protection in urban areas. Nat. Clim. Change 2017, 7, 642–646. [Google Scholar] [CrossRef]
- Ballesteros-Canovas, J.A.; Czajka, B.; Janecka, K.; Lempa, M.; Kaczka, R.J.; Stoffel, M. Flash floods in the Tatra Mountain streams: Frequency and triggers. Sci. Total Environ. 2015, 511, 639–648. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S. Trends in rainfall erosivity in NE Spain at annual, seasonal and daily scales, 1955–2006. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 6285–6309. [Google Scholar] [CrossRef]
- Blocken, B.; Carmeliet, J. A review of wind-driven rain research in building science. J. Wind Eng. Ind. Aerodyn. 2004, 92, 1079–1130. [Google Scholar] [CrossRef]
- Dave, N.; Mittelstet, A.; Korus, J.; Waszgis, M. Impact of an extreme flood event on streambank retreat: Cedar River, Nebraska, USA. J Am Water Resour Assoc. 2020, 56, 528–541. [Google Scholar] [CrossRef]
- Vahedifard, F.; AghaKouchak, A.; Ragno, E.; Shahrokhabadi, S.; Mallakpour, I. Lessons from the Oroville dam. Science 2017, 355, 1139–1140. [Google Scholar] [CrossRef]
- Liu, G.; Tong, F.; Tian, B.; Gong, J. Finite element analysis of flood discharge atomization based on water–air two-phase flow. Appl. Math. Model. 2020, 81, 473–486. [Google Scholar] [CrossRef]
- Gong, J.B.; Pi, J.H. Reflection and countermeasures of “7·19” flood event of Shuibuya dam. Dam Saf. 2018, 2, 20–26. [Google Scholar]
- Lian, J.J.; He, J.L.; Liu, F.; Ran, D.J.; Wang, X.Q.; Wang, C. An improved empirical model for flood discharge atomization and its application to optimize the flip bucket of the Nazixia Project. Int. J. Environ. Res. Public Health 2019, 16, 316. [Google Scholar] [CrossRef]
- Wang, F.H. Influence of discharging foggy and its protection at Ertan hydropower station. Dam Saf. 2011, 5, 42–46. [Google Scholar]
- Wu, W.Y.; Yang, Y.H.; Min, S.H. Analysis on collapse and sliding control of high slope in atomized area of right bank of Ertan hydropower station. Dam Saf. 2018, 4, 49–52. [Google Scholar]
- Li, Z. On landslide induced by water-fog from ski-jump energy dissipation of Longyangxia Hydropower Station. Dam Saf. 2001, 3, 17–20+29–56. [Google Scholar]
- Lian, J.J. Hydraulic Prototype Observation Test at Jinping Hydropower Station and Its Early Warning System Development with Real-Time Monitoring for Flood Discharge Security; Research report; Tianjin University: Tianjin, China, 2016. [Google Scholar]
- Lian, J.J.; Liu, D.; Liu, F. Research progress and frontiers on flood discharge atomization of Chinese high dam projects. J. Hydraul. Eng. 2019, 50, 283–293. [Google Scholar]
- Zeng, S.Y.; Zhang, Y.T.; Zhang, B.C.; Gu, L.; Dai, X.B.; Miao, B.G.; Wang, L.J. Discharge atomization and its affection analysis of Xiangjiaba Hydropower Station. Water Power 2019, 45, 54–58. [Google Scholar]
- Zhou, H.; Wu, S.Q.; Chen, H.L.; Zhou, J.; Wu, X.F. Similarity criterion of flood discharge atomization. Water Sci. Eng. 2008, 1, 59–65. [Google Scholar]
- Liu, H.T.; Sun, S.K.; Wang, X.S.; Xia, Q.F. Study on the distribution of splash intensity during nappe impingement. J. Hydrodyn. 2009, 24, 217–223. [Google Scholar]
- Yuan, H.; Xu, W.L.; Li, R.; Feng, Y.Z.; Hao, Y.F. Spatial distribution characteristics of rainfall for two-jet collisions in air. Water 2018, 10, 1600. [Google Scholar] [CrossRef]
- Duan, H.D.; Liu, S.H.; Luo, Q.S.; Huang, W. Rain intensity distribution in the splash region of atomized flow. J. Hydrodyn. Ser. 2006, 18, 362–366. [Google Scholar] [CrossRef]
- Liu, F.; Lian, J.J.; Zhang, X.J.; Li, C.Y. Experimental study of atomization and splashing caused by a ski-jump jet into scour pool. J. Hydroelectr. Eng. 2010, 29, 113–117. [Google Scholar]
- Liu, D.; Lian, J.J.; Liu, F.; Liu, D.; Ma, B.; Shi, J. An experimental study on the effects of atomized rain of a high velocity waterjet to downstream area in low ambient pressure environment. Water 2020, 12, 397. [Google Scholar] [CrossRef]
- Wu, X.F.; Wu, S.Q.; Zhou, H.; Chen, H.L. Atomization measurement for Wantang Hydroplant. Hydro Sci. Eng. 2001, 4, 71–74. [Google Scholar]
- Chen, D.; Jin, F.; Li, J. Study on model law for intensity of rainfall from atomization of flood discharging flow for high dam. Water Resour. Hydr. Eng. 2005, 36, 47–49. [Google Scholar]
- Liu, S.H.; Ran, Q.S.; Luo, Q.S.; Tai, W.; Fan, M. An in-depth study of partical size of atomization rainfall and generated flow on a slope. Eng. J. Wuhan Univ. 2013, 46, 1–5. [Google Scholar]
- Schwendner, P.; Schuerger, A.C. Exploring microbial activity in low-pressure environments. Curr. Issues Mol. Biol. 2020, 38, 163–196. [Google Scholar] [CrossRef]
- Rengel, B.; Àgueda, A.; Pastor, E.; Casal, J.; Planas, E.; Hu, L.; Palacios, A. Experimental and computational analysis of vertical jet fires of methane in normal and sub-atmospheric pressures. Fuel 2020, 265, 116878. [Google Scholar] [CrossRef]
- Cai, X.; Wang, X.S.; Liao, G.X. Experimental study on the effects of ambient pressure on spray characteristics of water mist. J. Disas. Prev. Mitig. Eng. 2012, 32, 235–241. [Google Scholar]
- Ersoy, N.E.; Eslamian, M. Phenomenological study and comparison of droplet impact dynamics on a dry surface, thin liquid film, liquid film and shallow pool. Exp. Therm. Fluid Sci. 2020, 112, 109977. [Google Scholar] [CrossRef]
- Ge, X.; Ge, Y.; Li, Q.; Cai, X.; Yang, W.; Du, Y. Effect of low air pressure on the durability of concrete. Constr. Build. Mater. 2018, 187, 830–838. [Google Scholar] [CrossRef]
- Lian, J.J.; Dong, Z.; Liu, F.; Liu, D. Experimental study on the influence of low atmospheric pressure on the dynamic pressure. J. Hydroelectr. Eng. 2019, 38, 1–13. [Google Scholar]
- Liu, X.L.; An, G.; Yao, Z.D. The investigation on the mechabism and sphere of influence of atomization by discharge flow. J. Tianjin Univ. 1991, 24, 30–36. [Google Scholar]
- Liang, Z.C. A analysis and computation for droplets-splashing region of atomization water flow. J. Yangtze River Sci. Res. Inst. 1996, 13, 9–13. [Google Scholar]
- Lian, J.J.; Li, C.Y.; Liu, F.; Wu, S.Q. A prediction method of flood discharge atomization for high dams. J. Hydraul. Res. 2014, 52, 274–282. [Google Scholar] [CrossRef]
- Liu, H.T.; Liu, Z.P.; Xia, Q.F.; Sun, S.K. Computational model of flood discharge splash in large hydropower stations. J. Hydraul. Res. 2015, 53, 576–687. [Google Scholar] [CrossRef]
- Xu, L.; Barcos, L.; Nagel, S.R. Splashing of Liquids: Interplay of surface roughness with surrounding gas. Phys. Rev. Stat. Nonlin. Soft Matter Phys. 2007, 76, 066311. [Google Scholar] [CrossRef]
- Latka, A.; Strandburg-Peshkin, A.; Driscoll, M.M.; Stevens, C.S.; Nagel, S.R. Creation of prompt and thin-sheet splashing by varying surface roughness or increasing air pressure. Phys. Rev. Lett. 2012, 109, 054501. [Google Scholar] [CrossRef]
- Song, C.; Zhou, Y.Q.; Wu, Z.H. Vertical profils of raindrop size distribution observed by Micro Rain Radar. J. Appl. Meteor. Sci. 2019, 30, 479–490. [Google Scholar]
- Li, H.; Yin, Y.; San, Y.P.; Jin, Q. Statistical characteristics of raindrop size distribution for stratiform and convective precipitation at different altitudes in Mt. Huangshan. Chin. J. Atmos. Sci. 2018, 42, 268–280. [Google Scholar]
- Sumesh, R.K.; Resmi, E.A.; Unnikrishnan, C.K.; Jash, D.; Sreekanth, T.S.; Resmi, M.C.M.; Rajeevan, K.; Nita, S.; Ramachandran, K.K. Microphysical aspects of tropical rainfall during Bright Band events at mid and high-altitude regions over Southern Western Ghats, India. Atmos. Res. 2019, 227, 178–197. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L. Statistical characteristics of raindrop size distribution in the Tibetan Plateau and southern China. Adv. Atmos. Sci. 2017, 34, 727–736. [Google Scholar] [CrossRef]
- Deegan, R.D.; Brunet, P.; Eggers, J. Complexities of splashing. Nonlinearity 2008, 21, C1–C11. [Google Scholar] [CrossRef]
- Chen, H.L. Study of flood discharge atomization for Xiaowan Hydropower Project. Yunnan Water Power 1998, 14, 51–55. [Google Scholar]
- Alessandro, B.; Elke, R.; Ali, T.; Ulrich, B.; Clemens, S. PARSIVEL snow observations: A critical assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar]
- Jaffrain, J.; Berne, A. Experimental quantification of the sampling uncertainty associated with measurements from Parsivel disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Serio, M.A.; Carollo, F.G.; Ferro, V. Raindrop size distribution and terminal velocity for rainfall erosivity studies. A review. J. Hydrol. 2019, 576, 210–228. [Google Scholar] [CrossRef]
- Qiu, H.J. Hydraulic Characteristics of Splash of Aerated Jet. Master’s Thesis, Hohai University, Nanjing, China, 2011. [Google Scholar]
- Löffler-Mang, M.; Joss, J. An optical disdrometer for measuring size and velocity of hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Luo, L.; Xiao, H.; Yang, H.L.; Chen, H.N.; Guo, J.; Sun, Y.; Feng, L. Raindrop size distribution and microphysical characteristics of a great rainstorm in 2016 in Beijing, China. Atmos. Res. 2020, 239, 104895. [Google Scholar] [CrossRef]
- Hill, M.; Grieser, J. How to express hail intensity-modeling the hailstone size distribution. J. Appl. Meteorol. Climatol. 2019, 58, 2329–2345. [Google Scholar]
- Huang, G.J.; Kleinkort, C.; Bringi, V.N.; Notaros, B.M. Winter precipitation particle size distribution measurement by Multi-Angle Snowflake Camera. Atmos. Res. 2017, 198, 81–96. [Google Scholar] [CrossRef]
- Zhang, A.; Hu, J.; Chen, S.; Hu, D.; Li, H. Statistical characteristics of raindrop size distribution in the monsoon season observed in southern China. Remote Sens. 2019, 11, 432. [Google Scholar] [CrossRef]
- Islam, T.; Rico-Ramirez, M.A.; Thurai, M.; Han, D. Characteristics of raindrop spectra as normalized gamma distribution from a Joss–Waldvogel disdrometer. Atmos. Res. 2012, 108, 57–73. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).